Improving the Temporal Resolution of Land Surface Temperature Using Machine and Deep Learning Models
Abstract
1. Introduction
2. Literature Review
3. Materials and Methods
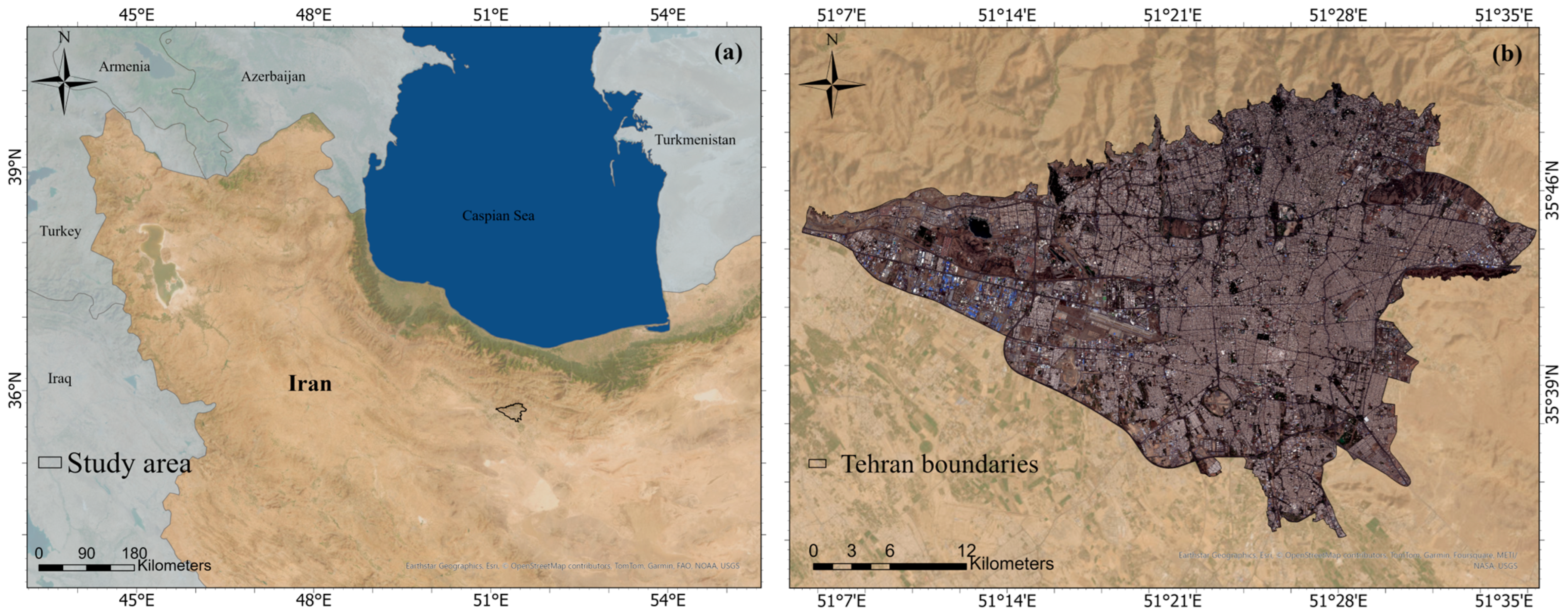
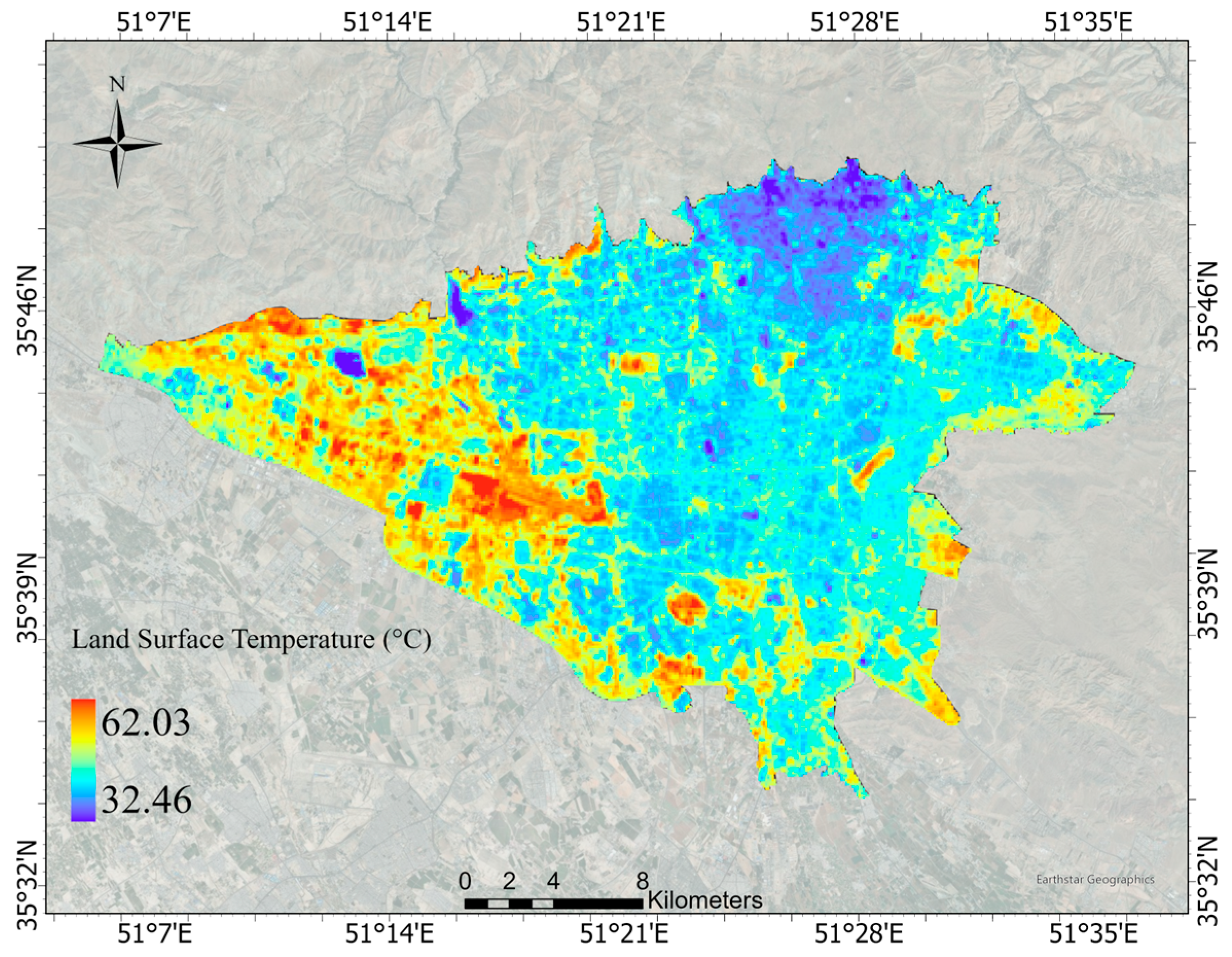
3.1. Study Area and Dataset
3.2. Methodology
3.2.1. LST Derivation from Landsat Imagery
3.2.2. Data Preparation and Feature Engineering
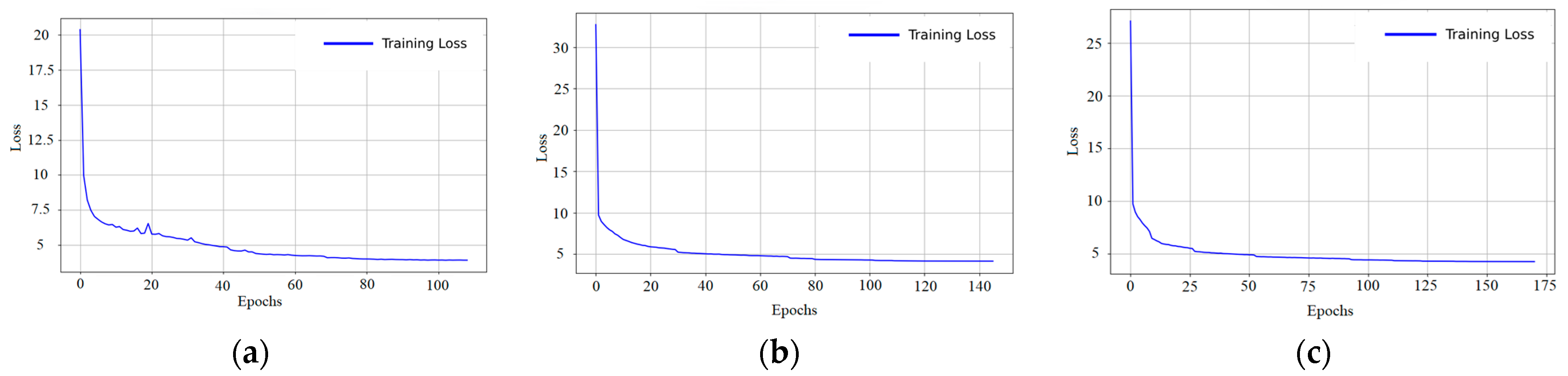
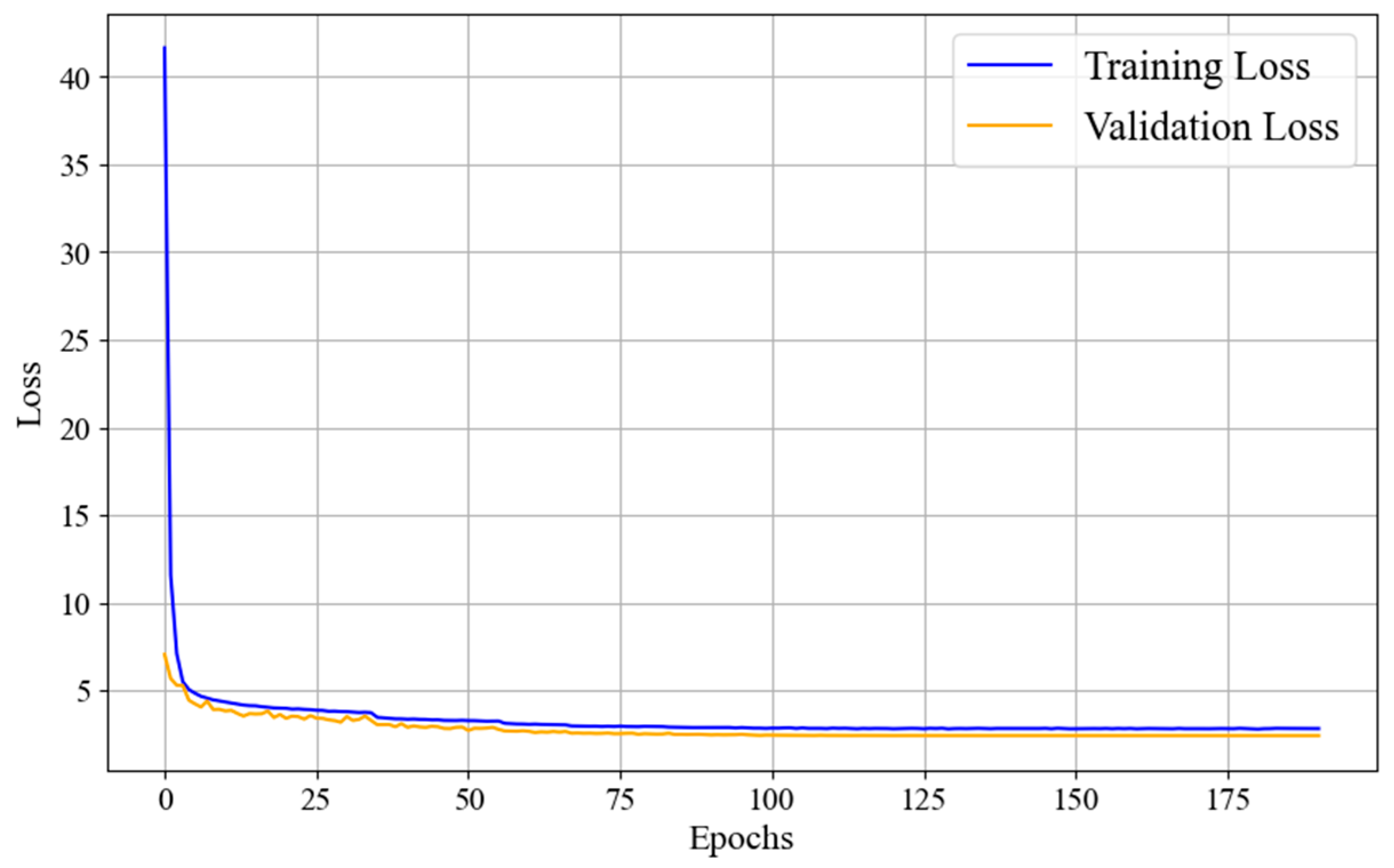
3.2.3. Model Training
Random Forest Regression (RFR)
Convolutional Neural Network (CNN)
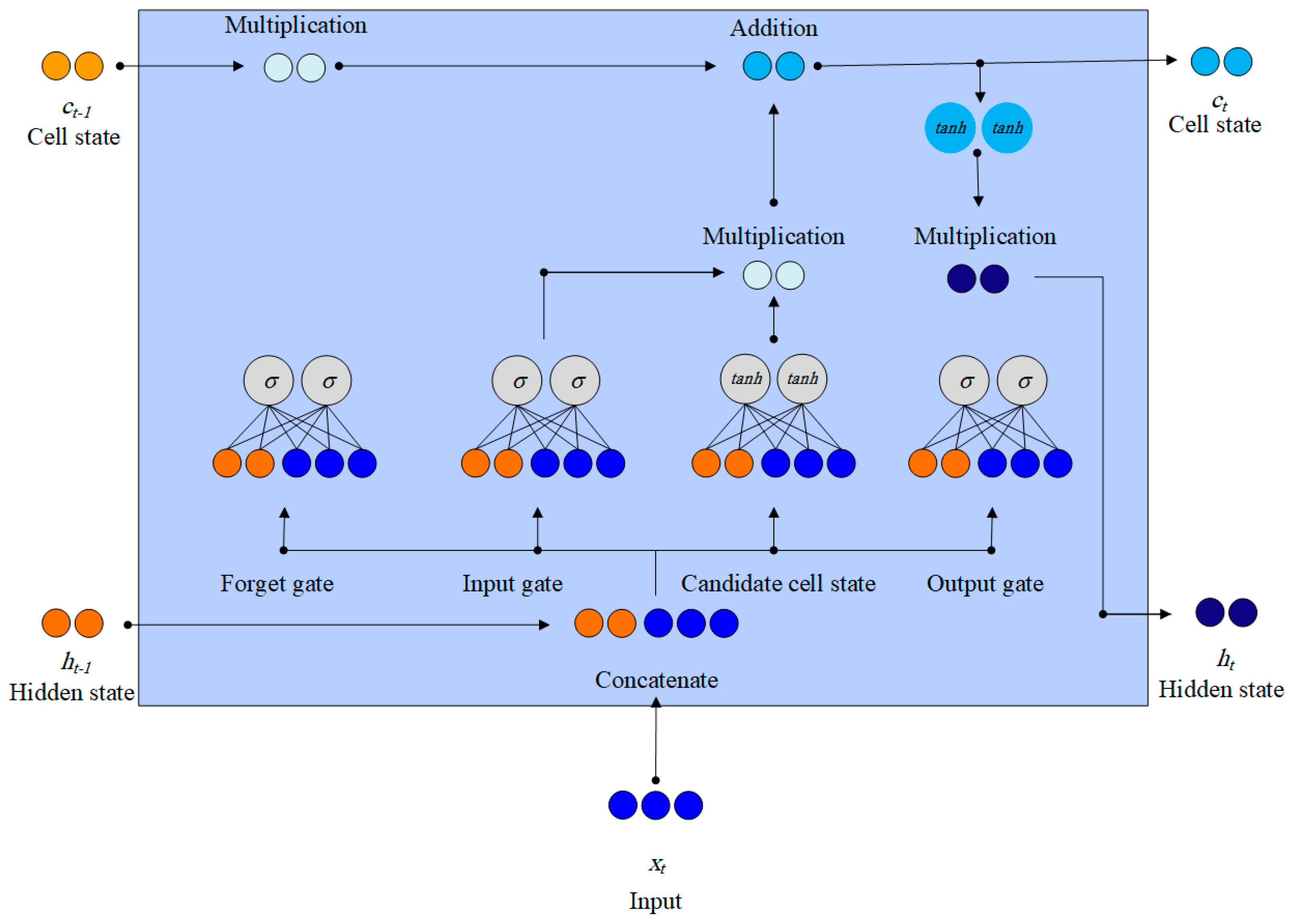
Long Short-Term Memory (LSTM)
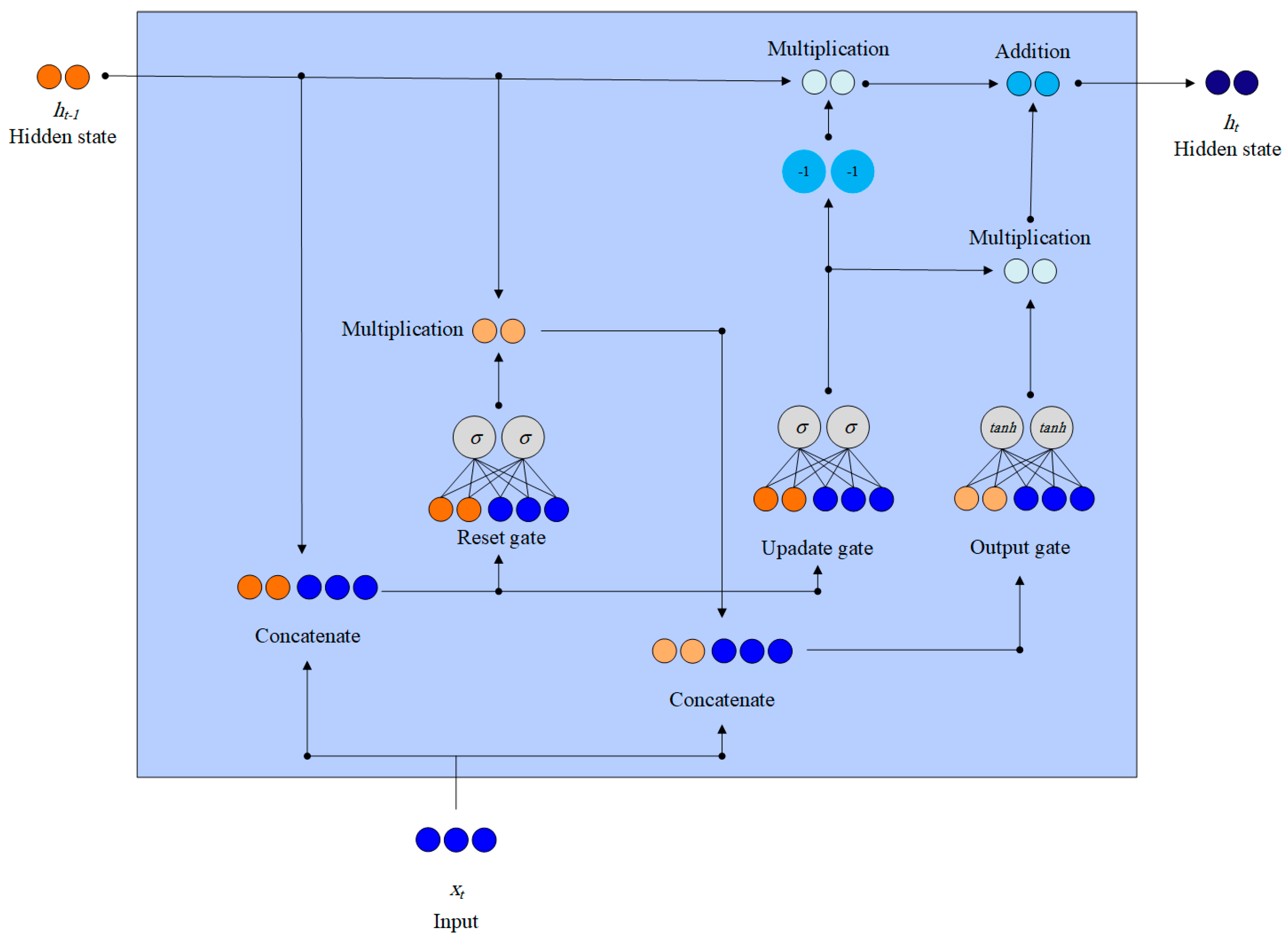
Gated Recurrent Units (GRUs)
3.2.4. Model Training Parameters
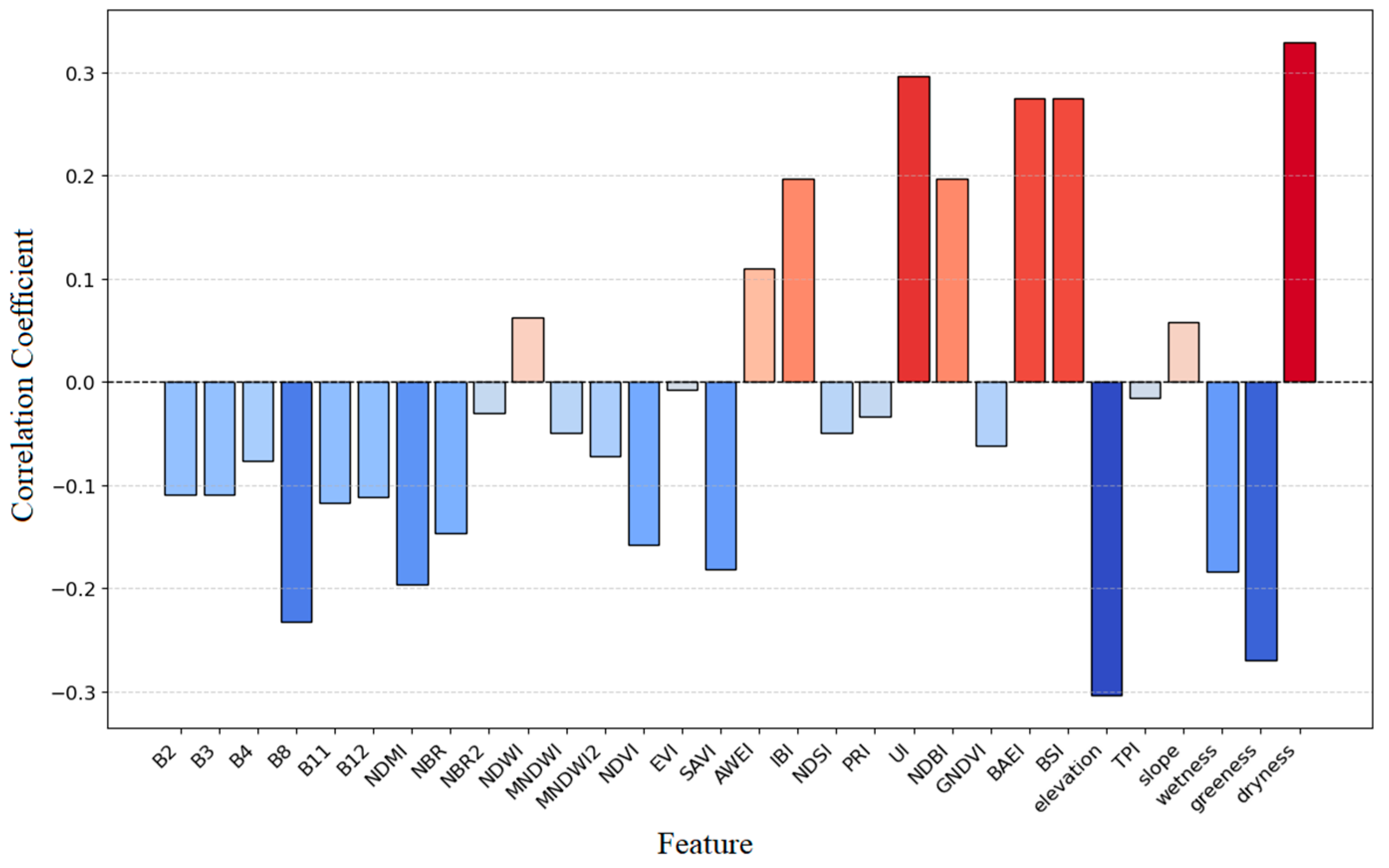
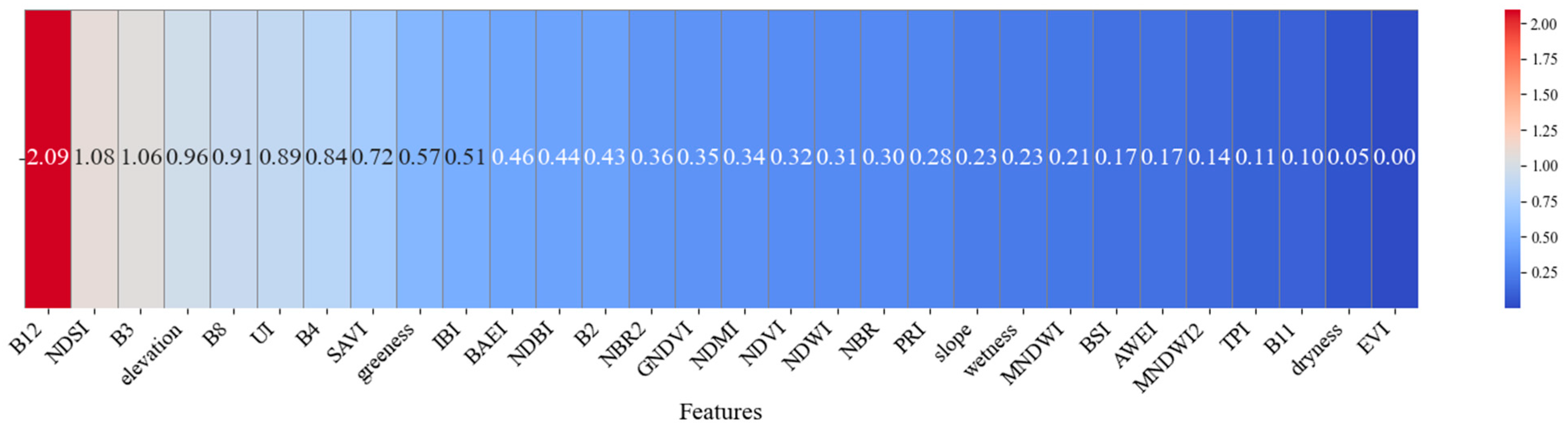
3.2.5. Feature Importance Analysis
3.2.6. Sharpening Thermal Imagery
3.2.7. Evaluation Metrics
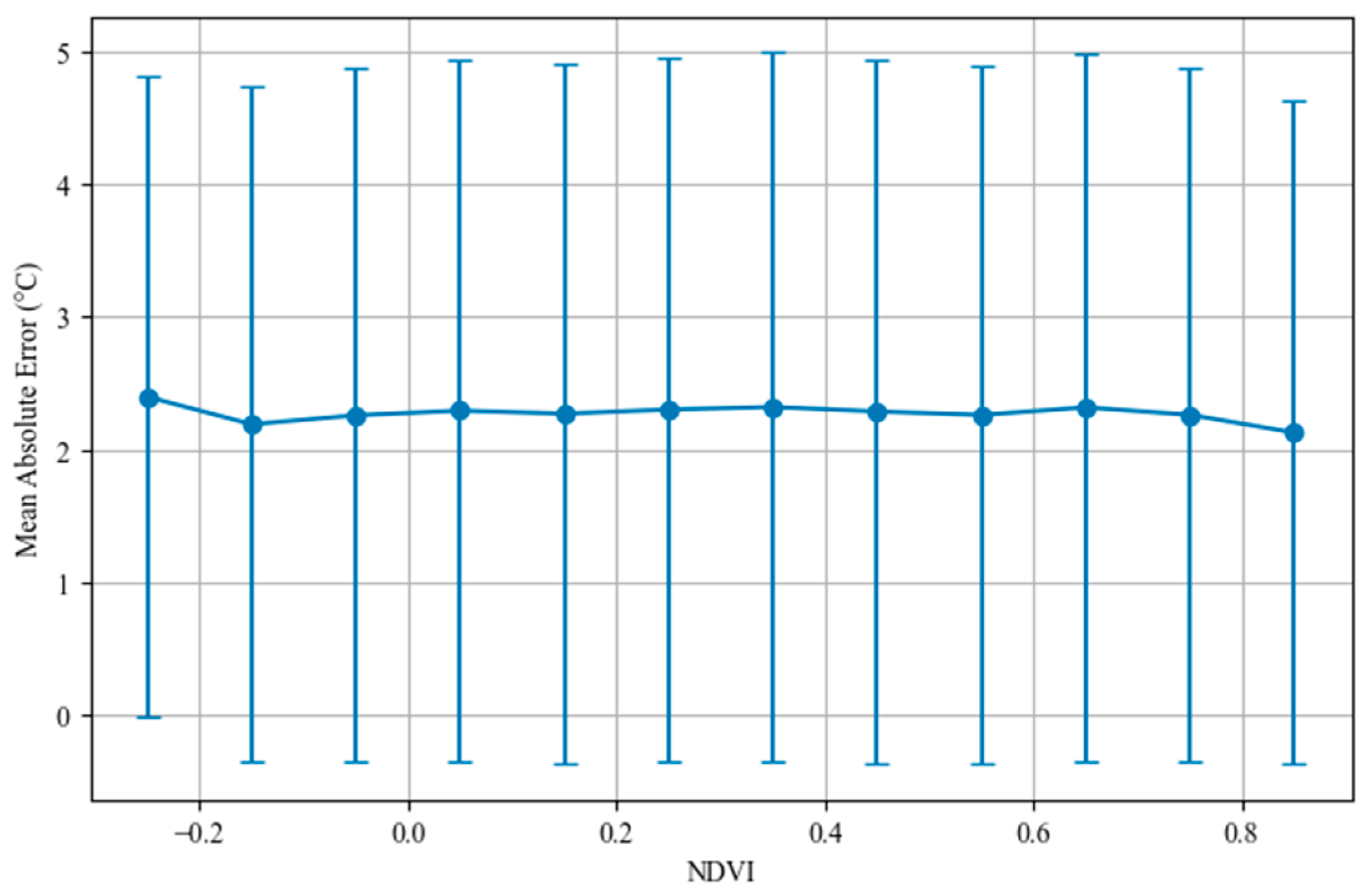
4. Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Mutiibwa, D.; Strachan, S.; Albright, T. Land surface temperature and surface air temperature in complex terrain. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 4762–4774. [Google Scholar] [CrossRef]
- Hu, J.; Fu, Y.; Zhang, P.; Min, Q.; Gao, Z.; Wu, S.; Li, R. Satellite retrieval of microwave land surface emissivity under clear and cloudy skies in China using observations from AMSR-E and MODIS. Remote Sens. 2021, 13, 3980. [Google Scholar] [CrossRef]
- Crossley, J.; Polcher, J.; Cox, P.; Gedney, N.; Planton, S. Uncertainties linked to land-surface processes in climate change simulations. Clim. Dyn. 2000, 16, 949–961. [Google Scholar] [CrossRef]
- Weng, Q.; Lu, D.; Schubring, J. Estimation of land surface temperature–vegetation abundance relationship for urban heat island studies. Remote Sens. Environ. 2004, 89, 467–483. [Google Scholar] [CrossRef]
- Li, Z.-L.; Tang, B.-H.; Wu, H.; Ren, H.; Yan, G.; Wan, Z.; Trigo, I.F.; Sobrino, J.A. Satellite-derived land surface temperature: Current status and perspectives. Remote Sens. Environ. 2013, 131, 14–37. [Google Scholar] [CrossRef]
- Meng, X.; Cheng, J.; Guo, H.; Guo, Y.; Yao, B. Accuracy evaluation of the Landsat 9 land surface temperature product. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 8694–8703. [Google Scholar] [CrossRef]
- Rozenstein, O.; Qin, Z.; Derimian, Y.; Karnieli, A. Derivation of land surface temperature for Landsat-8 TIRS using a split window algorithm. Sensors 2014, 14, 5768–5780. [Google Scholar] [CrossRef] [PubMed]
- Griffiths, P.; Nendel, C.; Hostert, P. Intra-annual reflectance composites from Sentinel-2 and Landsat for national-scale crop and land cover mapping. Remote Sens. Environ. 2019, 220, 135–151. [Google Scholar] [CrossRef]
- Bharathi, D.; Karthi, R.; Geetha, P. Blending of Landsat and Sentinel images using Multi-sensor fusion. In Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2023; Volume 2571, p. 012008. [Google Scholar]
- Chang, Y.; Xiao, J.; Li, X.; Middel, A.; Zhang, Y.; Gu, Z.; Wu, Y.; He, S. Exploring diurnal thermal variations in urban local climate zones with ECOSTRESS land surface temperature data. Remote Sens. Environ. 2021, 263, 112544. [Google Scholar] [CrossRef]
- Alexandris, N.; Piccardo, M.; Syrris, V.; Cescatti, A.; Duveiller, G. Downscaling sub-daily Land Surface Temperature time series for monitoring heat in urban environments. In Proceedings of the EGU General Assembly Conference Abstracts, Vienna, Austria, 4–8 May 2020; EGUsphere Platform: Göttingen, Germany; p. 21094. [Google Scholar]
- Li, W.; Ni, L.; Li, Z.-l.; Duan, S.-B.; Wu, H. Evaluation of machine learning algorithms in spatial downscaling of MODIS land surface temperature. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 2299–2307. [Google Scholar] [CrossRef]
- Ebrahimy, H.; Azadbakht, M. Downscaling MODIS land surface temperature over a heterogeneous area: An investigation of machine learning techniques, feature selection, and impacts of mixed pixels. Comput. Geosci. 2019, 124, 93–102. [Google Scholar] [CrossRef]
- Xu, S.; Zhao, Q.; Yin, K.; He, G.; Zhang, Z.; Wang, G.; Wen, M.; Zhang, N. Spatial downscaling of land surface temperature based on a multi-factor geographically weighted machine learning model. Remote Sens. 2021, 13, 1186. [Google Scholar] [CrossRef]
- Yin, Z.; Wu, P.; Foody, G.M.; Wu, Y.; Liu, Z.; Du, Y.; Ling, F. Spatiotemporal fusion of land surface temperature based on a convolutional neural network. IEEE Trans. Geosci. Remote Sens. 2020, 59, 1808–1822. [Google Scholar] [CrossRef]
- Wang, N.; Tian, J.; Su, S.; Tian, Q. A Downscaling Method Based on MODIS Product for Hourly ERA5 Reanalysis of Land Surface Temperature. Remote Sens. 2023, 15, 4441. [Google Scholar] [CrossRef]
- Li, X.; He, X.; Pan, X. Application of Gaofen-6 images in the downscaling of land surface temperatures. Remote Sens. 2022, 14, 2307. [Google Scholar] [CrossRef]
- Jamaluddin, I.; Chen, Y.-N.; Mahendra, W.K.; Awanda, D. Deep neural network regression for estimating land surface temperature at 10 meter spatial resolution using Landsat-8 and Sentinel-2 data. In Proceedings of the Seventh Geoinformation Science Symposium, Yogyakarta, Indonesia, 25–28 October 2021; SPIE: Bellingham, WA, USA, 2021; Volume 12082, pp. 31–41. [Google Scholar]
- Li, W.; Ni, L.; Li, Z.-L.; Wu, H. Downscaling land surface temperature by using random forest regression algorithm. In Proceedings of the IGARSS 2018–2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; IEEE: New York, NY, USA, 2018; pp. 2527–2530. [Google Scholar]
- Wang, F.; Qin, Z.; Song, C.; Tu, L.; Karnieli, A.; Zhao, S. An improved mono-window algorithm for land surface temperature retrieval from Landsat 8 thermal infrared sensor data. Remote Sens. 2015, 7, 4268–4289. [Google Scholar] [CrossRef]
- Wang, L.; Lu, Y.; Yao, Y. Comparison of three algorithms for the retrieval of land surface temperature from Landsat 8 images. Sensors 2019, 19, 5049. [Google Scholar] [CrossRef]
- Shen, Y.; Wang, Y.; Lv, H. Thin cloud removal for Landsat 8 OLI data using independent component analysis. In Proceedings of the 2015 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 26–31 July 2015; IEEE: New York, NY, USA; pp. 921–924. [Google Scholar]
- Louis, J.; Pflug, B.; Debaecker, V.; Mueller-Wilm, U.; Iannone, R.Q.; Boccia, V.; Gascon, F. Evolutions of Sentinel-2 Level-2A cloud masking algorithm Sen2Cor prototype first results. In Proceedings of the 2021 IEEE international geoscience and remote sensing symposium IGARSS, Brussels, Belgium, 11–16 July 2021; IEEE: New York, NY, USA; pp. 3041–3044. [Google Scholar]
- Immitzer, M.; Vuolo, F.; Atzberger, C. First experience with Sentinel-2 data for crop and tree species classifications in central Europe. Remote Sens. 2016, 8, 166. [Google Scholar] [CrossRef]
- Wang, Z.; Sun, Y.; Zhang, T.; Ren, H.; Qin, Q. Optimization of spectral indices for the estimation of leaf area index based on Sentinel-2 multispectral imagery. In Proceedings of the IGARSS 2018-2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; IEEE: New York, NY, USA; pp. 5441–5444. [Google Scholar]
- Imran, A.; Khan, K.; Ali, N.; Ahmad, N.; Ali, A.; Shah, K. Narrow band based and broadband derived vegetation indices using Sentinel-2 Imagery to estimate vegetation biomass. Glob. J. Environ. Sci. Manag. 2020, 6, 97–108. [Google Scholar]
- Jiang, W.; Ni, Y.; Pang, Z.; Li, X.; Ju, H.; He, G.; Lv, J.; Yang, K.; Fu, J.; Qin, X. An effective water body extraction method with new water index for sentinel-2 imagery. Water 2021, 13, 1647. [Google Scholar] [CrossRef]
- Hu, B.; Xu, Y.; Huang, X.; Cheng, Q.; Ding, Q.; Bai, L.; Li, Y. Improving urban land cover classification with combined use of sentinel-2 and sentinel-1 imagery. ISPRS Int. J. Geo-Inf. 2021, 10, 533. [Google Scholar] [CrossRef]
- Alcaras, E.; Costantino, D.; Guastaferro, F.; Parente, C.; Pepe, M. Normalized Burn Ratio Plus (NBR+): A new index for Sentinel-2 imagery. Remote Sens. 2022, 14, 1727. [Google Scholar] [CrossRef]
- Castaldi, F.; Chabrillat, S.; Don, A.; van Wesemael, B. Soil organic carbon mapping using LUCAS topsoil database and Sentinel-2 data: An approach to reduce soil moisture and crop residue effects. Remote Sens. 2019, 11, 2121. [Google Scholar] [CrossRef]
- Lefebvre, A.; Sannier, C.; Corpetti, T. Monitoring urban areas with Sentinel-2A data: Application to the update of the Copernicus high resolution layer imperviousness degree. Remote Sens. 2016, 8, 606. [Google Scholar] [CrossRef]
- Le Saint, T.; Lefebvre, S.; Hubert-Moy, L.; Nabucet, J.; Adeline, K. Sensitivity analysis of Sentinel-2 data for urban tree characterization using DART model. In Proceedings of the Remote Sensing Technologies and Applications in Urban Environments VIII, Edinburgh, Scotland, 3–4 September 2023; SPIE: Bellingham, WA, USA; pp. 116–129. [Google Scholar]
- Phiri, D.; Simwanda, M.; Salekin, S.; Nyirenda, V.R.; Murayama, Y.; Ranagalage, M. Sentinel-2 data for land cover/use mapping: A review. Remote Sens. 2020, 12, 2291. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Wu, H.; Li, W. Downscaling land surface temperatures using a random forest regression model with multitype predictor variables. IEEE Access 2019, 7, 21904–21916. [Google Scholar] [CrossRef]
- Mei, S.; Ji, J.; Bi, Q.; Hou, J.; Du, Q.; Li, W. Integrating spectral and spatial information into deep convolutional neural networks for hyperspectral classification. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; IEEE: New York, NY, USA; pp. 5067–5070. [Google Scholar]
- Jiang, X.; Lu, M.; Wang, S.-H. An eight-layer convolutional neural network with stochastic pooling, batch normalization and dropout for fingerspelling recognition of Chinese sign language. Multimed. Tools Appl. 2020, 79, 15697–15715. [Google Scholar] [CrossRef]
- Akila Agnes, S.; Anitha, J. Analyzing the effect of optimization strategies in deep convolutional neural network. In Nature Inspired Optimization Techniques for Image Processing Applications; Springer: Berlin/Heidelberg, Germany, 2019; pp. 235–253. [Google Scholar]
- Arora, R.; Basu, A.; Mianjy, P.; Mukherjee, A. Understanding deep neural networks with rectified linear units. arXiv 2016, arXiv:1611.01491. [Google Scholar]
- Garbin, C.; Zhu, X.; Marques, O. Dropout vs. batch normalization: An empirical study of their impact to deep learning. Multimed. Tools Appl. 2020, 79, 12777–12815. [Google Scholar] [CrossRef]
- Wang, Q.; Peng, R.-Q.; Wang, J.-Q.; Li, Z.; Qu, H.-B. NEWLSTM: An optimized long short-term memory language model for sequence prediction. IEEE Access 2020, 8, 65395–65401. [Google Scholar] [CrossRef]
- Van Houdt, G.; Mosquera, C.; Nápoles, G. A review on the long short-term memory model. Artif. Intell. Rev. 2020, 53, 5929–5955. [Google Scholar] [CrossRef]
- Ghojogh, B.; Ghodsi, A. Recurrent neural networks and long short-term memory networks: Tutorial and survey. arXiv 2023, arXiv:2304.11461. [Google Scholar] [CrossRef]
- Boardman, J.W.; Xie, Y. Radically Simplifying Gated Recurrent Architectures Without Loss of Performance. In Proceedings of the 2019 IEEE International Conference on Big Data (Big Data), Los Angeles, CA, USA, 9–12 December 2019; IEEE: New York, NY, USA; pp. 2615–2623. [Google Scholar]
- Lu, Y.; Salem, F.M. Simplified gating in long short-term memory (lstm) recurrent neural networks. In Proceedings of the 2017 IEEE 60th international midwest symposium on circuits and systems (MWSCAS), Boston, MA, USA, 6–9 August 2017; IEEE: New York, NY, USA; pp. 1601–1604. [Google Scholar]
- Ramadhan, M.M.; Sitanggang, I.S.; Nasution, F.R.; Ghifari, A. Parameter tuning in random forest based on grid search method for gender classification based on voice frequency. DEStech Trans. Comput. Sci. Eng. 2017, 10. [Google Scholar] [CrossRef]
- Agarap, A. Deep learning using rectified linear units (relu). arXiv 2018, arXiv:1803.08375. [Google Scholar]
- Agostinelli, F. Learning activation functions to improve deep neural networks. arXiv 2014, arXiv:1412.6830. [Google Scholar]
- Bock, S.; Goppold, J.; Weiß, M. An improvement of the convergence proof of the ADAM-Optimizer. arXiv 2018, arXiv:1804.10587. [Google Scholar] [CrossRef]
- Hu, L.; Wang, K. Computing SHAP Efficiently Using Model Structure Information. arXiv 2023, arXiv:2309.02417. [Google Scholar] [CrossRef]
- Sattari, F.; Hashim, M.; Sookhak, M.; Banihashemi, S.; Pour, A.B. Assessment of the TsHARP method for spatial downscaling of land surface temperature over urban regions. Urban Clim. 2022, 45, 101265. [Google Scholar] [CrossRef]
- Ly, A.; Marsman, M.; Wagenmakers, E.J. Analytic posteriors for Pearson’s correlation coefficient. Stat. Neerl. 2018, 72, 4–13. [Google Scholar] [CrossRef] [PubMed]
- Cheng, C.-L.; Garg, G. Coefficient of determination for multiple measurement error models. J. Multivar. Anal. 2014, 126, 137–152. [Google Scholar] [CrossRef]
- De Myttenaere, A.; Golden, B.; Le Grand, B.; Rossi, F. Mean absolute percentage error for regression models. Neurocomputing 2016, 192, 38–48. [Google Scholar] [CrossRef]





| Category | Feature | Description |
|---|---|---|
| Spectral Bands | B2, B3, B4 (Visible Bands) | Blue, Green, and Red bands for vegetation, soil, and water detection [24]. |
| B8 (NIR) | Near-Infrared for vegetation vigor analysis [25]. | |
| B11, B12 (SWIR) | Shortwave Infrared bands for moisture and geological analysis [26]. | |
| Spectral Indices | NDVI, EVI, SAVI, GNDVI | Measure vegetation health, density, and greenness [26]. |
| NDWI, MNDWI, AWEI, MNDWI2 | Identify and enhance water body detection [27]. | |
| NDBI, UI, IBI | Highlight urban and built-up areas [28]. | |
| NBR, NBR2 | Assess burned areas and vegetation stress [29]. | |
| BSI, PRI, BAEI | Indicate soil characteristics, dryness, and photosynthetic activity [30]. | |
| NDSI | Highlights snow-covered areas [31]. | |
| Topographic Data | Elevation | Height above sea level from digital elevation models (DEMs) [32]. |
| TPI (Topographic Position Index) | Classifies landforms based on elevation [32]. | |
| Slope | Measures terrain steepness [32]. | |
| Land Cover Data | Wetness | Derived from MNDWI2, indicating the presence of surface water [33]. |
| Greenness | Derived from NDMI, representing vegetated areas not classified as wet [33]. | |
| Dryness | Identifies dry surfaces as areas classified as neither wet nor green, with a smoothing filter applied [33]. |
| Model | Hyperparameter | Search Range | Selected Value |
|---|---|---|---|
| RFR | Number of estimators | 100, 150, 200, 250, 300 | 250 |
| Maximum depth | 10, 20, 30, 40, None | 30 | |
| Minimum samples split | 2, 5, 10 | 5 | |
| CNN | Number of convolutional layers | 2, 3, 4 | 3 layers |
| Filters per layer | 64, 128, 256 | 256, 128, 64 (from first to third layer) | |
| Kernel size | (3 × 3), (5 × 5) | (3 × 3) | |
| Batch size | 8, 16, 32 | 16 | |
| Learning rate | 10−3, 10−4, 10−5 | Fine-tuned to 3.9063 × 10−6 | |
| LSTM and GRU | Number of recurrent layers | 2, 3, 4 | 4 layers |
| Units per layer | 64, 128, 256 | 256, 128, 64, 32 (from first to fourth layer) | |
| Batch size | 8, 16, 32 | 16 | |
| Learning rate | 10−3, 10−4, 10−5 | 10−3 (initial), reduced to 10−6 upon plateau |
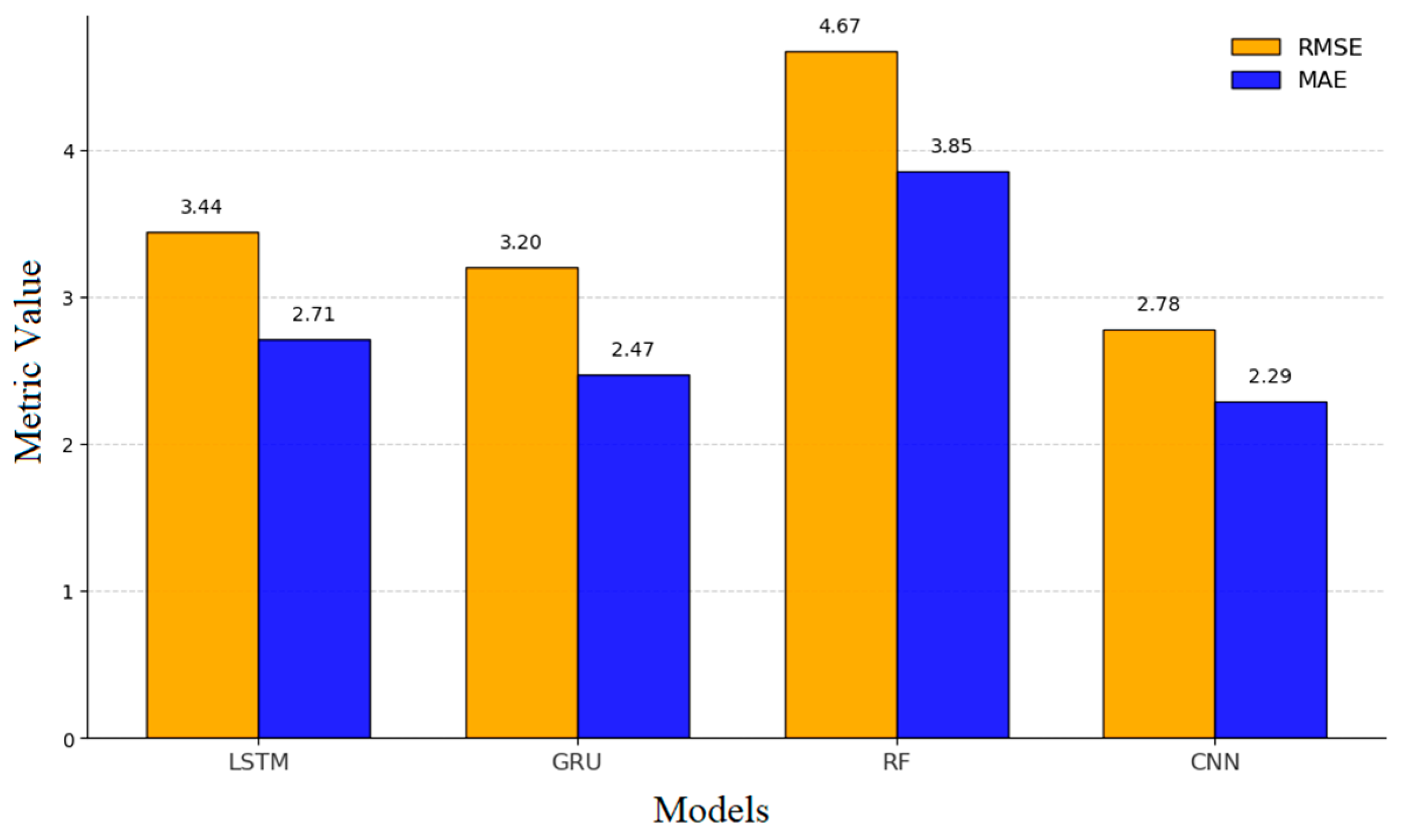
| Method | R2 | MAE (Celsius) |
|---|---|---|
| RFR | 55.75% | 2.3818 |
| CNN | 74.81% | 1.5880 |
| LSTM | 72.11% | 1.6151 |
| GRU | 71.01% | 1.6565 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Niroomand, M.; Pahlavani, P.; Bigdeli, B.; Ghorbanzadeh, O. Improving the Temporal Resolution of Land Surface Temperature Using Machine and Deep Learning Models. Geomatics 2025, 5, 50. https://doi.org/10.3390/geomatics5040050
Niroomand M, Pahlavani P, Bigdeli B, Ghorbanzadeh O. Improving the Temporal Resolution of Land Surface Temperature Using Machine and Deep Learning Models. Geomatics. 2025; 5(4):50. https://doi.org/10.3390/geomatics5040050
Chicago/Turabian StyleNiroomand, Mohsen, Parham Pahlavani, Behnaz Bigdeli, and Omid Ghorbanzadeh. 2025. "Improving the Temporal Resolution of Land Surface Temperature Using Machine and Deep Learning Models" Geomatics 5, no. 4: 50. https://doi.org/10.3390/geomatics5040050
APA StyleNiroomand, M., Pahlavani, P., Bigdeli, B., & Ghorbanzadeh, O. (2025). Improving the Temporal Resolution of Land Surface Temperature Using Machine and Deep Learning Models. Geomatics, 5(4), 50. https://doi.org/10.3390/geomatics5040050








