Spatial Variability and Geostatistical Modeling of Soil Physical Properties Under Eucalyptus globulus Plantations
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Site and Sampling
2.2. Measurement of the Physical Properties of the Evaluated Soil
2.3. Statistical Analysis
3. Results
3.1. Comparison of Vegetation Covers
3.2. Descriptive Statistical Analysis
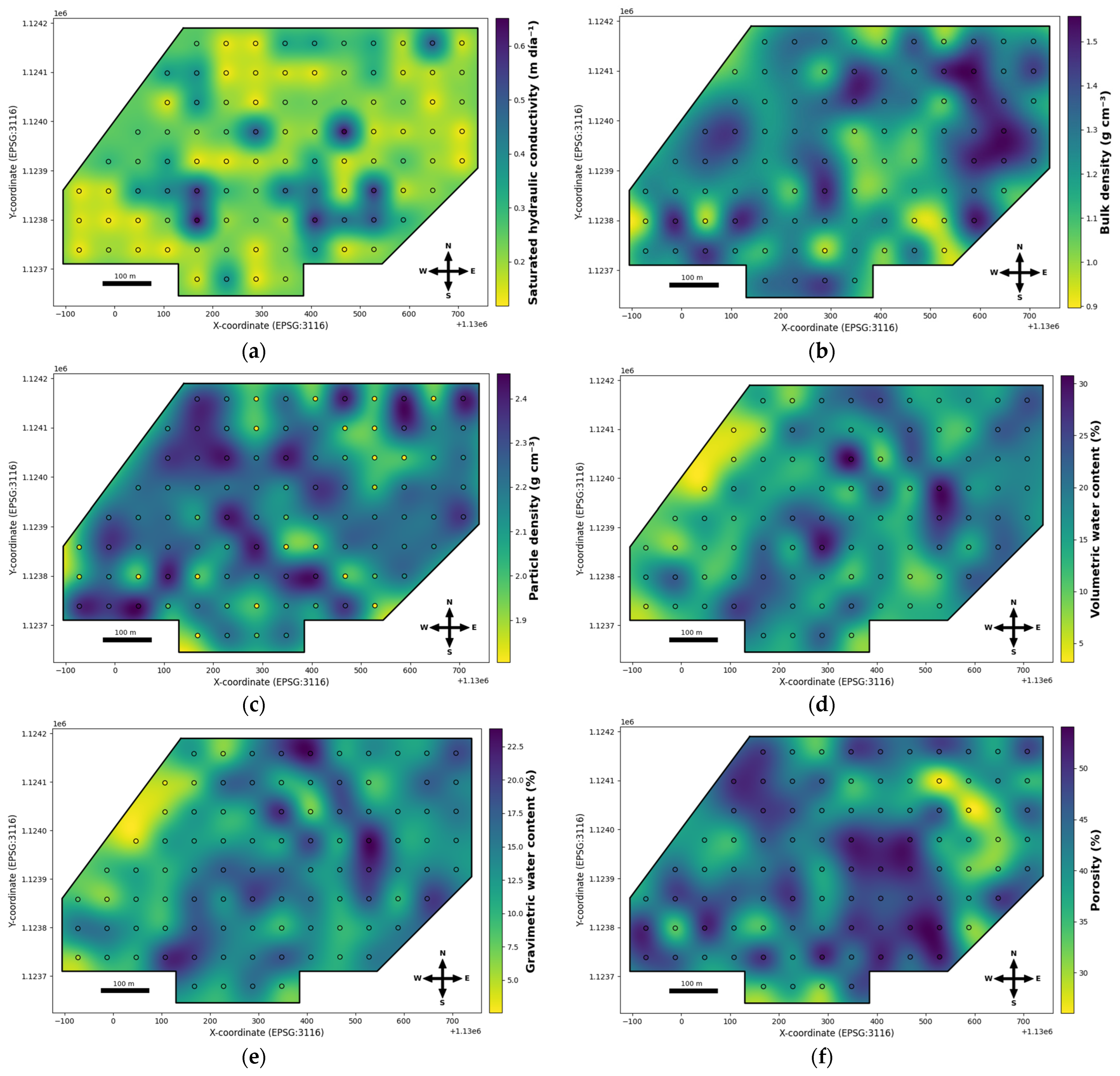
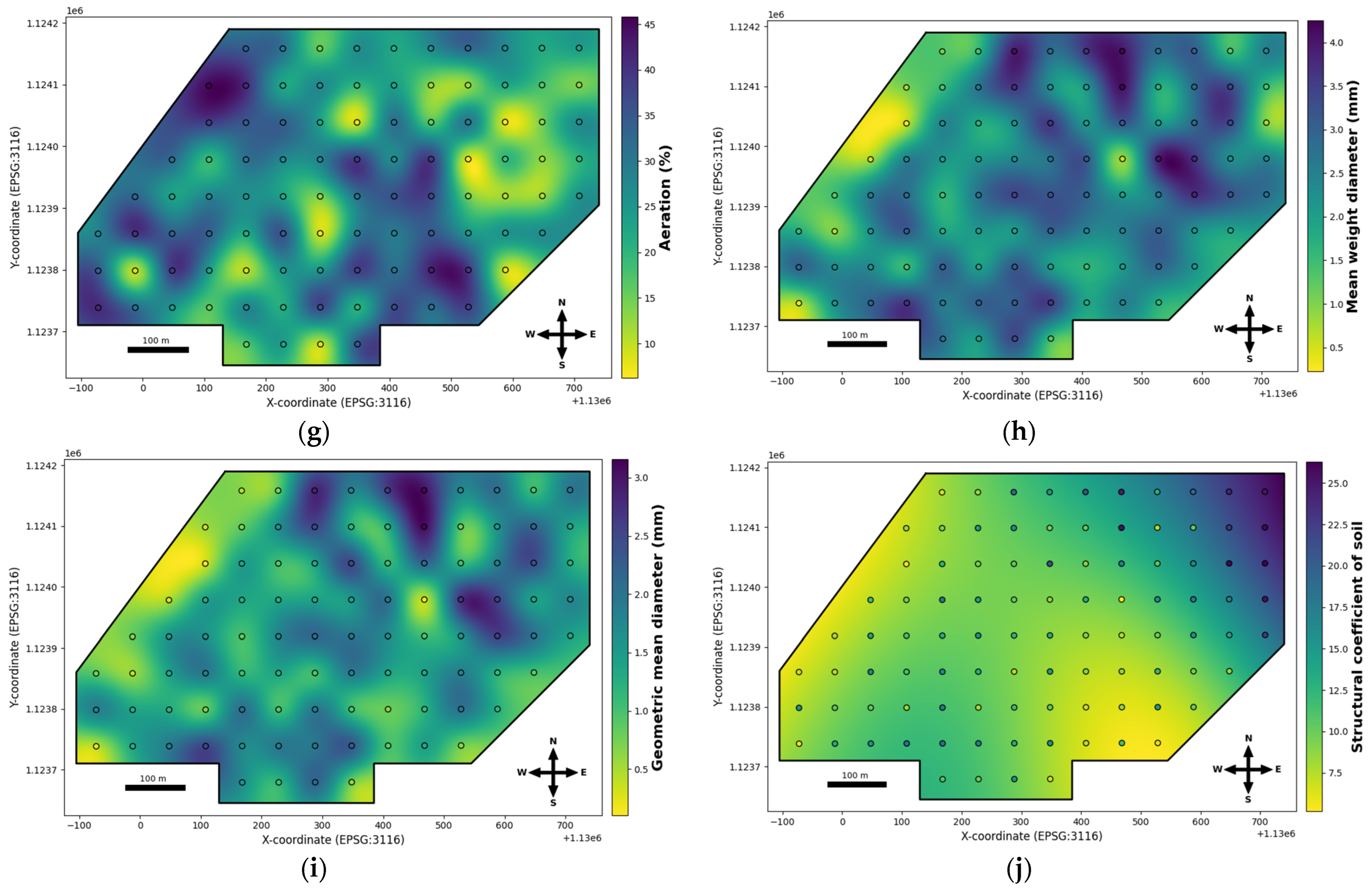
3.3. Geostatistical Analysis and Spatial Distribution of Soil Properties
3.3.1. Saturated Hydraulic Conductivity
3.3.2. Bulk Density (ρb)
3.3.3. Particle Density (ρs)
3.3.4. Volumetric Moisture Content (θV) and Gravimetric Moisture Content (θg)
3.3.5. Total Porosity (ft)
3.3.6. Aeration (A)
3.3.7. Mean Weight Diameter (MWD) and Geometric Mean Diameter (GMD)
3.3.8. Structural Coefficient (Ks)
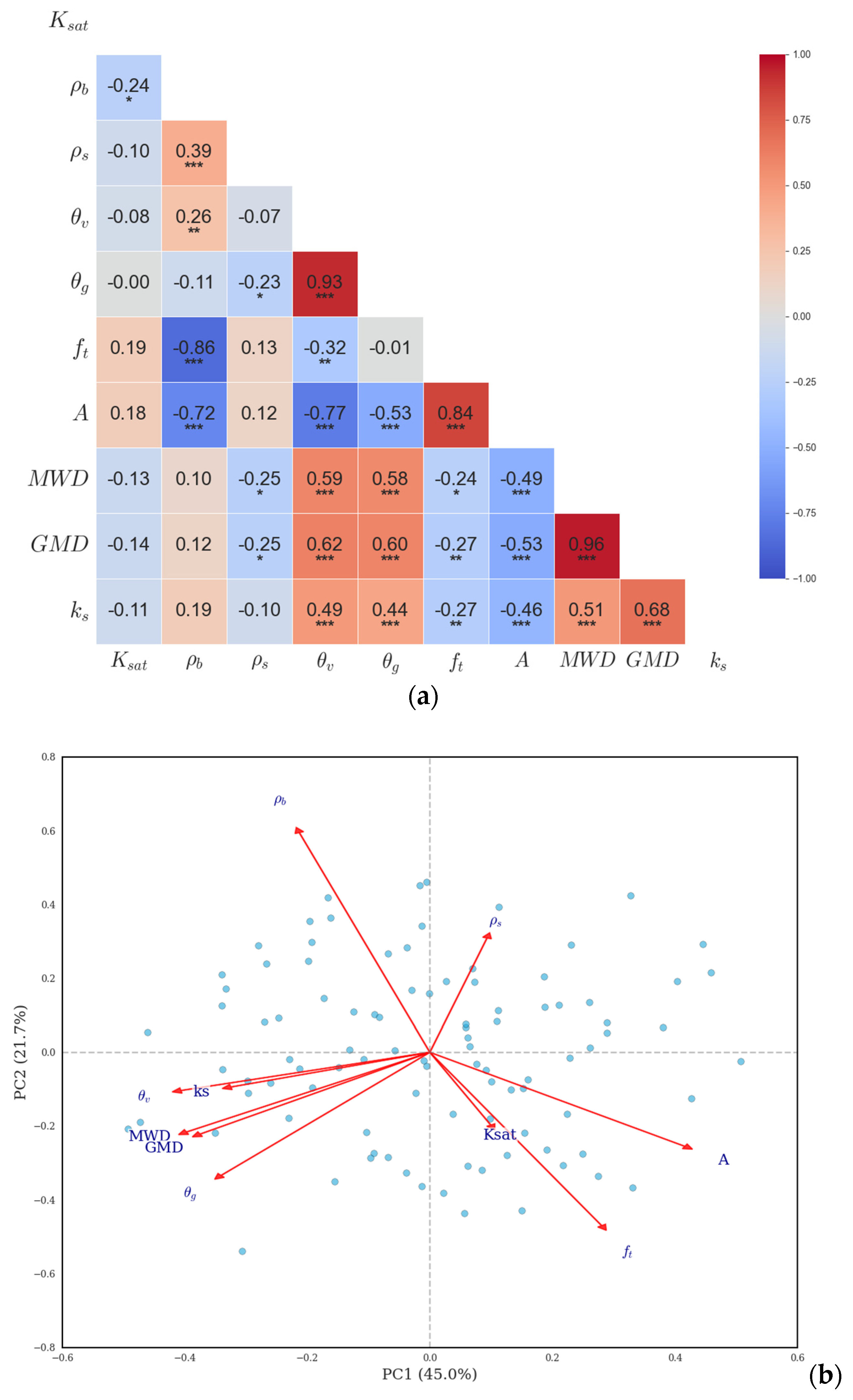
3.4. Correlation Analysis and Principal Component Analysis of Soil Physical Properties
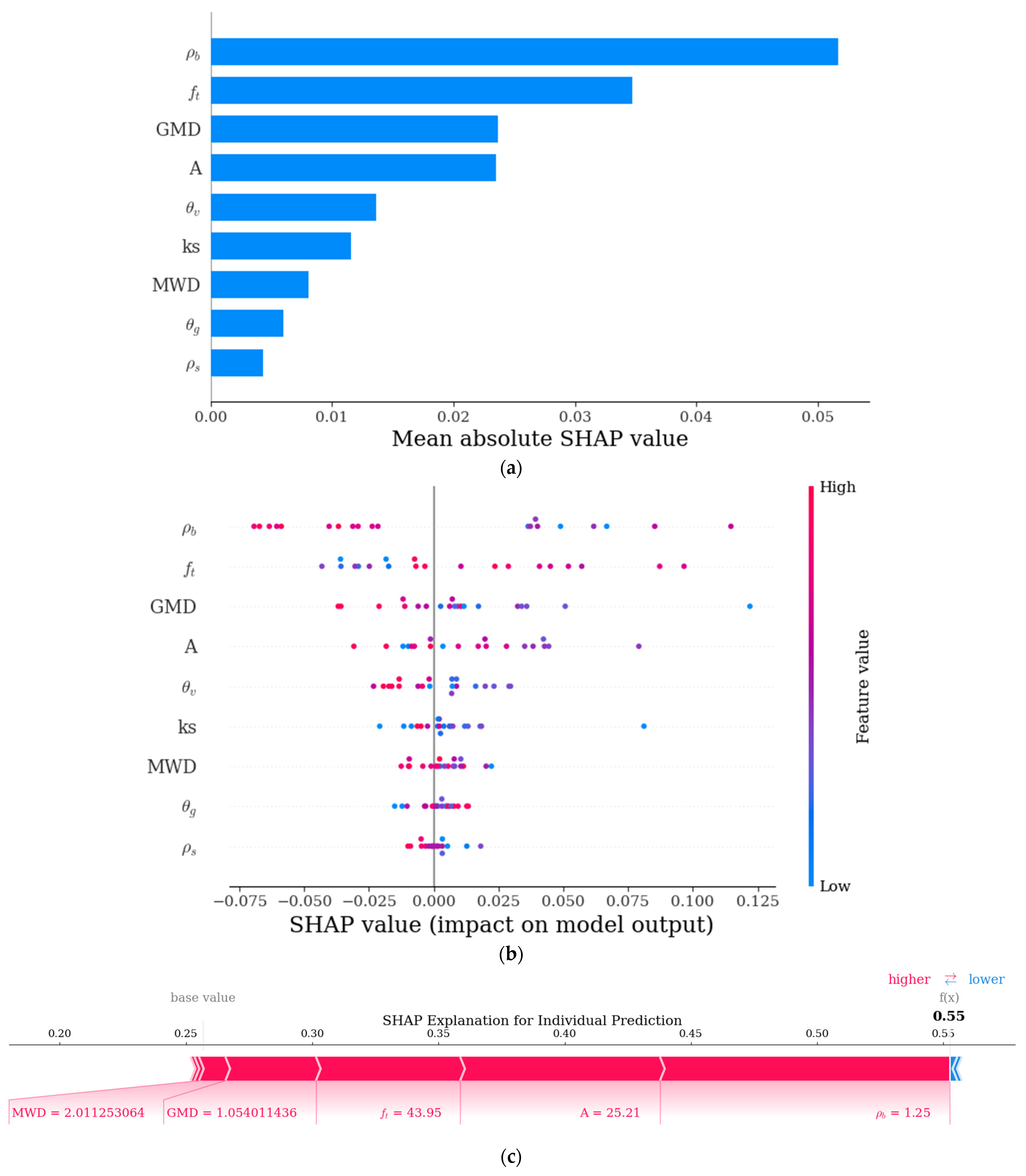
3.5. SHAP Values Analysis of Soil Physical Properties
4. Discussion
4.1. Comparison of Vegetation Covers and Descriptive Statistics
4.2. Geostatistical Analysis and Spatial Distribution of Soil Properties
4.2.1. Saturated Hydraulic Conductivity
4.2.2. Bulk Density (ρb) and Particle Density (ρs)
4.2.3. Moisture Content
4.2.4. Total Porosity (ft) and Aeration (A)
4.2.5. Aggregate Stability, and Structural Coefficient
4.3. Interpretation of Correlations and Model Contributions
4.3.1. Correlation and Principal Component Analysis
4.3.2. Correlation and Principal Component Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Awal, R.; Safeeq, M.; Abbas, F.; Fares, S.; Deb, S.K.; Ahmad, A.; Fares, A. Soil physical properties spatial variability under long-term no-tillage corn. Agronomy 2019, 9, 750. [Google Scholar] [CrossRef]
- Meshesha, D.T.; Belay, A.W.; Tiruneh, G.A.; Adgo, E.; Alemayehu, T.Y.; Chandrakala, M.; Reichert, J.M. Exploring and modeling the spatial variability of soil erosion in Tana Basin, Northwestern Ethiopia. Appl. Environ. Soil Sci. 2024, 2024, 2102727. [Google Scholar] [CrossRef]
- Oladipupo, R.A.; Munnaf, M.A.; Sanganta, P.; Borundia, A.; Mouazen, A.M. A Novel On-Line Dual Sensing System for Soil Property Measurement and Mapping. Smart Agric. Technol. 2024, 9, 100640. [Google Scholar] [CrossRef]
- Della Peruta, R.; Mereu, V.; Spano, D.; Marras, S.; Vezy, R.; Trabucco, A. Projecting Trends of Arabica Coffee Yield under Climate Change: A Process-Based Modelling Study at Continental Scale. Agric. Syst. 2025, 227, 104353. [Google Scholar] [CrossRef]
- Yang, Y.; Peng, B.; Guan, K.; Pan, M.; Franz, T.E.; Cosh, M.H.; Bernacchi, C.J. Within-field soil moisture variability and time-invariant spatial structures of agricultural fields in the US Midwest. Vadose Zone J. 2024, 23, e20337. [Google Scholar] [CrossRef]
- Wang, Y.; Yuan, F.; Cammarano, D.; Liu, X.; Tian, Y.; Zhu, Y.; Cao, W.; Cao, Q. Integrating Machine Learning with Spatial Analysis for Enhanced Soil Interpolation: Balancing Accuracy and Visualization. Smart Agric. Technol. 2025, 11, 101032. [Google Scholar] [CrossRef]
- Sarto, M.V.M.; Borges, W.L.B.; Bassegio, D.; Nunes, M.R.; Rice, C.W.; Rosolem, C.A. Deep soil water content and forage production in a tropical agroforestry system. Agriculture 2022, 12, 359. [Google Scholar] [CrossRef]
- Dzikiti, S.; Gush, M.B.; Le Maitre, D.C.; Maherry, A.; Jovanovic, N.Z.; Ramoelo, A.; Cho, M.A. Quantifying potential water savings from clearing invasive alien Eucalyptus camaldulensis using in situ and high resolution remote sensing data in the Berg River Catchment, Western Cape, South Africa. For. Ecol. Manag. 2016, 361, 69–80. [Google Scholar] [CrossRef]
- Salazar, M.P.; Lozano, L.A.; Villarreal, R.; Bellora, G.L.; Villeda, C.A.M.; Churquina, N.; Polich, N.G.; Soracco, C.G. Soil water repellency under Eucalyptus stands of different age and its relationship with soil hydrological function and soil organic matter. Catena 2024, 246, 108441. [Google Scholar] [CrossRef]
- Wang, Y.; He, C.; Shi, Y.; Li, H.; Tang, Y.; Chen, B.; Ke, Q.; Wu, L.; Chen, L. Short-term cultivation limiting soil aggregate stability and macronutrient accumulation associated with glomalin-related soil protein in Eucalyptus urophylla × Eucalyptus grandis plantations. Sci. Total Environ. 2023, 878, 163187. [Google Scholar] [CrossRef]
- Tesfaw, A.; Teferi, E.; Senbeta, F.; Alemu, D. The spatial distribution and expansion of Eucalyptus in its hotspots: Implications on agricultural landscapes. Heliyon 2023, 9, e14393. [Google Scholar] [CrossRef]
- Zárate, J.A.; Gutiérrez, O.J. Caracterización de maderas usadas en Boyacá de acuerdo con el Reglamento Colombiano de Construcción Sismo Resistente. Rev. Fac. Ing. 2012, 21, 73–91. [Google Scholar]
- Guzmán, S.D.M.; Drummond, J.A.; Barreto, C.G. Undesirable Neighbours: Eucalyptus and Protected Areas. In Protected Area Management—Recent Advances; IntechOpen: London, UK, 2022. [Google Scholar] [CrossRef]
- Peng, J.; Xiao, L.; Xu, Z.; Chen, B.; Zhou, G.; Qiao, C.; Sun, C.; Wu, Z. Effects of Different Land Use Change on Soil Aggregate and Aggregate Associated Organic Carbon: A Meta-Analysis. Pol. J. Environ. Stud. 2024, 33, 5263–5274. [Google Scholar] [CrossRef]
- Ye, L.; Ji, L.; Chen, H.; Chen, X.; Tan, W. Spatial contribution of environmental factors to soil aggregate stability in a small catchment of the Loess Plateau, China. Agronomy 2022, 12, 2557. [Google Scholar] [CrossRef]
- Li, S.; Wang, B.; Zhang, X.; Wang, H.; Yi, Y.; Huang, X.; Li, H.; Zhu, P.; Han, W. Soil particle aggregation and aggregate stability associated with ion specificity and organic matter content. Geoderma 2023, 429, 116285. [Google Scholar] [CrossRef]
- Álvarez Herrera, J.G.; Ruiz Berrío, H.D.; Acosta Tova, D.F. Evaluación geoestadística de atributos hidrofísicos del suelo en la granja Tunguavita, Paipa, Colombia. Cienc. Ing. Neogranadina 2021, 31, 127–140. [Google Scholar] [CrossRef]
- Stolt, M.H.; Needelman, B.A. Fundamental Changes in Soil Taxonomy. Soil Sci. Soc. Am. J. 2015, 79, 1001–1007. [Google Scholar] [CrossRef]
- Guatibonza, M.; Álvarez-Herrera, J.G.; Sanabria, J.E. Distribución espacial de la conductividad hidráulica en un lote de la granja Tunguavita (Paipa, Colombia). Agron. Colomb. 2009, 27, 261–271. [Google Scholar]
- Ćirić, V.; Manojlović, M.; Nešić, L.; Belić, M. Soil dry aggregate size distribution: Effects of soil type and land use. J. Soil Sci. Plant Nutr. 2012, 12, 689–703. [Google Scholar] [CrossRef]
- Warrick, A.W.; Nielsen, D. Spatial variability of soil physical properties in the field. In Applications of Soil Physics; Academic Press: New York, NY, USA, 1980; pp. 319–344. [Google Scholar] [CrossRef]
- Cambardella, C.A.; Moorman, T.B.; Novak, J.M.; Parkin, T.B.; Karlen, D.L.; Turco, R.F.; Konopka, A.E. Field-scale variability of soil properties in central Iowa soils. Soil Sci. Soc. Am. J. 1994, 58, 1501–1511. [Google Scholar] [CrossRef]
- Catoni, M.; D’Amico, M.E.; Zanini, E.; Bonifacio, E. Effect of pedogenic processes and formation factors on organic matter stabilization in alpine forest soils. Geoderma 2016, 263, 151–160. [Google Scholar] [CrossRef]
- Kooch, Y.; Ghorbanzadeh, N.; Haghverdi, K.; Francaviglia, R. Soil Quality Cannot Be Improved after Thirty Years of Land Use Change from Forest to Rangeland. Sci. Total Environ. 2023, 856, 159132. [Google Scholar] [CrossRef]
- Godoy, V.A.; Zuquette, L.V.; Gómez-Hernández, J.J. Spatial variability of hydraulic conductivity and solute transport parameters and their spatial correlations to soil properties. Geoderma 2019, 339, 59–69. [Google Scholar] [CrossRef]
- Soares, M.F.; Centeno, L.N.; Timm, L.C.; Mello, C.R.; Kaiser, D.R.; Beskow, S. Identifying covariates to assess the spatial variability of saturated soil hydraulic conductivity using robust cokriging at the watershed scale. J. Soil Sci. Plant Nutr. 2020, 20, 1491–1502. [Google Scholar] [CrossRef]
- Moratelli, F.A.; Alves, M.A.B.; Borella, D.R.; Kraeski, A.; Almeida, F.T.D.; Zolin, C.A.; Hoshide, A.K.; Souza, A.P.D. Effects of land use on soil physical-hydric attributes in two watersheds in the southern Amazon, Brazil. Soil Syst. 2023, 7, 103. [Google Scholar] [CrossRef]
- Monroy-Rodríguez, F.L.; Álvarez-Herrera, J.G.; Alvarado-Sanabria, Ó.H. Distribución espacial de algunas propiedades físicas del suelo en un transecto de la granja Tunguavita, Paipa. Rev. UDCA Actual. Divulg. Cient. 2017, 20, 91–100. [Google Scholar]
- Mentges, M.I.; Reichert, J.M.; Rodrigues, M.F.; Awe, G.O.; Mentges, L.R. Capacity and intensity soil aeration properties affected by granulometry, moisture, and structure in no-tillage soils. Geoderma 2016, 263, 47–59. [Google Scholar] [CrossRef]
- Yalin, D.; Schwartz, A.; Tarchitzky, J.; Shenker, M. Soil oxygen and water dynamics underlying hypoxic conditions in the root-zone of avocado irrigated with treated wastewater in clay soil. Soil Tillage Res. 2021, 212, 105039. [Google Scholar] [CrossRef]
- Ćirić, V.; Manojlović, M.; Belić, M.; Nešić, L.; Seremešić, S. Effects of land use conversion on soil aggregate stability and organic carbon in different soils. Agrociencias 2013, 47, 539–552. Available online: https://agrociencia-colpos.org/index.php/agrociencia/article/view/1038/1038 (accessed on 25 July 2025).
- Holtz, R.D.; Baroutaji, A. Construction Materials: Soil and Natural Materials. In Reference Module in Materials Science and Materials Engineering; Elsevier: Amsterdam, The Netherlands, 2016. [Google Scholar] [CrossRef]
- Piyaruwan, H.I.G.S.; Jayasinghe, P.K.S.C.; Leelamanie, D.A.L. Water repellency in eucalyptus and pine plantation forest soils and its relation to groundwater levels estimated with multi-temporal modeling. J. Hydrol. Hydromech. 2020, 68, 382–391. [Google Scholar] [CrossRef]
- Priori, S.; Pellegrini, S.; Vignozzi, N.; Costantini, E.A. Soil physical-hydrological degradation in the root-zone of tree crops: Problems and solutions. Agronomy 2021, 11, 68. [Google Scholar] [CrossRef]
- Panagos, P.; De Rosa, D.; Liakos, L.; Labouyrie, M.; Borrelli, P.; Ballabio, C. Soil bulk density assessment in Europe. Agric. Ecosyst. Environ. 2024, 364, 108907. [Google Scholar] [CrossRef]
- Díaz, J.C. Relación espacial entre propiedades de suelos y estrés hídrico en caña de azúcar en la hacienda Churimal-Roldanillo-Valle del Cauca, Colombia. Suelos Ecuat. 2019, 49, 65–74. Available online: https://dialnet.unirioja.es/servlet/articulo?codigo=7831530 (accessed on 1 September 2025). [CrossRef]
- Li, D.; Shao, M.; Zhang, S.; Zhang, K. The dynamics of soil moisture balance components and their relations with the productivity of natural vegetation in an arid region of northwestern China. Ecol. Eng. 2020, 143, 105672. [Google Scholar] [CrossRef]
- Rasheed, M.W.; Tang, J.; Sarwar, A.; Shah, S.; Saddique, N.; Khan, M.U.; Khan, M.I.; Nawaz, S.; Shamshiri, R.R.; Aziz, M.; et al. Soil moisture measuring techniques and factors affecting the moisture dynamics: A comprehensive review. Sustainability 2022, 14, 11538. [Google Scholar] [CrossRef]
- Zhao, C.J.; Wu, Z.; Kang, M.Y.; Fan, W.B.; Lin, Z.; Zhuo, Z.Q. Variation of soil moisture content for Eucalyptus forests and its response to stand ages in Western Hainan. Acta Ecol. Sin. 2015, 35, 1734–1742. [Google Scholar] [CrossRef][Green Version]
- Daka, Y.S.; Geleta, Z.T. Effect of Eucalyptus Tree on Selected Soil Physico-Chemical Properties in Gidami District, West Ethiopia. Preprint 2023. [Google Scholar] [CrossRef]
- Christina, M.; Nouvellon, Y.; Laclau, J.P.; Stape, J.L.; Bouillet, J.P.; Lambais, G.R.; Le Maire, G. Importance of deep water uptake in tropical eucalypt forest. Funct. Ecol. 2017, 31, 509–519. [Google Scholar] [CrossRef]
- Chu, S.; Jacobs, D.F.; Sloan, J.L.; Xue, L.; Wu, D.; Zeng, S. Changes in soil properties under Eucalyptus relative to Pinus massoniana and natural broadleaved forests in South China. J. For. Res. 2018, 29, 1299–1306. [Google Scholar] [CrossRef]
- Indoria, A.K.; Sharma, K.L.; Reddy, K.S. Hydraulic properties of soil under warming climate. In Climate Change and Soil Interactions; Elsevier: Amsterdam, The Netherlands, 2020; pp. 473–508. [Google Scholar] [CrossRef]
- Earl, J. Soil Physics: Fact Sheet 9. Local Land Services, New South Wales 2020. Available online: https://www.lls.nsw.gov.au/__data/assets/pdf_file/0009/1270539/9-Soil-Physics_FINAL.pdf (accessed on 25 July 2025).
- Shaheb, M.R.; Venkatesh, R.; Shearer, S.A. A review on the effect of soil compaction and its management for sustainable crop production. J. Biosyst. Eng. 2021, 46, 417–439. [Google Scholar] [CrossRef]
- Medeiros, P.L.D.; Pimenta, A.S.; Miranda, N.D.O.; Melo, R.R.D.; Amorim, J.D.S.; Azevedo, T.K.B.D. The myth that eucalyptus trees deplete soil water—A review. Forests 2025, 16, 423. [Google Scholar] [CrossRef]
- Frene, J.P.; Pandey, B.K.; Castrillo, G. Under pressure: Elucidating soil compaction and its effect on soil functions. Plant Soil 2024, 502, 267–278. [Google Scholar] [CrossRef]
- Futa, B.; Gmitrowicz-Iwan, J.; Skersienė, A.; Šlepetienė, A.; Parašotas, I. Innovative soil management strategies for sustainable agriculture. Sustainability 2024, 16, 9481. [Google Scholar] [CrossRef]
- Zhang, S.; Li, L.; Zhu, Z.; Zhang, P. Spatial distribution and relationship between slope micro-topography changes and soil aggregate stability under rainfall conditions. Water 2024, 16, 648. [Google Scholar] [CrossRef]
- Wang, Y.; Xu, Y.; Yang, H.; Shen, H.; Zhao, L.; Zhu, B.; Wang, J.; Guo, L. Effect of slope shape on soil aggregate stability of slope farmland in black soil region. Front. Environ. Sci. 2023, 11, 1127043. [Google Scholar] [CrossRef]
- Bouslihim, Y.; Rochdi, A.; Aboutayeb, R.; El Amrani-Paaza, N.; Miftah, A.; Hssaini, L. Soil aggregate stability mapping using remote sensing and GIS-based machine learning technique. Front. Earth Sci. 2021, 9, 748859. [Google Scholar] [CrossRef]
- Gan, F.; Shi, H.; Gou, J.; Zhang, L.; Dai, Q.; Yan, Y. Responses of soil aggregate stability and soil erosion resistance to different bedrock strata dip and land use types in the karst trough valley of Southwest China. Int. Soil Water Conserv. Res. 2024, 12, 684–696. [Google Scholar] [CrossRef]
- Maffia, A.; Oliva, M.; Marra, F.; Mallamaci, C.; Nardi, S.; Muscolo, A. Humic substances: Bridging ecology and agriculture for a greener future. Agronomy 2025, 15, 410. [Google Scholar] [CrossRef]
- Zeraatpisheh, M.; Ayoubi, S.; Mirbagheri, Z.; Mosaddeghi, M.R.; Xu, M. Spatial prediction of soil aggregate stability and soil organic carbon in aggregate fractions using machine learning algorithms and environmental variables. Geoderma Reg. 2021, 27, e00440. [Google Scholar] [CrossRef]
- Ramezani, N.; Sayyad, G.A.; Barzegar, A.R. Tractor Wheel Compaction Effect on Soil Water Infiltration, Hydraulic Conductivity and Bulk Density. Malays. J. Soil Sci. 2017, 21, 47–61. Available online: https://www.msss.com.my/mjss/Full%20Text/vol21/4.Ramezani.pdf (accessed on 25 July 2025).
- Kim, K.; Gil, J.; Ostrom, N.E.; Gandhi, H.; Oerther, M.S.; Kuzyakov, Y.; Guber, A.K.; Kravchenko, A.N. Soil pore architecture and rhizosphere legacy define N2O production in root detritusphere. Soil Biol. Biochem. 2022, 166, 108565. [Google Scholar] [CrossRef]
- Steponavičienė, V.; Bogužas, V.; Sinkevičienė, A.; Skinulienė, L.; Vaisvalavičius, R.; Sinkevičius, A. Soil water capacity, pore size distribution, and CO2 emission in different soil tillage systems and straw retention. Plants 2022, 11, 614. [Google Scholar] [CrossRef] [PubMed]
- Jarvis, N.; Coucheney, E.; Lewan, E.; Klöffel, T.; Meurer, K.H.; Keller, T.; Larsbo, M. Interactions between Soil Structure Dynamics, Hydrological Processes, and Organic Matter Cycling: A New Soil-Crop Model. Eur. J. Soil Sci. 2024, 75, e13455. [Google Scholar] [CrossRef]
| Parameter | Equation | Units |
|---|---|---|
| Bulk density | g cm−3 | |
| Particle density | g cm−3 | |
| Volumetric water content | % | |
| Gravimetric water content | % | |
| Porosity | % | |
| Aeration | % | |
| Mean weight diameter | mm | |
| Geometric mean diameter | mm | |
| Structural coefficient of soil | --- |
| Parameter | Dense Forest (n = 24) | Mosaic of Grasses and Crops (n = 31) | Weedy Pastures (n = 23) | Mosaic of Crops (n = 19) |
|---|---|---|---|---|
| Ksat | 0.2580 a | 0.3251 a | 0.2143 a | 0.1574 a |
| ρb | 1.2542 a | 1.2439 a | 1.2987 a | 1.2305 a |
| ρs | 2.2204 a | 2.1584 a | 2.2230 a | 2.2211 a |
| θV | 15.2738 a | 16.9739 a | 18.7583 a | 16.1495 a |
| θg | 12.1417 a | 13.6942 a | 14.7243 a | 13.0442 a |
| ft | 43.4146 a | 42.2723 a | 41.6083 a | 44.7216 a |
| Aeration | 28.1392 a | 25.2977 a | 22.8513 a | 28.5705 a |
| MWD | 2.2581 a | 2.5434 a | 2.7451 a | 2.2498 a |
| GMD | 1.4383 a | 1.5766 a | 1.7394 a | 1.3563 a |
| Ks | 10.9850 a | 10.6387 a | 13.2048 a | 9.0968 a |
| Parameter | Unit | Mean | Median | Min. | Max. | Skewness | Kurtosis | CV (%) | N |
|---|---|---|---|---|---|---|---|---|---|
| Ksat | m day−1 | 0.249 | 0.155 | 0.001 | 1.014 | 1.341 | 1.070 | 104.49 | ns |
| ρb | g cm−3 | 1.257 | 1.260 | 0.960 | 1.540 | −0.064 | −0.634 | 11.30 | * |
| ρs | g cm−3 | 2.201 | 2.220 | 2.000 | 2.440 | −0.074 | −0.793 | 5.85 | ns |
| θV | % | 16.815 | 16.200 | 5.180 | 30.510 | 0.286 | 0.023 | 30.78 | * |
| θg | % | 13.427 | 13.170 | 3.990 | 23.410 | 0.189 | −0.040 | 29.70 | * |
| ft | % | 42.877 | 43.760 | 26.120 | 52.130 | −0.509 | −0.440 | 14.27 | ns |
| Aeration | % | 26.062 | 26.550 | 8.450 | 45.010 | −0.182 | −0.805 | 35.21 | * |
| MWD | mm | 2.463 | 2.473 | 0.640 | 4.028 | −0.195 | −0.362 | 31.54 | * |
| GMD | mm | 1.538 | 1.423 | 0.353 | 3.048 | 0.333 | −0.222 | 38.72 | * |
| Ks | --- | 11.031 | 9.930 | 1.060 | 26.920 | 0.781 | −0.121 | 60.54 | ns |
| Parameter | Model | Nugget (C0) | Sill (C + C0) | Range (m) | SDL (C0/C + C0) | Interpolation Method | r2 |
|---|---|---|---|---|---|---|---|
| Ksat | Spherical | 0.0046 | 0.072 | 98 | 0.064 | Kriging | 0.682 |
| ρb | Linear | 0.0166 | 0.022 | 379 | 0.755 | IDW | 0.726 |
| ρs | Linear | 0.0148 | 0.017 | 379 | 0.873 | IDW | −0.192 |
| θV | Exponential | 5.47 | 16.24 | 214 | 0.337 | IDW | 0.998 |
| θg | Exponential | 2.66 | 27.5 | 154 | 0.097 | IDW | 0.939 |
| ft | Exponential | 5.10 | 39.4 | 207 | 0.129 | IDW | 0.858 |
| Aeration | Exponential | 10.1 | 88.01 | 195 | 0.115 | IDW | 0.987 |
| MWD | Linear | 0.434 | 0.641 | 379 | 0.677 | IDW | 0.832 |
| GMD | Linear | 0.260 | 0.386 | 379 | 0.674 | IDW | 0.797 |
| Ks | Gaussian | 24.59 | 49.19 | 470 | 0.499 | Kriging | 0.940 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Álvarez-Herrera, J.G.; Jaime-Guerrero, M.; Fernández-Pérez, C.J. Spatial Variability and Geostatistical Modeling of Soil Physical Properties Under Eucalyptus globulus Plantations. Geomatics 2025, 5, 41. https://doi.org/10.3390/geomatics5030041
Álvarez-Herrera JG, Jaime-Guerrero M, Fernández-Pérez CJ. Spatial Variability and Geostatistical Modeling of Soil Physical Properties Under Eucalyptus globulus Plantations. Geomatics. 2025; 5(3):41. https://doi.org/10.3390/geomatics5030041
Chicago/Turabian StyleÁlvarez-Herrera, Javier Giovanni, Marilcen Jaime-Guerrero, and Carlos Julio Fernández-Pérez. 2025. "Spatial Variability and Geostatistical Modeling of Soil Physical Properties Under Eucalyptus globulus Plantations" Geomatics 5, no. 3: 41. https://doi.org/10.3390/geomatics5030041
APA StyleÁlvarez-Herrera, J. G., Jaime-Guerrero, M., & Fernández-Pérez, C. J. (2025). Spatial Variability and Geostatistical Modeling of Soil Physical Properties Under Eucalyptus globulus Plantations. Geomatics, 5(3), 41. https://doi.org/10.3390/geomatics5030041






