Analytical Method for Modifying Compound Curves on Railway Lines

Abstract

The aim of the research presented in the article is to develop a method for modifying compound curves, i.e., geometric systems composed of two (or more) circular arcs with different radii, directed in the same direction and directly connected to each other. These curves are used when connecting two directions of the railway route where one circular arc is impossible due to permanent terrain obstacles. To solve the problem, an analytical method of designing track geometric systems was used, in which individual elements of these systems are described using mathematical equations. The modification itself involves introducing appropriate transition curves between the connecting arcs. Three possibilities for such a connection were presented, resulting from the method of considering conditions related to horizontal curvature of the track axis. A comparative analysis of the obtained solutions was conducted using the developed geometric test system. The analysis was based on the curvature values determined for the considered transition curves, after assuming varying lengths of these curves. For the recommended solution to the problem, it was necessary to verify the practical feasibility of horizontal ordinate values, which could not be too small relative to the implementation error. As stated, to limit the effects of this error, the transition curve lengths should be adjusted to specific geometric situations and excessively short curves should be avoided. As a result of the conducted research, the transition curve determined with strict curvature conditions was determined to be the most advantageous. It maintains curvature continuity along its entire length, there are no abrupt changes in curvature at the edges, and the changes in curvature along the length are much smoother than in the other curves considered. Therefore, this curve should be recommended for practical use.

1. Introduction

The field of railways has a very long history. Currently, the greatest interest is focused on high-speed railways (e.g., [1,2,3,4,5]). Numerous studies are also conducted on rolling stock and its maintenance (e.g., [6,7,8,9]). In the field of railway superstructure, the issue of interactions between the system rail vehicle—railway track is being developed on a large scale (e.g., [10,11,12,13,14,15]).

When it comes to track geometry, numerous simplifying assumptions have been introduced into design methodology over the decades. This was primarily due to limited computational capabilities. Progress in this field in the second half of the 20th century radically changed this situation and led to the development of computational algorithms that strictly correspond to a specific geometric situation. Currently, the development of design documentation in the field of railways is carried out using commercial computer software [16,17].

At the same time, for some time now one can get the impression that conducting research on the methodology of designing track geometric layouts is of lesser importance. Work in this field is, of course, conducted [18,19,20,21], but its scope is often limited to specific issues, such as transition curves [22,23,24,25] or railway turnouts [26,27,28,29].

Although high-speed railways are currently attracting the most attention, traditional railways, which were most often built in the 19th century, still dominate in terms of length. They are still in operation today, one may get the impression that they are disappearing from the field of research interest, and yet they should be modernized, adapting them to contemporary requirements. This remark applies especially to railway lines running in difficult terrain conditions (e.g., in mountainous terrain), which often feature such specific geometrical arrangements as compound curves and reverse curves. Improving the quality of these lines, leading to an increase in travel speed, requires appropriate modernization activities.

This article is a continuation of the study [30] and deals with the issue of designing modifications of compound curves, i.e., geometric systems consisting of two successive circular arches of different radii, directed in the same direction and directly connected to each other. Compound curves are currently used on tram lines. They were used on railways until the middle of the last century; then they were basically not made there anymore. However, those built earlier still exist on many railway lines, creating specific operational problems caused by the rapid changes in curvature that occur on them. They were also less affected by the progress in computational technology that occurred later. From a scientific point of view, the interest in the discussed problem is limited, and selected practical aspects of the issue are rather exposed [31].

In relation to railway lines, the first step is to be able to recreate (i.e., model) the existing geometric layout with compound curves, so that it is then possible to correct the horizontal ordinates in the area where the circular arches connect. For this purpose, it was necessary to develop an effective method for designing such a layout, which, however, by definition, will not be used to determine the coordinates of a new compound curve, but to model the existing layout with a view to its later modification.

In [30], an analytical method of modeling compound curves on railway lines was presented. In this method, individual elements of the discussed geometric systems are described using mathematical equations [32]. Its final effect is a set of horizontal coordinates in the appropriate global system (in Poland—in relation to flat coordinates—it is the national spatial reference system PL-2000 [33]). The actual design is carried out in the appropriate local Cartesian coordinate system, which is based on symmetrically set neighboring main directions of the route. In order to obtain such a setting of main directions, an appropriate transformation (i.e., shift and rotation) of the global system must be performed. The origin of the local coordinate system is located at the point of intersection of both main directions, whose Cartesian coordinates in the global system are known.

2. Compound Curve Modeling Procedure

Design activities carried out in the global rectangular coordinate system, i.e., creating a polygon of the main directions of the route and determining the mathematical equations of these directions, the coordinates of their intersection points (i.e., the main points W) and the angles of return, were presented in [30]. This work also explains the method of creating a local coordinate system for a given area of changing the route direction, which consists of shifting the origin of the global system to the point of intersection of two adjacent main directions (i.e., the point with coordinates Y_W, X_W), and then rotating the shifted system by such an angle β as to obtain a symmetrical setting of the main directions in the local coordinate system x, y.

It should be noted that the setting of the main directions of the route in the PL-2000 system can be very diverse. However, after the transformation to the local coordinate system, there are only two possibilities for the location of the designed geometric system: under the x axis, with negative ordinates and the convexity of the curvilinear elements directed upwards, and above the x axis, with positive ordinates and the convexity of the curvilinear elements directed downwards. Therefore, when determining the appropriate calculation algorithms, two possible cases had to be taken into account:

• Case I—for a geometric system located below the W vertex and resulting negative ordinates, and
• Case II—for a geometric system located above the W vertex and resulting positive ordinates.

In [30], when determining the formulas for the coordinates of characteristic points in the local coordinate system, both possible cases were taken into account. The design of the geometric system is carried out in several stages.

In order to be able to operate in the local coordinate system, it is necessary to first perform an auxiliary procedure, the purpose of which is to determine the basic calculation quantities. These quantities concern the regions of the geometric system connecting the ends of the extreme straight segments (i.e., the beginnings of the transition curves) with the connection point of both circular arcs. This refers to the lengths of the projections of both transition curves and circular arcs on the horizontal and vertical axis. The determined coordinates of the connection point of the circular arcs with each other are of key importance from the point of view of further actions.

Based on the above-mentioned calculation values, the connection of both existing horizontal arcs is carried out, first realized in the appropriate auxiliary system and then transferred to the local system. In [30] a set of formulas for the coordinates of characteristic points and formulas for determining the coordinates of the geometric system between these points is presented.

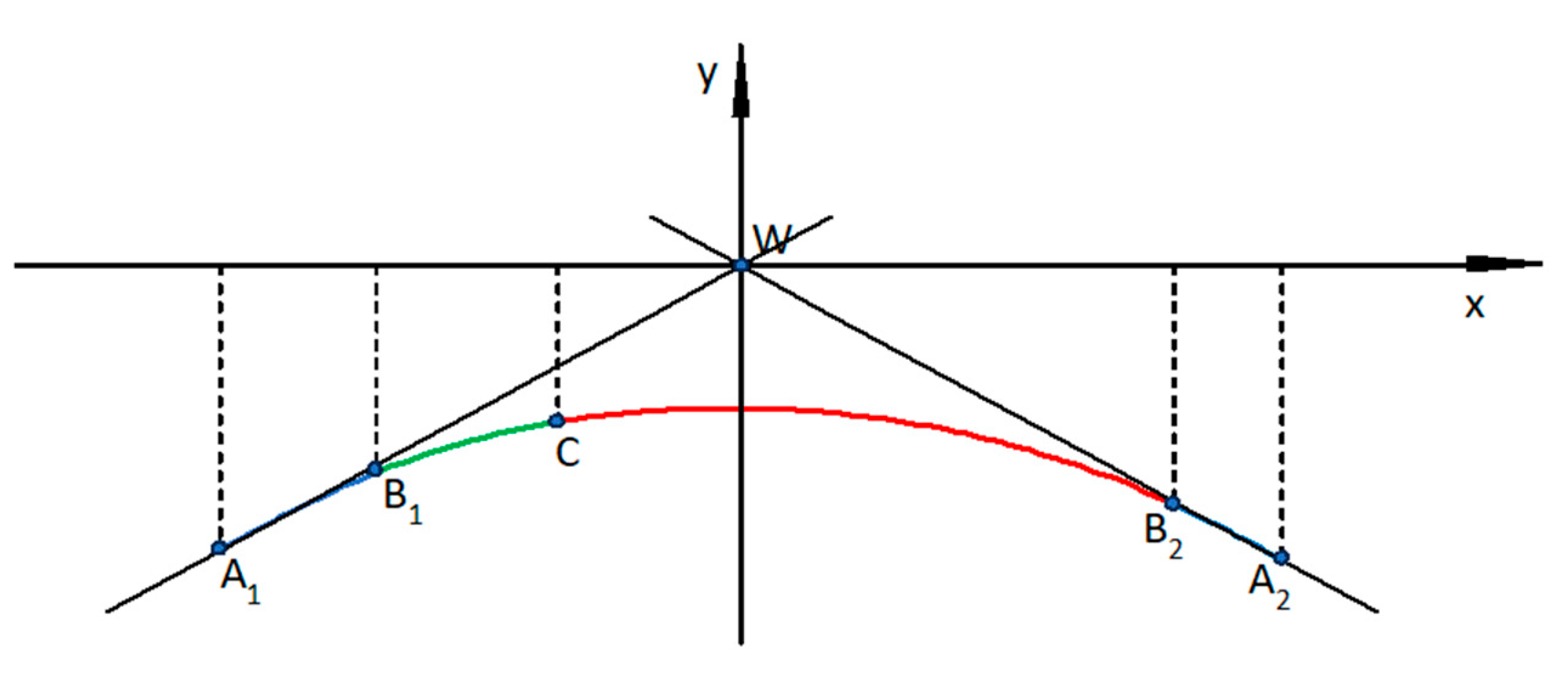
As a result of the design procedure, an appropriate geometric system is obtained in the local coordinate system. Figure 1 shows an example of such a system, in this case located under the x axis. In this figure, the first circular arc B₁C is marked in green, the second circular arc CB₂ in red, and the transition curves A₁B₁ and A₂B₂ in blue.

The designations of the characteristic points are as follows: A₁—assumed beginning of the geometric system (beginning of the first transition curve), B₁—end of the first transition curve, C—designated connection of both circular arcs, B₂—end of the second transition curve, A₂—end of the geometric system (beginning of the second transition curve). In this situation, between points A₁ and B₁ in Figure 1 there is a transition curve TC1, and between points A₂ and B₂ there is a transition curve TC2. These curves are related—respectively—to circular arcs CA1 (between points B₁ and C) and CA2 (between points C and B₂).

Finally, the obtained solution is transferred to the PL-2000 system using the transformation formulas given in [34].

3. Method of Modifying the Compound Curve

3.1. The Idea of Solving the Given Problem

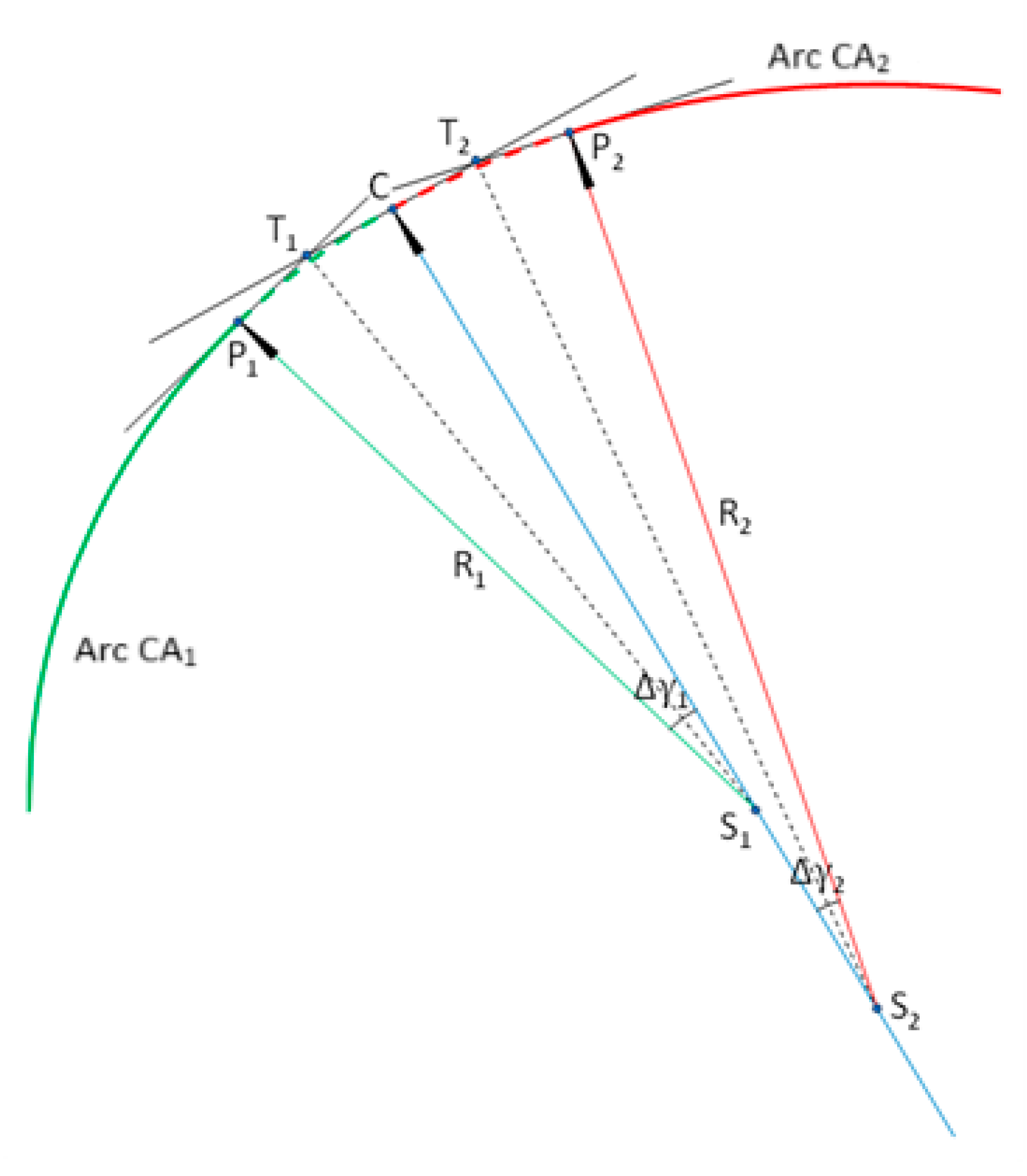
The modification of the compound curve consists of eliminating the direct connection of both horizontal arches by introducing an appropriate transition curve between them. It is marked as curve TC3 and will be located in the area of the connection of both circular arches (i.e., point C). The minimum length of this curve should meet the applicable kinematic conditions. After adopting the length l₃, the coordinates of the extreme points of the transition curve (i.e., points P₁ and P₂) should be determined (Figure 2).

The starting point P₁ is located on the arc CA1, at a distance of l₃/2 from point C. The ending point P₂ is located on the arc CA2, at the same distance from point C. Unfortunately, at this stage we do not yet know the equation of the transition curve, so when determining the coordinates of points P₁ and P₂ we must assume that the lengths l₃/2 also apply to the contacting segments of horizontal arcs (which are deleted). In the next stage, in the vacant space, between points P₁ and P₂, we should insert the curve TC3, determining its form based on the appropriate differential equations (when the required boundary conditions are met).

3.2. Determination of the Position of the Extreme Points of the Transition Curve TC3

To determine the coordinates of points P₁ and P₂, we must first determine the coordinates of the centers of both connected circular arcs in the local coordinate system. This is done using the knowledge of the calculation parameters of point C—the abscissa x_C, the ordinate y_C and the inclination of the tangent s_C [30]. The centers of both arcs (points S₁ and S₂)) lie on the line perpendicular to the tangent at point C, at distances R₁ and R₂ from this point (Figure 2). The corresponding formulas are presented in

Table 1. List of formulas for the coordinates of the centers of connected circular arcs.

Tangent	Case I	Case II
	$x_{S1}=x_C+{\displaystyle \frac{s_C}{\sqrt{1+s_C^2}}}{R}_1$	$x_{S1}=x_C-{\displaystyle \frac{s_C}{\sqrt{1+s_C^2}}}{R}_1$
sC > 0	$y_{S1}=y_C-{\displaystyle \frac{1}{\sqrt{1+s_C^2}}}{R}_1$	$y_{S1}=y_C+{\displaystyle \frac{1}{\sqrt{1+s_C^2}}}{R}_1$
	$x_{S2}=x_C+{\displaystyle \frac{s_C}{\sqrt{1+s_C^2}}}{R}_2$	$x_{S2}=x_C-{\displaystyle \frac{s_C}{\sqrt{1+s_C^2}}}{R}_2$
	$y_{S2}=y_C-{\displaystyle \frac{1}{\sqrt{1+s_C^2}}}{R}_2$	$y_{S2}=y_C+{\displaystyle \frac{1}{\sqrt{1+s_C^2}}}{R}_2$
	$x_{S1}=x_C-{\displaystyle \frac{s_C}{\sqrt{1+s_C^2}}}{R}_1$	$x_{S1}=x_C+{\displaystyle \frac{s_C}{\sqrt{1+s_C^2}}}{R}_1$
sC < 0	$y_{S1}=y_C-{\displaystyle \frac{1}{\sqrt{1+s_C^2}}}{R}_1$	$y_{S1}=y_C+{\displaystyle \frac{1}{\sqrt{1+s_C^2}}}{R}_1$
	$x_{S2}=x_C-{\displaystyle \frac{s_C}{\sqrt{1+s_C^2}}}{R}_2$	$x_{S2}=x_C+{\displaystyle \frac{s_C}{\sqrt{1+s_C^2}}}{R}_2$
	$y_{S2}=y_C-{\displaystyle \frac{1}{\sqrt{1+s_C^2}}}{R}_2$	$y_{S2}=y_C+{\displaystyle \frac{1}{\sqrt{1+s_C^2}}}{R}_2$

. In the formulas for the abscissa values, the sign of the inclination of the tangent s_C plays an important role.

When determining the position of point P₁, the central angle $\Delta {\gamma }_1$ plays a decisive role. It is for this point

$$\Delta {\gamma }_1={\displaystyle \frac{l_3}{2R_1}}$$

(1)

and for point P₂

$$\Delta {\gamma }_2={\displaystyle \frac{l_3}{2R_2}}$$

(2)

These angles are shown in Figure 2 for Case I, with s_C > 0. The values of the angles Δγ₁ and Δγ₂ directly result in the slopes of the tangent at points P₁ and P₂. For Case I, they are

$$s_{P1}=\tan \left(\arctan s_C+\Delta {\gamma }_1\right),$$

(3)

$$s_{P2}=\tan \left(\arctan s_C-\Delta {\gamma }_2\right).$$

(4)

and for Case II

$$s_{P1}=\tan \left(\arctan s_C-\Delta {\gamma }_1\right),$$

(5)

$$s_{P2}=\tan \left(\arctan s_C+\Delta {\gamma }_2\right).$$

(6)

When determining the coordinates of points P₁ and P₂, the sign of the inclination of the tangent at point C plays an important role. Knowing the coordinates of this point and the coordinates of the centers of both circular arcs, the coordinates of points T₁ and T₂ are first determined (Figure 2). After determining them, it is possible to determine formulas for the coordinates of the beginning and end of the transition curve. They have the same form for Case I and Case II. A list of these formulas is provided in

Table 2. List of formulas for the coordinates of the beginning and end of the transition curve TC3.

Tangent sC > 0	Tangent sC < 0
$x_{P1}=x_C-\left({\displaystyle \frac{1}{\sqrt{1+s_C^2}}}+{\displaystyle \frac{1}{\sqrt{1+s_{P1}^2}}}\right)R_1\cdot \tan {\displaystyle \frac{\Delta {\gamma }_1}{2}}$	$x_{P1}=x_C-\left({\displaystyle \frac{1}{\sqrt{1+s_C^2}}}+{\displaystyle \frac{1}{\sqrt{1+s_{P1}^2}}}\right)R_1\cdot \tan {\displaystyle \frac{\Delta {\gamma }_1}{2}}$
$y_{P1}=y_C-\left({\displaystyle \frac{s_C}{\sqrt{1+s_C^2}}}+{\displaystyle \frac{s_{P1}}{\sqrt{1+s_{P1}^2}}}\right)R_1\cdot \tan {\displaystyle \frac{\Delta {\gamma }_1}{2}}$	$y_{P1}=y_C+\left({\displaystyle \frac{s_C}{\sqrt{1+s_C^2}}}+{\displaystyle \frac{s_{P1}}{\sqrt{1+s_{P1}^2}}}\right)R_1\cdot \tan {\displaystyle \frac{\Delta {\gamma }_1}{2}}$
$x_{P2}=x_C+\left({\displaystyle \frac{1}{\sqrt{1+s_C^2}}}+{\displaystyle \frac{1}{\sqrt{1+s_{P2}^2}}}\right)R_2\cdot \tan {\displaystyle \frac{\Delta {\gamma }_2}{2}}$	$x_{P2}=x_C+\left({\displaystyle \frac{1}{\sqrt{1+s_C^2}}}+{\displaystyle \frac{1}{\sqrt{1+s_{P2}^2}}}\right)R_2\cdot \tan {\displaystyle \frac{\Delta {\gamma }_2}{2}}$
$y_{P2}=y_C+\left({\displaystyle \frac{s_C}{\sqrt{1+s_C^2}}}+{\displaystyle \frac{s_{P2}}{\sqrt{1+s_{P2}^2}}}\right)R_2\cdot \tan {\displaystyle \frac{\Delta {\gamma }_2}{2}}$	$y_{P2}=y_C-\left({\displaystyle \frac{s_C}{\sqrt{1+s_C^2}}}+{\displaystyle \frac{s_{P2}}{\sqrt{1+s_{P2}^2}}}\right)R_2\cdot \tan {\displaystyle \frac{\Delta {\gamma }_2}{2}}$

.

The equation of the linear curvature κ(l) on the TC3 transition curve would be:

$$\kappa (l)={\displaystyle \frac{1}{R_1}}+{\displaystyle \frac{1}{l_3}}\left({\displaystyle \frac{1}{R_2}}-{\displaystyle \frac{1}{R_1}}\right)\cdot l,\cdots l\in 〈0,l_3〉$$

and the parametric equations of the curve were described by the formulas given in [35]:

$$x(l)=l-{\displaystyle \frac{1}{6R_1^2}}{l}^3-{\displaystyle \frac{1}{8R_1{l}_3}}\left({\displaystyle \frac{1}{R_2}}-{\displaystyle \frac{1}{R_1}}\right)l^4+\left[{\displaystyle \frac{1}{120R_1^4}}-{\displaystyle \frac{1}{40l_3^2}}({\displaystyle \frac{1}{R_2}}-{\displaystyle \frac{1}{R_1}}{)}^2\right]l^5+{\displaystyle \frac{1}{72R_1^3{l}_3}}\left({\displaystyle \frac{1}{R_2}}-{\displaystyle \frac{1}{R_1}}\right)l^6-\dots$$

$$y(l)={\displaystyle \frac{1}{2R_1}}{l}^2+{\displaystyle \frac{1}{6l_3}}\left({\displaystyle \frac{1}{R_2}}-{\displaystyle \frac{1}{R_1}}\right)l^3-{\displaystyle \frac{1}{24R_1^3}}{l}^4-{\displaystyle \frac{1}{20R_1^2{l}_3}}\left({\displaystyle \frac{1}{R_2}}-{\displaystyle \frac{1}{R_1}}\right)l^5+\left[{\displaystyle \frac{1}{720R_1^5}}-{\displaystyle \frac{1}{48R_1{l}_3^2}}({\displaystyle \frac{1}{R_2}}-{\displaystyle \frac{1}{R_1}}{)}^2\right]l^6+\dots$$

However, there is a serious problem: we know the Cartesian coordinates of the connected points, but we do not know the transition curve corresponding to the length l₃, because the coordinates of points P₁ and P₂ were determined along a circular arc. Moreover, the parametric equations of the curve, determined in the manner given in [35], would not take into account the conditions of tangency at the initial and final points, which plays a key role in the case under consideration. Therefore, the problem should be solved by omitting the equation of the curvature κ(l), determining the coordinates y(x) of the transition curve directly. Since the curvature κ(l) will not constitute the initial basis, the adopted procedure may in some situations result in certain disturbances in the obtained curvature graph.

4. Determination of the TC3 Transition Curve

The introduction of a transition curve aims to smoothly connect adjacent geometric elements, which in this case are two congruent circular arcs with radii R₁ and R₂. The goal here is not only to ensure continuity of the connection but also to achieve a smooth change in curvature (ideally, it should be monotonic along the entire length of the curve). From the perspective of rail vehicle dynamics, the shape of the transition curve (i.e., the class of the function describing the curvature) and its length (the generated dynamic interactions decrease with increasing curve length) play a significant role.

The transition curve sought connects points P₁ and P₂, whose coordinates are defined by the formulas given in Table 2. The values of the tangent slope at these points are also known, determined using Formulas (3) and (4) or (5) and (6). In order to simplify the procedure of determining the transition curve, an auxiliary coordinate system $\overline{x}$,$\overline{y}$ was introduced, in which $\overline{x}=x-x_{P1}$, $\overline{y}=y-y_{P1}$. Additional symbols were also added: $\Delta \overline{x}=x_{P2}-x_{P1}=L$ and $\Delta \overline{y}=y_{P2}-y_{P1}$; this means that $\overline{x}\in 〈0,\Delta \overline{x}〉$ and $\overline{y}\in 〈0,\Delta \overline{y}〉$. The effects of using the determined equations of the transition curve will be analyzed in detail in the presented test geometric system. Inserting the transition curve into the local coordinate system x, y consists of taking into account the relations: $x=\overline{x}+x_{P1}$, $y=\overline{y}+y_{P1}$.

4.1. Transition Curve Determined Without Taking into Account Curvature Conditions

The elementary form of the transition curve (denoted as curve TC(a)) satisfies the following conditions:

$$\left\{\begin{array}{cc}\overline{y}(0)=0& \overline{y}(\Delta \overline{x})=\Delta \overline{y}\\ \overline{y}\prime (0)=s_{P1}& \overline{y}\prime (\Delta \overline{x})=s_{P2}\end{array}\right.$$

(7)

and the adopted differential equation

$${\overline{y}}^{(4)}(\overline{x})=0$$

(8)

The general solution of the differential problem (7), (8) is a third-degree polynomial

$$\overline{y}(\overline{x})=a_1\overline{x}+a_2{\overline{x}}^2+a_3{\overline{x}}^3$$

(9)

where

$$a_1=s_{P1}, a_2={\displaystyle \frac{3\cdot \Delta \overline{y}-(2s_{P1}+s_{P2})\cdot \Delta \overline{x}}{\Delta {\overline{x}}^2}}, a_3={\displaystyle \frac{(s_{P1}+s_{P2})\cdot \Delta \overline{x}-2\cdot \Delta \overline{y}}{\Delta {\overline{x}}^3}}$$

The general formula for the curvature of the determined curve is as follows:

$$\kappa (\overline{x})={\displaystyle \frac{\left|y″(\overline{x})\right|}{{\left\{\sqrt{1+{\left[y\prime (\overline{x})\right]}^2}\right\}}^3}},$$

(10)

where

$$\overline{y}\prime (\overline{x})=a_1+2a_2\overline{x}+3a_3{\overline{x}}^2,\overline{y}″(\overline{x})=2a_2+6a_3\overline{x}$$

4.2. Transition Curve with Simplified Curvature Conditions

Boundary conditions (7) do not include the curvature values at points P₁ and P₂. In order to take into account the curvature of the track axis to some extent, the approximate formula was used

$$\kappa (\overline{x})\approx \overline{y}″(\overline{x})$$

(11)

used in the past, among others, when determining the equations of transition curves on railway lines [36]. This allowed the extension of conditions (7) to the following form:

$$\left\{\begin{array}{cc}\overline{y}(0)=0& \overline{y}(\Delta \overline{x})=\Delta \overline{y}\\ \overline{y}\prime (0)=s_{P1}& \overline{y}\prime (\Delta \overline{x})=s_{P2}\\ \overline{y}″(0)={\kappa }_{P1}& \overline{y}″(\Delta \overline{x})={\kappa }_{P2}\end{array}\right.$$

(12)

where κ_P1 = 1/R₁, κ_P2 = 1/R₂. In a given situation, the differential equation should be assumed

$${\overline{y}}^{(6)}(\overline{x})=0$$

(13)

The solution of the differential problem (12), (13) is a fifth-degree polynomial (denoted as the curve TC(b))

$$\overline{y}(\overline{x})=a_1\overline{x}+a_2{\overline{x}}^2+a_3{\overline{x}}^3+a_4{\overline{x}}^4+a_5{\overline{x}}^5,$$

(14)

where

$$a_1=s_{P1}, a_2={\displaystyle \frac{{\kappa }_{P1}}{2}}$$

$$a_3={\displaystyle \frac{20\cdot \Delta \overline{y}-(12\cdot s_{P1}+8\cdot s_{P2})\cdot \Delta \overline{x}-\left(3\cdot {\kappa }_{P1}-{\kappa }_{P2}\right)\cdot \Delta {\overline{x}}^2}{2\cdot \Delta {\overline{x}}^3}}$$

$$a_4={\displaystyle \frac{(16\cdot s_{P1}+14\cdot s_{P2})\cdot \Delta \overline{x}+\left(3\cdot {\kappa }_{P1}-2\cdot {\kappa }_{P2}\right)\cdot \Delta {\overline{x}}^2-30\cdot \Delta \overline{y}}{2\cdot \Delta {\overline{x}}^4}}$$

$$a_5={\displaystyle \frac{12\cdot \Delta \overline{y}-6\cdot (s_{P1}+s_{P2})\cdot \Delta \overline{x}+\left({\kappa }_{P2}-{\kappa }_{P1}\right)\cdot \Delta {\overline{x}}^2}{2\cdot \Delta {\overline{x}}^5}}$$

To determine the curvature, use formula (10), inserting the values of the derivatives

$$\overline{y}\prime (\overline{x})=a_1+2a_2\overline{x}+3a_3{\overline{x}}^2+4a_4{\overline{x}}^3+5a_5{\overline{x}}^4, \overline{y}″(\overline{x})=2a_2+6a_3\overline{x}+12a_4{\overline{x}}^2+20a_5{\overline{x}}^3$$

4.3. Transition Curve with Strict Curvature Conditions

As it turns out, it is possible to use a strict formula for curvature in the considered design task. Based on formula (10), we can write that

$$y″(\overline{x})={\left\{\sqrt{1+{\left[y\prime (\overline{x})\right]}^2}\right\}}^3\kappa (\overline{x}).$$

At points P₁ and P₂ the values of $\kappa (\overline{x})$ and $y\prime (\overline{x})$ are known, which allows us to formulate strict conditions for the curvature. This leads to the correction of conditions (12); they take the form

$$\left\{\begin{array}{cc}\overline{y}(0)=0& \overline{y}(\Delta \overline{x})=\Delta \overline{y}\\ \overline{y}\prime (0)=s_{P1}& \overline{y}\prime (\Delta \overline{x})=s_{P2}\\ \overline{y}″(0)={\vartheta }_{P1}\cdot {\kappa }_{P1}& \overline{y}″(\Delta \overline{x})={\vartheta }_{P2}\cdot {\kappa }_{P2}\end{array}\right.$$

(15)

where

$${\vartheta }_{P1}={\left(\sqrt{1+s_{P1}^2}\right)}^3,{\vartheta }_{P2}=\left(\sqrt{1+s_{P2}^2}\right)$$

After solving the differential problem (13), (15), the general form of the transition curve (marked as the TC(c) curve) is obtained, written by Equation (14), where

$$a_1=s_{P1}, a_2={\displaystyle \frac{{\vartheta }_{P1}\cdot {\kappa }_{P1}}{2}}$$

$$a_3={\displaystyle \frac{20\cdot \Delta \overline{y}-(12\cdot s_{P1}+8\cdot s_{P2})\cdot \Delta \overline{x}-\left(3\cdot {\vartheta }_{P1}\cdot {\kappa }_{P1}-{\vartheta }_{P2}\cdot {\kappa }_{P2}\right)\cdot \Delta {\overline{x}}^2}{2\cdot \Delta {\overline{x}}^3}}$$

$$a_4={\displaystyle \frac{(16\cdot s_{P1}+14\cdot s_{P2})\cdot \Delta \overline{x}+\left(3\cdot {\kappa }_{P1}-2\cdot {\kappa }_{P2}\right)\cdot \Delta {\overline{x}}^2-30\cdot \Delta \overline{y}}{2\cdot \Delta {\overline{x}}^4}}$$

$$a_5={\displaystyle \frac{12\cdot \Delta \overline{y}-6\cdot (s_{P1}+s_{P2})\cdot \Delta \overline{x}+\left({\kappa }_{P2}-{\kappa }_{P1}\right)\cdot \Delta {\overline{x}}^2}{2\cdot \Delta {\overline{x}}^5}}$$

The curvature of the TC(c) curve is determined in a similar way as for the TC(b) curve.

5. Test Geometric System

The method of modifying the compound curve will be presented for the test geometric system shown in Figure 3. The assumed speed of trains on this system is V = 90 km/h. The compound curve is formed by two circular arches: the CA1 arch with radius R₁ = 450 m and the CA2 arch with radius R₂ = 600 m, together with the appropriate transition curves in the form of a clothoid: the TC1 curve with length l₁ = 115 m and the TC2 curve with length l₂ = 75 m. The coordinates of the centers of the existing circular arches are: x_S1 = −3.941 m, y_S1 = 507.321 m (for the CA1 arch) and x_S2 = −37.362 m, y_S2 = 653.550 m (for the CA2 arch). In a given situation, the modeled geometric system is located above the x axis (i.e., it is included in Case II).

Table 3. The values of the characteristic point parameters for the geometric system in the presented calculation example.

Parameter	Point A1	Point B1	Point C	Point B2	Point A2
Abscissa x [m]	−258.402	−153.681	96.319	198.774	266.420
Ordinate y [m]	130.286	82.964	68.632	01.971	134.328
Tangent s	−0.50420	−0.35286	0.22855	0.42811	0.50420

presents the parameter values of characteristic points.

The modification of the compound curve will concern the route area located before point C (in arc CA1) and after point C (in arc CA2). Therefore, it will be important to know the equations of both circular arcs. Arc CA1, for which $x\in 〈x_{B1},x_C〉$, is described by the equation

$$y(x)=y_{S1}-\sqrt{R_1^2-{\left(x-x_{S1}\right)}^2}$$

(16)

while the arc CA2, for which $x\in 〈x_C,x_{B2}〉$, is described by the equation

$$y(x)=y_{S2}-\sqrt{R_2^2-{\left(x-x_{S2}\right)}^2}$$

(17)

The transition curves with lengths l₃ = 40 m, 60 m, 80 m and 100 m will be subjected to a detailed analysis. Focusing on geometric aspects, dynamic effects, which decrease with increasing curve length, were not considered. The focus was on assessing the appropriate horizontal ordinates, or more precisely, the differences between these ordinates and the original state. This is related to the issue of feasibility, i.e., the accuracy of the corrected geometric layout.

Table 4. Coordinate values and slopes of the tangent for extreme points of transition curves.

Curve Length	l3 = 40 m	l3 = 60 m	l3 = 80 m	l3 = 100 m
xP1 [m]	76.730	66.872	56.980	47.058
yP1 [m]	64.611	62.927	61.464	60.220
sP1	0.182221	0.159349	0.136640	0.114067
xP2 [m]	115.730	125.386	134.988	144.542
yP2 [m]	73.412	76.044	78.837	81.789
sP2	0.263904	0.281811	0.299888	0.318147

gives the coordinates and tangent values of the corresponding points P₁ and P₂.

6. General Assessment of the Situation

In order to make a general assessment of the obtained solutions, the determined ordinates of the transition curves TC(a), TC(b) and TC(c) with length l₃ = 60 m were considered. As it turns out, on an uncontaminated scale the corresponding graphs basically coincide; moreover, this also applied to the removed sections of both circular arcs. Therefore, there is only one possibility to assess the situation: comparing the relative differences of the horizontal ordinates, with respect to the original state. 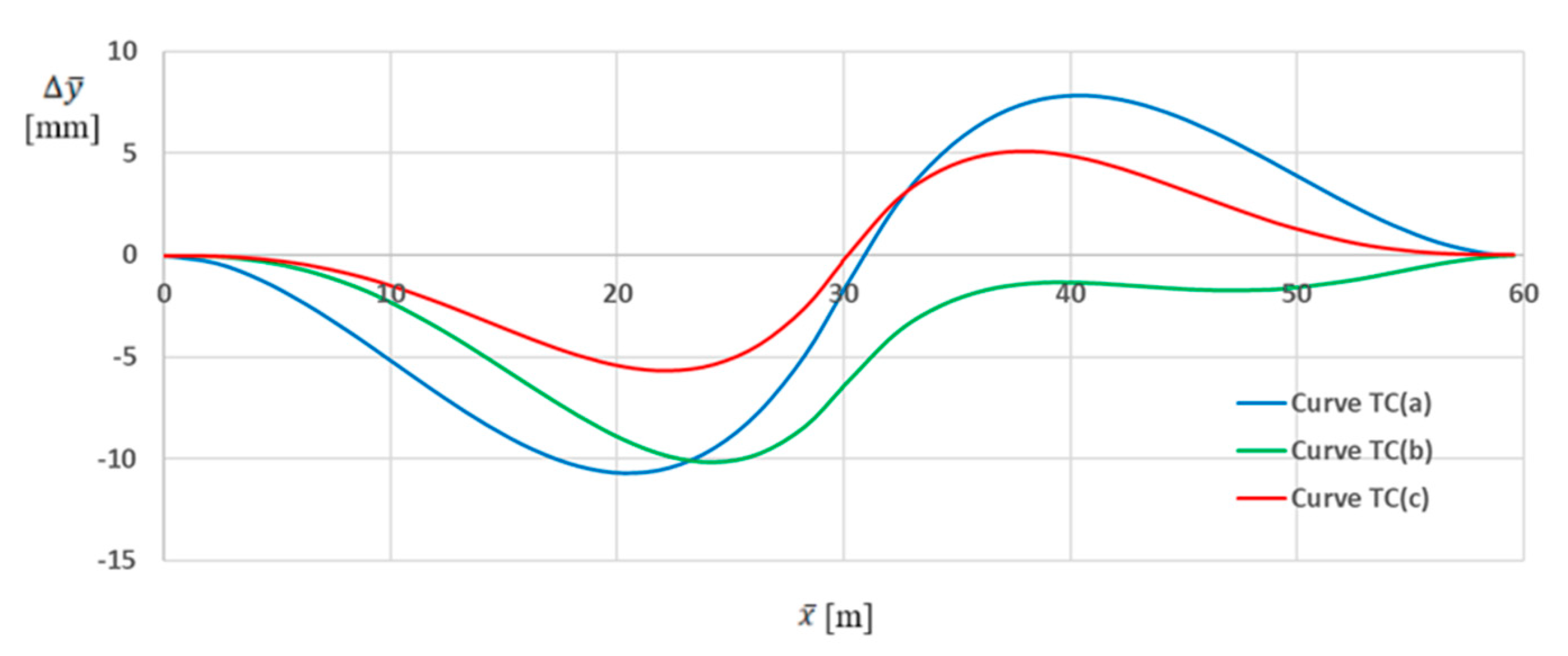Figure 4 shows the graphs $\Delta \overline{y}(\overline{x})$ for the considered transition curves.

As can be seen, the values $\Delta \overline{y}(\overline{x})$ for l₃ = 60 m are small, although their nature for the individual transition curves is different. The TC(a) curve deviates the most from the original shape in this situation (the difference is bilateral, in the range of $〈-11,+8〉$ mm). For the TC(b) curve, the difference is unilateral and reaches the order of 10 mm, while for the TC(c) curve, it is bilateral and in the range of $〈–6,+5〉$ mm. However, it would be difficult to draw final conclusions on this basis without checking the curvature that occurs. The corresponding graphs $\kappa (\overline{x})$ are shown in Figure 5. The black horizontal lines indicate the values of the constant curvature on the CA1 arc (left side) and the CA2 arc (right side).

The graphs in Figure 5 show that the matter is more complicated. Transition curves provide a change in curvature at the connection of circular arcs, but this does not always happen smoothly. The abrupt changes in curvature in the initial and/or final regions question the usefulness of using some transition curves. This will be discussed in detail for individual curves.

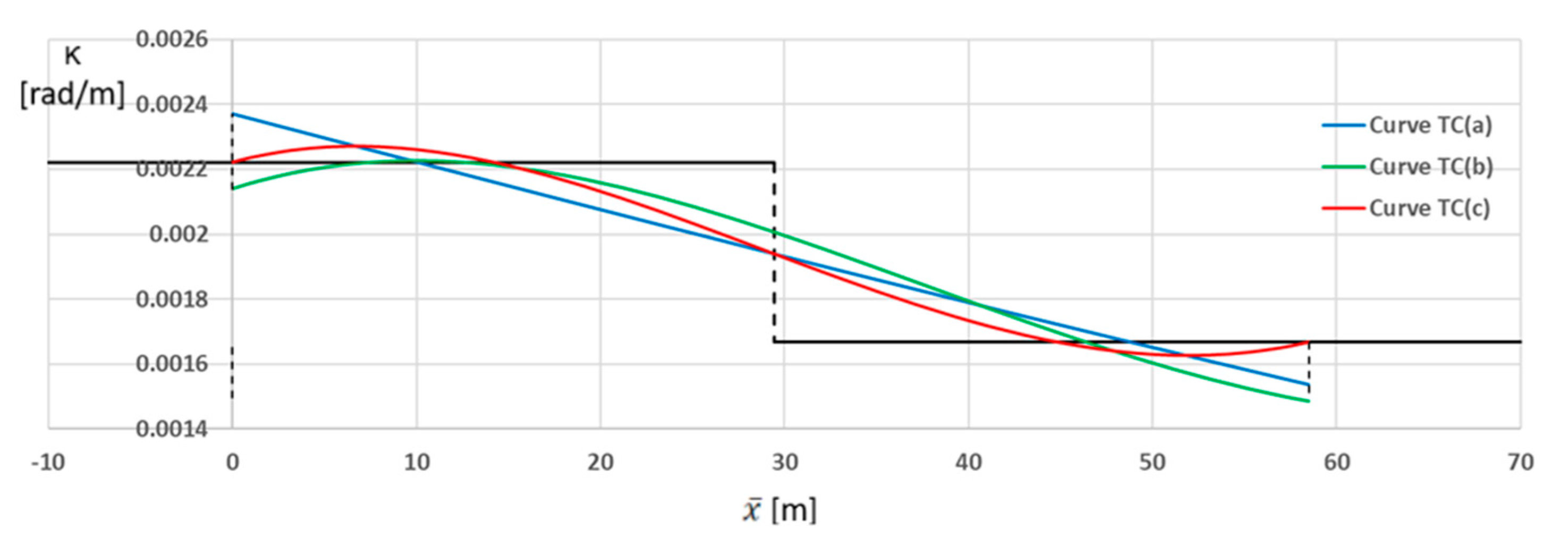
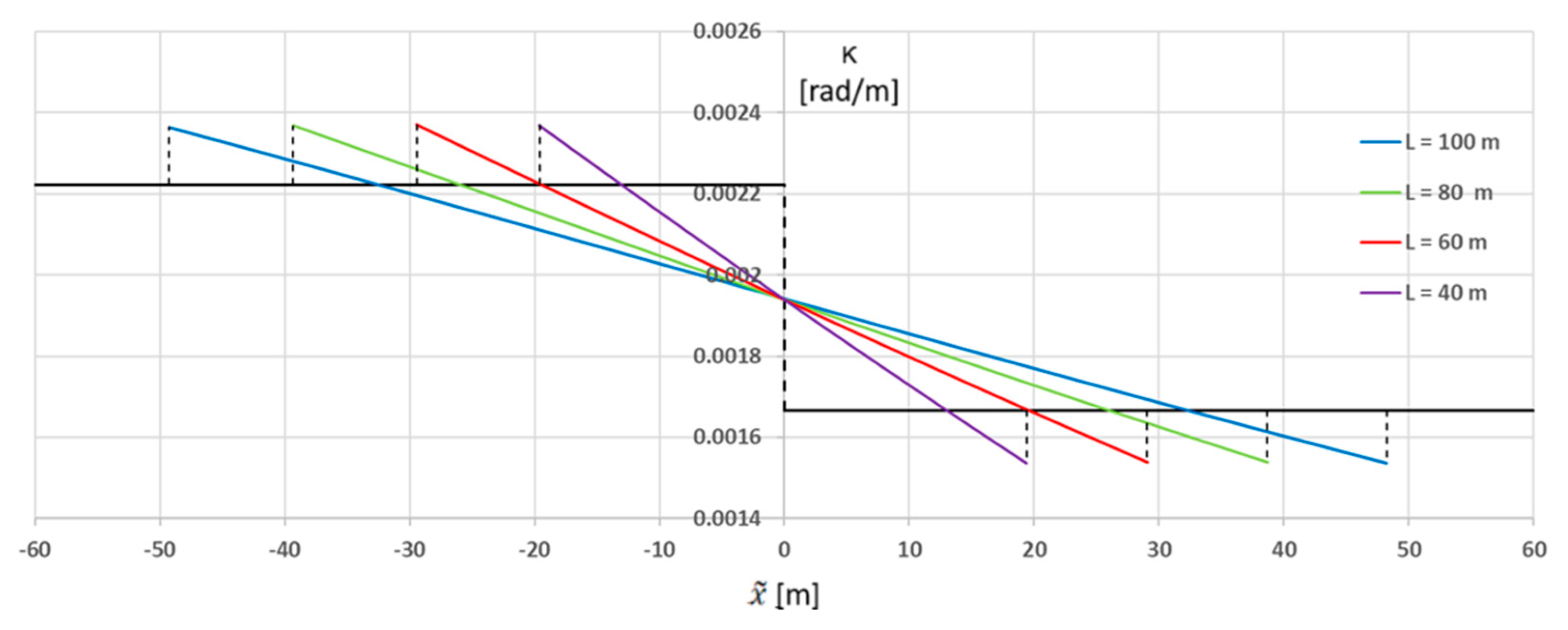
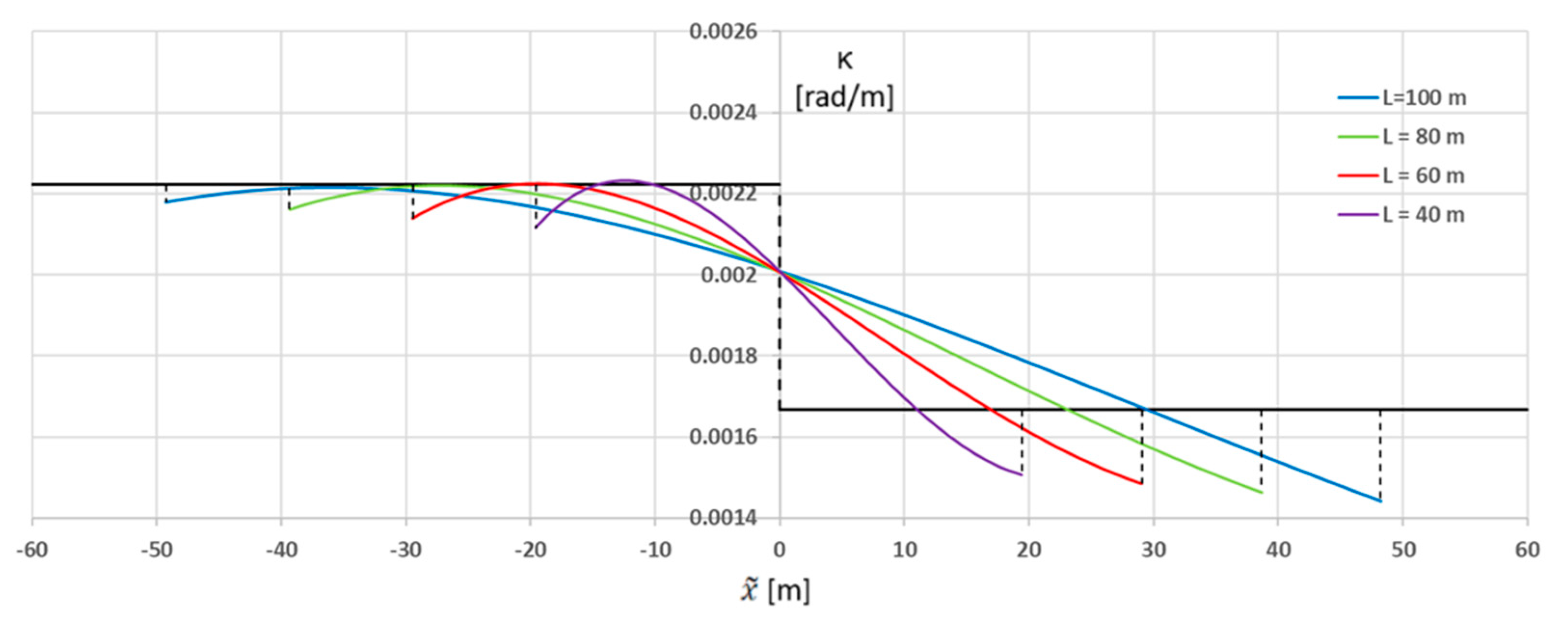
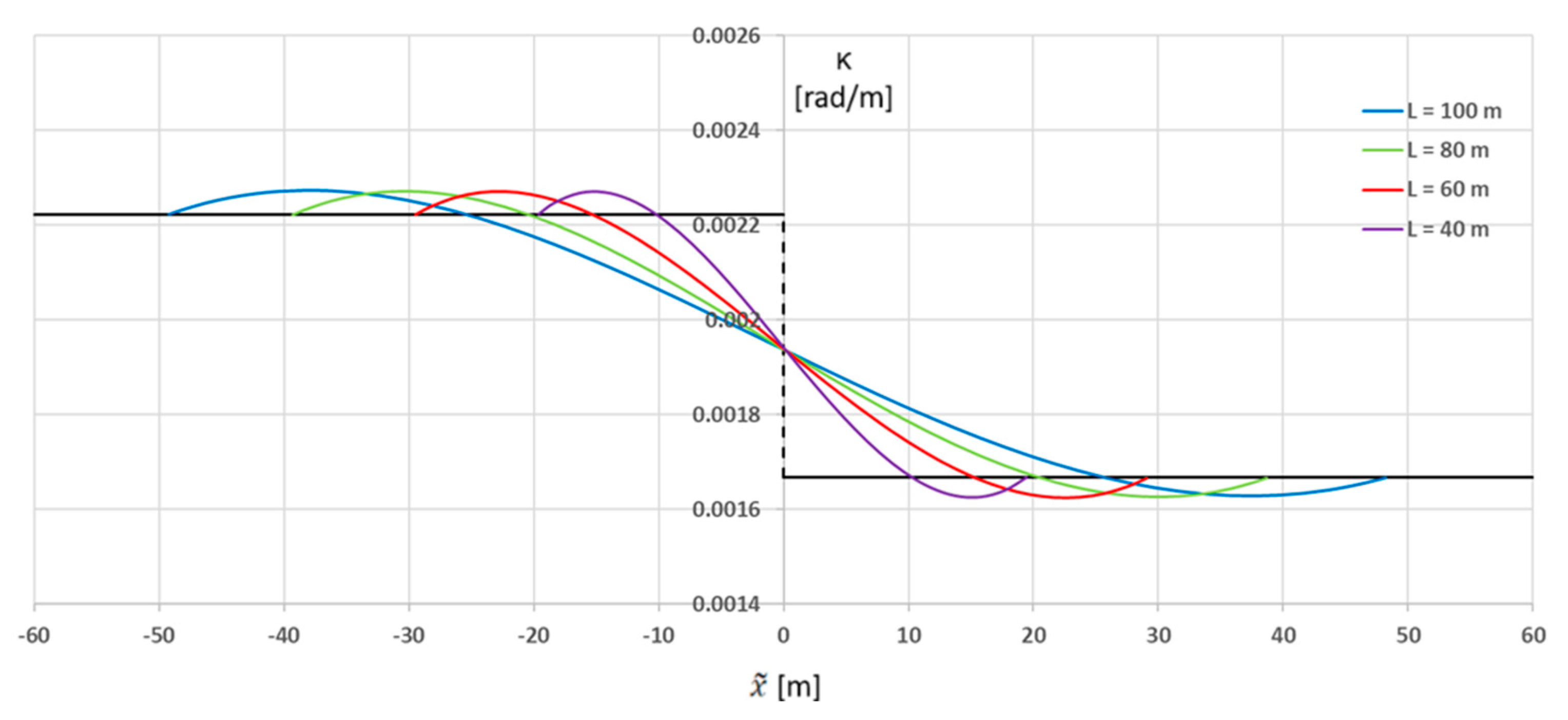
7. Determination of the Curvature Occurring

For the considered transition curves, the curvature values were determined using Formula (10), assuming the lengths of these curves given in Table 4. The corresponding collective curvature graphs (for curves TC(a), TC(b) and TC(c)) are presented in Figure 6, Figure 7 and Figure 8. The abscissa of the original connection point of both arcs (i.e., point C) was assumed as zero there. This means that in these figures the abscissa values are $\tilde{x}=\overline{x}-{\overline{x}}_C$. In the above figures, the black horizontal lines indicate the values of the constant curvature on the CA1 arc and the CA2 arc (as in Figure 5).

The graphs $\kappa (\tilde{x})$ for the TC(a) transition curve shown in Figure 6 are linear. There are abrupt changes in curvature at the start and end points. It is true that the extension of the curve smooths the transition between the circular arcs, but in this solution the original one abrupt change in curvature is replaced by two smaller ones (i.e., the problem still remains). It is therefore doubtful that the TC(a) curve can be recommended for practical use.

The graphs $\kappa (\tilde{x})$ for the TC(b) transition curve in Figure 7 are non-linear. However, they can hardly be considered more advantageous than the analogous graphs shown in Figure 6. The change in curvature along the length is more abrupt here than for the TC(a) curve. The abrupt changes in the initial region are smaller, while in the final region they are more pronounced. This can be easily explained by using the approximate Formula (11) for the TC(b) curve, which shows that the condition $\overline{y}\prime (\overline{x})=0$ is valid along its entire length. Since the s_P1 values for the transition curves in Figure 7 were much smaller than the s_P2 values, the influence of the simplifying assumption was more evident at the final point. In specific situations, due to the more abrupt change in curvature along the length, the TC(b) curve may be less advantageous than the TC(a) curve and then it also could not be recommended for practical use.

The graphs $\kappa (\tilde{x})$ for the TC(c) transition curve shown in Figure 8 are—like the graphs in Figure 7—non-linear. However, they differ significantly from the graphs shown in Figure 6 and Figure 7 in that they do not show any abrupt changes in curvature, while its changes along the length are much milder. There can be no doubt that the TC(c) curve should be recommended as the most advantageous solution to the problem. All that needs to be checked is the practical possibilities of implementing this curve related to the values of the horizontal ordinates. They cannot be too small in relation to the occurring implementation error.

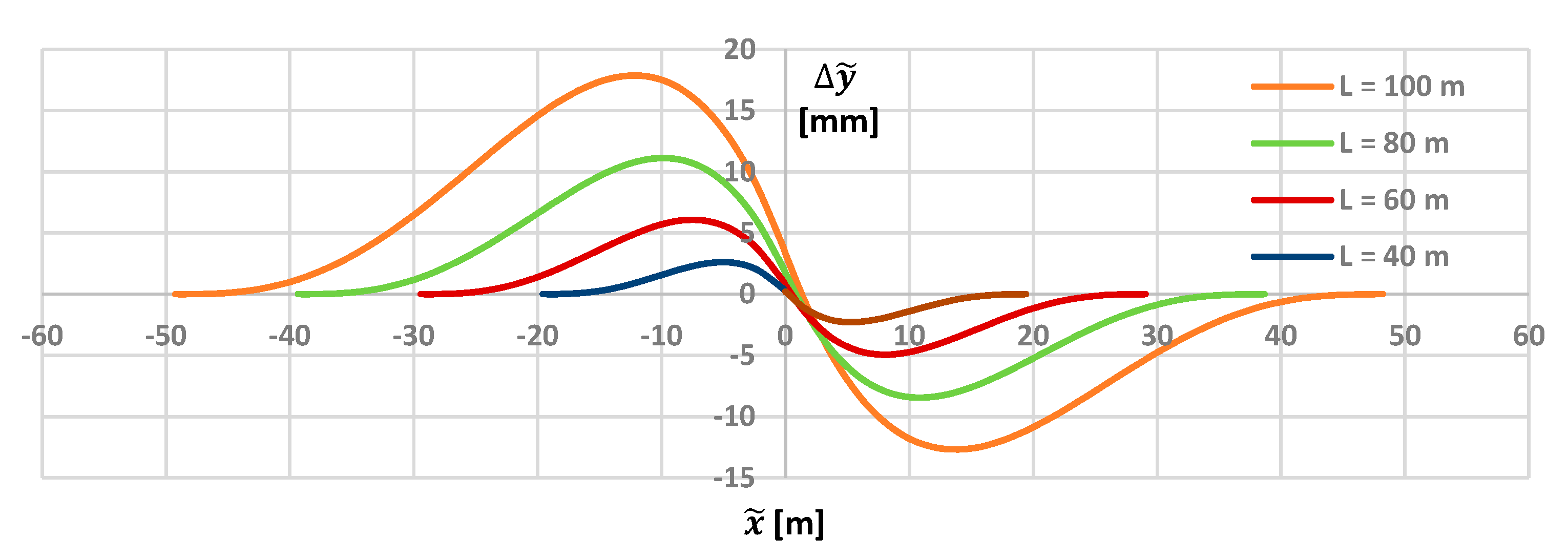
8. Horizontal Ordinates of the Recommended Transition Curve

Figure 9 shows graphs of relative differences in the horizontal ordinates of the TC(c) transition curve with respect to the original state, for the assumed different curve lengths. Similarly to Chapter 7, the abscissa of the original connection point of both arcs (i.e., point C) was assumed as zero in these graphs.

The graphs $\Delta \tilde{y}(\tilde{x})$ in Figure 9 indicate the regular nature of the required deviations of the geometric system from the original state. At the same time, these differences are very small: in the given case for L = 100 m they do not even reach 20 mm, and for L = 80 m they only slightly exceed 10 mm. This may indicate a certain problem related to the accuracy of the corrected system. In order to limit the effects of a possible error in this area, the lengths of the transition curves should be adjusted to specific situations and the use of too short curves should be avoided. It seems that for the situation shown in Figure 9, the length of the transition curve should not be less than 80 m.

Of course, each geometrical system should be considered individually. There is no doubt, however, that the presented method is universal and allows to modify each compound curve, eliminating the disturbance caused by a sudden change in curvature in the area of direct connection of two horizontal circular arcs of different radii.

9. Conclusions

Although currently the main interest is focused on high-speed railways, traditional lines, whose layout was most often created in the 19th century, still dominate in terms of length. The latter are still in use today, but one may get the impression that they are disappearing from the field of research interest, and yet they should be modernized and adapted to contemporary requirements. This applies especially to railway lines running in difficult terrain conditions (e.g., in mountainous terrain), which often have specific geometric layouts, such as compound curves and reverse curves.

This article refers to the analytical method of modeling compound curves on railway lines, which was presented in [30]. This method—in principle—was to serve to create the basis for subsequent modification of the existing geometric system, consisting in correcting the horizontal ordinates in the area of connection of both circular arches. This analytical approach highlights the innovative nature of the presented research and allows for the consideration of detailed issues that are difficult to address traditionally. The issue of practical application of the presented method is limited to computational issues (the given formulas for determining Cartesian coordinates can be directly applied to determine the appropriate geometric system).

The modification of the compound curve consists of eliminating the direct connection of both horizontal arches by introducing an appropriate transition curve between them. After determining the position of the extreme points of this curve (resulting from the assumed length of the curve), the appropriate mathematical equations are determined by solving the appropriate differential problem. The article presents three possibilities of connecting the occurring circular arches, guided by the criterion of the degree to which the nature of the curvature of a given curve is taken into account. The transition curve determined without taking into account the conditions concerning the curvature, the transition curve taking into account simplified conditions concerning the curvature and the transition curve taking into account strict conditions concerning the curvature were considered. A detailed analysis of the obtained solutions was carried out using the developed test geometric system.

On the transition curve determined without taking into account the conditions concerning curvature (with linear curvature), abrupt changes in curvature were found at the initial and final points. Although the extension of the curve softens the transition between the circular arcs, in this solution the originally occurring one abrupt change in curvature (at the point of connection of the circular arcs) is replaced by two smaller ones. The situation is similar, although to a slightly smaller extent of disturbances, for the transition curve taking into account simplified conditions concerning curvature, created after introducing the appropriate simplifying assumption (still used on the railway). It should therefore be recognized that these curves do not solve the problem and therefore cannot be recommended for practical use.

The third transition curve under consideration, with non-linear curvature, determined in a strict manner, maintains the continuity of the curvature along its entire length. It does not have abrupt changes in curvature in the extreme regions, and the changes along the length are much milder than in the case of the two previously discussed curves. In order to avoid difficulties in its practical implementation related to the values of horizontal ordinates (which differ little from the original state), the lengths of the transition curves should be adjusted to specific situations and the use of curves that are too short should be avoided. The point here is to limit the impact of the implementation error. There can be no doubt that this curve should be recommended as the most advantageous solution to the problem.

The detailed calculations performed are based on regulations applicable in Poland. However, similar operating conditions prevail in other countries in this respect. Railway lines containing compound curves are characterized by relatively low train speeds, and similar permissible values for kinematic parameters apply to their design. Therefore, the presented method is universal, and the obtained results may be useful internationally.