Effects of Training Parameter Concept and Sample Size in Possibilistic c-Means Classifier for Pigeon Pea Specific Crop Mapping
Abstract
:1. Introduction
2. Study Area and Datasets
2.1. Study Area
2.2. Datasets
3. Methods
3.1. Possibilistic c-Means Algorithm (PCM)
3.2. CBSI-MSAVI2 Indices
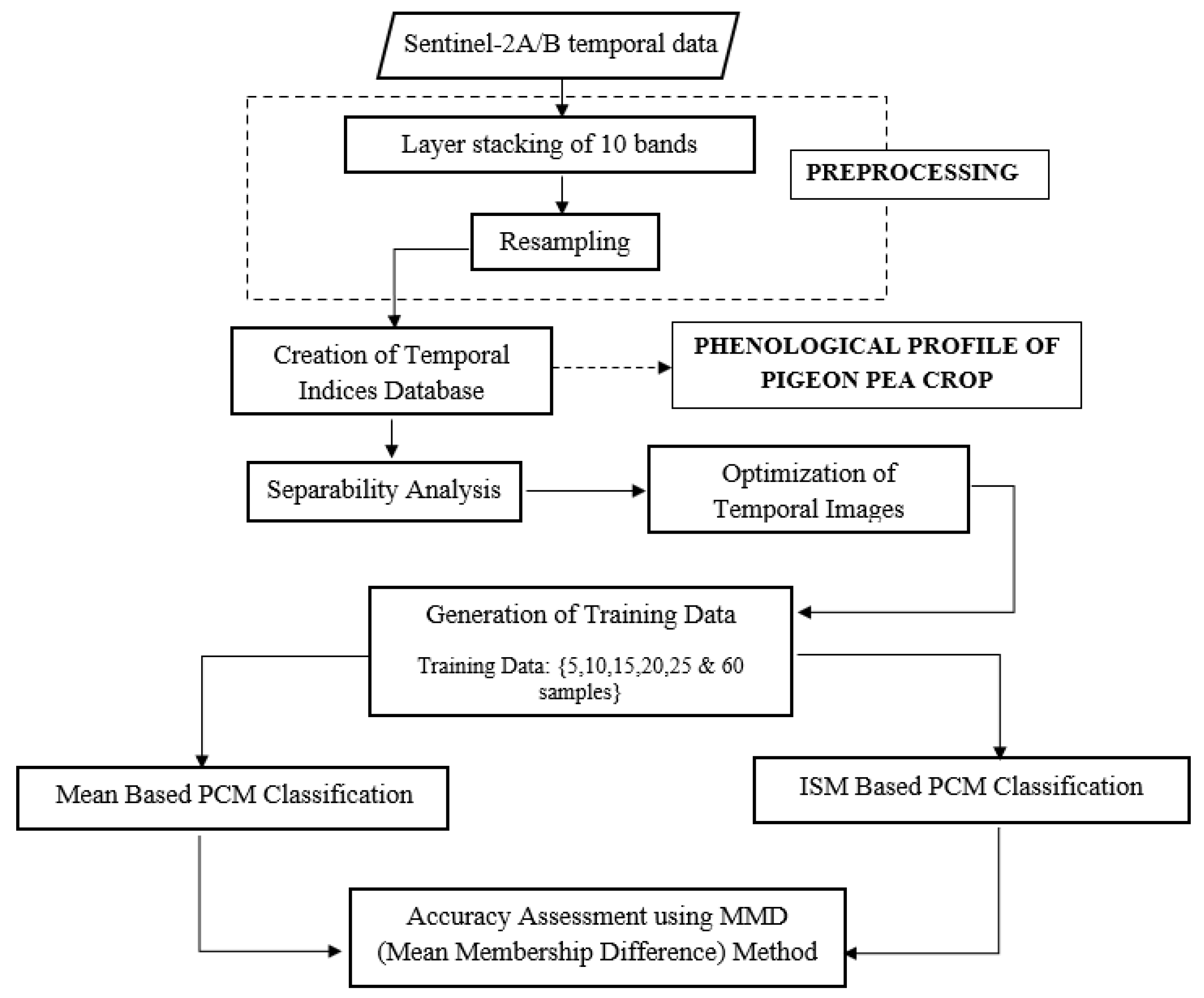
3.3. Methodology Adopted
4. Results& Discussion
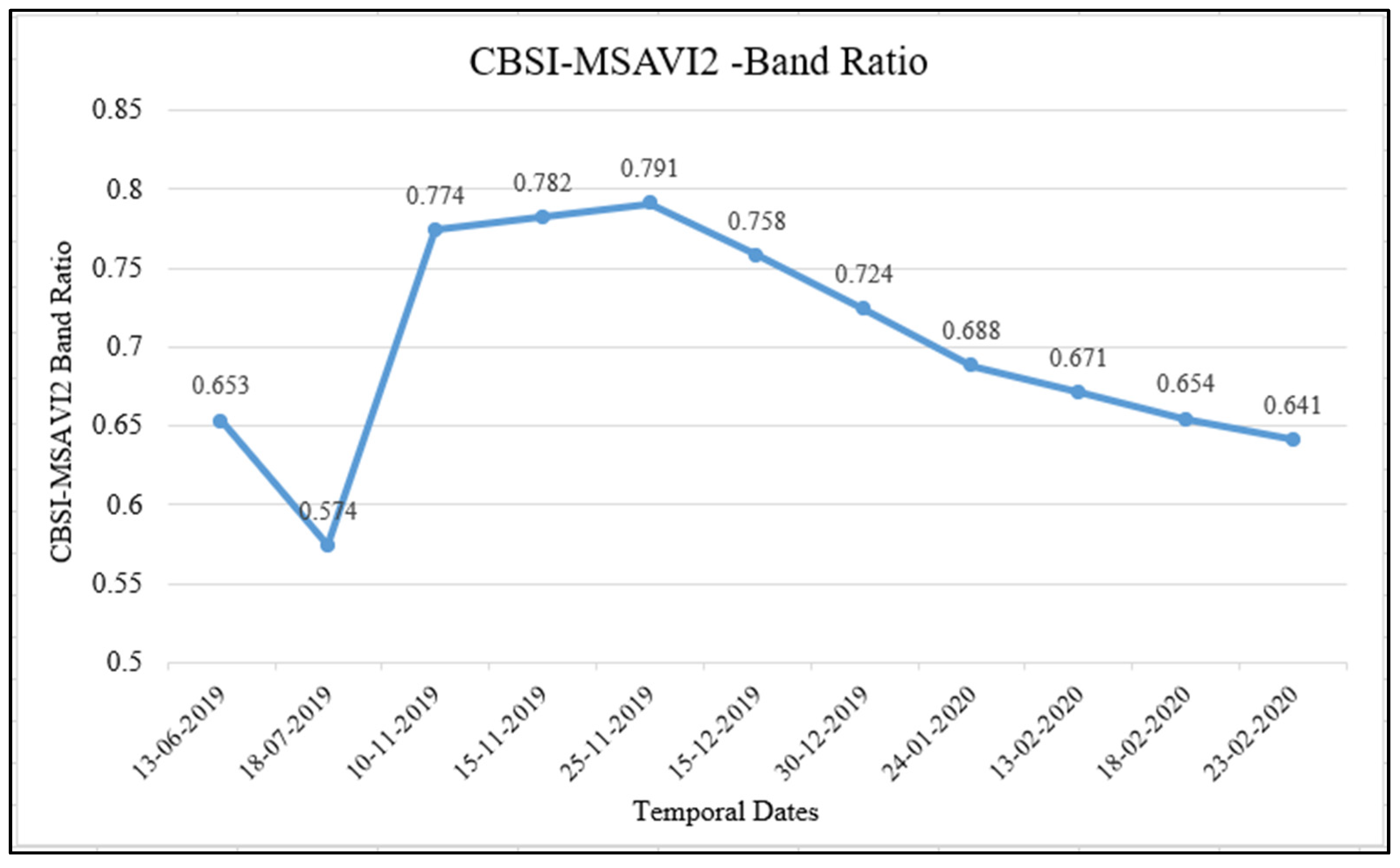
4.1. Database of Generated Temporal Indices—CBSI-MSAVI2
4.2. Separability Analysis and Selection of Optimal Dates
4.3. Optimising Weighted Exponent (m) Parameter
4.4. Classification Results
4.5. Accuracy Assessment Using MMD
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- GoI. Annual Report 2018-19. Ministry of Agriculture & Farmers Welfare; Government of India: New Delhi, India, 2019; pp. 1–224.
- Pigeonpea_E.pdf. Available online: https://farmer.gov.in/imagedefault/Other_Pulses/Pigeonpea_E.pdf (accessed on 19 November 2021).
- Rosenthal, G. Economic and Social Council. Oxford Handb. United Nations 2008, 00424, 135–148. [Google Scholar] [CrossRef]
- Xue, Y.; Li, Y.; Guang, J.; Zhang, X.; Guo, J. Small satellite remote sensing and applications—History, current and future. Int. J. Remote Sens. 2008, 29, 4339–4372. [Google Scholar] [CrossRef]
- Millan, R.M.; von Steiger, R.; Ariel, M.; Bartalev, S.; Borgeaud, M.; Campagnola, S.; Castillo-Rogez, J.C.; Fléron, R.; Gass, V.; Gregorio, A.; et al. Small satellites for space science: A COSPAR scientific roadmap. Adv. Space Res. 2019, 64, 1466–1517. [Google Scholar] [CrossRef]
- Weiss, M.; Jacob, F.; Duveiller, G. Remote sensing for agricultural applications: A meta-review. Remote Sens. Environ. 2019, 236, 111402. [Google Scholar] [CrossRef]
- Naik, P.; Kumar, A. A Stochastic Approach for Automatic Collection of Precise Training Data for a Soft Machine Learning Algorithm Using Remote Sensing Images. In Soft Computing for Problem Solving. Advances in Intelligent Systems and Computing; Tiwari, A., Ahuja, K., Yadav, A., Bansal, J.C., Deep, K., Nagar, A.K., Eds.; Springer: Singapore, 2021; Volume 1393, pp. 285–297. [Google Scholar] [CrossRef]
- Lark, T.; Schelly, I.; Gibbs, H. Accuracy, Bias, and Improvements in Mapping Crops and Cropland across the United States Using the USDA Cropland Data Layer. Remote Sens. 2021, 13, 968. [Google Scholar] [CrossRef]
- Paliwal, A.; Jain, M. The Accuracy of Self-Reported Crop Yield Estimates and Their Ability to Train Remote Sensing Algorithms. Front. Sustain. Food Syst. 2020, 4, 25. [Google Scholar] [CrossRef] [Green Version]
- Gong, J.; Sui, H.; Ma, G.; Zhou, Q. A review of multi-temporal remote sensing data change detection algorithm. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci.-ISPRS Arch. 2008, 37, 757–762. [Google Scholar]
- Ghamisi, P.; Rasti, B.; Yokoya, N.; Wang, Q.; Hofle, B.; Bruzzone, L.; Bovolo, F.; Chi, M.; Anders, K.; Gloaguen, R.; et al. Multisource and Multitemporal Data Fusion in Remote Sensing. arXiv 2018, arXiv:1812.08287. [Google Scholar]
- Naik, P.; Dalponte, M.; Bruzzone, L. A comparison on the use of different satellite multispectral data for the prediction of aboveground biomass. In Image and Signal Processing for Remote Sensing XXVI; International Society for Optics and Photonics: Bellingham, WC, USA, 2020; Volume 11533, p. 1153315. [Google Scholar] [CrossRef]
- Naik, P.; Dalponte, M.; Bruzzone, L. Prediction of Forest Aboveground Biomass Using Multitemporal Multispectral Remote Sensing Data. Remote Sens. 2021, 13, 1282. [Google Scholar] [CrossRef]
- Shu, C.; Sun, L. Automatic target recognition method for multitemporal remote sensing image. Open Phys. 2020, 18, 170–181. [Google Scholar] [CrossRef]
- Yan, S.; Yao, X.; Zhu, D.; Liu, D.; Zhang, L.; Yu, G.; Gao, B.; Yang, J.; Yun, W. Large-scale crop mapping from multi-source optical satellite imageries using machine learning with discrete grids. Int. J. Appl. Earth Obs. Geoinf. 2021, 103, 102485. [Google Scholar] [CrossRef]
- Sun, C.; Bian, Y.; Zhou, T.; Pan, J. Using of Multi-Source and Multi-Temporal Remote Sensing Data Improves Crop-Type Mapping in the Subtropical Agriculture Region. Sensors 2019, 19, 2401. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pôças, I.; Calera, A.; Campos, I.; Cunha, M. Remote sensing for estimating and mapping single and basal crop coefficientes: A review on spectral vegetation indices approaches. Agric. Water Manag. 2020, 233, 106081. [Google Scholar] [CrossRef]
- Campos, I.; Gómez, L.G.; Villodre, J.; Calera, M.; Campoy, J.; Jiménez, N.; Plaza, C.; Sánchez-Prieto, S.; Calera, A. Mapping within-field variability in wheat yield and biomass using remote sensing vegetation indices. Precis. Agric. 2018, 20, 214–236. [Google Scholar] [CrossRef]
- Moumni, A.; Lahrouni, A. Machine Learning-Based Classification for Crop-Type Mapping Using the Fusion of High-Resolution Satellite Imagery in a Semiarid Area. Scientifica 2021, 2021, 8810279. [Google Scholar] [CrossRef] [PubMed]
- Kumari, M.; Pandey, V.; Choudhary, K.K.; Murthy, C.S. Object-based machine learning approach for soybean mapping using temporal sentinel-1/sentinel-2 data. Geocarto Int. 2021, 1–19. [Google Scholar] [CrossRef]
- Kobayashi, N.; Tani, H.; Wang, X.; Sonobe, R. Crop classification using spectral indices derived from Sentinel-2A imagery. J. Inf. Telecommun. 2020, 4, 67–90. [Google Scholar] [CrossRef]
- Viskovic, L.; Kosovic, I.N.; Mastelic, T. Crop Classification using Multi-spectral and Multitemporal Satellite Imagery with Machine Learning. In Proceedings of the 2019 International Conference on Software, Telecommunications and Computer Networks (SoftCOM), Split, Croatia, 19–21 September 2019; p. 8903738. [Google Scholar]
- Saini, R.; Ghosh, S.K. Crop classsification on single date Sentinel-2 Imagery using Random Forest and Suppor Vector Machine. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2018, 42, 683–688. [Google Scholar] [CrossRef] [Green Version]
- Kamilaris, A.; Prenafeta-Boldú, F.X. Deep learning in agriculture: A survey. Comput. Electron. Agric. 2018, 147, 70–90. [Google Scholar] [CrossRef] [Green Version]
- Melgani, F.; Bruzzone, L. Classification of hyperspectral remote sensing images with support vector machines. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1778–1790. [Google Scholar] [CrossRef] [Green Version]
- Fawagreh, K.; Gaber, M.M.; Elyan, E. Random forests: From early developments to recent advancements. Syst. Sci. Control Eng. Open Access J. 2014, 2, 602–609. [Google Scholar] [CrossRef] [Green Version]
- Liakos, K.G.; Busato, P.; Moshou, D.; Pearson, S.; Bochtis, D. Machine learning in agriculture: A review. Sensors 2018, 18, 2674. [Google Scholar] [CrossRef] [Green Version]
- Scheer, C.; Guder, L. Deep Learning in Agriculture: A Systematic Literature Review Deep Learning in Agriculture Três de Maio. Bachelor Thesis, Faculty of Três de Maio, Tres de Maio, Brazil, 2019. [Google Scholar] [CrossRef]
- Saleem, M.H.; Potgieter, J.; Arif, K.M. Automation in Agriculture by Machine and Deep Learning Techniques: A Review of Recent Developments; Springer: New York, NY, USA, 2021; Volume 22. [Google Scholar]
- Naik, P.; Dalponte, M.; Bruzzone, L. A Disentangled Variational Autoencoder for Prediction of Above Ground Biomass from Hyperspectral Data. In Proceedings of the 2021 IEEE International Geoscience and Remote Sensing Symposium IGARSS, Brussels, Belgium, 11–16 July 2021; pp. 2991–2994. [Google Scholar] [CrossRef]
- Tilson, L.; Excell, P.; Green, R. A Generalisation of the Fuzzy C-means Clustering Algorithm. In Proceedings of the International Geoscience and Remote Sensing Symposium, Remote Sensing: Moving Toward the 21st Century, Edinburgh, UK, 12–16 September 1988; Volume 3, pp. 1783–1784. [Google Scholar] [CrossRef]
- Hung, M.-C.; Yang, D.-L. An efficient Fuzzy C-Means clustering algorithm. In Proceedings of the 2001 IEEE International Conference on Data Mining, Maebashi City, Japan, 9–12 December 2002; pp. 225–232. [Google Scholar] [CrossRef]
- Sandhya, P.; Kumar, A. A Survey on Fuzzy C-means Clustering Techniques. Ijedr 2017, 5, 1151–1155. [Google Scholar]
- Krishnapuram, R.; Keller, J. The possibilistic C-means algorithm: Insights and recommendations. IEEE Trans. Fuzzy Syst. 1996, 4, 385–393. [Google Scholar] [CrossRef]
- Singh, A.; Kumar, A.; Upadhyay, P. Modified possibilistic c- means with constraints (MPCM-S) approach for incorporating the local information in a remote sensing image classification. Remote Sens. Appl. Soc. Environ. 2020, 18, 100319. [Google Scholar] [CrossRef]
- Singh, A.; Kumar, A.; Upadhyay, P. A novel approach to incorporate local information in Possibilistic c-Means algorithm for an optical remote sensing imagery. Egypt. J. Remote Sens. Space Sci. 2020, 24, 151–161. [Google Scholar] [CrossRef]
- Singh, A.; Kumar, A. Identification of Paddy Stubble Burnt Activities Using Temporal Class-Based Sensor-Independent Indices Database: Modified Possibilistic Fuzzy Classification Approach. J. Indian Soc. Remote Sens. 2019, 48, 423–430. [Google Scholar] [CrossRef]
- Louis, J. Sentinel 2 MSI—Level 2A Product Definition. Eur. Sp. Agency 2016, 49. Available online: https://sentinel.esa.int/documents/247904/1848117/Sentinel-2-Level-2A-Product-Definition-Document.pdf (accessed on 22 January 2022).
- Jankowski, J.A. (Ed.) Inflammation and Gastrointestinal Cancers; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011. [Google Scholar] [CrossRef]
- Qi, J.; Chehbouni, A.; Huete, A.R.; Kerr, Y.H.; Sorooshian, S. A modified soil adjusted vegetation index. Remote Sens. Environ. 1994, 48, 119–126. [Google Scholar] [CrossRef]
- Vincent, A.; Kumar, A.; Upadhyay, P. Effect of Red-Edge Region in Fuzzy Classification: A Case Study of Sunflower Crop. J. Indian Soc. Remote Sens. 2020, 48, 645–657. [Google Scholar] [CrossRef]
- Kumar, A.; Ghosh, S.; Dadhwal, V. ALCM: Automatic land cover mapping. J. Indian Soc. Remote Sens. 2010, 38, 239–245. [Google Scholar] [CrossRef]
- Krishnapuram, R.; Keller, J. A possibilistic approach to clustering. IEEE Trans. Fuzzy Syst. 1993, 1, 98–110. [Google Scholar] [CrossRef]
- Upadhyay, P.; Kumar, A.; Roy, P.S.; Ghosh, S.; Gilbert, I. Effect on specific crop mapping using WorldView-2 multispectral add-on bands: Soft classification approach. J. Appl. Remote Sens. 2012, 6, 063524-1. [Google Scholar] [CrossRef]
- Rawat, A.; Kumar, A.; Upadhyay, P.; Kumar, S. Multisensor temporal approach for transplanted paddy fields mapping using fuzzy-based classifiers. J. Appl. Remote Sens. 2020, 14, 024524. [Google Scholar] [CrossRef]
- Nandan, R.; Kamboj, A.; Kumar, A.; Kumar, S.; Reddy, K.V. Formosat-2 with Landsat-8 Temporal-Multispectral Data for Wheat Crop Identification using Hypertangent Kernel based Possibilistic classifier. J. Geomat. 2016, 10, 89–95. [Google Scholar]
- Jensen, J.R.; Lulla, K. Introductory Digital Image Processing: A Remote Sensing Perspective, 3rd ed.; Prentice Hall Series in Geographic Information Science; Pearson Prentice Hall: Upper Saddle River, NJ, USA, 2005; ISBN 0-13-145361-0. [Google Scholar]
- Misra, G.; Kumar, A.; Patel, N.R.; Zurita-Milla, R. Mapping a Specific Crop—A Temporal Approach for Sugarcane Ratoon. J. Indian Soc. Remote Sens. 2013, 42, 325–334. [Google Scholar] [CrossRef]
- Devinda, C.S.; Kumar, A. Application of fuzzy machine learning algorithm in agro-geography. Khoj Int. Peer Rev. J. Geogr. 2020, 7, 30–46. [Google Scholar] [CrossRef]
- Najafabadi, M.M.; Villanustre, F.; Khoshgoftaar, T.M.; Seliya, N.; Wald, R.; Muharemagic, E. Deep learning applications and challenges in big data analytics. J. Big Data 2015, 2, 1. [Google Scholar] [CrossRef] [Green Version]




| Study Site | Sentinel 2A (L2A Product) | Sentinel 2B (L2A Product) |
|---|---|---|
| J Bhupalpally District (Telangana) | 13 June2019 | 18 July 2019 |
| 10 November 2019 | 15 November 2019 | |
| 20 December 2019 | 25 November 2019 | |
| 30 December 2019 | 15 December 2019 | |
| 18 February 2020 | 24 January 2020 | |
| 13 February 2020 | ||
| 23 February 2020 |
| Band Details | Resolution |
|---|---|
| Band 2-Blue (490 nm) | 10 m |
| Band 3-Green (560 nm) | 10 m |
| Band 4-Red (665 nm) | 10 m |
| Band 5-Red edge (705 nm) | 20 m |
| Band 6-Red edge (740 nm) | 20 m |
| Band 7-Red edge (783 nm) | 20 m |
| Band 8-NIR (842 nm) | 10 m |
| Band 8A-Red Edge (865 nm) | 20 m |
| Band 11-SWIR (1610 nm) | 20 m |
| Band 12-SWIR (2190 nm) | 20 m |
| Date | Minimum Band | Maximum Band |
|---|---|---|
| 13 June 2019 | Band 2—Blue | Band 11—SWIR |
| 18 July 2019 | Band 2—Blue | Band 8A—Red Edge |
| 10 November 2019 | Band 2—Blue | Band 7—Red Edge |
| 15 November 2019 | Band 2—Blue | Band 8A—Red Edge |
| 25 November | Band 2—Blue | Band 8A—Red Edge |
| 15 December 2019 | Band 2—Blue | Band 8A—Red Edge |
| 30 December 2019 | Band 2—Blue | Band 8A—Red Edge |
| 24 January 2020 | Band 2—Blue | Band 11—SWIR |
| 13 February 2020 | Band 2—Blue | Band 11—SWIR |
| 18 February 2020 | Band 2—Blue | Band 11—SWIR |
| 23 February 2020 | Band 2—Blue | Band 11—SWIR |
| No. of Images | Date Combinations | Min Separability Distance |
|---|---|---|
| 1 | 5 | 15 |
| 2 | 2, 5 | 40 |
| 3 | 1, 2, 5 | 47 |
| 4 | 1, 2, 4, 5 | 54 |
| 5 | 1, 2, 4, 5, 8 | 57 |
| 6 | 1, 2, 4, 5, 8, 10 | 59 |
| 7 | 1, 2, 3, 4, 5, 8, 10 | 60 |
| 8 | 1, 2, 3, 4, 5, 7, 8, 10 | 60 |
| 9 | 1, 2, 3, 4, 5, 7, 8, 9, 10 | 60 |
| 10 | 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 | 60 |
| ‘M’ Value | Membership Values from Testing Site—Pigeon Pea | Mean Value at Test Site | Mean Value at Training Site | MMD | |||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | ||||
| 1.1 | 0.996078 | 0.996078 | 0.996078 | 0.996078 | 0.996078 | 0.992157 | 0.995425 | 0.99607843 | 0.000654 |
| 1.5 | 0.992157 | 0.992157 | 0.996078 | 0.996078 | 0.996078 | 0.992157 | 0.994118 | 0.99542484 | 0.001307 |
| 2.0 | 0.937255 | 0.945098 | 0.956863 | 0.945098 | 0.941176 | 0.945098 | 0.945098 | 0.94705882 | 0.001961 |
| 2.1 | 0.921569 | 0.929412 | 0.941176 | 0.929412 | 0.92549 | 0.941176 | 0.931373 | 0.93202614 | 0.000654 |
| 2.2 | 0.905882 | 0.917647 | 0.929412 | 0.917647 | 0.909804 | 0.92549 | 0.917647 | 0.91830065 | 0.000654 |
| 2.3 | 0.890196 | 0.901961 | 0.913725 | 0.901961 | 0.894118 | 0.901961 | 0.900654 | 0.90261438 | 0.001961 |
| 2.4 | 0.870588 | 0.890196 | 0.886275 | 0.909804 | 0.866667 | 0.886275 | 0.884967 | 0.88823529 | 0.003268 |
| 2.5 | 0.854902 | 0.870588 | 0.866667 | 0.898039 | 0.85098 | 0.870588 | 0.868627 | 0.87385621 | 0.005229 |
| 2.6 | 0.839216 | 0.835294 | 0.858824 | 0.882353 | 0.835294 | 0.854902 | 0.85098 | 0.85947712 | 0.008497 |
| 2.7 | 0.827451 | 0.819608 | 0.843137 | 0.870588 | 0.823529 | 0.843137 | 0.837908 | 0.84705882 | 0.00915 |
| 2.8 | 0.811765 | 0.807843 | 0.831373 | 0.858824 | 0.811765 | 0.831373 | 0.82549 | 0.83398693 | 0.008497 |
| 2.9 | 0.8 | 0.796078 | 0.819608 | 0.847059 | 0.8 | 0.819608 | 0.813725 | 0.82156863 | 0.007843 |
| 3.0 | 0.788235 | 0.784314 | 0.807843 | 0.835294 | 0.788235 | 0.807843 | 0.801961 | 0.81111111 | 0.00915 |
| ‘M’ Value | Membership Values from Testing Site—Pigeon Pea | Mean Value at Test Site | Mean Value at Training Site | MMD | |||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | ||||
| 1.1 | 0.996078 | 0.996078 | 0.996078 | 0.996078 | 0.996078 | 0.996078 | 0.996078 | 0.996078 | 0 |
| 1.5 | 0.976471 | 0.976471 | 0.980392 | 0.976471 | 0.980392 | 0.976471 | 0.977778 | 0.976471 | 0.001307 |
| 2.0 | 0.87451 | 0.866667 | 0.878431 | 0.870588 | 0.870588 | 0.866667 | 0.871242 | 0.869281 | 0.001961 |
| 2.1 | 0.854902 | 0.847059 | 0.858824 | 0.85098 | 0.85098 | 0.847059 | 0.851634 | 0.84902 | 0.002614 |
| 2.2 | 0.835294 | 0.827451 | 0.839216 | 0.831373 | 0.831373 | 0.827451 | 0.832026 | 0.830065 | 0.001961 |
| 2.3 | 0.815686 | 0.807843 | 0.823529 | 0.811765 | 0.811765 | 0.811765 | 0.813725 | 0.810458 | 0.003268 |
| 2.4 | 0.8 | 0.792157 | 0.803922 | 0.796078 | 0.796078 | 0.792157 | 0.796732 | 0.794771 | 0.001961 |
| 2.5 | 0.784314 | 0.776471 | 0.788235 | 0.780392 | 0.788235 | 0.780392 | 0.783007 | 0.779085 | 0.003922 |
| 2.6 | 0.768627 | 0.764706 | 0.776471 | 0.764706 | 0.764706 | 0.764706 | 0.76732 | 0.766013 | 0.001307 |
| 2.7 | 0.756863 | 0.74902 | 0.760784 | 0.752941 | 0.752941 | 0.752941 | 0.754248 | 0.752288 | 0.001961 |
| 2.8 | 0.745098 | 0.737255 | 0.74902 | 0.741176 | 0.741176 | 0.741176 | 0.742484 | 0.74183 | 0.000654 |
| 2.9 | 0.733333 | 0.729412 | 0.741176 | 0.729412 | 0.729412 | 0.729412 | 0.732026 | 0.730719 | 0.001307 |
| 3.0 | 0.72549 | 0.717647 | 0.729412 | 0.721569 | 0.721569 | 0.717647 | 0.722222 | 0.720261 | 0.001961 |
| ‘M’ Value | Membership Values from Testing Site—Cotton | Mean Value at Test Site | Mean Value at Training Site | MMD | |||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | ||||
| 1.1 | 0.011765 | 0.015686 | 0.019608 | 0.019608 | 0.011765 | 0.019608 | 0.01634 | 0.996078431 | 0.979739 |
| 1.5 | 0.298039 | 0.309804 | 0.313725 | 0.313725 | 0.290196 | 0.317647 | 0.30719 | 0.995424837 | 0.688235 |
| 2.0 | 0.392157 | 0.4 | 0.4 | 0.4 | 0.388235 | 0.403922 | 0.397386 | 0.947058824 | 0.549673 |
| 2.1 | 0.403922 | 0.407843 | 0.411765 | 0.411765 | 0.4 | 0.415686 | 0.408497 | 0.932026144 | 0.523529 |
| 2.2 | 0.411765 | 0.415686 | 0.415686 | 0.415686 | 0.407843 | 0.419608 | 0.414379 | 0.918300654 | 0.503922 |
| 2.3 | 0.415686 | 0.423529 | 0.423529 | 0.423529 | 0.415686 | 0.427451 | 0.421569 | 0.902614379 | 0.481046 |
| 2.4 | 0.423529 | 0.427451 | 0.427451 | 0.427451 | 0.419608 | 0.431373 | 0.426144 | 0.888235294 | 0.462092 |
| 2.5 | 0.427451 | 0.431373 | 0.435294 | 0.435294 | 0.423529 | 0.435294 | 0.431373 | 0.873856209 | 0.442484 |
| 2.6 | 0.431373 | 0.435294 | 0.439216 | 0.439216 | 0.431373 | 0.439216 | 0.435948 | 0.859477124 | 0.423529 |
| 2.7 | 0.435294 | 0.439216 | 0.439216 | 0.439216 | 0.435294 | 0.443137 | 0.438562 | 0.847058824 | 0.408497 |
| 2.8 | 0.439216 | 0.443137 | 0.443137 | 0.443137 | 0.435294 | 0.447059 | 0.44183 | 0.833986928 | 0.392157 |
| 2.9 | 0.443137 | 0.447059 | 0.447059 | 0.447059 | 0.439216 | 0.45098 | 0.445752 | 0.821568627 | 0.375817 |
| 3.0 | 0.443137 | 0.45098 | 0.45098 | 0.45098 | 0.443137 | 0.45098 | 0.448366 | 0.811111111 | 0.362745 |
| ‘M’ Value | Membership Values from Testing Site—Cotton | Mean Value at Test Site | Mean Value at Training Site | MMD | |||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | ||||
| 1.1 | 0.003922 | 0.007843 | 0.003922 | 0.003922 | 0.003922 | 0.003922 | 0.004575 | 0.996078 | 0.991503 |
| 1.5 | 0.270588 | 0.278431 | 0.270588 | 0.270588 | 0.258824 | 0.278431 | 0.271242 | 0.976471 | 0.705229 |
| 2.0 | 0.380392 | 0.380392 | 0.380392 | 0.380392 | 0.372549 | 0.380392 | 0.379085 | 0.869281 | 0.490196 |
| 2.1 | 0.388235 | 0.392157 | 0.388235 | 0.388235 | 0.384314 | 0.392157 | 0.388889 | 0.84902 | 0.460131 |
| 2.2 | 0.396078 | 0.4 | 0.396078 | 0.396078 | 0.392157 | 0.4 | 0.396732 | 0.830065 | 0.433333 |
| 2.3 | 0.403922 | 0.407843 | 0.403922 | 0.403922 | 0.4 | 0.407843 | 0.404575 | 0.810458 | 0.405882 |
| 2.4 | 0.411765 | 0.415686 | 0.411765 | 0.411765 | 0.407843 | 0.415686 | 0.412418 | 0.794771 | 0.382353 |
| 2.5 | 0.415686 | 0.419608 | 0.419608 | 0.419608 | 0.411765 | 0.419608 | 0.417647 | 0.779085 | 0.361438 |
| 2.6 | 0.423529 | 0.423529 | 0.423529 | 0.423529 | 0.419608 | 0.423529 | 0.422876 | 0.766013 | 0.343137 |
| 2.7 | 0.427451 | 0.427451 | 0.427451 | 0.427451 | 0.423529 | 0.427451 | 0.426797 | 0.752288 | 0.32549 |
| 2.8 | 0.431373 | 0.431373 | 0.431373 | 0.431373 | 0.427451 | 0.431373 | 0.430719 | 0.74183 | 0.311111 |
| 2.9 | 0.435294 | 0.435294 | 0.435294 | 0.435294 | 0.431373 | 0.435294 | 0.434641 | 0.730719 | 0.296078 |
| 3.0 | 0.439216 | 0.439216 | 0.439216 | 0.439216 | 0.435294 | 0.439216 | 0.438562 | 0.720261 | 0.281699 |
| Number of Samples | Membership Values from Testing Site—Pigeon Pea | Mean Value at Test Site | Mean Value at Training Site | MMD | Variance | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |||||
| 5 | 0.960784 | 0.956863 | 0.980392 | 0.968627 | 0.960784 | 0.976471 | 0.96732 | 0.968409586 | 0.019608 | 0.019172 |
| 10 | 0.956863 | 0.956863 | 0.980392 | 0.964706 | 0.956863 | 0.976471 | 0.965359 | 0.966775599 | 0.018954 | 0.024074 |
| 15 | 0.964706 | 0.960784 | 0.984314 | 0.968627 | 0.964706 | 0.980392 | 0.970588 | 0.971568627 | 0.017647 | 0.019281 |
| 20 | 0.968627 | 0.964706 | 0.984314 | 0.972549 | 0.968627 | 0.980392 | 0.973203 | 0.973965142 | 0.016993 | 0.012309 |
| 25 | 0.972549 | 0.964706 | 0.988235 | 0.976471 | 0.972549 | 0.984314 | 0.976471 | 0.977124183 | 0.015686 | 0.015686 |
| 60 | 0.980392 | 0.972549 | 0.988235 | 0.984314 | 0.984314 | 0.992157 | 0.98366 | 0.984204793 | 0.013072 | 0.019695 |
| Number of Samples | Membership Values from Testing Site—Cotton | Mean Value at Test Site | Mean Value at Training Site | MMD | |||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | ||||
| 5 | 0.705882 | 0.670588 | 0.705882 | 0.682353 | 0.603922 | 0.643137 | 0.668627 | 0.968409586 | 0.318301 |
| 10 | 0.705882 | 0.670588 | 0.705882 | 0.682353 | 0.603922 | 0.643137 | 0.668627 | 0.966775599 | 0.315686 |
| 15 | 0.701961 | 0.666667 | 0.701961 | 0.682353 | 0.603922 | 0.639216 | 0.666013 | 0.971568627 | 0.322222 |
| 20 | 0.698039 | 0.662745 | 0.698039 | 0.678431 | 0.6 | 0.639216 | 0.662745 | 0.973965142 | 0.327451 |
| 25 | 0.694118 | 0.658824 | 0.694118 | 0.670588 | 0.592157 | 0.635294 | 0.657516 | 0.977124183 | 0.334641 |
| 60 | 0.701961 | 0.666667 | 0.705882 | 0.682353 | 0.603922 | 0.639216 | 0.666667 | 0.984204793 | 0.330065 |
| Number of Samples | Membership Values from Testing Site—Pigeon Pea | Mean Value at Test Site | Mean Value at Training Site | MMD | Variance | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |||||
| 5 | 0.964706 | 0.952941 | 0.976471 | 0.968627 | 0.972549 | 0.984314 | 0.969935 | 0.994118 | 0.024183 | 0.024401 |
| 10 | 0.968627 | 0.988235 | 0.980392 | 0.980392 | 0.980392 | 0.976471 | 0.979085 | 1 | 0.020915 | 0.008388 |
| 15 | 0.968627 | 0.988235 | 0.980392 | 0.980392 | 0.980392 | 0.976471 | 0.979085 | 0.996732 | 0.017647 | 0.008715 |
| 20 | 0.968627 | 0.988235 | 0.980392 | 0.980392 | 0.980392 | 0.976471 | 0.979085 | 0.996732 | 0.017647 | 0.008715 |
| 25 | 0.980392 | 0.972549 | 0.988235 | 0.984314 | 0.984314 | 0.992157 | 0.98366 | 1 | 0.01634 | 0.009695 |
| 60 | 0.980392 | 0.972549 | 0.988235 | 0.984314 | 0.984314 | 0.992157 | 0.98366 | 1 | 0.01634 | 0.009695 |
| Number of Samples | Membership Values from Testing Site—Cotton | Mean Value at Test Site | Mean Value at Training Site | MMD | |||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | ||||
| 5 | 0.670588 | 0.643137 | 0.678431 | 0.658824 | 0.588235 | 0.619608 | 0.643137 | 0.994118 | 0.35098 |
| 10 | 0.654902 | 0.694118 | 0.647059 | 0.65098 | 0.717647 | 0.643137 | 0.667974 | 1 | 0.332026 |
| 15 | 0.643137 | 0.686275 | 0.643137 | 0.639216 | 0.713725 | 0.635294 | 0.660131 | 0.996732 | 0.336601 |
| 20 | 0.643137 | 0.686275 | 0.643137 | 0.639216 | 0.713725 | 0.635294 | 0.660131 | 0.996732 | 0.336601 |
| 25 | 0.72549 | 0.690196 | 0.733333 | 0.705882 | 0.627451 | 0.658824 | 0.690196 | 1 | 0.309804 |
| 60 | 0.72549 | 0.690196 | 0.733333 | 0.705882 | 0.627451 | 0.658824 | 0.690196 | 1 | 0.309804 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sivaraj, P.; Kumar, A.; Koti, S.R.; Naik, P. Effects of Training Parameter Concept and Sample Size in Possibilistic c-Means Classifier for Pigeon Pea Specific Crop Mapping. Geomatics 2022, 2, 107-124. https://doi.org/10.3390/geomatics2010007
Sivaraj P, Kumar A, Koti SR, Naik P. Effects of Training Parameter Concept and Sample Size in Possibilistic c-Means Classifier for Pigeon Pea Specific Crop Mapping. Geomatics. 2022; 2(1):107-124. https://doi.org/10.3390/geomatics2010007
Chicago/Turabian StyleSivaraj, Priyadarsini, Anil Kumar, Shiva Reddy Koti, and Parth Naik. 2022. "Effects of Training Parameter Concept and Sample Size in Possibilistic c-Means Classifier for Pigeon Pea Specific Crop Mapping" Geomatics 2, no. 1: 107-124. https://doi.org/10.3390/geomatics2010007
APA StyleSivaraj, P., Kumar, A., Koti, S. R., & Naik, P. (2022). Effects of Training Parameter Concept and Sample Size in Possibilistic c-Means Classifier for Pigeon Pea Specific Crop Mapping. Geomatics, 2(1), 107-124. https://doi.org/10.3390/geomatics2010007






