Optimization of Cogeneration Supercritical Steam Power Plant Design Based on Heat Consumer Requirements
Abstract
1. Introduction
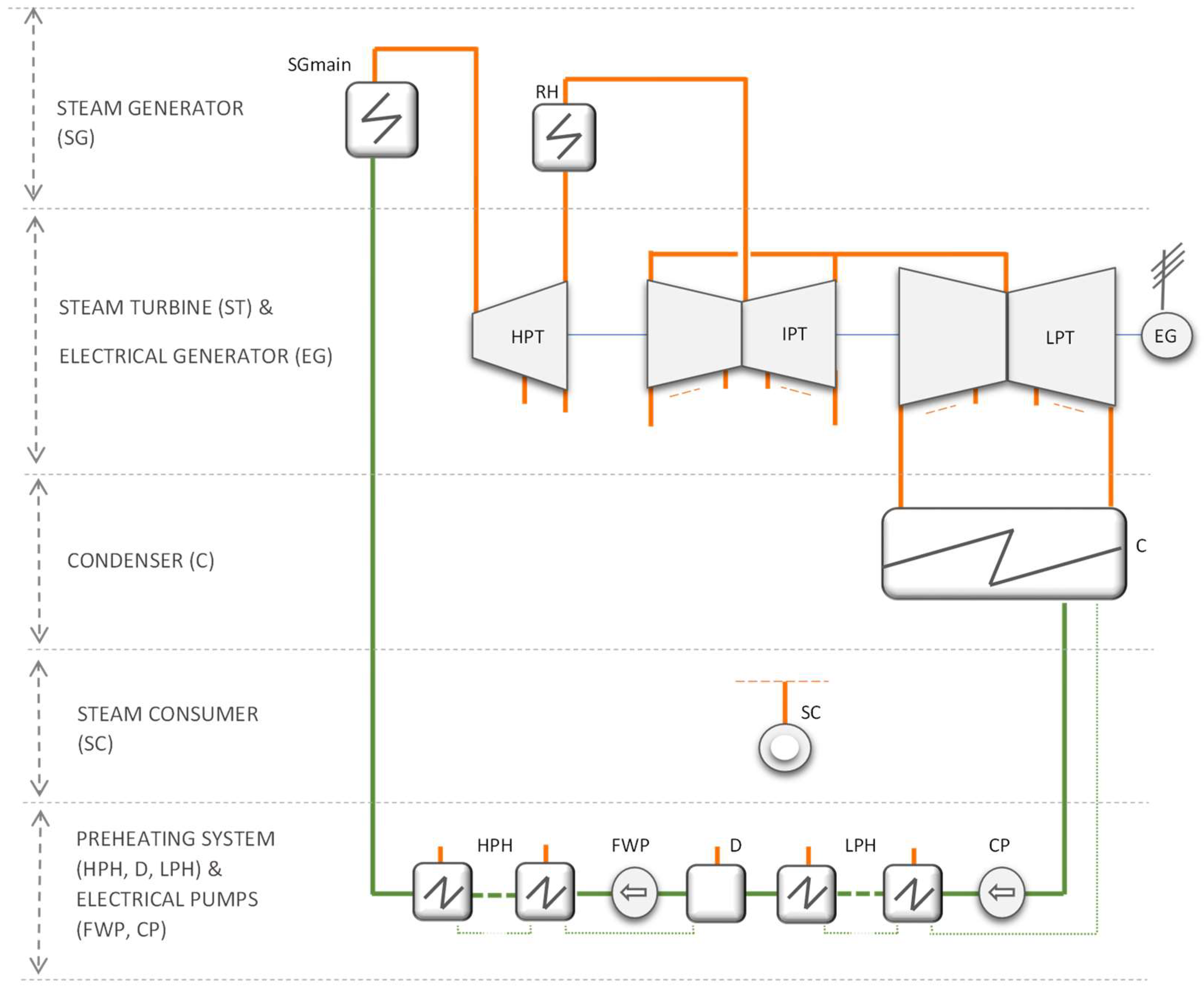
2. Thermodynamic Cycle
- The steam generator (SG), which comprises two main parts: the main part of the SG (mainSG), which generates steam with supercritical parameters, and the steam reheater (RH), where steam is reheated after its expansion in the first cylinder of the turbine.
- The steam turbine (ST) and the electrical generator (EG). The ST has three distinct cylinders through which steam passes and expands, namely the high-, intermediate-, and low-pressure turbines (HPTs, IPTs, LPTs). All these cylinders contain one or more steam extractions that provide steam to the preheating system and the steam consumer. This study considers HPTs with steam extraction. However, the number of steam extractions from IPTs and LPTs is variable, depending on the preheating system design optimization. In the electrical generator (EG), mechanical energy is transformed into electrical energy.
- The condenser (C) condenses the steam that exits the LPTs into water by using a cooling water circuit. The condensing pressure is below the atmospheric pressure to maximize the steam expansion in the ST.
- The steam consumer (SC) requires a specific heat flow rate with specific steam parameters. To ensure this requirement, the ST should have a steam extraction whose position from the ST depends on the steam pressure to the SC.
- The preheating system. Feedwater is heated through a series of low-pressure heaters (LPHs), a deaerator (D), and a series of high-pressure heaters (HPHs). Steam for the preheating system is extracted from the ST. The condensate from the HPHs is carried in cascade toward D, and the condensate from the LPHs is carried in cascade toward C.
- Electrical pumps. There are the following electrical pumps along the thermodynamic circuit: the condensate pumps (CPs), which introduce the condensate into the LPHs and send it toward D, and the feedwater pumps (FWPs), which send the feedwater through the HPHs toward the SG.
3. Materials and Methods
3.1. Input Data, Assumptions, and Restrictions
- For the steam generator, the use of the same known fuel, with a given heat flow rate of fuel (QSG); the efficiency of the SG is constant (0.95).
- For the steam turbine, there is a bleed steam in the HPT; the steam quality at the LPT exit must be higher than the minimum accepted value (0.88).
- For the electrical generator, the mechanical efficiency of the turbine and electrical generator (ηmg) depends on the internal power of the ST.
- For the condenser, the condenser steam pressure (pc) is an input parameter (Table 1), which varies within a given interval.
- For the steam consumer, the steam pressure at the SC and the heat flow rate at the SC are input values (Table 1), modified according to the SC requirements. The SC condensate is replaced by the supply water at the condenser (C).
- For the preheating system, equal temperature increases in preheaters, lower than the maximum imposed value of 32 °C (except for preheaters next to the SC); use of the lowest number of preheaters; the number of HPHs should not exceed the number of LPHs; the deaerator pressure should be lower than the maximum imposed value (12 bar); steam extraction pressure to preheaters closest to the SC is adjusted to be equal to the SC pressure.
- For the pumps, the electrical motor overall efficiencies of the pumps are constant (0.85 for the FWP and 0.8 for the CP).
3.2. Modeling Equations
3.2.1. Steam Generator (SG, SGmain, RH)
3.2.2. Steam Turbine (ST)
- The dimensionless ratio between the reheating pressure and the main steam pressure:
- The difference between the reheat and the main steam temperature, in °C:where —reheat steam temperature, in °C; —main steam temperature, in °C.
3.2.3. Electrical Generator (EG)
3.2.4. Preheating System (HPH, D, LPH) and Condenser (C)
3.2.5. Electrical Pumps (FWP, CP)
3.3. Performance Indicators
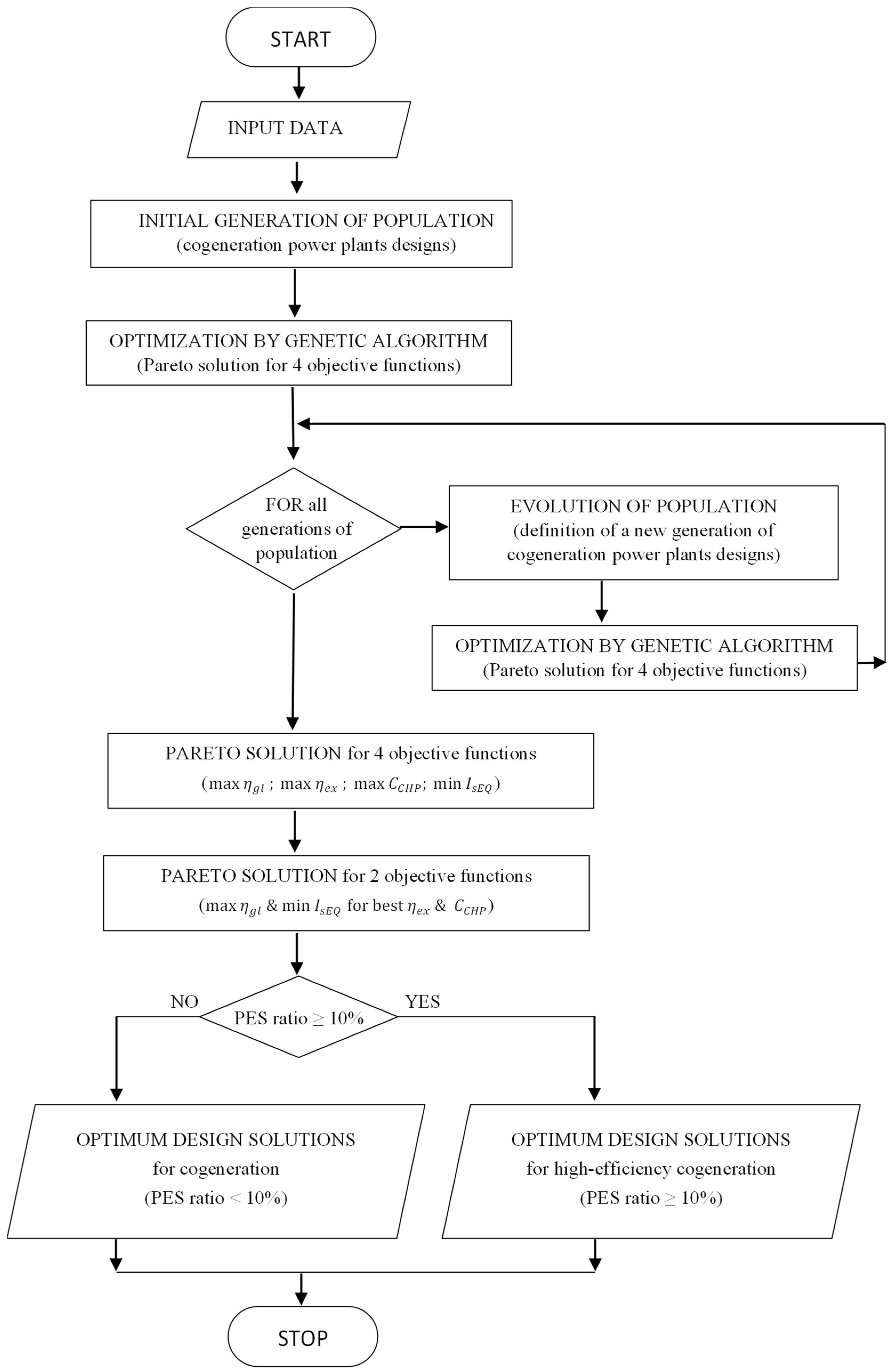
3.4. Thermodynamic Cycle Optimization
- Heuristic optimization of the four objective functions, Objective_function_4, shown in Equation (19): the simultaneous maximization of global efficiency, exergetic efficiency, and power-to-heat ratio in full cogeneration mode, and minimization of specific investment in equipment.
- Two-objective Pareto optimization, chosen from the four objective Pareto solutions, involving simultaneous maximization of global efficiency and minimization of specific investment in equipment:Pareto_2/4 = {ηgl = max; ηex = max}.
- Selection of high-efficiency cogeneration schemes from the two objective Pareto solutions (Equation (21)).
4. Results and Discussion
4.1. Input Data
- Low heat flow rate to the SC: QSC = 0.1QSG = 170 MW;
- Medium heat flow rate to the SC: QSC = 0.2QSG = 340 MW;
- High heat flow rate to the SC: QSC = 0.4QSG = 680 MW.
4.2. Pareto Design Solutions for Low Heat Flow Rate to SC
4.3. Pareto Design Solutions for Medium Heat Flow Rate to SC
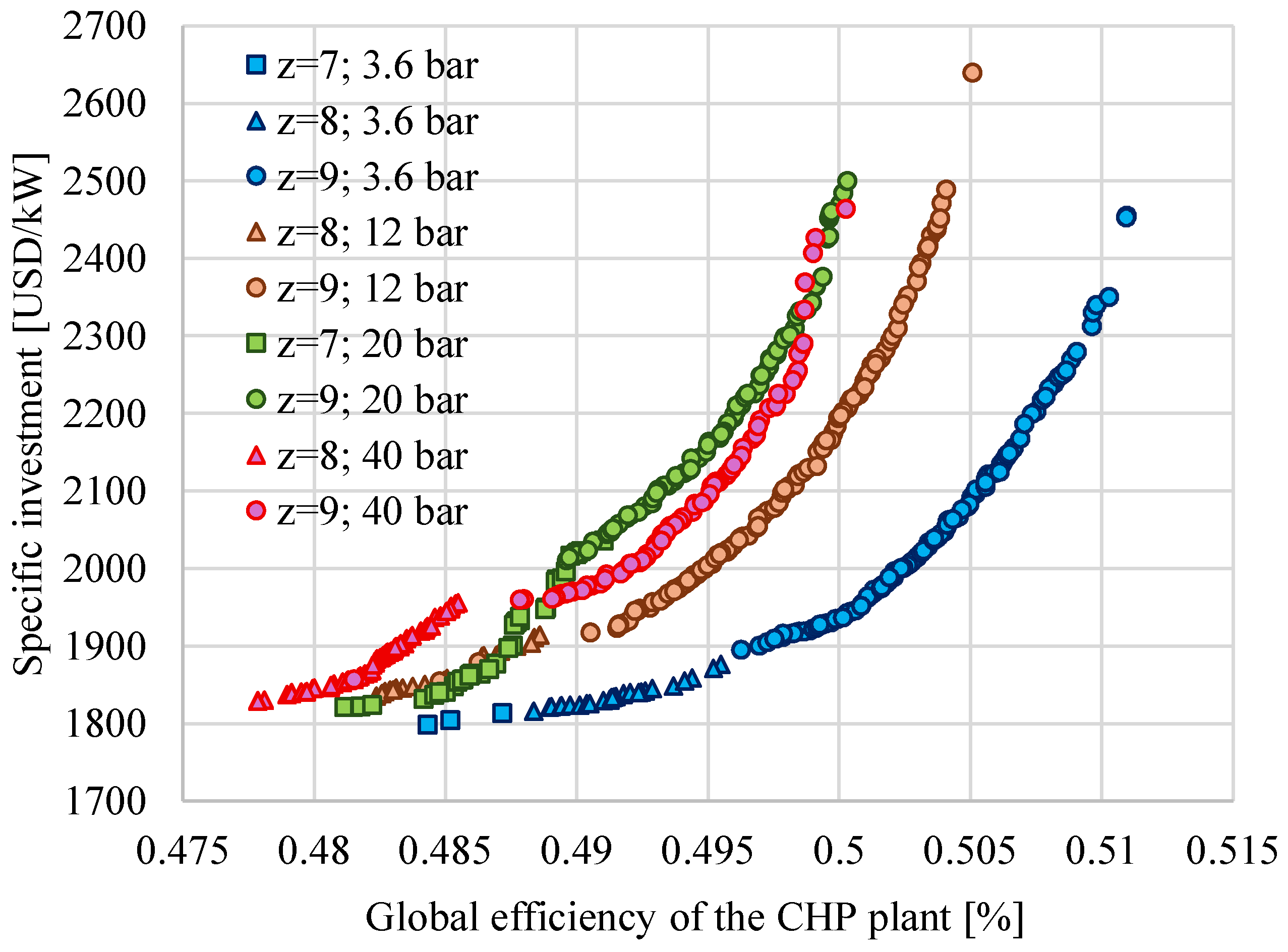
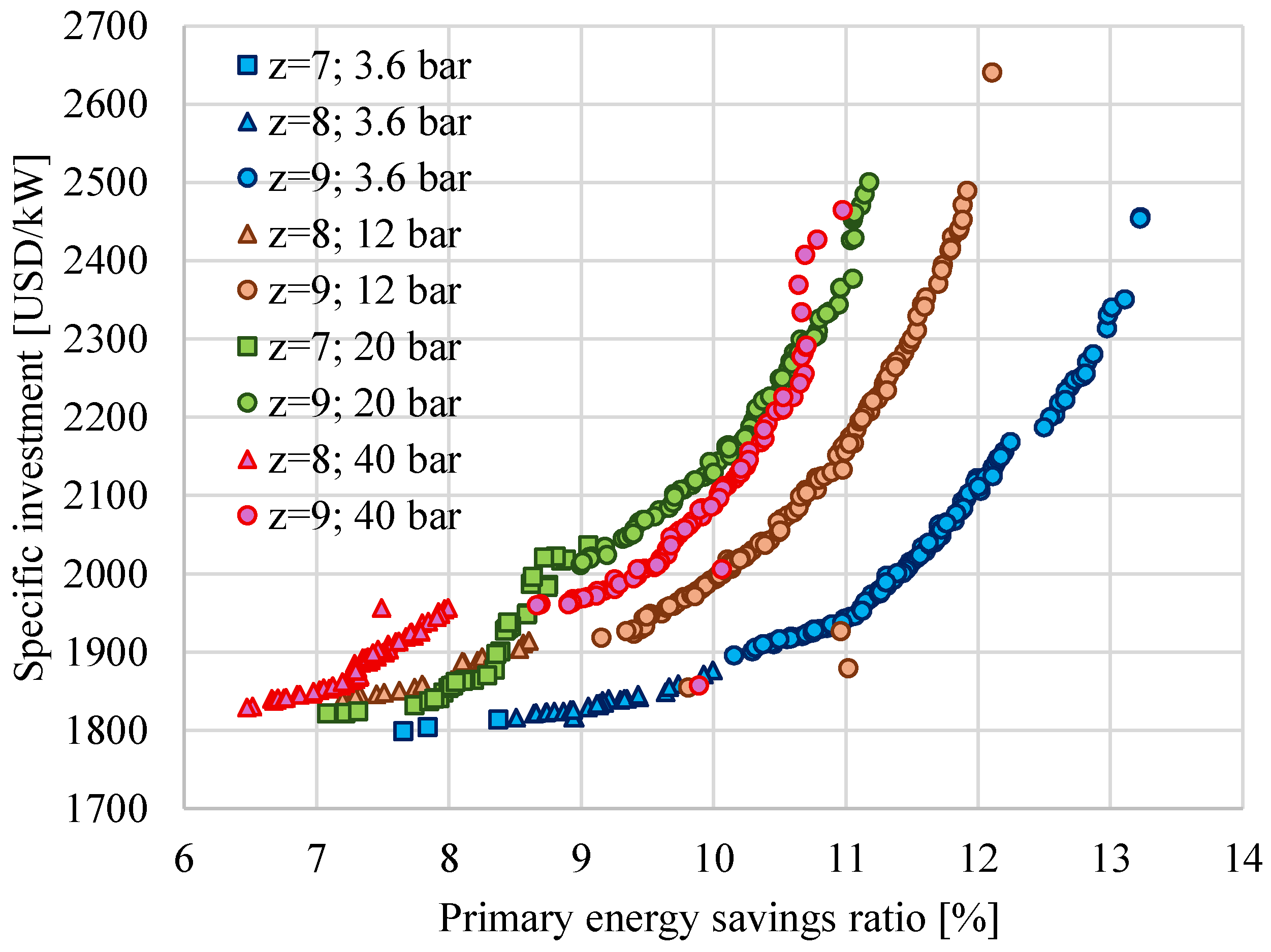
4.4. Pareto Design Solutions for High Heat Flow Rate to SC
- -
- If z = 8, the SC is fed from the steam extraction somewhere along the HPT, with the pressure at the HPT exit able to vary freely between the limits imposed for .
- -
- If z = 9, the SC is fed from the steam extraction at the exit of the HPT, thus fixing the pressure at the HPT exit at 40 bar, as required by the SC.
5. Conclusions
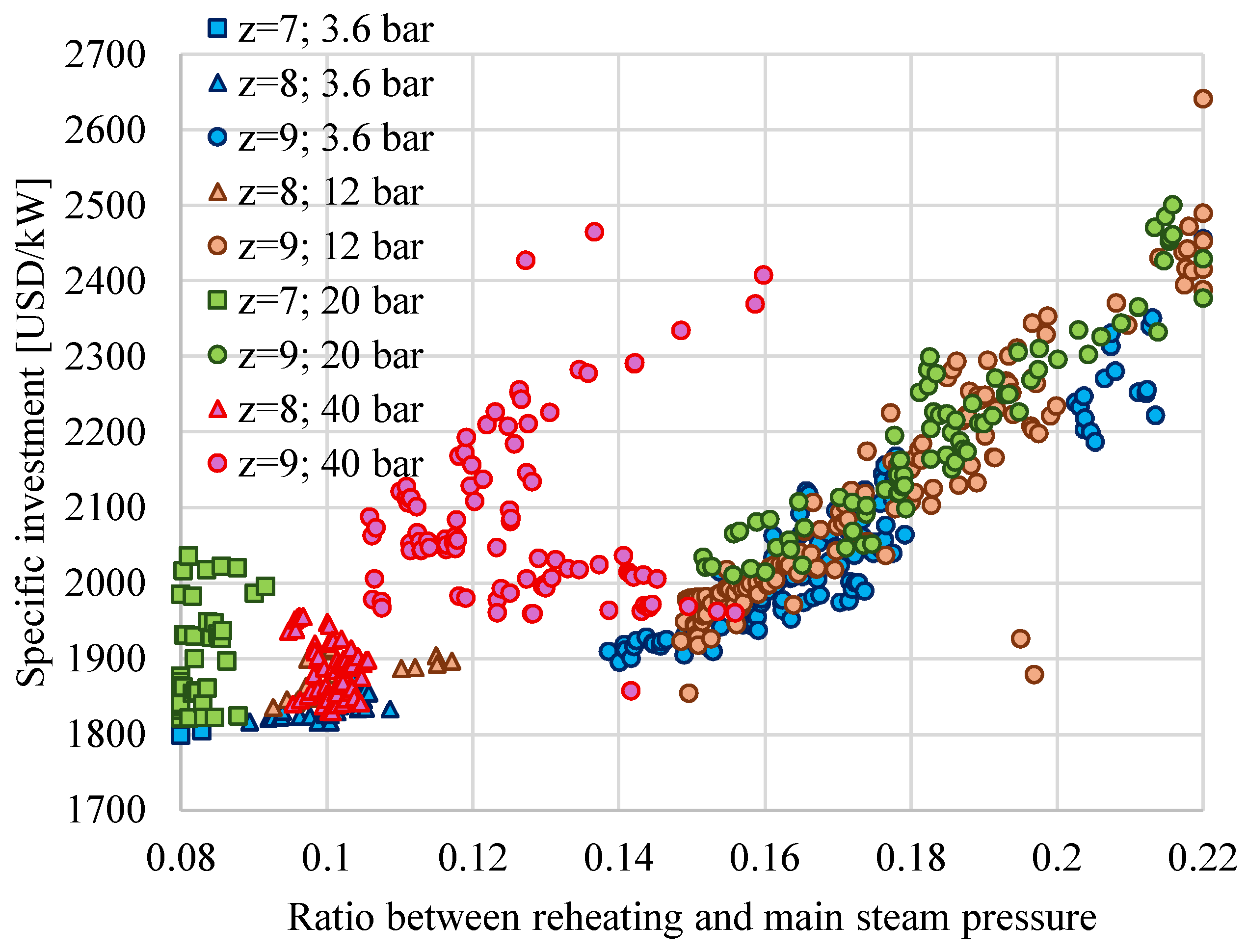
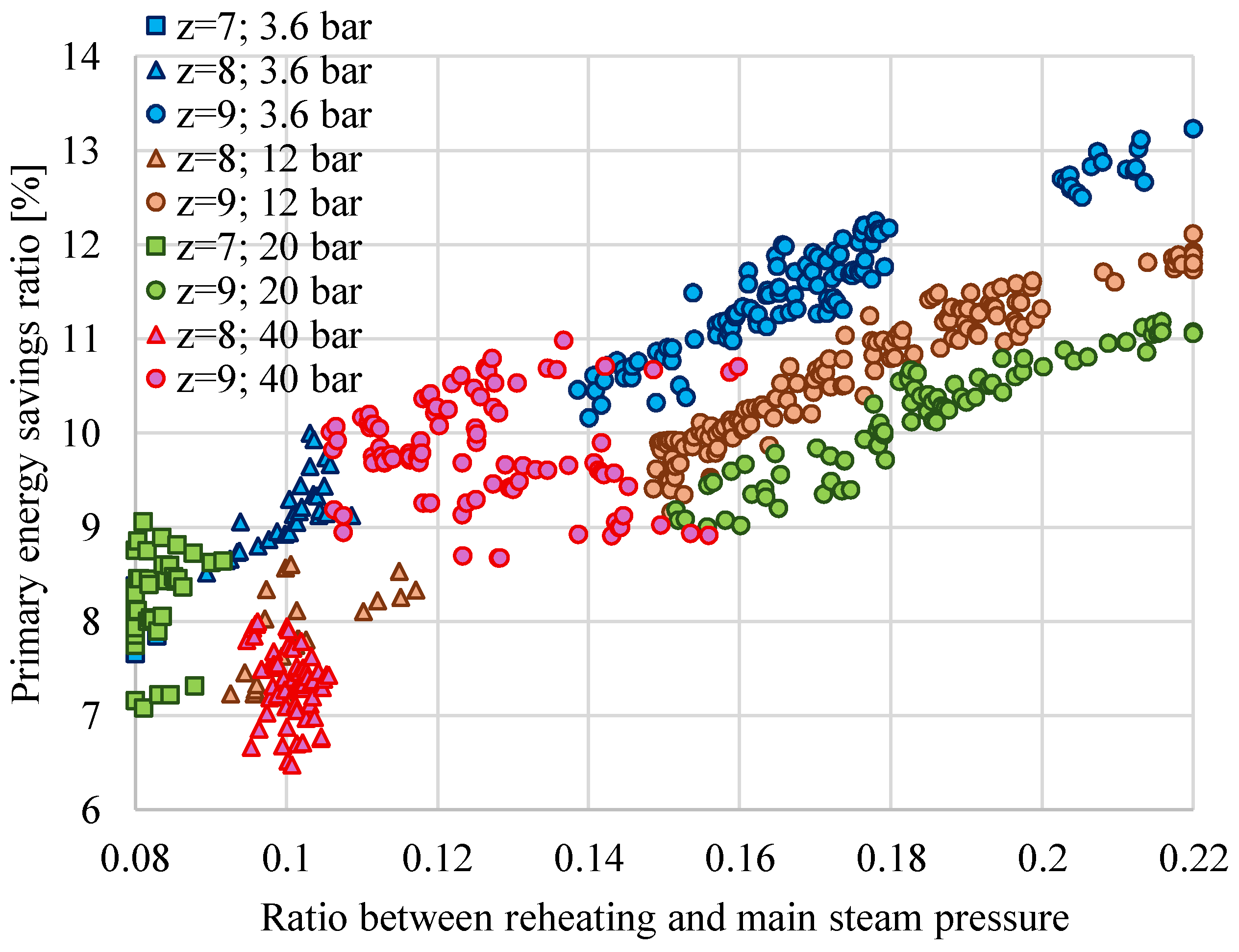
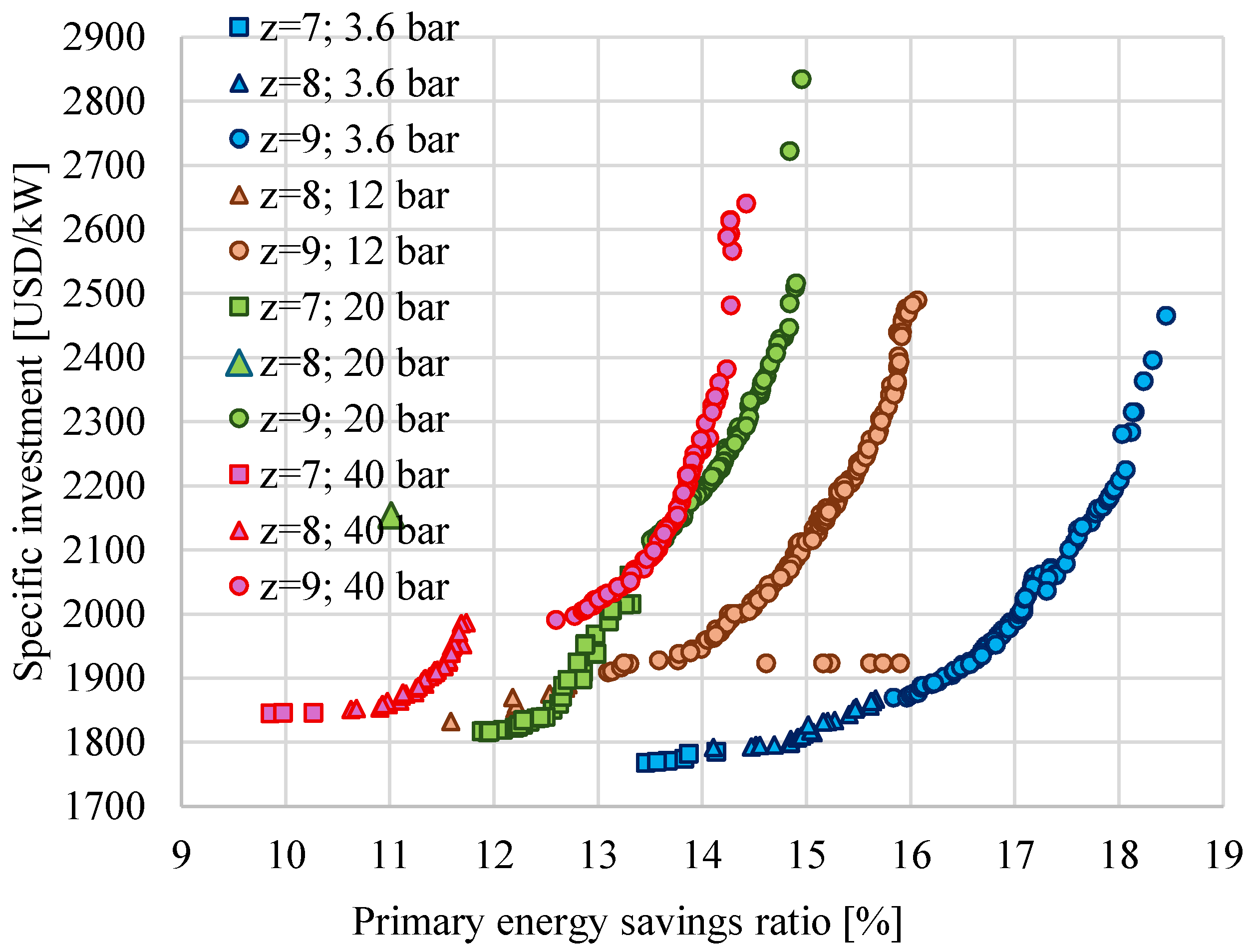
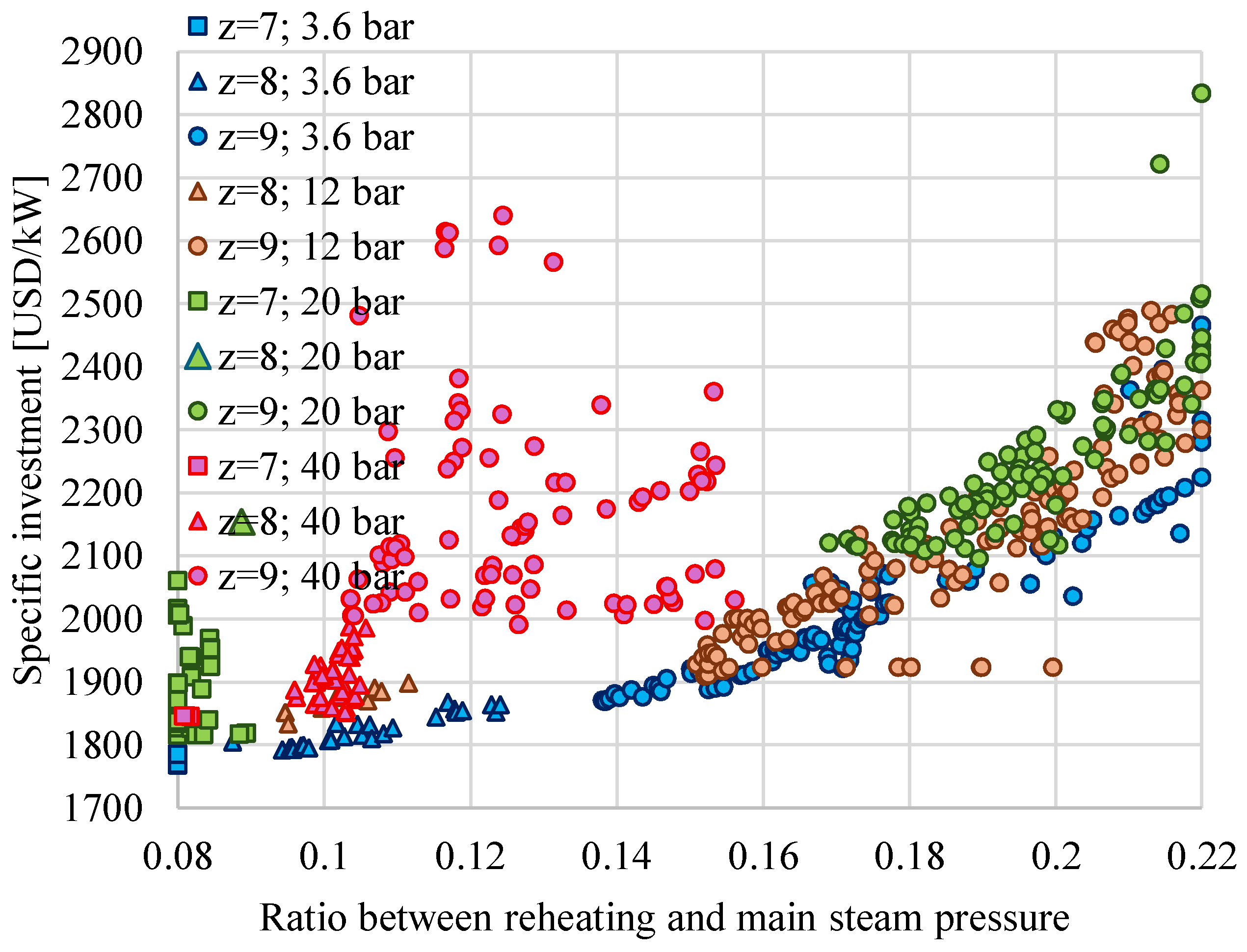
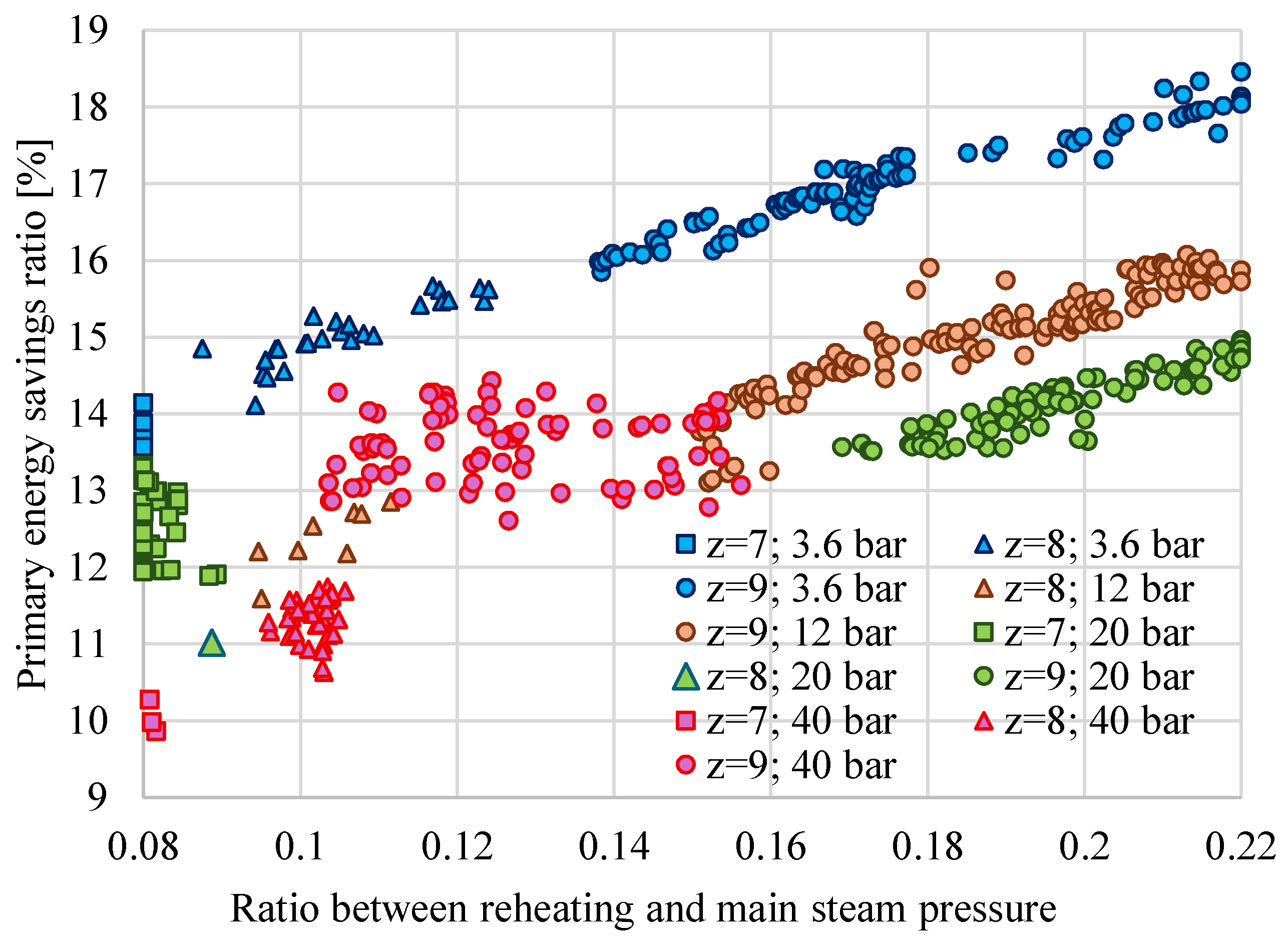
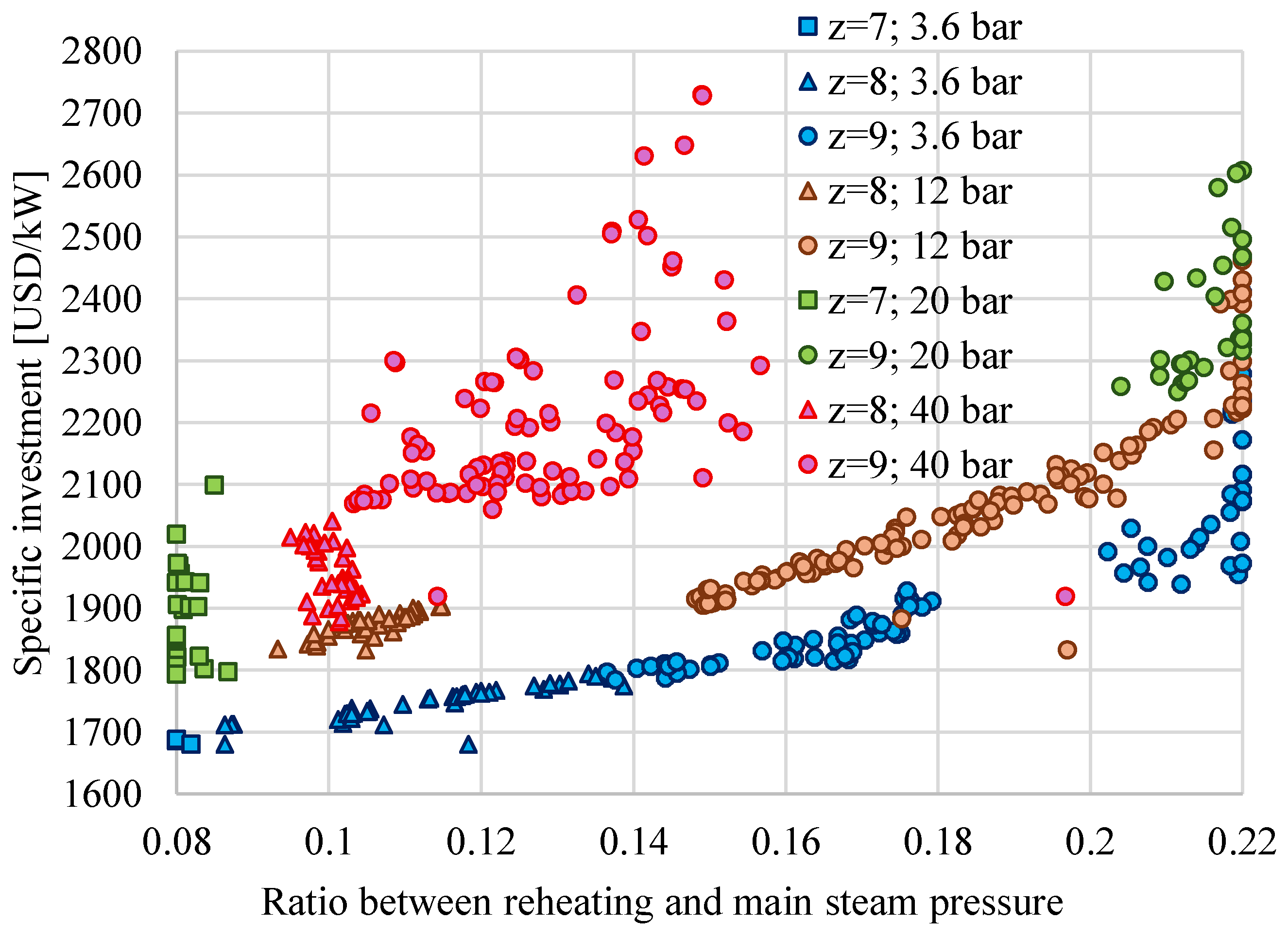
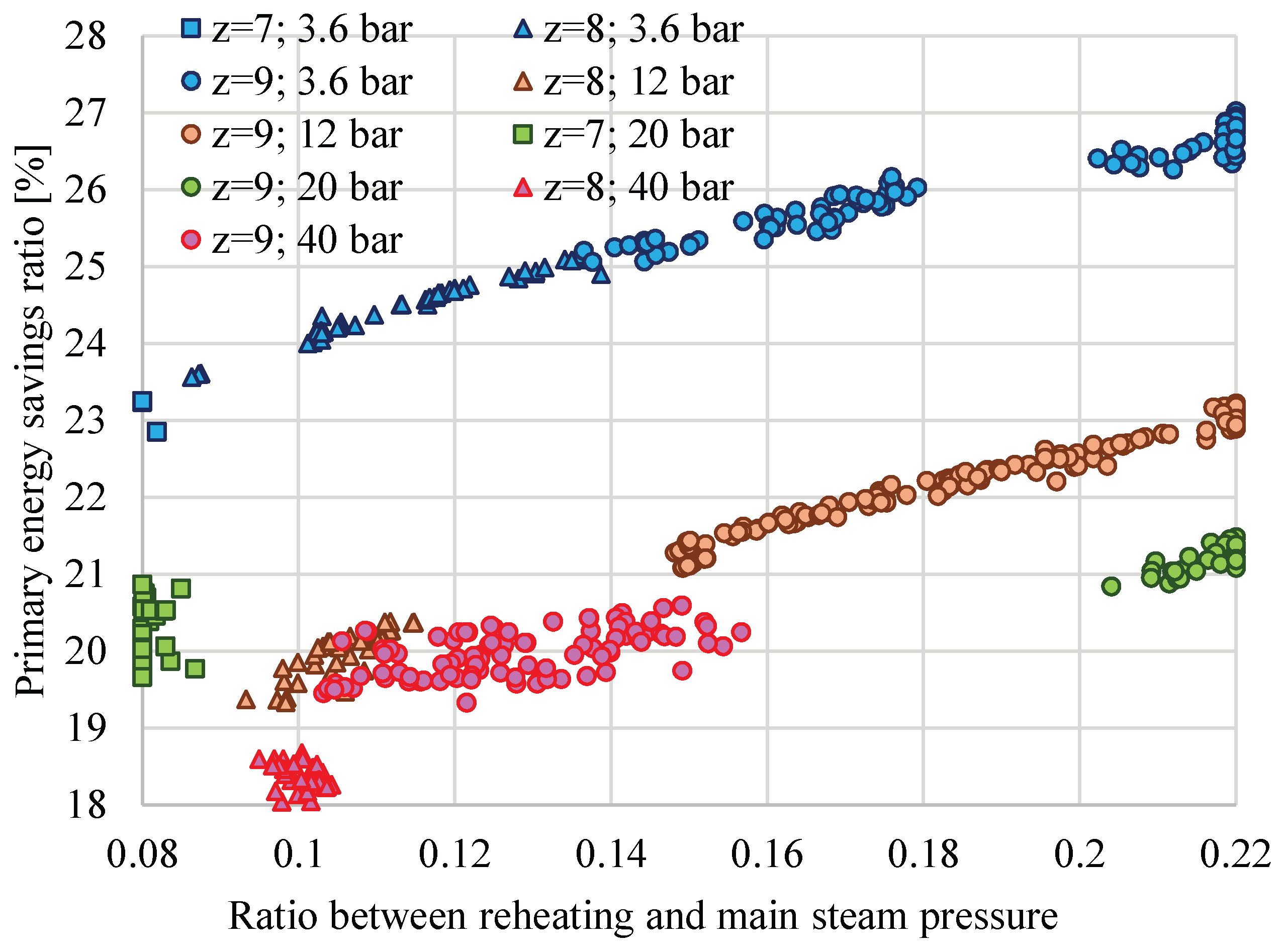
- The ratio between the reheating pressure and the main steam pressure (rp) depends strongly on the number of preheaters (z); higher z corresponds to a higher optimal rp.
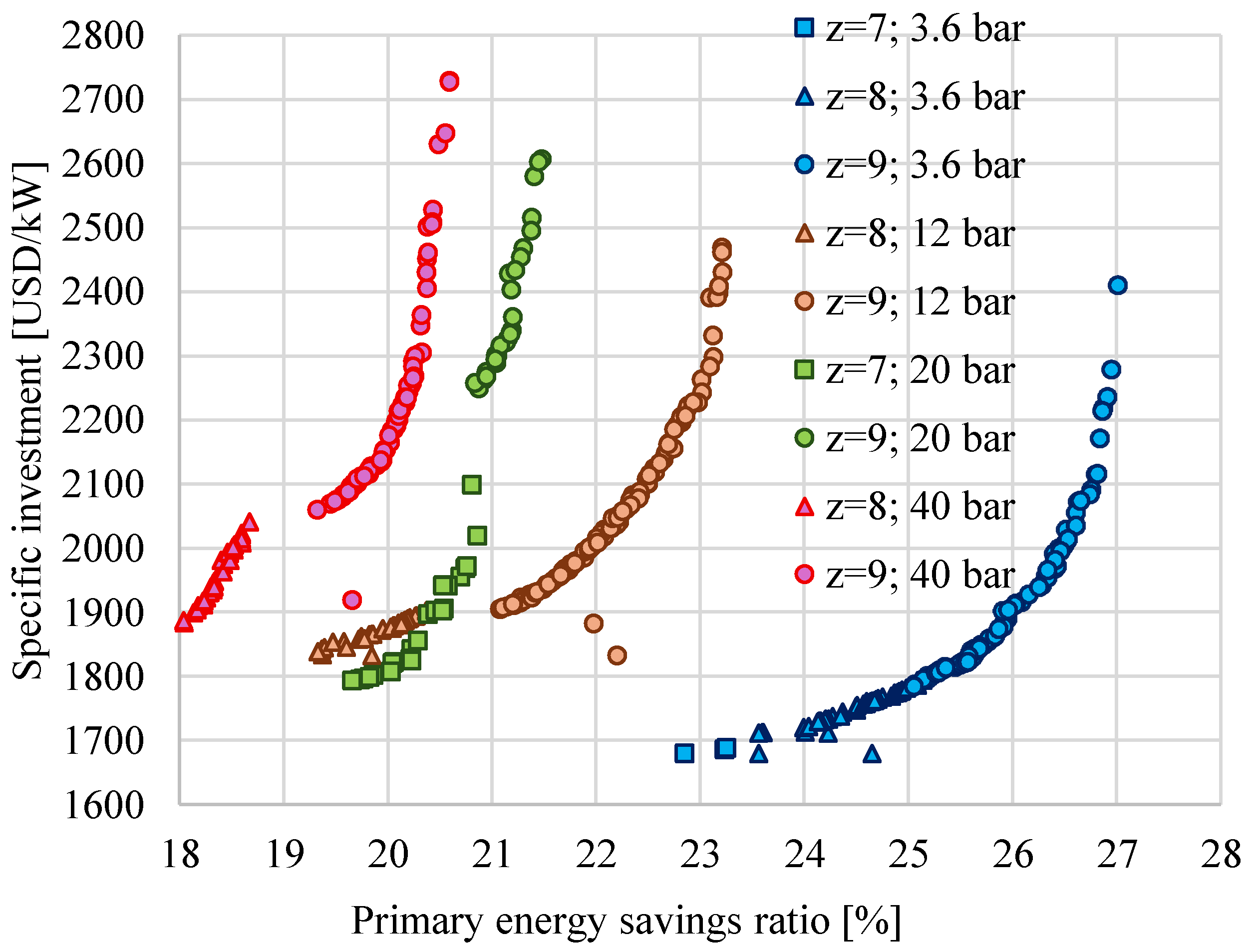
- The PESratio depends strongly on SC requirements. When QSC increases, the PESratio also increases from values below 10% (for QSC = 0.1QSG and a small number of preheaters) to values above 25% (for QSC = 0.4QSG, pSC = 3.6 bar, and z = 9).
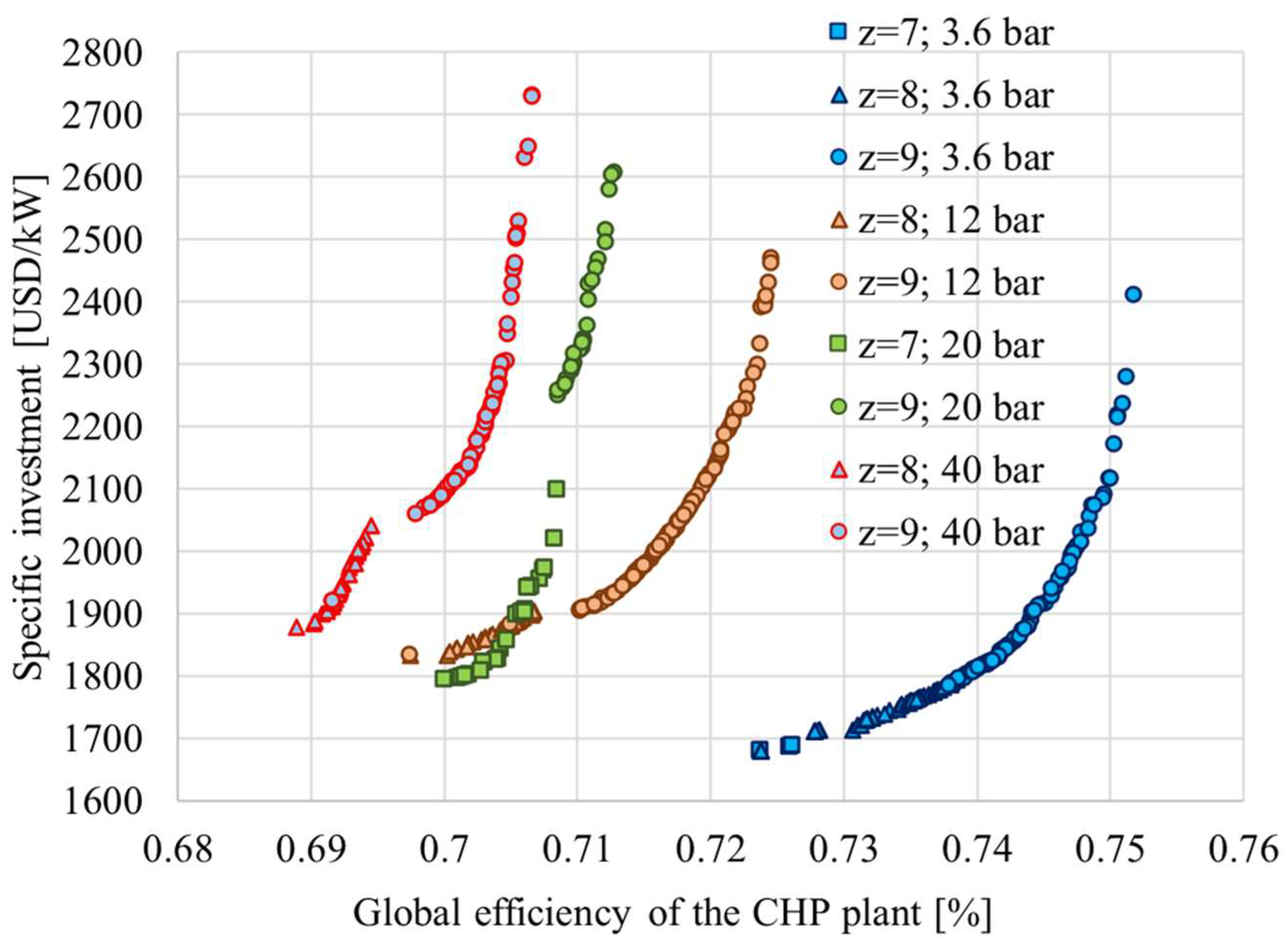
- For a medium-heat consumer (QSC = 0.2QSG) at IsEQ = 2000 USD/kW and z = 9, ηgl increases by 4.3% if pSC decreases from 40 bar to 3.6 bar.
- For the same QSC, CCHP increases with the decrease in pSC due to the supplementary power produced in cogeneration.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Directive 2012/27/EU of the European Parliament and of the Council of 25 October 2012 on Energy Efficiency, Amending Directives 2009/125/EC and 2010/30/EU and Repealing Directives 2004/8/EC and 2006/32/EC. Off. J. Eur. Union 2012, L 315/1, 14.11.2012. Available online: https://eur-lex.europa.eu/legal-content/EN/TXT/HTML/?uri=CELEX:32012L0027 (accessed on 28 June 2025).
- Kurmayer, N.J. New EU Energy Efficiency Directive Sets 11.7% Reduction Target by 2030. Euractiv. 10 March 2023. Available online: https://www.euractiv.com/section/energy-environment/news/new-eu-energy-efficiency-directive-sets-11-7-reduction-target-by-2030/ (accessed on 28 June 2025).
- Caglayan, H.; Caliskan, H.; Hong, H.; Caliskan, N.; Kale, U.; Kilikevičius, A. Advanced exergoeconomic analysis and mathematical modelling of the natural gas fired gas turbine unit used for industrial cogeneration system. Case Stud. Therm. Eng. 2024, 61, 104969. [Google Scholar] [CrossRef]
- Da Silva, L.M.C.; Alcântara, M.T.; Higa, M. Cogeneration and thermal integration of multiple effect evaporator in sugarcane industry. Therm. Sci. Eng. Prog. 2025, 63, 103715. [Google Scholar] [CrossRef]
- Lozano, M.A.; dos Santos, R.; Santos, J.J.C.S.; Serra, L.M. Optimal modes of operation and product cost allocation in sugarcane steam cogeneration plants. Therm. Sci. Eng. Prog. 2024, 52, 102686. [Google Scholar] [CrossRef]
- Wu, X.L.; Yang, Y.; Li, K.; Xu, Y.W.; Peng, J.; Chi, B.; Wang, Z.; Li, X. Performance prediction of gasification-integrated solid oxide fuel cell and gas turbine cogeneration system based on PSO-BP neural network. Renew. Energy 2024, 237, 121711. [Google Scholar] [CrossRef]
- Iodice, P.; Langella, G.; Amoresano, A.; Senatore, A. Comparative exergetic analysis of solar integration and regeneration in steam power plants. J. Energy Eng. 2017, 143, 04017042. [Google Scholar] [CrossRef]
- Hajabdollahi, H.; Saleh, A.; Yadollahi, N.K. Multi-objective optimization of a solar-assisted cogeneration system in hot climate: An exergoeconomic and exergoenvironmental assessment. Therm. Sci. Eng. Prog. 2025, 62, 103656. [Google Scholar] [CrossRef]
- Michaelides, E.E. Power and Energy Requirements for Carbon Capture and Sequestration. Thermo 2025, 5, 8. [Google Scholar] [CrossRef]
- Guo, P.; Hua, J.; Xue, Q.; Zhao, X.; Hu, J.; Duan, P. A study on the integration and flexible operation strategy of sodium-based CO2 capture system in cogeneration power plants and economic analysis. Energy Convers. Manag. 2025, 326, 119491. [Google Scholar] [CrossRef]
- Zhi, L.H.; Hu, P.; Chen, L.X.; Zhao, G. Performance analysis and optimization of engine waste heat recovery with an improved transcritical-subcritical parallel organic Rankine cycle based on zeotropic mixtures. Appl. Therm. Eng. 2020, 181, 115991. [Google Scholar] [CrossRef]
- Abolghasem, M.; Sadeghi, K.; Ghazaie, S.H.; Sokolova, E.; Sergeev, V.; Ksenia, N.; Peng, W. Enhancing nuclear cogeneration efficiency using the low-grade waste heat recovery from nuclear hydrogen production system. Nucl. Eng. Des. 2025, 441, 114166. [Google Scholar] [CrossRef]
- Huang, Z.; You, H.; Han, J.; Li, G.; Xiao, Y.; Hu, B.; Chen, Z.H.; Chen, D. Techno-economic evaluation and multi-objective optimization of a cogeneration system integrating solid oxide fuel cell with steam Rankine and supercritical carbon dioxide Brayton cycles. Fuel 2025, 382, 133675. [Google Scholar] [CrossRef]
- Wu, Y.; Fu, L.; Zhang, S.; Tang, D. Study on a novel co-operated heat and power system for improving energy efficiency and flexibility of cogeneration plants. Appl. Therm. Eng. 2019, 163, 114429. [Google Scholar] [CrossRef]
- Sharew, S.S.; Di Pretoro, A.; Yimam, A.; Negny, S.; Montastruc, L. Combining Exergy and Pinch Analysis for the Operating Mode Optimization of a Steam Turbine Cogeneration Plant in Wonji-Shoa, Ethiopia. Entropy 2024, 26, 453. [Google Scholar] [CrossRef]
- Sharew, S.S.; Di Pretoro, A.; Yimam, A.; Negny, S.; Montastruc, L. Exploiting exergy and exergoeconomic analysis as decisional tool for cogeneration plant optimal operating mode: A sugar factory case study. Energy Rep. 2024, 12, 143–157. [Google Scholar] [CrossRef]
- Shen, F.; Zhao, L.; Du, W.; Zhong, W.; Qian, F. Large-scale industrial energy systems optimization under uncertainty: A data-driven robust optimization approach. Appl. Energy 2020, 259, 114199. [Google Scholar] [CrossRef]
- Ali, R.H.; Samee, A.A.A.; Attalla, M.; Maghrabie, H.M. Energy-exergy approach of a cogeneration system in pulp and paper industry with a chemical recovery of black liquor and soda. Case Stud. Therm. Eng. 2023, 42, 102712. [Google Scholar] [CrossRef]
- Zeitoun, O.; Orfi, J.; Khan, S.U.-D.; Al-Ansary, H. Desalinated Water Costs from Steam, Combined, and Nuclear Cogeneration Plants Using Power and Heat Allocation Methods. Energies 2023, 16, 2752. [Google Scholar] [CrossRef]
- Choi, S.; Kim, S.; Jung, M.; Lee, J.; Lim, J.; Kim, M. Comparative analysis of exergy-and enthalpy-based allocation methods for cogeneration businesses in the industrial complex of South Korea. Energy 2022, 240, 122837. [Google Scholar] [CrossRef]
- Li, D.; Wang, J. Study of supercritical power plant integration with high temperature thermal energy storage for flexible operation. J. Energy Storage 2018, 20, 140–152. [Google Scholar] [CrossRef]
- Manesh, M.K.; Navid, P.; Baghestani, M.; Abadi, S.K.; Rosen, M.A.; Blanco, A.M.; Amidpour, M. Exergoeconomic and exergoenvironmental evaluation of the coupling of a gas fired steam power plant with a total site utility system. Energy Convers. Manag. 2014, 77, 469–483. [Google Scholar] [CrossRef]
- Mousavi Rabeti, S.A.; Khoshgoftar Manesh, M.H.; Blanco-Marigorta, A.M.; Del Río Gamero, B. Multi-objective Optimization, Techno-economic Analysis, and Life Cycle Assessment of an Innovative Solar-Biomass-Driven Cogeneration System Integrated with MED-RO-MD: A Case Study of the Canary Islands. Renew. Energy 2025, 256, 123757. [Google Scholar] [CrossRef]
- Nikolaidis, P. Mixed Thermal and Renewable Energy Generation Optimization in Non-Interconnected Regions via Boolean Mapping. Thermo 2024, 4, 445–460. [Google Scholar] [CrossRef]
- Wang, X.; Wang, C.; Zhu, J.; Wang, H.; Dai, C.; Sun, L. Dynamic Exergy Analysis of Heating Surfaces in a 300 MW Drum-Type Boiler. Thermo 2025, 5, 17. [Google Scholar] [CrossRef]
- Saari, J.; Martinez, C.M.; Kaikko, J.; Sermyagina, E.; Mankonen, A.; Vakkilainen, E. Techno-economic optimization of a district heat condenser in a small cogeneration plant with a novel greedy cuckoo search. Energy 2022, 239, 122622. [Google Scholar] [CrossRef]
- Panowski, M.; Zarzycki, R.; Kobyłecki, R. Conversion of steam power plant into cogeneration unit—Case study. Energy 2021, 231, 120872. [Google Scholar] [CrossRef]
- Wang, Z.; Gu, Y.; Liu, H.; Li, C. Optimizing thermal–electric load distribution of large-scale combined heat and power plants based on characteristic day. Energy Convers. Manag. 2021, 248, 114792. [Google Scholar] [CrossRef]
- Wang, X.; Duan, L. Comparative study of multiple-mode collaborative operation strategy and traditional heat and power decoupling technologies for cogeneration system based on GTCC. Case Stud. Therm. Eng. 2023, 49, 103213. [Google Scholar] [CrossRef]
- Cenușă, V.E.; Opriș, I. Design optimization of cogeneration steam power plants with supercritical parameters. Sustain. Energy Technol. Assess. 2024, 64, 103727. [Google Scholar] [CrossRef]
- Opriş, I.; Cenuşă, V.E.; Norişor, M.; Darie, G.; Alexe, F.N.; Costinaş, S. Parametric optimization of the thermodynamic cycle design for supercritical steam power plants. Energy Convers. Manag. 2020, 208, 112587. [Google Scholar] [CrossRef]
- Opriș, I.; Cenușă, V.E. Parametric and heuristic optimization of multiple schemes with double-reheat ultra-supercritical steam power plants. Energy 2023, 266, 126454. [Google Scholar] [CrossRef]
- Kler, A.M.; Zharkov, P.; Epishkin, N.O. Parametric optimization of supercritical power plants using gradient methods. Energy 2019, 189, 116230. [Google Scholar] [CrossRef]
- Scilab Enterprises. Scilab 6.0.1. Available online: https://www.scilab.org/ (accessed on 4 May 2025).
- Bondarenko, O. XSteam. Water and Steam Properties According to IAPWS IF-97. 2020. Available online: https://fileexchange.scilab.org/toolboxes/502000 (accessed on 4 May 2025).
- Lai, F.; Wang, S.; Liu, M.; Yan, J. Operation optimization on the large-scale CHP station composed of multiple CHP units and a thermocline heat storage tank. Energy Convers. Manag. 2020, 211, 112767. [Google Scholar] [CrossRef]
- Zhang, K.; Liu, M.; Zhao, Y.; Zhang, S.; Yan, H.; Yan, J. Thermo-economic optimization of the thermal energy storage system extracting heat from the reheat steam for coal-fired power plants. Appl. Therm. Eng. 2022, 215, 119008. [Google Scholar] [CrossRef]
- Liu, H.; Geng, Z.; Gu, Y.; Mo, Z.; Yu, Z.; He, X.; Lu, S. A regional integrated energy system with a coal-fired CHP plant, screw turbine and solar thermal utilization: Scenarios for China. Energy Convers. Manag. 2020, 212, 112812. [Google Scholar] [CrossRef]
- Daneh-Dezfuli, A.; Ghanad-Dezfuli, M.; Changizian, M. A novel 4E-based optimization framework for circular biomass multi-generation systems integrating NSGA-II and ANN to enhance resource efficiency and sustainability. Int. Commun. Heat Mass Transf. 2025, 164, 108849. [Google Scholar] [CrossRef]
- Wang, L.; Yang, Y.; Dong, C.; Morosuk, T.; Tsatsaronis, G. Parametric optimization of supercritical coal-fired power plants by MINLP and differential evolution. Energy Convers. Manag. 2014, 85, 828–838. [Google Scholar] [CrossRef]
- Cenușă, V.E.; Opriș, I. Optimal Design Parameters for Supercritical Steam Power Plants. Thermo 2025, 5, 1. [Google Scholar] [CrossRef]
- Jiang, Q.; Wang, P. NSGA-II algorithm based control parameters optimization strategy for megawatt novel nuclear power systems. Energy 2025, 316, 134444. [Google Scholar] [CrossRef]

| Parameter | Symbol | Units |
|---|---|---|
| Heat flow rate to steam generator | QSG | kW |
| Main steam pressure | pms | bar |
| Main steam temperature | tms | °C |
| Difference between reheat and main steam temperature | Δtrh | °C |
| Ratio between the reheating pressure and the main steam pressure | rp | - |
| Steam pressure at condenser | pc | bar |
| Heat flow rate at SC | QSC | kW |
| Steam pressure at SC | pSC | bar |
| Performance Indicator | Symbol | Units | Equation | Legend |
|---|---|---|---|---|
| global efficiency of the CHP plant | ηgl | % | ηgl = (PEG − PEP + QSC)/QSG × 100 | PEG—power at EG, in kW; PEP—motor power of EP; QSC—heat flow rate to SC, in kW; QSG—fuel heat flow rate in SG, in kW. |
| exergetic efficiency | ηex | % | ηex = (PEG − PEP + ExSC)/Exf × 100 * | PEG—power at EG, in kW; PEP—motor power of EP; ExSC—exergy of SC, in kW; Exf—input exergy of the fuel, in kW |
| power-to-heat ratio in full cogeneration mode | CCHP | - | CCHP = PeCHP/QSC | PeCHP—power in full cogeneration mode, in kW |
| specific investment in equipment | IsEQ | USD/kW | IsEQ = CEQ fm/PEG | CEQ—cost of equipment (SGmain, RH, HPT, IPT, LPT, C, HPH, D, LPH, FWP, CP, EG), in USD; fm—multiplying factor to consider other costs and construction costs (fm = 2.08) [33]; PEG—power at EG, in kW. |
| Parameter | Units | Domain of Variation |
|---|---|---|
| pms | bar | 240–280 |
| tms | °C | 550–600 |
| Δtrh | °C | 0–20 |
| rp | - | 0.08–0.22 |
| pc | bar | 0.04–0.05 |
| pSC [bar] | Statistical Analysis | rp [-] | pms [bar] | tms [°C] | Δtrh [°C] | pc [bar] |
|---|---|---|---|---|---|---|
| 3.6 | med ± σ | 0.16 ± 0.03 | 272.3 ± 5.4 | 576.8 ± 7.1 | 15.1 ± 3.2 | 0.047 ± 0.003 |
| min–max | 0.08–0.22 | 246.4–279.9 | 558.6–591.7 | 5.5–19.4 | 0.04–0.05 | |
| 12 | med ± σ | 0.17 ± 0.03 | 274.3 ± 4.6 | 578.8 ± 6.3 | 15 ± 2.3 | 0.045 ± 0.003 |
| min–max | 0.09–0.22 | 254.6–279.2 | 566–596.2 | 4.7–19.7 | 0.04–0.05 | |
| 20 | med ± σ | 0.15 ± 0.05 | 272.1 ± 6.8 | 579.4 ± 5.5 | 14.9 ± 3.4 | 0.045 ± 0.003 |
| min–max | 0.08–0.22 | 244.1–278.9 | 559.8–591.4 | 4.1–19.1 | 0.04–0.05 | |
| 40 | med ± σ | 0.12 ± 0.02 | 274.2 ± 3.7 | 577 ± 7 | 15.7 ± 1.6 | 0.047 ± 0.003 |
| min–max | 0.09–0.16 | 263.5–279.3 | 557.9–595.9 | 6.9–18.8 | 0.04–0.05 |
| pSC [bar] | Statistical Analysis | PESratio [%] | ηgl [%] | IsEQ [USD/kW] | CCHP [-] | ηex [%] |
|---|---|---|---|---|---|---|
| 3.6 | med ± σ | 11 ± 1.3 | 50.1 ± 0.6 | 2005 ± 143 | 0.71 ± 0.04 | 40.3 ± 0.5 |
| min–max | 7.7–13.2 | 48.4–51.1 | 1799–2455 | 0.6–0.76 | 38.9–41.3 | |
| 12 | med ± σ | 10.2 ± 1.2 | 49.6 ± 0.6 | 2080 ± 167 | 0.56 ± 0.03 | 40.6 ± 0.5 |
| min–max | 7.2–12.1 | 48.2–50.5 | 1836–2640 | 0.48–0.61 | 39.4–41.4 | |
| 20 | med ± σ | 9.5 ± 1.1 | 49.2 ± 0.5 | 2102 ± 179 | 0.53 ± 0.03 | 40.4 ± 0.6 |
| min–max | 7.1–11.2 | 48.1–50 | 1821–2500 | 0.48–0.57 | 39.2–41.2 | |
| 40 | med ± σ | 8.8 ± 1.3 | 48.9 ± 0.6 | 2003 ± 135 | 0.48 ± 0.07 | 40.3 ± 0.6 |
| min–max | 6.5–11 | 47.8–50 | 1829–2464 | 0.38–0.55 | 39.2–41.3 |
| pSC [bar] | Statistical Analysis | rp [-] | pms [bar] | tms [°C] | Δtrh [°C] | pc [bar] |
|---|---|---|---|---|---|---|
| 3.6 | med ± σ | 0.16 ± 0.04 | 273.4 ± 5.1 | 576.4 ± 5.8 | 15.8 ± 2.9 | 0.047 ± 0.003 |
| min–max | 0.08–0.22 | 252.8–278.5 | 563.4–593.7 | 4.9–19.7 | 0.04–0.05 | |
| 12 | med ± σ | 0.18 ± 0.03 | 275.2 ± 2.4 | 580.3 ± 8 | 14.7 ± 2.6 | 0.045 ± 0.003 |
| min–max | 0.09–0.22 | 258.1–279.8 | 559–599.6 | 4.8–18 | 0.04–0.05 | |
| 20 | med ± σ | 0.16 ± 0.05 | 274.3 ± 4.8 | 579.8 ± 6.2 | 14.8 ± 2.1 | 0.045 ± 0.004 |
| min–max | 0.08–0.22 | 254.5–278.4 | 563.9–598.8 | 8.3–18.6 | 0.04–0.05 | |
| 40 | med ± σ | 0.12 ± 0.02 | 273.7 ± 3.8 | 580 ± 7.8 | 15.2 ± 2.6 | 0.046 ± 0.003 |
| min–max | 0.08–0.16 | 256–279.9 | 556.2–598.2 | 4.1–19.3 | 0.04–0.05 |
| pSC [bar] | Statistical Analysis | PESratio [%] | ηgl [%] | IsEQ [USD/kW] | CCHP [-] | ηex [%] |
|---|---|---|---|---|---|---|
| 3.6 | med ± σ | 16.5 ± 1.1 | 58.1 ± 0.6 | 1971 ± 144 | 0.74 ± 0.04 | 41 ± 0.5 |
| min–max | 13.5–18.5 | 56.5–59.2 | 1767–2465 | 0.65–0.8 | 39.7–42 | |
| 12 | med ± σ | 14.9 ± 0.9 | 57.1 ± 0.5 | 2136 ± 176 | 0.61 ± 0.03 | 41.4 ± 0.4 |
| min–max | 11.6–16.1 | 55.5–57.8 | 1833–2489 | 0.52–0.65 | 40.1–42 | |
| 20 | med ± σ | 13.7 ± 0.9 | 56.5 ± 0.4 | 2152 ± 204 | 0.56 ± 0.01 | 41.2 ± 0.6 |
| min–max | 11–15 | 55.5–57.2 | 1815–2834 | 0.54–0.58 | 40–42 | |
| 40 | med ± σ | 12.8 ± 1.2 | 56 ± 0.6 | 2085 ± 191 | 0.52 ± 0.04 | 41.1 ± 0.6 |
| min–max | 9.9–14.4 | 54.5–56.9 | 1845–2640 | 0.45–0.56 | 39.6–41.9 |
| pSC [bar] | Statistical Analysis | rp [-] | pms [bar] | tms [°C] | Δtrh [°C] | pc [bar] |
|---|---|---|---|---|---|---|
| 3.6 | med ± σ | 0.16 ± 0.04 | 274.4 ± 3.3 | 572.3 ± 6.3 | 15.5 ± 2.6 | 0.047 ± 0.003 |
| min–max | 0.08–0.22 | 252–279.3 | 561.5–594.9 | 4.3–19.4 | 0.04–0.05 | |
| 12 | med ± σ | 0.17 ± 0.04 | 275.2 ± 3.1 | 572.7 ± 6.1 | 12.3 ± 2.3 | 0.047 ± 0.003 |
| min–max | 0.09–0.22 | 254.5–279.7 | 557.2–591.2 | 5–18.3 | 0.04–0.05 | |
| 20 | med ± σ | 0.15 ± 0.07 | 273.9 ± 4.3 | 578.3 ± 7.7 | 13.8 ± 3.4 | 0.044 ± 0.004 |
| min–max | 0.08–0.22 | 263.8–278.7 | 558.2–591.9 | 1.4–18.2 | 0.04–0.05 | |
| 40 | med ± σ | 0.12 ± 0.02 | 276.6 ± 1.9 | 578.9 ± 6.8 | 13.9 ± 2.5 | 0.045 ± 0.003 |
| min–max | 0.09–0.2 | 269.3–279.5 | 566.3–597.3 | 6.5–19 | 0.04–0.05 |
| pSC [bar] | Statistical analysis | PESratio [%] | ηgl [%] | IsEQ [USD/kW] | CCHP [-] | ηex [%] |
|---|---|---|---|---|---|---|
| 3.6 | med ± σ | 25.4 ± 0.9 | 74 ± 0.7 | 1856 ± 132 | 0.76 ± 0.04 | 42.2 ± 0.5 |
| min–max | 22.9–27 | 72.4–75.2 | 1680–2410 | 0.67–0.82 | 41.1–43.2 | |
| 12 | med ± σ | 21.7 ± 1 | 71.4 ± 0.7 | 2022 ± 137 | 0.62 ± 0.03 | 42.5 ± 0.4 |
| min–max | 19.3–23.2 | 69.7–72.5 | 1832–2469 | 0.53–0.67 | 41.3–43.3 | |
| 20 | med ± σ | 20.76 ± 0.5 | 70.8 ± 0.3 | 2146 ± 263 | 0.58 ± 0.01 | 41.5 ± 0.8 |
| min–max | 19.65–21.48 | 70–71.3 | 1793–2607 | 0.56–0.6 | 41.2–43.4 | |
| 40 | med ± σ | 19.53 ± 0.78 | 70 ± 0.5 | 2139 ± 174 | 0.54 ± 0.03 | 42.3 ± 0.5 |
| min–max | 17.81–20.59 | 68.9–70.7 | 1878–2730 | 0.49–0.57 | 41.4–43.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cenușă, V.-E.; Opriș, I. Optimization of Cogeneration Supercritical Steam Power Plant Design Based on Heat Consumer Requirements. Thermo 2025, 5, 29. https://doi.org/10.3390/thermo5030029
Cenușă V-E, Opriș I. Optimization of Cogeneration Supercritical Steam Power Plant Design Based on Heat Consumer Requirements. Thermo. 2025; 5(3):29. https://doi.org/10.3390/thermo5030029
Chicago/Turabian StyleCenușă, Victor-Eduard, and Ioana Opriș. 2025. "Optimization of Cogeneration Supercritical Steam Power Plant Design Based on Heat Consumer Requirements" Thermo 5, no. 3: 29. https://doi.org/10.3390/thermo5030029
APA StyleCenușă, V.-E., & Opriș, I. (2025). Optimization of Cogeneration Supercritical Steam Power Plant Design Based on Heat Consumer Requirements. Thermo, 5(3), 29. https://doi.org/10.3390/thermo5030029





