Heat Exchanger Improvement of a Counter-Flow Dew Point Evaporative Cooler Through COMSOL Simulations
Abstract
:1. Introduction
2. Literature Review
3. M-Cycle’s Theoretical Background
4. Modeling and Simulation
4.1. Mathematical Descripcion
- -
- Along the x-direction (∆x), the airflow is evenly distributed.
- -
- The airflow is turbulent.
- -
- Material properties (air, water, and duct material) are constant within each temperature/humidity range for each experiment.
- -
- Radiative heat flux from the surface to the environment is negligible.
- -
- Evaporation rates are constant throughout the experiment (each range).
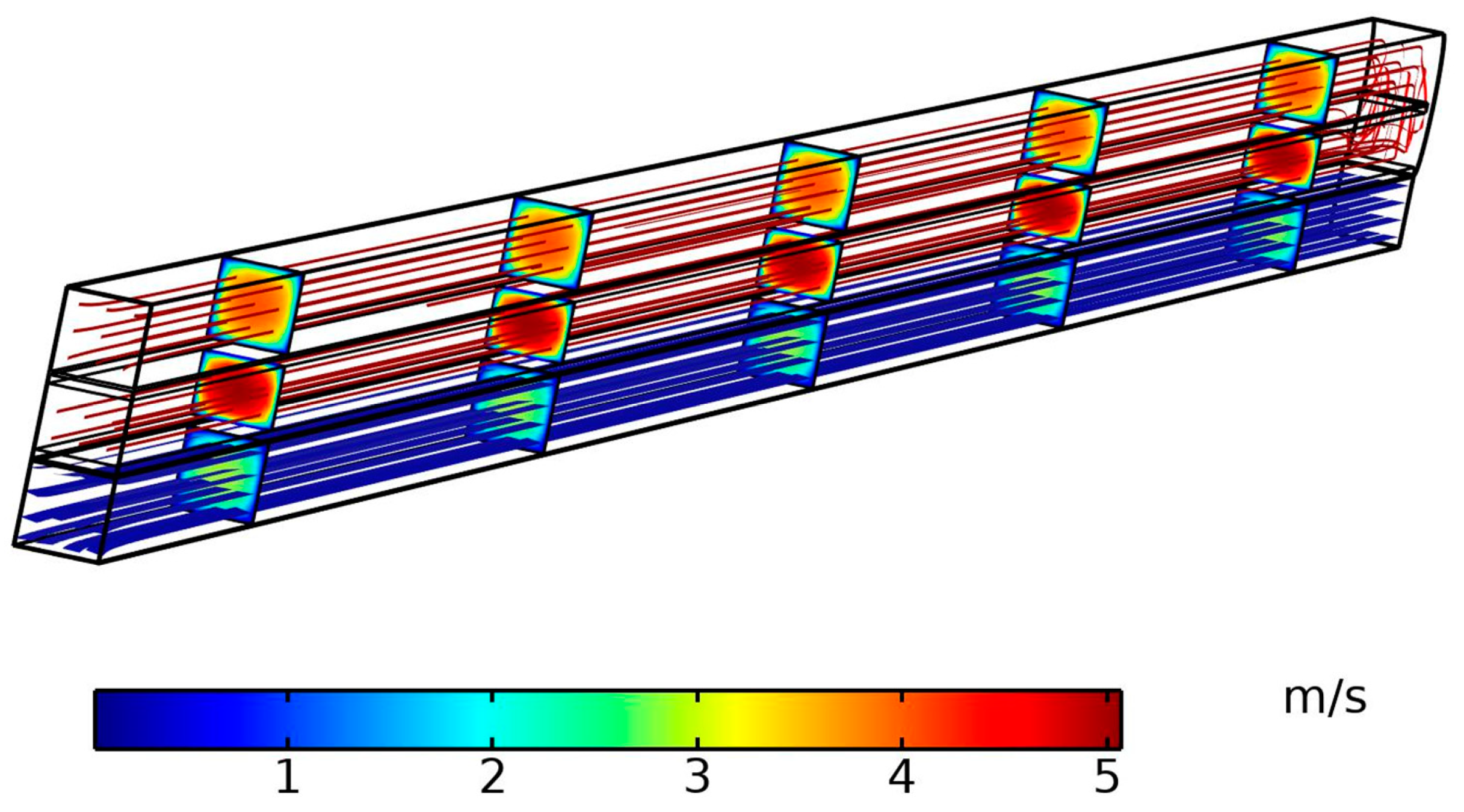
4.2. Simulation
4.3. Model Validation
5. Results and Discussion
5.1. Transient Response of Temperature and Humidity
5.2. Dynamic Performance Under External Weather Conditions
5.3. Analysis of the Physical Parameters of the Heat Exchanger
5.3.1. Channel Size
5.3.2. Material of Heat Exchanger
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Symbols | |
| x | x-axis |
| y | y-axis |
| z | z-axis |
| Δx | section at x-axis |
| temperature at the dry channel at j instant, °C | |
| enthalpy at the dry channel at j instant, J/kg | |
| temperature at the dry channel at j + 1 instant, °C | |
| enthalpy at the dry channel at j + 1 instant, J/kg | |
| j | instant |
| heat transfer rate at the dry channel at j instant, W | |
| temperature at the wet channel at j instant, °C | |
| enthalpy at the wet channel at j instant, J/kg | |
| temperature at the wet channel at j + 1 instant, °C | |
| enthalpy at the wet channel at j + 1 instant, J/kg | |
| humidity at the wet channel at j instant (after evaporation), kg/kg | |
| humidity at the wet channel at j + 1 instant (air from dry channel), kg/kg | |
| heat transfer rate at the wet channel at j instant, W | |
| mass transfer rate at the wet channel at j instant, kg/s | |
| heat transfer coefficient at the dry channel at j instant, W/m2K | |
| heat transfer coefficient at the wet channel at j instant, W/m2K | |
| mass flow at the wet channel, kg/s | |
| mass flow at the dry channel, kg/s | |
| u | velocity, m/s |
| A | area, m2 |
| ∆Twlm | Log Mean Temperature Difference at wet channel |
| ∆Tdlm | Log Mean Temperature Difference at dry channel |
| a | water density |
| ∆HVap | constant water latent heat of vaporization |
| molar mass of water vapor | |
| Twater | water temperature, °C |
| ρvs,j | surface vapor |
| ρvm,j | mean vapor |
| mass flow rate at dry channel, kg/s | |
| mass flow rate at wet channel, kg/s | |
| air density, kg/m3 | |
| velocity in dry channel, m/s | |
| velocity in wet channel, m/s | |
| channel height, m | |
| Log mean density difference at j instant | |
| Cv | vapor concentration |
| Csat | saturation concentration |
| evaporation rate | |
| latent heat source | |
| mass transfer coefficient at j instant, m/s |
References
- Lin, J.; Wang, R.Z.; Kumja, M.; Bui, T.D.; Chua, K.J. Multivariate scaling and dimensional analysis of the counter-flow dew point evaporative cooler. Energy Conv. Manag. 2017, 150, 172–187. [Google Scholar] [CrossRef]
- Amer, O.; Boukhanouf, R.; Ibrahim, H.G. A Review of Evaporative Cooling Technologies. Int. J. Environ. Sci. Dev. 2015, 6, 111–117. [Google Scholar] [CrossRef]
- Pistochini, T.; Modera, M. Water-use efficiency for alternative cooling technologies in arid climates. Energy Build. 2011, 43, 631–638. [Google Scholar] [CrossRef]
- International Energy Agency. Buildings. Available online: https://www.iea.org/energy-system/buildings (accessed on 2 October 2024).
- Duan, Z. Investigation of a Novel Dew Point Indirect Evaporative Air Conditioning System for Buildings. Ph.D. Thesis, University of Nottingham, Nottingham, UK, 2011. [Google Scholar]
- Tertipis, D.; Rogdakis, E. Maisotsenko cycle: Technology overview and energy-saving potential in cooling systems. Energy Emiss. Control. Technol. 2015, 3, 15–22. [Google Scholar] [CrossRef]
- Statista. U.S. Household Electricity Prices. 2023. Available online: https://www.statista.com/statistics/200199/residential-sector-electricity-prices-in-the-us-since-1975/ (accessed on 9 October 2024).
- Bernal, B.; Molero, J.C.; Perez De Gracia, F. Impact of fossil fuel prices on electricity prices in Mexico. J. Econ. Stud. 2019, 46, 356–371. [Google Scholar] [CrossRef]
- Energy. Office of Energy Efficiency & Renewable Energy. Heating, Ventilation, and Air Conditioning (HVAC). Available online: https://rpsc.energy.gov/tech-solutions/hvac (accessed on 2 October 2024).
- Mahmood, M.H.; Sultan, M.; Miyazaki, T.; Koyama, S.; Maisotsenko, V.S. Overview of the Maisotsenko cycle—A way towards dew point evaporative cooling. Renew. Sustain. Energy Rev. 2016, 66, 537–555. [Google Scholar] [CrossRef]
- Glanville, P.; Kozlov, A.; Maisotsenko, V. Dew Point Evaporative Cooling: Technology Review and Fundamentals. Ashrae Trans. 2011, 117, 111–118. [Google Scholar]
- Bom, J.; Foster, R.; Dijkstra, E.; Tummers, M. Evaporative Air-conditioning: Applications for Environmentally Friendly Cooling. World Bank Tech. Pap. 1999, 421, 1–69. [Google Scholar]
- Xu, P.; Ma, X.; Zhao, X.; Fancey, K. Experimental Investigation of a Super Performance Dew Point Air Cooler. Appl. Energy 2017, 203, 761–777. [Google Scholar] [CrossRef]
- Youssef, A.; Hamid, A. Energy saving potential of indirect evaporative cooling as fresh air pre-cooling in different climatic conditions in Saudi Arabia. In Proceedings of the 1st International Conference on Energy and Indoor Environment for Hot Climates, Doha, Qatar, 24–26 February 2014; pp. 256–263. [Google Scholar]
- Hsu, S.T.; Lavan, Z.; Worek, W.M. Optimization of wet-surface heat exchangers. Energy 1989, 14, 757–770. [Google Scholar] [CrossRef]
- Riangvilaikul, B.; Kumar, S. An experimental study of a novel dew point evaporative cooling system. Energy Build. 2010, 42, 637–644. [Google Scholar] [CrossRef]
- Chun, L.; Gong, G.; Peng, P.; Wan, Y.; Chua, K.J.; Fang, X.; Li, W. Research on thermodynamic performance of a novel building cooling system integrating dew point evaporative cooling, air-carrying energy radiant air conditioning and vacuum membrane-based dehumidification (DAV-cooling system). Energy Conv. Manag. 2021, 245, 114551. [Google Scholar] [CrossRef]
- Xiao, X.; Liu, J. A state-of-art review of dew point evaporative cooling technology and integrated applications. Renew. Sustain. Energy Rev. 2024, 191, 114142. [Google Scholar] [CrossRef]
- De Antonellis, S.; Cignatta, L.; Facchini, C.; Liberati, P. Effect of heat exchanger plates geometry on performance of an indirect evaporative cooling system. Appl. Therm. Eng. 2020, 173, 115200. [Google Scholar] [CrossRef]
- Badiei, A.; Akhlaghi, Y.; Zhaoa, X.; Li, J.; Yi, F.; Wang, Z. Can whole building energy models outperform numerical models, when forecasting performance of indirect evaporative cooling systems? Energy Convers. Manag. 2020, 213, 112886. [Google Scholar] [CrossRef]
- Liu, Y.; Akhlaghi, Y.G.; Zhao, X.; Li, J. Experimental and numerical investigation of a high-efficiency dew-point evaporative cooler. Energy Build. 2019, 197, 120–130. [Google Scholar] [CrossRef]
- Chen, Y.; Yang, H.; Luo, Y. Parameter sensitivity analysis and configuration optimization of indirect evaporative cooler (IEC) considering condensation. Appl. Energy 2017, 194, 440–453. [Google Scholar] [CrossRef]
- Golizadeh Akhlaghi, Y.; Aslansefat, K.; Zhao, X.; Sadati, S.; Badiei, A.; Xiao, X.; Shittu, S.; Fan, Y.; Ma, X. Hourly performance forecast of a dew point cooler using explainable Artificial Intelligence and evolutionary optimisations by 2050. Appl. Energy 2021, 281, 116062. [Google Scholar] [CrossRef]
- Wang, B.C.; Garcia, M.; Wei, C.D.; Cheng, G.G.; Pang, W.; Bui, T. Development and performance analysis of a compact counterflow dew-point cooler for tropics. Therm. Sci. Eng. 2023, 46, 102218. [Google Scholar] [CrossRef]
- Thermal Engineering. What is Logarithmic Mean Temperature Difference—LMTD—Definition. Available online: https://www.thermal-engineering.org/what-is-logarithmic-mean-temperature-difference-lmtd-definition/ (accessed on 9 October 2024).
- Lin, J.; Bui, D.T.; Wang, R.; Chua, K.J. On the fundamental heat and mass transfer analysis of the counter-flow dew point evaporative cooler. Appl. Energy 2018, 217, 126–142. [Google Scholar] [CrossRef]
- COMSOL. Tutorial Model of the Evaporative Cooling of Water. Available online: https://www.comsol.com/model/evaporative-cooling-of-water-6192 (accessed on 2 October 2024).
- Weather Spark. The Weather Year Round Anywhere on Earth—Weather Spark. Available online: https://weatherspark.com/ (accessed on 2 October 2023).




| Configuration | Characteristics | Limitations |
|---|---|---|
| Direct (DEC) | Direct configurations add moisture to the inlet air (air supplied to rooms for cooling) | - It is only suitable for use in dry and hot climates. - Wet-bulb effectiveness of 70–80% |
| Indirect (IEC) | It can reduce the air temperature to dry bulb temperature. This system avoids adding moisture to the air (inlet air humidity remains constant). | - Wet-bulb effectiveness of 40–80%. - It is only suitable for use in dry and hot climates. |
| Configuration | Characteristics |
|---|---|
| M-Cycle | - Indoor air and outdoor air work together, but without mixing. - 50–80% dew-point effectiveness. - Up to 80% of energy savings compared with conventional systems. - Wet-bulb effectiveness of 90–130%. - 10–30% higher effectiveness than conventional heat exchangers. |
| Parameter | Nominal Value | Range |
|---|---|---|
| Inlet Air Temperature | 25 °C | 25–40 °C |
| Air Humidity | 40% (8.02918 g/kg) | 20–80% |
| Air Speed | Wet Channel—3 m/s | 1–4 m/s |
| Working Air Ratio | Dry Channel—2 m/s | 1–4 m/s |
| Channel Length | 500 mm | Constant |
| Channel (Height/Width) | 5 mm | 3–7 mm |
| Channel Thickness | 0.1 mm | Constant |
| Water film Thickness | 0.2 mm | Constant |
| Channel Length(in) | P Model (°C) | H Model (°C) | Error (%) |
|---|---|---|---|
| 0 | 34.4 | 34.4 | 0 |
| 4 | 22.2588 | 28.2 | −21.0681 |
| 8 | 19.161 | 21.5 | −10.8791 |
| 12 | 16.746 | 16.2 | 3.3704 |
| 16 | 14.4886 | 14.47 | 0.1285 |
| 20 | 12.5461 | 11.2 | 12.0188 |
| 40 °C | 35 °C | 30 °C | 25 °C | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RH (%) | OT P Model | OT R Model | Error (%) | OT P Model | OT R Model | Error (%) | OT P Model | OT R Model | Error (%) | OT P Model | OT R Model | Error (%) |
| 40 | 23.1 | 17 | 26 | 19.36 | 16 | 14 | 15.48 | 16.3 | 5 | 11.81 | 16 | 35 |
| 60 | 30.16 | 21.5 | 29 | 25.77 | 21 | 19 | 21.3 | 20 | 6 | 16.94 | 19 | 12 |
| 80 | 35.61 | 27.5 | 23 | 30.85 | 27 | 12 | 26.06 | 26.5 | 2 | 21.3 | 26 | 22 |
| RH (%) | Dew Point Effectiveness | Wet Bulb Effectiveness |
|---|---|---|
| 20 | 78.16 | 153.17 |
| 40 | 90.34 | 153.08 |
| 60 | 97.10 | 146.62 |
| 80 | 99.91 | 138.46 |
| City | RH (%) | Inlet Temp. P Model | Outlet Temp. P Model |
|---|---|---|---|
| Beijing, China | 76.5 | 31.06 | 26.508 |
| Xi’an, China | 75 | 31.615 | 26.521 |
| Shenyang, China | 68.33 | 27.949 | 21.564 |
| Cairo, Egypt | 62 | 34.947 | 23.08 |
| Hermosillo, Mexico | 54.25 | 39.947 | 33.574 |
| Baltimore, USA | 53.25 | 30.948 | 20.326 |
| Chicago, USA | 43 | 27.949 | 14.891 |
| Roma, Italy | 39.75 | 30.504 | 15.82 |
| Mexicali, Mexico | 21 | 35.247 | 13.947 |
| Las Vegas, USA | 4 | 39.946 | 3.8361 |
| Madrid, Spain | 10 | 32.725 | 2.7611 |
| Channel Size (W × H) | Geometry | Volumetric Flow Rate, m3/s | Outlet Temperature, °C |
|---|---|---|---|
| 3 × 3 | square | 0.000018 | 13.99 |
| 4 × 4 | square | 0.000032 | 14.10 |
| 5 × 5 | square | 0.00005 | 14.35 |
| 6 × 6 | square | 0.000072 | 15.97 |
| 7 × 7 | square | 0.000098 | 19.04 |
| 5 × 4 | rectangular | 0.00004 | 15.46 |
| 5 × 6 | rectangular | 0.00006 | 16.91 |
| 4 × 5 | rectangular | 0.00004 | 16.19 |
| 6 × 5 | rectangular | 0.00006 | 17.6 |
| Material | Outlet Temperature |
|---|---|
| Aluminum | 14.353 |
| Alum/Polythene | 15.2 |
| Polyethylene | 17.545 |
| Polyethylene/Fiber | 19.146 |
| Fiber | 19.159 |
| Polyester | 19.182 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
García-González, M.; Cheng, G.; Bui, D.T.; López-Leyva, J.A. Heat Exchanger Improvement of a Counter-Flow Dew Point Evaporative Cooler Through COMSOL Simulations. Thermo 2024, 4, 475-489. https://doi.org/10.3390/thermo4040026
García-González M, Cheng G, Bui DT, López-Leyva JA. Heat Exchanger Improvement of a Counter-Flow Dew Point Evaporative Cooler Through COMSOL Simulations. Thermo. 2024; 4(4):475-489. https://doi.org/10.3390/thermo4040026
Chicago/Turabian StyleGarcía-González, Mario, Guanggui Cheng, Duc Thuan Bui, and Josué Aarón López-Leyva. 2024. "Heat Exchanger Improvement of a Counter-Flow Dew Point Evaporative Cooler Through COMSOL Simulations" Thermo 4, no. 4: 475-489. https://doi.org/10.3390/thermo4040026
APA StyleGarcía-González, M., Cheng, G., Bui, D. T., & López-Leyva, J. A. (2024). Heat Exchanger Improvement of a Counter-Flow Dew Point Evaporative Cooler Through COMSOL Simulations. Thermo, 4(4), 475-489. https://doi.org/10.3390/thermo4040026






