Effects of Preheating on Thermal Behavior in Inconel 718 Processed by Additive Manufacturing
Abstract
1. Introduction
2. Numerical Approach: Finite Element Analysis (FEA)
2.1. Temperature-Dependent Properties
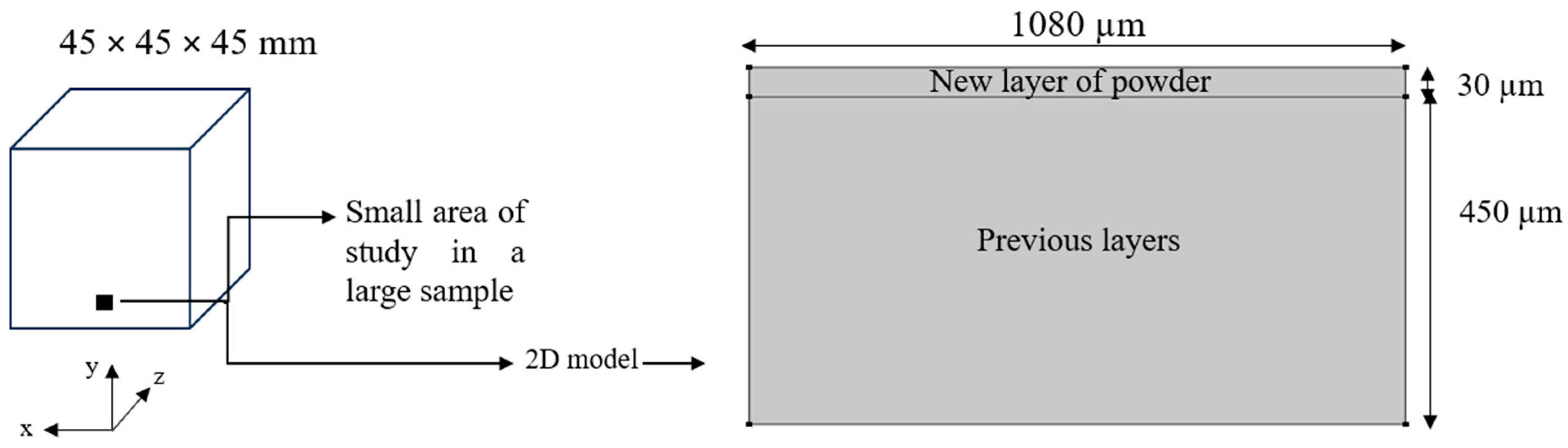
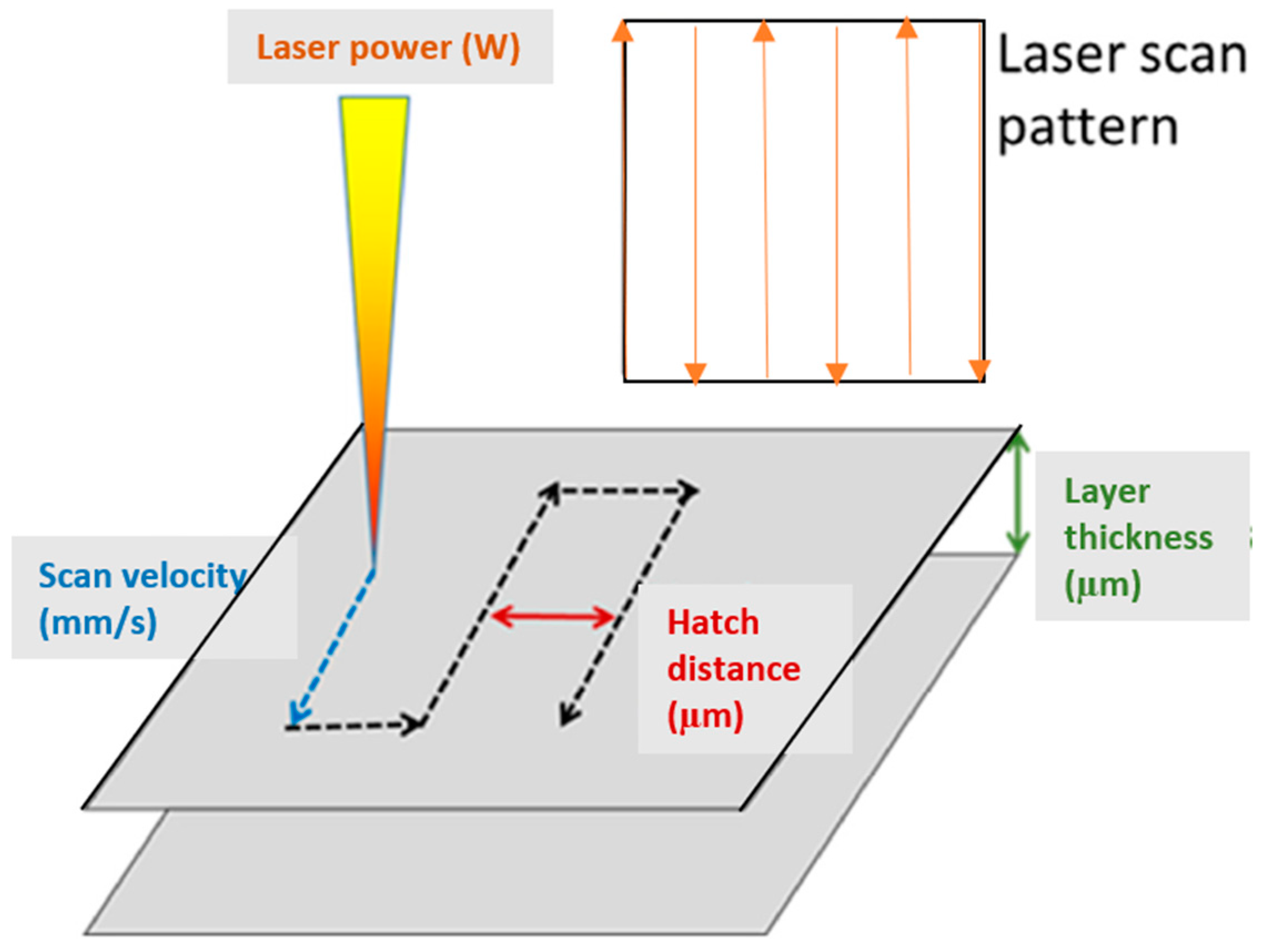
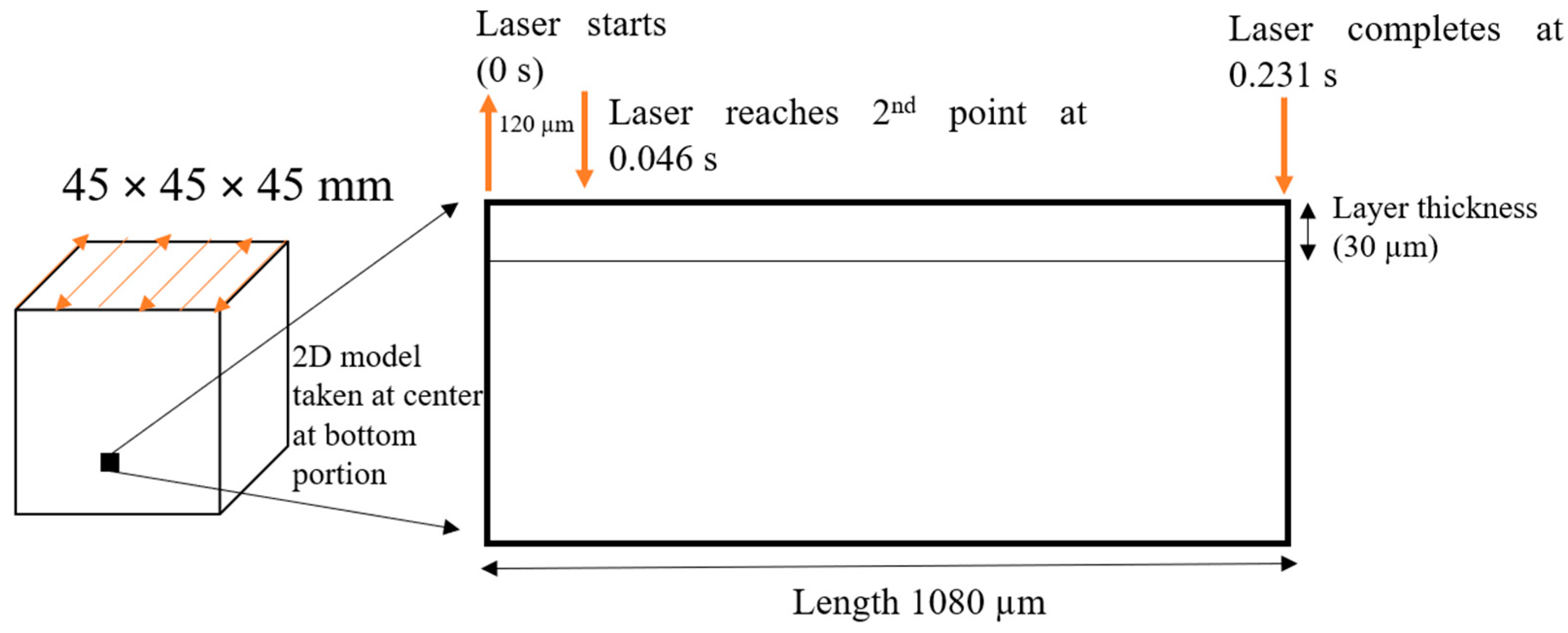
2.2. FEM Simulation
2.3. Experimental Setup
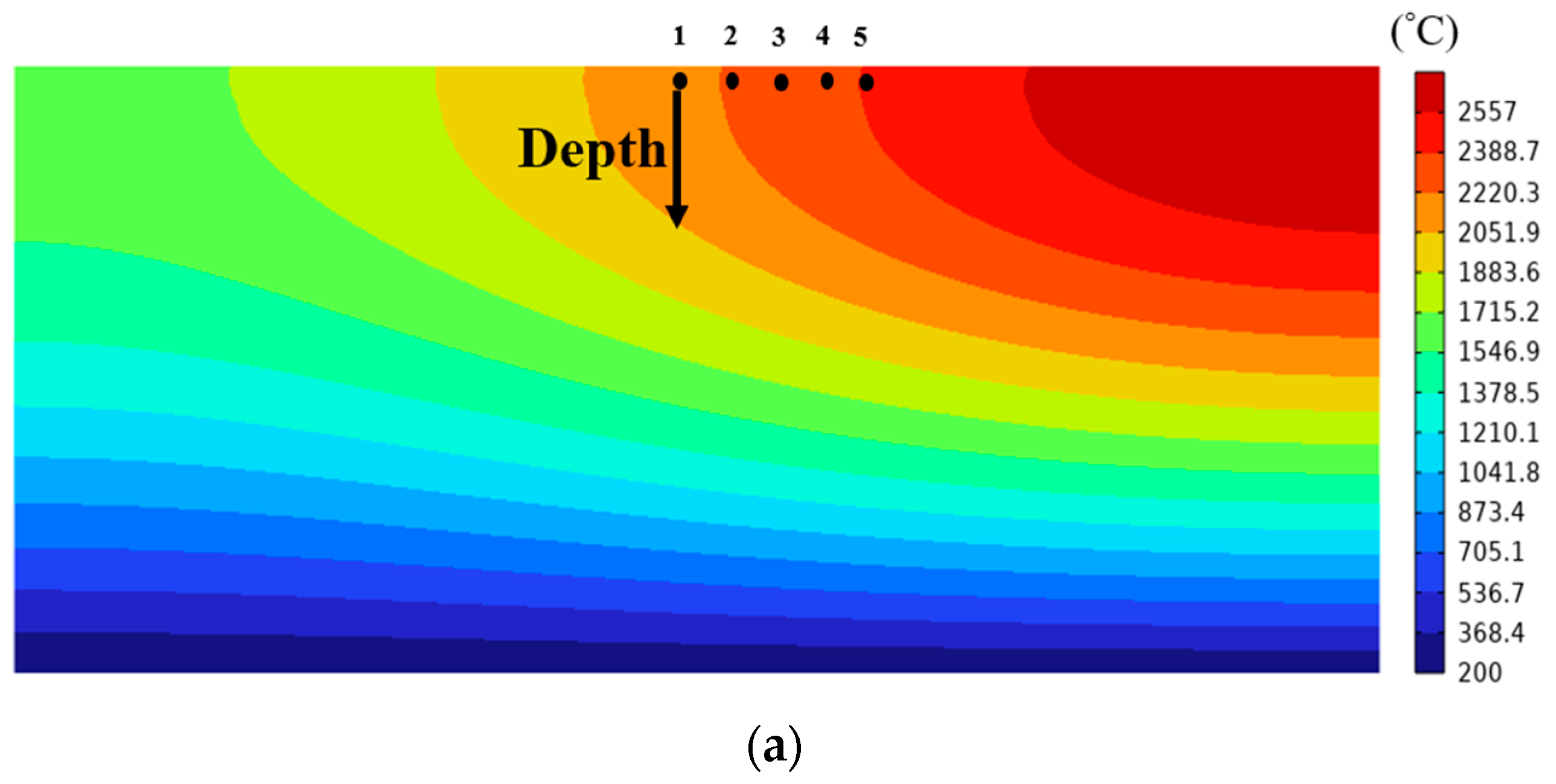
3. Results
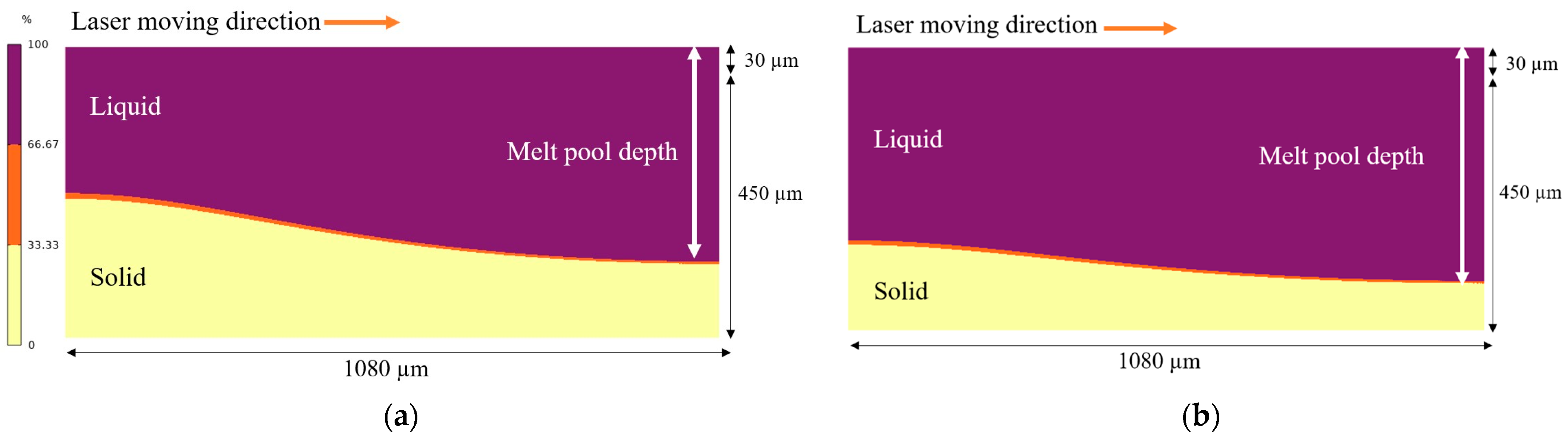
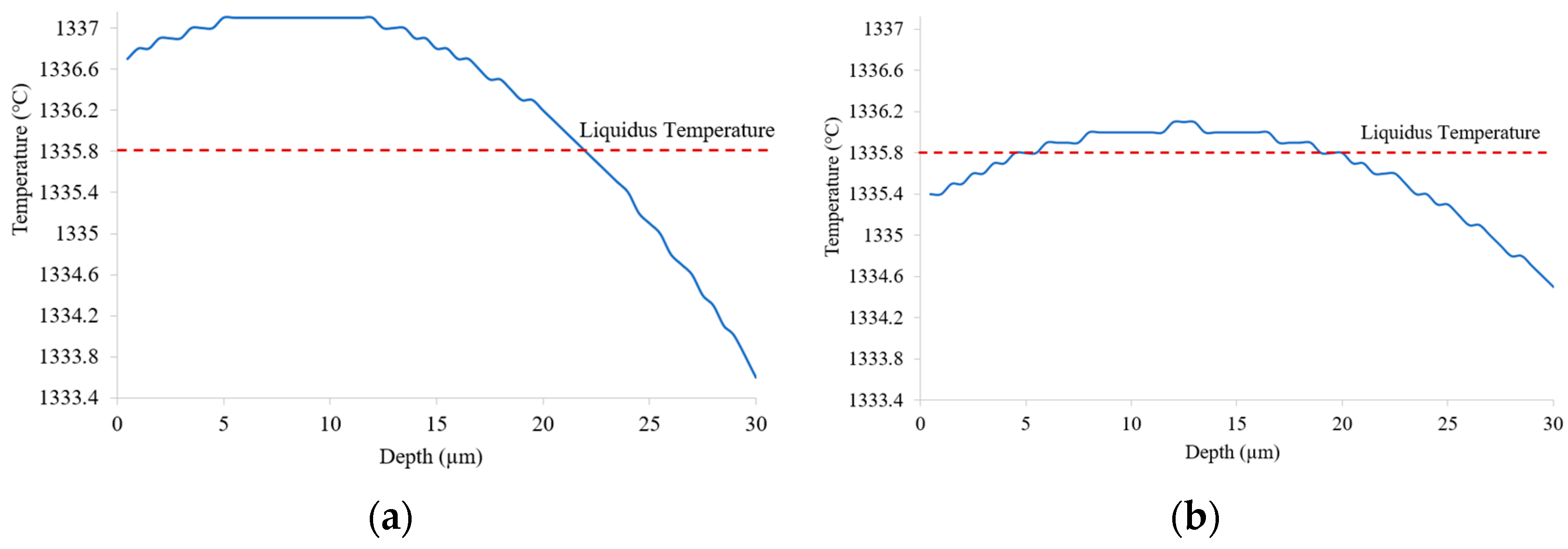
3.1. Change in Melt Pool
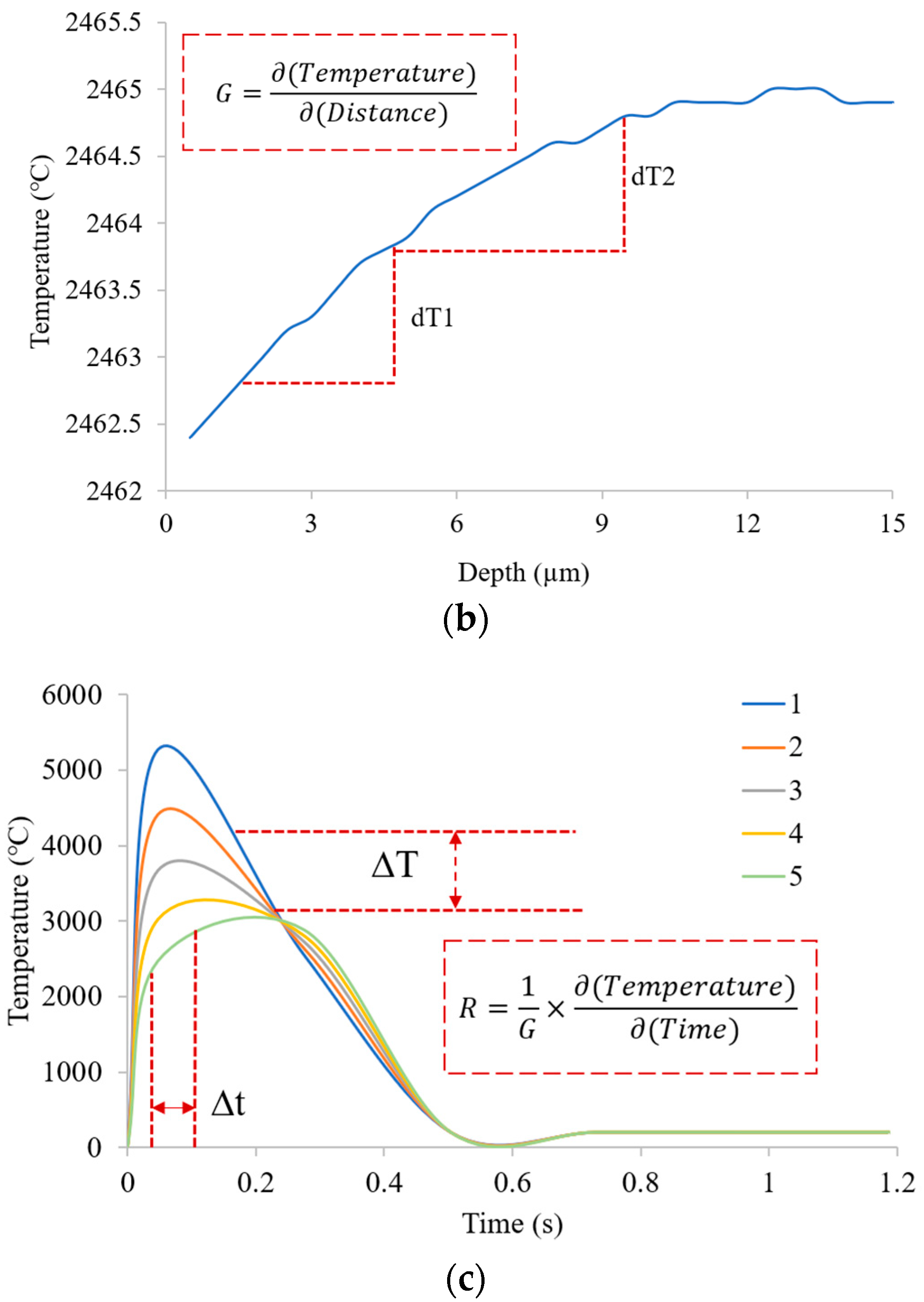
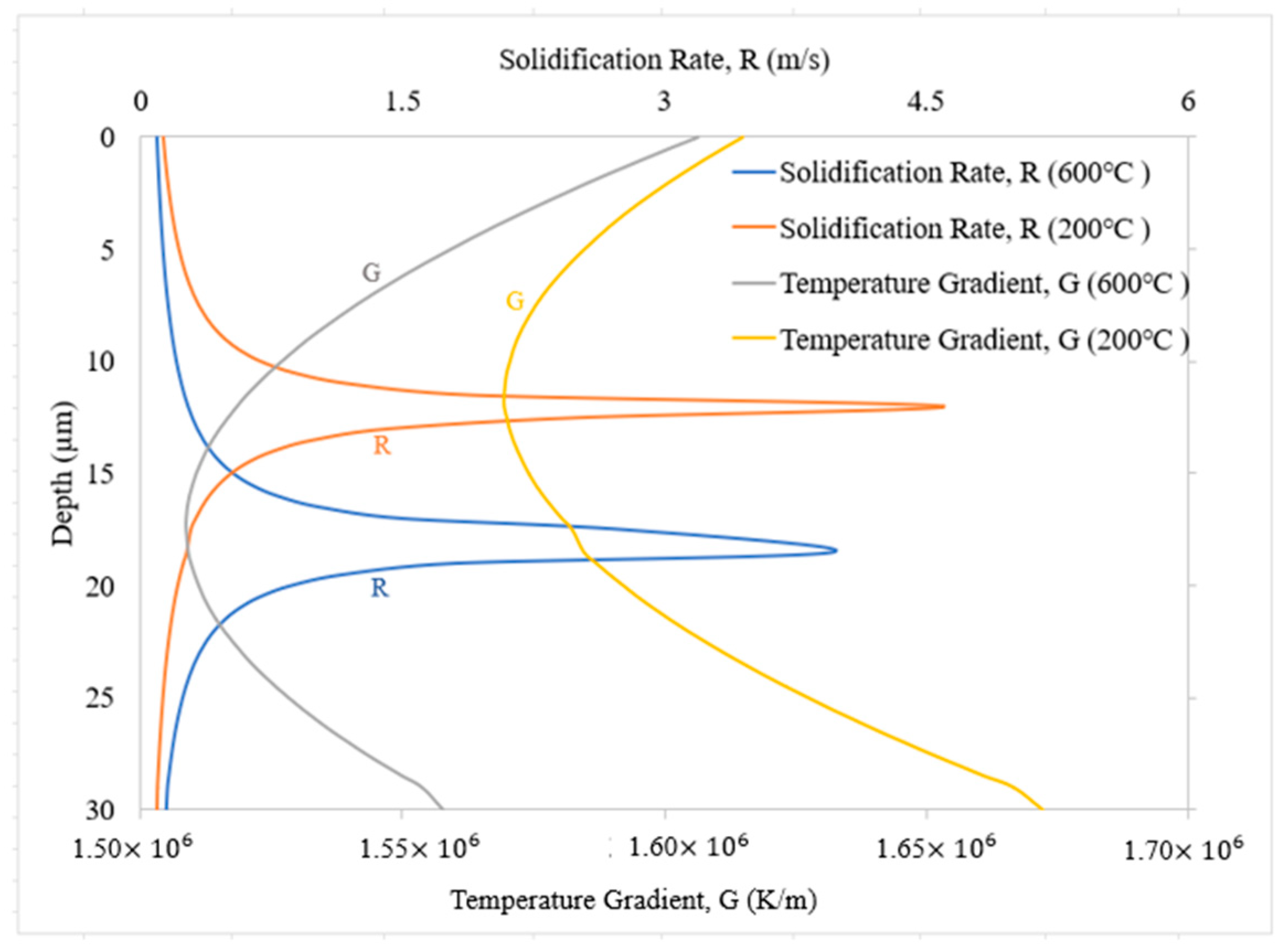
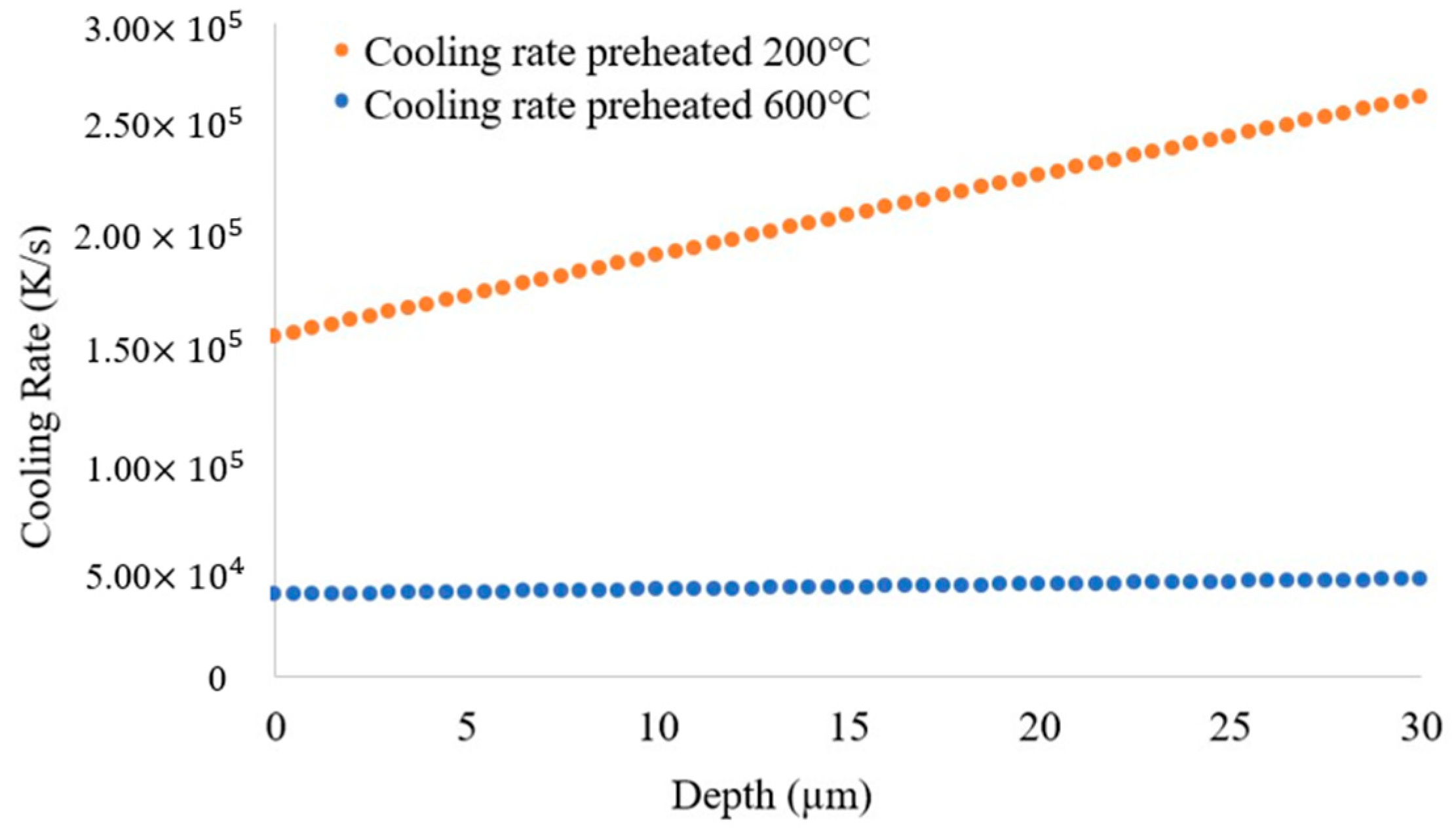
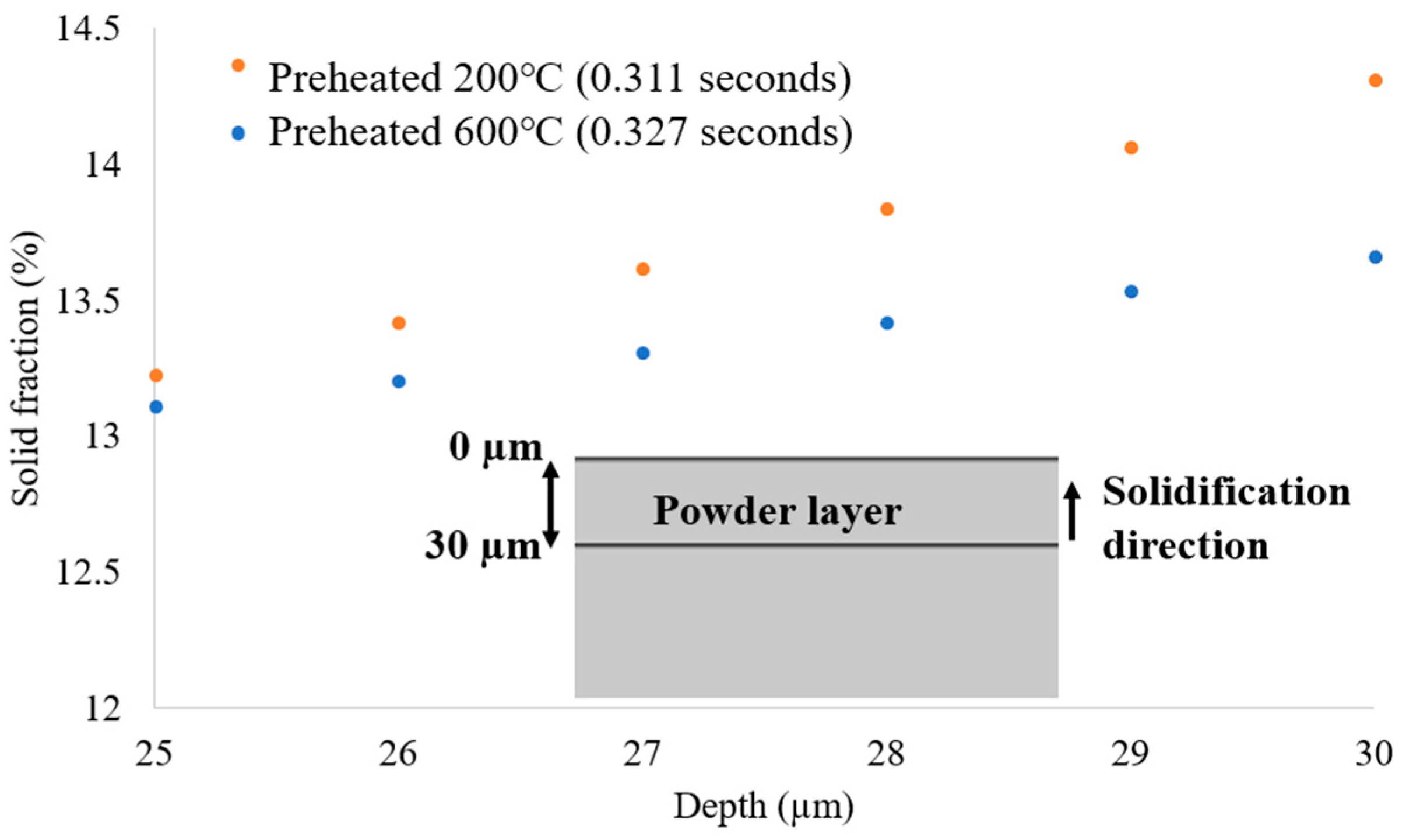
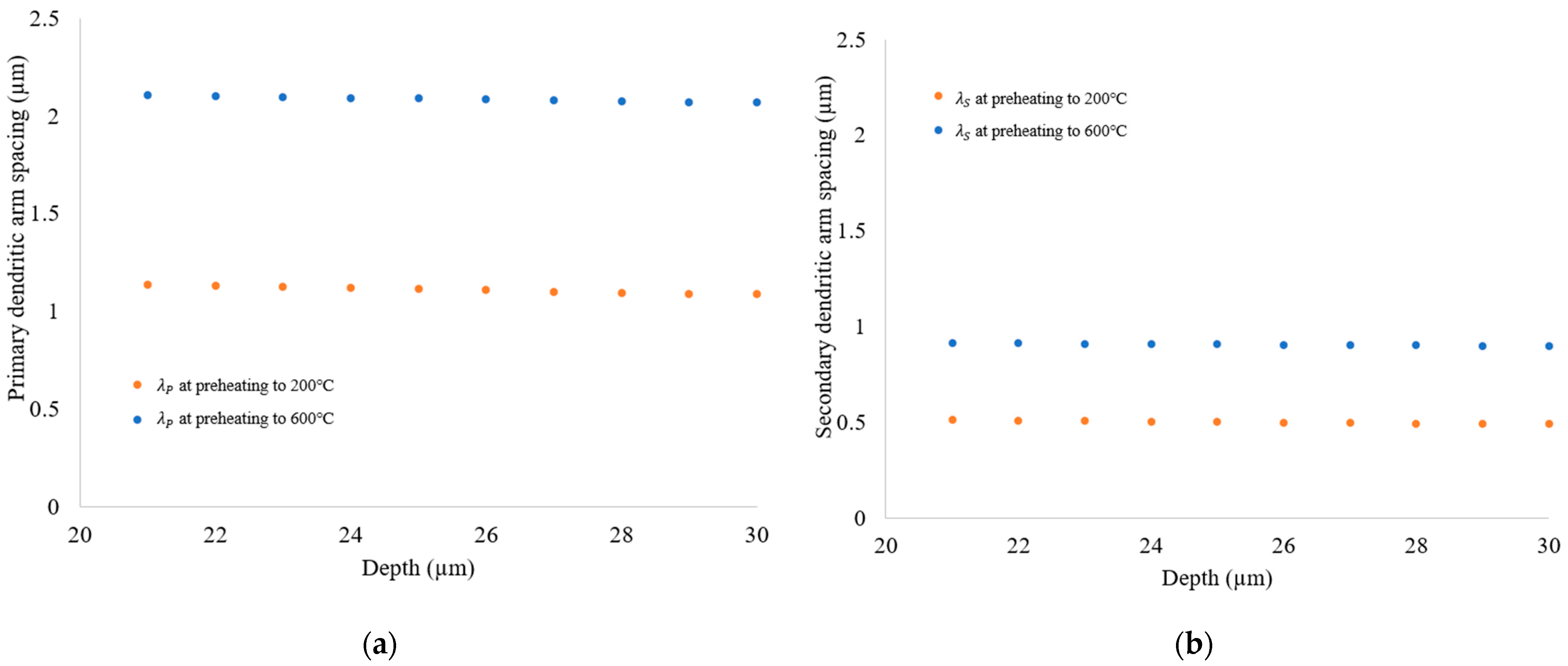
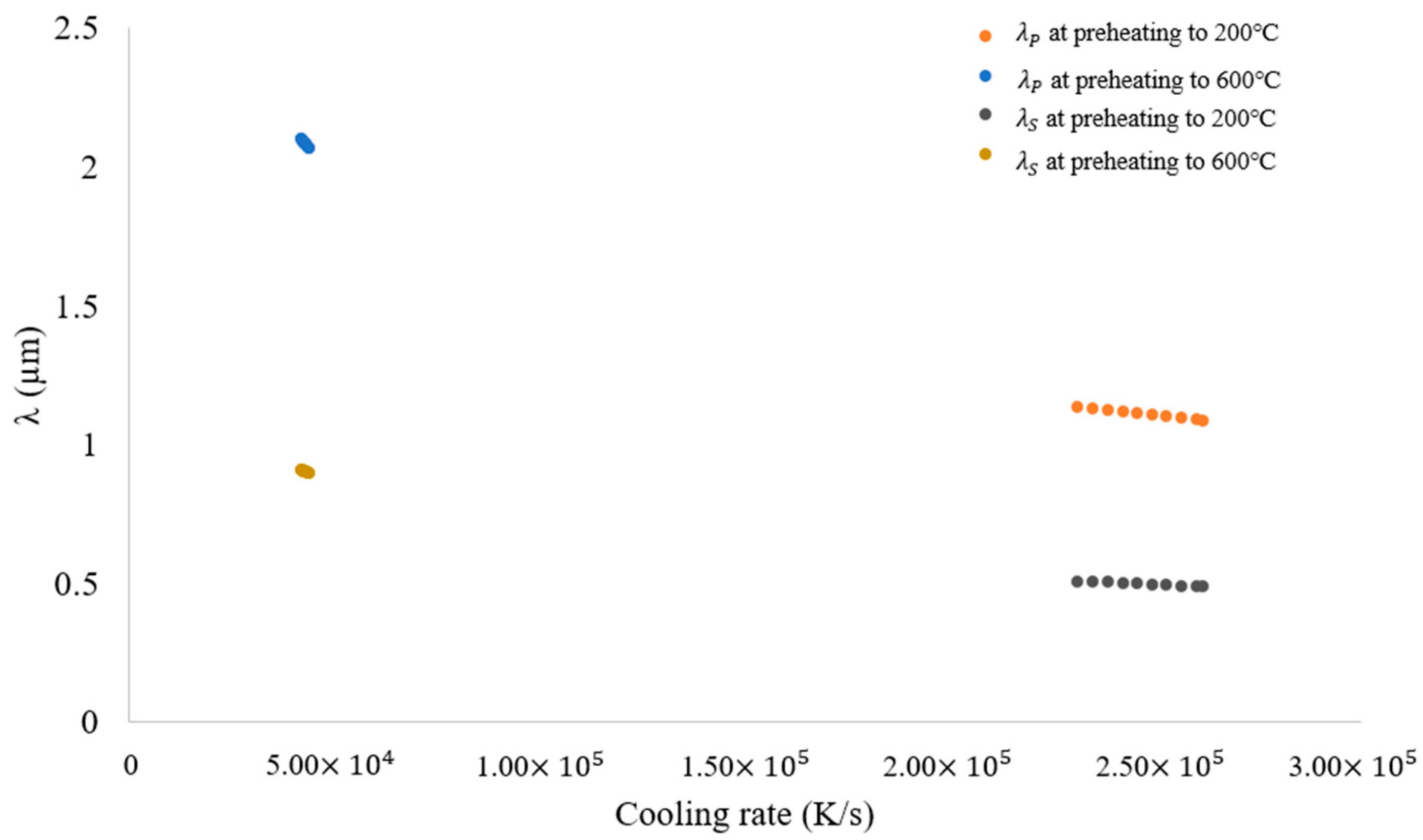
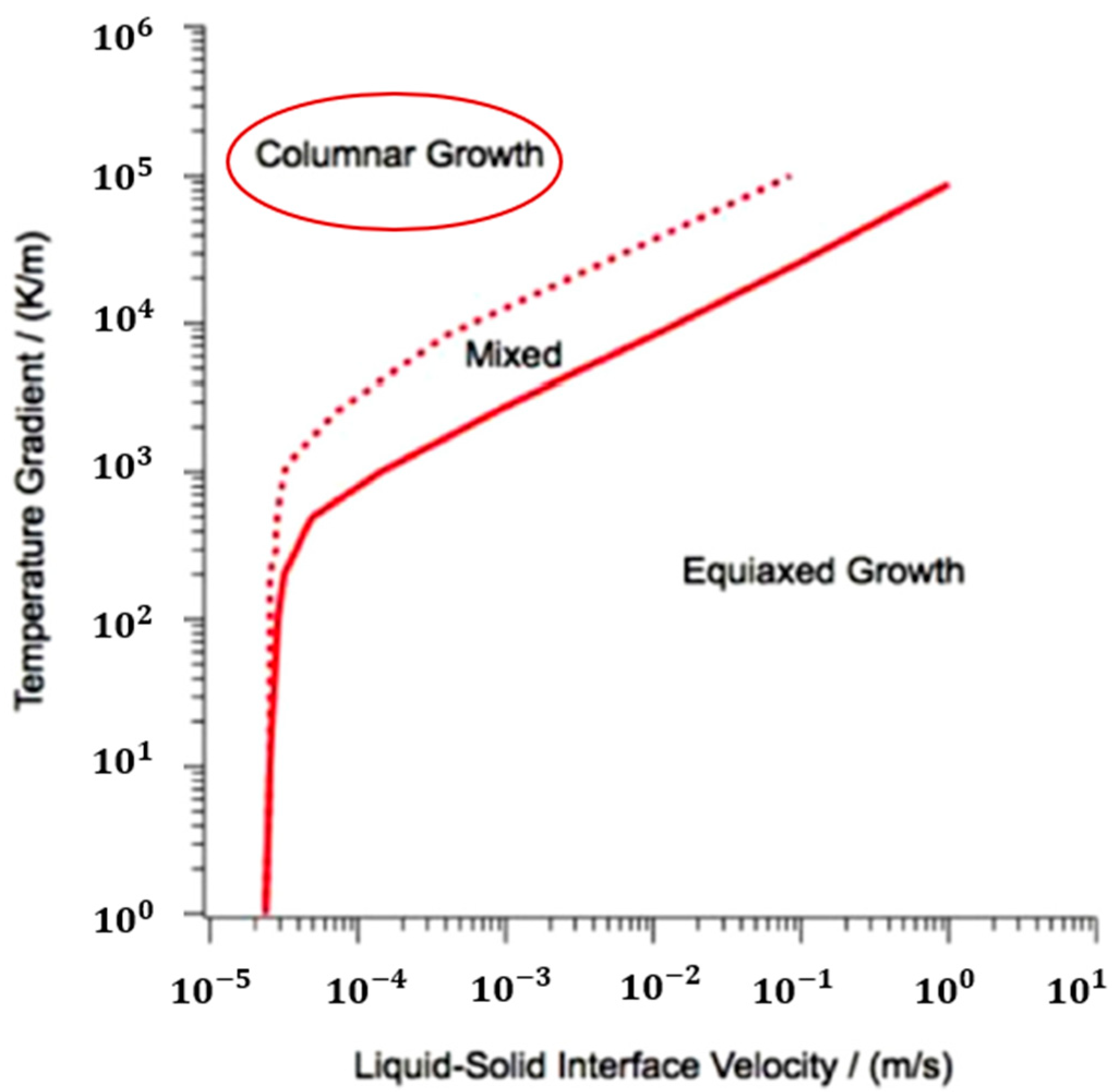
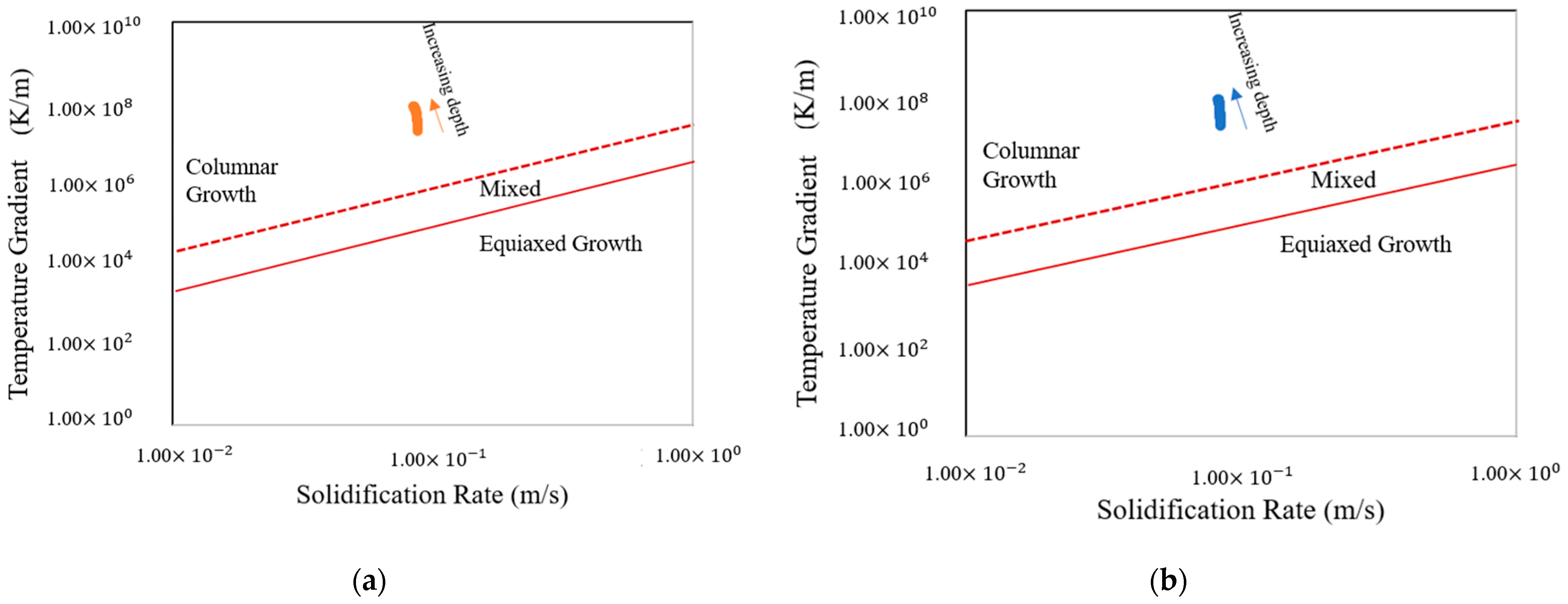
3.2. Solidification Parameters
4. Discussion
5. Conclusions
- Blocks built with preheating to 600 °C have a slower cooling rate and higher primary dendritic arm spacing (λ) than those preheated to 200 °C. This indicates a change in the microstructure by preheating to 600 °C.
- The solidification map shows columnar microstructures for base plates preheated to both temperatures.
- The melt pool depth is greater in the preheating to 600 °C model than in the 200 °C model. Analysis of the solid percentage at the same points reveals that the model preheating to 200 °C undergoes a quicker transformation from liquid to solid compared to preheating to 600 °C.
- Preheating increased the size of the dendrite structure and reduced elemental segregation, but it did not affect crystal grain morphology or size. A simulation confirmed that grain structure is unaffected by preheating.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yap, C.Y.; Chua, C.K.; Dong, Z.L.; Liu, Z.H.; Zhang, D.Q.; Loh, L.E.; Sing, S.L. Review of selective laser melting: Materials and applications. Appl. Phys. Rev. 2015, 2, 041101. [Google Scholar] [CrossRef]
- Guraya, T.; Singamneni, S.; Chen, Z. Microstructure formed during selective laser melting of IN738LC in keyhole mode. J. Alloys Compd. 2019, 792, 151–160. [Google Scholar] [CrossRef]
- Park, J.-H.; Bang, G.B.; Lee, K.-A.; Son, Y.; Song, Y.H.; Lee, B.-S.; Kim, W.R.; Kim, H.G. Effect of Preheating Temperature on Microstructural and Mechanical Properties of Inconel 718 Fabricated by Selective Laser Melting. Met. Mater. Int. 2022, 28, 2836–2848. [Google Scholar] [CrossRef]
- Li, C.; Liu, Z.; Fang, X.; Guo, Y. Residual Stress in Metal Additive Manufacturing. Procedia CIRP 2018, 71, 348–353. [Google Scholar] [CrossRef]
- Zhang, W.; Abbott, W.M.; Sasnauskas, A.; Lupoi, R. Process Parameters Optimisation for Mitigating Residual Stress in Dual-Laser Beam Powder Bed Fusion Additive Manufacturing. Metals 2022, 12, 420. [Google Scholar] [CrossRef]
- Popovich, V.; Borisov, E.; Sufiiarov, V.; Masaylo, D.; Alzina, L. Impact of heat treatment on mechanical behaviour of Inconel 718 processed with tailored microstructure by selective laser melting. Mater. Des. 2017, 131, 12–22. [Google Scholar] [CrossRef]
- Pollock, T.M.; Tin, S. Nickel-Based Superalloys for Advanced Turbine Engines: Chemistry, Microstructure and Properties. J. Propuls. Power 2006, 22, 361–374. [Google Scholar] [CrossRef]
- Cao, M.; Zhang, D.; Gao, Y.; Chen, R.; Huang, G.; Feng, Z.; Poprawe, R.; Schleifenbaum, J.H.; Ziegler, S. The effect of homogenization temperature on the microstructure and high temperature mechanical performance of SLM-fabricated IN718 alloy. Mater. Sci. Eng. A 2021, 801, 140427. [Google Scholar] [CrossRef]
- Song, B.; Zhao, X.; Li, S.; Han, C.; Wei, Q.; Wen, S.; Liu, J.; Shi, Y. Differences in microstructure and properties between selective laser melting and traditional manufacturing for fabrication of metal parts: A review. Front. Mech. Eng. 2015, 10, 111–125. [Google Scholar] [CrossRef]
- Cheng, Y.; Xiao, Z.; Zhu, H.; Zeng, X.; Wang, G. Influence of substrate characteristics on residual stress of SLMed Inconel 718. Rapid Prototyp. J. 2019, 25, 792–799. [Google Scholar] [CrossRef]
- Jia, Q.; Gu, D. Selective laser melting additive manufacturing of Inconel 718 superalloy parts: Densification, microstructure and properties. J. Alloys. Compd. 2014, 585, 713–721. [Google Scholar] [CrossRef]
- Mazzarisi, M.; Angelastro, A.; Latte, M.; Colucci, T.; Palano, F.; Campanelli, S.L. Thermal monitoring of laser metal deposition strategies using infrared thermography. J. Manuf. Process. 2023, 85, 594–611. [Google Scholar] [CrossRef]
- Mazzarisi, M.; Campanelli, S.L.; Angelastro, A.; Palano, F.; Dassisti, M. In situ monitoring of direct laser metal deposition of a nickel-based superalloy using infrared thermography. Int. J. Adv. Manuf. Technol. 2021, 112, 157–173. [Google Scholar] [CrossRef]
- Ansari, J.; Nguyen, D.-S.; Park, H.S. Investigation of SLM Process in Terms of Temperature Distribution and Melting Pool Size: Modeling and Experimental Approaches. Materials 2019, 12, 1272. [Google Scholar] [CrossRef]
- Pfaff, A.; Schäffer, S.; Jäcklein, M.; Balle, F. Measuring the Cooling Behavior of Melt Pools in L-PBF by Pyrometry. Materials 2023, 16, 3647. [Google Scholar] [CrossRef]
- Loh, L.-E.; Chua, C.-K.; Yeong, W.-Y.; Song, J.; Mapar, M.; Sing, S.-L.; Liu, Z.-H.; Zhang, D.-Q. Numerical investigation and an effective modelling on the Selective Laser Melting (SLM) process with aluminium alloy 6061. Int. J. Heat Mass Transf. 2015, 80, 288–300. [Google Scholar] [CrossRef]
- Mills, K.C. “Ni—IN 718,” in Recommended Values of Thermophysical Properties for Selected Commercial Alloys. In Woodhead Publishing Series in Metals and Surface Engineering; Mills, K.C., Ed.; Woodhead Publishing: Cambridge, UK, 2002; pp. 181–190. [Google Scholar] [CrossRef]
- Zhao, X.; Iyer, A.; Promoppatum, P.; Yao, S.-C. Numerical modeling of the thermal behavior and residual stress in the direct metal laser sintering process of titanium alloy products. Addit. Manuf. 2017, 14, 126–136. [Google Scholar] [CrossRef]
- Tang, M.; Pistorius, P.C.; Beuth, J.L. Prediction of lack-of-fusion porosity for powder bed fusion. Addit. Manuf. 2017, 14, 39–48. [Google Scholar] [CrossRef]
- Willy, H.J.; Li, X.; Chen, Z.; Herng, T.S.; Chang, S.; Ong, C.Y.A.; Li, C.; Ding, J. Model of laser energy absorption adjusted to optical measurements with effective use in finite element simulation of selective laser melting. Mater. Des. 2018, 157, 24–34. [Google Scholar] [CrossRef]
- Continuous Casting—Apparent Heat Capacity Method. Available online: https://www.comsol.jp/model/continuous-casting-8212-apparent-heat-capacity-method-382 (accessed on 22 May 2023).
- Oliveira, J.P.; LaLonde, A.D.; Ma, J. Processing parameters in laser powder bed fusion metal additive manufacturing. Mater. Des. 2020, 193, 108762. [Google Scholar] [CrossRef]
- Promoppatum, P.; Yao, S.-C.; Pistorius, P.C.; Rollett, A.D. A Comprehensive Comparison of the Analytical and Numerical Prediction of the Thermal History and Solidification Microstructure of Inconel 718 Products Made by Laser Powder-Bed Fusion. Engineering 2017, 3, 685–694. [Google Scholar] [CrossRef]
- Li, H.; Huang, Y.; Jiang, S.; Lu, Y.; Gao, X.; Lu, X.; Ning, Z.; Sun, J. Columnar to equiaxed transition in additively manufactured CoCrFeMnNi high entropy alloy. Mater. Des. 2021, 197, 109262. [Google Scholar] [CrossRef]
- Chen, J.; Liu, H.; Peng, Z.; Tang, J. Study on the Solidification Behavior of Inconel617 Electron Beam Cladding NiCoCrAlY: Numerical and Experimental Simulation. Coatings 2022, 12, 58. [Google Scholar] [CrossRef]
- Hogan, L.M. Crystals, Dendritic Solidification of. In Encyclopedia of Materials: Science and Technology; Buschow, K.H.J., Cahn, R.W., Flemings, M.C., Ilschner, B., Kramer, E.J., Mahajan, S., Veyssière, P., Eds.; Elsevier: Oxford, UK, 2001; pp. 1913–1918. [Google Scholar] [CrossRef]
- Körber, S.; Fleck, M.; Völkl, R.; Glatzel, U. Anisotropic Growth of the Primary Dendrite Arms in a Single-Crystal Thin-Walled Nickel-Based Superalloy. Adv. Eng. Mater. 2022, 24, 2101332. [Google Scholar] [CrossRef]
- Cui, C.; Liu, W.; Deng, L.; Wang, Y.; Liu, Y.; Wang, S.; Tian, L.; Su, H. Primary dendrite arm spacing and preferential orientations of the Ni–Si hypereutectic composites at different solidification rates. Appl. Phys. A 2020, 126, 1–9. [Google Scholar] [CrossRef]
- Formenti, A.; Eliasson, A.; Fredriksson, H. On the Dendritic Growth and Microsegregation in Ni-Base Superalloys Ιn718, In625 and In939. High Temp. Mater. Process. 2005, 24, 221–238. [Google Scholar] [CrossRef]
- Tao, P.; Li, H.; Huang, B.; Hu, Q.; Gong, S.; Xu, Q. The crystal growth, intercellular spacing and microsegregation of selective laser melted Inconel 718 superalloy. Vacuum 2019, 159, 382–390. [Google Scholar] [CrossRef]
- Nagahari, T.; Nagoya, T.; Kakehi, K.; Sato, N.; Nakano, S. Microstructure and Creep Properties of Ni-Base Superalloy IN718 Built up by Selective Laser Melting in a Vacuum Environment. Metals 2020, 10, 362. [Google Scholar] [CrossRef]
- Zhang, S.; Wang, L.; Lin, X.; Yang, H.; Huang, W. The formation and dissolution mechanisms of Laves phase in Inconel 718 fabricated by selective laser melting compared to directed energy deposition and cast. Compos. Part B Eng. 2022, 239, 109994. [Google Scholar] [CrossRef]
- Wei, H.L.; Mukherjee, T.; DebRoy, T. Grain Growth Modeling for Additive Manufacturing of Nickel Based Superalloys. In Proceedings of the 6th International Conference on Recrystallization and Grain Growth (ReX&GG 2016); Springer: Cham, Switzarland, 2016; pp. 265–269. [Google Scholar] [CrossRef]





| 255 W | |
| Laser spot radius | 80 µm |
| Layer thickness | 30 µm |
| Scanning velocity | 980 mm/s |
| Hatch spacing | 120 µm |
| Flow Velocity in the connecting Pipe * | 23 m/s |
| Pressure | 470.81 Pa |
| Temperature | 45 °C |
| 0.3 | |
| 65 µm | |
| 0.36 | |
| Heat transfer coefficient | |
| 1571 K | |
| Solidus temperature | 1443 K |
| Liquidus temperature | 1609 K |
| Latent heat of fusion | 210 J/g |
| Preheated temperatures | 200 °C, 600 °C |
| Initial Conditions | Boundary Conditions | |
|---|---|---|
| Previously solidified layers and the new layer → Room temperature (25 °C) | Top surface of powder → | Convection (convective heat transfer coefficient and using heat flux node) |
| Velocity field (laminar flow node) → 0 m/s | Argon cooling effect (external forced convection and using heat flux node) | |
| Pressure (laminar flow node) → 0 Pa | Radiation (using surface-to-ambient radiation node) | |
| Bottom surface of powder → Preheated temperature (200 °C, 600 °C) (using temperature node) | ||
| No-slip condition (using wall in laminar flow node) | ||
| Conduction from powder to solid material | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chowdhury, H.T.; Palleda, T.N.; Kakuta, N.; Kakehi, K. Effects of Preheating on Thermal Behavior in Inconel 718 Processed by Additive Manufacturing. Thermo 2024, 4, 48-64. https://doi.org/10.3390/thermo4010005
Chowdhury HT, Palleda TN, Kakuta N, Kakehi K. Effects of Preheating on Thermal Behavior in Inconel 718 Processed by Additive Manufacturing. Thermo. 2024; 4(1):48-64. https://doi.org/10.3390/thermo4010005
Chicago/Turabian StyleChowdhury, Hasina Tabassum, Thaviti Naidu Palleda, Naoto Kakuta, and Koji Kakehi. 2024. "Effects of Preheating on Thermal Behavior in Inconel 718 Processed by Additive Manufacturing" Thermo 4, no. 1: 48-64. https://doi.org/10.3390/thermo4010005
APA StyleChowdhury, H. T., Palleda, T. N., Kakuta, N., & Kakehi, K. (2024). Effects of Preheating on Thermal Behavior in Inconel 718 Processed by Additive Manufacturing. Thermo, 4(1), 48-64. https://doi.org/10.3390/thermo4010005







