Abstract
The isobaric heat capacity of solid eutectic mixtures LiCl-KCl-CsCl, LiBr-CsBr and LiBr-KBr-CsBr was investigated from room temperature up to melting point. The molar heat capacity of all mixtures under study was found to be close to the additive sum of that of pure salts. The heat accumulated up to melting temperature is directly dependent on the melting point.
1. Introduction
Eutectic mixtures comprising halide salts are used as phase-change materials. The melting temperatures of eutectics are much lower than those of pure salts [1]. Low temperatures have certain advantages including a low vapour pressure in molten state and low corrosion activity.
It makes halide eutectics very attractive for use in solar energy production [2,3,4,5,6] or power sources [7]. Heat capacity is very important since it indicates the amount of energy that a given system can possess under certain conditions.
Heat capacity has been shown to be temperature independent in a molten state according to many studies [8,9,10,11], but in solids, the heat capacity rises with temperature. There are scarce data on the heat capacity of solid eutectic halide mixtures. FLINAK, a well-known eutectic mixture was measured in a solid state [12,13].
The aim of the present research was to investigate the heat capacity of the solid halide eutectic mixtures within temperature interval from room temperature up to melting point. The study was focused on the mixtures with melting temperatures below 600 K.
2. Materials and Methods
Alkali halide salts classified as ‘‘chemically pure” (99.5% of main substance) were used for mixture preparation. Lithium chloride was provided by FMC (UK), caesium salts were from Vekton, Russia. and lithium and potassium bromides were from Reachim, Russia. Chloride salts were purified by zone melting [14,15]. LiBr was purified from moisture and other admixtures through double recrystallization from anhydrous acetonitrile solution with additional treatment with molecular sieves. KBr and CsBr were purified from moisture by stepwise with vacuum drying. The detailed procedure was given in our previous work [1]. The mixtures prepared were subjected to thermal and gravimetric analysis in order to verify the melting temperature and sample mass stability. The samples were homogenous, and the melting temperature difference was within 5 degrees. The compositions of eutectic mixtures are given in Table 1.

Table 1.
Compositions and melting points.
The study of heat capacity was carried out on the samples of the prepared mixtures using the STA 449C Jupiter synchronous thermal analyser (NETZSCH). The experiments were carried out under the following conditions: heating rate 10K/min; argon atmosphere; and Pt–Rh crucibles with a perforated lid. The heat capacity was determined in three stages: first stage—measurement of the base curve when the crucibles were empty; second stage—measurement with a standard sample (sapphire); and final stage—measurement with test sample. The detailed description of the experimental procedure has been described elsewhere [1]. The uncertainty of heat capacity determination was 5%.
3. Results and Discussion
The heat capacity of solid eutectic mixtures under investigation is given in Table 2 according to temperature.

Table 2.
Heat capacity of solid eutectics.
The isobaric heat capacities of solid eutectic mixtures were measured up to melting temperature.
The results for LiCl-KCl-CsCl are shown in Figure 1. The calculation of molar heat capacity according to the Neumann–Kopp rule [16,17] is also presented as Cp mixture = ∑Cp component salt.
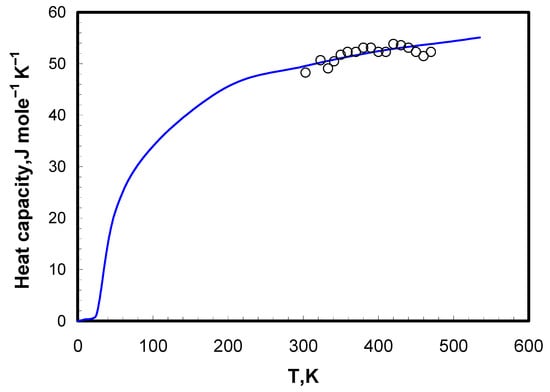
Figure 1.
Heat capacity of LiCl-KCl-CsCl solid eutectic. ○—our data, line—values calculated according to the additive law based on the data available from the literature [8,19].
The usage of this rule for halide salt mixtures can be justified by the similarity of the halide salts’ thermodynamic properties [18]. The experimental and calculated values were in good agreement. The pure salt data were taken from the available literature [8,19]. Experimental and calculated data were used for the calculation of the enthalpy accumulated by eutectic mixture up to the melting temperature. Calculation of the integral (by the standard trapezoid method [20]) from the LSQM-line produced a value of 21.9 kJ mole–1 for LiCl-KCl-CsCl. The accuracy of the calculations was approximately ±7.5%.
Molten bromide eutectics possess certain advantages in comparison with chloride systems, primarily, due to lower temperatures. For this reason, they were also interesting subjects for study. The isobaric heat capacities of solid eutectic mixtures LiBr-KBr and LiBr-KBr-CsBr were measured up to melting point.
The heat capacities of the bromide eutectics being investigated are shown in Figure 2 and Figure 3. The enthalpy of samples was calculated for bromide eutectics for premelting temperature. Calculation of the integral gave the value of 21.4 kJ mole–1 for LiBr-KBr-CsBr and 23.95 kJ mole–1 for LiBr-CsBr. Comparison of enthalpy and melting temperature indicated their dependency. The data for eutectic mixtures can be considered as a derivative of pure salts and, thus, they have the same dependency as that of individual salts. The results for eutectic mixtures are given in Table 3 and Figure 4. The enthalpy and melting points of chloride, bromide, and iodide salts were taken from literature [21] and are shown in Table 4 and Figure 4.
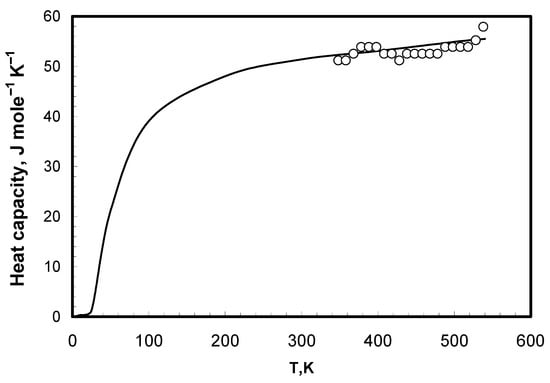
Figure 2.
Heat capacity of the solid LiBr-CsBr eutectic mixture. ○—our data, line—values calculated according to additive law using literature data [8,19].
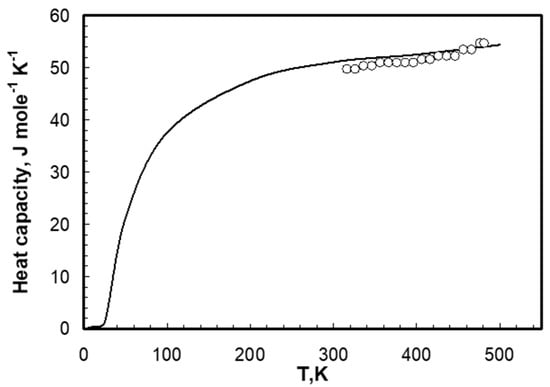
Figure 3.
Heat capacity of solid the LiBr-KBr-CsBr eutectic mixture. ○—our data, line—values calculated according to additive law using literature data [8,19].

Table 3.
Melting points and enthalpy before the melting of the eutectics.
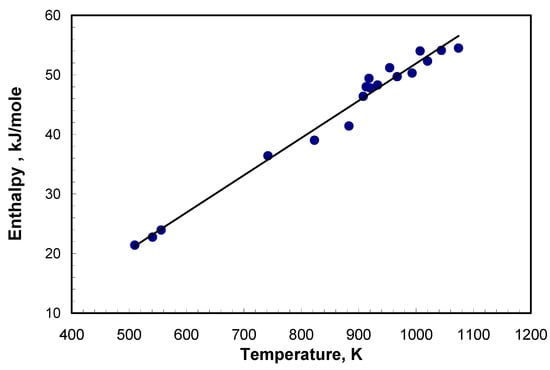
Figure 4.
Enthalpy of salts and eutectics before melting versus melting point.

Table 4.
Enthalpy (H) of solid halide salts before melting point (Tm) [17].
The fitting was carried out by two mathematical methods: LSQM and the interval method. LSQM is well known and provides reliable fitting parameters of data under treatment, but it gives only the maximal (by modulus) bounds emax of measuring errors. Consequently, the parameters calculated by the standard least square method (LSQM) gives too broad an uncertainty interval. Under given conditions of uncertainty, interval analysis methods [22,23] give the guaranteed estimates of parameters (the information sets) which defines the area of possible values of property under investigation.
The fitting line was as follows: H (T) = A × T + B, where H is the enthalpy of the solid eutectic near melting point, T is the melting temperature, and A and B are the empirical coefficients.
The results of data treatment are shown in Figure 5 and Figure 6. Figure 5 demonstrates the information set (the possible values of coefficients A and B). According to interval analysis, the minimal coefficient B is 5.48 × 10−2 kJ mole−1 K−1, which relates to the maximal coefficient A equal to 23.9 KJ mole−1. Maximal coefficient B is 6.95 × 10−2 kJ mole−1 K−1, which relates to 18.3 kJ mole−1. The optimal coefficients correspond to the central point (Acnt = 6.22 × 10−2 kJ mole−1 K−1, Bcnt = 21.169 kJ mole−1). The results of LSQM are close (A = 6.26 × 10−2 kJ mole−1 K−1, B = 21.208 kJ mole−1).
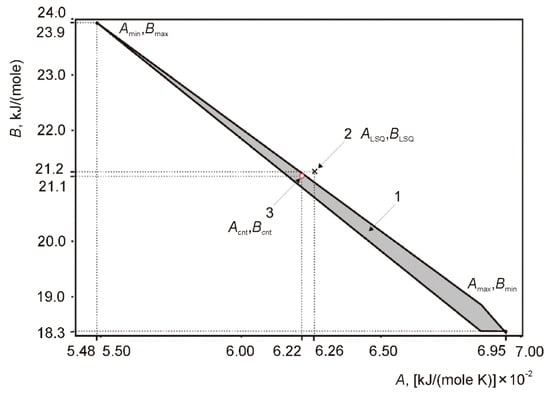
Figure 5.
Results of estimation of admissible values of parameters for the approximation function H (T) = A × T + B. (1) Information set; (2) LSQM—estimate ALSQ, BLSQ; (3) central point Acnt and Bcnt of the information set. Grey area is an area of possibleA and B coefficientsts according interval analysis, red circle is a point of fiiting coefficients related to to LSQM.
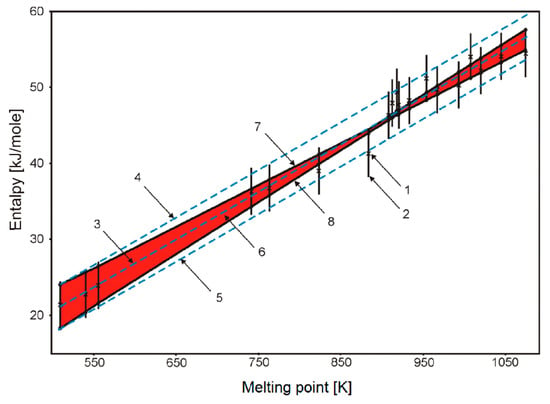
Figure 6.
Input data and results of their processing.(1) measurements; (2) uncertainty interval Hn of each measurement; (3) line of the LSQM—approximation; (4,5) boundaries “+2σ” and “–2σ” of the LSQM—admissible curves of the process; (6) the tube of admissible curves according to the interval approach estimation; (7,8) the upper and lower boundaries of admissible curves according to interval approach estimation. Red area is an area of possible fitting lines according to interval analysis.
These results were related to the temperature interval 510–1074, and the constants were related to 510 K. At recalculating to zero point by temperature, the equation is as follows: LSQM results:
ALSQ = 6.26 × 10−2 kJ mole−1 K−1, BLSQ = −10.655 kJ mole−1
The results of estimation on the basis of the interval approach are the following:
Acnt = 6.22 × 10−2 kJ mole−1 K−1, Bcnt = −10.718 J mole−1
The results obtained demonstrated the independence of fitting results from the treatment method.
Thus, the amount of heat accumulated by solid halide eutectic mixtures up to melting point can be described by the following linear equation:
H = 62.2 × Tm − 10.718 J mole−1
The enthalpy of the melting of halide eutectics is also dependent on the melting point [24] according to the following formula:
where H is enthalpy of fusion, and Tm is melting point.
H = 38 × Tm − 11.220 J mole−1,
Thus, it is possible to calculate the amount of energy accumulated by salt or eutectic mixture before and just after melting as follows (Figure 7):
H = 98.6 × Tm − 21.855 J mole−1
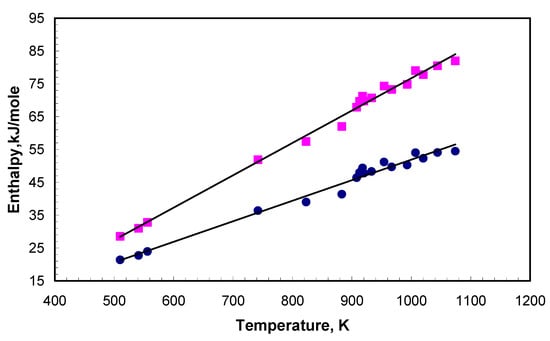
Figure 7.
Enthalpy of salts and mixtures before (navy) and after melting (magenta).
This is the heat that the system possesses just after melting. This equation allows for the estimation of the amount of heat that the eutectic mixture can accumulate for heat storage.
4. Conclusions
- The molar heat capacity of all mixtures under study was found to be close to the additive sum of that of pure salts.
- The enthalpy of the solid eutectic mixtures closes to melting temperature was directly dependent on the melting point.
- The results obtained allow for the estimation of the amount of energy that the eutectic mixture can accumulate for storage.
Author Contributions
Conceptualization, A.R.; methodology, A.R., I.K., T.Y. and O.R.; validation, T.Y., O.R. and A.R.; formal analysis, S.K.; investigation, T.Y., O.R. and I.K.; data curation, A.R.; data treatment, S.K.; writing—original draft preparation, A.R.; writing—review and editing, A.R., O.R. and A.K.; supervision and project administration Y.Z. All authors have read and agreed to the published version of the manuscript.
Funding
The research was funded as the frame of the scientific theme of Institute of High Temperature Electrochemistry UB RAS (number FUME-2021-0001, registration number 1211111126-9) and the Institute of Solid State Chemistry, Urals Branch, Russian Academy of Sciences (theme number 0320-2019-0005, registration number NIOKTR АААА-А19-119102990044-6).
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Redkin, A.; Korzun, I.; Yaroslavtseva, T.; Reznitskikh, O.; Zaikov, Y. Isobaric heat capacity of molten halide eutectics. J. Therm. Anal. Calorim. 2017, 128, 621–626. [Google Scholar] [CrossRef]
- Fernandez, A.; Velis, S.; Galleguillos, H. Thermal characterization of solar salts from north of Chile and variations of their properties over time at high temperature. J. Therm. Anal. Calorim. 2017, 128, 1241–1249. [Google Scholar] [CrossRef]
- Fernández, A.; Vidal, J.; Oró, E.; Kruisenga, A.; Solé, A.; Cabeza, L. Mainstreaming commercial CSP systems: A Technology Review. Renew. Energy 2019, 140, 152–176. [Google Scholar] [CrossRef]
- Badenhorst, H.; Böhmer, T. Enthalpy of fusion prediction for the economic optimisation of salt based latent heat thermal energy stores. J. Energy Storage 2018, 20, 459–472. [Google Scholar] [CrossRef]
- Wei, X.; Song, M.; Peng, O.; Ding, J.; Yang, J. Quaternary chloride eutectic mixture for thermal energy storage at high temperature. Energy Procedia 2015, 75, 417–422. [Google Scholar] [CrossRef]
- Wei, X.; Song, M.; Peng, O.; Ding, J.; Yang, J. A new ternary chloride eutectic mixture and its thermo-physical properties for solar thermal energy storage. Energy Procedia 2014, 61, 1314–1317. [Google Scholar] [CrossRef]
- Masset, P.; Guidotti, R. Thermal activated (thermal) battery technology: Part II. Molten Salt Electrolytes. J. Power Sources 2007, 164, 397–414. [Google Scholar] [CrossRef]
- Glushko, V. Thermodynamic Properties of Individual Substances; Book 2; Nauka: Moscow, Russia, 1982; Volume 4, 559p. [Google Scholar]
- Grimes, W. Reactor Chemistry Division Annual Progress Report for Period Ending: December 31, 1965; ORNL-3913; Oak Ridge National Laboratory: Oak Ridge, TN, USA, 1966; p. 29.
- Gaune-Escard, M.; Bogacz, M.; Rycerz, L.; Szczepaniak, W. Heat capacity of LaCI3, CeC13, PrC13, NdCI3, GdC13, DyC13. J. Alloys Compd. 1996, 235, 176–181. [Google Scholar] [CrossRef]
- Beilmann, M.; Beneš, O.; Capelli, E.; Reuscher, V.; Konings, R.; Fanghänel, T. Excess Heat Capacity in Liquid Binary Alkali-Fluoride Mixtures. Inorg. Chem. 2013, 52, 2404–2411. [Google Scholar] [CrossRef] [PubMed]
- Rogers, D.; Yoko, T.; Janz, G. Fusion properties and heat capacities of the eutectic LiF-NaF-KF. J. Chem. Eng. Data 1982, 27, 366–367. [Google Scholar] [CrossRef]
- Kosaka, M.; Asahina, T.; Taoda, H.; Kushi, A. Heat of fusion and heat capacities of MX and M2Y (M=Li, Na, K; X=F, Cl, I; Y=CO3, SO4) ternary eutectic salts. Nippon Kagaku Kayshi 1982, 6, 977–982. [Google Scholar] [CrossRef]
- Mullabaev, A.; Kovrov, V.; Kholkina, A.A.; Zaikov, Y. Anode processes on Pt and ceramic anodes in chloride and oxide-chloride melts. Nucl. Eng. Technol. 2022, 54, 965–974. [Google Scholar] [CrossRef]
- Nikolaev, A.; Mullabaev, A.; Suzdaltsev, A.; Kovrov, V.; Kholkina, A.; Shishkin, V.; Zaikov, Y. Purification alkali metal chlorides by zone recrystallisation for use in pyrochemical processing of spent nuclear fuel. At. Energy 2022, 131, 195–201. [Google Scholar] [CrossRef]
- Leitner, J.; Vonka, P.; Sedmidubsky, D.; Svoboda, P. Application of Neumann-Kopp rule for estimation of heat capacity of mixed oxides. Thermochim. Acta 2010, 497, 7–13. [Google Scholar] [CrossRef]
- Il’ina, E.; Raskovalov, A.; Reznitskikh, O. Thermodynamic properties of solid electrolyte Li7La3Zr2O12. J. Chem. Thermodyn. 2019, 128, 68–73. [Google Scholar] [CrossRef]
- Redkin, A.; Zaykov, Y. Relation between the thermal expansion coefficient and the heat capacity in halide melts. Russ. Metall. 2017, 2017, 75–78. [Google Scholar] [CrossRef]
- Berg, W.T.; Morrison, J.A. The Thermal Properties of Alkali Halide Crystals. I. The Heat Capacity of Potassium Chloride, Potassium Bromide, Potassium Iodide and Sodium Iodide between 2, 8 and 270 °K. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1957, 242, 467–477. [Google Scholar]
- Atkinson, K.E. An Introduction to Numerical Analysis, 2nd ed.; John Wiley & Sons: New York, NY, USA, 1989; 693p. [Google Scholar]
- Galwey, A. A view and a review of the melting of alkali metal halide crystals: Part 1. A melt model based on density and energy changes. J. Therm. Anal. Calorim. 2005, 82, 23–40. [Google Scholar] [CrossRef]
- Jaulin, L.; Kieffer, M.; Didrit, O.; Walter, E. Applied Interval Analysis; Springer: New York, NY, USA, 2001; 379p. [Google Scholar]
- Kumkov, S.I.; Nikitin, V.S.; Ostanina, T.N.; Rudoy, V.M. Interval processing of electrochemical data. J. Comput. Appl. Math. 2020, 380, 112961. [Google Scholar] [CrossRef]
- Redkin, A.; Korzun, I.; Reznitskikh, O.; Yaroslavtseva, T.; Zaikov, Y.; Kumkov, S. Heat of fusion of halide salts and their eutectics. J. Therm. Anal. Calorim. 2018, 131, 2021–2026. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).