Abstract
The group combustion characteristics of core–shell nanothermite particles differ from other dispersed solid or liquid fuels. In a core–shell structure, each discrete nanothermite particle can undergo an exothermic reaction as the oxygen atoms in the metal oxide shell undergo a solid state diffusion to oxidize the metal core. This feature allows the spherical core–shell nanothermites to react in the absence of gaseous oxygen, thus modifying their group combustion characteristics compared to char or liquid fuels. Using a number of simplifying assumptions, a theoretical framework was established—based on existing group combustion theory—to examine the characteristics of mass and heat diffusion in nanothermite combustion. First, a model for the quasi-steady state single-particle combustion, in quiescent air, was established. The isolated particle combustion theory serves as the basis for the combustion interaction and mass transfer in a spherical cloud of dispersed nanothermite particles. The type of group combustion is strongly dependent on the diffusion of vapour products, i.e., the interaction is more pronounced when the diffusion of vapour products is higher. The group combustion regimes in dispersed nanothermites were identified and delineated.
1. Introduction
Nanothermites are a Metastable Intermolecular Composite (MIC) which are often made of a metal and metal oxide—mixed at a nanoscale—that can undergo an exothermic chemical reaction with sufficient energy input. The nanosized constituents, namely the metal fuel and solid oxidizer, are often physically mixed to promote a rapid ignition and reaction [1]; the chemical reactions in MIC occur due to the solid-state diffusion of oxygen [2]. More recently, spherical core–shell nanothermites were developed wherein a nanosized metallic core was wrapped in a thin oxidizing shell [3,4,5], which can be either metallic or non-metallic. As the contact area between the fuel and oxidizer was maximized, the diffusion length and timescales were minimized. Thus, the core–shell nanothermites presents many advantages, most notably that the outer shell is thermodynamically stable and therefore reactions can occur as discrete solid-state particle combustion in the absence of gaseous oxygen. This differs from classical, physically-mixed nanothermite combustion which requires physical proximity between the fuel and oxidizer particles, and thus cannot react in a dispersed phase.
Nanothermites are characterized by their high reactivity and energetic density [6], and can be tailored to specific applications. As they undergo highly exothermic reactions, a dispersed group of core–shell structured nanothermites can result in self-sustaining combustion due to the thermal diffusion and convection of the heated products of combustion, which ignite the neighboring particles. However, most interestingly, as the particle reactions are driven by solid-state oxygen diffusion [2], the combustion in the dispersed phase is not limited by the availability of gaseous oxygen. Instead, it is limited by the inter-particle heat and mass transfer. Furthermore, reactions can occur in vacuum, water and any other inert environment, assuming the continuum phase does not chemically impact the core–shell structure of the MIC. These characteristics make the core–shell nanothermites well suited for many novel applications, including space technologies.
A substantial amount of research has focused on the combustion of closely packed nanothermite particles [2]. The physically mixed solid-phase fuel and oxidizer particles are often mechanically compressed, and their combustion characteristics have been investigated. The packing density, measured in terms of Theoretical Maximum Density (TMD), greatly impacts the flame propagation speed [1,7] through a consolidated pellet. The flame front advances predominantly due to convective (at low TMD) or conductive (at high TMD) [8] means, with the flame speed varying from m/s at high TMD [1], to m/s at low TMD [9]. The sensitivity of the flame propagation speed to TMD was recently assessed using numerical models [10]. However, the combustion characteristics of dispersed core–shell nanothermites, in which the ignition and combustion of the individual particles are predicated upon the inter-particle heat and mass transfer, are not well established and represent the focus of the present work which applied a theoretical perspective to the problem.
Under sufficient heating, the combustion of a single, core–shell nanothermite particle shares many characteristics with single-particle char or droplet combustion, the primary difference being the solid-state diffusion of oxygen that occurs within a particle in the nanothermite. As the dispersed core–shell nanothermite reactions are not limited by the presence of gaseous oxygen (due to the solid-phase oxidizer transport from the shell), the combustion dynamic of multiple dispersed particles differs greatly from the classical multi-phase combustion regimes. Group combustion is the burning characteristic of the collection of particles [11] and is helpful in modeling of dispersed particle combustion. Several different ‘modes’ of group combustion have been recognized for the case of dispersed droplets [12] and solid particles [13]. Classically, these different modes of group combustion are governed by the availability of oxygen within the dispersed cluster. Thus, dispersed core–shell nano-energetic particles will have different group combustion characteristics.
The theory and models of metal combustion in a gaseous oxidizer have long been subject to mathematical study [14]. Yetter and Dryer [15] examined metal particle combustion regimes and concluded that the oxidizer and pressure have a significant impact on the thermodynamics of combustion and particle combustion regimes. The metal vapours react instantly with oxygen upon contact, and vapour pressures of metals are only substantial when close to flame temperatures. It can be difficult to imagine a scenario in which a cloud of metal vapour would burn with external oxygen in a group combustion process. However, metal vapour can still burn with external oxygen caused by high-temperature plasma, laser-induced plasma, electrostatic discharge, the chemical reaction zone behind a detonation front, and other non-typical combustion applications. Emission from metal vapors (e.g., Al, B) and oxidized species (e.g., AlO, BO2) has been observed under these conditions. Lam et al. [16] investigated the scaling of the flame propagation in a particulate cloud. They adopted the following two models: a continuum model for an analytical study and a discrete source model for a numerical investigation. They discovered that the flame propagation could not be deterministically predicted in the limit of fast combustion compared to the interparticle diffusion time.
In very dense metal clouds [17], the reaction is more like that of metal particle agglomerate wherein the reaction rate can be restricted by the availability of oxidizer, something that does not occur in the case of nanothermites. An increase in local temperature within the particle suspension due to a reaction at multiple particle sites is referred to as the collective effect [18]. This leads to less heat loss to its surroundings, since the particles are self-heating as they react at multiple particle sites [19]. Compared to isolated particles, the collective effect accelerates the heating rate within a cloud, as is discussed in Section 3, resulting in faster combustion. Unlike previous work conducted by Soo et al. [17], Mi et al. [20] found that particles combust at all sizes and there is no minimum size for ignition.
Clusters of dispersed particles can emerge in turbulent flows where the discrete particles can be preferentially concentrated due to the kinematics of the turbulence [21,22]. This preferential clustering of discrete particles becomes particularly important under external radiative [23] or inductive [24] heating. The particle heating locally heats the fluid phase and may locally generate turbulence [25] and even further enhance clustering. The inhomogeneous particle distribution can impede the interphase heat transfer, generating hot and cold zones in the continuum phase [23,24,26,27,28]. This is a particularly important problem in particle-laden solar collectors [29]. If these particles are reactive, the clustering can impact the combustion dynamics of these dispersed particles [13], especially if the group combustion is oxygen constrained. For core–shell nanothermite particles, the implication of local clustering on the group combustion characteristics remains unclear.
In this research, we proposed a theoretical study of the group combustion characteristics of dispersed, spherical core–shell nanothermites that built on the analytical work developed by Annamalai and co-workers [13]. This work differs from the classical group combustion theory in that core–shell nanothermites, as they contain both fuel and oxidizer within a discrete particle, do not undergo an oxygen-limiting group combustion behaviour. The role of group combustion theory is not limited to understanding the combustion of a group of dispersed reactive particles, but it can also help understand the ignition time, burning rates, heat release, flame structures and other combustion characteristics. For tractability, we simplified the combustion kinetics to a single-step with approximated kinetic parameters and neglected any additional forces emerging at the nanoscale. Most dispersed nanoparticles agglomerate into microsized particles containing hundreds or thousands of discrete core–shell nanosized particles. These simplifications provide a tractable framework to study the inter-particle heat transfer of dispersed core–shell nanothermites. This work is organized as follows: Section 2 considers the combustion of an isolated particle within a carrier gas. Thereafter, in Section 3, we focus on the mass conservation and group combustion characteristics in a dispersed particle cluster. In Section 4, we present classifications of the various group combustion regimes specific to core–shell nanothermites. Finally, in Section 5, we develop a group combustion model for non-spherical particle distribution of nanothermites entrained from the nozzle. The conclusions and discussions are included in Section 6.
2. Single Isolated Particle Combustion
For the present study, we considered spherical core–shell nanoparticles consisting of an aluminium core and a copper oxide shell. However, the theory developed herein is generalizable to any core–shell nanothermite material. In a dispersed phase, nanoparticles have a tendency to aggregate—due to the intermolecular and electrostatic forces—into agglomerations of particles that have a diameter on the micrometer scale. Although for most practical applications we use core–shell particles on the nanoscale, we considered the nanoparticle aggregates as isolated particles for the present combustion theory study. This simplification allowed us to neglect any nanoscale forces that would hinder the tractability of the analysis. It should be noted that, above the nanometer scale, the analysis is scale-independent, as shown in Figure 1. However, the combustion time changed with the length scales (size) of the particle agglomerate. As is seen in Equation (17), which corresponds to the particle consumption time, if the particle size () is doubled, the consumption time () of the particle quadruples.
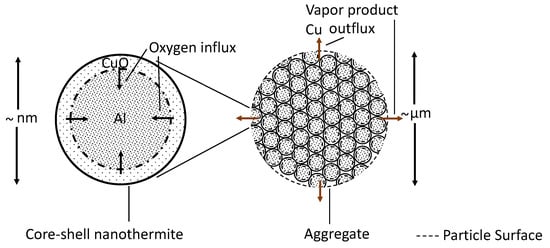
Figure 1.
Illustration of the core–shell nanothermite and corresponding nanothermite agglomerate, which can disperse in the carrier phase for combustion.
Quasi-Steady Assumptions of Single Particle Combustion—We first considered the simplest case of the combustion of an isolated core–shell nanothermite particle. Under sufficient heating, the oxygen from the shell undergoes solid-state diffusion and a chemical reaction with the pure metal core takes place, as shown in Figure 1. We considered only the heterogeneous redox reaction near the surface involving the aluminium core with the oxygen in the copper oxide shell. It is to be noted that this reaction is independent of the gaseous oxygen availability around the particle surface. To simplify the analysis, a perfectly spherical particle was considered where the solid-state reaction occurred at the edge. Depending on the composition of the nanothermites, gas is formed as a product of combustion [30] in addition to a solid or liquid phase metal oxide. In the specific case of an aluminium core with a copper oxide shell, copper vapors are formed, as shown in Figure 2. Thus, a concentration gradient in the gas phase is established, which results in the diffusion of copper vapors away from the particle surface. We were interested in obtaining the concentration profile of copper vapors. Under steady conditions, this profile must adjust in such a way that the combustion of nanothermite must equal the stoichiometric release of copper vapors at the particle surface. The transfer rate of copper vapors can then be evaluated using the mass conservation equations. With conservation of mass considerations, the regression rate of the particle is proportional to the vapor generation under the quasi-steady assumption. Thus, the temperature-dependent heat release, which was used in the work of Soo et al. [17], is implicitly accounted for within the gaseous formation. Furthermore, given the low thermal mass of these particles and the rapid timescale of combustion, we assumed a non-constant but uniform temperature within the particle. Similarly, the thermophysical properties of the solid, such as specific heat, were assumed to be temperature independent. Finally, using stoichiometry, the nanothermite burn rate was be evaluated.

Figure 2.
Combustion of a single solid nanothermite; surface denotes nanothermite pellet surface. This combustion of a single-particle behaves the same as a highly concentrated group combustion event (sheath combustion as discussed in Section 4.3.3).
There are some other assumptions considered in this formulation. The radiative heat release from combustion and hot particles is considered to be negligible—a simplification that may not be valid in all cases. The kinetic energy of the carrier phase as well as its shear work are neglected. Finally, there was no chemical reaction with the copper vapors in the carrier phase. With these assumptions, we considered the mass conservation, vapor product transport, and energy equation. The rate of mass consumption of the solid particle () is as follows:
where is the radius of the particle, is the density of the particle, is the density of the gas phase including vapor density of copper species (kg/m), u is the velocity of the gas mixture at any spherical cross-section in the gas phase, is the mass flux rate at any spherical cross-section in the gas phase, and is the mass production rate of the vapor products. Here, the mass of the particle () decreases with time, thus a negative value, , is obtained; similarly, the mass flux is positive. The conservation of species per unit surface area in a quiescent environment of the gas phase is as follows:
where Y is the mass fraction of copper vapor species at a given location, is the binary diffusion coefficient of copper vapor species in the carrier phase, is the vapor density of the copper species, and is the mass fraction gradient of the copper vapor. We also simplified the above equation by considering from Equation (1). It is to be noted that the two ways to integrate the above equation are as follows: (1) from the particle surface () to a radial location, r or (2) from a radial location, r, to a far away location (). However, adopting any of the boundary conditions will produce the same final result. An expression of the above conservation law after integration can be written as follows:
where is the copper vapor mass fraction of the ambient gas adjacent to the particle surface and is the mass fraction of copper vapor at a location far from the nanothermite particle. We can rewrite the above equation by defining the mass transfer number B as follows:
The higher the mass combustion rate of the nanothermites, the higher the mass transfer number (B). This gives us the exact value of the constant mass flow rate () parameter in terms of the known boundary conditions:
Above is the constant mass flow rate at any spherical cross-section of radius, r, for a given mass fraction of the vapor product in the immediate vicinity of the particle () and mass fraction of the vapor product located far from the particle (). The general case of the above equation is that leads to outwards mass flow rate () from the particle. We can also review the limiting case in which , which means there is no mass flow rate as . Thus, the final solution of the mass fraction variation of the vapor product (Y) at any radius (r) location is obtained by substituting Equation (5) into Equation (3) to obtain:
This can be further simplified as follows: if we consider that no mass fraction of the vapor product is located far from the particle, . The conservation of energy in the domain is given by the following formula:
where T is the thermodynamic temperature at radial location (r). Similarly, and are the thermal conductivity and specific heat of the gas-mixture, respectively.
By considering the boundary condition of , Equation (1), the solution of the above equation is given as:
where the parameter is given as:
Thus, the solution of the temperature is:
We can verify the limit cases from the above equation. For example, at the particle surface (), we have , which expresses the exact boundary condition at the particle surface. A similar sanity check can be performed at a radial location far from the solid particle (). Additionally, for the limiting case when the temperature at the surface and the temperature at the freestream are equal, the solution of the above equation can be simplified to .
The diffusion of the combustion products into the surrounding carrier gas is characterized by the Lewis number, , which relates the mixture thermal diffusivity ) to the mass diffusivity (). An assumption of the unity Lewis number was made to retain mathematical tractability. This means that the mass (mass diffusivity of the copper vapors relative to the gas mixture) and thermal diffusion were approximately equal. Considering a unity Lewis number, where the mixture thermal diffusivity is () and the species diffusivity is () and equal, (), the above equation simplifies to:
where the thermal transfer number () is as follows:
To decipher the physical implication of the thermal transfer number (), let us posit that the copper vapor product leaves with an energy of . If this thermal energy is supplied to the copper vapors at , the potential amount of energy that is transferred is . The higher the number, the higher the potential for heat transfer in the surrounding gas phase.
2.1. Comparison with Other Single-Particle Combustion Models
Previous works developed analytical models for quasi-steady single-particle combustion for a variety of fuels. Here, these models were compared to the core–shell nanothermite combustion model; the comparison is summarized in Table 1.

Table 1.
Comparison with other single-particle combustion models.
2.1.1. Spray Combustion
The spray combustion has the following two fundamental elements: combustion of an individual fluid droplet and a collection of droplets [31]. Intuitively, single droplet combustion generally appears in dilute sprays, whereas droplet clusters are found at higher concentration flows. It should be noted that the size of these clusters is much smaller than the integral length scale of the turbulent flow [32]. Much research has been conducted to investigate the steady-state burning of individual drops and the two-stage ignition—particularly in microgravity [33,34]. However, the literature on group combustion is rather limited. In the case of single droplet combustion, the thermal transfer number, equivalent to Equation (12) for nanothermites, becomes [35]:
In the above equation T, , , , and are the temperature at a distance from the fuel drop, the boiling point of the liquid fuel, the specific heat of the gas, the specific enthalpy of the combustion reaction, and the latent heat of vaporization, respectively. Likewise, represents the oxygen mass fraction at locations far from the fluid drop, and represents the oxygen stoichiometric coefficient in the reaction. Therefore, in order to elucidate the physical interpretation of B, the energy () of the reaction products that escape from the surface was considered. By providing this thermal energy to a noncombustible liquid fuel at a temperature of , the physical quantity of the fuel that can potentially be vaporized is (). In droplet combustion, the potential of converting liquid fuel into vapors, measured in the mass of fuel per mass of the stoichiometric amount of air, is known as the transfer number B. In this sense, a greater value of B depicts a higher level of overall evaporation and consequently, a higher combustion of the fluid particles.
2.1.2. Coal/Char Combustion
Annamalai and Ramalingam [13] conducted a theoretical analysis in order to decipher the combustion characteristics of char particle clusters in a quiescent flow. In their case, they determined the mass transfer number of a single coal/char particle as follows:
here, , , , , and represent the carbon dioxide (CO) mass fraction, carbon dioxide (CO) mass fraction at the char particle surface, oxygen (O) mass fraction, oxygen (O) mass fraction at the particle surface, oxygen and carbon dioxide stoichiometric coefficient in the reaction. In this combustion reaction, the main product is carbon dioxide, while the reaction of carbon and oxygen is trivial. Furthermore, each particle releases carbon monoxide based on the oxidation of the carbon atoms and reduction of carbon dioxide. This carbon monoxide later oxidates to create carbon dioxide provided a homogeneous gas phase. Hence, they proposed a one-step reaction scheme as follows: CO + O→ CO. Considering this reaction, if the rate of oxidation of carbon monoxide is high, then the concentration of oxygen in the particle cloud will dwindle. Moreover, the global rate of the char cloud combustion was deemed independent of carbon monoxide oxidation, if the diffusion control is ensured for the combustion of every char particle in the group.
2.2. Particle Consumption Time and D-Square Law
Considering Equations (1) and (4) at the surface of a particle and simplifying by replacing radius of the particle with its diameters (), we get:
where is a constant corresponding to the linear slope of the relationship between the diameter square () and time (t). Physically, represents the combustion rate of the nanothermite particle. It is noteworthy that the right-hand terms of the above equation are constant in time, and the solution of the above linear differential equation is as follows:
where is the initial size of the particle. Thus, the time taken for the particle to become completely consumed () is (assuming that complete and idealized combustion occurs) is calculated as follows:
The particle diameter decays linearly with time. There is a finite time when the particle is completely consumed, given by . This is an order-of-magnitude approximation given the heterogeneous makeup of the core–shell nanothermite. For other solid and liquid fuels, the scaling relation between the lifetime and diameter of the particle () was shown previously.
Returning to our initial assumption of quasi-steady combustion, we implicitly assumed that the particle was stationary and the gas generation and expansion were perfectly symmetrical. The above analysis does not account for the relative velocity of a nanothermite particle to the gas phase. However, it was found empirically for other fuels [36] that even if there is a superimposed gas velocity, the scaling relationship, Equation (17), holds. The study conducted by Frssling [37], who developed correlations of droplet evaporation, described the correction factor in the presence of a free-stream gas velocity (). Thus, the modification ratio of as a correction in the presence of some flow divided by is as follows , where is the Reynolds number, a is typically about and b is also about to in droplet evaporation. With these values, there is a relatively weak dependence on for various . Hence, the above relation can serve as a motivation for researchers to implement more detailed measurements of the variation of the nanothermite diameter with time during its combustion.
3. Mass Conservation and Group Combustion
The previous section provided a simplified analytical framework with which to characterize the combustion of a discrete, quasi-steady, spherical core–shell nanothermite particle. In this section, we derive an analytical approach to describe nanothermite cloud combustion. The initial part of this section presents the derivations, while the later part describes the group combustion trends. Although extensive research has been carried out on group combustion theory, no study exists on the thermally-driven particularities of core–shell nanothermite combustion. The theoretical approach adopted in this study follows similar lines of inquiry used for spray [35] and coal powder combustion [13], but adapted to the specific characteristics of nanothermites.
Distributed core–shell nanothermites are considered to be a spherical group of particles (although the results could be easily extended to cylindrical and planar clouds). Consider a group of radius containing nanothermite particles as shown in Figure 3. The group is essentially a two-phase region, consisting of discrete solids and a continuous gas phase. The gas phase inside the group can be divided into the film region (region C, in the particle’s vicinity) and the gaseous middle region (region B—shown in Figure 3). There is a separation of length l between the particles. As in the previous section, we considered dispersed aggregates of core-=shell Al/CuO nanothermites, which produce copper vapor when the aluminium core oxidizes. The copper vapor is formed at the particle surface, and it diffuses into the gaseous middle region through the film region. The rate of heat transfer and nanothermite combustion is dictated by the diffusion of copper vapor, which eventually diffuses into the outer region (region A). For the purpose of simplifying the group combustion analysis, we made two additional assumptions. The first assumption is , which translated to a continuum in the group region. Consequently, the particles are perceived as point sources. The second assumption is the presence of a uniform monodispersed cloud of nanothermite particles.
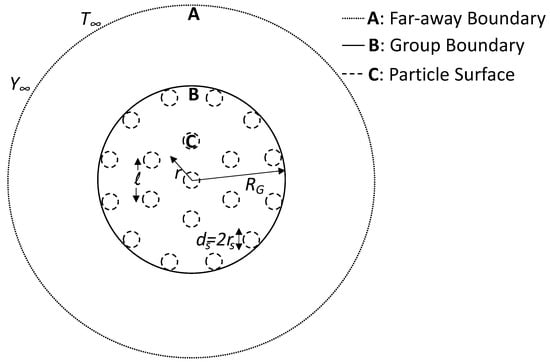
Figure 3.
Illustration of combustion for a group of nanothermites and the different regions of A, B and C.
In the classical group combustion regime, an internal zone of unburnable fuel is created by the evaporation of liquid fuels or pyrolysis of solid fuels (due to lack of oxygen), which establishes a flame around a cluster of these particles. During this change, the individual particles’ flames transitions to a flame around a group of particles. In the case of nanothermites, which are a type of nanoreactors that do not have limitations in terms of oxidizer availability, since it is available within each particle, each particle acts as a microreactor with the ability to ignite when it reaches above its ignition temperature. Thus, the combustion dynamics of the group are a purely heat and mass transfer problem.
It is noteworthy that heat release is a function of temperature. The temperature variation within a cloud plays an important role in group combustion, which depends on the mass transfer of copper vapor above the ignition temperature. It is reasonable to assume that combustion reactions in region B (of Figure 3) take place uniformly since it is the domain of mean mass and mean temperature within the interstitial field. Thus, the group is considered as a homogeneous phase. It was previously demonstrated for a group interaction system that all the particles must be at the same temperature () for the thermodynamic equilibrium to occur at a steady-state [38]. Therefore, the reaction rate in each configuration was considered constant in our model.
The group or cloud method described in this section involves obtaining the statistical mean of the mass source. The conservation of mass [39] of copper vapors of all particles for the control volume bounded within cross-sections of radii r and is given as:
Quasi-Steady Assumptions of Group Combustion—The above governing equation of group combustion holds under the following assumptions. The combustion time of each particle is sufficiently long to establish a steady state over a continuous gas field of size O(). The combustion and its effect of every particle can be viewed as point sources of mass and energy for the gas field. The ignition of each particle is governed by the surrounding temperature of the gas phase.
An appropriate inter-particle vapor product propagation model can determine how the steady combustion field is realized within the group combustion theory. We arrived at the solution of the above governing equation following the approach adopted in the literature [40,41]. Here, the solution is presented for a monodispersed and uniformly distributed group. The radial variation of mass fraction and temperature is as follows:
where is the non-dimensional rate of sheath combustion as is defined in Equation (30) and the group combustion number (G) can be expressed as follows:
where n is the density of particles (with units of m), is the radius of the particle, N is the total number of particles in the group, is the surface area of the particles in a unit volume, is the ratio of fuel to air volume, is the total mass of particles in the group and is the virtual porosity of the particles in the group, wherein is the theoretical group density.
The G number expresses a relationship between the total number of particles (N) and normalized interparticle spacing of within a cluster. As the core–shell particles are local sources of heat and mass, the physical implication of G can also be determined as the ratio of the characteristic heat release rate of the exothermic reaction to the heat transport rate of products (as copper vapors) in the group/cloud, from Equations (19) and (20).
The normalized mass-fraction and temperature of nanothermite group combustion, determined using Equations (19) and (20), are plotted in Figure 4. These normalized plots are similar to the non-dimensional temperature distribution and non-dimensional vapor mass fraction of group evaporation [42]—this is a reasonable observation as both droplet evaporation and core–shell nanothermite combustion depend primarily on temperature, not the availability of the oxidizer. The variations of the temperature (T) and mass fraction (Y) of the nanothermite combustion products, as in Equations (19) and (20), differ from both spray [39] and char combustion [43]. However, the normalized Shvab–Zeldovich variables [43] of the spray combustion (, where [39]) and char combustion (, where [13]) are similar to that of the non-dimensional temperature (and non-dimensional mass-fraction) of the nanothermites (Equations (19) and (20)).

Figure 4.
Variation of the quasi-steady non-dimensional temperature of the gas and non-dimensional mass fraction of copper vapors with a non-dimensional radius of nanothermite group. represents the temperature in proximity to isolated particle combustion as defined in Equation (10).
Group Mass-Loss Rate and Correction Factor
The outflux of copper vapors progressively increases radially (r) from the cloud center () to the cloud periphery () because of the symmetry. The clouds mass flow rate at a radial location (r) is determined by summing up the overall particle sources (from Equation (4)) as follows:
Further, the total mass flow rate () at the boundary and outside of the cloud is as follows:
Thus, the normalized radial mass outflux rate of the group is given by the following formula:
Figure 5 plots the normalized radial mass flow rate against the normalized radius for different group combustion numbers (G). We observed that as the G increased, the majority of the combustion occurred near the group perimeter, for instance in sheath combustion for ).
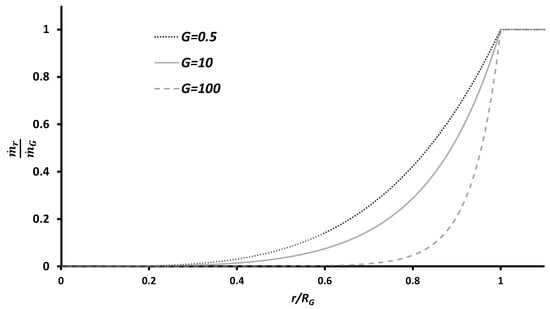
Figure 5.
Plot of normalized radial mass flow rate against the normalized radius for different group combustion numbers (G).
Furthermore, the non-dimensional mass group rate () can be obtained as follows:
The mass flux in the cloud is normalized by (), analogous to the normalizing term of single particle combustion presented in Equation (5). The normalized mass flux considered in the nanothermite group combustion was described so that the conditions of the cloud versus the single particle combustion could be compared. The solution for the group mass-loss rate is provided in two forms. First, the ratio of non-dimensional nanothermite group combustion () with the non-dimensional sheath combustion rate () [43] is defined as follows:
where the non-dimensional rate of sheath combustion () is obtained from Equation (4) as follows:
With the increasing magnitudes of G, the above fraction () tends to reach a unitary value as shown by the trend of Figure 6. The limiting cases (e.g., and ) can be approximated as . Before proceeding to the next form of the group mass-loss rate, it is important to note that we classified nanothermite group combustion based on the magnitude of , which in turn was based on the group combustion number (G). Secondly, the group mass-loss rate can be normalized by integrating the isolated group burn rate () as follows:
where the non-dimensional isolated group combustion is provided by considering Equation (5) of single particle combustion as follows:
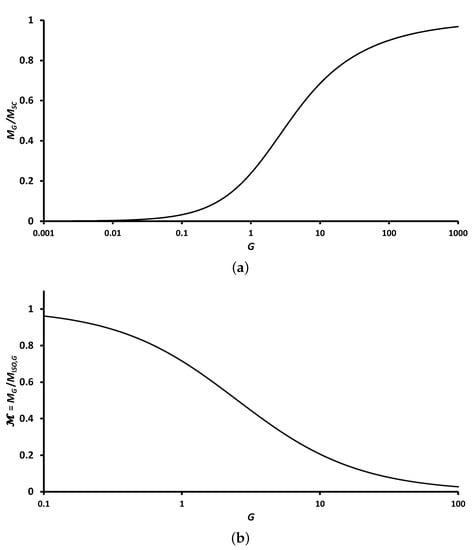
Figure 6.
(a) The fraction variation of cloud combustion rate to sheath combustion for a spherical nanothermite group with group combustion number. (b) The fraction variation of cloud combustion rate to isolated individual particle combustion for a spherical nanothermite group.
Figure 6b plots the variation of with G considering a monodispersed and uniform group of nanothermites. When the magnitude of G is approximately , equates to roughly 80% of the isolated particle combustion. The rate of particle combustion accounts for only about 10% of the isolated particle combustion rate for a group combustion number (G) of 100. As G approaches zero, the ratio tends towards one.
In this study, the diffusion of species was treated as being controlled, and the problem was considered from a thermal point of view. Based on Figure 4 for , group combustion is essentially a cloud of hot burning particles that loses heat to its surroundings. Figure 6a shows the results for group mass-loss rate in the form of variation with the group number (G). Figure 6b shows the group mass-loss rate in the form of variation with the group number (G).
In a group of particles where G approaches zero, each particle in the group is enclosed in a gas at the temperature of , with considered for a range of . This case of isolated group combustion corresponds to group numbers of with for magnitudes of . As the magnitude of G increases, each particle inside the group has the same temperature as the particle surface (), and the concentration of copper vapors corresponds to the saturated condition. Therefore, a compact group of particles acts as a single, large, isolated particle placed in an ambient fluid at and . Under these conditions, the group of particles is considered to combust in the sheath combustion (SC) regime. As the magnitude of G increases, the fraction reaches one, which is considered for a range of . This corresponds to group number of with for a range of . This variation in does not indicate that the combustion rate of nanothermites reduces as G increases.
The above ranges of group number (G) assist in classifying the group mass loss rate to the sheath combustion mode ( for ) and the isolated combustion mode ( for ) as defined in Equations (29) and (31), respectively. Whilst this variation of group mass-loss rates ( and ) with group number (G) is already established for spray [44] and char combustion [13], it helps to establish that these variations are the same and consistent for nanothermite combustion as well.
This section described the analytical approach adopted in modeling the group combustion of the nanothermites. We established a solution for the normalized mass-fraction and temperature of nanothermite group combustion (Figure 4). Additionally, we established the classical combustion modes of isolated and sheath combustion modes based on the group combustion numbers of and , respectively. In the following section, the group combustion modes of nanothermites are further refined.
4. Group Classification
The following part of this paper describes, in greater detail, the classification of nanothermite group combustion modes. As mentioned in the previous section, this classification is based on the magnitude range of the group mass-loss rate , which further depends on the group combustion number (G). We can redefine G as the ratio of mass transfer between the particles in the group (Region A, Figure 3) to the mass transfer between the group and its surroundings (Region B, Figure 3). This assists with the classification of different nanothermite combustion modes. When the mass transfer along the group boundary and ambient region (Region A, Figure 3) is extremely rapid in comparison to the net transfer among the particles and surrounding gaseous phase in the group (Region B, Figure 3), G is small and likely attributable to an isolated combustion (ISOC, Zone i) mode. When the mass transfer along the group boundary and ambient region is significantly low in comparison to the net transfer among the particles and the surrounding gaseous phase in the group, G is large and it is suitable to adopt the sheath combustion (SC, Zone iv) mode.
Other than the isolated combustion (ISOC) model and the sheath combustion (SC) model, Table 2 also classifies the intermediate models of nanothermite combustion. Overall, we can classify nanothermite groups simply into internal group combustion—representing Regime I of with —and external group combustion representing Regime II of and with as shown in Figure 7. The other modes are individual to partial group combustion in the upper limit of internal group combustion with the group combustion number in the range of which represents Zone ii of and in Table 2. Further, the group combustion number in the range of represents Zone iii of and . Zone iii is in the lower limit of external group combustion, depicting the modes of critical particle combustion (CPC) and external particle combustion (EPC). Next, we discuss the classification of minor regimes of nanothermite group combustion.

Table 2.
Summary of classifications of nanothermite groups based on range of group combustion number (G). represents the lower limit and represents the upper limit of the group combustion regimes, respectively.
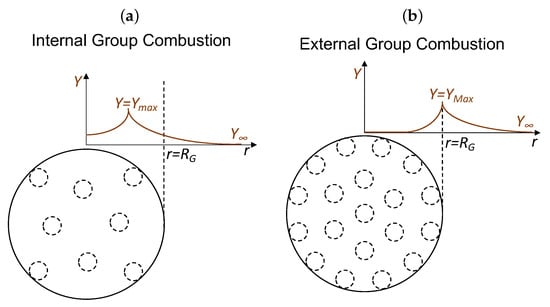
Figure 7.
Illustration of major group combustion modes of nanothermites.
4.1. Isolated Particle Combustion (ISOC)
In the case when particles are sufficiently distant from each another, they combust in an isolated mode of combustion. The existence of neighbouring particles has no effect on the combustion characteristics of an individual particle. This is discussed in detail in Section 2.
4.2. Internal Group Combustion (IGC)
It is hard to delineate the zones of cloud combustion for nanothermite as the species in the gaseous phase do not chemically react and there is no requirement to find oxygen-deficient regions. Thus, the various minor modes of nanothermite combustion (IPG, IGC and PG, as well as CGC, EPC and SC) are placed into the same groups. Internal Group Combustion (IGC) and External Group Combustion (EGC) were also established in spray combustion [45]. In the case of Internal Group Combustion (IGC), the highest mass fraction of copper (vapour product), , is located inside the group cloud ().
4.2.1. Individual Particle Combustion (IPC)
If the number density (n) of nanothermite increases, the burning characteristics of the constituent particles change owing to the rise in temperature within the region. However, suppose the inter-particle distance (l) is large. In such a case, each particle still maintains its own combustion characteristics, with the temperature of the cloud being higher than the temperature of isolated particle combustion. This is termed IPC, as demonstrated in Figure 8a.
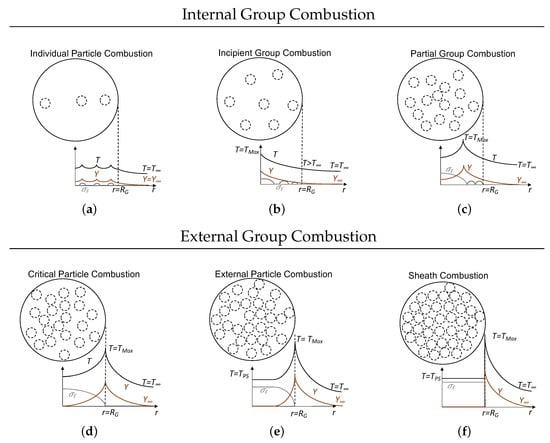
Figure 8.
Illustration of minor group combustion modes for a cluster of nanothermites. is the particle surface temperature.
4.2.2. Incipient Group Combustion (IGC)
The outermost nanothermites continue to combust in IPC as the magnitude of n increases. These nanothermites produce copper vapors, resulting in increased copper vapors () within the cloud. As this continues, the copper vapors reach the maximum mass fraction of saturation located at the cloud’s core. Further, the temperature at this location is at its maximum due to the maximum mass fraction of combustion products. This is termed IGC, as shown in Figure 8b.
4.2.3. Partial Group Combustion (PGC)
As n increases even further, the inner particles are starved of outer vapors (by extension, thermal energy) and ignite at a slow pace. The vapors from the inner region diffuse outwards and establish a maximum temperature inside the cloud. However, the nanothermites located in the outer region of the cloud combust in the form of IPC. This phenomenon is denoted as PGC, see Figure 8c.
4.3. External Group Combustion (EGC)
Suppose we further increase the concentration of nanothermites (n), such that, it causes a decrease in the copper vapor concentration within the cloud, and the location at which moves radially outwards from the cloud’s core. Furthermore, the mass fraction of fuel around the group’s center increases with an increase in the number density. For the regime of EGC, the maximum mass fraction of the copper vapors () is located at the group cloud radius ().
4.3.1. Critical Group Combustion (CGC)
As the magnitude of n increases further, the flux of copper vapor is such that it cannot penetrate to the cloud’s core and prevent the combustion of the nanothermites at the center. The maximum temperature is located only at the cloud surface. This is termed CGC, as shown in Figure 8d.
4.3.2. External Particle Combustion (EPC)
When n is further increased, the flux of inner copper vapors prevents outer copper vapors (and heat) from penetrating into the cloud center (and its surroundings). A maximum temperature is still determined at the group radius (). This is called EGC, as shown in Figure 8e.
4.3.3. Sheath Combustion (SC)
When n increases to large magnitudes, thereby forming a compact group, a state is achieved in which the temperature at the boundary of the particle group is at the ignition temperature of the nanothermite. The group acts similarly to an individual large particle of radius that has a group mass density similar to single particle density (). This combustion mode is known as sheath combustion, as shown in Figure 8f. Thus, we can use the single-particle results presented in Section 2 for a highly dense spherical cloud.
In practical cases, is lower than the ignition temperature of the considered core–shell nanothermites. Figure 8 demonstrates that the core–shell nanothermite combustion results in net heat release to the initial ambient gas because the magnitudes of the temperature profile are greater than the ambient temperature ().
As shown in Figure 7a, the mass fraction (Y) profiles are indicative of combustion occurring inside the thermite cloud since every particle in the system has access to an oxidizer. Figure 7b also shows combustion in an area bordering the thermite cloud. Additionally, the temperature profiles in Figure 8 are at their maximum at or within the cloud boundary and decrease to that of a distant temperature (). Regardless of the mode of external combustion in the second row of Figure 8, maximum temperature mainly occurs at the boundary because of the high particle concentration, which causes greater heat flux to the surrounding gas than the heat influx into the cloud interior. If we consider that the single particle completely burns instantly, then the time for single particle combustion is zero (), Equation (17), which is not the case for nanothermites.
It is important to emphasize that the combustion of nanothermites is not oxidizer limited. The model implicitly assumes that the stoichiometry of the nanothermite is balanced, i.e., the copper oxide content in the core–shell is neither more nor less in comparison to the aluminium content. This is an important distinction compared to spray and coal combustion. Owing to this property, internal particles of the cloud boundary may react via heat diffusion or the mass convection of products. Figure 9a illustrates the external sheath combustion (ESC), while Figure 9b depicts the internal sheath combustion (ISC) mode of nanothermites.
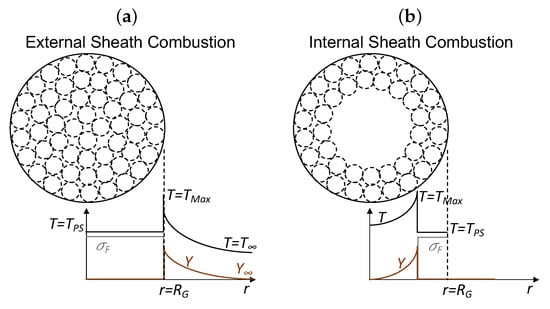
Figure 9.
Illustration of external and internal combustion modes of nanothermites.
Figure 10a shows the required number of particles (N), and Figure 10b shows the fraction of cloud radius to particle radius () with interparticle spacing () for different group combustion numbers (G). The variation in G represents different group combustion modes. The data representing , , and are theoretical and have no physical implications. As shown in Figure 10a, is fixed and increasing N results in a larger group radius. Hence at , the mode of isolated particle combustion occurs when , internal group combustion occurs when , external group combustion takes place if 15,450, and sheath combustion develops for 15,450. Likewise, considering Figure 10b where is chosen, the mode of isolated particle combustion takes place when (e.g., µm, mm), internal group combustion takes place if , (1 mm mm), external group combustion occurs for 146 464, (4.6 mm mm), and sheath combustion develops if ( mm). As the combustion rate reaches isolated particle combustion, the reducing group radius () correlates to a higher combustion rate of each particle. Note that the quasi-steady assumption underpins all of the plots in this section, and also the time-dependent considerations reduce the interaction.
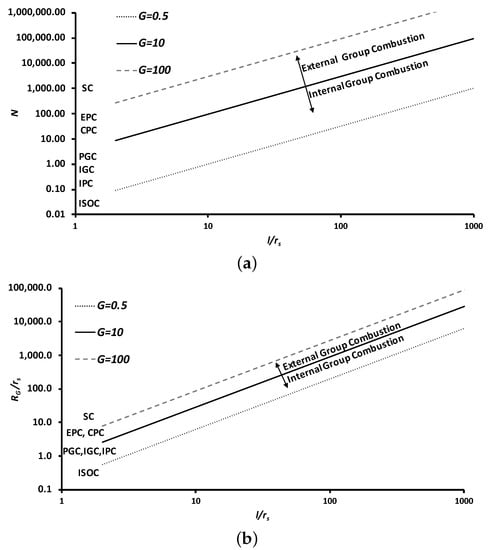
Figure 10.
(a) The variation of the overall number of particles (N) with normalized interparticle distance () for various group combustion numbers (G) corresponding to different group combustion modes. (b) The variation of non-dimensional group radius () with normalized interparticle distance () for various group combustion numbers (G) corresponding to different group combustion modes.
4.4. Comparison with Other Group Combustion Models
Table 3 classifies various nanothermite group combustion regimes with the lower limit and upper limit of the group combustion number (G). The upper limit of the regime corresponds to the lower limit of the next regime. The regime before the Individual Particle Combustion (IPC) corresponds to Isolated Particle Combustion (ISOG), where particles burn without interaction. We can observe in Table 3 that the magnitude of nanothermite regimes varies exponentially from IPC of 0.5 to CPC of 10 to SC of 100. It is apparent from this table that the magnitudes of G are higher for nanothermite regimes than for spray combustion. These higher magnitudes of G occur because the combustion is not limited by the oxygen availability in the gas phase.

Table 3.
Comparison of group number with other combustion models.
Laster and Annamalai [46] analyzed the transient combustion of a quiescent droplet cloud. They reported that a cloud ignites with ease in comparison to a single droplet. Additionally, if the cluster is dense, ignition is limited to within a narrow band along the outer surface of the cluster. Similarly, the ignition of a fuel spray was investigated by Bellan and Harstad [47]. Here, the influence of convection was determined to be less crucial in a cloud of high spray concentration. In this case, until a considerable quantity of fuel evaporates and saturates the environment, combustion does not begin. In this regard, Chiu and Lin [44] numerically studied the time-dependent ignition of a cold spray as it was suddenly exposed to a hot environment. It was found that ignition and combustion within a cloud can take place even if the cloud is non-diluted (). This aberrant combustion contradicts the typical norms of group combustion.
5. Group Combustion of Non-Spherical Particle Distribution
In order to model the combustion of nanothermites, we developed a group combustion model for the simple geometry of spherical particle distribution in the previous section. A hypothetical group combustion of nanothermites is shown in Figure 11, where we considered a two-dimensional flux of nanothermites entrained from the nozzle along with a laminar flow surrounding it. This injection of nanothermites was distributed with a greater concentration near the nozzle and a lesser concentration further away. Symmetry conditions around the midline can be taken into account. The resulting temperature of the gas mixture is higher in a region when the concentration of nanothermites is higher. Having nanothermite particles distributed randomly in such a system and the complexities of the flow fields makes it difficult to obtain a closed-form solution to this problem. To be able to identify the parameters governing the group behavior in such a system, it is helpful to achieve explicit solutions for the burn rate and correction factor for simple geometry, as discussed previously in Section 4 (and Figure 8).
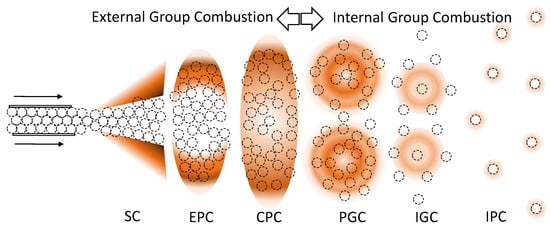
Figure 11.
Schematic of group combustion in nanothermite jet suspension considering convective heating.
The particle distribution of nanothermites is shown in Figure 11, along with the contour map of the heat release for the corresponding regions. We can, for the most part, classify the combustion flow regimes as either an external group combustion regime or an internal group combustion regime. The zones under these regimes are considered equivalent to simple geometry zones (SC, EPC, etc.) from Section 4. As long as there are particles within the boundaries of such particle distributions but no particles outside, then there is a mass source term for particles within the boundary but not for particles outside. In other words, there is a variation in the number density, which is indirectly the mass source. By assuming that we reshape these zones to a spherical shape and there is no convective flow across the zones, we obtained a closed-form solution to the burn rate of clouds.
When ignited, the nanothermites burn mostly along the boundary of the distribution in external group combustion. Because the nanothermite core is too cold for ignition at the nozzle exit, it was hypothesized that ignition begins further downstream. As nanothermites are highly dense (SC), heat transfer and ignition are not possible within the distribution boundary, resulting in ignition occurring outside this boundary. The increasing separation of particles (EPC) results in heat penetration of the inner side of the cloud and ignition of those particles. After a sufficiently large separation of the particles is reached, heat penetrates to the mid-area of the jet, intersecting and igniting the entire cluster (CPC). After this zone, internal group combustion may exist outside of the external group combustion. There may be an individual combustion zone (PGC) or a nested combustion zone (IGC) around a group of particles. This is followed by the terminal zone, where unburned nanothermite particles are consumed individually (IPC).
It is important to emphasize that we began this study by focusing on aluminium-copper oxide. However, this framework can be applied to a variety of different nanothermite compositions, such as aluminium-bismuth trioxide and aluminium-iron oxide. Some of these fuels are more gas generating, while others are predominantly energy generating. Aluminium-copper oxide does not generate a lot of vapors compared to the other types of nanothermites. Thus, all these different effects could also be expanded to the present study, including the high amount of gas generations as well as studying the high threshold values for enthalpy and observing their impact on the results.
6. Conclusions
A combustion model was developed to examine the combustion characteristics of a cloud of spherical, core–shell, nanothermite particles. The present framework characterized the burning configuration in different combustion modes. The burning characteristics of each particle are dependent on the diffusion rate of heat and copper vapors, and the overall combustion rate of the group is independent of oxygen availability due to the dispersed phase reaction of nanothermites. The theoretical results provided insight into the characteristics of combustion and emissions, which are dictated by the combustion mode. There are two regimes of combustion, namely (I) Internal Group Combustion (IGC), and (II) External Group Combustion (EGC). The correct regime can be established based on the mass flow of the fuel, the particle distribution, and the mass flows of species in the carrier gas. The IGC regime is defined based on small magnitudes of G, in which smaller particle sizes lead to a higher average burning rate per unit area. Hence, for a given mass within a group of a certain radius (), smaller particle sizes yield an increase in the burning rate.
Although the model developed involves a number of assumptions that facilitate the theoretical tractability, the qualitative features of the experimental study of the nanothermites combustion are expected to follow the trends reported herein. However, for the accurate prediction of the combustion features and emission characteristics—especially for engineering relevant designs—the present laminar model must be extended to include turbulent features of the carrier phase, with added complexities, such as a finite rate chemical reaction, particle–fluid interaction mechanics, and swirling/recirculating flow features. Much of the group combustion phenomena reported in the paper were derived from theoretical investigations and should be verified experimentally to confirm the validity of the model.
Author Contributions
Conceptualization: M.M.R. and J.-P.H.; methodology: M.M.R. and J.-P.H.; writing—original draft preparation: M.M.R. and A.S.; writing—review and editing: M.M.R., A.S., M.F.K. and J.-P.H.; visualization: M.M.R., A.S. and M.F.K.; supervision: J.-P.H.; funding acquisition: J.-P.H. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by Columbiad Launch Services and the NSERC CRD program. Ahmed Saieed was supported by the NSERC Vanier Canada Graduate Scholarship award. Computations were performed on the Niagara supercomputer at the SciNet HPC Consortium as part of Compute Canada.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data that support the findings of this study are available from the corresponding author, M.M.R., upon reasonable request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Saceleanu, F.; Idir, M.; Chaumeix, N.; Wen, J.Z. Combustion Characteristics of Physically Mixed 40 nm Aluminum/Copper Oxide Nanothermites Using Laser Ignition. Front. Chem. 2018, 6, 465. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rogachev, A.; Mukasyan, A. Combustion of heterogeneous nanostructural systems (review). Combust. Explos. Shock Waves 2010, 46, 243–266. [Google Scholar] [CrossRef]
- Qin, L.; Gong, T.; Hao, H.; Wang, K.; Feng, H. Core–shell-structured nanothermites synthesized by atomic layer deposition. J. Nanopart. Res. 2013, 15, 2150. [Google Scholar] [CrossRef]
- Zhang, Y.; Sui, H.; Li, Y.; Wen, J.Z. Energetic characteristics of the Al/CuO core–shell composite micro-particles fabricated as spherical colloids. Thermochim. Acta 2020, 689, 178656. [Google Scholar] [CrossRef]
- Ma, X.; Li, Y.; Hussain, I.; Shen, R.; Yang, G.; Zhang, K. Core–Shell Structured Nanoenergetic Materials: Preparation and Fundamental Properties. Adv. Mater. 2020, 32, 2001291. [Google Scholar] [CrossRef]
- Zhou, X.; Torabi, M.; Lu, J.; Shen, R.; Zhang, K. Nanostructured energetic composites: Synthesis, ignition/combustion modeling, and applications. ACS Appl. Mater. Interfaces 2014, 6, 3058–3074. [Google Scholar] [CrossRef]
- Ahn, J.Y.; Kim, J.H.; Kim, J.M.; Lee, D.W.; Park, J.K.; Lee, D.; Kim, S.H. Combustion characteristics of high-energy Al/CuO composite powders: The role of oxidizer structure and pellet density. Powder Technol. 2013, 241, 67–73. [Google Scholar] [CrossRef]
- Weismiller, M.; Malchi, J.; Yetter, R.; Foley, T. Dependence of flame propagation on pressure and pressurizing gas for an Al/CuO nanoscale thermite. Proc. Combust. Inst. 2009, 32, 1895–1903. [Google Scholar] [CrossRef]
- Sanders, V.E.; Asay, B.W.; Foley, T.J.; Tappan, B.C.; Pacheco, A.N.; Son, S.F. Reaction propagation of four nanoscale energetic composites (Al/MoO3, Al/WO3, Al/CuO, and Bi2O3). J. Propul. Power 2007, 23, 707–714. [Google Scholar] [CrossRef]
- Epps, J.M.; Hickey, J.P.; Wen, J.Z. Modelling reaction propagation for Al/CuO nanothermite pellet combustion. Combust. Flame 2021, 229, 111374. [Google Scholar] [CrossRef]
- Chiu, H.; Kim, H.; Croke, E. Internal group combustion of liquid droplets. Symp. Combust. 1982, 19, 971–980. [Google Scholar] [CrossRef]
- Candel, S.; Lacas, F.; Darabiha, N.; Rolon, J.C. Group combustion in spray flames. Multiph. Sci. Technol. 1999, 11, 1–18. [Google Scholar] [CrossRef]
- Annamalai, K.; Ramalingam, S. Group combustion of char/carbon particles. Combust. Flame 1987, 70, 307–332. [Google Scholar] [CrossRef]
- Frank-Kamenetskii, D.A. Diffusion and Heat Exchange in Chemical Kinetics; Princeton University Press: Princeton, NJ, USA, 1955. [Google Scholar]
- Yetter, R.A.; Dryer, F.L. Metal particle combustion and classification. In Microgravity Combustion: Fire in Free Fall; Academic Press: Cambridge, MA, USA, 2001; pp. 419–478. [Google Scholar]
- Lam, F.Y.; Mi, X.; Higgins, A.J. Dimensional scaling of flame propagation in discrete particulate clouds. Combust. Theor. Model. 2020, 24, 486–509. [Google Scholar] [CrossRef]
- Soo, M.; Mi, X.; Goroshin, S.; Higgins, A.J.; Bergthorson, J.M. Combustion of particles, agglomerates, and suspensions—A basic thermophysical analysis. Combust. Flame 2018, 192, 384–400. [Google Scholar] [CrossRef]
- Rumanov, E.; Khaikin, B. Critical autoignition conditions for a system of particles. Combust. Explos. Shock Waves 1969, 5, 88–91. [Google Scholar] [CrossRef]
- Cassel, H.; Liebman, I. The cooperative mechanism in the ignition of dust dispersions. Combust. Flame 1959, 3, 467–475. [Google Scholar] [CrossRef]
- Mi, X.; Fujinawa, A.; Bergthorson, J.M. A quantitative analysis of the ignition characteristics of fine iron particles. Combust. Flame 2022, 240, 112011. [Google Scholar] [CrossRef]
- Monchaux, R.; Bourgoin, M.; Cartellier, A. Analyzing preferential concentration and clustering of inertial particles in turbulence. Int. J. Multiphas. Flow 2012, 40, 1–18. [Google Scholar] [CrossRef]
- Rahman, M.M.; Cheng, W.; Samtaney, R. Generation and sustenance of electric fields in sandstorms. Phys. Rev. Res. 2021, 3, L012008. [Google Scholar] [CrossRef]
- Pouransari, H.; Mani, A. Particle-to-fluid heat transfer in particle-laden turbulence. Phys. Rev. Fluids 2018, 3, 074304. [Google Scholar] [CrossRef]
- Mouallem, J.; Hickey, J.P. Induction heating of dispersed metallic particles in a turbulent flow. Int. J. Multiphas. Flow 2020, 132, 103414. [Google Scholar] [CrossRef]
- Zamansky, R.; Coletti, F.; Massot, M.; Mani, A. Radiation induces turbulence in particle-laden fluids. Phys. Fluids 2014, 26, 071701. [Google Scholar] [CrossRef]
- Pouransari, H.; Kolla, H.; Chen, J.H.; Mani, A. Spectral analysis of energy transfer in turbulent flows laden with heated particles. J. Fluid Mech. 2017, 813, 1156–1175. [Google Scholar] [CrossRef]
- Saieed, A.; Rahman, M.M.; Hickey, J.P. Role of Viscosity in the Preferential Concentration of Heated, Bidispersed Particles. Int. J. Multiphas. Flow 2022, 155, 104185. [Google Scholar] [CrossRef]
- Rahman, M.M.; Chamkha, A.J.; Elmasry, Y.; Ullah, I.; Pasha, A.A.; Sadeghi, M.S.; Galal, A.M. The heat transfer behavior of MHD micro-polar MWCNT-Fe3O4/Water Hybrid Nano-fluid in an inclined shaped cavity with semi-circular heat source inside. Case Stud. Therm. Eng. 2022, 2214-157X, 102316. [Google Scholar] [CrossRef]
- Pouransari, H.; Mani, A. Effects of preferential concentration on heat transfer in particle-based solar receivers. J. Sol. Energy Eng. 2017, 139, 021008. [Google Scholar] [CrossRef]
- Baijot, V.; Glavier, L.; Ducéré, J.M.; Djafari Rouhani, M.; Rossi, C.; Esteve, A. Modeling the Pressure Generation in Aluminum-Based Thermites. Propell. Explos. Pyrot. 2015, 40, 402–412. [Google Scholar] [CrossRef]
- Law, C.K. Combustion Physics; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Sahu, S.; Hardalupas, Y.; Taylor, A. Interaction of droplet dispersion and evaporation in a polydispersed spray. J. Fluid Mech. 2018, 846, 37–81. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.C.; Xu, Y.; Hicks, M.C.; Avedisian, C.T. Comprehensive study of initial diameter effects and other observations on convection-free droplet combustion in the standard atmosphere for n-heptane, n-octane, and n-decane. Combust. Flame 2016, 171, 27–41. [Google Scholar] [CrossRef]
- Nayagam, V.; Dietrich, D.L.; Ferkul, P.V.; Hicks, M.C.; Williams, F.A. Can cool flames support quasi-steady alkane droplet burning? Combust. Flame 2012, 159, 3583–3588. [Google Scholar] [CrossRef]
- Chiu, H.; Liu, T. Group combustion of liquid droplets. Combust. Sci. Technol. 1977, 17, 127–142. [Google Scholar] [CrossRef]
- Zhao, Y.; Yang, L.; Ge, K.; Li, Y. Numerical simulation of impacts of gas flow temperature on combustion characteristics of single droplet. J. Combust. Sci. Technol. 2014, 20, 77–83. [Google Scholar]
- Frossling, N. Uber die verdunstung fallernder tropfen. Gerl. Beitr. Geophys. 1938, 52, 170–216. [Google Scholar]
- Labowsky, M. The effects of nearest neighbor interactions on the evaporation rate of cloud particles. Chem. Eng. Sci. 1976, 31, 803–813. [Google Scholar] [CrossRef]
- Annamalai, K.; Ryan, W. Interactive processes in gasification and combustion. Part I: Liquid drop arrays and clouds. Prog. Energ. Combust. 1992, 18, 221–295. [Google Scholar] [CrossRef]
- Samson, R.; Bedeaux, D.; Saxton, M.; Deutch, J. A simple model of fuel spray burning I: Random sprays. Combust. Flame 1978, 31, 215–221. [Google Scholar] [CrossRef]
- Labowsky, M.; Rosner, D.E. “Group” Combustion of Droplets in Fuel Clouds. I. Quasi-steady Predictions. In Evaporation—Combustion of Fuels; ACS Publications: Washington, DC, USA, 1978; Chapter 4; pp. 63–79. [Google Scholar]
- Tishkoff, J.M. A model for the effect of droplet interactions on vaporization. Int. J. Heat Mass Transf. 1979, 22, 1407–1415. [Google Scholar] [CrossRef]
- Annamalai, K.; Ryan, W.; Dhanapalan, S. Interactive processes in gasification and combustion—Part III: Coal/char particle arrays, streams and clouds. Prog. Energy Combust. Sci. 1994, 20, 487–618. [Google Scholar] [CrossRef]
- Chiu, H.; Lin, C. Anomalous group combustion of premixed clusters. Symp. Combust. 1996, 26, 1653–1661. [Google Scholar] [CrossRef]
- Chigier, N. Group combustion models and laser diagnostic methods in sprays: A review. Combust. Flame 1983, 51, 127–139. [Google Scholar] [CrossRef]
- Laster, W.; Annamalai, K. Ignition delay of droplet clouds: Results from group combustion theory. Chem. Eng. Commun. 1991, 105, 201–219. [Google Scholar] [CrossRef]
- Bellan, J.; Harstad, K. Ignition of non dilute clusters of drops in convective flows. Combust. Sci. Technol. 1987, 53, 75–87. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).