1. Introduction
Liquid lead-bismuth eutectic (LBE, 55 wt% Bi and 45 wt% Pb, melting point of 125.5 °C) is an attractive nuclear coolant for application in fast neutron systems. Several of its properties are advantageous for reactor operation and safety, such as its low vapor pressure, high heat transport capability, and compatibility with water [
1].
Fast-spectrum nuclear reactors cooled by LBE are seen as an intermediate step in the roadmap towards the deployment of commercial lead-cooled fast reactors (LFR), because they allow coolant technology development at lower temperatures than with lead. The LFR is one of the Generation IV reactor concepts, with an expected improved sustainability, efficiency, and cost compared to existing nuclear reactors [
2]. LBE is also foreseen to be used in accelerator-driven systems (ADS) [
3]. An ADS consists of a subcritical nuclear reactor core coupled to a high-energy proton accelerator. The protons interacting with Pb and Bi in the LBE cause spallation reactions, which result in the extra neutrons that are used to sustain the nuclear reaction in the subcritical core. The operational flexibility of an ADS allows for the efficient burning of minor actinides to shorter-lived fission products. It is therefore one of the key technologies for reducing the radiotoxicity and volume of minor actinide waste.
When LBE is used as coolant, polonium is produced in it in relatively large quantities, mainly by activation of stable bismuth. Polonium, in particular the isotope
210Po, is expected to build up to concentrations of ~0.1 ppm. Because of its radiotoxicity, it is the main contributor to the primary radioactive source term in the LBE. Moreover, polonium is a relatively volatile element in its metallic state (estimated atmospheric boiling point 949 °C) [
4]. In safety evaluations used for design and licensing of LBE cooled nuclear systems, it is therefore required to assess polonium release by evaporation from LBE in various reactor operation and accidental conditions.
A consistent thermochemical description of the equilibria between polonium in the LBE and its vapor forms the basis for conservative release estimations. It further allows one to determine the driving forces for more detailed release evaluations, which may also take into account time-dependent processes such as mass transfer.
The required thermochemical properties of relevant polonium phases and species are available in databases. However, it was found that there are inconsistencies of these properties with primary experimental data, i.e., vapor pressure data and measured properties of the gas phase species. Moreover, additional information has recently become available on polonium evaporation from LBE and its vapor species, based on both experimental work and ab initio computational studies.
In the present work, we first revisit the vapor pressure of pure metallic polonium, and provide a set of thermodynamic data that is consistent with primary experimental measurements and recent ab initio data. Subsequently, the activity coefficient of polonium in LBE is derived by matching a thermochemical model with measurements of the Henry constant of a solution of polonium in LBE. Because of its potentially important role in chemical equilibria with polonium in LBE, the thermochemical properties of solid lead polonide are furthermore estimated. Based on this new information, the validity of Henry’s law for polonium in LBE is examined and its expected range of applicability determined.
2. Vapor Pressure of Metallic Polonium
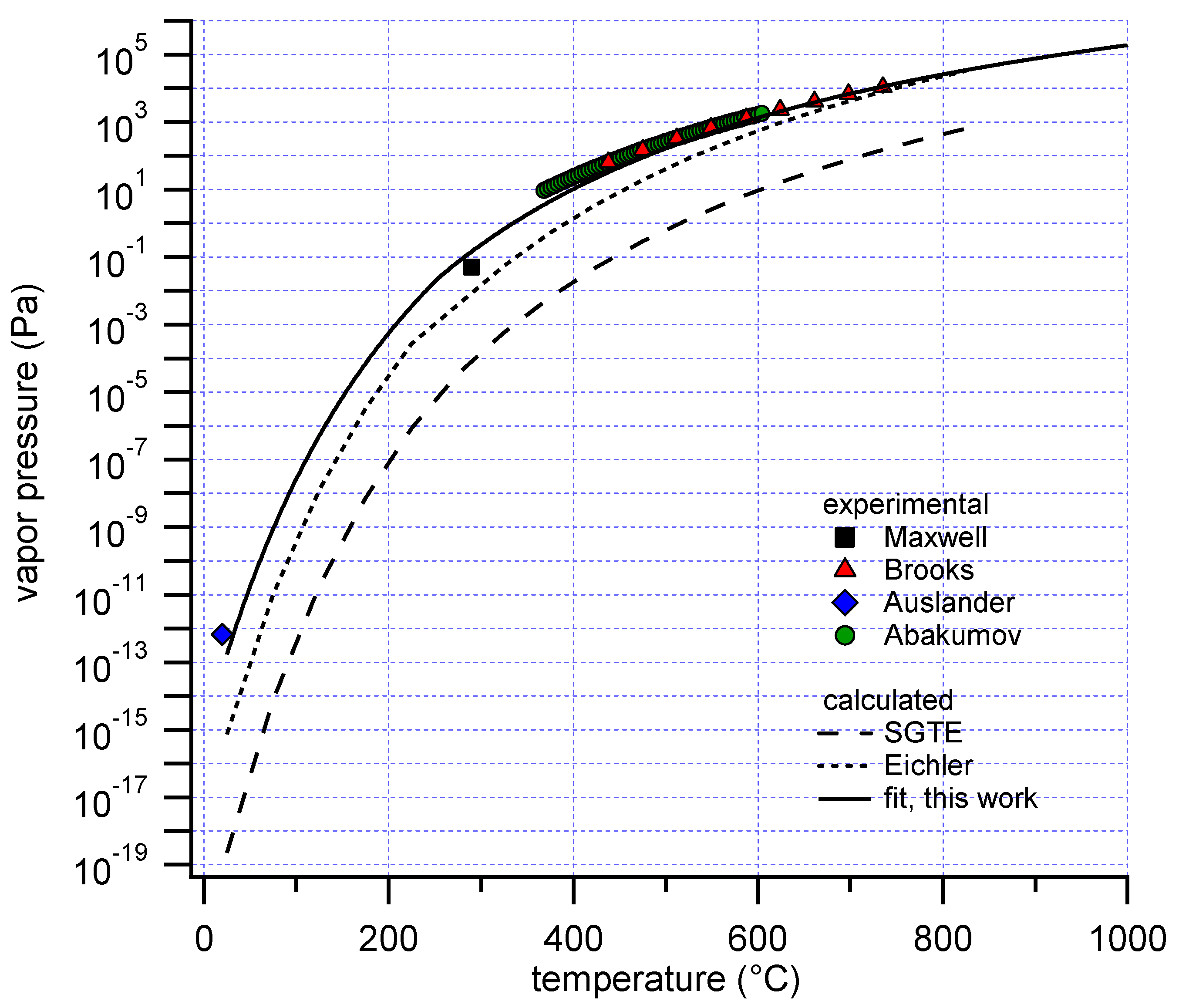
Only a limited number of experimental measurements of the vapor pressure of polonium exist (
Table 1,
Figure 1).
The earliest report of the vapor pressure of polonium is a value at a single temperature, which is attributed to Beamer and Maxwell, as cited in [
5]. A vapor pressure-temperature correlation of metallic Po was subsequently reported by Brooks in 1955 [
6]. The correlation was determined by fitting 9 direct pressure measurements with a quartz Bourdon gauge between 438 and 735 °C. Ausländer and Georgescu measured the vapor pressure of Po at room temperature (18–22 °C) by a radiometric method [
7]. As of today, this is the only available experimental result for solid polonium. The most recent determination dates from 1974, in which Abakumov and Ershova provided a temperature correlation for the vapor pressure of Po based on 64 experimental data points between 368 and 604 °C, using a radiometric method [
5]. The correlations by Brooks and Abakumov are in very good agreement. An additional correlation has been reported by Bagnall [
8] with reference to a report by Moyer, [
9] but that correlation could not be found in the original reference, and has therefore been omitted in the present study.
The vapor in equilibrium with metallic Po in inert conditions is thought to contain both monoatomic Po(g) as well as diatomic Po
2(g) vapor species. In thermochemical databases, such as that compiled by the Scientific Group Thermodata Europe (SGTE) [
10], entries for condensed polonium and these gaseous species are available. However, with the SGTE data, the experimental vapor pressure measurements are not reproduced, showing deviations up to several orders of magnitude (
Figure 1). Eichler performed a critical review of the thermodynamic properties relevant to polonium evaporation [
4], and suggested new values based on extrapolation of trends from the lighter homologues of polonium in the periodic system. However, his correlation for the vapor pressure of polonium also is not consistent with the experimental results (
Figure 1), although the deviation is less than when SGTE data are used.
Besides these vapor pressure measurements, a single experimental result exists of the dissociation enthalpy Δ
Hdiss of Po
2(g) to 2Po(g), having a value of 1.895 eV or 182.8 kJ/mol. This result was obtained by Charles et al. using vibrational spectroscopy [
11].
These experimentally determined equilibrium properties are complemented by recent results from high level ab initio calculations by Mertens et al. He studied various binary polonium vapor species with a method that was extensively validated by comparison with tabulated properties of the lighter homologues of polonium [
12,
13]. In direct support of the accuracy of the approach by Mertens et al. for polonium species, it was found that the calculated dissociation enthalpy of Po
2(g) was in good agreement with the experimentally observed value.
In the present work a model was set up and matched with the available experimental data, also taking into account recent
ab inito results for the gas-phase species. In the model, it was assumed that the vapor pressure of polonium metal is established by the following equilibria:
The gas phase was assumed ideal. The vapor pressure
that is compared with experiment is calculated as the sum of the partial pressures of the two gas species:
where
is the Gibbs energy of formation of the gas species, which is calculated between 298.15 K and 1400 K from
,
,
at 298.15 K and the heat capacity
of the involved phases and species. The following data were chosen (
Table 2):
Po(s) and Po(l): enthalpy of formation (
of Po(s) at 298.15 K = 0 as it is the reference state), entropy
, heat capacity, and properties of the solid (s)-liquid (l) phase transition as listed by SGTE were used for the solid and liquid Po metal phases [
10].
Po(g)
- ○
The enthalpy of formation (
at 298 K of Po(g) is the only property in the model that is treated as a fit parameter. We assume that the measured dissociation enthalpy
is accurate, as well as the estimated entropy of this species.
of Po(g) is therefore assumed to be the main contributor to the discrepancy between the vapor pressure calculated from SGTE data and experimental results. Eichler already recognized that there are large inconsistencies in literature for this property [
4].
- ○
The entropy
at 298 K was taken from Mertens et al., a value that is in good agreement with both SGTE data and the extrapolation result by Eichler [
4].
- ○
The heat capacity as entered in the SGTE database is also assumed to be accurate. As expected, it is close to the heat capacity of an ideal gas (constant volume heat capacity = 3/2).
Po2(g)
- ○
The enthalpy of formation at 298 K of Po2(g) is calculated from the optimized enthalpy of formation of Po(g) and the experimental dissociation enthalpy.
- ○
The entropy at 298 K and heat capacity of this species are taken from the ab initio results by Mertens et al. A correlation for the calculated heat capacity at different temperatures was derived (see
Supplementary Material).
The model was implemented in the Python programming language. The result of the optimization is shown in
Figure 1. The best fit, minimizing the sum of squared differences (SSD) between data and experiment, showed good agreement with the data by Brooks and Abakumov, in contrast with calculations only based on data by SGTE or Eichler. The SSD was calculated directly from the pressure values, and not from their logarithm. The contribution of the high pressure, high temperature data to the SSD is therefore dominant. Despite this emphasis on the high pressure data, the experimental data points at lower temperature by Maxwell and Ausländer were also in good agreement with the calculated result.
The fitted enthalpy of formation for Po(g) at 298.15 K was 165 kJ/mol. This value is significantly lower than that listed in the database by SGTE, 182 kJ/mol. Estimates reported in various other (secondary) sources, as summarized by Eichler, were of the order of 145 kJ/mol [
4]. Eichler himself derived a larger value of 188.9 kJ/mol, by extrapolation of the properties of the lighter homologues. The enthalpy of formation for Po
2(g) similarly showed a lower value than previously reported.
Since the presently derived data are consistent with primary experimental observations, and further rely on well-validated ab initio data, we assume that these are current best estimates for the properties of the condensed phase-vapor system of polonium. These data will be used further in this work.
3. Partial Pressure and Activity Coefficient of Polonium Dissolved in LBE
The partial pressure of polonium in equilibrium with a dilute mixture of polonium in LBE has been measured by various authors. A summary of experimental studies can be found in Ref. [
14]. The apparent Henry constant of polonium, determined in the presence of inert (Ar) or reducing cover gas (Ar/5–7%H
2), follows a single correlation in the temperature range 235–1000 °C, and it was observed that Henry’s law is applicable in a concentration range of
xPo = 10
–13…10
–8 (mol fraction). The recommended correlation for the temperature dependence of the Henry constant of polonium in LBE is that proposed by Gonzalez et al. [
15]:
The polonium-containing vapor species in equilibrium with LBE are expected to be Po(g), Po
2(g), PbPo(g), and BiPo(g) [
16]. Thermochemical properties for Po(g) and Po
2(g) have been derived in
Section 2 of the present work. Properties for PbPo(g) and BiPo(g) (
Table 3) have been derived from the dissociation enthalpies [
13], entropies, and heat capacities calculated by the ab initio method by Mertens et al. [
12,
13], and the properties of Po(g).
With this information, the activity coefficient of dissolved Po in LBE at low concentrations was estimated, by fitting the experimental correlation of the Henry constant with a model, taking into account the following condensed-gas equilibria:
The gas phase was modeled as ideal, containing besides the polonium species of Equation (4), the dominant species in equilibrium with LBE, viz. Pb(g), Bi(g) and Bi
2(g) [
14]. The LBE phase was modeled as an ideal-dilute solution of polonium in Pb and Bi. Metallic Pb, Bi, and Po were also included in the model as pure phases.
The polonium pressure over a solution in LBE was calculated on a monoatomic basis, to describe the experimental pressure, which is measured by α-counting, and given by:
In terms of thermochemical properties, this becomes:
where
and
are the mole fractions, resp. activity coefficients in the solution of Po, and of Pb and Bi at the eutectic composition.
For the activity coefficients of Pb and Bi in LBE, the correlations derived from Gokcen’s work are taken [
14,
17]. References for the activity coefficients are the pure liquid phases of Po, Pb, and Bi as listed in the SGTE database [
10]. The temperature dependence of the activity coefficient of Po in LBE was approximated by the equation:
where
and
are the partial molar excess enthalpy and entropy (assumed temperature independent) whose values were optimized to fit the experimental Henry constant correlation (Equation (3)). This was done using the Gibbs Energy Minimization (GEM) functions of the HSC Chemistry software to calculate the equilibrium composition and Henry constant at different temperatures, coupled with least squares fitting.
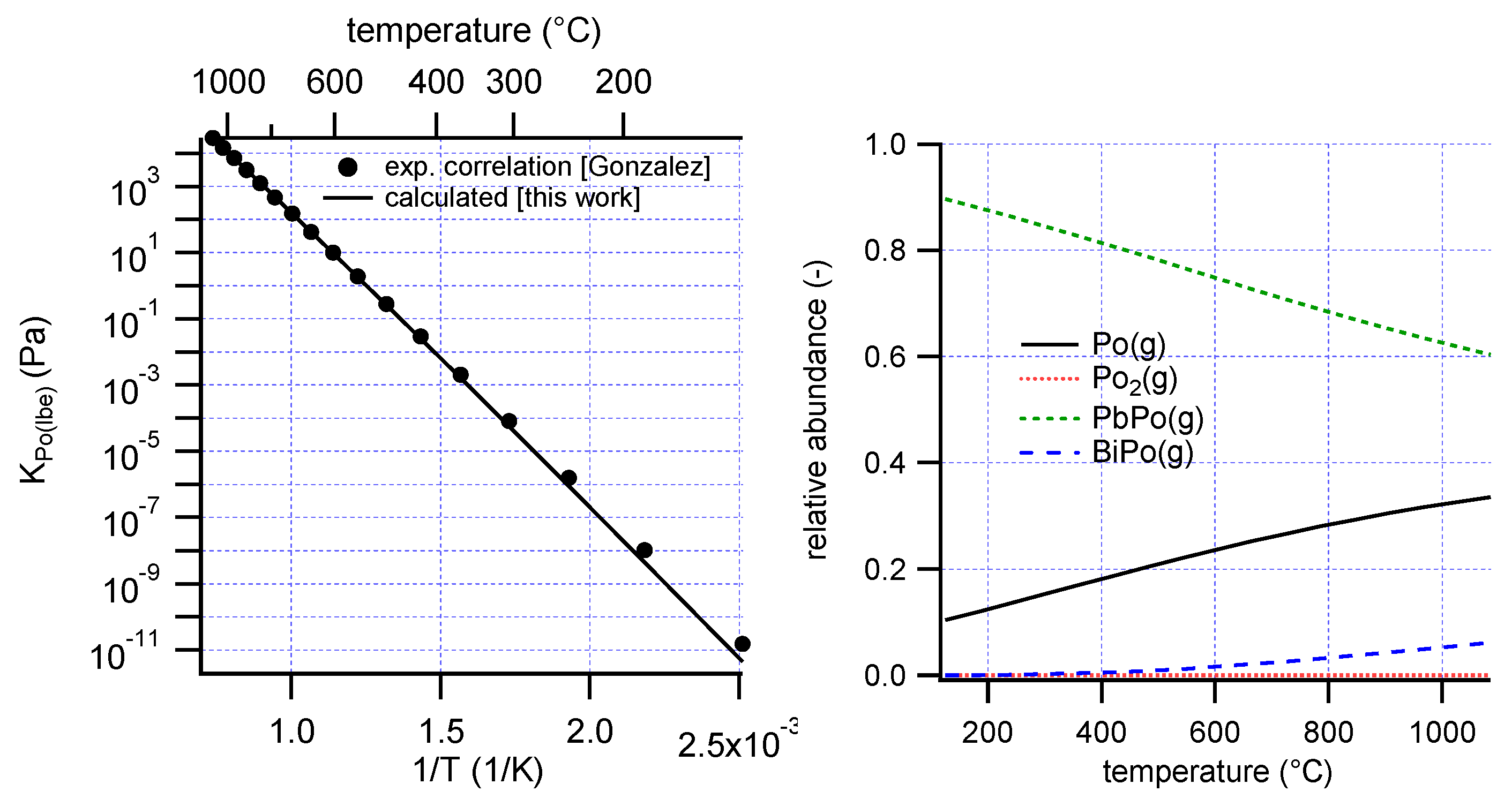
A best fit was obtained with Δ
HPo(lbe)xs = −24 kJ/mol and Δ
SPo(lbe)xs = −11 J/mol/K (
Figure 2, left). The calculated enthalpy may be compared with the work by Neuhausen et al., who estimated a value of −10 kJ/mol for the partial molar enthalpy of polonium in liquid LBE using the semi-empirical Miedema model [
18]. Rijpstra et al. found a solution enthalpy of Po in solid LBE of −26 kJ/mol using a DFT method, and found that Po in LBE is preferentially sited in a Pb-rich environment [
19]. Although it remains difficult to assess its accuracy, the current result appears to be reasonable given these previous estimations.
The dominant species in the gas phase below 1000 °C are predicted to be PbPo(g) and Po(g) (
Figure 2, right), comparable to an earlier calculation [
12].
Deviations from Henry’s law will occur when Po2(g) starts contributing significantly to the total vapor pressure. The contribution of this species is expected to increase with increasing polonium concentration. From the present analysis it is found that Po2(g) does not contribute to more than 1% of the total polonium partial pressure below dissolved polonium concentrations xPo(lbe) ≈ 10−3, assuming the activity coefficient of Po is concentration-independent up to that concentration.
4. Lead Polonide and Its Solubility in LBE
Lead polonide, PbPo(s), is thought to be the most stable compound that may form with polonium and Pb or Bi, and may therefore limit polonium solubility in LBE. This is expected from the phase behavior of tellurium-lead and bismuth systems, and confirmed by density functional theory calculations of the corresponding systems with polonium [
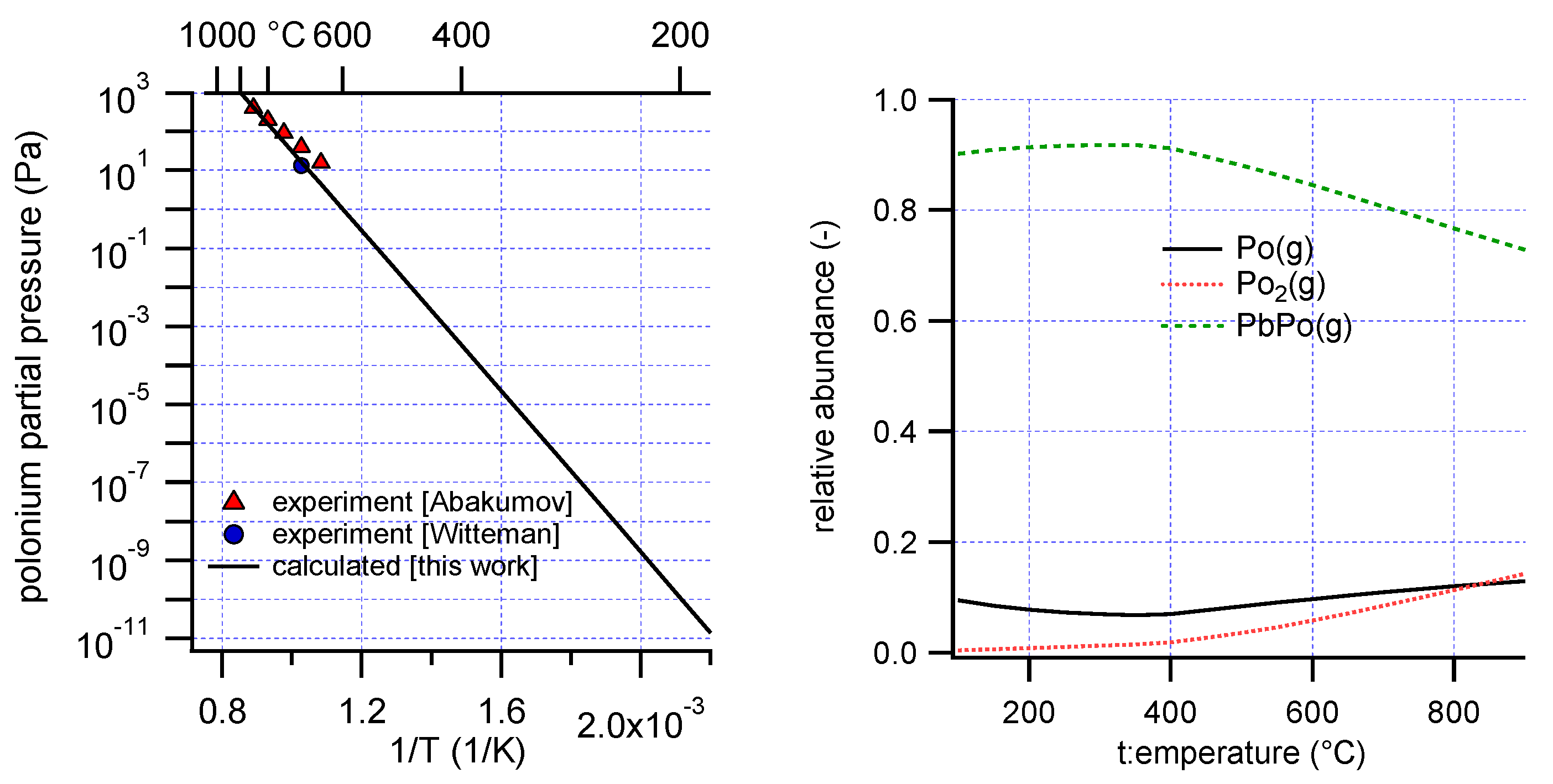
20]. Vapor pressure data exist for the compound PbPo(s): Witteman reported a single data point (0.1 mmHg at 700 °C) [
21]. Abakumov suggested the correlation log p (mm) = −(7270 ± 80)/T + (6.9360 ± 0.0700) in the temperature interval 640 °C to 850 °C, based on a limited number of experimental data points [
5].
Using extrapolation of the properties of the lower-mass homologues, Eichler derived the thermochemical properties of PbPo(s) [
16]. The result was dependent on an earlier estimation of the properties of Po(g) [
4], since a correlation between the formation entropy and enthalpy of the solid from the monoatomic gas species was used in the extrapolation. In view of the new estimations of the present work, the thermochemical properties of PbPo(s) are re-evaluated, by adjusting them to fit the experimental vapor pressure results.
Again, a model was set-up, in which the vapor in equilibrium with solid PbPo was assumed to be ideal and composed of the polonium gas species Po(g), Po
2(g) and PbPo(g). The properties of these molecules have been derived in the previous Sections (
Table 2 and
Table 3). A Pb(g) species was included in the gas phase. Pb(s;l) and Po(s;l) were included to account for thermal decomposition of PbPo(s) into elemental pure condensed phases.
The formation enthalpy and entropy of PbPo(s) were then varied to match the vapor pressure, calculated by the GEM method, to the experimental data. Calculations were only performed below 1100 K, the estimated melting temperature of PbPo.
Optimized values are listed in
Table 4 and the calculated polonium partial pressure and composition of the gas phase are plotted in
Figure 3. The most abundant polonium vapor species is found to be PbPo(g). Above 400 °C, the contribution of PbPo(g) to the total polonium pressure decreased. This coincided with the formation of a pure Pb phase, indicative of dissociative evaporation reactions of the form:
It is conceivable that the liquid Pb formed by dissociation of PbPo(s) will contain dissolved polonium. To verify the influence of this polonium dissolution on the results, a liquid solution phase was added to the model. This solution consisted of Pb(l) and dissolved Po. The activity coefficient derived above for Po in LBE was taken as an approximation for the activity coefficient of Po in liquid Pb. The tendency for Po to associate with Pb rather than with Bi [
19] indicated that this approximation is not unrealistic. This resulted in slight changes of the relative abundance of the polonium gas species only, and the resulting properties of PbPo(s) (<1% difference of its formation enthalpy and entropy).
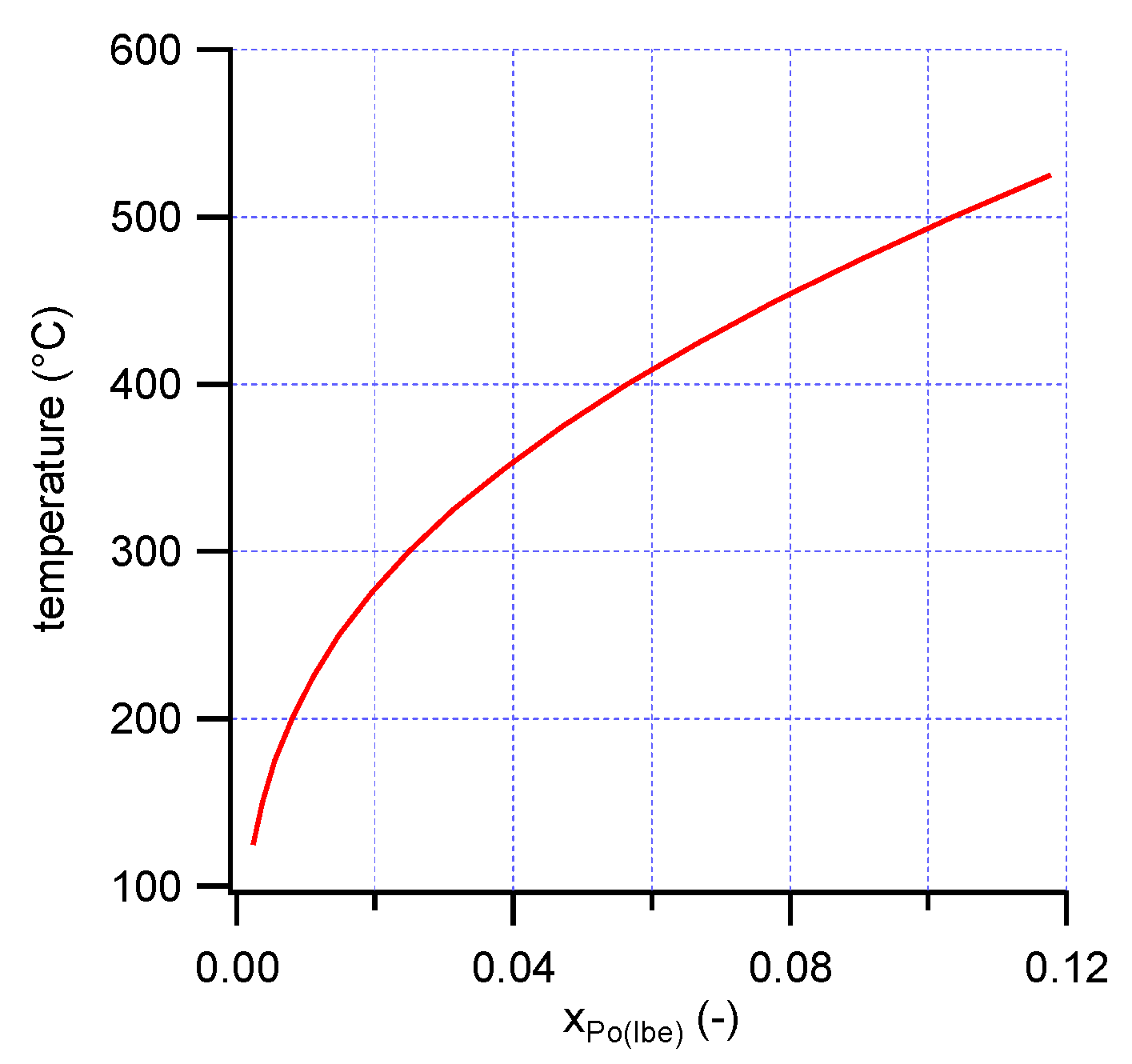
The partial molar excess quantities for dissolution of polonium in LBE indicated that dissolution is energetically favorable at these low concentrations. However, Po solubility in liquid LBE may be limited by formation of PbPo(s) (Bi
2Po
3, the most stable Po-Bi compound, is less stable than PbPo, in line with the Pb-Te and Bi-Te systems) [
20]. Using the activity coefficient of Po in LBE and the thermodynamic properties of PbPo(s), the solubility of PbPo in LBE was estimated (
Figure 4). The solubility, even near the melting point of LBE, is much higher than typical polonium concentrations used in experiments to measure the Henry constant of polonium in LBE, and higher than the concentrations that are expected in LBE-cooled nuclear systems. The present results thus indicate that both in experimental studies of Po evaporation from LBE, and in LBE-cooled reactors (operating typically between 200 °C and 400 °C), polonium is expected to be fully dissolved in LBE.