Mechanical Characterization of Natural Polymers Using Brillouin Spectroscopy: A Comprehensive Review
Abstract
1. Introduction
2. History of Brillouin Spectroscopy
3. Brillouin Scattering
3.1. Physical Principles
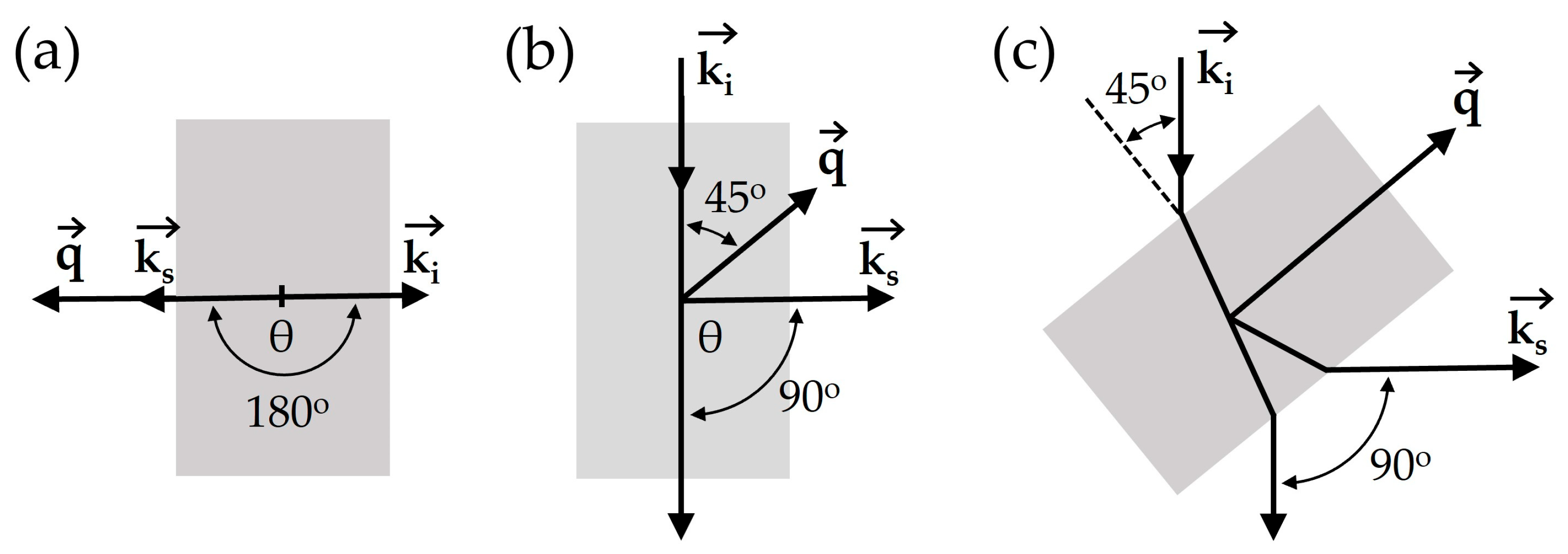
3.2. Scattering Geometries
3.3. Mechanical Considerations in Brillouin Scattering of Natural Polymers
4. Brillouin Spectroscopy Experimental Setup
4.1. Laser
4.2. Spectrometer
4.2.1. Tandem Fabry–Perot Interferometer
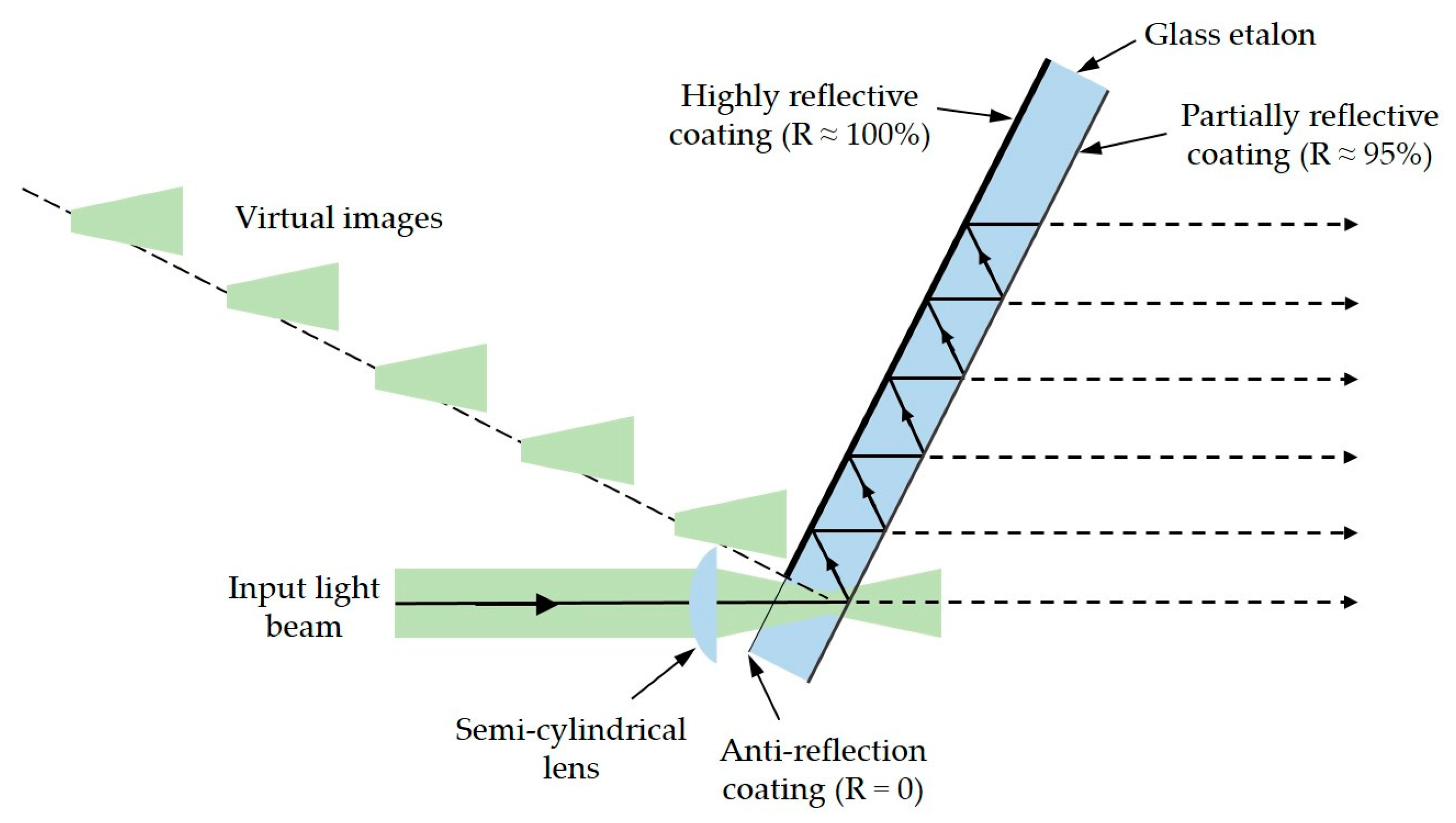
4.2.2. Virtually Imaged Phased Array
4.3. Detector
5. Natural Polymers
5.1. Collagen
5.2. Cellulose
5.3. Chitin and Chitosan
5.4. Silk
5.5. Keratin
5.6. Starch
5.7. Gelatin
5.8. Agar-Agar
5.9. Hyaluronic Acid
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ghasemi-Mobarakeh, L.; Kolahreez, D.; Ramakrishna, S.; Williams, D. Key terminology in biomaterials and biocompatibility. Curr. Opin. Biomed. Eng. 2019, 10, 45–50. [Google Scholar] [CrossRef]
- Marin, E.; Boschetto, F.; Pezzotti, G. Biomaterials and biocompatibility: An historical overview. J. Biomed. Mater. Res. Part A 2020, 108, 1617–1633. [Google Scholar] [CrossRef]
- Williams, D.F. Definitions in Biomaterials. In Proceedings of a Consensus Conference of the European Society for Biomaterials, Chester, England, 3–5 March 1986; Williams, D.F., Ed.; Elsevier: Amsterdam, The Netherlands, 1987; Volume 4. [Google Scholar]
- Bergmann, C.P.; Stumpf, A. Dental Ceramics, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Marjanović-Balaban, Ž.; Jelić, D. Polymeric Biomaterials in Clinical Practice. In Biomaterials in Clinical Practice, 1st ed.; Zivic, F., Affatato, S., Trajanovic, M., Schnabelrauch, M., Grujovic, N., Choy, K.L., Eds.; Springer: Cham, Switzerland, 2017; Chapter 4; pp. 101–117. [Google Scholar]
- Paul, S. Biomedical Engineering and Its Applications in Healthcare, 1st ed.; Springer: Singapore, 2019. [Google Scholar]
- Bharadwaj, A. An Overview on Biomaterials and Its Applications in Medical Science. In International Conference on Futuristic and Sustainable Aspects in Engineering and Technology, Mathura, India, 18–19 December 2020; IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2021; Volume 1116, p. 012178. [Google Scholar]
- Bhatia, S. Natural Polymers vs. Synthetic Polymer. In Natural Polymer Drug Delivery Systems, 1st ed.; Springer: Cham, Switzerland, 2016; pp. 95–118. [Google Scholar]
- Shaw, M.T.; MacKnight, W.J. Introduction to Polymer Viscoelasticity, 3rd ed.; Wiley: Hoboken, NJ, USA, 2005. [Google Scholar]
- Bottani, C.E.; Fioretto, D. Brillouin scattering of phonons in complex materials. Adv. Physics X 2018, 3, 1467281. [Google Scholar] [CrossRef]
- Palombo, F.; Fioretto, D. Brillouin Light Scattering: Applications in Biomedical Sciences. Chem. Rev. 2019, 119, 7833–7847. [Google Scholar] [CrossRef]
- Kojima, S. 100th Anniversary of Brillouin Scattering: Impact on Materials Science. Materials 2022, 15, 3518. [Google Scholar] [CrossRef]
- Brillouin, L. Diffusion de la lumière et des rayons X par un corps transparent homogène. Ann. Phys. 1922, 9, 88–122. [Google Scholar] [CrossRef]
- Meng, Z.; Traverso, A.J.; Ballmann, C.W.; Troyanova-Wood, M.A.; Yakovlev, V.V. Seeing cells in a new light: A renaissance of Brillouin spectroscopy. Adv. Opt. Photon. 2016, 8, 300–327. [Google Scholar] [CrossRef]
- Mandelstam, L.I. Light scattering by inhomogeneous media. Zh. Russ. Fiz. Khim. Ova. 1926, 58, 381–391. (In Russian) [Google Scholar]
- Gross, E. Change of Wave-length of Light due to Elastic Heat Waves at Scattering in Liquids. Nature 1930, 126, 201–202. [Google Scholar] [CrossRef]
- Singaraju, A.B.; Bahl, D.; Stevens, L.L. Brillouin Light Scattering: Development of a Near Century-Old Technique for Characterizing the Mechanical Properties of Materials. AAPS PharmSciTech 2019, 20, 109. [Google Scholar] [CrossRef] [PubMed]
- Perot, A.; Fabry, C. On the Application of Interference Phenomena to the Solution of Various Problems of Spectroscopy and Metrology. Astrophys. J. 1899, 9, 87. [Google Scholar] [CrossRef]
- Venkateswaran, C.S. Interferometric studies of light scattering in mobile liquids. Proc. Indian Acad. Sci. Sect. A 1942, 15, 322–337. [Google Scholar] [CrossRef]
- Maiman, T.H. Stimulated Optical Radiation in Ruby. Nature 1960, 187, 493–494. [Google Scholar] [CrossRef]
- Rioboó, R.J.J.; Gontán, N.; Sanderson, D.; Desco, M.; Gómez-Gaviro, M.V. Brillouin Spectroscopy: From Biomedical Research to New Generation Pathology Diagnosis. Int. J. Mol. Sci. 2021, 22, 8055. [Google Scholar] [CrossRef] [PubMed]
- Chiao, R.Y.; Stoicheff, B.P. Brillouin Scattering in Liquids Excited by the He–Ne Maser. J. Opt. Soc. Am. 1964, 54, 1286–1287. [Google Scholar] [CrossRef]
- Sandercock, J.R. Brillouin scattering study of SbSI using a double-passed, stabilised scanning interferometer. Opt. Commun. 1970, 2, 73–76. [Google Scholar] [CrossRef]
- Sandercock, J.R. Trends in brillouin scattering: Studies of opaque materials, supported films, and central modes. In Light Scattering in Solids III, 1st ed.; Cardona, M., Güntherodt, G., Eds.; Springer: Berlin/Heidelberg, Germany, 1982; pp. 173–206. [Google Scholar]
- Dil, J.G.; van Hijningen, N.C.J.A.; van Dorst, F.; Aarts, R.M. Tandem multipass Fabry-Perot interferometer for Brillouin scattering. Appl. Opt. 1981, 20, 1374–1381. [Google Scholar] [CrossRef]
- Prevedel, R.; Diz-Muñoz, A.; Ruocco, G.; Antonacci, G. Brillouin microscopy: An emerging tool for mechanobiology. Nat. Methods 2019, 16, 969–977. [Google Scholar] [CrossRef] [PubMed]
- Shirasaki, M. Large angular dispersion by a virtually imaged phased array and its application to a wavelength demultiplexer. Opt. Lett. 1996, 21, 366–368. [Google Scholar] [CrossRef] [PubMed]
- Scarcelli, G.; Yun, S.H. Confocal Brillouin microscopy for three-dimensional mechanical imaging. Nat. Photon. 2007, 2, 39–43. [Google Scholar] [CrossRef]
- Poon, C.; Chou, J.; Cortie, M.; Kabakova, I. Brillouin imaging for studies of micromechanics in biology and biomedicine: From current state-of-the-art to future clinical translation. J. Phys. Photon. 2020, 3, 012002. [Google Scholar] [CrossRef]
- Mattana, S.; Mattarelli, M.; Urbanelli, L.; Sagini, K.; Emiliani, C.; Serra, M.D.; Fioretto, D.; Caponi, S. Non-contact mechanical and chemical analysis of single living cells by microspectroscopic techniques. Light Sci. Appl. 2017, 7, 17139. [Google Scholar] [CrossRef]
- Mattarelli, M.; Capponi, G.; Passeri, A.A.; Fioretto, D.; Caponi, S. Disentanglement of Multiple Scattering Contribution in Brillouin Microscopy. ACS Photon. 2022, 9, 2087–2091. [Google Scholar] [CrossRef]
- Filippidi, E.; Dhiman, A.K.; Li, B.; Athanasiou, T.; Vlassopoulos, D.; Fytas, G. Multiscale Elasticity of Epoxy Networks by Rheology and Brillouin Light Spectroscopy. J. Phys. Chem. B 2024, 128, 12628–12637. [Google Scholar] [CrossRef]
- Bailey, M.; Alunni-Cardinali, M.; Correa, N.; Caponi, S.; Holsgrove, T.; Barr, H.; Stone, N.; Winlove, C.P.; Fioretto, D.; Palombo, F. Viscoelastic properties of biopolymer hydrogels determined by Brillouin spectroscopy: A probe of tissue micromechanics. Sci. Adv. 2020, 6, eabc1937. [Google Scholar] [CrossRef] [PubMed]
- Speziale, S.; Marquardt, H.; Duffy, T.S. Brillouin Scattering and its Application in Geosciences. Rev. Miner. Geochem. 2014, 78, 543–603. [Google Scholar] [CrossRef]
- Rouxel, D.; Thevenot, C.; Nguyen, V.S.; Vincent, B. Brillouin spectroscopy of polymer nanocomposites. In Spectroscopy of Polymer Nanocomposites, 1st ed.; Thomas, S., Rouxel, D., Ponnamma, D., Eds.; William Andrew: Norwich, NY, USA, 2016; pp. 362–392. [Google Scholar]
- Krüger, J.K.; Müller, U.; Bactavatchalou, R.; Liebschner, D.; Sander, M.; Possart, W.; Wehlack, C.; Baller, J.; Rouxel, D. Mechanical Interphases in Epoxies as seen by Nondestructive High-Performance Brillouin Microscopy. In Adhesion; Possart, W., Ed.; Wiley-VCH: New York, NY, USA, 2005; pp. 125–142. [Google Scholar]
- Hammoud, B.; Schumacher, J.S.; Zhang, H.; Dutra, B.A.; Susanna, B.N.; Scarcelli, G.; Randleman, J.B. Brillouin microscopy for focal biomechanical measurements in normal and keratoconic corneas: A narrative review. Surv. Ophthalmol. 2025. [CrossRef]
- Aluculesei, A.; Zhang, Y.; Huang, S.; Wang, Z.; Cang, Y.; Min, Y.; Fytas, G. Elasticity Anisotropy of Bombyx mori Silkworm Silk Fiber by Brillouin Light Spectroscopy. Biomacromolecules 2025, 26, 2479–2486. [Google Scholar] [CrossRef] [PubMed]
- Antonacci, G.; Beck, T.; Bilenca, A.; Czarske, J.; Elsayad, K.; Guck, J.; Kim, K.; Krug, B.; Palombo, F.; Prevedel, R.; et al. Recent progress and current opinions in Brillouin microscopy for life science applications. Biophys. Rev. 2020, 12, 615–624. [Google Scholar] [CrossRef] [PubMed]
- Webb, J.N.; Zhang, H.; Roy, A.S.; Randleman, J.B.; Scarcelli, G. Detecting Mechanical Anisotropy of the Cornea Using Brillouin Microscopy. Transl. Vis. Sci. Technol. 2020, 9, 26. [Google Scholar] [CrossRef]
- So, P. Brillouin bioimaging. Nat. Photon. 2008, 2, 13–14. [Google Scholar] [CrossRef]
- Zhang, J.; Scarcelli, G. Mapping mechanical properties of biological materials via an add-on Brillouin module to confocal microscopes. Nat. Protoc. 2021, 16, 1251–1275. [Google Scholar] [CrossRef]
- Scarcelli, G.; Yun, S.H. Multistage VIPA etalons for high-extinction parallel Brillouin spectroscopy. Opt. Express 2011, 19, 10913–10922. [Google Scholar] [CrossRef]
- Zhu, X.; Lin, D.; Zhang, Z.; Xie, X.; He, J. Dispersion Characteristics of the Multi-mode Fiber-fed VIPA Spectrograph. Astron J. 2023, 165, 228. [Google Scholar] [CrossRef]
- Ng, R.C.; El Sachat, A.; Cespedes, F.; Poblet, M.; Madiot, G.; Jaramillo-Fernandez, J.; Florez, O.; Xiao, P.; Sledzinska, M.; Sotomayor-Torres, C.M.; et al. Excitation and detection of acoustic phonons in nanoscale systems. Nanoscale 2022, 14, 13428–13451. [Google Scholar] [CrossRef] [PubMed]
- Edrei, E.; Gather, M.C.; Scarcelli, G. Integration of spectral coronagraphy within VIPA-based spectrometers for high extinction Brillouin imaging. Opt. Express 2017, 25, 6895–6903. [Google Scholar] [CrossRef]
- Fiore, A.; Zhang, J.; Shao, P.; Yun, S.H.; Scarcelli, G. High-extinction virtually imaged phased array-based Brillouin spectroscopy of turbid biological media. Appl. Phys. Lett. 2016, 108, 203701. [Google Scholar] [CrossRef] [PubMed]
- Shao, P.; Besner, S.; Zhang, J.; Scarcelli, G.; Yun, S.-H. Etalon filters for Brillouin microscopy of highly scattering tissues. Opt. Express 2016, 24, 22232–22238. [Google Scholar] [CrossRef]
- Meng, Z.; Yakovlev, V.V. Optimizing signal collection efficiency of the VIPA-based Brillouin spectrometer. J. Innov. Opt. Health Sci. 2015, 8, 1550021. [Google Scholar] [CrossRef]
- Doppalapudi, S.; Katiyar, S.; Domb, A.J.; Khan, W. Biodegradable Natural Polymers. In Advanced Polymers in Medicine, 1st ed.; Puoci, F., Ed.; Springer: Cham, Switzerland, 2014; pp. 33–66. [Google Scholar]
- Fan, J.; Abedi-Dorcheh, K.; Vaziri, A.S.; Kazemi-Aghdam, F.; Rafieyan, S.; Sohrabinejad, M.; Ghorbani, M.; Adib, F.R.; Ghasemi, Z.; Klavins, K.; et al. A Review of Recent Advances in Natural Polymer-Based Scaffolds for Musculoskeletal Tissue Engineering. Polymers 2022, 14, 2097. [Google Scholar] [CrossRef]
- Adamiak, K.; Sionkowska, A. Current methods of collagen cross-linking: Review. Int. J. Biol. Macromol. 2020, 161, 550–560. [Google Scholar] [CrossRef]
- Ghomi, E.R.; Nourbakhsh, N.; Kenari, M.A.; Zare, M.; Ramakrishna, S. Collagen-based biomaterials for biomedical applications. J. Biomed. Mater. Res. Part B Appl. Biomater. 2021, 109, 1986–1999. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, Z.; Dong, Y. Collagen-Based Biomaterials for Tissue Engineering. ACS Biomater. Sci. Eng. 2023, 9, 1132–1150. [Google Scholar] [CrossRef] [PubMed]
- Chattopadhyay, S.; Raines, R.T. Collagen-based biomaterials for wound healing. Biopolymers 2014, 101, 821–833. [Google Scholar] [CrossRef]
- Chen, H.; Xue, L.; Gong, G.; Pan, J.; Wang, X.; Zhang, Y.; Guo, J.; Qin, L. Collagen-based materials in reproductive medicine and engineered reproductive tissues. J. Leather Sci. Eng. 2022, 4, 3. [Google Scholar] [CrossRef]
- Palombo, F.; Winlove, C.P.; Edginton, R.S.; Green, E.; Stone, N.; Caponi, S.; Madami, M.; Fioretto, D. Biomechanics of fibrous proteins of the extracellular matrix studied by Brillouin scattering. J. R. Soc. Interface 2014, 11, 20140739. [Google Scholar] [CrossRef]
- Harley, R.; James, D.; Miller, A.; White, J.W. Phonons and the elastic moduli of collagen and muscle. Nature 1977, 267, 285–287. [Google Scholar] [CrossRef]
- Cusack, S.; Miller, A. Determination of the elastic constants of collagen by Brillouin light scattering. J. Mol. Biol. 1979, 135, 39–51. [Google Scholar] [CrossRef] [PubMed]
- Randall, J.T.; Vaughan, J.M. Brillouin scattering in systems of biological significance. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Sci. 1979, 293, 341–348. [Google Scholar] [CrossRef]
- Lees, S.; Tao, N.-J.; Lindsay, S.M. Studies of Compact Hard Tissues and Collagen by Means of Brillouin Light Scattering. Connect. Tissue Res. 1990, 24, 187–205. [Google Scholar] [CrossRef]
- Edginton, R.S.; Green, E.M.; Winlove, C.P.; Fioretto, D.; Palombo, F. Dual scale biomechanics of extracellular matrix proteins probed by Brillouin scattering and quasistatic tensile testing. In Biophysics, Biology and Biophotonics III: The Crossroads, SPIE BiOS, San Francisco, CA, USA, 27–28 January 2018; Wax, A., Backman, V., Eds.; SPIE: San Francisco, CA, USA, 2018; Volume 10504, pp. 33–39. [Google Scholar]
- Heinze, T. Cellulose: Structure and Properties. In Cellulose Chemistry and Properties: Fibers, Nanocelluloses and Advanced Materials, 1st ed.; Rojas, O.J., Ed.; Springer: Cham, Switzerland, 2015; pp. 1–52. [Google Scholar]
- Gibson, L.J. The hierarchical structure and mechanics of plant materials. J. R. Soc. Interface 2012, 9, 2749–2766. [Google Scholar] [CrossRef]
- Salmén, L. Wood Cell Wall Structure and Organisation in Relation to Mechanics. In Plant Biomechanics, 1st ed.; Geitmann, A., Gril, J., Eds.; Springer: Cham, Switzerland, 2018; Chapter 1; pp. 3–19. [Google Scholar]
- Wüstenberg, T. Cellulose. In Cellulose and Cellulose Derivatives in the Food Industry; Wüstenberg, T., Ed.; Wiley-VCH: New York, NY, USA, 2014; Volume 24, pp. 91–142. [Google Scholar]
- Patterson, G.D. Brillouin scattering from polymer films. J. Polym. Sci. Polym. Phys. Ed. 1976, 14, 143–149. [Google Scholar] [CrossRef]
- Sui, L.; Huang, L.; Podsiadlo, P.; Kotov, N.A.; Kieffer, J. Brillouin Light Scattering Investigation of the Mechanical Properties of Layer-by-Layer Assembled Cellulose Nanocrystal Films. Macromolecules 2010, 43, 9541–9548. [Google Scholar] [CrossRef]
- Williams, D.R.; Nurco, D.J.; Rahbar, N.; Koski, K.J. Elasticity of bamboo fiber variants from Brillouin spectroscopy. Materialia 2019, 5, 100240. [Google Scholar] [CrossRef]
- Elsayad, K.; Urstöger, G.; Czibula, C.; Teichert, C.; Gumulec, J.; Balvan, J.; Pohlt, M.; Hirn, U. Mechanical Properties of cellulose fibers measured by Brillouin spectroscopy. Cellulose 2020, 27, 4209–4220. [Google Scholar] [CrossRef]
- Klemm, D.; Heublein, B.; Fink, H.-P.; Bohn, A. Cellulose: Fascinating Biopolymer and Sustainable Raw Material. Angew. Chem. Int. Ed. 2005, 44, 3358–3393. [Google Scholar] [CrossRef] [PubMed]
- Ganser, C.; Weber, F.; Czibula, C.; Bernt, I.; Schennach, R.; Teichert, C. Tuning hardness of swollen viscose fibers. Bioinspired Biomim. Nanobiomaterials 2014, 3, 131–138. [Google Scholar] [CrossRef]
- Czibula, C.; Ulz, M.H.; Wagner, A.; Elsayad, K.; Hirn, U.; Koski, K.J. The elastic stiffness tensor of cellulo-sic viscose fibers measured with Brillouin spectroscopy. J. Phys. Phot. 2024, 6, 035012. [Google Scholar] [CrossRef]
- Samalova, M.; Melnikava, A.; Elsayad, K.; Peaucelle, A.; Gahurova, E.; Gumulec, J.; Spyroglou, I.; Zemlyanskaya, E.V.; Ubogoeva, E.V.; Balkova, D.; et al. Hormone-regulated expansins: Expression, localization, and cell wall biomechanics in Arabidopsis root growth. Plant Physiol. 2023, 194, 209–228. [Google Scholar] [CrossRef]
- Pachernegg-Mair, L.; Schaubeder, J.B.; Brandberg, A.; Thoman, M.; Urstöger, G.; Rüggeberg, M.; Koski, K.J.; Plank, H.; Hirn, U.; Spirk, S.; et al. Ionic liquid treatment of flax fibers and the effects on morphology and mechanical properties. Mater. Sci. Eng. A 2025, 942, 148675. [Google Scholar] [CrossRef]
- Tharanathan, R.N.; Kittur, F.S. Chitin—The Undisputed Biomolecule of Great Potential. Crit. Rev. Food Sci. Nutr. 2003, 43, 61–87. [Google Scholar] [CrossRef]
- Lv, J.; Lv, X.; Ma, M.; Oh, D.-H.; Jiang, Z.; Fu, X. Chitin and chitin-based biomaterials: A review of advances in processing and food applications. Carbohydr. Polym. 2023, 299, 120142. [Google Scholar] [CrossRef] [PubMed]
- Giraldo, J.D.; García, Y.; Vera, M.; Garrido-Miranda, K.A.; Andrade-Acuña, D.; Marrugo, K.P.; Rivas, B.L.; Schoebitz, M. Alternative processes to produce chitin, chitosan, and their oligomers. Carbohydr. Polym. 2024, 332, 121924. [Google Scholar] [CrossRef]
- Yoshihara, A.; Miyazaki, A.; Maeda, T.; Imai, Y.; Itoh, T. Spectroscopic characterization of dragonfly wings common in Japan. Vib. Spectrosc. 2012, 61, 85–93. [Google Scholar] [CrossRef]
- Holland, C.; Numata, K.; Rnjak-Kovacina, J.; Seib, F.P. The Biomedical Use of Silk: Past, Present, Future. Adv. Healthc. Mater. 2018, 8, 1800465. [Google Scholar] [CrossRef]
- Laity, P.R.; Holland, C. Native Silk Feedstock as a Model Biopolymer: A Rheological Perspective. Biomacromolecules 2016, 17, 2662–2671. [Google Scholar] [CrossRef] [PubMed]
- Koski, K.J.; Akhenblit, P.; McKiernan, K.; Yarger, J.L. Non-invasive determination of the complete elastic moduli of spider silks. Nat. Mater. 2013, 12, 262–267. [Google Scholar] [CrossRef]
- Schneider, D.; Gomopoulos, N.; Koh, C.Y.; Papadopoulos, P.; Kremer, F.; Thomas, E.L.; Fytas, G. Nonlinear control of high-frequency phonons in spider silk. Nat. Mater. 2016, 15, 1079–1083. [Google Scholar] [CrossRef]
- Lee, B.W.; Ryeom, J.; Ko, J.-H.; Kim, D.W.; Park, C.H.; Park, J.; Ko, Y.H.; Kim, K.J. Pressure and temperature dependences of the acoustic behaviors of biocompatible silk studied by using Brillouin spectroscopy. J. Korean Phys. Soc. 2016, 69, 213–219. [Google Scholar] [CrossRef]
- Wang, Z.; Cang, Y.; Kremer, F.; Thomas, E.L.; Fytas, G. Determination of the Complete Elasticity of Nephila pilipes Spider Silk. Biomacromolecules 2020, 21, 1179–1185. [Google Scholar] [CrossRef]
- Wang, B.; Yang, W.; McKittrick, J.; Meyers, M.A. Keratin: Structure, mechanical properties, occurrence in biological organisms, and efforts at bioinspiration. Prog. Mater. Sci. 2016, 76, 229–318. [Google Scholar] [CrossRef]
- Feroz, S.; Muhammad, N.; Ratnayake, J.; Dias, G. Keratin-Based materials for biomedical applications. Bioact. Mater. 2020, 5, 496–509. [Google Scholar] [CrossRef] [PubMed]
- McLellan, J.; Thornhill, S.G.; Shelton, S.; Kumar, M. Keratin-Based Biofilms, Hydrogels, and Biofibers. In Keratin as a Protein Biopolymer, 1st ed.; Sharma, S., Kumar, A., Eds.; Springer: Cham, Switzerland, 2019; Chapter 7; pp. 187–200. [Google Scholar]
- Shavandi, A.; Silva, T.H.; Bekhit, A.A.; Bekhit, A.E.-D.A. Keratin: Dissolution, extraction and biomedical application. Biomater. Sci. 2017, 5, 1699–1735. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Shang, Y.; Zhang, J.; Yuan, J.; Shen, J. Recent advances in keratin for biomedical applications. Adv. Colloid Interface Sci. 2023, 321, 103012. [Google Scholar] [CrossRef]
- Correa, N.; Cardinali, M.A.; Bailey, M.; Fioretto, D.; Pudney, P.D.A.; Palombo, F. Brillouin microscopy for the evaluation of hair micromechanics and effect of bleaching. J. Biophotonics 2021, 14, e202000483. [Google Scholar] [CrossRef]
- Morrison, W.R.; Karkalas, J.; Starch. Methods in Plant Biochemistry; Dey, P.M., Ed.; Academic Press: San Diego, CA, USA, 1990; pp. 323–352. [Google Scholar]
- Hemamalini, T.; Dev, V.R.G. Comprehensive review on electrospinning of starch polymer for biomedical applications. Int. J. Biol. Macromol. 2018, 106, 712–718. [Google Scholar] [CrossRef] [PubMed]
- Rakymzhan, A.; Yakupov, T.; Yelemessova, Z.; Bukasov, R.; Yakovlev, V.V.; Utegulov, Z.N. Monitoring of vegetation drying by Brillouin and Raman spectroscopies. In Sensing for Agriculture and Food Quality and Safety IX, SPIE Commercial + Scientific Sensing and Imaging, Baltimore, MD, USA, 17–21 April 2016; Kim, M.S., Chao, K., Chin, B.A., Cho, B.-K., Eds.; SPIE: Anaheim, CA, USA, 2017; Volume 10217, pp. 88–93. [Google Scholar]
- Rakymzhan, A.; Yakupov, T.; Yelemessova, Z.; Bukasov, R.; Yakovlev, V.V.; Utegulov, Z.N. Time-resolved assessment of drying plants by Brillouin and Raman spectroscopies. J Raman Spectrosc. 2019, 50, 1881–1889. [Google Scholar] [CrossRef]
- Haug, I.J.; Draget, K.I. Gelatin. In Handbook of Hydrocolloids, 2nd ed.; Phillips, G.O., Williams, P.A., Eds.; Woodhead Publishing: Cambridge, England, 2009; pp. 142–163. [Google Scholar]
- Ahart, M.; Hemley, R.J. Sound Velocity and Equation of State of Ballistic Gelatin by Brillouin Scattering. Materials 2023, 16, 1279. [Google Scholar] [CrossRef]
- Liu, D.; Nikoo, M.; Boran, G.; Zhou, P.; Regenstein, J.M. Collagen and Gelatin. Annu. Rev. Food Sci. Technol. 2015, 6, 527–557. [Google Scholar] [CrossRef]
- Alipal, J.; Pu’AD, N.M.; Lee, T.; Nayan, N.; Sahari, N.; Basri, H.; Idris, M.; Abdullah, H. A review of gelatin: Properties, sources, process, applications, and commercialisation. Mater. Today Proc. 2021, 42, 240–250. [Google Scholar] [CrossRef]
- Bedborough, D.; Jackson, D. Brillouin scattering study of gelatin gel using a double passed Fabry-Perot spectrometer. Polymer 1976, 17, 573–576. [Google Scholar] [CrossRef]
- Bot, A.; Schram, R.P.C.; Wegdam, G.H. Brillouin light scattering from a biopolymer gel: Hypersonic sound waves in gelatin. Colloid Polym. Sci. 1995, 273, 252–256. [Google Scholar] [CrossRef]
- Zhao, P.; Vanderwal, J. Brillouin scattering study of gelatin gel. Polym. Gels Networks 1997, 5, 23–36. [Google Scholar] [CrossRef]
- Meng, Z.; Thakur, T.; Chitrakar, C.; Jaiswal, M.K.; Gaharwar, A.K.; Yakovlev, V.V. Assessment of Local Heterogeneity in Mechanical Properties of Nanostructured Hydrogel Networks. ACS Nano 2017, 11, 7690–7696. [Google Scholar] [CrossRef] [PubMed]
- Correa, N.; Harding, S.; Bailey, M.; Brasselet, S.; Palombo, F. Image analysis applied to Brillouin images of tissue-mimicking collagen gelatins. Biomed. Opt. Express 2019, 10, 1329–1338. [Google Scholar] [CrossRef]
- Laktionova, A.V.; Dobrynina, E.A.; Zykova, V.A.; Surovtsev, N.V. Brillouin Scattering Study of Gelatin Films with Different Water Concentrations. Bull. Russ. Acad. Sci. Phys. 2023, 87, S66–S70. [Google Scholar] [CrossRef]
- Armisén, R.; Gaiatas, F. Agar. In Handbook of Hydrocolloids, 2nd ed.; Phillips, G.O., Williams, P.A., Eds.; Woodhead Publishing: Cambridge, England, 2009; pp. 82–107. [Google Scholar]
- Selby, H.H.; Whistler, R.L. Agar. In Industrial Gums, 3rd ed.; Whistler, R.L., Bemiller, J.N., Eds.; Academic Press: San Diego, CA, USA, 1993; pp. 87–103. [Google Scholar]
- Esteves, B.; Rocha, A.; Silva, M.; Correia, J.; Rodrigues, J. Non-contact determination of the viscoelastic properties of agar culture media by Brillouin spectroscopy. Materialia 2023, 30, 101858. [Google Scholar] [CrossRef]
- Kogan, G.; Šoltés, L.; Stern, R.; Gemeiner, P. Hyaluronic acid: A natural biopolymer with a broad range of biomedical and industrial applications. Biotechnol. Lett. 2006, 29, 17–25. [Google Scholar] [CrossRef]
- Necas, J.; Bartosikova, L.; Brauner, P.; Kolar, J. Hyaluronic acid (hyaluronan): A review. Vet. Med. 2008, 53, 397–411. [Google Scholar] [CrossRef]
- Lee, S.A.; Oliver, W.F.; Rupprecht, A.; Song, Z.; Lindsay, S.M. Observation of a phase transition in wet-spun films of Na-hyaluronate. Biopolymers 1992, 32, 303–306. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.A.; Flowers, M.R.; Oliver, W.F.; Rupprecht, A.; Lindsay, S.M. Brillouin-scattering study of hyaluronic acid: Dynamic coupling with the water of hydration and phase transitions. Phys. Rev. E 1993, 47, 677–683. [Google Scholar] [CrossRef] [PubMed]
- Hauck, N.; Seixas, N.; Centeno, S.P.; Schlüßler, R.; Cojoc, G.; Müller, P.; Guck, J.; Wöll, D.; Wessjohann, L.A.; Thiele, J. Droplet-Assisted Microfluidic Fabrication and Characterization of Multifunctional Polysaccharide Microgels Formed by Multicomponent Reactions. Polymers 2018, 10, 1055. [Google Scholar] [CrossRef] [PubMed]




| Biomaterials | Polymers | Natural (e.g., collagen, agar) |
| Biodegradable synthetic (e.g., polylactic acid) | ||
| Non-biodegradable synthetic (e.g., polyamide) | ||
| Ceramics | Bioinert (e.g., alumina) | |
| Bioactive (e.g., apatite-wollastonite glass ceramics) | ||
| Bioresorbable (e.g., calcium phosphate) | ||
| Metal | Biodegradable (e.g., magnesium alloys) | |
| Nonbiodegradable (e.g., titanium) | ||
| Composites | Polymeric (e.g., polyamide 6/poly(l-lactic acid)) | |
| Metallic (e.g., CoCrWNi) | ||
| Ceramic (e.g., Ca7MgSi4O16) |
| Year | Event | Ref. |
|---|---|---|
| 1899 | A. Perot and C. Fabry developed the Fabry–Perot interferometer | [18] |
| 1922 | Léon Brillouin predicted inelastic light scattering by thermally induced acoustic waves | [13] |
| 1926 | L. Mandelstam independently predicted light scattering from thermally excited acoustic waves | [15] |
| 1930 | Eugenii Gross empirically confirmed the Brillouin effect with the first experimental study | [16] |
| 1942 | Venkateswaran used the Fabry–Perot interferometer as a dispersive element for high-resolution frequency analysis in Brillouin scattering | [19] |
| 1960 | Theodore H. Maiman presents the world’s first operating laser | [20] |
| 1964 | Raymond Chiao developed a Brillouin spectrometer which incorporates a laser, Fabry–Perot interferometer, and photomultiplier tube detection | [22] |
| 1970 | John Sandercock showed for the first time that contrast can be significantly improved by the multipass Fabry–Perot interferometer | [23] |
| 1982 | John Sandercock proposed the tandem multi-pass Fabry–Perot interferometer | [24] |
| 1996 | Shirasaki proposed the virtual imaged phased array (VIPA) | [27] |
| 2008 | First high-resolution spectrometer based on VIPA | [28] |
| Natural Polymer | Sample Type | Brillouin Frequency Shift (GHz) | Excitation Light (nm) | Ref. |
|---|---|---|---|---|
| Collagen | Rat tail tendon (dried) | 10.65–18.9 | 514 or 488 | [58,62] |
| Rat tail tendon (hydrated) | 9–10.29 | |||
| Cellulose | Fibers | 8.4–9.4 | 532 | [70] |
| Chitin | Dragonfly wing | 19.5 | 488 | [79] |
| Silk | Fibers | 15–17.5 | 532 | [83] |
| Keratin | Horsehair (dried) | 11.2 | 488 | [60] |
| Horsehair (hydrated) | 7.7–8.7 | |||
| Starch | Geranium leaf (dried) | 7.7 | 532 | [95] |
| Geranium leaf (live) | 7.4 | |||
| Gelatin | 4–18% (w/w) gel | 7.4–8.4 | 532 | [105] |
| Agar-agar | 0.5–3.7 (w/w) gel | 7.55–7.61 | 532 | [108] |
| Hyaluronic acid | 75% hydrated film | 12 | 514 | [111] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rodrigues, J.A.; Esteves, B.; Costa, P.; Correia, J.H. Mechanical Characterization of Natural Polymers Using Brillouin Spectroscopy: A Comprehensive Review. Photochem 2025, 5, 34. https://doi.org/10.3390/photochem5040034
Rodrigues JA, Esteves B, Costa P, Correia JH. Mechanical Characterization of Natural Polymers Using Brillouin Spectroscopy: A Comprehensive Review. Photochem. 2025; 5(4):34. https://doi.org/10.3390/photochem5040034
Chicago/Turabian StyleRodrigues, José A., Bruno Esteves, Patrícia Costa, and José H. Correia. 2025. "Mechanical Characterization of Natural Polymers Using Brillouin Spectroscopy: A Comprehensive Review" Photochem 5, no. 4: 34. https://doi.org/10.3390/photochem5040034
APA StyleRodrigues, J. A., Esteves, B., Costa, P., & Correia, J. H. (2025). Mechanical Characterization of Natural Polymers Using Brillouin Spectroscopy: A Comprehensive Review. Photochem, 5(4), 34. https://doi.org/10.3390/photochem5040034





