The Effect of Orientation Angle of Center Facing Arm on Elongation of 3D-Printed Auxetic-Structure Textiles

Abstract

This study aimed to examine the effect of the orientation angle of center facing arms on the elongation and strength of 3D-printed textiles with two different re-entrant cellular auxetic structures. An experimental research design, consisting of 6 (auxetic-structure textiles) × 3 (repetition), was employed. Star-shaped re-entrant auxetic structures (star re-entrant) with orientation angles of 25°, 30°, and 35° and floral-based star-shaped re-entrant auxetic structures (floral re-entrant) with orientation angles of 55°, 60°, and 65° were developed using the fused deposition modeling 3D-printing method through identifying commonly used auxetic structures in the 3D-printed textiles’ development. A statistically significant relationship was found between load and elongation of both star re-entrant and floral re-entrant. The findings indicated that 3D-printed textiles with both star re-entrant and floral re-entrant structures exhibited an enhanced elongation with the increase in orientation angle, making the textile products more flexible and potentially providing better wear comfort. However, the strength of both star re-entrant and floral re-entrant textiles was not significantly affected by the orientation angle of center facing arms. The findings demonstrated the potential to enhance the elongation of 3D-printed auxetic-structure textiles without compromising their strength for ensuing comfort by adjusting the orientation angle of center facing arms.

1. Introduction

Recent technological advancements have expanded the application of 3D printing (3DP) in wearable product development, leading to its increased popularity over the past several years both in academia and industry [1,2]. According to Sheikh et al., the 3DP market has expanded astonishingly, rising from 3.07 billion dollars in 2014 to 21 billion dollars by 2020 [3]. Moreover, the 3DP market is anticipated to grow from USD 5 billion in sales in 2017 to USD 23 billion in global sales by 2029 [4,5]. From the supply chain viewpoint, 3DP promises shorter production times, reduced inventory needs, and decreased disassembly requirements, as well as offering options of customization and personalization for users. Specifically, 3DP decentralizes production nearer to the end user and minimizes the amount of labor input required for both production and transportation [6,7]. Due to its transformative influence on design and manufacturing 3DP is often referred to as ‘third industrial’ revolution [8].

In addition, 3DP has potential to enhance the functionality of wearable products by enabling the production of intricate and complex geometric structures with a high precision, which cannot be achieved through traditional subtractive manufacturing, thereby opening up opportunities for high-performance textile applications in the fashion industry [9,10]. For example, Lee and Li developed a dress using flexible 3D-printed textiles to emulate the drapability of conventional lace fabrics [11]. Beecroft utilized selective laser sintering with nylon powder to produce flexible 3D-printed weft knitted textiles aiming to simulate the flexibility of traditional knit textiles [12]. Although 3D-printed textiles are expected to revolutionize the design and development of wearable products [2,3], ensuring essential properties such as elongation and strength, which influence wear comfort, remains as the main obstacle to the widespread adoption of 3D-printed wearable products [13].

Wear comfort, the most crucial aspect of wearable textiles that come into direct contact with human skin, determines how pleasant clothing feels to the wearer [14]. It is defined as how effectively clothing supports body functions such as movement or minimally interferes with them [15]. To ensure wear comfort, textiles need to elongate effortlessly with body movement and maintain their original shape without deformation [16]. Elongation, a vital factor that impacts wear comfort, provides textiles with the ability to facilitate the body movement by elongating to their fullest extent and putting the least amount of pressure on the body [17]. Textile strength represents the maximum elongation that textiles can endure before breaking, and it is a factor closely associated with elongation and that significantly influences wearability of textile products and wear comfort [18]. Specifically, the association between textile strength and elongation determines the wearability and wear comfort of final textile products [18,19]. Therefore, it is of paramount importance to develop 3D-printed textiles with sufficient elongation and strength for wearers’ comfort and satisfaction [16].

With continuous research, significant progress has been made in developing flexible 3D-printed textiles for wearable products [20]. Auxetic structures, specialized flexible geometric textile structures used in previous studies, can offer four-way elongation and greatly improve the tensile performance of 3D-printed textiles [21]. The properties of auxetic-structure textiles greatly depend on their structural geometry, particularly the orientation of center facing arms, concave lines that direct toward the center or midpoint of the auxetic structure [22]. Consequently, it is assumed that the elongation and strength of 3D-printed auxetic structure textiles are also influenced by the orientation angle of center facing arms, an angle between the center facing arm and the borderline that joins the outer corner points of the repeating unit of the auxetic structure.

Previous studies have explored the potential of employing different auxetic structures (e.g., re-entrant cellular structures, nodule and fibril structures, rotating unit structures) in 3D-printed textiles’ development [21,23,24]. However, no research has been identified to examine how the orientation angle of center facing arms influences the strength and elongation of 3D-printed auxetic-structure textiles, specifically star-shaped re-entrant cellular structures and their variations. These structures are the most typical re-entrant cellular structures used in 3D-printed textiles’ development. Thus, this study aimed to examine the effect of the orientation angle of center facing arms on the elongation and strength of 3D-printed re-entrant cellular auxetic-structure textiles. The specific objectives of this study were to (a) examine the effect of the orientation angle of center facing arms on the elongation of various 3D-printed re-entrant cellular auxetic-structure textiles by analyzing the relationship between load and elongation within the elastic region of the load-elongation curve, and (b) examine the effect of the orientation angle of center facing arms on the strength of two different 3D-printed re-entrant cellular auxetic-structure textiles by measuring the variation in maximum force across different orientation angles in the final plastic region of the load–elongation curve.

2. Literature Review

2.1. Development of 3D-Printed Textiles

The innovative design technology of 3D printing (3DP) has already attracted considerable interest from both academia and industry [13]. Recent technological advancements are expanding the horizons of 3DP applications in wearable product development. Due to its ability to create complex structures, 3DP offers a promising avenue for creating high-performance textiles [10]. To further enhance the wearability of 3D-printed textiles, designers have employed various approaches that include using flexible 3DP materials and adapting flexible textile structures [20].

A wide variety of 3DP materials are available nowadays, including plastic, rubber, resin, ceramics, gold, platinum, silver, iron, and titanium [20]. Polymers or polymer composites, such as polylactide, acrylonitrile butadiene styrene, and nylon, are the primary sources of 3DP materials for developing 3D-printed textiles [20,25]. For example, Nervous System’s Kinematics dress used 3D-printed textiles with rigid hinge-joint interfaces made out of nylon [26]. However, due to their stiffness and hardness, traditional polymer materials cannot guarantee an adequate flexibility in 3D-printed textile products [20].

Recently, the development of 3D-printed textile products has increasingly embraced novel flexible polymer materials such as thermoplastic polyurethane (TPU), which is considered an ideal option for developing 3D-printed wearable products due to its inherent flexibility, the key desired quality in wearable textile products [27]. Associating the fused deposition modeling (FDM) 3DP method with flexible TPU filaments, designers can develop flexible textiles that offer an enhanced comfort and flexibility comparable to conventional textiles [28]. For instance, Valtas and Sun utilized 3DP with flexible polyurethane filament to develop commercial and wearable garments [29]. Other researchers such as Lee and Li and Spahiu et al. also designed 3D-printed dresses featuring diverse geometric structures using an FDM 3D printer with flexible 3DP filaments [11,23].

Different flexible structures are also being explored for use in developing 3D-printed textiles in an attempt to simulate the comfort and flexibility of conventional fabrics. Auxetic structures are one of flexible textile structures that have a unique property of becoming fatter when stretched and thinner when compressed due to their special geometric structure [30]. This special geometry enables auxetic structures to possess unique elongation properties, showcasing their potential to simulate the comfort and flexibility of conventional textiles when developing 3D-printed textiles [23].

2.2. Auxetic Structure

The development of materials using auxetic structures is rapidly growing, with significant potential to revolutionize various industries due to their distinctive mechanical properties. These structures exhibit behaviors that defy conventional material mechanics, opening up exciting possibilities for product innovation and development [30,31]. Conventional materials typically contract laterally when stretched and expand laterally when compressed lengthwise. In contrast, when auxetic-structure materials are stretched lengthwise, they tend to become thicker in widthwise directions. Conversely, when compressed along their length, they become thinner widthwise [30,32,33].

This unique auxetic behavior is attained through the special geometric design of auxetic structures. The key component of auxetic structures is the individual arms, their dimension and the way they are connected to each other, which collectively produce the auxetic behavior [22,34]. Because auxetic structures can expand in both lengthwise and widthwise directions when tensional force is applied, they offer a unique four-way elongation [21]. This distinctive deformation characteristic of auxetic-structure materials endows them with a range of exceptional mechanical properties [30,32,35]. Thus, their increased elongation, along with other enhanced mechanical properties, makes auxetic-structure materials highly appealing for various applications across numerous fields, including textiles, where they can significantly enhance wear comfort [35].

2.3. Auxetic-Structure 3D-Printed Textiles

Integrating auxetic structures in 3D-printed textiles holds great potential to improve their wearability and meet diverse user needs [23]. The exceptional mechanical properties of 3D-printed auxetic-structure textiles can be further manipulated by adjusting the geometry of auxetics in the 3DP process to address specific user requirements [23,33,36]. The development structures of 3D-printed auxetic-structure textiles are rapidly expanding, as their unique auxetic properties enhance the mechanical performance of textiles [37]. Specifically, different auxetic structures used in 3D-printed textiles can mimic the wearability of conventional lace fabrics, making them suitable for a range of wearable items and home décor [35,38].

Previous studies have identified different auxetic structures (e.g., re-entrant cellular structures, nodule and fibril structures, and rotating unit structures) with great potential for developing 3D-printed wearable products [34,39]. The re-entrant cellular structure consists of multiple cells that unfold outward from their original shape under tension, resulting in an expansion of the bulk specimen, with their auxetic behavior significantly affected by the orientation angle of center facing arms [40].

Specifically, star-shaped re-entrant auxetic structures, one of the most typically used re-entrant cellular auxetic structures, consist of interconnected star-shaped units forming 2D periodic structures [41,42]. Other re-entrant cellular auxetic structures, such as floral-based star-shaped re-entrant auxetic structures, a classic variation of the star-shaped re-entrant design, have also been widely employed in 3D-printed textiles’ development. For example, researchers have adapted star-shaped re-entrant auxetic structures when developing 3D-printed textiles to provide consistent pressure during the joint movement of pressure garments [43]. The nodule and fibril structures consist of an interconnected network of nodules and fibrils, which produces an expansion in the transverse direction, while the fibrils cause the nodules to be pushed apart [44]. For example, 3D-printed mesh textiles with nodule and fibril structures were developed by researchers to offer a high flexibility for supporting softer tissues such as muscles and tendons as personalized wearable supports [45]. The rotating unit structures include geometric shapes such as rigid squares, triangles, and rectangles connected at their vertices by hinges, with their auxetic behavior achieved through the rotation of these shapes relative to each other [46]. For example, Maria Alejandra Mora Sanchez’s collection used rotating unit structures in 3D-printed textiles to create a wearable dress that expands under longitudinal strain and contracts when compressed [47].

2.4. Elongation and Strength of 3D-Printed Auxetic-Structure Textiles

The adoption of 3DP in clothing is indeed a transformative trend in the apparel and textiles industry, with numerous benefits [20,48]. Researchers have been examining the mechanical properties of 3D-printed textiles that hinder their widespread adoption in developing wearable products [48]. Specifically, it is essential to identify the key mechanical properties of 3D-printed textiles to ensure their quality and performance, thereby enhancing user satisfaction [49]. Among different mechanical properties, strength and elongation are the two crucial properties that affect the performance and functionality of wearable textiles, which experience multi-directional stress and strain during use [50,51].

Elongation denotes the percentage increase in the length of textiles when subjected to force or stress, providing insights into how textiles perform under stress to offer comfort and ease of movement [18,52]. Textile strength represents the maximum resistance of textiles to tensional forces, which can be understood as the elongation of the textile product at the point of rupture [18]. Thus, the strength and elongation of 3D-printed textiles should be examined during the material development process to achieve their optimal performance [52].

The strength and elongation of 3D-printed textiles are assessed through tensile testing, which generates a load–elongation curve that characterizes the material’s tensile properties [19]. Typically, the load–elongation curve of textiles exhibits three main segments. Initially, there is a linear region signifying elastic deformation, followed by a non-linear segment representing elastoplastic deformation. The final linear segment signifies the occurrence of permanent deformation in the textile sample [49]. In the elastic region, the initial part of the load–elongation curve, textiles endure a low load and display elastic properties, meaning they can return to their original shape once the applied force is removed [17,49].

Elongation, which contributes to wear comfort by enabling textiles to stretch fully and exert minimal pressure on the body during movement, is evaluated by analyzing the elastic region. This is because the pressure exerted by body movement on textiles resembles the pressure experienced by textiles in the elastic region [17,49]. Alternatively, the maximum force or breaking load, the key measure of textile strength, occurs when the force needed to break the textile sample is applied [19,49]. The final plastic region, where permanent deformation occurs, indicates the maximum force and elongation at break, which provides researchers with insights to understand textiles’ strength [49].

With their special geometric structures, 3D-printed auxetic-structure textiles have great potential to improve these essential mechanical properties [23]. Specifically, the auxetic behavior of 3D-printed auxetic-structure textiles results from the deformation of individual arms and their rotation around joints when subjected to stretching. As auxetic-structure textiles stretch in a particular direction, the angles between the arms alter, leading to expansion in both lengthwise and widthwise directions. Conversely, when compressed, auxetic-structure textiles contract in both dimensions due to changes in the angles between their individual arms [53]. The mechanical properties of auxetic-structure textiles are greatly influenced by their structural geometry, specifically the orientation angle of center facing arms [22]. Therefore, the auxetic property can be adjusted by modifying the sizes of the arms and their orientation angle, which may affect textiles’ strength and elongation [22,34].

Prior research has leveraged 3DP to develop auxetic structures and examine their mechanical characteristics [30,34,37]. For example, 3D-printed textiles with auxetic structures offer improved permeability, enhanced indentation resistance, increased fracture toughness, and superior synclastic behavior [34]. Turkoglu et al. created auxetic structures using an FDM 3D printer and examined their strength and energy absorption properties. Their research revealed that 3D-printed auxetic structures possess notable advantages in terms of strength, stiffness, and energy absorption capabilities [54]. Li and Yu [33] fabricated 3D-printed auxetic-structure textiles and performed experiments demonstrating that these structures exhibit auxetic behavior when stretched in multiple directions. The study concluded that the influence of the diameter or thickness of the textiles on the deformation behavior of 3D-printed auxetic structure textiles was significant. However, limited attention has been given to examining how the orientation angle of center facing arms in 3D-printed auxetic-structure textiles influences their mechanical properties, particularly textile strength and elongation. Thus, this study aimed to address this gap by investigating the effect of the orientation angle of center facing arms on the strength and elongation of 3D-printed textiles with two different re-entrant cellular structures, the most common auxetic structures used in the 3D-printed textiles’ development.

3. Materials and Methods

An experimental research design consisting of 6 (auxetic structure textiles) × 3 (repetition) was used to examine the effect of the orientation angle of center facing arms on the elongation and strength of 3D-printed re-entrant cellular auxetic-structure textiles to showcase the possibility of manipulating the mechanical properties of 3D-printed auxetic-structure textiles to maximize 3D-printed textile products’ wearability and functionality by adjusting the orientation angle of center facing arms in the textile structure design and 3D modeling stages.

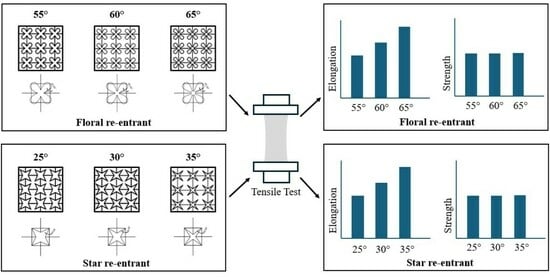
3.1. Textile Sample Development

As shown in Figure 1, 6 auxetic-structure textiles were purposefully identified, consisting of (a) 3 star-shaped re-entrant auxetic structures (star re-entrant-25, star re-entrant-30, and star re-entrant-35) with orientation angles of 25°, 30°, and 35°, respectively, and (b) 3 floral-based star-shaped re-entrant auxetic structures with curvilinear edges inspired by floral patterns (floral re-entrant-55, floral re-entrant-60 and floral re-entrant-65) with orientation angles of 55°, 60°, and 65°, respectively. Star re-entrant and floral re-entrant are among the most commonly used re-entrant cellular auxetic structures in 3D-printed textiles’ development, offering designers diverse options for fulfilling different user needs [41,42]. Additionally, Kabir et al. demonstrated the potential for developing 3D-printed textiles with different re-entrant cellular auxetic structures, including star re-entrant and floral re-entrant, to improve drapability [21]. Therefore, star re-entrant and floral re-entrant were adapted from the existing literature and modified with varying sizes of center facing arms and orientation angles for this experiment.

In this study, Kabir et al.’s procedure for developing 3D-printed textiles was followed for prototyping 3D-printed auxetic-structure textiles [21]. The 2D drawings of 6 auxetic structures, each featuring an identical unit size (0.6 inches for diagonal distance) but varying orientation angles, were created using Rhino 7 software. Different methods for measuring the orientation angle were used based on the geometric differences between the star re-entrant and the floral re-entrant, particularly the straight or curved center facing arm in each unit. To measure the orientation angle, a boundary line was drawn connecting the four outer corner points of the repeating unit in both star re-entrant and floral re-entrant, as shown in Figure 1. For the star re-entrant with a straight center facing arm, the orientation angle between the center facing arm and the borderline was measured. For the floral re-entrant with a curved center facing arm, a straight line was drawn alongside the curved line, and the orientation angle between the straight center facing arm and the borderline was measured. Subsequently, the orientation angle, the angle between the center facing arm and the border, was adjusted to 25°, 30°, and 35° for the star re-entrant and to 55°, 60°, and 65° for the floral re-entrant, respectively. The orientation angles for this study were purposefully chosen for the 3D-printed textiles not to compromise their auxetic behavior.

All the 2D drawings of the 6 auxetic structures were extruded into 3D models with a thickness of 0.4 mm. The final 3D models of the auxetic-structure textile samples were customized with dimensions of 7″ × 3″, suitable for use in tensile testing. All the textile samples with different orientation angles were fabricated using an FDM 3D printer equipped with a direct-drive extruder with a 0.4 mm nozzle diameter. Due to their special material properties, TPU 3DP filaments with a diameter of 1.75 mm, the most commonly used material for 3D-printed wearables, were purposefully chosen to print all the 3D-printed textile samples. To ensure optimal printing quality and performance in the 3DP process, the FDM 3D printer settings were adjusted to a nozzle temperature of 220 °C, bed temperature of 60 °C, and a layer height of 0.2 mm. Later, a tensile test was performed on the 3D-printed auxetic-structure textiles.

3.2. Tensile Test

To measure textile elongation and strength at breaking point, a tensile test following the ISO 13934-2:1999 [55]: tensile properties of fabrics (grab method) was performed. All the textile samples of 7″ × 3″ were placed in a constant rate of extension machine (INSTRON 5565, 68TM-10, Instron, Norwood, MA, USA) with a maintained load of 5000 N, extension speed of 76 mm/min, and clamp distance of 3″. As the upper head of the machine moved up at a constant rate of 76 mm/min, measurements were taken for elongation and force. As the pressure that the body movement places on wearable textiles is relatively small and below the breaking point, the elongation of the textile samples was measured within the range of elasticity under low load conditions so that no permanent deformation of the textile samples takes place, and the sample can self-reverse once the applied load is removed [17,49]. Thus, for this experiment, 6 N and 4 N were set as the low load condition for the 3D-printed textile samples with star re-entrant and floral re-entrant structures, respectively, to simulate real-life usage. The strength of the 3D-printed textile samples was measured in terms of maximum force, the maximum amount of force the textile samples endure before they break.

3.3. Data Analysis Procedures

SPSS 29 statistical software was used for statistical analysis at p < 0.05. Simple linear regression analysis was performed to uncover the relationship between load and elongation for the 3D-printed textile samples with various orientation angles within the elastic region. A one-way ANOVA was conducted to compare the maximum force of different 3D-printed textile samples with varying orientation angles of center facing arms. The analysis was used to determine whether there are statistically significant differences in textile strength among the star re-entrant and the floral re-entrant based on the orientation angle variations.

4. Results and Discussion

This study explored the effect of the orientation angle of center facing arms on the elongation and strength of 3D-printed auxetic structure textiles, specifically focusing on star re-entrant and floral re-entrant structures. The investigation focused on two main aspects: (a) the relationship between force load and elongation within the elastic region of the load–elongation curve and (b) the difference in maximum force within the final linear plastic segment of the load–elongation curve.

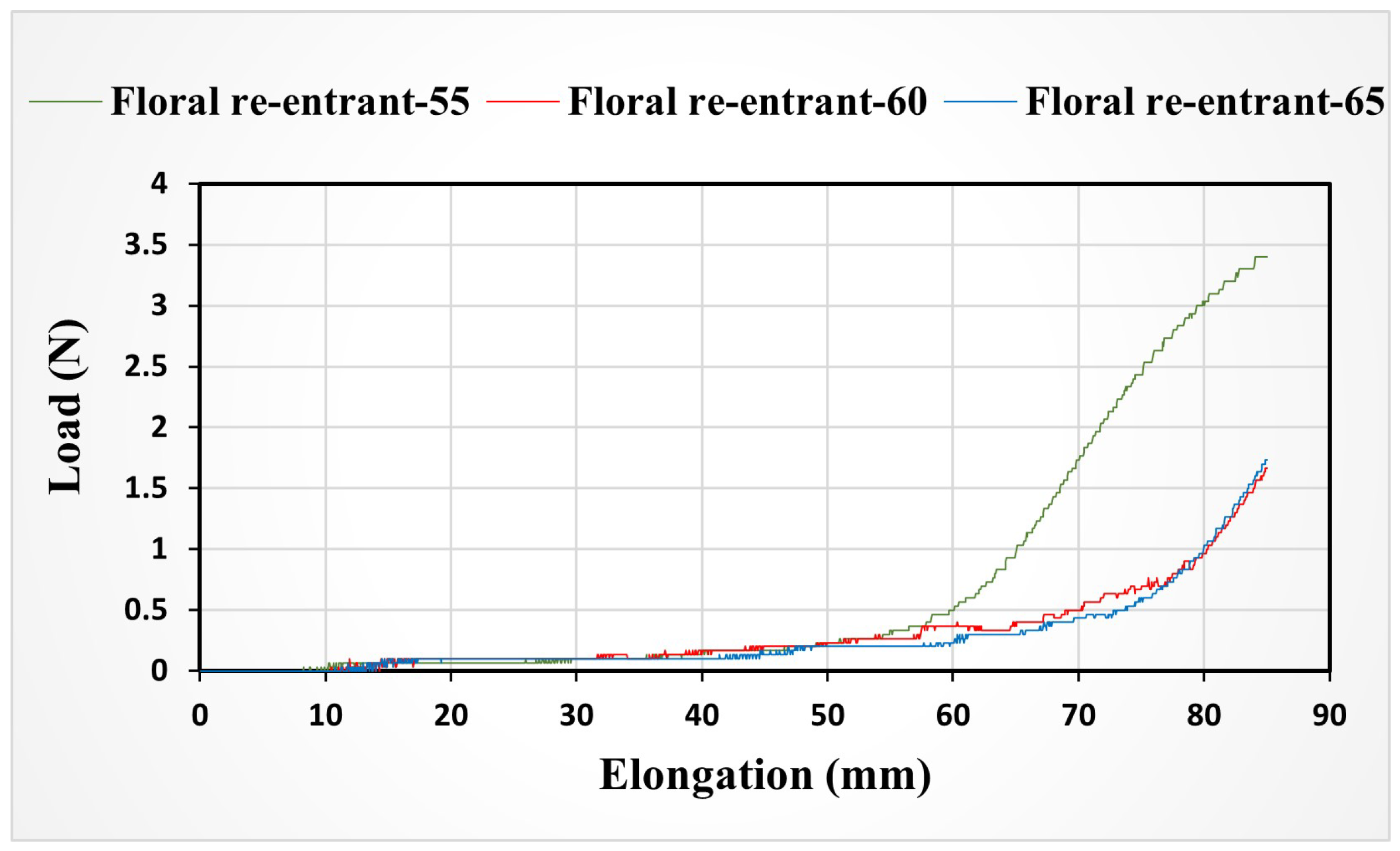
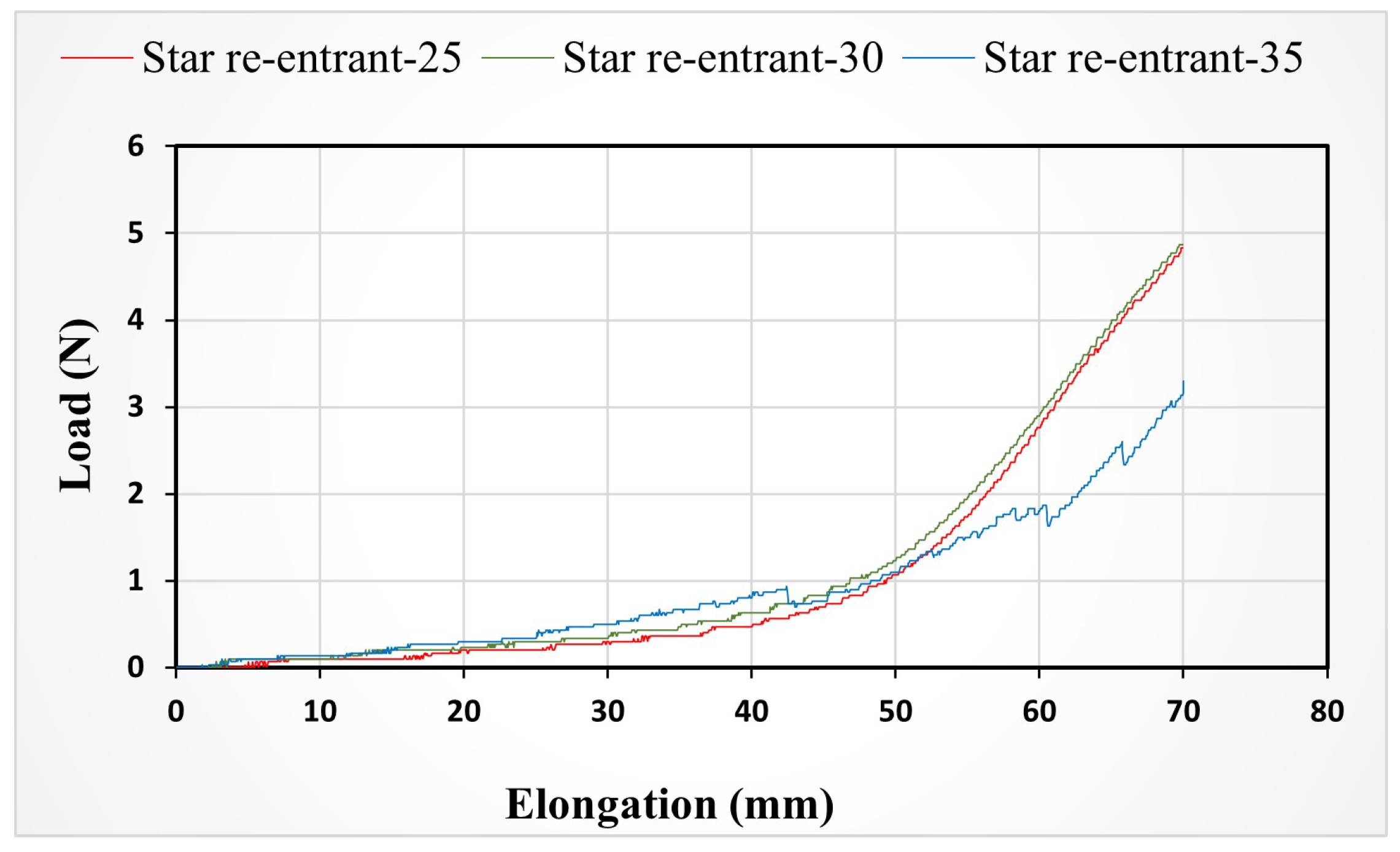
4.1. The Effect of Orientation Angle on Elongation

As shown in Figure 2, the load–elongation slope decreases in steepness when increasing the orientation angle for the floral re-entrant, indicating that less force is needed to elongate the sample as the orientation angle rises. Initially, all three load–elongation curves were linearly overlapping each other. However, when the applied load reached about 1 N, the textile samples with a higher orientation angle (e.g. floral re-entrant-60 and floral re-entrant-65) started displaying a higher elongation. This indicates that the textile samples with a higher orientation angle possess better elongation properties, as materials with the enhanced elongation property elongate more with a given applied load [19].

The results of simple linear regression revealed a statistically significant relationship between load and elongation for floral re-entrant-55 (F(1,1673) = 3168.18, p <.001), floral re-entrant-60 (F(1,1673) = 3898.59, p <.001), and floral re-entrant-65 (F(1,1673) = 2478.87, p <.001). Additionally, elongation explained 65%, 70%, and 60% of the variance in the applied load for floral re-entrant-55, floral re-entrant-60, and floral re-entrant-65, respectively.

To investigate the relationship between load and elongation within the elastic region, this study also examined how variations in load affect elongation. The regression analysis results showed that as the orientation angle increases, the required load to elongate the textile sample decreases. For example, every 1 mm elongation of floral re-entrant-55 required a load of 0.03 N, while a 0.01 N load was needed to elongate floral re-entrant-60 and floral re-entrant-65 by the same amount. Generally, textiles with enhanced elongation properties typically require less load to elongate, whereas textiles with poor elongation properties necessitate more force to achieve the same elongation [19]. Therefore, it can be interpreted that as the orientation angle of center facing arms increases, the necessary force to elongate the floral re-entrant decreases, leading to better elongation performance.

A similar trend between load and elongation was observed for the star re-entrant. As presented in Figure 3, as the orientation angle increases, the slope of the load–elongation curve decreases in steepness, suggesting that less force is necessary to elongate the sample as the orientation angle increases. As shown in Figure 3, the load–elongation curves initially overlapped. However, once the applied load reached about 2 N, the textile sample with a higher orientation angle began to demonstrate higher elongation, as materials with enhanced elongation properties elongate more with a given applied load [19].

A statistically significant relationship was found between load and elongation for star re-entrant-25 (F(1,1377) = 3391.99, p <.001), star re-entrant-30 (F(1,1377) = 3933.27, p <.001), and star re-entrant-35 (F(1,1379) = 8414.62, p <.001). Elongation accounted roughly for 71%, 74%, and 86% of the variance in the applied load for star entrant-25, star re-entrant-30, and star re-entrant-35, respectively. Furthermore, according to the regression analysis, every 1 mm elongation of star re-entrant-25 and star re-entrant-30 required a load of 0.06 N, whereas every 1 mm elongation of star re-entrant-35 required a 0.04 N load. Thus, for the star re-entrant, the required load to elongate the sample decreases as the orientation angle of center facing arms increases, resulting in improved elongation.

The results indicated that the elongation of both 3D-printed cellular auxetic-structure textiles (the star re-entrant and the floral re-entrant) was positively influenced by the orientation angle of center facing arms in their geometric structures. The results are consistent with the findings from previous studies, indicating that the elongation of 3D-printed auxetic structure textiles results from the deformation of central facing arms and their rotation around joints when subjected to stretching [53,56]. As the star re-entrant and the floral re-entrant are stretched in a specific direction, the cells unfold outward gradually, straightening up indented center facing arms from their original shape, and orientation angles gradually decrease towards zero, creating space for the structure to expand in both lengthwise and widthwise directions [22,40,56]. In addition, as the orientation angle increases, so does the size of the center facing arm. For instance, as shown in Figure 4, the size of center facing arms for floral re-entrant-55, floral re-entrant-60, and floral re-entrant-65 was 7.84 mm, 8.37 mm, and 8.79 mm, respectively, while the size of the arms for star re-entrant-25, star re-entrant-30, and star re-entrant-35 was 5.94 mm, 6.23 mm, and 6.73 mm, respectively. Auxetic structures with longer center facing arms can provide more space for expansion, leading to enhanced elongation. Consequently, all the re-entrant cellular units in this study, with sufficiently sized center facing arms, create space to expand when stretched. Therefore, the auxetic structures with higher orientation angles form longer center facing arms, leading to greater elongation properties.

The enhancement in elongation becomes evident both visually and quantitatively with a specific change in orientation angle. When the orientation angle difference is minimal, the enhancement in elongation is not apparent. For instance, the load–elongation curves for floral re-entrant-60 and floral re-entrant-65 were nearly indistinguishable visually (see Figure 2). Likewise, the load–elongation curves for star re-entrant-25 and star re-entrant-30 showed almost no visible difference (see Figure 3). As shown in Figure 2 and Figure 3, a 10° increment in orientation angle resulted in visible changes in the load–elongation curve, indicating the observable improvement in elongation.

In addition, the quantitative data from the regression analysis revealed that floral re-entrant-60 and floral re-entrant-65 behave similarly, with each requiring a load of 0.01 N to elongate by 1 mm. Similarly, both star re-entrant-25 and star re-entrant-30 required a load of 0.06 N to elongate by 1 mm. However, with a 10° increase in orientation angle, the required load to elongate the textile samples decreased. For instance, floral re-entrant-55 required a load of 0.03 N, compared to 0.01 N for floral re-entrant-65. Likewise, star re-entrant-25 required a load of 0.06 N, whereas star re-entrant-35 required 0.04 N. The findings demonstrate that the enhancement in elongation becomes obvious only with a specific degree of change in orientation angle.

4.2. The Effect of Orientation Angle on Strength

A one-way ANOVA was conducted to compare the maximum force among different orientation angles of center facing arms for both 3D-printed cellular auxetic-structure textiles (the star re-entrant and the floral re-entrant). The results showed no statistically significant difference in textile strength for the star re-entrant with different orientation angles of center-facing arms (F(2,6) =3.16, p = 0.12), and the floral re-entrant with different orientation angles of center-facing arms (F(2,6) =4.09, p = 0.08). Specifically, the mean maximum force sustained before break for star re-entrant-25 was 16.57 N, compared to 20.58 N for star re-entrant-30, and 19.03 N for star re-entrant-35. Similarly, the mean maximum force endured before break for floral re-entrant-55 was 16.61 N, while it was 14.9 N for floral re-entrant-60, and it was 12.08 N for floral re-entrant-65. These results indicated no significant variation in textile strength across different angles for both star re-entrant and floral re-entrant auxetic-structure textiles in this study.

Unlike their elongation, the strength of the star re-entrant and the floral re-entrant was not significantly affected by the orientation angle of center facing arms. One possible explanation for these results is that the consistent material properties of TPU and the triangular architecture of both star re-entrant and floral re-entrant structures provide an inherent strength that is independent of the specific orientation of center facing arms. The lack of significant differences in maximum force across orientation angles may imply robustness in star re-entrant and floral re-entrant structures, highlighting their potential for practical applications for wearables that require consistent performance under the varying comfort and functional needs of wearers.

5. Conclusions

This study examined the effect of the orientation angle of center facing arms on the strength and elongation of 3D-printed auxetic-structure textiles. Specifically, this study experimented with two different types of re-entrant cellular auxetic structures (star re-entrant and floral re-entrant), the most common auxetic structures used in 3D-printed textiles’ development. The findings of this study offer multiple implications for designers and scholars in both industry and academia, providing guidelines to optimize the geometric design in auxetic structures and improve the performance of 3D-printed auxetic-structure textiles.

The study results revealed that as the orientation angle increases, the elongation of 3D-printed textiles with star re-entrant and floral re-entrant structures improves, making the final textile products more flexible and potentially providing better wear comfort. The findings also highlight potential for researchers and designers to manipulate the elongation of 3D-printed auxetic structure textiles for different applications by adjusting the orientation angle of center facing arms. Specifically, by using different auxetic structures with varying angles of center facing arms in 3D-printed textiles, it is possible to create wearable products with a tailored elongation, allowing specific areas of the human body, such as joints, knees, and elbows, to move freely and comfortably. The method outlined in this study to control the elongation of 3D-printed auxetic-structure textiles is suitable for designing customized 3D-printed wearables, significantly enhancing their functionality and wear comfort.

The study results demonstrated no significant variation in the maximum force of 3D-printed textiles with star re-entrant and floral re-entrant structures across different orientation angles, which indicates the potential of using re-entrant cellular structures with different angles of center facing arms to tailor the elongation of 3D-printed textiles while maintaining a consistent strength across different applications. This exploratory study provides a comprehensive guideline for designers and industry professionals to fabricate 3D-printed wearables with an adjustable elongation tailored to specific product needs, while ensuring that the strength of the wearables remains consistent to meet user requirements and enhance wear comfort.

Although this study provides valuable insights for researchers and designers by investigating the elongation and strength of 3D-printed auxetic structure textiles with various orientation angles, it is limited by the use of only two geometries of auxetic structures (star re-entrant and floral re-entrant) with three orientation angle options. Further research is needed to explore different geometries of 3D-printed auxetic structures. Additionally, this study was constrained by the manipulation of auxetic structures with only three different orientation angles, each with a 5° increment. This narrow range of variation might have restricted the validity and generalizability of the study findings. Future studies should incorporate a wider range of orientation angles to investigate their impact on both elongation and strength more comprehensively. Furthermore, the auxetic-structure textile samples in this study were developed only using an FDM 3D printer with TPU filaments. Future investigations also need to consider different 3DP methods and materials, such as stereolithography and nylon, to assess their effect on the property of 3D-printed auxetic-structure textiles. This study focused solely on the impact of the orientation angle of center facing arms on elongation and strength. The influence of orientation angle on other important textile properties, such as drapability, stiffness, and dimensional stability, should also be examined in future research to obtain a more thorough understanding of the relationship between orientation angle and mechanical properties, thereby enhancing the application of 3D-printed auxetic-structure textiles for wearable products’ development. Despite the study limitations, the study design, methods, and results presented in this paper provide an important reference point for other researchers to validate their study findings when conducting similar studies in the future.