Abstract
Stretch fabric provides good formability and does not restrict the movement of the body for increased tension levels. The major expectations of a wearer in an apparel fabric are a high level of mechanical comfort and good aesthetics. The prediction of shrinkage in stretch fabric is a very complex and unexplored topic. There are no existing formulas that can effectively predict the shrinkage of stretch fabrics. The purpose of this paper is to develop a novel model based on an artificial neural network to predict the shrinkage of stretch fabrics. Different stretch fabrics (core-spun lycra yarn) with stretch in the weft direction were manufactured in the industry using a miniature weaving machine. A model was built using an artificial neural network method, including training of the data set, followed by testing of the model on the test data set. The correlation of factors, such as warp count, weft count, greige PPI, greige EPI, and greige width, was established with respect to boil-off width.
1. Introduction
Stretch textiles, which range from infant clothes to upholstery, provide a better fit for a wide range of products. Some fabrics offer tremendous control, while others offer ease of movement or a comfortable fit. These stretch fabrics can be divided into two types. One type is power stretch, which can be found in support garments, swimsuits, and other items. The other is comfort, sometimes known as action stretch. It can be found in athletic and casual wear, and other products with a lot of mobility and a smooth fit [,]. Stretch fabric is a fabric that stretches when force is applied in a single or several directions during normal wear. Power stretching is well known, while comfort stretching is a relatively recent notion []. Stretch fabric is made from materials that have specialized extension qualities, with at least 20% elongation in the warp direction []. Cotton fabrics are used along with spandex to provide greater stretch and recovery than cotton alone can provide. Cotton/spandex blends are most common in women’s clothing, but are now spreading into other product categories, such as knit products, skirts, leggings, and tops, as well as almost all sorts of woven fabrics, such as stretch jeans. Spandex is typically found in woven textiles as a core spun yarn; however, the form in which the spandex is used relies on the fabric construction, performance needs, and designer’s knowledge. Cotton knit fabrics with spandex often have stretch qualities ranging from 50 to 100%; this figure is typically 15 to 50% for woven structures.
In general, a ’stretch fabric’ is defined as a material with a minimum stretch of 20% in the warp direction. Natural rubber is the main choice for adding elasticity to fibers, and mercerization and texturization are used to process normal woven fabrics to develop elasticity. Since conventional rubber is used, there is a need for other synthetic materials to take on increasing demand, and spandex has emerged as a solution to this problem. A popular way to produce stretch fabrics is to use elastane yarns, because the desired properties can be achieved by using 2–3% of elastane yarns. Spandex-containing stretch fabrics are less stiff, more easily stretchable, and more recoverable than non-spandex fabrics. Value may be added to garments due to spandex by emerging properties such as wash and wear, which add comfort during wear [].
Stretch fabrics have lower drapability and wrinkle recoverability. Stretch textiles can be compressed more than others and have larger surface volumes when it comes to compression. Furthermore, their higher compression recovery reflects the inherent property of stretch materials as opposed to non-stretch fabrics in general []. Stretch fabric is either a two-way stretch or a four-way stretch. According to researchers, a stretch range of 20 to 45% from the wearer’s comfort viewpoint depends on the end use []. Stretch fabrics can be woven as well as knitted fabrics. The various methods used in the production of stretch fabric can be listed as slack, the mercerization of fabrics, weaving fabric with high twist yarn, using textured synthetic yarn, using covered rubber yarns, using spandex yarns, and so on []. In one study, the linear density of weft threads and the preliminary tension of the ground yarn, which produced a pillar stitch, were found to affect the stretch qualities of elastic warp knitted fabrics, the full deformation, and the constituent parts [].
As spandex is generally used in the weft direction in stretch fabrics, the properties based on weft input become crucial in testing the performance of stretch fabrics. These parameters include fabric growth, fabric stretch, and elastic recovery of the stretch fabric. Stretch fabric is popular among sportswear companies. Stretch fabrics have a wide range of applications in sports apparel, including yoga suits, bicycle shorts, skiwear, swimsuits, leotards, sports bras, and all other types of apparel designed for intense stretching of body parts.
Cotton and spandex fabrics will always default to a lower energy level. Relaxing the cloth from intrinsic construction and processing tensions improves dimensional stability. The boil-off bath should contain a good textile detergent or the scouring agents to be used in processing. A useful way to quickly determine the relaxed state is to "boil-off" a two yard long, full-width sample. Following the boil-off, the samples can be dried in a sample oven and the fabric width measured. This is the absolute smallest width to which the fabric will shrink. This understanding will prohibit the finisher from attempting to complete the fabric at a width less than the relaxed width.
Stretch fabric, when subjected to heat and moisture during processing, tends to release its internal stresses and shrink to a certain extent. This shrinkage is dependent on the following parameters: yarn count, fabric construction (EPI, PPI), weave structure, the percentage content of spandex in the fabric, loom width, and so on. Shrinkage occurs when moisture, heat, and mechanical action (movement during fabric formation, drying, and washing) are mixed [,,,]. The combination of these factors causes the fibers to release the stresses created during the fabrication of the stretch fabric. Higher moisture content also increases the rate of shrinkage. There are two methods to control fabric shrinkage. First, shrinkage is appropriately controlled at feeding and is reduced with length and width to apply clothing with lower or greater feed speed. The maximum is controlled using 70–75% shrinkage. Second, shrinkage fiber is raised to its original position in the thermoplastic and cooled after the reaction of a hot steam process [,,]. This process will mold the fiber to its original position. Shrinkage percentage plays a very important role in stretch fabric manufacturing as the stretch of the fabric is indirectly dependent on it, and stretch is very important in specific end-use fabrics, such as sportswear and infant wears. Therefore, it is very essential to predict the shrinkage percentage of stretch fabrics in the manufacturing textile industries.
In one study based on the basic fabric constructional variables, it was discovered that an artificial neural network can accurately assess the tear strength of a bed sheet fabric. The weave structure of the material was discovered to be significantly related to the tearing strength properties. Including the weave factor parameter as a training input can improve prediction performance even further. Therefore, artificial neural networks have great importance in the textile industry for advanced fabric manufacturing, product development, etc., wherein developing new specialty fabrics is vital (Ahirwar and Behera, 2022).
Artificial intelligence (AI) is a machine’s abiltiy to carry out tasks in a way that would be considered smart. The AI approach is founded on the assumption that data are fed into machine learning models which then gain intuition on their own, with no manual intervention [,,,]. ANNs, or artificial neural networks, are forms of neural networks based on a collection of units called artificial neurons which are connected to the next layer’s units, as shown in Figure 1. Arrows represent the connection or interchange of information through an arrow from one layer to another, and on the other side, we obtain the output of our neural network [,,,]. This design is based on our brains. Numerical information from these neurons passes on through deeper layer neurons.
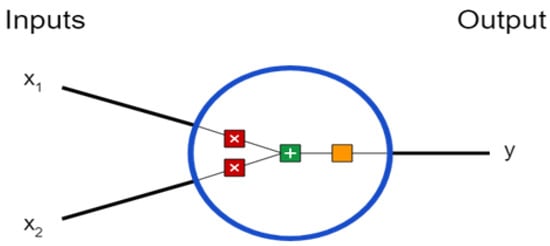
Figure 1.
Two input, one output model.
Algorithms in machine learning are primarily based on methods to easily process a wide variety of data that are difficult to process manually. In the production of stretch fabric, stretch yarns were used. These yarns are very sensitive to low-standard spinning methods compared with core-spun yarns. Due to improper heat settings or machine parameters, some problems may occur, such as variation of dyeability or shrinkage throughout the fabric or color fading or stripe effect. Since a two-dimensional fabric is used to mimic the surface of a three-dimensional body, the result can be problematic, and the main important thing is the shape and the frequent posture of the person and how our fabric performs in that condition. The shrinkage in the stretch fabric is dependent on every factor that comes into account in its production. A lot of these variables are unable to derive a formula for shrinkage manually. Additionally, other studies predict fabric properties that are hard to predict manually using machine learning models. This gives us a direction of research for predicting shrinkage using machine learning. In light of the above discussion, the present study focuses on predicting the shrinkage of stretch fabrics by using machine-learning-based artificial neural networks.
2. Materials and Methods
2.1. Materials
Stretch fabrics (core-spun lycra yarn) with stretch in the weft direction were manufactured by Vardhman Industries, India. The fiber blends used were 96–98% cotton and 2–4% elastane. Different samples were manufactured in an industry using a miniature weaving machine. The parameters and their numerical range are given in Table 1 and were used as the data points in the artificial neural network.

Table 1.
Particulars of fabric samples.
2.2. Methodology
2.2.1. Process Sequence
The grey fabrics were processed using the standard process settings used in commercial production, as shown below.
Grey fabric → Grey wash → Heat Set→ Pre-treatment → Mercerization → Peach → Wash → Dry pad → Pad steam → Finish→ Dry
2.2.2. Artificial Neural Network to Predict Shrinkage
Machine learning-based artificial neural networks, are now widely being used to forecast the performance of any parameter. The artificial intelligence (AI) concept is based on the idea that data are supplied to machine learning models which then learn intuitively, on their own, with no manual intervention [,,,]. Artificial neural networks are varieties of neural networks based on a collection of units called artificial neurons that are connected to the next layer’s units [,,,].
The important steps in the ANN methodology include the building of the model, training, and testing of data points, and authentication of the model. These steps are to be performed very specifically to obtain precise results. The characterization of properties is considered for the shrinkage of stretch fabrics. The input parameters, such as yarn count, construction parameters, weave structure, and on-loom width were measured. Spandex% was also taken into consideration. Shrinkage% is measured using the ANN model. These five input parameters and one output parameter data were stored in MS Excel and were fed to the model accordingly. As weave structure cannot be represented in a numerical value, weave factor is used as a numerical representation of the weave structure. It is the number of interlacements of warp and weft in each repeat. The formula used for weave factor is:
M = E/I
E = number of threads per repeat;
I = number of interactions per repeat.
In the case of irregular weave patterns, the weave interlacements of warp and weft yarns may be different; hence, two weave factors, M1 and M2, are considered:
where E1 and I2 can be measured by observing a pick in fabric, and E2 and I1 can be measured by observing ends in the repeat.
M1 = E1/I2 M2 = E2/I1
2.2.3. Significance of Backpropagation
Backpropagation is a learning technique used by artificial neural networks to generate a gradient descent for weights. A comparison is made between the desired and realized system outputs, and then connection weights are adjusted to reduce the discrepancy as much as is feasible. In this method, weights are changed in reverse order, from output to input. The different factors that need to be taken into consideration while training a machine learning model are very important, as they can significantly affect the prediction. A wide range of factors that could affect the shrink age behavior were considered, and then later ranked based on their affectability. The different input parameters selected here are, warp and weft count, ends/inch, and picks/inch, spandex percentage, and greige width of the fabrics. Following that, the fabric was cleaned and preprocessed using several scikit-learn data pre-processing packages. Preprocessing data is an important step in machine learning since it enhances the quality of the data and makes it easier to extract meaningful information. Data preprocessing in machine learning is the process of preparing raw data for use in the building and training of machine learning models. Data pre-processing in machine learning is essentially a data mining strategy that converts raw data into a more comprehensible and legible form. Standardization and normalization are used to ensure the accuracy of a dataset. As the precursor to many machine learning models, standardization is an important pre-processing step that is used to equalize the range of features in the input data set.
2.2.4. Building a Machine Learning Model to Predict Shrinkage Behavior Using ANN
Traditionally, neural networks have only three layers, which are the input layers, hidden layers, and output layers. Input layers are fed external data and, output layers feed their data to an external output, which is used in prediction. All these three layers are commonly referred to as dense layers. All the neurons are connected to each neuron in the next layers, and the output neuron has no forward connection to another layer, as shown in Figure 2.
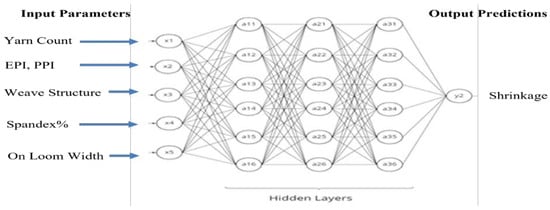
Figure 2.
Model architecture for shrinkage prediction.
The architecture of the model is very important for the prediction of numerical output using machine learning. This architecture depends on how much depth the input data are related to the output data. The number of interrelated parameters might be the best choice for the number of deep layers in the neural network. The deeper the layer, the greater the number of weights required to manage a deeper neural network, which can result in predicting a good result. Four layers of neural networks were chosen, three of which will be hidden. Five neurons are chosen for each layer, and the output neuron will have shrinkage as an output. The number of epochs will be taken as four initially and will be changed as the model becomes accurate.
2.2.5. Training the Artificial Neural Network Model
Training a model for predictive analysis gives the model an intuition about how the output parameters will depend on input parameters. Data points are divided into two sets: one is a train set, and the other is a test set. Train sets were used to train the model, and a test set to test the model for unseen data and prediction. The number of times this process is repeated is the number of epochs. A higher number of epochs will increase time but also increase accuracy for current data. Training a model takes most of the time, and models are generally deployed on cloud storage, such as AWS and Google Cloud. These cloud storages are also equipped with TPU (tensor processing unit), which is very good for matrix multiplication and other operations. Nvidia GeForce GTX 1050 was used in this study.
2.2.6. Testing the Model on a Test Data Set
After building and training the model, the model accuracy was tested. The data set was divided into a test set and a train set. Twenty percent of the data were used for the test set. The model will predict the accuracy of model prediction on test data for each epoch. If low accuracy is obtained for the train set, then the time hyperparameters are changed accordingly, and if both the train and test set have low accuracy, then a different architecture for the model is to be developed. This will determine how the model predicts the test set data.
2.2.7. Authentication and Using the Model for the Prediction of a New Data Set
Experimental testing data are used for evaluating the accuracy of the model. This will give an idea of the error of the model concerning real-world scenarios, and corrections will be incorporated according to the type of error. These errors are mainly there if there is an unknown factor that exists, but is not in our inputs. Generally, these errors are negligible, but in case of very high accuracy, this can be added to the model as an input. The development of stretch fabric is an important factor as the prediction of the model’s performance is based on these results. The error in the development of the fabric will lead to an error in the evaluation of the model. The error measurement of the machine learning model was used with respect to experimental results as a factor in this evaluation. If there are no significant results in the model, then the model architecture and parameters are reshaped. Evaluating the model is the final step in this study. Statistical results, such as the p-test, were used to test our model’s accuracy and significance. The evaluation gives an idea about how much the model is reliable and precise in a real-world scenario.
3. Results and Discussion
3.1. Error Backpropagation Algorithm for Shrinkage Percentage
The algorithm related to the error backpropagation method to determine shrinkage percentage is given below.
The error signal at the output neuron j at the iteration n is defined by ej(n) = dj(n) − yj(n).
The internal activity level vj(n) produced at the input vj(n) = ∑i = 0p wji(n)yi(n).
The output of the neuron j at iteration n is yj(n) = φj (vj(n)).
The local gradient is δj(n) = [dj(n) − oj(n)] oj(n) [1 − oj(n)].
For the hidden neuron j, the local gradient is δj(n) = yI(n) [1 − yI(n)] ∑k δk(n) wkj(n).
The correction Δwji(n) applied to the synaptic weight is Δwji(n) = η × δj(n) × yi(n).
In forward pass, the synaptic weights remain unaltered throughout the network. In nonlinear functions, the below functions were included:
The log function is yI(n) = 1/(1 + exp(−vj(n)).
The hyperbolic tangent function is φj (v) = 2a/(1 − exp(bv)) − a.
The momentum constant is Δwji(n) = αΔwji (n − 1) + η δj(n) yi(n).
3.2. Correlation of Factors with Respect to Boil-Off Width
The correlation of factors with respect to boil-off width was established. The factors include warp count, weft count, greige PPI, greige EPI, and greige width. The R-value and p-value of fabrics were found with respect to boil-off width, and are given in Table 2. The R-value donates the correlation between the boil-off width and the different construction parameters of the fabric. The error matrices obtained from the machine learning model with respect to experimental shrinkage and shrinkage predicted by using Equations (1)–(4) are given in Table 3. The graphs depicting the correlation of warp and weft count with respect to boil-off width are shown in Figure 3. A low degree of negative correlation was observed between the boil-off width and warp count of 100% cotton. This means that as the warp count increases and the fineness of the yarn increases, the boil-off width decreases. A low degree of negative correlation was also observed between the boil-off width and weft count of cotton-spandex. As the weft count increases and the fineness of the yarn increases, the boil-off width decreases, and it can be seen from Figure 3 that the points are scattered over the region, depicting low correlation. The graphs depicting the correlation of greige EPI and PPI with respect to boil-off width are shown in Figure 4. A high degree of negative correlation was found between EPI and boil-off width. As the greige EPI increases, the boil-off width of the fabric decreases. A high degree of positive correlation was found between PPI and boil-off width. As the greige PPI increases, the boil-off width of the fabric also increases. The graph depicting the correlation of spandex percentage with boil-off width is shown in Figure 5. A low degree of negative correlation was observed between boil-off width and spandex percentage in weft core. This means that as the percentage of spandex in the weft yarn increases, the boil-off width of the fabric decreases. The graph depicting the correlation of greige width with boil-off width is shown in Figure 6. A high degree of positive correlation was observed between boil-off width and greige width. As the greige width of the fabric increases, the boil-off width of the fabric also increases. It can be witnessed from Figure 6 that a cluster of dense points occurs in the graph, depicting high correlation.

Table 2.
R-value and p-value of fabrics with respect to boil-off width.

Table 3.
The error values for experimental and predicted shrinkage.
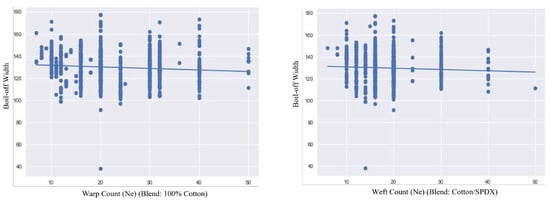
Figure 3.
Warp and weft count with respect to boil-off width.
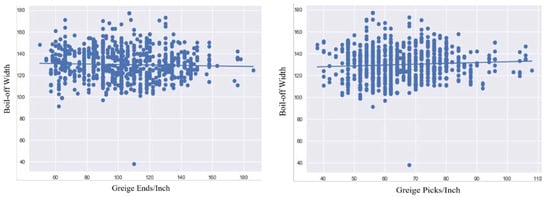
Figure 4.
Greige EPI and PPI with respect to boil-off width.
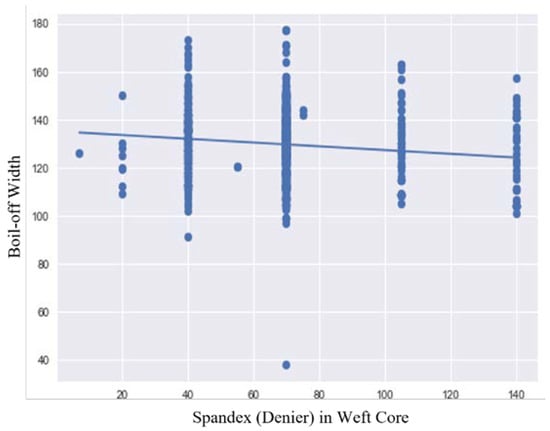
Figure 5.
Spandex% with respect to boil-off width.
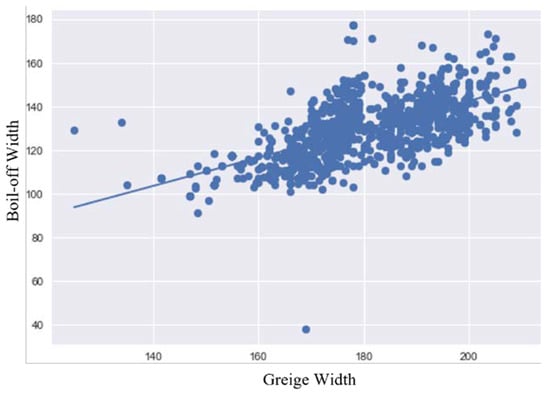
Figure 6.
Greige width with respect to boil-off width.
Using an error measure, one may determine the forecasting model error. These are used to objectively compare the performance of opposing models. The error metrics that are employed here include MSE, RMSE, MAE, and MSE root mean squared error (RMSE) (SE). The correlation coefficient “r” is a unit-free value between −1 and 1. The statistical significance is indicated with a p-value.
Mean squared error (MSE) (average of the squares of the errors):
where n is the number of data points, is the observed value, and is the predicted value.
Mean absolute error (MAE) (a measure of errors between paired observations expressing the same phenomenon):
where n is the number of data points, is the predicted value, and is the true value.
Mean standard error (SE) (standard deviation of its sampling distribution):
where n is the number of observations, and is the standard deviation.
Root mean squared deviation (RMSD) is a measure of the differences between values (sample or population values) predicted by a model:
where i is a variable, n is the number of data points, is the observed value, and is the predicted value.
The mean absolute error percentage was found to be 4.21, which is within the acceptable range; the root mean squared error was also within the acceptable bounds. As a result, this model can accurately forecast the shrinkage behavior of stretch fabrics, allowing industries to use this tool to predict shrinkage behavior prior to the beginning of actual manufacturing. This is an advantageous tool for product development, quality assurance, and advanced fabric manufacturing.
4. Conclusions
It was determined that the artificial neural network can accurately forecast stretch fabric qualities based on basic fiber characteristics and fabric constructional parameters. The main input parameters that were considered to influence fabric shrinkage percentage were yarn count, construction of fabric (EPI, PPI), weave structure, the percentage content of spandex in the fabric, and the on-loom width. These factors have a significant effect on shrinkage percentage, which is predicted through the ANN model. The network prediction correlates well with the actual experimental results. The prediction of fabric qualities from constructional parameters has some uncertainty. The shrinkage properties are highly correlated with the weave structure of the fabric. The network projected opposing trends in a few cases, which are difficult to explain. However, the model prediction accuracy on training data reached 99.2%; therefore, using ANN is effective for numerical prediction of fabric parameters and determination of shrinkage percentage.
Author Contributions
Conceptualization, methodology, software, validation, formal analysis, writing, M.A.; visualization, supervision, project administration, B.K.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
No data linked to this research.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Pannu, S.; Ahirwar, M.; Jamdigni, R.; Behera, B.K. Effect of Spandex Denier of Weft Core Spun Yarn on Properties of Finished Stretch Woven Fabric. Int. J. Eng. Technol. Manag. Res. 2020, 7, 21–32. [Google Scholar] [CrossRef]
- Ahirwar, M.; Behera, B.K. Objective Hand Evaluation of Stretch Fabrics Using Artificial Neural Network and Computational Model. J. Nat. Fibers 2022, 19, 13640–13652. [Google Scholar] [CrossRef]
- Aratani, Y.; Kojima, T. Stretch Fabrics. Sen’i Gakkaishi 1984, 40, 352–355. [Google Scholar] [CrossRef]
- Varghese, N.; Thilagavathi, G. Development of woven stretch fabrics and analysis on handle, stretch, and pressure comfort. J. Text. Inst. 2015, 106, 242–252. [Google Scholar]
- Ishimaru, S.; Isogai, Y.; Matsui, M.; Furuichi, K.; Nonomura, C.; Yokoyama, A. Prediction method for clothing pressure distribution by the numerical approach: Attention to deformation by the extension of knitted fabric. Text. Res. J. 2011, 81, 1851–1870. [Google Scholar] [CrossRef]
- Kim, H.A.; Ryu, H.S. Hand and Mechanical Properties of Stretch Fabrics. Fibers Polym. 2008, 9, 574–582. [Google Scholar] [CrossRef]
- Gurarda, A.; Meric, B. The Effects of Silicone and Pre-Fixation Temperature on the Elastic Properties of Cotton/Elastane Woven Fabrics. AATCC Rev. 2005, 5, 53–56. [Google Scholar]
- Choi, M.S.; Ashdown, S.P. Effect of Changes in Knit Structure and Density on the Mechanical and Hand Properties of Weft-Knitted Fabrics for Outerwear. Text. Res. J. 2000, 70, 1033–1045. [Google Scholar] [CrossRef]
- Kyzymchuk, O.; Melnyk, L. Stretch properties of elastic knitted fabric with pillar stitch. J. Eng. Fiber Fabr. 2018, 13, 1558925018820722. [Google Scholar] [CrossRef]
- Varghese, N.; Thilagavathi, G. Handle, fit and pressure comfort of silk/hybrid yarn woven stretch fabrics. Fibers Polym. 2016, 17, 484–494. [Google Scholar] [CrossRef]
- Ogulata, S.N.; Sahin, C.; Ogulata, R.T.; Balci, O. The prediction of elongation and recovery of woven bi-stretch fabric using artificial neural network and linear regression models. Fibres Text. East. Eur. 2006, 14, 46–49. [Google Scholar]
- Kaynak, H.K. Optimization of stretch and recovery properties of woven stretch fabrics. Text. Res. J. 2017, 87, 582–592. [Google Scholar] [CrossRef]
- Majumdar, P.K.; Majumdar, A. Predicting the breaking elongation of ring spun cotton yarns using mathematical, statistical, and artificial neural network models. Text. Res. J. 2004, 74, 652–655. [Google Scholar] [CrossRef]
- ASTM D3107-07; Standard Method of Test for Stretch Properties of Fabrics Woven from Stretch Yarns. ASTM: Philadelphia, PA, USA, 1975.
- Senthilkumar, M.; Anbumani, N.; Hayavadana, J. Elastane fabrics—A tool for stretch applications in sports. Indian J. Fibre Text. Res. 2011, 36, 300. [Google Scholar]
- Behera, B.K.; Militky, J.; Mishra, R.; Kremenakova, D. Modeling of Woven Fabrics Geometry and Properties. In Woven Fabrics; IntechOpen: Rijeka, Croatia, 2012. [Google Scholar]
- Tsai, Y.J. The influence of woven stretch fabric properties on garment and pattern design. Taiwan Text. Res. J. 2006, 16, 55–61. [Google Scholar] [CrossRef]
- Park, S.W.; Hwang, Y.G.; Kang, B.C.; Yeo, S.W. Applying Fuzzy Logic and Neural Networks to Total Hand Evaluation of Knitted Fabrics. Text. Res. J. 2000, 70, 675–681. [Google Scholar] [CrossRef]
- Noor, A.; Saeed, M.A.; Ullah, T.; Uddin, Z.; Ullah Khan, R.M.W. A review of artificial intelligence applications in apparel industry. J. Text. Inst. 2022, 113, 505–514. [Google Scholar]
- Nwobi-Okoye, C.C.; Anyichie, M.K.; Atuanya, C.U. RSM and ANN Modeling for Production of Newbouldia Laevies Fibre and Recycled High Density Polyethylene Composite: Multi Objective Optimization Using Genetic Algorithm. Fibers Polym. 2020, 21, 898–909. [Google Scholar]
- Raheel, M.; Liu, J. An Empirical Model for Fabric Hand: Part I: Objective Assessment of Light Weight Fabrics. Text. Res. J. 1991, 61, 31–38. [Google Scholar] [CrossRef]
- Park, S.W.; Hwang, Y.G.; Kang, B.C.; Yeo, S.W. Total handle evaluation from selected mechanical properties of knitted fabrics using neutral network. Int. J. Cloth. Sci. Technol. 2001, 13, 106–114. [Google Scholar] [CrossRef]
- Raheel, M.; Jiang, L. An Empirical Model for Fabric Hand. Text. Res. J. 1991, 61, 79–82. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).