The Influence of Several Carbon Fiber Architecture on the Drapability Effect
Abstract
1. Introduction
2. Materials and Methods
2.1. Fiber Reinforcements Characteristics
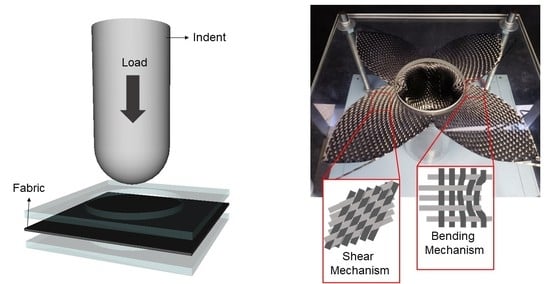
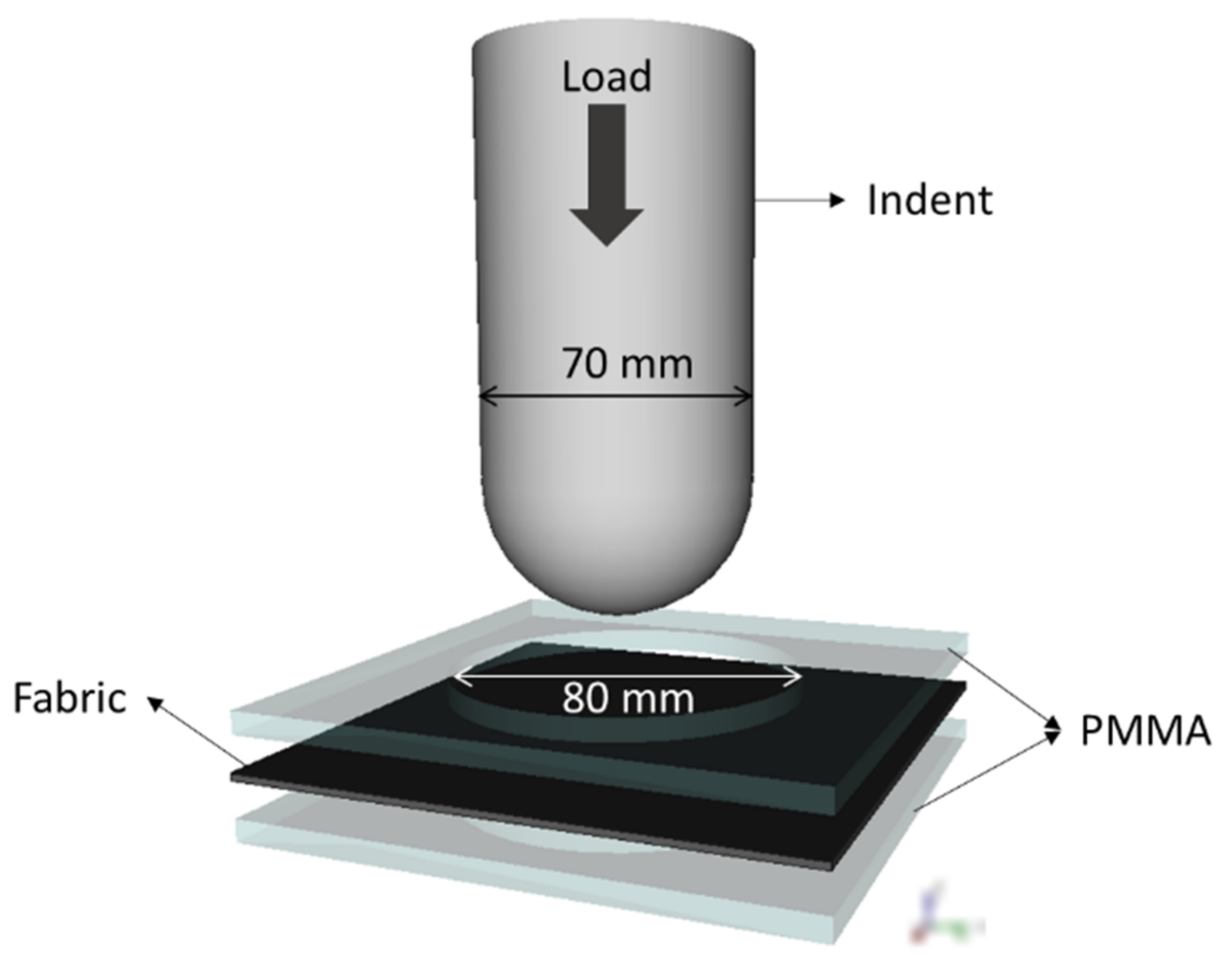
2.2. Experimental Structure
2.3. Optical Microscopy
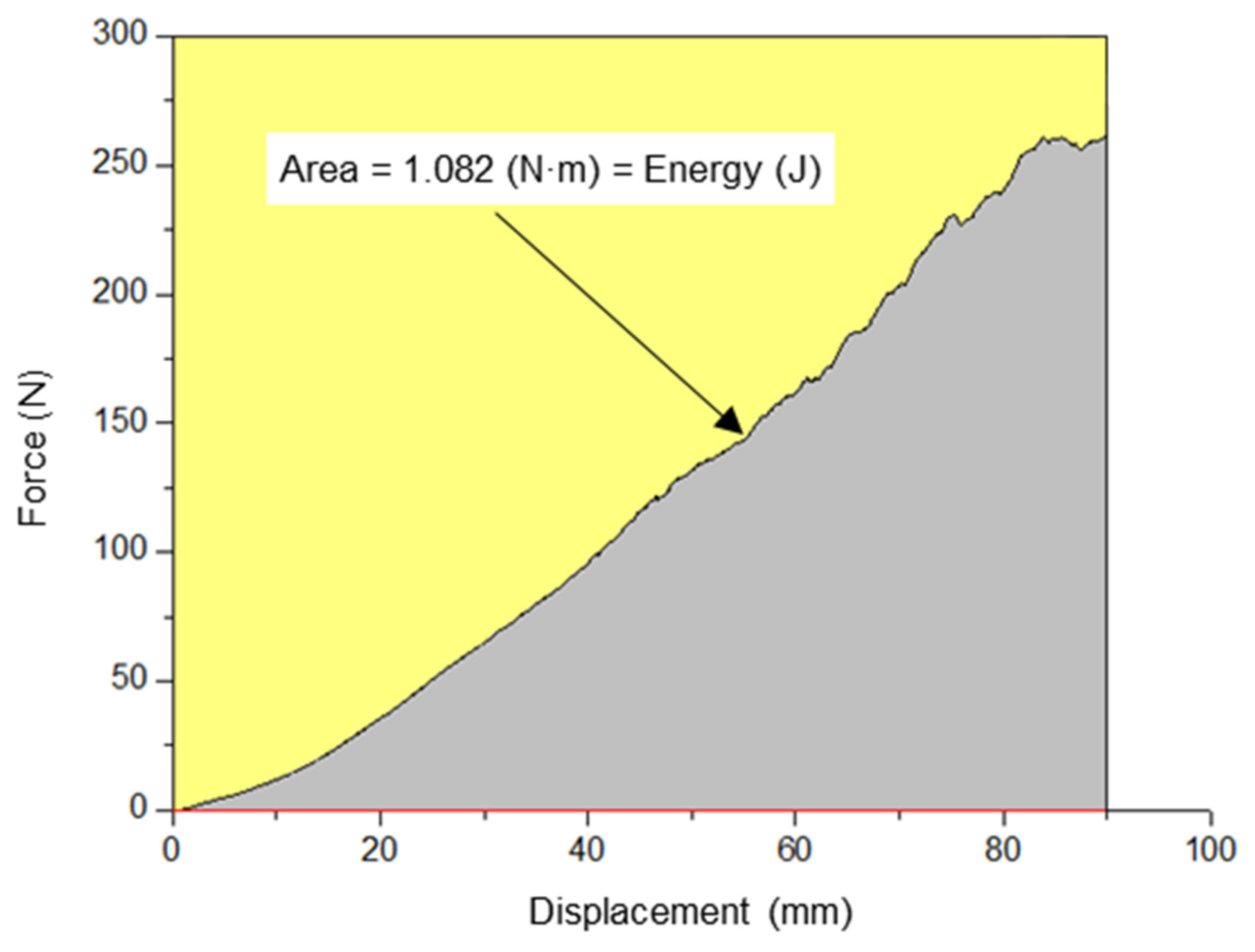
2.4. Deformation Energy Determination
3. Results
3.1. Drapability: Qualitative Analysis
3.2. Drapability: Quantitative Analysis
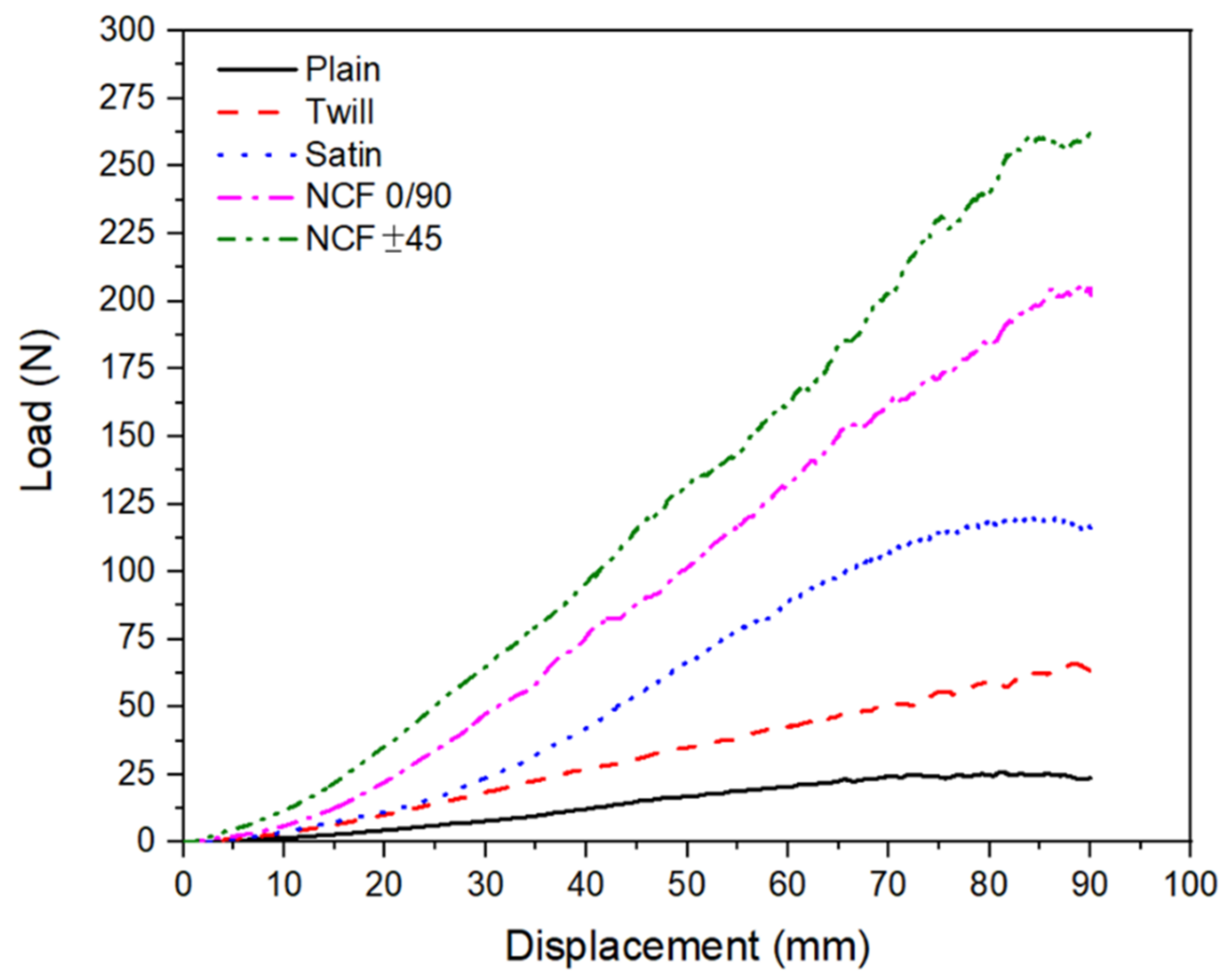
3.3. Drapability Deformation Energy
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Almeida, J.H.S.; Bittrich, L.; Jansen, E.; Tita, V.; Spickenheuer, A. Buckling optimization of composite cylinders for axial compression: A design methodology considering a variable-axial fiber layout. Compos. Struct. 2019, 222, 110928. [Google Scholar] [CrossRef]
- Almeida, J.H.S.; Angrizani, C.C.; Botelho, E.C.; Amico, S.C. Effect of fiber orientation on the shear behavior of glass fiber/epoxy composites. Mater. Des. 2015, 65, 789–795. [Google Scholar] [CrossRef]
- Potluri, R.; Dheeraj, R.S.; Vital, G.V.V.N. Effect of stacking sequence on the mechanical & thermal properties of hybrid laminates. Mater. Today Proc. 2018, 5, 5876–5885. [Google Scholar] [CrossRef]
- Monticeli, F.M.; Almeida, J.H.S.A., Jr.; Neves, R.M.; Ornaghi, F.G.; Ornaghi, H.L. On the 3D void formation of hybrid carbon/glass fiber composite laminates: A statistical approach. Compos. Part A Appl. Sci. Manuf. 2020, 137, 106036. [Google Scholar] [CrossRef]
- Kim, H.J.; Kim, H.S.; Lee, G.Y.; Kim, M.S.; Min, S.H.; Keller, R.; Ihn, J.B.; Ahn, S.H. Three-dimensional carbon fiber composite printer for CFRP repair. Compos. Part B Eng. 2019, 174, 106945. [Google Scholar] [CrossRef]
- Härter, F.V.; Souza, J.A.; Isoldi, L.A.; Santos, E.D.D.; Amico, S.C. Transverse permeability determination and influence in resin flow through an orthotropic medium in the RTM process. Rev. Mater. 2017, 22, e-11851. [Google Scholar] [CrossRef]
- Ashir, M.; Hahn, L.; Kluge, A.; Nocke, A.; Cherif, C. Development of innovative adaptive 3D Fiber Reinforced Plastics based on Shape Memory Alloys. Compos. Sci. Technol. 2016, 126, 43–51. [Google Scholar] [CrossRef]
- Molnár, P.; Ogale, A.; Lahr, R. Mitschang, Influence of drapability by using stitching technology to reduce fabric deformation and shear during thermoforming. Compos. Sci. Technol. 2007, 67, 3386–3393. [Google Scholar] [CrossRef]
- Friedrich, K.; Maier, M.; Neitzel, M. Manufacturing and testing of composite materials and structures. European cooperative research examples. Mech. Compos. Mater. 2000, 36, 429–438. [Google Scholar] [CrossRef]
- Hosseini, M.R.; Taheri-Behrooz, F.; Salamat-talab, M. Mode I interlaminar fracture toughness of woven glass/epoxy composites with mat layers at delamination interface. Polym. Test. 2019, 78, 105943. [Google Scholar] [CrossRef]
- Rozant, O.; Bourban, P.E.; Månson, J.A.E. Drapability of dry textile fabrics for stampable thermoplastic preforms. Compos. Part A Appl. Sci. Manuf. 2000, 31, 1167–1177. [Google Scholar] [CrossRef]
- Omeroglu, S.; Karaca, E.; Becerir, B. Comparison of Bending, Drapability and Crease Recovery Behaviors of Woven Fabrics Produced from Polyester Fibers Having Different Cross-sectional Shapes. Text. Res. J. 2010, 80, 1180–1190. [Google Scholar] [CrossRef]
- Kurita, H.; Suganuma, M.; Wang, Y.; Narita, F. k-Means Clustering for Prediction of Tensile Properties in Carbon Fiber-Reinforced Polymer Composites. Adv. Eng. Mater. 2022, 24, 2101072. [Google Scholar] [CrossRef]
- Shaik, F.; Ramakrishna, M.; Varma, P.D. A review on fabrication of thermoset prepreg composites using out-of-autoclave technology. INCAS Bull. 2021, 13, 133–149. [Google Scholar] [CrossRef]
- Tanaka, K.; Ushiyama, R.; Katayama, T.; Enoki, S.; Sakamoto, H. Formability Evaluation of Carbon Fiber NCF by a Non-Contact 3D Strain Measurement System and the Effects of Blank Folder Force on its Formability. In High Performance and Optimum Design of Structures and Materials; WIT Press: Southampton, UK, 2014; pp. 317–326. [Google Scholar]
- Hesseler, S.; Stapleton, S.E.; Appel, L.; Schöfer, S.; Manin, B. 11—Modeling of Reinforcement Fibers and Textiles. In Advances in Modeling and Simulation in Textile Engineering; Woodhead Publishing: Cambridge, UK, 2021; pp. 267–299. [Google Scholar]
- Malysheva, G.V.; Tumasova, M.S.; Tepishkina, E.S. Evaluation of forming properties of fabrics from carbon, glass, and organic fibers. Polym. Sci. Ser. D 2016, 9, 223–227. [Google Scholar] [CrossRef]
- Mehdikhani, M.; Gorbatikh, L.; Verpoest, I.; Lomov, S.V. Voids in fiber-reinforced polymer composites: A review on their formation, characteristics, and effects on mechanical performance. J. Compos. Mater. 2019, 53, 1579–1669. [Google Scholar] [CrossRef]
- Windhammer, A.; Wuchner, R.; Bletzinger, K.-U. Drape Simulation for Non-Developable Multi-Layered CFRP Structures Focusing on Optimized Cutting Patterns. In Proceedings of the European Congress on Computational Methods in Applied Sciences and Engineering, ECCOMAS 2012, Vienna, Austria, 10–14 September 2012. [Google Scholar]
- Yang, L.; Kim, K.O.; Takatera, M. Measurement of local shear deformation in fabric drape using three-dimensional scanning. Text. Res. J. 2021, 91, 885–898. [Google Scholar] [CrossRef]
- Pil, L.; Bensadoun, F.; Pariset, J.; Verpoest, I. Why are designers fascinated by flax and hemp fibre composites? Compos. Part A Appl. Sci. Manuf. 2016, 83, 193–205. [Google Scholar] [CrossRef]
- Allaoui, S.; Boisse, P.; Chatel, S.; Hamila, N.; Hivet, G.; Soulat, D.; Vidal-salle, E. Experimental and numerical analyses of textile reinforcement forming of a tetrahedral shape. Compos. Part A 2011, 42, 612–622. [Google Scholar] [CrossRef]
- Ahmad, F.; Yuvaraj, N.; Bajpai, P.K. Effect of reinforcement architecture on the macroscopic mechanical properties of fiberous polymer composites: A review. Polym. Compos. 2020, 41, 2518–2534. [Google Scholar] [CrossRef]
- Huang, Z.; Ma, W.; Jia, C.; Lei, X.; Zhang, Z. A deformation model and draping behavior analysis of plain weave fabric with low-twist yarn on continuous surface. Mater. Res. Express. 2022, 9, 055303. [Google Scholar] [CrossRef]
- Rath, J.-E.; Schwieger, L.-S.; Schüppstuhl, T. Robotic Die-Less Forming Strategy for Fiber-Reinforced Plastic Composites Production. Procedia CIRP 2022, 107, 1281–1286. [Google Scholar] [CrossRef]
- Bai, R.; Chen, B.; Colmars, J.; Boisse, P. Physics-based evaluation of the drapability of textile composite reinforcements. Compos. Part B 2022, 242, 110089. [Google Scholar] [CrossRef]
- ATaieb, H.; Mshali, S.; Sakli, F. Predicting fabric drapability property by using an artificial neural network. J. Eng. Fiber. Fabr. 2018, 13, 87–93. [Google Scholar] [CrossRef]
- Hubner, M.; Diestel, O.; Sennewald, C.; Gereke, T.; Cherif, C. Simulation of the Drapability of Textile Semi-Finished Products with Gradient-Drapability Characteristics by Varying the Fabric Weave. Fibres Text. East. Eur. 2011, 20, 88–93. [Google Scholar]
- Hineno, S.; Yoneyama, T.; Tatsuno, D.; Kimura, M. Fiber deformation behavior during press forming of rectangle cup by using plane weave carbon fiber reinforced thermoplastic sheet. Procedia Eng. 2014, 81, 1614–1619. [Google Scholar] [CrossRef]
- Kondratiev, A.; Haidachuck, O.; Tsaritsynskyi, A. Research of Safe Technology of Impregnation of Heated Reinforcing Materials with Binder. Mater. Sci. Forum 2021, 1038, 119–128. [Google Scholar] [CrossRef]
- Tan, J.; Jiang, G.; Gao, Z.; Ma, P.; Zheng, P. Development and mechanical properties of three-dimensional flat-knitted fabrics with reinforcement yarns. J. Ind. Text. 2022, 51, 2071–2088. [Google Scholar] [CrossRef]
- Hassan, M.H. A mini review on manufacturing defects and performance assessments of complex shape prepreg-based composites. Int. J. Adv. Manuf. Technol. 2021, 115, 3393–3408. [Google Scholar] [CrossRef]
- Amor, N.; Noman, M.T.; Petru, M. Classification of textile polymer composites: Recent trends and challenges. Polymers 2021, 13, 2592. [Google Scholar] [CrossRef]
- Saboktakin, A. 3D textile preforms and composites for aircraft strcutures: A review. Int. J. Aviat. Aeronaut. Aerosp. 2019, 6, 2. [Google Scholar] [CrossRef]
- Kissinger, C.; Neitzel, M.M. Advanced Materials for RTM-Processing-Characterization and Application of Non Crimp Fabrics (NCF). In Materials for Transportation Technology; Wiley: Hoboken, NJ, USA, 2005; pp. 176–182. [Google Scholar] [CrossRef]
- Uhlig, K.; Bittrich, L.; Spickenheuer, A.; Almeida, J.H.S., Jr. Waviness and fiber volume content analysis in continuous carbon fiber reinforced plastics made by tailored fiber placement. Compos. Struct. 2019, 222, 110910. [Google Scholar] [CrossRef]
- Van de Werken, n.; Tekinalp, H.; Khanbolouki, P.; Ozcan, S.; Williams, A.; Tehrani, M. Additively manufactured carbon fiber-reinforced composites: State of the art and perspective. Addit. Manuf. 2020, 31, 100962. [Google Scholar] [CrossRef]
- Kim, D.J.; Yu, M.H.; Lim, J.; Nam, B.; Kim, H.S. Prediction of the mechanical behavior of fiber-reinforced composite structure considering its shear angle distribution generated during thermo-compression molding process. Compos. Struct. 2019, 220, 441–450. [Google Scholar] [CrossRef]
- Bodaghi, M.; Cristóvão, C.; Gomes, R.; Correia, N.C. Experimental characterization of voids in high fibre volume fraction composites processed by high injection pressure RTM. Compos. Part A Appl. Sci. Manuf. 2016, 82, 88–99. [Google Scholar] [CrossRef]
- Yokozeki, T.; Ogasawara, T.; Ishikawa, T. Effects of fiber nonlinear properties on the compressive strength prediction of unidirectional carbon-fiber composites. Compos. Sci. Technol. 2005, 65, 2140–2147. [Google Scholar] [CrossRef]
- Yurgartis, S.W. Measurement of small angle fiber misalignments in continuous fiber composites. Compos. Sci. Technol. 1987, 30, 279–293. [Google Scholar] [CrossRef]
- Li, Y.; Stier, B.; Bednarcyk, B.; Simon, J.W.; Reese, S. The effect of fiber misalignment on the homogenized properties of unidirectional fiber reinforced composites. Mech. Mater. 2016, 92, 261–274. [Google Scholar] [CrossRef]
- Joshuva, A.; Sugumaran, V. A study of various blade fault conditions on a wind turbine using vibration signals through histogram features. J. Eng. Sci. Technol. 2018, 13, 102–121. [Google Scholar]
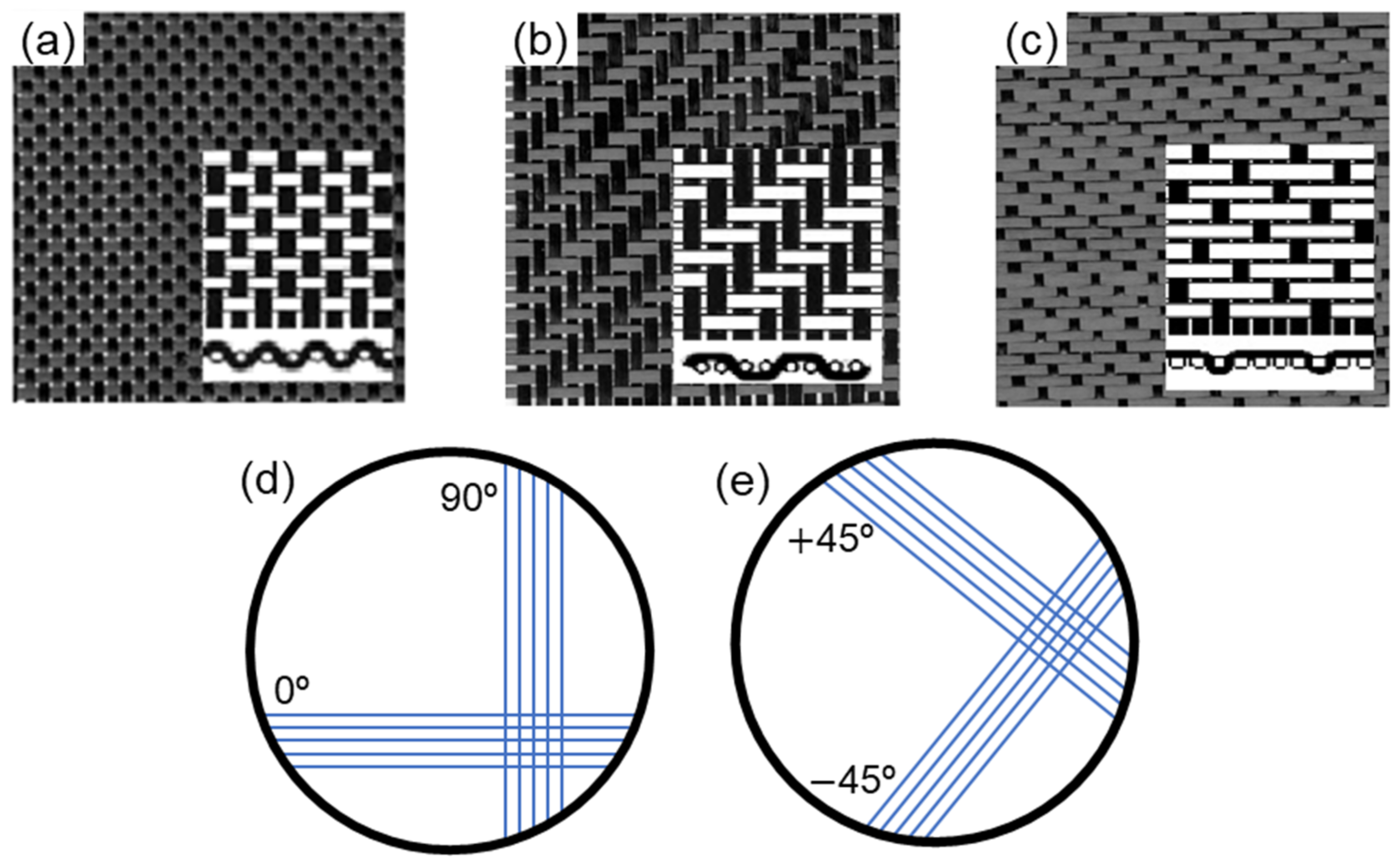




| Fabric | Architecture | Fibers | Height (mm) | Dimension (mm) |
|---|---|---|---|---|
| Plain | 1 × 1 | IM7 GP | 0.31 | 250 × 250 |
| Twill | 2 × 2 | IM7 GP | 0.30 | 250 × 250 |
| Satin | 4 × 1 | IM7 GP | 0.32 | 250 × 250 |
| NCF | Biaxial (0/90) | IM7 5131 | 0.57 | 250 × 250 |
| NCF | Biaxial (±45) | IM7 5131 | 0.48 | 250 × 250 |
| Warp/Weft Space (mm) | Before | After | Average Difference (%) | ||
|---|---|---|---|---|---|
| X-Axis | Y-Axis | X-Axis | Y-Axis | ||
| Plain | 0.5 ± 0.1 | 0.5 ± 0.1 | 0.6 ± 0.4 | 1.4 ± 0.5 | 88.6 ↑ |
| Twill | 0.5 ± 0.2 | 0.3 ± 0.1 | 0.7 ± 0.3 | 0.5 ± 0.2 | 32.5 ↑ |
| Satin | 0.2 ± 0.1 | 0.2 ± 0.1 | 0.3 ± 0.2 | 0.3 ± 0.2 | 0.1 ↑ |
| NCF 0/90 | 5.9 ± 0.6 | 1.7 ± 0.3 | 5.8 ± 0.7 | 1.2 ± 0.2 | 8.0 ↓ |
| NCF ± 45 | 4.8 ± 0.1 | 1.8 ± 0.1 | 4.6 ± 0.2 | 1.2 ± 0.4 | 18.7 ↓ |
| Warp/Weft Angle (°) | Before | After | Difference (%) |
|---|---|---|---|
| Plain | 90.0 | 56.1 | 37.7 |
| Twill | 90.0 | 80.5 | 10.6 |
| Satin | 90.0 | 84.5 | 5.5 |
| NCF 0/90 | 90.0 | 79.4 | 11.8 |
| NCF ± 45 | 90.0 | 68.8 | 23.6 |
| Energy | Plain | Twill | Satin | NCF 0/90 | NCF ± 45 |
|---|---|---|---|---|---|
| Average | 1.8 | 2.1 | 5.4 | 8.2 | 10.7 |
| a SD | 0.05 | 0.05 | 0.59 | 0.29 | 0.50 |
| Parameter | F | p-Value | Fcritical | PC |
|---|---|---|---|---|
| Deformation (mm) | 582.65 | 6.8 × 10−10 | 4.60 | 39.54 |
| Angle change (%) | 495.43 | 1.0 × 10−2 | 4.45 | 33.62 |
| Energy (J) | 5.95 | 1.0 × 10−2 | 3.84 | 26.84 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chuves, Y.P.; Pitanga, M.; Grether, I.; Cioffi, M.O.; Monticeli, F. The Influence of Several Carbon Fiber Architecture on the Drapability Effect. Textiles 2022, 2, 486-498. https://doi.org/10.3390/textiles2030027
Chuves YP, Pitanga M, Grether I, Cioffi MO, Monticeli F. The Influence of Several Carbon Fiber Architecture on the Drapability Effect. Textiles. 2022; 2(3):486-498. https://doi.org/10.3390/textiles2030027
Chicago/Turabian StyleChuves, Yuri Pereira, Midori Pitanga, Inga Grether, Maria Odila Cioffi, and Francisco Monticeli. 2022. "The Influence of Several Carbon Fiber Architecture on the Drapability Effect" Textiles 2, no. 3: 486-498. https://doi.org/10.3390/textiles2030027
APA StyleChuves, Y. P., Pitanga, M., Grether, I., Cioffi, M. O., & Monticeli, F. (2022). The Influence of Several Carbon Fiber Architecture on the Drapability Effect. Textiles, 2(3), 486-498. https://doi.org/10.3390/textiles2030027