A Review on Tough Soft Composites at Different Length Scales
Abstract
:1. Introduction
2. Fabrication
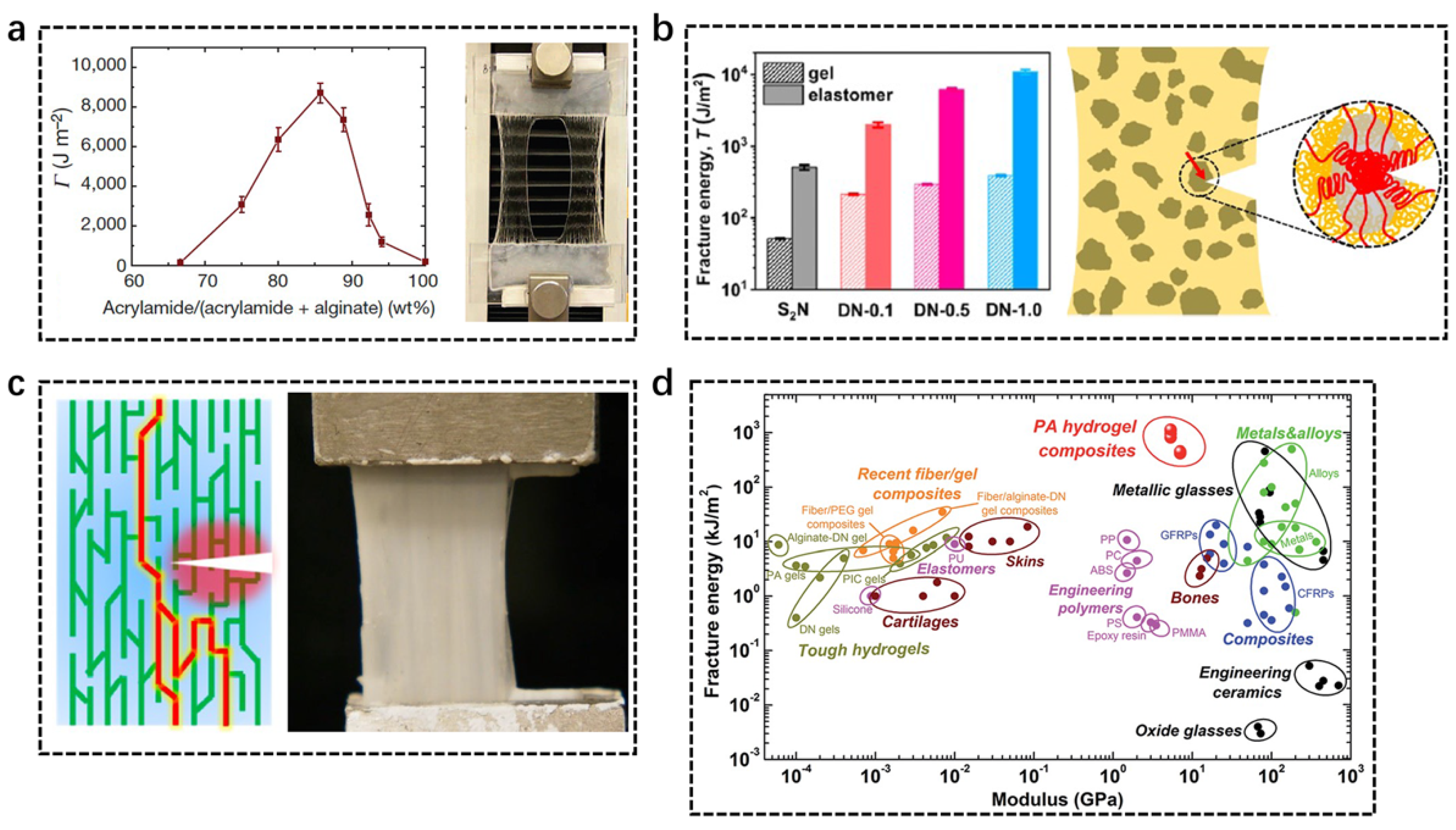
2.1. Double Network
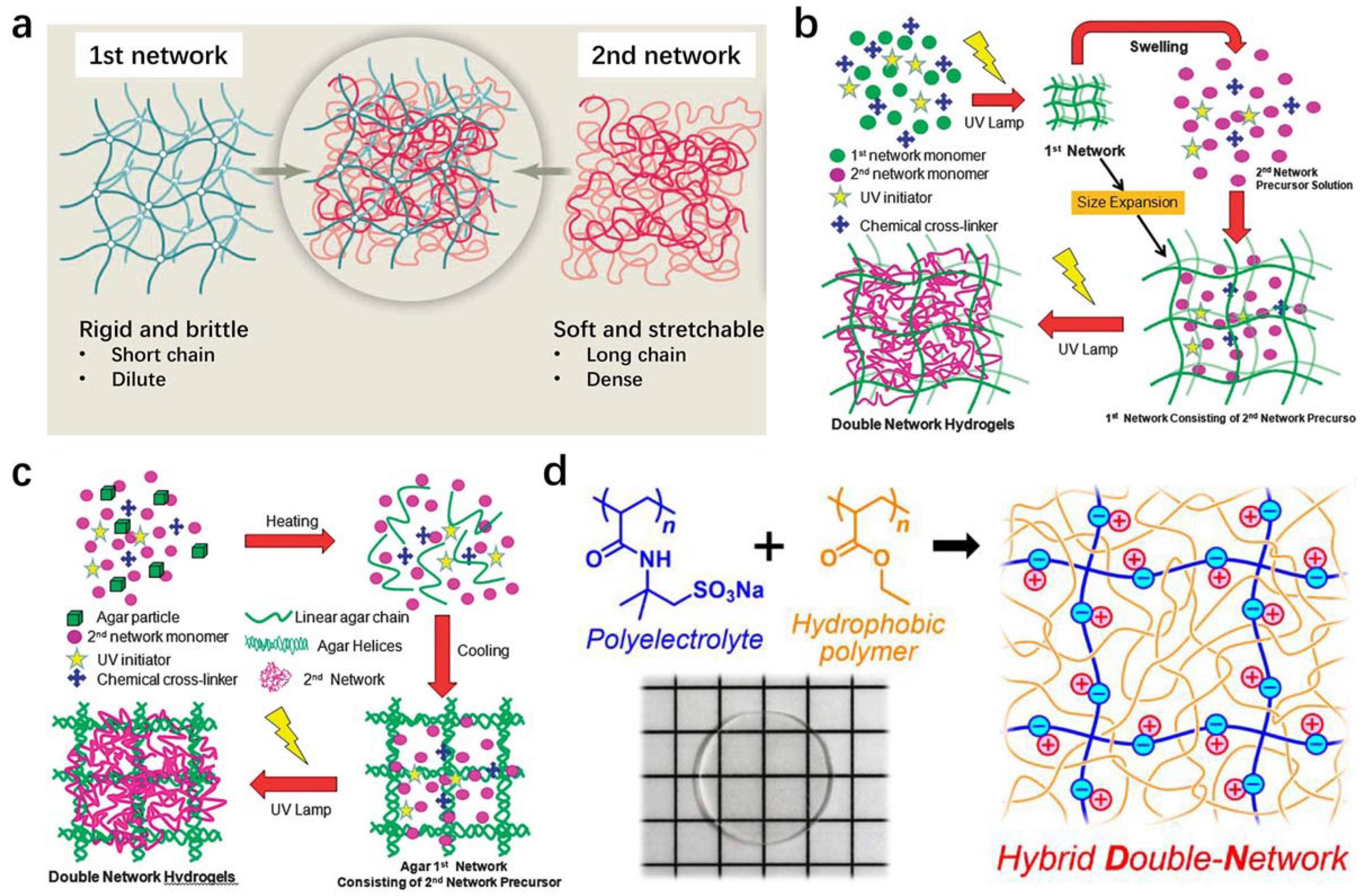
2.2. Phase Separation
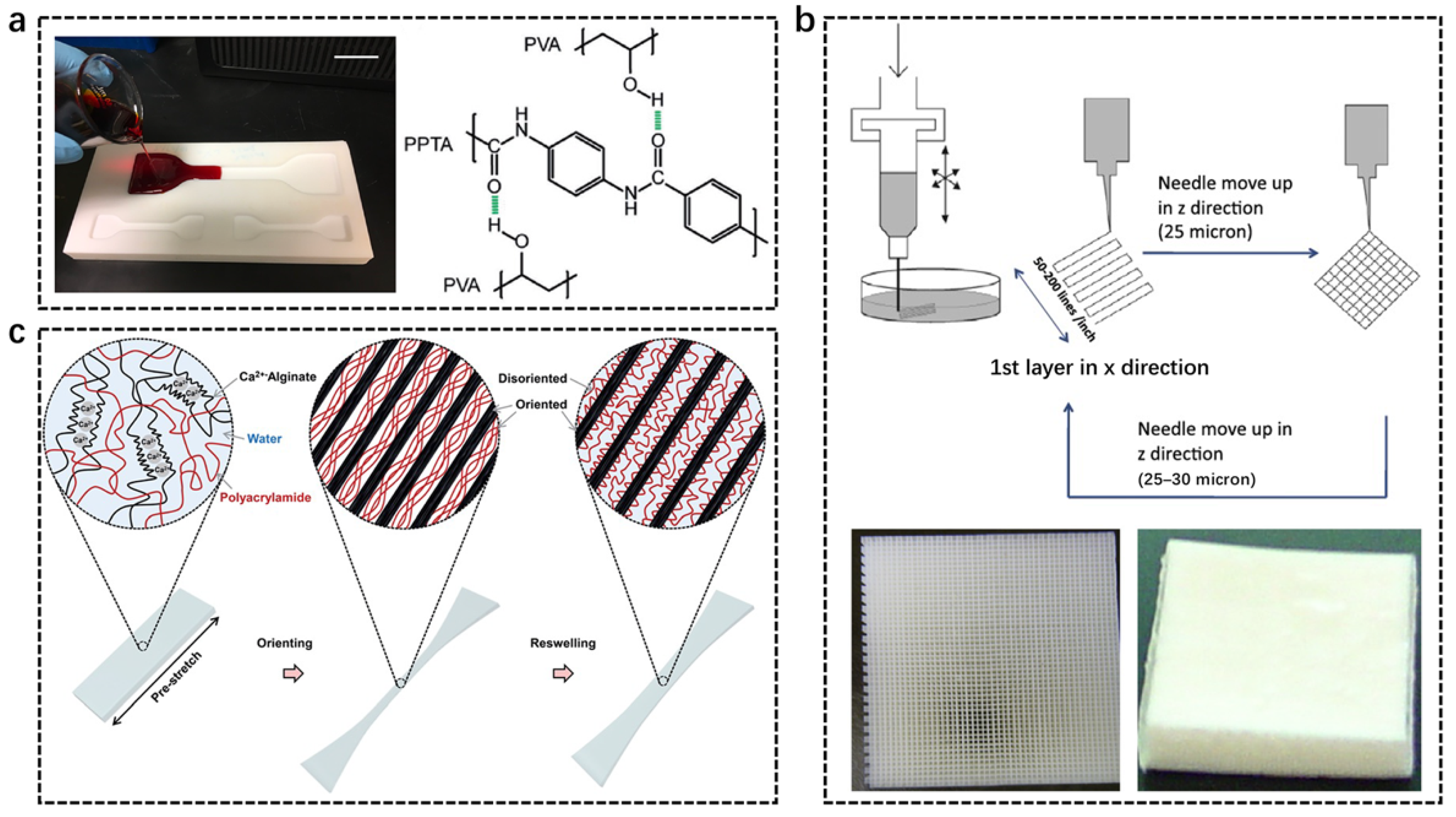
2.3. Microscopic Reinforcement
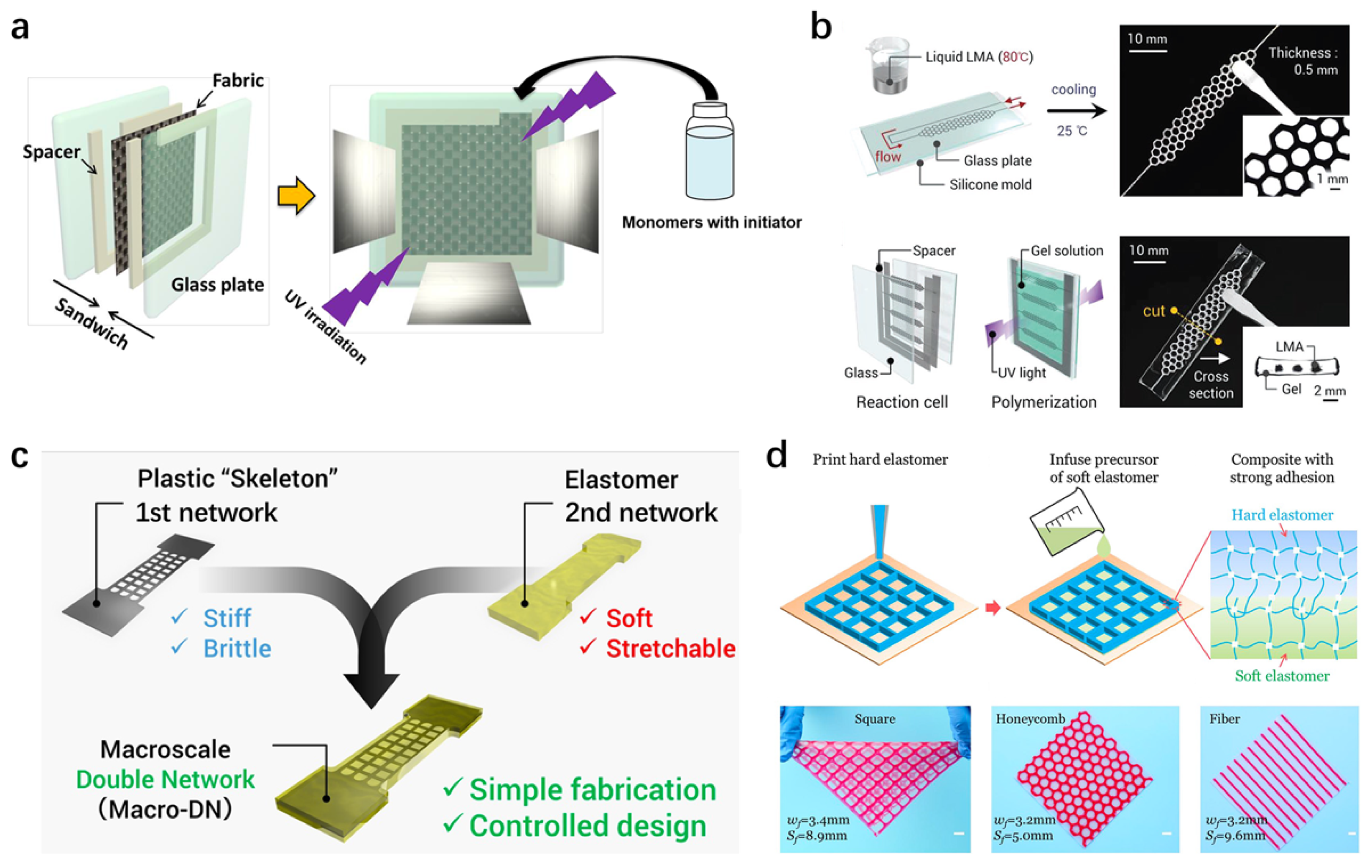
2.4. Macroscopic Reinforcement
3. Mechanical Property
3.1. Tensile Performance

3.2. Fracture Toughness
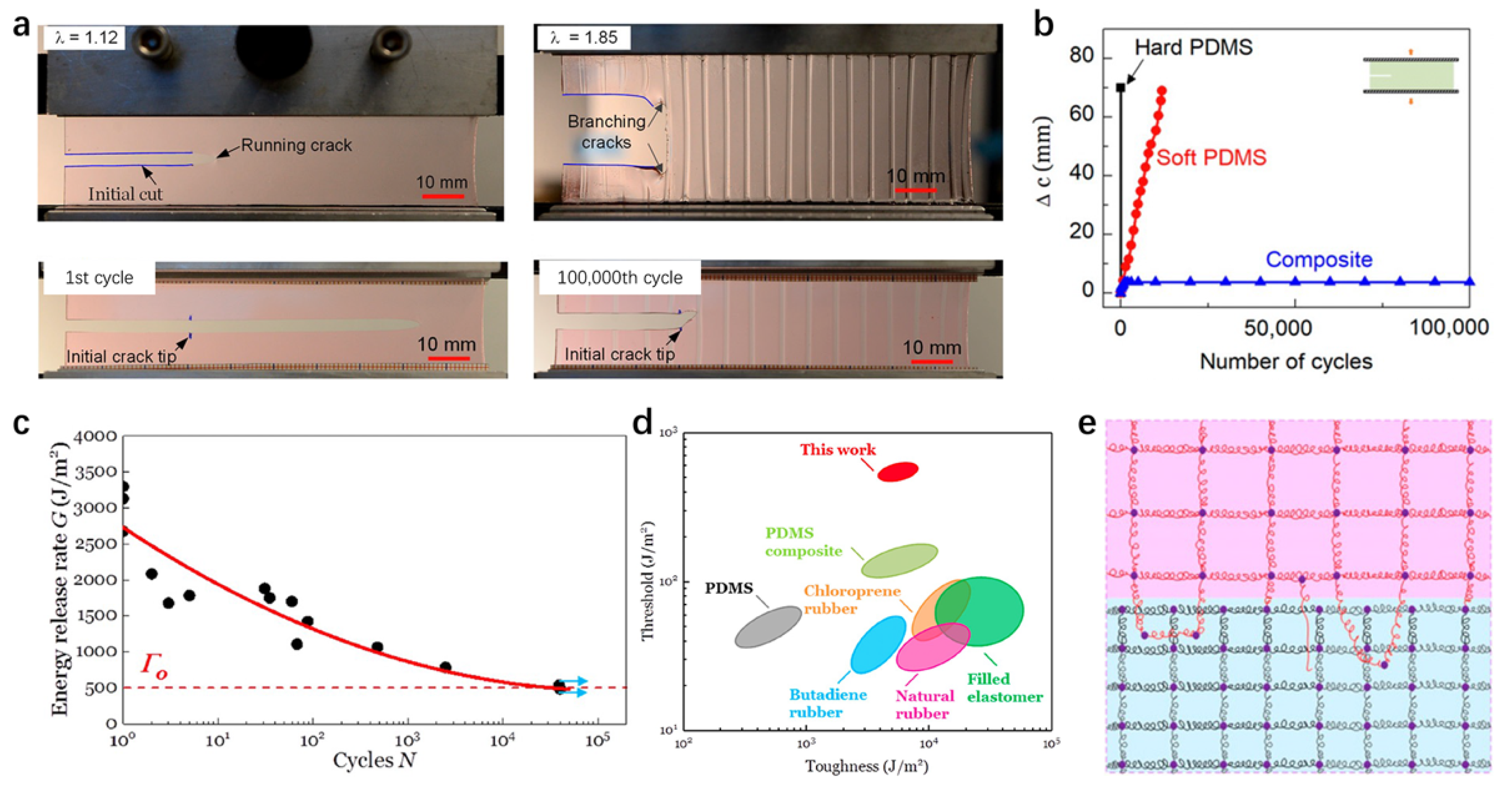
3.3. Fatigue Resistance

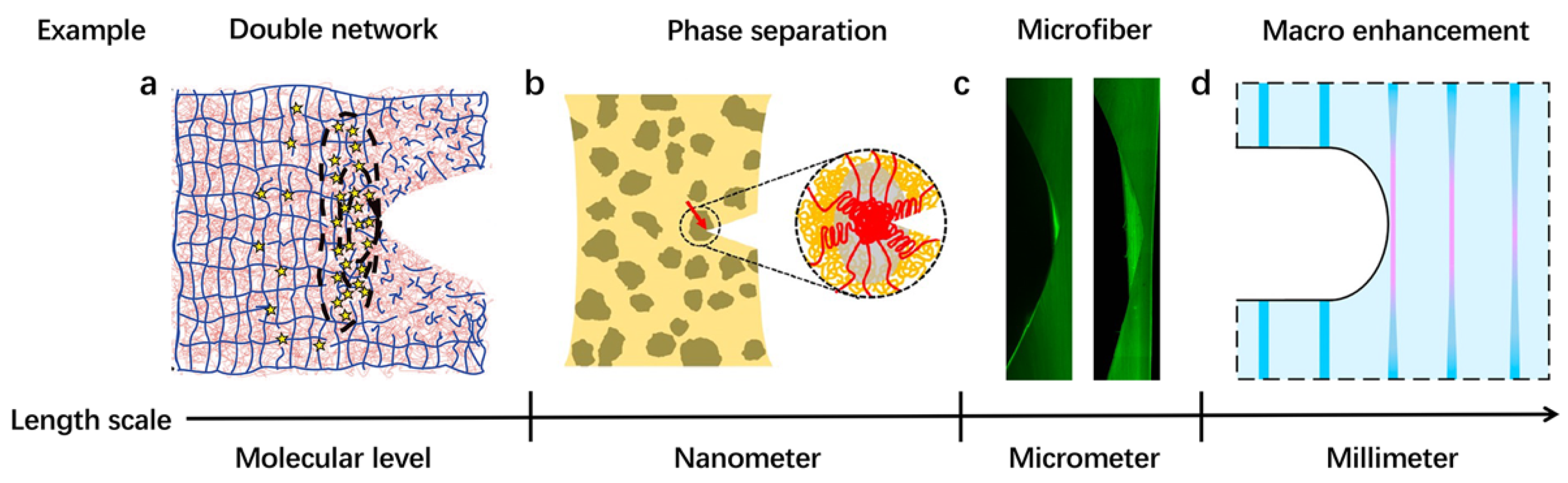
4. Toughening Mechanisms
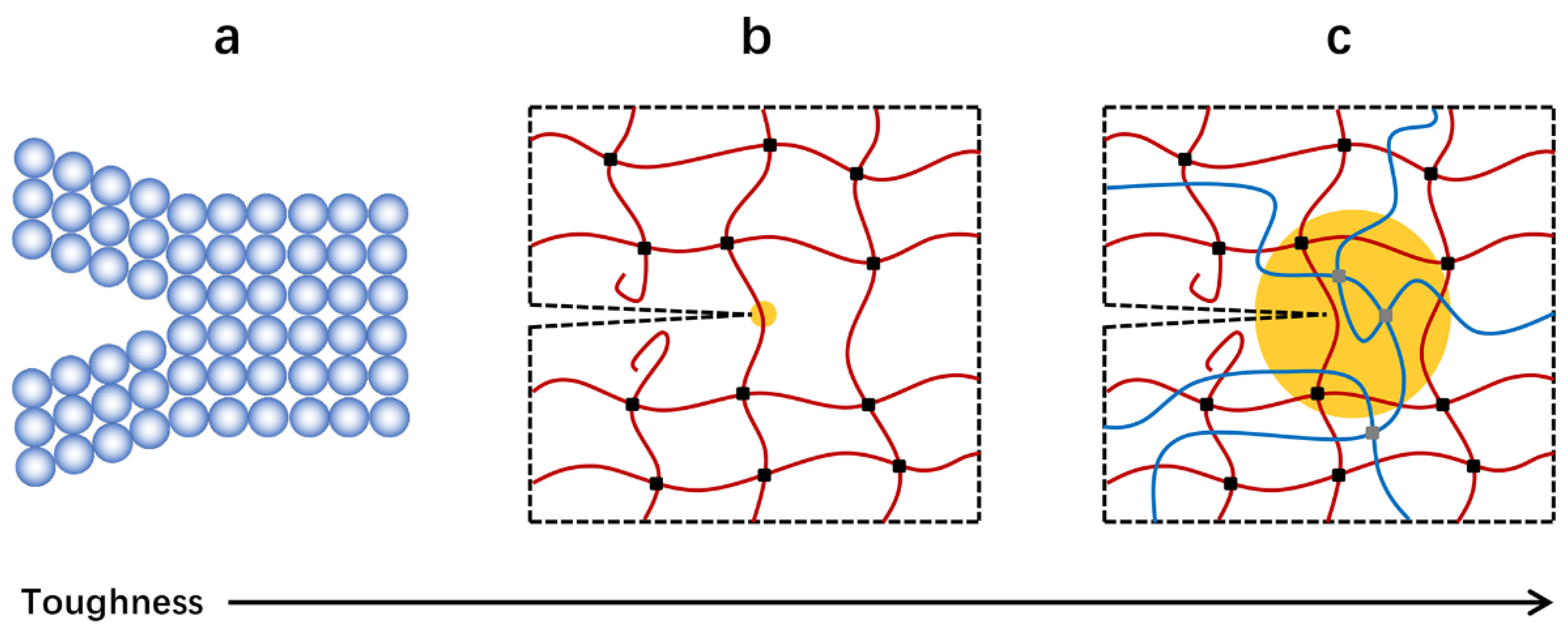
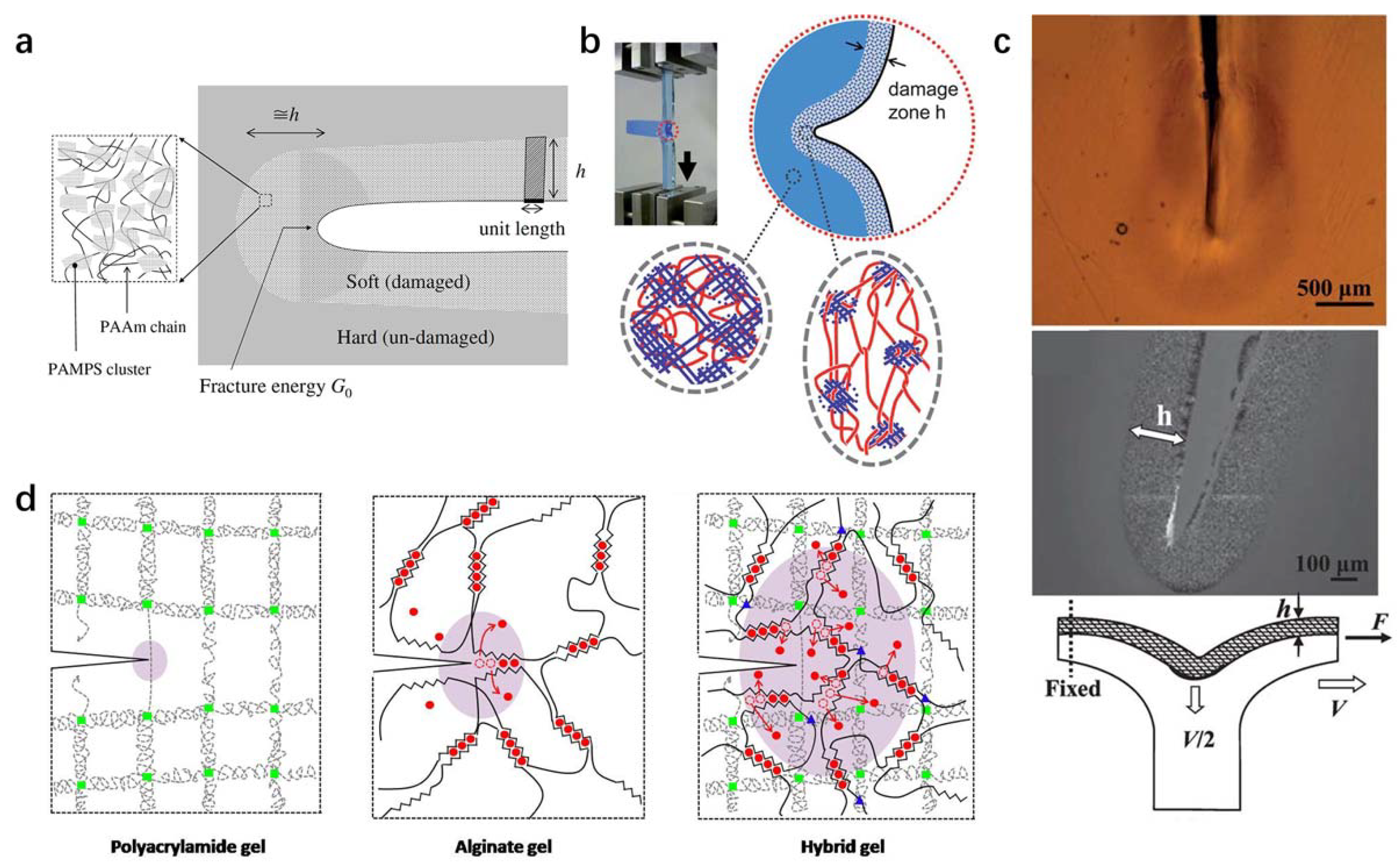
4.1. Molecular Cluster
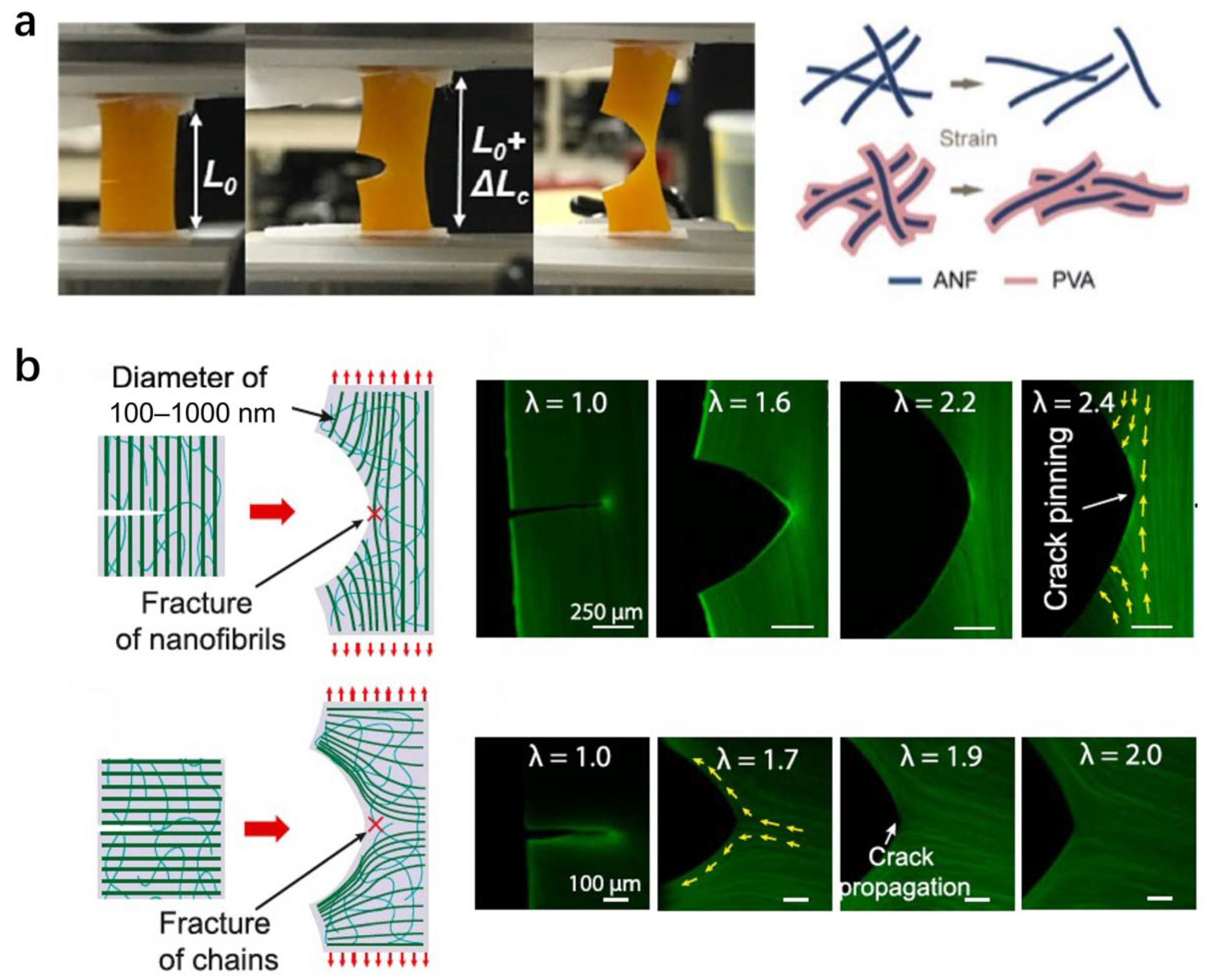
4.2. Nanophse Pinning
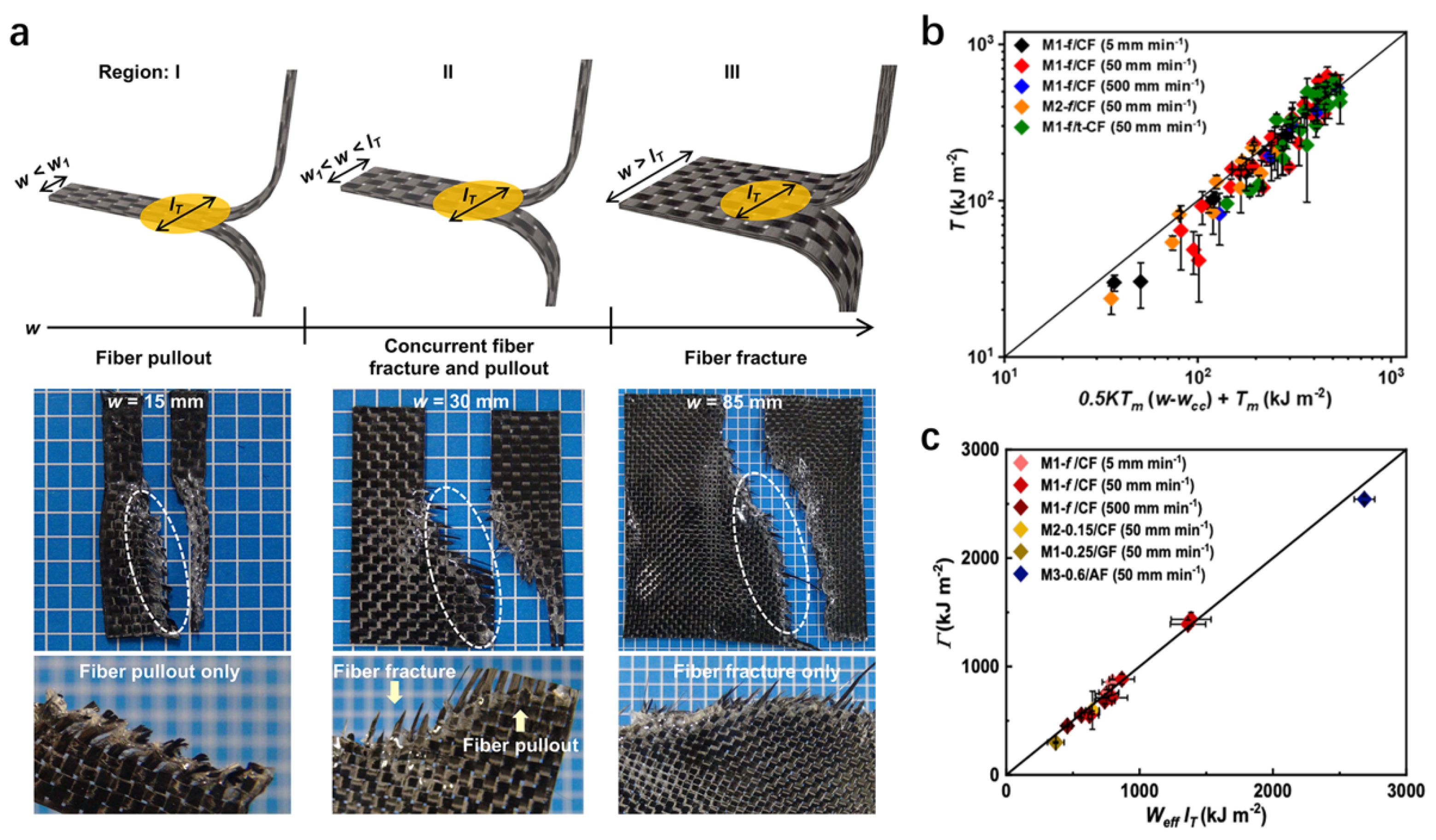
4.3. Microfiber Enhancement
4.4. Macroscale Bulk Dissipation
5. Applications
| Soft Composite | Length Scale for Energy Dissipation | Fracture Stress (MPa) | Fracture Toughness (kJ m−2) | Fatigue Threshold (kJ m−2) | Application | Reference |
|---|---|---|---|---|---|---|
| DN materials | Molecular level | 10−1–100 | 10−1–100 | 10−2 | Tissue engineering, sensors | [21,23,29,44,46,51,81,94,95] |
| Phase-separated materials | Nanometer | 10−1–100 | 100–101 | 10−1 | Adhesives | [31,32,33,52,55,70,86] |
| Microfiber-reinforced gels | Micrometer | 100–101 | 100–102 | 100–101 | Conductor, artificial muscles | [34,37,61,62,64,72,100,103] |
| Macrophase-reinforced composites | Millimeter | 100–102 | 100–103 | 10−1 | Actuators | [12,18,38,39,65,66,67,77,92] |
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Coleman, J.N.; Khan, U.; Blau, W.J.; Gun’ko, Y.K. Small but strong: A review of the mechanical properties of carbon nanotube–polymer composites. Carbon 2006, 44, 1624–1652. [Google Scholar] [CrossRef]
- Akil, H.; Omar, M.; Mazuki, A.M.; Safiee, S.; Ishak, Z.M.; Bakar, A.A. Kenaf fiber reinforced composites: A review. Mater. Des. 2011, 32, 4107–4121. [Google Scholar] [CrossRef]
- Miracle, D. Metal matrix composites–from science to technological significance. Compos. Sci. Technol. 2005, 65, 2526–2540. [Google Scholar] [CrossRef]
- Summerscales, J.; Virk, A.; Hall, W. A review of bast fibres and their composites: Part 3–Modelling. Compos. Part A Appl. Sci. Manuf. 2013, 44, 132–139. [Google Scholar] [CrossRef] [Green Version]
- Ku, H.; Wang, H.; Pattarachaiyakoop, N.; Trada, M. A review on the tensile properties of natural fiber reinforced polymer composites. Compos. Part B Eng. 2011, 42, 856–873. [Google Scholar] [CrossRef] [Green Version]
- Thomas, W. High Strength Glass Fibre-Resin Composites. Nature 1973, 242, 455–456. [Google Scholar] [CrossRef]
- McLoughlin, J. New high temperature carbon fibre composite. Nature 1970, 227, 701. [Google Scholar] [CrossRef] [PubMed]
- Whitesides, G.M. Soft robotics. Angew. Chem. Int. Ed. 2018, 57, 4258–4273. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.A.-C.; Gillen, J.H.; Mishra, S.R.; Evans, B.A.; Tracy, J.B. Photothermally and magnetically controlled reconfiguration of polymer composites for soft robotics. Sci. Adv. 2019, 5, eaaw2897. [Google Scholar] [CrossRef] [Green Version]
- Horne, J.; McLoughlin, L.; Bury, E.; Koh, A.S.; Wujcik, E.K. Interfacial phenomena of advanced composite materials toward wearable platforms for biological and environmental monitoring sensors, armor, and soft robotics. Adv. Mater. Interfaces 2020, 7, 1901851. [Google Scholar] [CrossRef]
- Kim, S.Y.; Choo, Y.; Bilodeau, R.A.; Yuen, M.C.; Kaufman, G.; Shah, D.S.; Osuji, C.O.; Kramer-Bottiglio, R. Sustainable manufacturing of sensors onto soft systems using self-coagulating conductive Pickering emulsions. Sci. Robot. 2020, 5, eaay3604. [Google Scholar] [CrossRef] [PubMed]
- Hubbard, A.M.; Cui, W.; Huang, Y.; Takahashi, R.; Dickey, M.D.; Genzer, J.; King, D.R.; Gong, J.P. Hydrogel/elastomer laminates bonded via fabric interphases for stimuli-responsive actuators. Matter 2019, 1, 674–689. [Google Scholar] [CrossRef] [Green Version]
- Cox, H. The elasticity and strength of paper and other fibrous materials. Br. J. Appl. Phys. 1952, 3, 72. [Google Scholar] [CrossRef]
- Lake, G.; Thomas, A. The strength of highly elastic materials. Proc. Math. Phys. Eng. Sci. 1967, 300, 108–119. [Google Scholar]
- Thomas, A.; Whittle, J. Tensile rupture of rubber. Rubber Chem. Technol. 1970, 43, 222–228. [Google Scholar] [CrossRef]
- Hui, C.-Y.; Liu, Z.; Phoenix, S.L.; King, D.R.; Cui, W.; Huang, Y.; Gong, J.P. Mechanical behavior of unidirectional fiber reinforced soft composites. Extrem. Mech. Lett. 2020, 35, 100642. [Google Scholar] [CrossRef]
- Volokh, K.; Trapper, P. Fracture toughness from the standpoint of softening hyperelasticity. J. Mech. Phys. Solids 2008, 56, 2459–2472. [Google Scholar] [CrossRef]
- Cui, W.; King, D.R.; Huang, Y.; Chen, L.; Sun, T.L.; Guo, Y.; Saruwatari, Y.; Hui, C.Y.; Kurokawa, T.; Gong, J.P. Fiber-reinforced viscoelastomers show extraordinary crack resistance that exceeds metals. Adv. Mater. 2020, 32, 1907180. [Google Scholar] [CrossRef]
- Sih, G.; Liebowitz, H. On the Griffith energy criterion for brittle fracture. Int. J. Solids Struct. 1967, 3, 1–22. [Google Scholar] [CrossRef]
- Greensmith, H. Rupture of rubber. XI. Tensile rupture and crack growth in a noncrystallizing rubber. J. Appl. Polym. Sci. 1964, 8, 1113–1128. [Google Scholar] [CrossRef]
- Gong, J.P. Why are double network hydrogels so tough? Soft Matter 2010, 6, 2583–2590. [Google Scholar] [CrossRef]
- Gong, J.P.; Katsuyama, Y.; Kurokawa, T.; Osada, Y. Double-network hydrogels with extremely high mechanical strength. Adv. Mater. 2003, 15, 1155–1158. [Google Scholar] [CrossRef]
- Sun, J.-Y.; Zhao, X.; Illeperuma, W.R.; Chaudhuri, O.; Oh, K.H.; Mooney, D.J.; Vlassak, J.J.; Suo, Z. Highly stretchable and tough hydrogels. Nature 2012, 489, 133–136. [Google Scholar] [CrossRef] [PubMed]
- Davey, C.L.; Gilbert, K. Tensile strength and the tenderness of beef sternomandibularis muscle. Meat Sci. 1977, 1, 49–61. [Google Scholar] [CrossRef]
- Kuthe, C.D.; Uddanwadiker, R.; Ramteke, A. Experimental evaluation of fiber orientation based material properties of skeletal muscle in tension. Mol. Cell. Biomech. 2014, 11, 113. [Google Scholar]
- Bennett1, M.; Ker1, R.; Imery, N.J.; Alexander1, R.M. Mechanical properties of various mammalian tendons. J. Zool. 1986, 209, 537–548. [Google Scholar] [CrossRef]
- Yang, W.; Sherman, V.R.; Gludovatz, B.; Schaible, E.; Stewart, P.; Ritchie, R.O.; Meyers, M.A. On the tear resistance of skin. Nat. Commun. 2015, 6, 1–10. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhao, X.; Chen, X.; Yuk, H.; Lin, S.; Liu, X.; Parada, G. Soft Materials by Design: Unconventional Polymer Networks Give Extreme Properties. Chem. Rev. 2021, 121, 4309–4372. [Google Scholar] [CrossRef]
- Ducrot, E.; Chen, Y.; Bulters, M.; Sijbesma, R.P.; Creton, C. Toughening elastomers with sacrificial bonds and watching them break. Science 2014, 344, 186–189. [Google Scholar] [CrossRef]
- Brown, H.R. A model of the fracture of double network gels. Macromolecules 2007, 40, 3815–3818. [Google Scholar] [CrossRef]
- Zheng, Y.; Kiyama, R.; Matsuda, T.; Cui, K.; Li, X.; Cui, W.; Guo, Y.; Nakajima, T.; Kurokawa, T.; Gong, J.P. Nanophase Separation in Immiscible Double Network Elastomers Induces Synergetic Strengthening, Toughening, and Fatigue Resistance. Chem. Mater. 2021, 33, 3321–3334. [Google Scholar] [CrossRef]
- Sun, T.L.; Kurokawa, T.; Kuroda, S.; Ihsan, A.B.; Akasaki, T.; Sato, K.; Haque, M.A.; Nakajima, T.; Gong, J.P. Physical hydrogels composed of polyampholytes demonstrate high toughness and viscoelasticity. Nat. Mater. 2013, 12, 932–937. [Google Scholar] [CrossRef] [Green Version]
- Cui, K.; Sun, T.L.; Liang, X.; Nakajima, K.; Ye, Y.N.; Chen, L.; Kurokawa, T.; Gong, J.P. Multiscale energy dissipation mechanism in tough and self-healing hydrogels. Phys. Rev. Lett. 2018, 121, 185501. [Google Scholar] [CrossRef]
- Hua, M.; Wu, S.; Ma, Y.; Zhao, Y.; Chen, Z.; Frenkel, I.; Strzalka, J.; Zhou, H.; Zhu, X.; He, X. Strong tough hydrogels via the synergy of freeze-casting and salting out. Nature 2021, 590, 594–599. [Google Scholar] [CrossRef] [PubMed]
- Guo, Y.Z.; Nakajima, T.; Mredha, M.T.I.; Guo, H.L.; Cui, K.; Zheng, Y.; Cui, W.; Kurokawa, T.; Gong, J.P. Facile preparation of cellulose hydrogel with Achilles tendon-like super strength through aligning hierarchical fibrous structure. Chem. Eng. J. 2022, 428, 132040. [Google Scholar] [CrossRef]
- Liu, R.; Xu, X.; Zhuang, X.; Cheng, B. Solution blowing of chitosan/PVA hydrogel nanofiber mats. Carbohydr. Polym. 2014, 101, 1116–1121. [Google Scholar] [CrossRef]
- Lin, S.; Liu, J.; Liu, X.; Zhao, X. Muscle-like fatigue-resistant hydrogels by mechanical training. Proc. Natl. Acad. Sci. USA 2019, 116, 10244–10249. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z.; Xiang, C.; Yao, X.; Le Floch, P.; Mendez, J.; Suo, Z. Stretchable materials of high toughness and low hysteresis. Proc. Natl. Acad. Sci. USA 2019, 116, 5967–5972. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- King, D.R.; Sun, T.L.; Huang, Y.; Kurokawa, T.; Nonoyama, T.; Crosby, A.J.; Gong, J.P. Extremely tough composites from fabric reinforced polyampholyte hydrogels. Mater. Horiz. 2015, 2, 584–591. [Google Scholar] [CrossRef] [Green Version]
- Huang, Y.; King, D.R.; Sun, T.L.; Nonoyama, T.; Kurokawa, T.; Nakajima, T.; Gong, J.P. Energy-dissipative matrices enable synergistic toughening in fiber reinforced soft composites. Adv. Funct. Mater. 2017, 27, 1605350. [Google Scholar] [CrossRef] [Green Version]
- Cantwell, W.J.; Morton, J. The impact resistance of composite materials—a review. Composites 1991, 22, 347–362. [Google Scholar] [CrossRef]
- De Zanet, A.; Casalegno, V.; Salvo, M. Laser surface texturing of ceramics and ceramic composite materials–A review. Ceram. Int. 2021, 47, 7307–7320. [Google Scholar] [CrossRef]
- Yu, X.; Manthiram, A. A review of composite polymer-ceramic electrolytes for lithium batteries. Energy Stor. Mater. 2021, 34, 282–300. [Google Scholar] [CrossRef]
- Gong, J.P. Materials both tough and soft. Science 2014, 344, 161–162. [Google Scholar] [CrossRef]
- Chen, Q.; Chen, H.; Zhu, L.; Zheng, J. Engineering of tough double network hydrogels. Macromol. Chem. Phys. 2016, 217, 1022–1036. [Google Scholar] [CrossRef]
- Chen, Q.; Chen, H.; Zhu, L.; Zheng, J. Fundamentals of double network hydrogels. J. Mater. Chem. B 2015, 3, 3654–3676. [Google Scholar] [CrossRef]
- Zhang, H.J.; Sun, T.L.; Zhang, A.K.; Ikura, Y.; Nakajima, T.; Nonoyama, T.; Kurokawa, T.; Ito, O.; Ishitobi, H.; Gong, J.P. Tough physical double-network hydrogels based on amphiphilic triblock copolymers. Adv. Mater. 2016, 28, 4884–4890. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Murai, J.; Nakajima, T.; Matsuda, T.; Tsunoda, K.; Nonoyama, T.; Kurokawa, T.; Gong, J.P. Tough double network elastomers reinforced by the amorphous cellulose network. Polymer 2019, 178, 121686. [Google Scholar] [CrossRef]
- Nakajima, T.; Ozaki, Y.; Namba, R.; Ota, K.; Maida, Y.; Matsuda, T.; Kurokawa, T.; Gong, J.P. Tough double-network gels and elastomers from the nonprestretched first network. ACS Macro Lett. 2019, 8, 1407–1412. [Google Scholar] [CrossRef]
- Wang, W.; Zhang, Z.; Davris, T.; Liu, J.; Gao, Y.; Zhang, L.; Lyulin, A.V. Simulational insights into the mechanical response of prestretched double network filled elastomers. Soft Matter 2017, 13, 8597–8608. [Google Scholar] [CrossRef] [Green Version]
- Matsuda, T.; Nakajima, T.; Gong, J.P. Fabrication of tough and stretchable hybrid double-network elastomers using ionic dissociation of polyelectrolyte in nonaqueous media. Chem. Mater. 2019, 31, 3766–3776. [Google Scholar] [CrossRef]
- Cui, K.; Ye, Y.N.; Sun, T.L.; Yu, C.; Li, X.; Kurokawa, T.; Gong, J.P. Phase separation behavior in tough and self-healing polyampholyte hydrogels. Macromolecules 2020, 53, 5116–5126. [Google Scholar] [CrossRef]
- Durmaz, S.; Okay, O. Phase separation during the formation of poly (acrylamide) hydrogels. Polymer 2000, 41, 5729–5735. [Google Scholar] [CrossRef]
- Broguiere, N.; Husch, A.; Palazzolo, G.; Bradke, F.; Madduri, S.; Zenobi-Wong, M. Macroporous hydrogels derived from aqueous dynamic phase separation. Biomaterials 2019, 200, 56–65. [Google Scholar] [CrossRef]
- Cui, W.; Zhu, R.; Zheng, Y.; Mu, Q.; Pi, M.; Chen, Q.; Ran, R. Transforming non-adhesive hydrogels to reversible tough adhesives via mixed-solvent-induced phase separation. J. Mater. Chem. A 2021, 9, 9706–9718. [Google Scholar] [CrossRef]
- Ihsan, A.B.; Sun, T.L.; Kuroda, S.; Haque, M.A.; Kurokawa, T.; Nakajima, T.; Gong, J.P. A phase diagram of neutral polyampholyte–from solution to tough hydrogel. J. Mater. Chem. B 2013, 1, 4555–4562. [Google Scholar] [CrossRef] [PubMed]
- Yodmuang, S.; McNamara, S.L.; Nover, A.B.; Mandal, B.B.; Agarwal, M.; Kelly, T.-A.N.; Chao, P.-h.G.; Hung, C.; Kaplan, D.L.; Vunjak-Novakovic, G. Silk microfiber-reinforced silk hydrogel composites for functional cartilage tissue repair. Acta Biomater. 2015, 11, 27–36. [Google Scholar] [CrossRef] [Green Version]
- Caves, J.M.; Cui, W.; Wen, J.; Kumar, V.A.; Haller, C.A.; Chaikof, E.L. Elastin-like protein matrix reinforced with collagen microfibers for soft tissue repair. Biomaterials 2011, 32, 5371–5379. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Surajarusarn, B.; Hajjar-Garreau, S.; Schrodj, G.; Mougin, K.; Amornsakchai, T. Comparative study of pineapple leaf microfiber and aramid fiber reinforced natural rubbers using dynamic mechanical analysis. Polym. Test. 2020, 82, 106289. [Google Scholar] [CrossRef]
- Caves, J.M.; Kumar, V.A.; Martinez, A.W.; Kim, J.; Ripberger, C.M.; Haller, C.A.; Chaikof, E.L. The use of microfiber composites of elastin-like protein matrix reinforced with synthetic collagen in the design of vascular grafts. Biomaterials 2010, 31, 7175–7182. [Google Scholar] [CrossRef] [Green Version]
- Xu, L.; Zhao, X.; Xu, C.; Kotov, N.A. Water-rich biomimetic composites with abiotic self-organizing nanofiber network. Adv. Mater. 2018, 30, 1703343. [Google Scholar] [CrossRef] [PubMed]
- Agrawal, A.; Rahbar, N.; Calvert, P.D. Strong fiber-reinforced hydrogel. Acta Biomater. 2013, 9, 5313–5318. [Google Scholar] [CrossRef]
- Mredha, M.T.I.; Guo, Y.Z.; Nonoyama, T.; Nakajima, T.; Kurokawa, T.; Gong, J.P. A facile method to fabricate anisotropic hydrogels with perfectly aligned hierarchical fibrous structures. Adv. Mater. 2018, 30, 1704937. [Google Scholar] [CrossRef]
- Cui, W.; Pi, M.; Zhu, R.; Xiong, Z.; Ran, R. Strong anisotropic hydrogels with ion transport capability via reswelling contrast of two oriented polymer networks. J. Mater. Chem. A 2021, 9, 20362–20370. [Google Scholar] [CrossRef]
- Takahashi, R.; Sun, T.L.; Saruwatari, Y.; Kurokawa, T.; King, D.R.; Gong, J.P. Creating Stiff, Tough, and Functional Hydrogel Composites with Low-Melting-Point Alloys. Adv. Mater. 2018, 30, 1706885. [Google Scholar] [CrossRef] [PubMed]
- King, D.R.; Okumura, T.; Takahashi, R.; Kurokawa, T.; Gong, J.P. Macroscale double networks: Design criteria for optimizing strength and toughness. ACS Appl. Mater. Interfaces 2019, 11, 35343–35353. [Google Scholar] [CrossRef]
- Li, C.; Yang, H.; Suo, Z.; Tang, J. Fatigue-resistant elastomers. J. Mech. Phys. Solids 2020, 134, 103751. [Google Scholar] [CrossRef]
- Zhang, G.; Yin, T.; Nian, G.; Suo, Z. Fatigue-resistant polyurethane elastomer composites. Extrem. Mech. Lett. 2021, 48, 101434. [Google Scholar] [CrossRef]
- Cui, W.; Ji, J.; Cai, Y.; Li, H.; Ran, R. Robust, anti-fatigue, and self-healing graphene oxide/hydrophobically associated composite hydrogels and their use as recyclable adsorbents for dye waste water treatment. J. Mater. Chem. A 2015, 3, 17445–17458. [Google Scholar] [CrossRef]
- Cui, W.; Cai, Y.; Zheng, Y.; Ran, R. Mechanical enhancement of hydrophobically associating hydrogels by solvent-regulated phase separation. Polymer 2020, 210, 123042. [Google Scholar] [CrossRef]
- Sato, K.; Nakajima, T.; Hisamatsu, T.; Nonoyama, T.; Kurokawa, T.; Gong, J.P. Phase-separation-induced anomalous stiffening, toughening, and self-healing of polyacrylamide gels. Adv. Mater. 2015, 27, 6990–6998. [Google Scholar] [CrossRef] [Green Version]
- Zhalmuratova, D.; Chung, H.-J. Reinforced gels and elastomers for biomedical and soft robotics applications. ACS Appl. Polym. Mater. 2020, 2, 1073–1091. [Google Scholar] [CrossRef]
- Long, R.; Hui, C.-Y. Fracture toughness of hydrogels: Measurement and interpretation. Soft Matter 2016, 12, 8069–8086. [Google Scholar] [CrossRef] [PubMed]
- Long, R.; Hui, C.-Y.; Gong, J.P.; Bouchbinder, E. The fracture of highly deformable soft materials: A tale of two length scales. Annu. Rev. Condens. Matter Phys. 2021, 12, 71–94. [Google Scholar] [CrossRef]
- Creton, C.; Ciccotti, M. Fracture and adhesion of soft materials: A review. Rep. Prog. Phys. 2016, 79, 046601. [Google Scholar] [CrossRef]
- Zhang, T.; Lin, S.; Yuk, H.; Zhao, X. Predicting fracture energies and crack-tip fields of soft tough materials. Extrem. Mech. Lett. 2015, 4, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Huang, Y.; King, D.R.; Cui, W.; Sun, T.L.; Guo, H.; Kurokawa, T.; Brown, H.R.; Hui, C.-Y.; Gong, J.P. Superior fracture resistance of fiber reinforced polyampholyte hydrogels achieved by extraordinarily large energy-dissipative process zones. J. Mater. Chem. A 2019, 7, 13431–13440. [Google Scholar] [CrossRef]
- Li, Z.; Liu, Z.; Ng, T.Y.; Sharma, P. The effect of water content on the elastic modulus and fracture energy of hydrogel. Extrem. Mech. Lett. 2020, 35, 100617. [Google Scholar] [CrossRef]
- Yang, C.; Yin, T.; Suo, Z. Polyacrylamide hydrogels. I. Network imperfection. J. Mech. Phys. Solids 2019, 131, 43–55. [Google Scholar] [CrossRef]
- Liu, J.; Yang, C.; Yin, T.; Wang, Z.; Qu, S.; Suo, Z. Polyacrylamide hydrogels. II. Elastic dissipater. J. Mech. Phys. Solids 2019, 133, 103737. [Google Scholar] [CrossRef]
- Zhang, W.; Liu, X.; Wang, J.; Tang, J.; Hu, J.; Lu, T.; Suo, Z. Fatigue of double-network hydrogels. Eng. Fract. Mech. 2018, 187, 74–93. [Google Scholar] [CrossRef] [Green Version]
- Hou, J.; Ren, X.; Guan, S.; Duan, L.; Gao, G.H.; Kuai, Y.; Zhang, H. Rapidly recoverable, anti-fatigue, super-tough double-network hydrogels reinforced by macromolecular microspheres. Soft Matter 2017, 13, 1357–1363. [Google Scholar] [CrossRef]
- Chen, Q.; Yan, X.; Zhu, L.; Chen, H.; Jiang, B.; Wei, D.; Huang, L.; Yang, J.; Liu, B.; Zheng, J. Improvement of mechanical strength and fatigue resistance of double network hydrogels by ionic coordination interactions. Chem. Mater. 2016, 28, 5710–5720. [Google Scholar] [CrossRef]
- Chen, Q.; Zhu, L.; Chen, H.; Yan, H.; Huang, L.; Yang, J.; Zheng, J. A novel design strategy for fully physically linked double network hydrogels with tough, fatigue resistant, and self-healing properties. Adv. Funct. Mater. 2015, 25, 1598–1607. [Google Scholar] [CrossRef]
- Chen, Q.; Zhu, L.; Zhao, C.; Wang, Q.; Zheng, J. A robust, one-pot synthesis of highly mechanical and recoverable double network hydrogels using thermoreversible sol-gel polysaccharide. Adv. Mater. 2013, 25, 4171–4176. [Google Scholar] [CrossRef]
- Li, X.; Cui, K.; Sun, T.L.; Meng, L.; Yu, C.; Li, L.; Creton, C.; Kurokawa, T.; Gong, J.P. Mesoscale bicontinuous networks in self-healing hydrogels delay fatigue fracture. Proc. Natl. Acad. Sci. USA 2020, 117, 7606–7612. [Google Scholar] [CrossRef] [PubMed]
- Tanaka, Y. A local damage model for anomalous high toughness of double-network gels. Europhys. Lett. 2007, 78, 56005. [Google Scholar] [CrossRef]
- Tominaga, T.; Tirumala, V.R.; Lee, S.; Lin, E.K.; Gong, J.P.; Wu, W.-l. Thermodynamic interactions in double-network hydrogels. J. Phys. Chem. B 2008, 112, 3903–3909. [Google Scholar] [CrossRef] [PubMed]
- Tominaga, T.; Tirumala, V.R.; Lin, E.K.; Gong, J.P.; Furukawa, H.; Osada, Y.; Wu, W.-l. The molecular origin of enhanced toughness in double-network hydrogels: A neutron scattering study. Polymer 2007, 48, 7449–7454. [Google Scholar] [CrossRef]
- Yu, Q.M.; Tanaka, Y.; Furukawa, H.; Kurokawa, T.; Gong, J.P. Direct observation of damage zone around crack tips in double-network gels. Macromolecules 2009, 42, 3852–3855. [Google Scholar] [CrossRef]
- Liang, S.; Wu, Z.L.; Hu, J.; Kurokawa, T.; Yu, Q.M.; Gong, J.P. Direct observation on the surface fracture of ultrathin film double-network hydrogels. Macromolecules 2011, 44, 3016–3020. [Google Scholar] [CrossRef]
- Cui, W.; Huang, Y.; Chen, L.; Zheng, Y.; Saruwatari, Y.; Hui, C.-Y.; Kurokawa, T.; King, D.R.; Gong, J.P. Tiny yet tough: Maximizing the toughness of fiber-reinforced soft composites in the absence of a fiber-fracture mechanism. Matter 2021, 4, 3646–3661. [Google Scholar] [CrossRef]
- Hui, C.-Y.; Liu, Z.; Phoenix, S.L. Size effect on elastic stress concentrations in unidirectional fiber reinforced soft composites. Extrem. Mech. Lett. 2019, 33, 100573. [Google Scholar] [CrossRef]
- Haque, M.A.; Kurokawa, T.; Gong, J.P. Super tough double network hydrogels and their application as biomaterials. Polymer 2012, 53, 1805–1822. [Google Scholar] [CrossRef]
- Yue, Y.; Kurokawa, T.; Haque, M.A.; Nakajima, T.; Nonoyama, T.; Li, X.; Kajiwara, I.; Gong, J.P. Mechano-actuated ultrafast full-colour switching in layered photonic hydrogels. Nat. Commun. 2014, 5, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Yue, Y.F.; Haque, M.A.; Kurokawa, T.; Nakajima, T.; Gong, J.P. Lamellar Hydrogels with High Toughness and Ternary Tunable Photonic Stop-Band. Adv. Mater. 2013, 25, 3106–3110. [Google Scholar] [CrossRef] [PubMed]
- Ye, Y.N.; Haque, M.A.; Inoue, A.; Katsuyama, Y.; Kurokawa, T.; Gong, J.P. Flower-like Photonic Hydrogel with Superstructure Induced via Modulated Shear Field. ACS Macro Lett. 2021, 10, 708–713. [Google Scholar] [CrossRef]
- Haque, M.A.; Kurokawa, T.; Kamita, G.; Yue, Y.; Gong, J.P. Rapid and reversible tuning of structural color of a hydrogel over the entire visible spectrum by mechanical stimulation. Chem. Mater. 2011, 23, 5200–5207. [Google Scholar] [CrossRef]
- Haque, M.A.; Kurokawa, T.; Gong, J.P. Anisotropic hydrogel based on bilayers: Color, strength, toughness, and fatigue resistance. Soft Matter 2012, 8, 8008–8016. [Google Scholar] [CrossRef] [Green Version]
- Kong, W.; Wang, C.; Jia, C.; Kuang, Y.; Pastel, G.; Chen, C.; Chen, G.; He, S.; Huang, H.; Zhang, J. Muscle-Inspired Highly Anisotropic, Strong, Ion-Conductive Hydrogels. Adv. Mater. 2018, 30, 1801934. [Google Scholar] [CrossRef]
- Zhou, Y.; Wan, C.; Yang, Y.; Yang, H.; Wang, S.; Dai, Z.; Ji, K.; Jiang, H.; Chen, X.; Long, Y. Highly stretchable, elastic, and ionic conductive hydrogel for artificial soft electronics. Adv. Funct. Mater. 2019, 29, 1806220. [Google Scholar] [CrossRef]
- Park, H.; Lee, K.; Kim, Y.; Ambade, S.; Noh, S.; Eom, W.; Hwang, J.; Lee, W.; Huang, J.; Han, T. Dynamic assembly of liquid crystalline graphene oxide gel fibers for ion transport. Sci. Adv. 2018, 4, eaau2104. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kanik, M.; Orguc, S.; Varnavides, G.; Kim, J.; Benavides, T.; Gonzalez, D.; Akintilo, T.; Tasan, C.C.; Chandrakasan, A.P.; Fink, Y. Strain-programmable fiber-based artificial muscle. Science 2019, 365, 145–150. [Google Scholar] [CrossRef] [PubMed]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cui, W.; Zhu, R. A Review on Tough Soft Composites at Different Length Scales. Textiles 2021, 1, 513-533. https://doi.org/10.3390/textiles1030027
Cui W, Zhu R. A Review on Tough Soft Composites at Different Length Scales. Textiles. 2021; 1(3):513-533. https://doi.org/10.3390/textiles1030027
Chicago/Turabian StyleCui, Wei, and Ruijie Zhu. 2021. "A Review on Tough Soft Composites at Different Length Scales" Textiles 1, no. 3: 513-533. https://doi.org/10.3390/textiles1030027
APA StyleCui, W., & Zhu, R. (2021). A Review on Tough Soft Composites at Different Length Scales. Textiles, 1(3), 513-533. https://doi.org/10.3390/textiles1030027







