Fitting Quality of NMR Relaxation Data to Differentiate Asphalt Binders

Abstract

Asphalt binder performance grades (PGs) are important metrics in designing pavements for effective transportation infrastructure. The PG system relies on the binder’s stiffness and is determined through energy- and time-intensive physical testing. Physical properties, like stiffness, can also be determined by spin–lattice NMR relaxometry, a non-destructive chemical method. NMR relaxometry can quantify the molecular mobility of materials by determining relaxation times from exponential decays of excited nuclear magnetization. While relaxation times have been used to determine physical properties of materials, a quantitative relation to the PG grades of asphalt binder is yet to be established. In this study, T₁ NMR relaxation analyses were used to differentiate between solid asphalt binders and determine the fastest yet still-reliable method of modeling exponential decay data. Algorithms that fit exponential decay relaxation data using one, two, or three independent relaxation times were compared with a 128-coefficient discrete inverse Laplace transformation to determine the best mathematical fit for a comparative analysis. The number of data points was then reduced from 256 to 64 to 16 and finally to 8 data points on a relaxation curve to reduce the testing time and determine the minimum number of data points needed for comparison. Two batches of PG 64-22 asphalt binder, along with samples of PG 76-22 and 94-10 binders, were investigated. The best compromise between measuring time and data reliability was found by acquiring 64 data points and then using a biexponential model to fit the experimental data. The PG 64-22 sources provided similar results, indicating similar physical properties. The PG 64-22 and PG 76-22 binders could also be compared via monoexponential data fits, but the PG 94-10 samples required an additional relaxation parameter for comparison. To differentiate all three binder grades, the primary relaxation times, along with their relative ratios, were utilized.

1. Introduction

Asphalt binder grades are critical to pavement design. The current classification system, Superpave performance grading (PG), differentiates binders according to their susceptibility to failures that occur at high and low temperatures. The first number in a grade indicates the high-temperature performance. The higher this temperature, the stiffer the binder and the less susceptible the binder is to permanent deformation at high temperatures. The second, negative number, indicates the low-temperature performance. The lower this temperature, the less susceptible the binder is to thermal cracking at low temperatures. At higher temperatures, the preferred performance is a stiffer binder to resist permanent deformation. At lower temperatures, the preferred performance is a softer binder to resist thermal cracking. The PG system guides pavement design according to the temperature range that the road will experience. The larger the range between the two numbers, the better performing the binder.

To determine the PG of a binder for pavement design, at least two days of testing are needed. The binder undergoes different aging simulations that require hours of time and energy. The high PG is determined by the initial and the short-term aged viscoelastic properties. Short-term aging requires the heating and rotating of a sample of binder for 85 min at 163 °C. This aging process mimics the mixing and compaction process. The viscoelastic testing requires about an hour depending on how many temperatures are evaluated. The low PG evaluates the binder that is prepared with the pressure aging vessel (PAV). The PAV keeps the sample at 100 °C (moderate climates) and 2.07 MPA for 20 h. Using chemical methods to indicate physical properties could save time, energy, and money.

NMR relaxometry has been developed over the years to fit industry applications. From paint aging to SBS determination in asphalt pavement, polymer systems have been shown to have distinct NMR relaxation times that can be related to physical properties [1,2,3,4,5,6,7,8,9,10]. While investigating asphalt is a relatively new application, most studies have relied on T₂ relaxation methods. T₂ methods have indicated characteristic NMR relaxation times for components of asphalt binder [11,12]. T₂ analysis has also been used to describe asphaltene aggregation [13] and indicate penetration grades [14]. While T₂ is a faster method, it relies on solvents that destroy the structural integrity of the sample [15]. Additionally, since T₂ acquisition is so fast, solid-state relaxation can be hard to detect at higher field strength. Therefore, to probe into the asphalt structural integrity, this work focuses on the lesser-used T₁ relaxation.

Recently, T₁ NMR relaxometry has been shown to indicate viscoelastic changes in asphalt binder due to additives [16] and aging [17]. Generally, a longer relaxation time describes a stiffer binder. Additionally, rejuvenation mechanisms [18] and mixture properties [19] have been detected. T₁ relaxometry is a superior method since solvents and heat are not needed, preserving the molecular integrity. The major drawback of T₁ NMR relaxometry testing is the time and knowledge needed to analyze the results. One dataset acquisition can require up to 10 h, and analysis can take several extra hours. Previous NMR work conducted on asphalt field testing resulted in a testing time of 20 min per location [20]. Compared to physical testing which requires days, NMR is a superior acquisition method.

In this study, different grades and sources of asphalt binder are compared with NMR relaxometry. The complexity and time of this analysis was varied to determine the best and fastest fit of NMR T₁ relaxation data using sum-of-squares analysis (X²). This analysis is used to separate chemical information from physical noise [21]. Further, a least squares analysis was used to determine the relaxation constants. This analysis aims to compare PG asphalt binders quickly and effectively using NMR T₁ relaxation times from noisy experimental data.

2. Materials and Methods

Performance grade (PG) 64-22, 76-22, and 94-10 binders were sourced from Philips 66 in Granite City, IL, USA. Two separate batches of PG 64-22 were considered: PG 64-22 and 64-22 B. PG 64-22 binders are commonly found in the Midwest, while the stiffer qualities of the PG 76-22 could be utilized in warmer climates. The PG 94-10 would be too stiff to use practically but represents very aged binders.

In our study, 2 mm capillary tubes were dipped in the heated binders to ensure a uniform testing area, using the chocolate-covered pretzel method [16,17,18,19]. The 2 mm capillaries were then placed in 5 mm NMR sample tubes. A Bruker Avance DRX 200-MHz spectrometer was used to collect the ¹H NMR T₁ relaxation data. The SIP-R pulse sequence was used to obtain exponential decays to zero instead of the traditional rise to maximum [22]. The recovery delays were equidistant on a log scale to determine the shape of the exponential decay. Four scans, 5 s pre-delay, and 100 µs dead time were also used for data acquisition. The delay-dependent signals were fitted to 128 predefined coefficients logarithmically spaced from 0.1 ms to 1 s using an inverse Laplace transform (ILT). These parameters, relaxation times, and intensities are traditionally solved with an iterative inverse Laplace transform [11,23,24]. The ILT results in an equation, as seen in Equation (1), but many of the 128 coefficients are zero. In Equation (1), S(τ) is the signal intensity for a given delay time τ; T₁ values indicate the relaxation times.

$$S(\tau )=S_1{e}^{{\displaystyle \frac{-\tau }{T_{\mathrm{1,1}}}}}+S_2{e}^{{\displaystyle \frac{-\tau }{T_{\mathrm{1,2}}}}}+\dots S_n{e}^{{\displaystyle \frac{-\tau }{T_{\mathrm{1,128}}}}}$$

(1)

Since this analysis of 128 coefficients can take hours, simple multiexponential fits were also used to fit 1, 2, and 3 relaxation times to compare them to the best fit ILT. These multiexponential fits were developed using the curve fit function provided by the SciPy python library to model the relaxation data. The maximum number of solvable parameters depends on the number of data points acquired. Mono, bi, and tri exponential fits are simpler and faster ways to approximate complex exponential decays. Most relaxation data of asphalt binders contain one reliable primary relaxation time. These relaxation times are related to physical properties of a material [16,17]. After the primary T₁ relaxation time is determined, the relative ratio (R₁) can also be calculated by Equation (2). S₁ and S₂ are the signal intensities of the primary and secondary relaxation times, T_1,1 and T_1,2, respectively.

$$R_1={\displaystyle \frac{S_1}{S_1+S_2}}, S_1>S_2$$

(2)

The number of data points was also reduced from 256, 64, 16, and 8. The reduced datasets were selected from the original 256, spaced equidistant on a log scale. Unlike the ILT analysis, which requires no a priori information, initial conditions and parameter bounds had to be specified. The initial intensity condition was set to the first, highest intensity. The initial conditions were set to 0.5, 0.005, and 0.0005 for the first, second, and third T₁ times. These values were chosen by visually examining the exponential decays for approximate relaxation times. The goodness of fit was investigated for 256, 64, 16, and 8 data points. One, two, and three exponentials were considered using the minimum least squares method, as shown in Equation (3). O_i is the observed value, E_i the expected value, and X² the sum of error squared. The expected value was derived from fitting the T₁ and intensity constants in the multiexponential decay. Observed data are considered experimental data.

$$X^2=\sum _{i=1}^n{\left(O_i-E_i\right)}^2$$

(3)

The objective of this study was to determine the optimal number of terms that would best fit the experimental data, specifically assessing how many exponentials were needed for an accurate fit. All parameters were bound to be greater than zero since intensities and time constants cannot have negative values. The average primary relaxation time and standard deviation (error bars) of three samples were compared in all experiments.

3. Results

All binders had a primary inflection point/relaxation time around 0.4–0.6 s, but this value shifts slightly. This shifting depended on the influence of noise from the device, the fit used, the number of points acquired, and the type of binder. The testing that would require the most time was the 256 data points transformed through the ILT. Eight data points transformed with a monoexponential fit would require the least amount of time and analysis. The objective of this analysis was a balance between time and fitting quality.

3.1. Noise

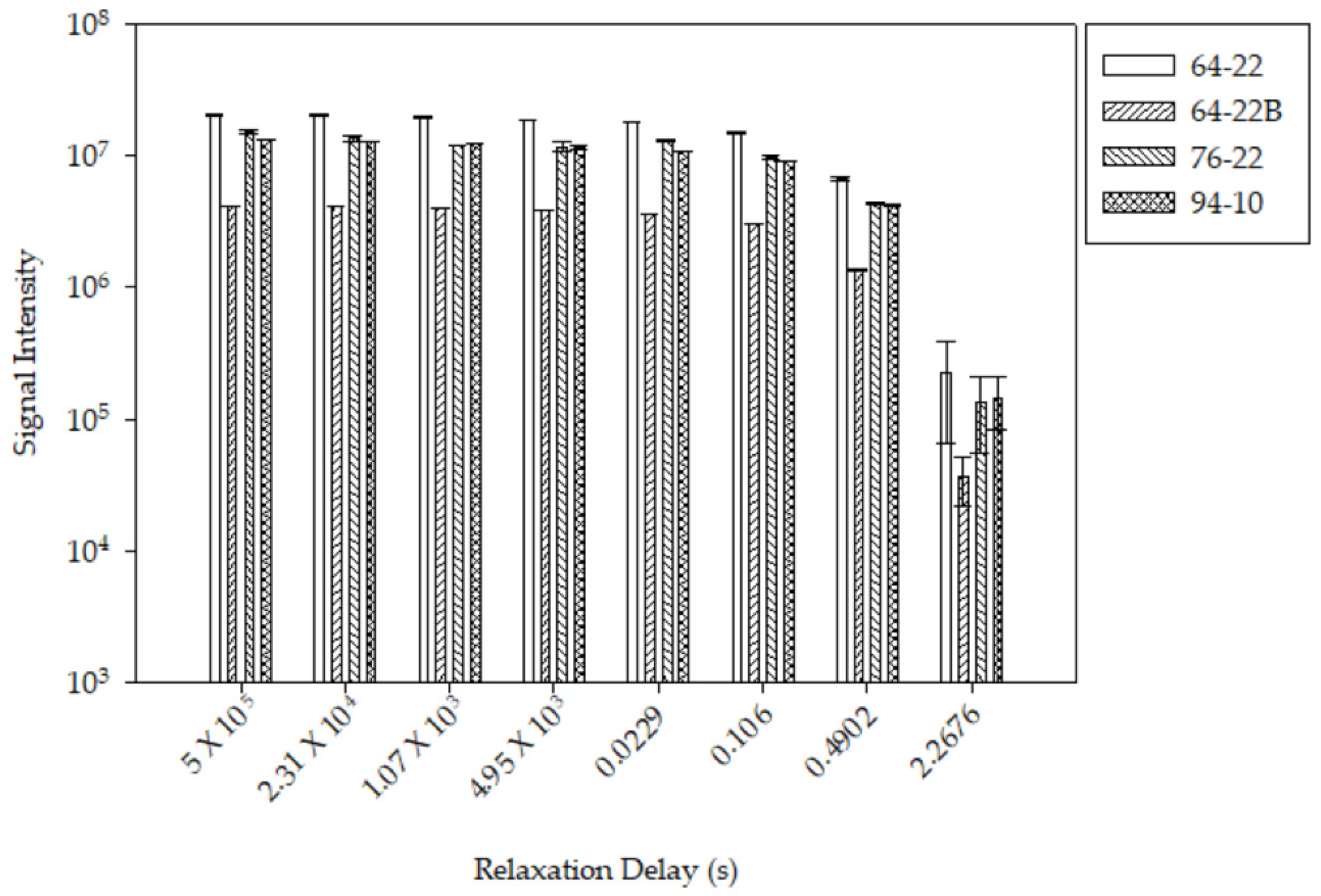
The noise from the device was not as impactful in the shifting of T₁ times, considering the scale of the intensities, as seen in Figure 1. The average intensity of 32 scans of the same eight points was used to compare the standard deviation (error bars) of each sample. The most noise was seen at the 2.27 s relaxation delay. This occurred since the main signal had completely decayed at that point and the only thing remaining was noise.

3.2. Goodness of Fit

Goodness of fit is defined as the square of the difference between the expected value and the observed value. This criterion was used to determine the best-fitting algorithm between 1, 2, and 3 exponentials, as shown in Figure 2. Unlike other statistical tests like ANOVA and t-test, where a hypothesis is being tested, the least squares criterion provides the maximum likelihood estimator for quality of fit [21]. Reference graphs can be found in Appendix A. For all PG binders, the monoexponential fit was the worst. The biexponential and triexponential fit produced comparable results. In general, the triexponential was slightly better but did not provide much confidence when eight data points were used. Additionally, the triexponential fit overfit the 64-22 binders, skewing the primary ratio. Therefore, the best comparative fit for the binders was a biexponential fit. These values were acquired by fitting the curve against the objective function then squaring the difference between the predicted curve and the dataset. This pattern repeats for 256, 64, 16, and 8 data points.

3.3. Number of Data Points

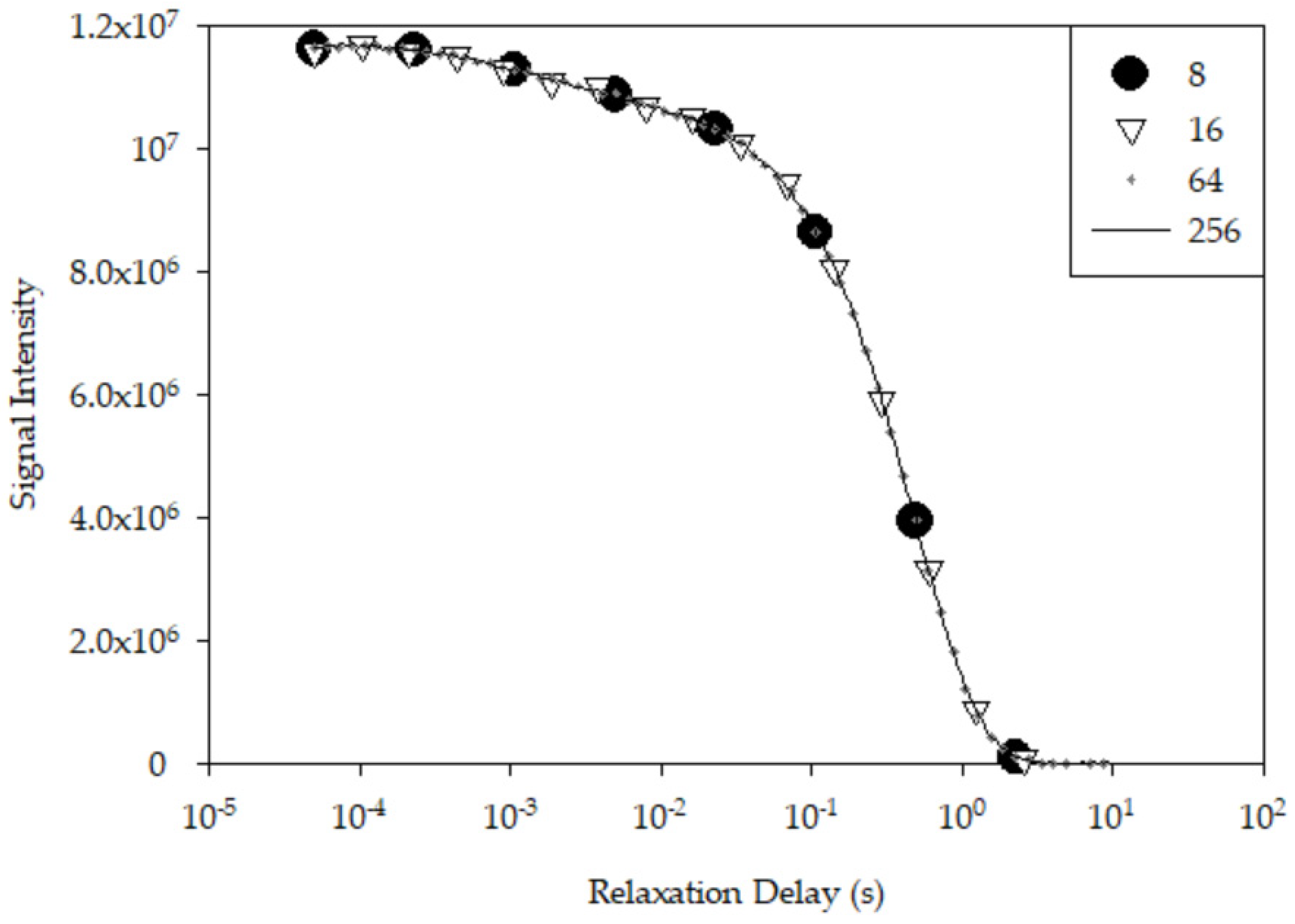
A total of 256 data points were acquired from an exponential decay for each binder sample. Out of those points, 64, 16, and 8 equally log-spaced points were sampled, as displayed in Figure 3. Reducing the number of data points reduced the required testing time, as summarized in

Table 1. Time needed for acquisition of data.

Number of Data Points	Approximate Time for Data Acquisition (Min)
256	214
64	50
16	5
8	3

. However, as the number of data points decreased, so did the ability to catch certain relaxation times, which appear as inflection points on the log scale. When reduced to eight data points, the standard deviation of some of the samples greatly increased. Sixty-four and sixteen points are viable reductions to consider as they reduce testing time and still allow for some differentiation. Eight points can be used to differentiate the PG 64-22 from the 76-22, but due to additional relaxation times, the 94-10 required more points to fit the relaxation times accurately.

3.4. Best and Fastest T₁ Fits

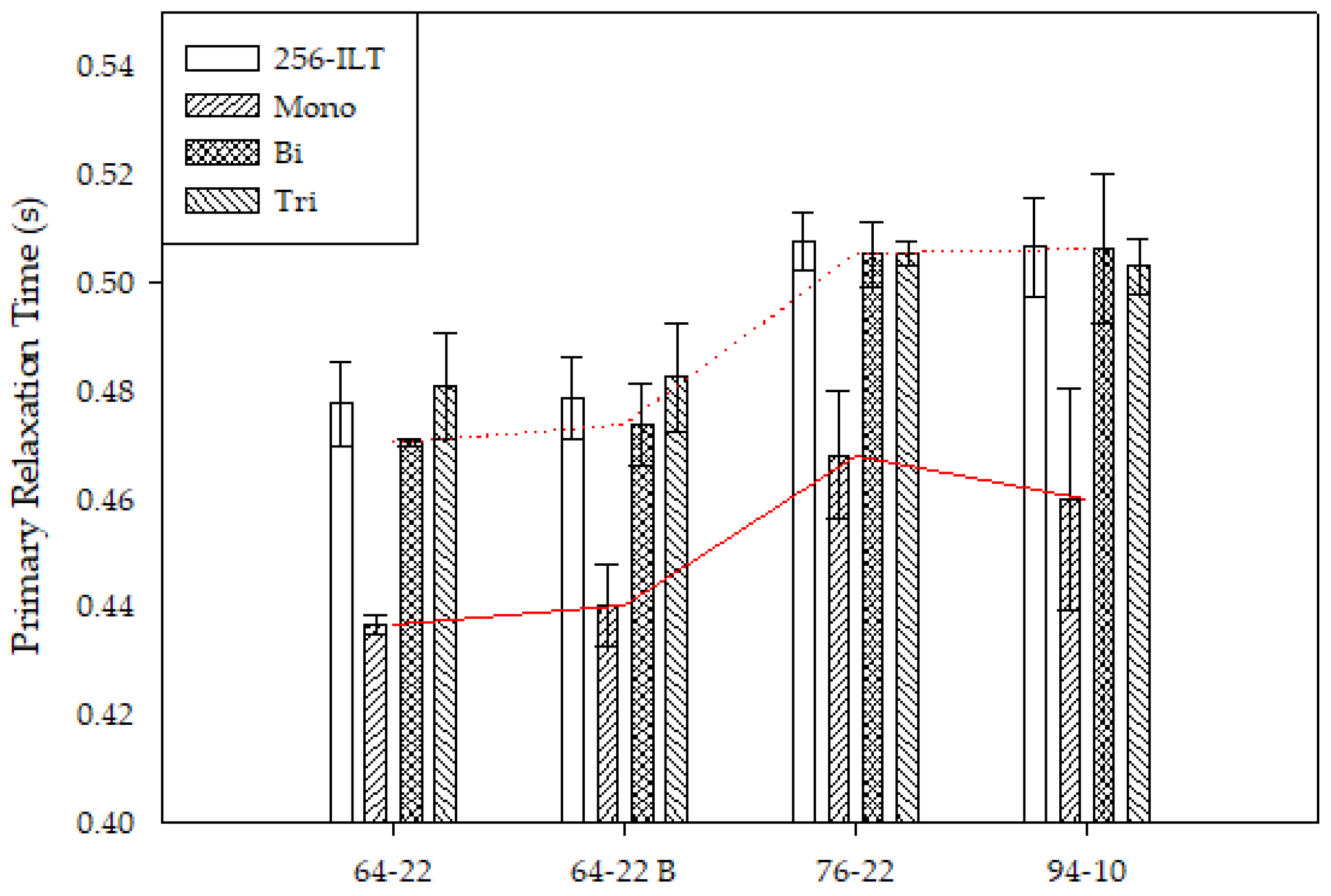
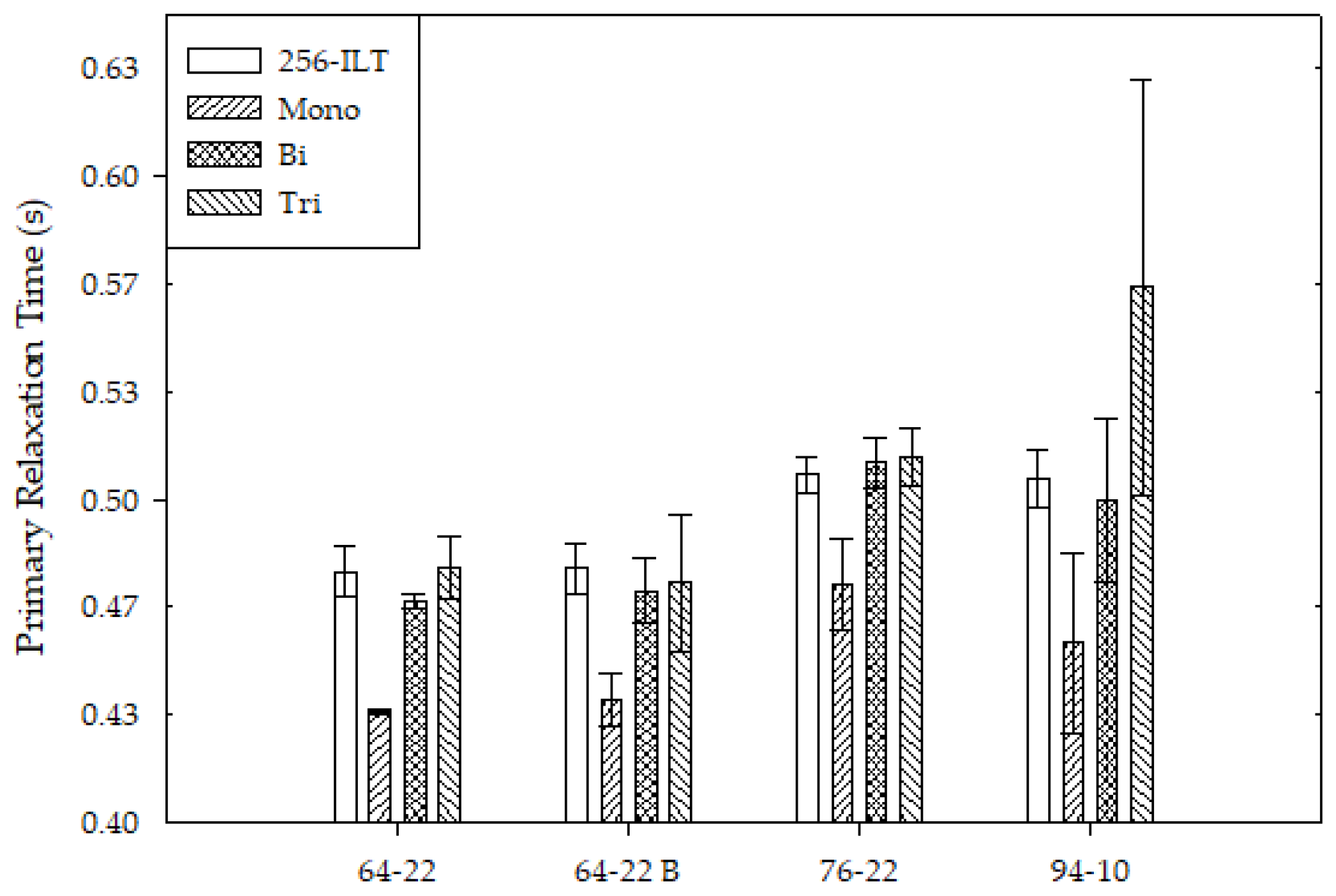
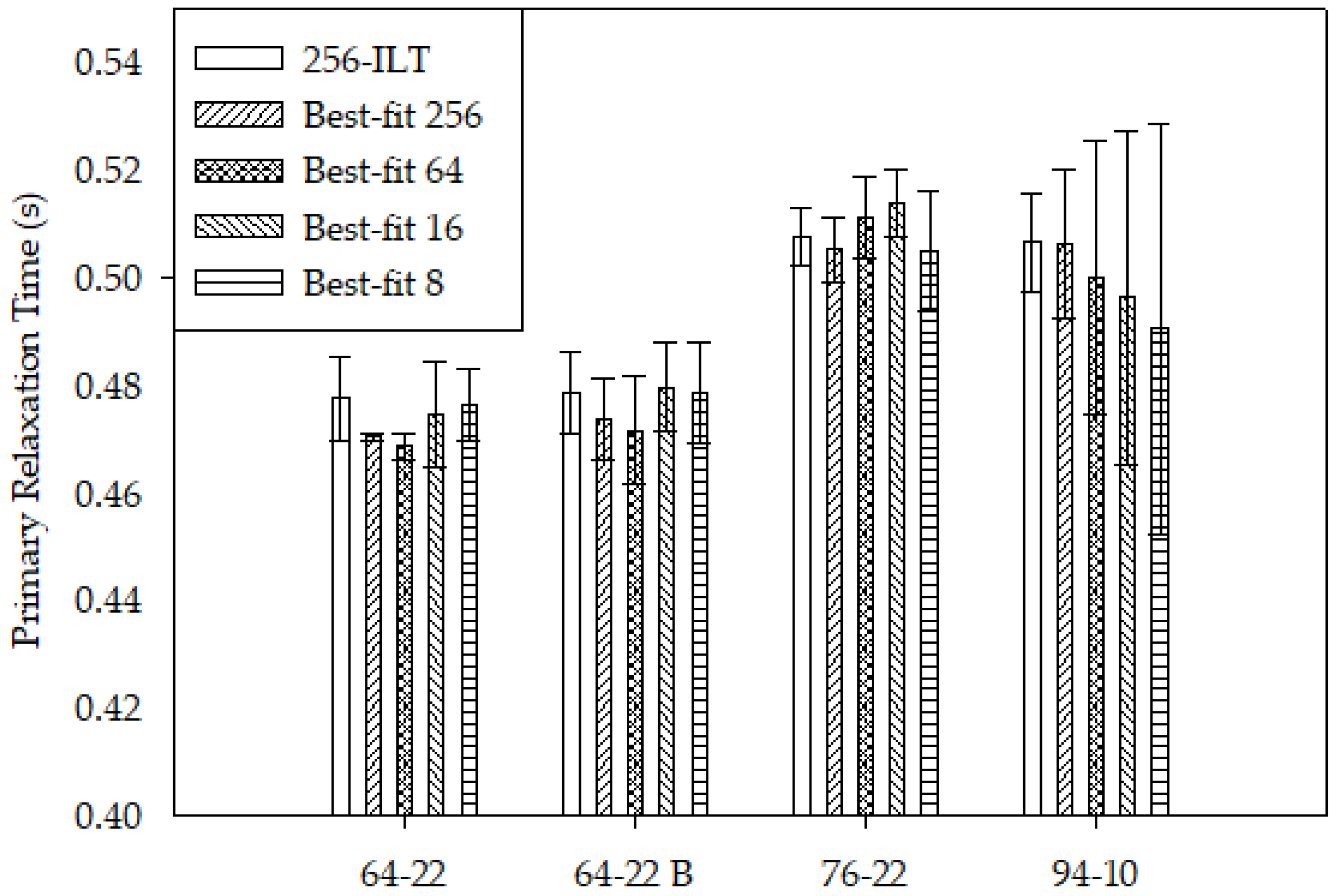
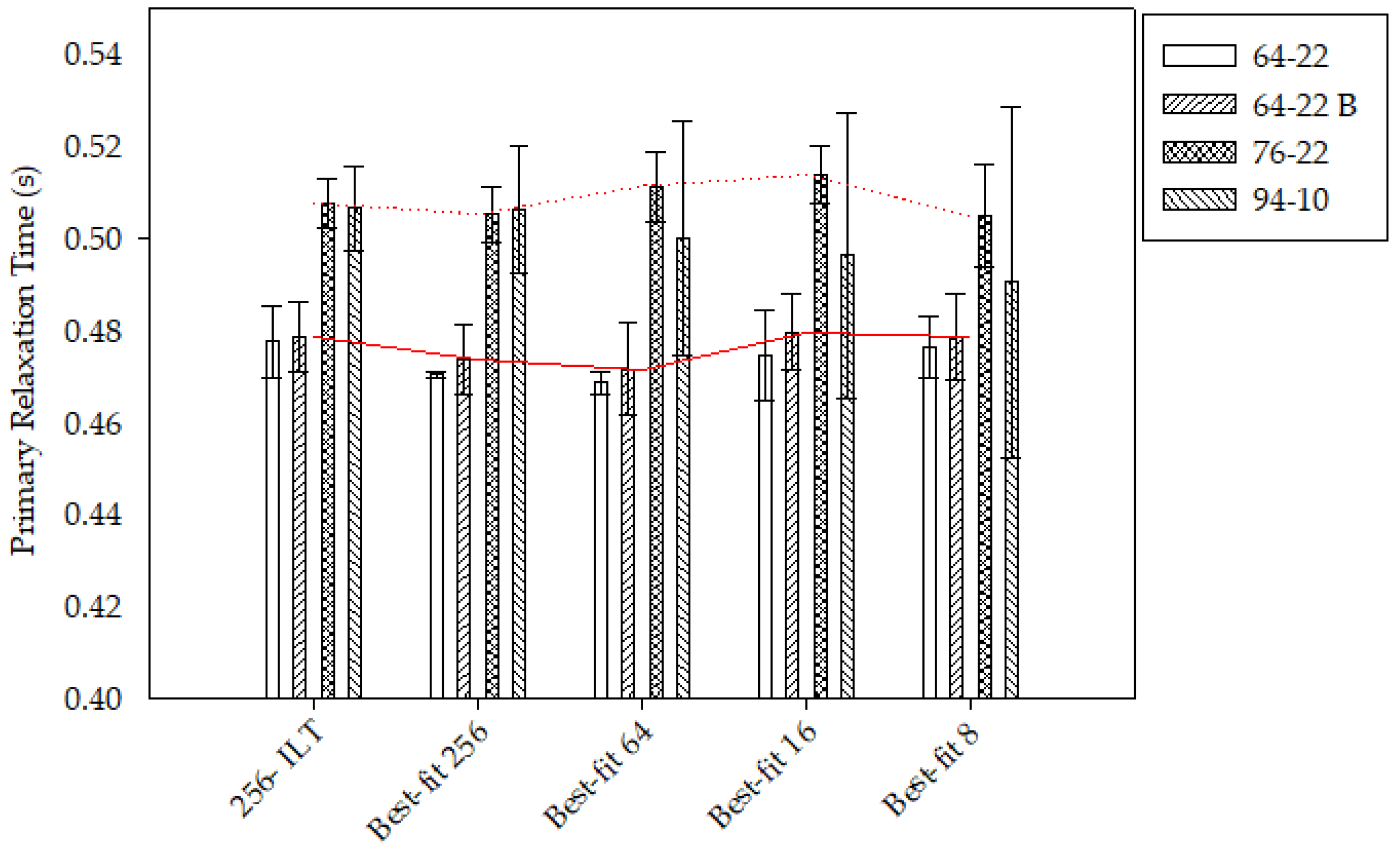
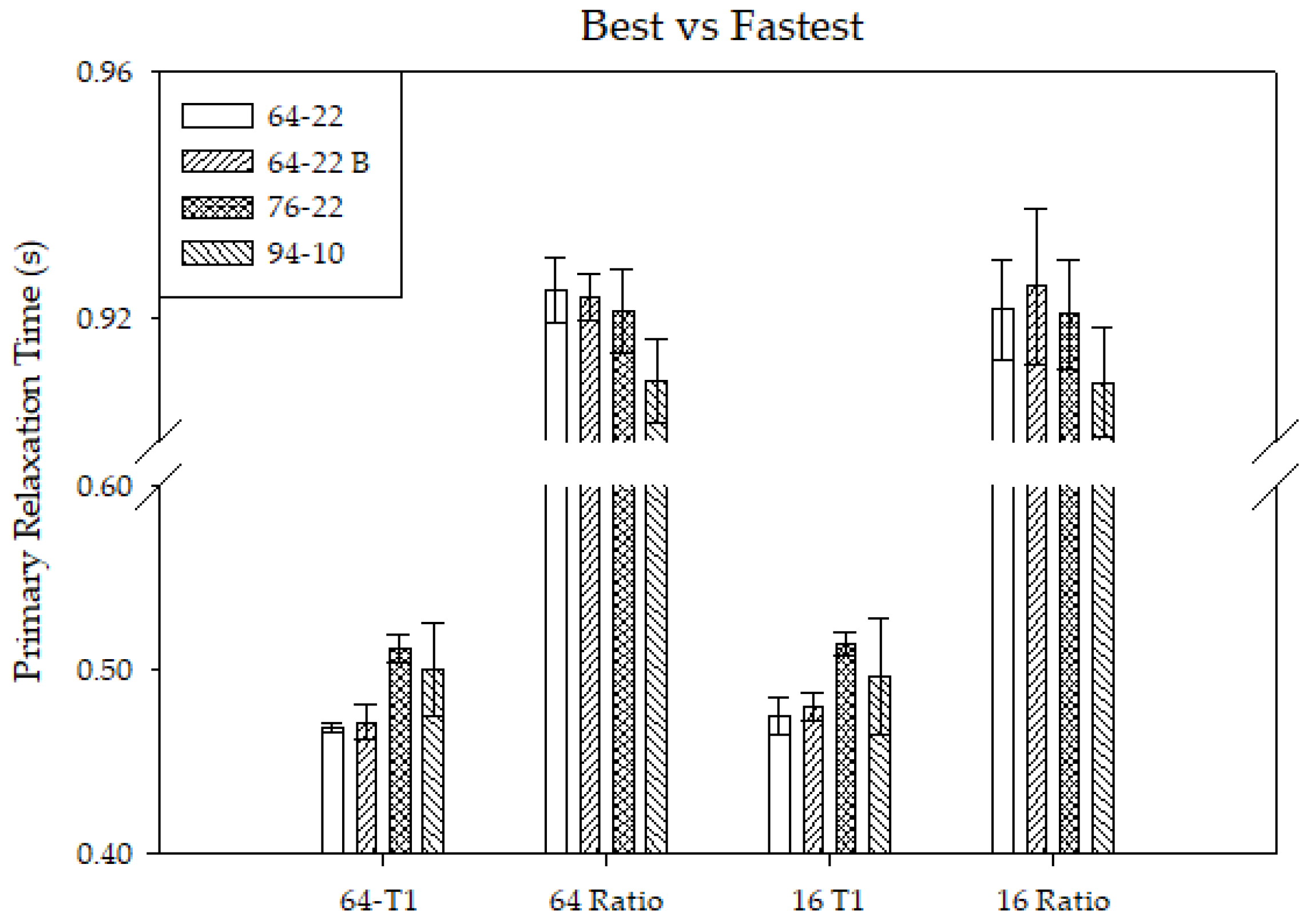
To reduce analysis time, the acquisition time must be reduced, but to differentiate binders, a comparable fit must be used. Since the best fit was determined to be biexponential, the number of data points was then decreased for comparison, as seen in Figure 4 and Figure 5. Figure 4 indicates how decreasing the number of data points impacts comparability. Since the ILT is commonly considered the best fit, the accuracy of each fit could be compared. Reducing the number of data points of the PG 64-22 binders and the PG 76-22 resulted in slight fluctuations in the standard deviation. As the number of data points was reduced for the PG 94-10 sample, the standard deviation continued to increase. This clearly shows how additional data is needed for the 94-10 sample, indicating that multiple hydrogen environments exist that cannot be fit as well with less data. Figure 5 compares the number of data points across the binders. The general trend, shown in red, indicates that the PG 64-22 sources were comparable while the 76-22 and 94-10 were comparable with slight differences. While the PG 64-22 samples could be clearly differentiated from the PG 76-22 samples, none of the fits could differentiate the PG 76-22 from the 94-10.

3.5. Best and Fastest T₁ Ratios

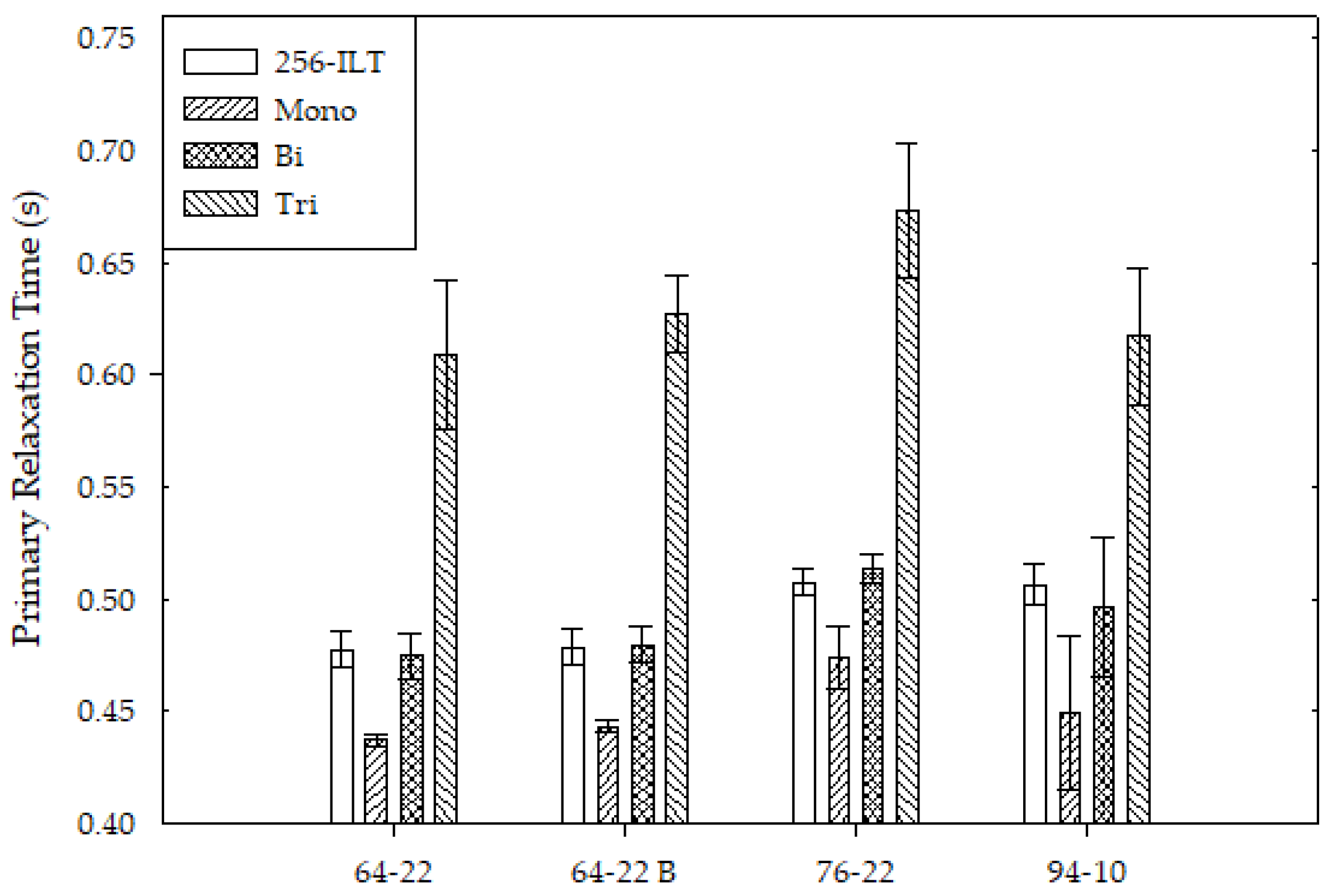
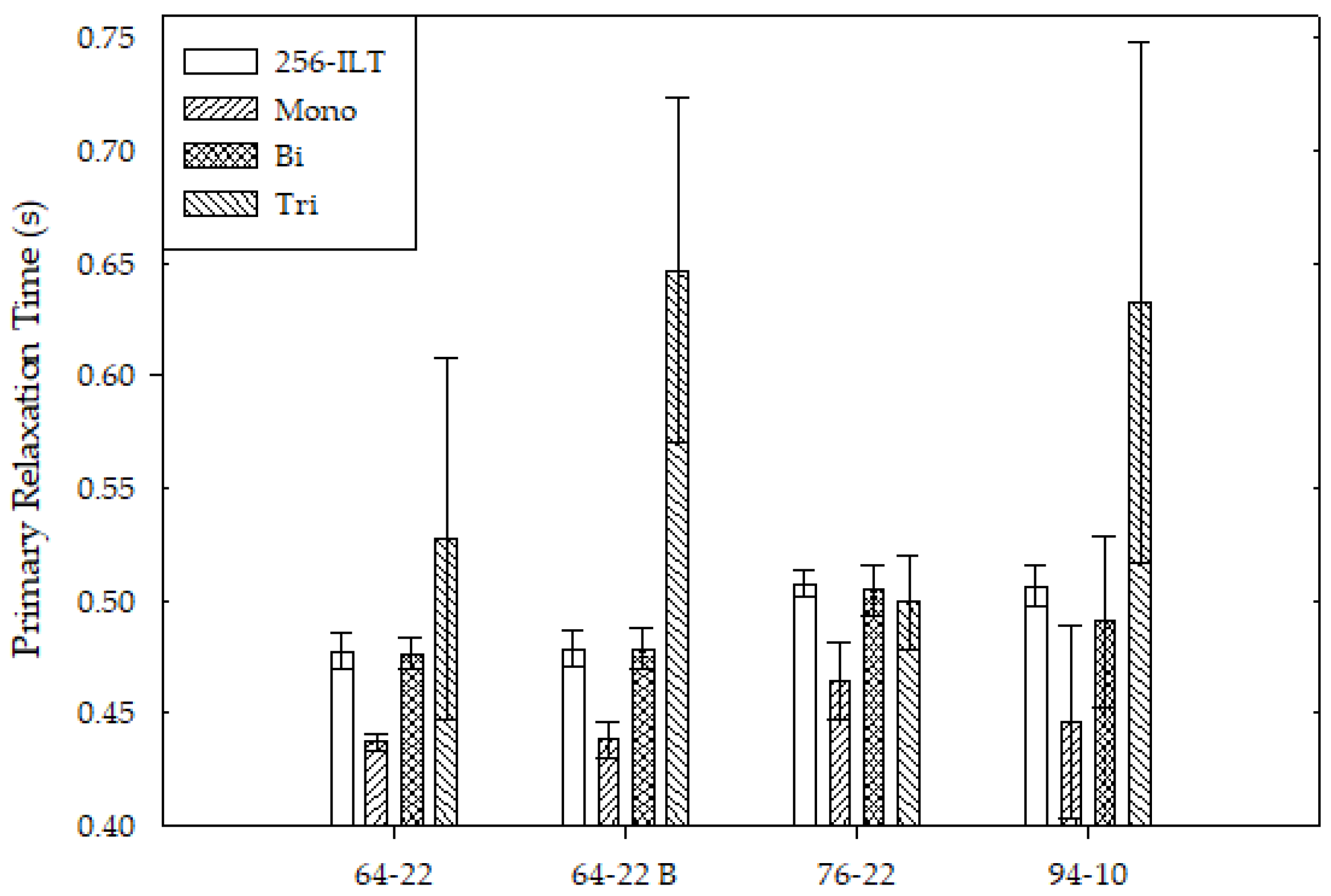
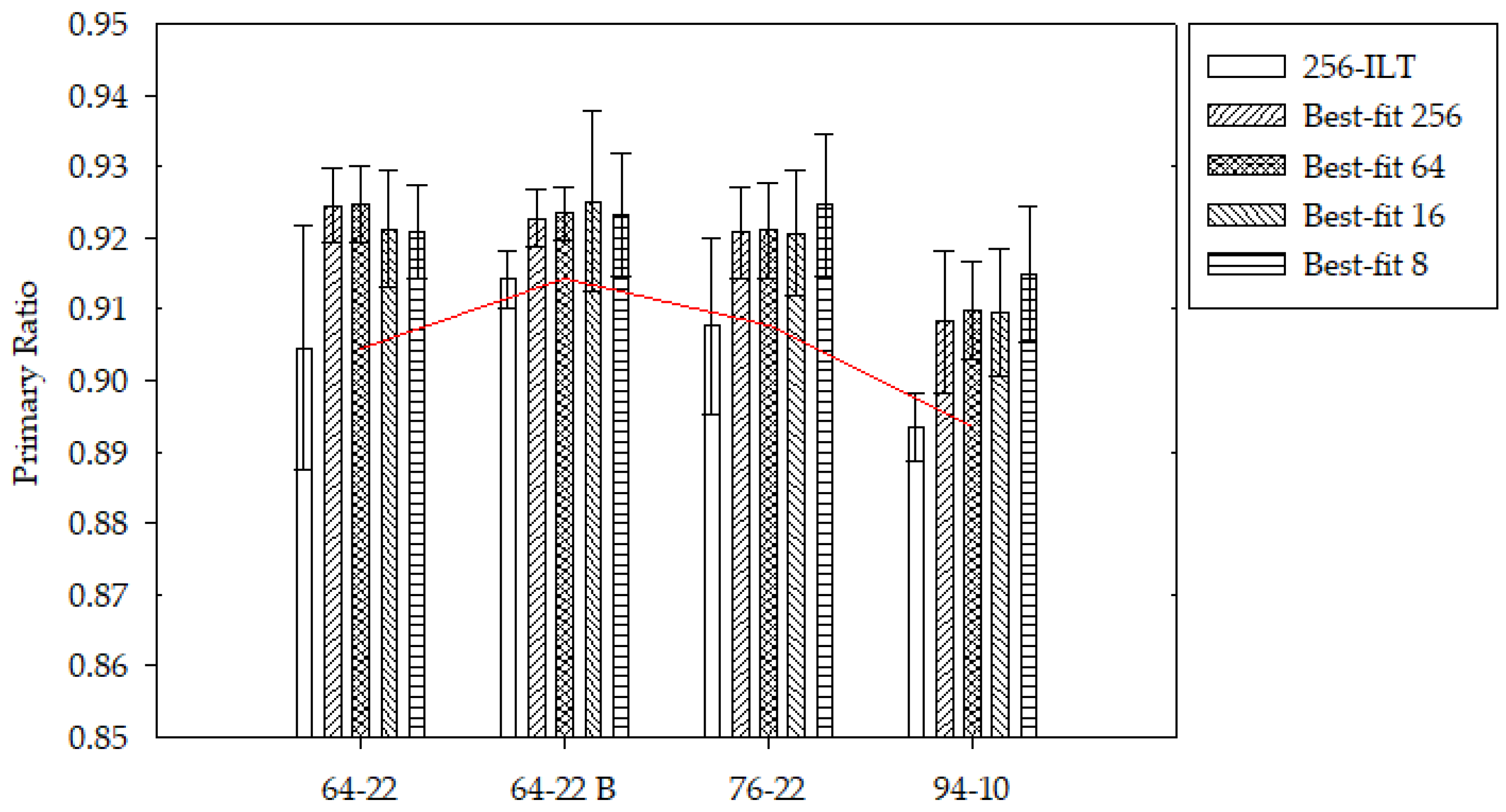
By comparing the primary relaxation time, the PG 64-22 binders could be differentiated from the 76-22 binder, but not the 94-10. Therefore, another parameter must be considered. The relative ratio of the primary relaxation time for each binder, the primary ratio, was determined. While this parameter is not entirely effective in differentiating the PG 76-22 from the 94-10, it is a better estimate than just the relaxation time. This comparison is seen in Figure 6. While the PG 64-22 and 76-22 samples had similar primary ratios, the primary ratio of the PG 94-10 sample was consistently lower than the other samples, as indicated by the general trend (red line) in Figure 7. The primary ratio is an indication of the number of distinct hydrogen environments present. The ILT considers the highest number of hydrogen environments, while the other fits consider two due to the biexponential fit. In both analyses, there can be a lot of variability in the hydrogen environments between samples.

The number of data points also impacted the variability in the samples, as displayed in Figure 7. Both samples of the PG 64-22 and the one sample of PG 76-22 experienced less variability when 256 and 64 data points were considered. Alternatively, the PG 94-10 displayed less variability when the inverse Laplace transform was used with 256 data points. While the ILT included more noise in the other samples, there may be more signal for the ILT to catch in the PG 94-10 samples. This is further supported due to the increase in variability and the decrease in overlap with the ILT as fewer data points were considered.

4. Discussion

4.1. Noise and Goodness of Fit

The differentiation of asphalt binders by NMR relaxometry depends on the noise, the type of fit, and the number of data points needed. The best mathematical fit of all samples would be the ILT. This mathematical iterative procedure will find the best match to the experimental data. However, since the data are noisy, some fitted relaxation times may not actually exist or be helpful. Therefore, this testing relied mainly on the most distinct relaxation time, the primary relaxation time.

The noise from the device was not a large component in the differences seen in the relaxation times of asphalt binders. When comparing the number of exponential fits, analysis indicated that a monoexponential fit is suboptimal, as shown by high X² values, suggesting a poor representation of the data. In contrast, a biexponential fit substantially improves the model’s accuracy, evident from significantly lower X² values and clearer alignment with the observed data, as seen in Appendix A. While the triexponential fit provided a similar goodness-of-fit, as evidenced by comparable X² values, the additional complexity does not greatly enhance the model’s performance. Therefore, the biexponential fit is preferred for the comparison of the primary relaxation time and ratio.

4.2. Best and Fastest Comparison (T₁ and Ratios)

It was shown that the type of fit and number of data points acquired did impact the primary relaxation time as well as the relative ratio, but to a lesser degree. Most of the samples had a smaller standard deviation with the mono-, bi-, or triexponential fits, not the ILT. This is occurring due to the averaging of the additional relaxation times that are resolved from the ILT. A monoexponential fit must summarize all noise into one relaxation time, so the most influential times will have the greatest impact, reducing the impact of noise. The number of relaxation times that can be resolved depends on the number of data points available. Three relaxation times is the maximum number of times that can be determined with eight data points with little confidence. While PG 64-22 and 76-22 could be differentiated, the 94-10 falls into the ranges of the other grades. Further testing should determine the best location of the data points since equally log-spaced data did not represent the data well, resulting in larger standard deviations of both the primary relaxation time and ratio.

At least a biexponential is needed to consider the relative ratio, which is needed to differentiate the PG 76-22 from the 94-10. Therefore, a biexponential fit of 64 or 16 acquired points can indicate binder grades, as seen in Figure 8. This is consistent with previous findings of asphalt that utilized a biexponential fit [20]. The best comparison requires 64 points since the ratios between the PG 76-22 and 94-10 have the least overlap.

The major difference between binder grades is the stiffness of each binder. Since the process of assigning grades is standard, it is assumed that the PG 64-22 had the lowest viscosity, while the PG 94-10 had the largest. The idea that increased stiffness leads to longer relaxation times [16,17] is somewhat supported by this study. The relaxation time increased from the PG 64-22 to 76-22 but then decreased in the PG 94-10 samples. This anomaly can be explained by the decrease in the primary ratio seen in the PG 94-10 samples. Since the primary ratio decreased, more distinct hydrogen environments are present at faster relaxation times, reducing the primary relaxation time. Therefore, both the primary relaxation time and ratio are needed to differentiate asphalt binders.

5. Conclusions

The asphalt binder is a major design consideration for essential infrastructure. In differentiating asphalt binders, it takes considerable time and energy to simulate failure conditions. Chemical testing has been considered for binder characterization, but often requires intense or destructive analysis. NMR relaxometry is emerging as a potential tool for asphalt performance determination. This study concludes that asphalt binders can be differentiated using NMR analysis, but the degree of this differentiation depends on the number of data points used and the type of fit. The best mathematical fit is the ILT, but across samples, this fit was not as effective in differentiating samples since the standard deviation was very high. While the variability between samples can be high (i.e., high standard deviation), the primary relaxation time and ratio were effective in differentiating the binders. The most comparable fit with a reliable amount of data points was a biexponential fit of 64 data points. This analysis method would reduce the testing time from 214 to 50 min.

Further testing should determine the best location for fewer data points to be considered. Additionally, other parameters should be developed to describe NMR data as a powerful tool for engineering use.