Abstract
The geometrical re parameters of trans-azobenzene (E-AB) free molecule were refined by gas electron diffraction (GED) method using available experimental data obtained previously by S. Konaka and coworkers. Structural analysis was carried out by various techniques. First of all, these included the widely used molecular orbital constrained gas electron diffraction method and regularization method. The results of the refinements using different models were also compared—a semirigid model, three variants of one-dimensional dynamic models, and a two-dimensional pseudoconformer model. Several descriptions have been used due to the fact that E-AB has a shallow potential energy surface along the rotation coordinates of phenyl groups. Despite this, it turned out that the semirigid model is suitable for use for E-AB and allows good agreement with experimental data to be achieved. According to the results of GED structural analysis, coupled with the results of DLPNO-CCSD(T0) calculations, E-AB has a planar structure. Based only on GED data, it is impossible to unambiguously determine the rotational angle of the phenyl group due to the facts that (i) with rotation over a wide range of angles, the bonded distances in the molecule change insignificantly and (ii) potential function in a structural analysis within a dynamic model is not determined with the necessary accuracy. This work also examines the sensitivity of the GED method to structural changes caused by trans-cis isomerization. The paper also analyzes the applicability of different variants of density functional theory (DFT) calculations in GED structural analysis using E-AB as an example. There are not enough similar methodological works in the literature. This experimental and methodological information is especially important and relevant for planning and implementing GED experiments and corresponding processing of the results for azobenzene derivatives, in which the conformer and isomeric diversity are even more complicated due to the presence of different substituents.
1. Introduction
Azo compounds R1-N=N-R2, and especially azobenzenes, receive much attention as promising compounds for creating functional and “smart” materials [1,2]. Perhaps the main object of research in this area is photoisomerization (trans ⇄ cis or E ⇄ Z), which makes azo compounds suitable for use in a different range of applications, such as the development of various sensors, molecular switches, optical data storage, nonlinear optics, color-changing materials [3,4,5,6,7,8], etc. Of course, much attention is paid to modifying these compounds by adding special functional groups [9,10,11,12,13]. In this regard, structural studies play a huge role in describing and predicting physicochemical properties. It is logical and self-explanatory that the “parent” azobenzene (AB) has been the subject of plenty of structural and spectral studies.
The current consensus is that E-AB (Figure 1) is characterized by a flat structure. However, the planarity of the E-AB structure has been the subject of controversial studies. There were several articles [14,15] describing azobenzene as a distorted molecule and many more modern works [16,17,18,19,20,21,22] proving the planar structure of the E-AB molecule. At the same time, in the crystalline state and in solutions, these molecules can undergo significant distortions [23,24,25,26,27]. It should be noted that structures in the solid and liquid phases are usually distorted due to intermolecular interactions. Structures determined by the gas electron diffraction (GED) method do not suffer from these interactions and reflect the properties of a free molecule. The first interpretation of the results of the GED experiment for AB was carried out in 1977 by Traetteberg and coworkers [28]. According to their interpretation, the molecule E-AB in the gas phase is nonplanar and phenyl groups twisted about φ ≈ 30°. Also, the authors of ref. [28] suggested that there are two conformers of Ci and C2 symmetries corresponding to phenyl rings rotated in the opposite and in the same direction, respectively. Vibrations corresponding to rotations of phenyl rings (Au and Bg irreducible representations under C2h point group) have frequencies of 15–21 and 95–111 cm−1 [19,20]. Potential energy surface (PES) of E-AB is shallow along the N=N-C-C torsional coordinates [19]. Studying the consequences of conformations in diffraction, the authors of ref. [29] came to the conclusion that for trans-stilbene (an E-AB-like molecule) and other molecules with flat PES, the pseudoconformer approach must be used to properly describe the diffraction pattern. In 2001, Konaka and coworkers [30] repeated the GED experiment for E-AB and interpreted their results within the framework of a dynamic model constructed using pseudoconformers: the stable form of E-AB was found to be planar. In that structural analysis, data from MP2/6-31+G* calculations were used, according to which the minimum on the PES corresponds to a distorted structure. Apparently, it is an artifact resulting from the use of a deficient ab initio approach [19,29].
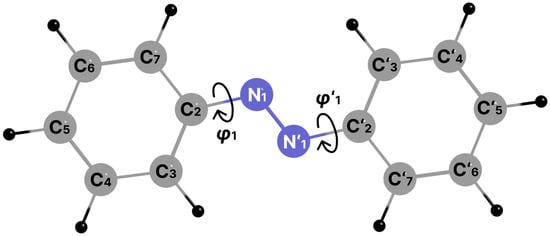
Figure 1.
Structure and atom labels of E-AB. φ1 and φ1’ are torsion angles N’1-N1-C2-C3 and N1-N’1-C’2-C’3.
Quantum chemical (QC) calculations are powerful tools for the determination of molecular structure and specificity of intramolecular dynamics. Nowadays, a lot of variants of approaches to the solution of such problems based on both ab initio and density functional theory (DFT) methods have been created. The method of coupled clusters can be called the most preferable at the moment. However, such calculations are very computationally expensive and realistically applicable only for molecules with a small number of atoms. Far less computationally expensive DFT methods can serve as an alternative but choosing the optimal functional/basis set combination from the many existing variants is a challenging task.
The structure determined experimentally by GED is of indisputable value. The experimental data available in the literature [30] operate with thermal averaged distances rg, but these parameters are trigonometrically inconsistent and cannot be directly compared with parameters determined by QC calculations [31]. The transition from the experimentally observed thermally average structure to the equilibrium structure requires solving the problem of accounting for the specificity of intramolecular dynamics. This work considers the issue of the applicability of QC data obtained by various DFT functionals in structure refinement using GED data. In general, the choice of one or another DFT functional should not affect the structural analysis. However, under GED structural refinement for large molecules, nonvariable vibrational corrections re − ra (or rh1 − ra) and nonvariable differences between the nonequivalent structural parameters in case of the MOCED (molecular orbital constrained gas electron diffraction) method [32] may influence the final results. The purpose of this work is to determine the equilibrium structure of the E-AB in terms of re parameters. Experimental data (molecular scattering intensities and background function) for the corresponding analysis were taken from [30]. It should be noted that in the works carried out twenty years ago and earlier (including ref. [28,30]), the re structures for medium-sized molecules were rarely determined due to the lack of the necessary computer power that is currently available. This information about re structural parameters of the “parent” molecule will be relevant for the subsequent comparison of experimentally and theoretically obtained structural parameters for substituted azobenzenes. A careful structural analysis of the parent AB is the first step toward planned studies of the gas phase molecular structure of phthalonitrile-based azodyes (e.g., [20]), in which the GED analysis will be further complicated by the need to consider tautomerism and a larger number of internal rotations. The present work also continues the studies [33,34,35,36] devoted to determining the sensitivity of the GED method to different kinds of conformational transitions caused by the rotation of various groups.
2. Methods
2.1. Computational Details
DFT calculations of the molecular geometries and Hessian of AB were performed using the Gaussian 09 program package [37]. To assess the applicability of the calculation results in the GED structural analysis, a large number of calculations were carried out using various DFT functionals—B3LYP [38,39], B97D [40], B98 [41], BMK [42], BP86 [43,44], CAM-B3LYP [45], LC-wPBE [46,47,48], M05 [49], M06 [50], M06HF [51,52], mPW1PW91 [53], PBE0 [54], PBE [55], TPSSh [56,57], VSXC [58], and X3LYP [59]. The basis set pcseg-2 [60] from the Basis Set Exchange software [61] was used in all DFT calculations. These basis sets were optimized for use in the DFT theory and were recommended for using in geometry optimizations and calculations of energies, vibrational frequencies, etc. [62]. “Tight” optimization convergence criterion and an “ultrafine” grid (pruned, 99 radial shells and 590 angular points per shell) were used. In a recent paper [63], it was declared that empirical dispersion corrections are not beneficial for medium-sized carbene systems. This is also true for planar E-AB. For an adequate comparison of DFT functionals, it was decided not to use empirical dispersion corrections. Nevertheless, cubic force fields from B3LYP calculations with Grimme’s dispersion corrections D3 [64] were used to generate the starting internuclear distances, vibration amplitudes, and corrections (re − ra), which were utilized in the final GED structural analysis.
The domain-based local pair natural orbital coupled cluster method with single, double, and semicanonical perturbative triples corrections DLPNO-CCSD(T0) [65,66,67,68] with TightPNO thresholds was used for single-point (SP) energy calculations in the ORCA program [69]. DLPNO-CCSD(T0) calculations were performed using corresponding optimized geometries from DFT/pcseg-2 calculations. SCF convergence was set to “VeryTight”. The calculations utilize correlation consistent basis sets cc-pVTZ [70] and cc-pVQZ [70]. The computational effort was reduced by making use of the resolution of the identity with the auxiliary basis sets cc-pVnZ/C (n = T, Q) [71]. Equation (1) [72] was used for two-point complete basis set (CBS) extrapolations with cc-pVnZ (n = T, Q) basis sets.
where n = 3 for cc-pVTZ and n = 4 for cc-pVQZ, A—constant, determined by solving a system of two equations.
Fractional occupation number weighted density (FOD) calculations were also carried out using ORCA [69]. The FOD was conducted by finite-temperature DFT calculations with a smearing temperature of 5000K using a TPSS [56] functional and def2-TZVP [73] basis set, as recommended by the authors of ref. [74].
2.2. Structural Analysis
2.2.1. Approaches
The experimental data (molecular scattering intensities and background function) obtained by the authors of ref. [30] were used to carry out the structural analysis. The procedure of the GED data refinement was performed using the UNEX program [75]. The Z-matrix was constructed according to the C2h-symmetry group (Table S1). Harmonic and cubic force fields were used for the generation of vibrational amplitudes and corrections (rh1 − ra and re − ra) by the VibModule program [76]. We will call the obtained structural parameters semiexperimental, since the vibrational corrections to the equilibrium geometry have an exclusively theoretical nature. Two approaches of structure refinement were applied to refine the structural parameters: molecular orbital constrained gas electron diffraction (MOCED) [32] using Euation (2) and the regularization method (RM) [77,78,79] using Equation (3).
where siM(si)exp—experimental molecular scattering intensities from [30]; siM(si)theor—theoretical molecular scattering intensities; αreg—regularization constant; —individual weight; —reference (restraining) value; and —the model (refining) value of the k-th structural parameter of the molecule.
For the MOCED variant, refinements were carried out in a way that parameter differences were constrained within sorted groups. Under the current study, four types of internuclear distances (N1=N’1, N1-C2, C2-C3, C3-H3) and two types of bond angles (C2-N1=N’1, N1-C2-C3) were refined independently. The remaining distances C-C and C-H were tied to the appropriate parameters mentioned above by the difference between the nonequivalent structural parameters of the same type. Angles C-C-C were tied to the angle N1-C2-C3. The amplitudes were refined in five groups corresponding to the different peaks on the radial distribution curve.
The RM imposes softer constraints. Compared to Equation (2) for the MOCED method, a penalty functional αreg∙ΦQC(αreg) based on the computed quantum chemical parameter has been added to the equation of refinement in the framework of RM. The second term in Equation (3) essentially restricts the k-th parameter to some limits determined by the αreg coefficient. Thus, a choice of the αreg value is decisive in the framework of this refinement approach. Under this investigation for different starting sets of internuclear distances, vibrational amplitudes and corrections, the regularization constants αreg were adjusted as a minimum for Equation (4) [80].
In a least squares (LS) analysis, the disagreement factor Rf between experimental and theoretical scattering intensity was calculated as
where siM(si)theor—theoretical molecular scattering intensities; siM(si)exp—experimental molecular scattering intensities from [30]; and kM—the scale factor.
The weights of the parameters in (3) were obtained () from their ascribed standard deviations (σk): 0.005 Å for bond lengths (0.01 Å for hydrogen bonds) and 0.5° for valence and dihedral angles. Contributions of the terms of Equation (2) to the refined parameters were estimated using the W2 method described in ref. [81].
In this work, structural analysis was carried out using: (i) a semirigid (static) model [31,82]; (ii) one-dimensional dynamic models constructed using pseudoconformers and potential energy function [31,82,83]; and (iii) a two-dimensional pseudoconformer model constructed using a mixture of molecules [29].
2.2.2. One-Dimensional Dynamic Models
We have carried out a one-dimensional dynamic version of GED data processing in three variants: (DM1) pseudoconformers obtained by rotation of only one phenyl group were considered (similar to the original work [30]); (DM2) pseudoconformers belonging to the C2 point group of symmetry, obtained by synchronous rotations of two phenyl groups or rotational vibration of Au symmetry, were considered; and (DM3) pseudoconformers belonging to the point group of symmetry Ci, obtained by synchronous rotations of two phenyl groups or vibration of Bg symmetry, were considered. The fully relaxed scan of the φ = 0°–90° coordinates at intervals of 15° and appropriate calculations of harmonic frequencies of vibrations at the B3LYP-D3/pcseg-2 level were carried out. The potential function was approximated by Equation (6), consistent with the need for the function to be symmetrical with respect to φ = 0 and π/2:
Abundances of the pseudoconformers were calculated using relative energies of structures and Boltzmann distribution. Vibrational amplitude l and vibrational corrections rh1 − ra were computed using the VibModule program from quadratic force fields with the exception of (i) in the case of (DM1) and (DM2) variants—the vibrational mode corresponding to lowest mode of Au symmetry under C2h point group—and (ii) in case of (DM3) variant—the vibrational mode corresponding to lowest mode belonging to the Bg irreducible representation under C2h point group.
2.2.3. 2D Pseudoconformer Model
The 2D pseudoconformer model was based on 190 rotational pseudoconformers with φ1 ∈ [−90°; 90°] and φ’1 ∈ [0°; 90°] with a step of Δφ = 10° (Figure 2). Due to the fact that the remaining part of the PES is symmetrical to the considered region, the remaining structures were not considered separately but were taken into account by correspondingly changing values for mole fractions. Abundances of the pseudoconformers were calculated using Boltzmann distribution on the basis of B3LYP-D3/pcseg-2 relaxed scan calculations and were fixed in the structural refinement. Vibrational amplitude l and vibrational corrections rh1 − ra for pseudoconformers marked in Figure 2 with circles were computed from quadratic force fields with the exclusion of two vibrational modes corresponding to phenyl rotations. For the remaining structures (correspond to the points in Figure 2), the corresponding parameters were calculated using the force field of the nearest structure, for which the harmonic vibration frequencies were calculated (corresponding to the circles in Figure 2).
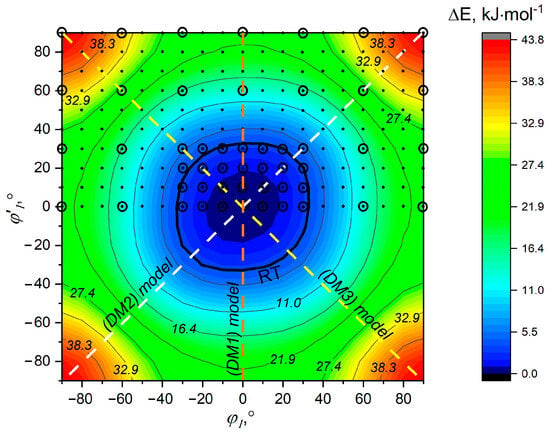
Figure 2.
PES obtained at the B3LYP-D3/pcseg-2 level of theory as a function of rotations of two phenyl moieties around N-C bonds. Bold line RT corresponds to the temperature of GED experiment (Texp = 407 K) [30]. The points correspond to the structures taken into account in the 2D pseudoconformer model. Circles mark structures for which harmonic frequencies were calculated for subsequent evaluation of vibrational amplitudes and corrections for 2D pseudoconformer model analysis. The dashed lines indicate geometries on the PES that are actually described by the structural analyses using dynamic models.
3. Results and Discussion
3.1. Multireference Nature of the Electronic Wave Function
In order to determine the multireference nature of the electronic wave function, an analysis of well-known diagnostic parameters (the Euclidean norm of the vector of t1 amplitudes or T1 [84], value of the largest double excitation amplitudes or T2 [85,86], NFOD) was carried out. It is noted that to apply a single-reference approach to describe a system, T1 and T2 values should not exceed 0.02 [84] and 0.1–0.2 [87]. The T1 (0.011 for both isomers) and T2 (0.046—for E-, 0.063—for Z-isomers) values were also within acceptable limits for the use of single-reference methods. FOD are largely localized on the nitrogen atoms (Figure S1). FOD diagnostic provides values of 0.344 and 0.299 for E- and Z-isomers, respectively. These indicators can be compared with data on nitroxoline and anthracene molecules (NFOD = 0.215 and 0.249), for which the applicability of single-reference methods was previously justified [88].
3.2. Evaluation of Optimized Geometries
MP2/6-31+G* predicted a twisted structure of E-AB [30]. DLPNO-CCSD(T0)/CBS // MP2/6-31+G* calculations indicate that the planar structure is energetically advantageous by 1.4 kJ∙mol−1. According to all DFT calculations mentioned in Section 2, as expected, E-AB has a flat structure of C2h symmetry. It is worth noting that the M05 calculation gave one imaginary frequency for the structure of C2h symmetry and the minimum turned out to be very close to it. However, by increasing the grid size, this problem was solved: all frequencies for the C2h symmetry structure are real.
QC calculations predict the structural parameters of E-AB with large uncertainty. Internuclear distances from DFT/pcseg-2 calculations are lower than those obtained [30] in MP2/6-31+G*. The use of different DFT functionals leads to quite strong differences in geometry (Table S2), primarily in the value of the N=N bond length from 1.221 Å (M06HF) to 1.267 Å (BP86). In this study, the quality of different DFT geometries is evaluated by calculating the DLPNO-CCSD(T0)/CBS energies for all optimized structures in a similar manner as the authors of ref. [63]. The lowest-energy (DLPNO-CCSD(T0)) structure is provided by the BMK functional (Table S3). Energy differences within 0.5 kJ∙mol−1 were derived for structures optimized by B3LYP, B98, and TPSSh calculations. More than 3.0 kJ∙mol−1 higher energy corresponds to the structures obtained by the LC-wPBE and M06HF (underestimating internuclear distances compared to BMK results), BP86, and PBE (overestimating internuclear distances compared to BMK results) functionals. Similar results were achieved within the framework of the analysis of optimized geometries of Z-AB (Table S4).
3.3. E-AB vs. Z-AB: Capabilities of GED Method
E-AB is energetically much more preferable compared to Z-AB. According to the DFT calculations considered, the gain in energy of the E-AB ranges from 43 to 63 kJ∙mol−1, while higher-level DLPNO-CCSD(T0)/CBS calculations predict this value to be ca. 51 kJ∙mol−1 (Table S5). The E-AB→Z-AB transition significantly affects the N1-C2 and N1-N’1 bond lengths: the difference in the values of these parameters in the two isomers are ca. 0.01 and ca. 0.02 Å, respectively [20]. The simulated radial distribution curves f(r) for E-AB and Z-AB differ significantly (Figure S2). Therefore, it is possible to distinguish cis- and trans-isomers of azobenzene and its derivatives. The structural analysis carried out in this work with assumptions of the cis-structure of AB poorly describes the experimental data presented in the work [30]. Modeling mixtures of trans- and cis-isomers in structural analysis also indicates the absence of Z-AB in the vapors under experimental conditions.
3.4. Does the Quality of Starting Parameters for GED Analysis Strongly Depend on the Choice of DFT Functional?
In GED structural refinement, three groups of parameters derived from theoretical calculations are used: internuclear distances, vibrational amplitudes, and corrections to internuclear distances. The first two groups usually vary during the LS procedure. In order to determine the spread of the starting parameters obtained by different QC calculations, the relative ranges R determined by Equations (7) and (8) were used for analysis.
where p is one of the parameters for pairs of atoms Xi and Yj (Xi, Yj = H, C, N): (i) internuclear distances re; (ii) differences between internuclear distances Δre equal to re(Ci-Cj)−re(C2-C3) or re(Ci-Cj)−re(N1-C2) or re(Xi-Xj)−re(N1=N’1); pmax and pmin are maximal and minimal values of the parameter p among those found by considered QC calculations; and <re> is the average value of the internuclear distance re for term Xi-Xj according to calculations using various functionals. Since the internuclear distances from the BMK calculations turned out to be approximately average among their analogues obtained in the considered set of calculations, we can use re(BMK) instead of the <re> in Formula (7). Thus, to analyze the ranges of vibrational amplitudes and vibrational corrections, Equation (8) was used.
where p is one of the parameters for pairs of atom Xi and Yj (Xi, Yj = H, C, N): vibrational amplitudes l, vibrational corrections (re − ra) or (rh1 − ra); pmax and pmin are maximal and minimal values of the parameter p among those found by QC calculations; and re(BMK) is the value of internuclear distance re by BMK calculations.
3.4.1. Internuclear Distances
Within the framework of the widely used MOCED method [32], in order to reduce the correlation between the independent parameters and improve the stability of the LS procedure, internuclear distances are combined into groups by the constraining differences (in general, Δr = r(Xi − Xj) − r(Xm − Xn)) between them within each group. In this case, obviously false differences taken from the theory will spoil GED structural refinement. It is worth mentioning that this problem can be solved by using the regularization procedure [77,78,79] but then it is necessary to decide the issue of choosing a suitable regularization factor αreg as carried out in this work by using Equation (4), or in other possible ways [89].
Previously, researchers [30] used four groups of bonded atom pairs: N=N, N-C, C-C, and C-H, despite the fact that a significant correlation (−0.79) was observed between the groups N-C and C-C. In this approach, differences between internuclear distances Δre should be kept only for terms C-C (i.e., Δre(Ci − Cj) = re(Ci − Cj) − re(C2 − C3)). The maximum spread in the Δre parameters equal to Δre = 0.012 Å (Δrmin = ΔrB97D = −0.015 Å, Δrmax = ΔrM06HF = −0.003 Å) was found for the distance C6-C7. This deviation corresponds to R(Δr) = 0.8% of the internuclear distance. When combining groups C-C and N-C, the maximum spread in the Δr will already be 0.033 Å, which corresponds to R(Δr) = 2.4% (Table S1). In the case of a rough constraining of all distances of the molecular framework (combining groups N=N, N-C and C-C), the maximum spread in the Δr becomes equal to 0.056 Å (or R(Δr) = 4%, Table S1). This can lead to optimization problems within the framework of structural analysis. For AB, the variant of dividing all bonding distances into four groups is justified based on the data presented and was used in current work for all MOCED refinements.
3.4.2. Vibrational Amplitudes
LC-wPBE calculations predict a shallow potential function of E-AB along the N=N-C-C torsional coordinates and a low vibrational frequency, ωrot.Ph = 6.6 cm−1, corresponding to the rotation of the phenyl rings (Table S6). A quite low frequency (ωrot.Ph < 13 cm−1) is also obtained in the calculations using M05 and M06HF functionals. This results in overestimated vibrational amplitudes and corrections that are very different from those obtained on the base of all other calculations. When comparing the acquired amplitude values for all remaining calculations (13 functionals), it can be noted that the average spread in the vibrational amplitudes is R(l)ave = 0.39% (Figure S3). The average relative range in vibrational corrections is rh1 − ra is 0.65% (Figure S4). The maximal ranges in vibrational amplitudes (corrections) were found only for six (twenty four) unbonded distances X∙∙∙H3,7,3′,7′: R(l) = 2–5% (R(rh1 − ra) = 2–8%) (Figures S3 and S4). Due to the poor determination of the position of hydrogen atoms in the GED method, these differences in the predicted parameters should not play a large role in the convergence of the LS procedure and the resulting final semiexperimental structure. The spread of the obtained vibrational corrections (re − ra) and (rh1 − ra) is similar (Figures S4 and S5). Ignoring the first low frequency when calculating vibrational amplitudes and corrections leads to very similar values (R(l)ave = 0.19%, R(rh1 − ra)ave = 0.22%), regardless of the functional used in QC calculations (even in the case of functionals LC-wPBE, M05 and M06HF) (Figures S6 and S7). Such vibrational parameters are suitable for use in a dynamic model.
Next, we checked how significant the found ranges in the values of the starting parameters would be for the LS analysis. LS procedures carried out within the framework of the MOCED method gave results that were in good agreement with each other and with the results of the work [30]. In almost all cases, it was possible to achieve both a low disagreement factor, Rf, and the same semiexperimental structural parameters of the molecule. The exceptions were analyses that used overestimated starting parameters taken from LC-wPBE, M05, and M06HF calculations (Tables S7 and S8, Figures S8 and S9). Thus, we can note the relatively good stability of the structural analysis to the choice of starting values of internuclear distances, vibrational amplitudes, and corrections.
In the case of structural analysis using the regularization method, one of the important fundamental actions is the choice of αreg. In this work, αreg was chosen separately for each set of starting values used in LS analysis. However, this approach showed less stability than within the MOCED method. RM still gives some ranges in the resulting disagreement factors, Rf, and, accordingly, in the structural parameters rg (Tables S9 and S10, Figures S10 and S11). With all this, the structures corresponding to an acceptably low Rf are very close to each other. It is also worth noting the stability of the structural analysis when changing the harmonic field to a cubic one: the structural parameters in terms of rg within the error limits are in good agreement (Tables S7–S10).
3.5. GED Analysis: Semirigid, One-Dimensional Dynamic and Two-Dimensional Dynamic Models
The rotational vibration of Au symmetry (symmetrical relative to the C2 axis) of the phenyl rings has a low frequency ~17 cm−1 (Table S6). According to the DLPNO-CCSD(T0)/CBS // B3LYP-D3/pcseg-2 calculation, the rotation barrier of one phenyl group is estimated to be about 19 kJ∙mol−1. Within the framework of the simultaneous rotation of two phenyl rings (along the τ(N1=N’1-C’2-C’3) + τ(N1=N’1-C’2-C’7) + τ(N’1=N1-C2-C3) + τ(N’1=N1-C2-C7) torsional coordinate), the barrier becomes equal to ca. 37 kJ∙mol−1 (Figure S12). It is important to note that different DFT calculations yield a large range in the barrier value—from 32 (LC-wPBE) to 72 kJ∙mol−1 (VSXC). The rotation of the phenyl rings is accompanied by the breaking of the π conjugation and the corresponding lengthening of the N-C bonds and shortening of the N1-N’1 bond (Figure S13). However, in the extensive area near the minimum in the PES of E-AB (at least with −30° < φ < 30°), the geometric changes are insignificant (Figure S13) and do not lead to a strong increase in the relative energy (Figure 2 and Figure S12). Based on the softness of potential along the phenyl rotation vibration coordinate, it is indeed justified to consider these rotations as large-amplitude motions and using dynamic a GED model in structural analysis.
It turned out that in dynamic GED analysis, the refined values of the parameters V0, V2, V4 from Equation (4) had large standard deviations and were unreliable. Therefore, it was decided to fix the parameters of the potential function in the structural refinement. All three structural analyses using different dynamic models DM1, DM2, and DM3 give almost identical structural parameters of the molecule and the values of Rf equal to 3.5–3.6%. However, these approaches to accounting for large-amplitude motions are also limited in that they describe the PES profile in Figure 2 under restrictions marked by dashed lines only. To eliminate this shortcoming, a structural analysis in the framework of a 2D pseudoconformer model can be performed, as recommended in the work for stilbene [29]. According to this consideration, the same structure of E-AB was obtained as in the case of previous analyses but with a slightly larger disagreement factor Rf = 3.7%.
In the next step, a structural analysis using a static model was performed. A semirigid model agreed well with experimental data giving Rf = 3.5%. The smaller Rf in the case of the semirigid model should not come as a surprise. Previously, the authors of ref. [90] studying the diaziridine derivative explained similar results due to two reasons: (i) dynamic models required a large number of not-refined constraints taken from theoretical calculations; and (ii) the fallacy of the theoretical potential used.
Additionally, we checked the possibility of determining the torsion angles φ1 and φ’1 using a semirigid model, for which we carried out (i) a comparison of the theoretical radial distribution curves f(r) for pseudoconformers, discussed above in the study of individual phenyl moiety rotation and synchronous rotations of two phenyl groups; and (ii) least-squares analyses for pseudoconformers using a static model with freezing dihedral angle values φ1 and φ’1. Models of considered pseudoconformers with 0° < |φ1; φ’1| < 30° should equally describe the experimental data, as indicated by minor differences in the theoretical radial distribution curves f(r) and the corresponding small values of Rftheor (Figures S14–S16). An analysis of the experimental data using the planar structure of C2h symmetry and pseudoconformers with rotation angles φ up to ~30° as a starting approximation makes it possible to obtain almost the same disagreement factors, Rf ≈ 3.5% (Figure S17). Using Hamilton’s criterion [91] shows that the uncertainty in determining the angle φ is about 40°. This value agrees well with the results of the DLPNO/CCSD(T0) calculated potential energy: the thermal energy, RTexp, corresponds to the relative energy of the conformer with φ1 = 37° and φ’1 = 0°.
3.6. Semiexperimental Equilibrium Structure
A structural analysis within the framework of dynamic and 2D pseudoconformer models provide similar structural parameters and disagreement factors Rf as the refinement using a semirigid model. Based on the results of this work, the structure refined from the B3LYP-D3/pcseg-2 calculated a geometry within the MOCED method using a semirigid model was chosen as the final semiexperimental equilibrium structure (Table 1 and Table S11).

Table 1.
Structural parameters a of E-AB according to QC b and GED.
Comparing the results of the GED structural analyses obtained by us (using the experimental data of [30]) and by the authors of refs. [28,30], it can be concluded that the internuclear distances in terms of rg are in good agreement with each other within the experimental error (Table 1). If the work in ref. [30] concluded that E-AB was planar, then the older work in ref. [28] stated that the molecules have distorted conformations with the phenyl groups twisted approximately 30° around the N-C bonds. Moreover, as reported by the authors of ref. [28], it was not possible to decide whether the phenyl groups were rotated to the same or to the opposite side relative to the azo bridge. Numerous variants of structural analysis carried out in this work indicate that the GED experiment unreliably determines the torsion angles φ1 and φ’1 as well as parameters Vi of potential function. This can be attributed to the facts that (i) flat and twisted (with 0° < |φ1; φ’1| < 30°) structures have internuclear distances close to each other; and (ii) the PES of E-AB is shallow along the N=N-C-C torsional coordinates. However, accompanied by high-level QC calculations, it can be stated that equilibrium structure of E-AB is planar. In this work, we also defined for the first time the GED structure of E-AB in terms of the re parameters that we recommend for terminologically correct comparison with QC optimized structural parameters for AB and its derivatives.
4. Conclusions
The AB considered in the work is the parent compound of many practically important compounds. It serves as a reference point in the search for new substances and materials, promising for practical application and for prediction of their physicochemical properties. The special importance is the knowledge about accurate molecular structure since it is the basis for all stereochemical constructions.
The semiexperimental equilibrium structure of the E-AB molecule was obtained and can be recommended as the most accurate to date. We can conclude that, according to the GED experiment, E-AB has a planar structure. High-level DLPNO-CCSD(T0) calculations confirmed that the flat geometry corresponds to the minimum on the PES. It is shown that, despite some nonrigidity of the E-AB molecule, the structural analysis using a dynamic model and an even more expensive 2D model is redundant. These variants of structural analyses did not lead to any noticeable decrease in the disagreement factor Rf compared to using the semirigid model. The resulting structural parameters of the planar pseudoconformer are almost identical according to these refinements. Determination of the experimental potential along the rotation coordinate of phenyl fragments using a dynamic model is associated with high errors in the coefficients Vi, which actually indicates the impossibility of this determination by means of GED. Rotation of the phenyl rings around the N-C bond at φ ≈ −40° ÷ 40° is probable under the experimental conditions but does not lead to significant changes in the bonded distances in the molecule. It is also noted that the relative energy of the Z-AB isomer is much greater than the thermal energy RTexp, so there is no need to consider the cis isomer as a component of the vapor under the experiment. These conclusions are recommended to be used to simplify the nontrivial structural analysis of the conformationally more complex azobenzene derivatives.
The influence of the DFT functional choice for the prediction starting parameters (distances, amplitudes, corrections) on the GED structural analysis results was considered. Despite the good agreement between the energetic parameters (the barriers of phenyl rotations, the relative energies of the Z- and E- isomers) obtained using LC-wPBE, M05, and M06 calculations with higher-level data of DLPNO-CCSD(T0), molecular structures and vibrational parameters (l, re − ra, rh1 − ra) from the LC-wPBE, M05, and M06 results turned out to be unsuitable for refinement using a semirigid model. The remaining DFT calculations generally performed well in structural analysis. Despite the above, M05 predicted a structure that is in good agreement with the GED results. B3LYP, mPW1PW91, PBE0, TPSSh, and X3LYP calculations also predict the structure to within the error of a GED experiment, while GGA calculations (B97D, BP86, and PBE) overestimate NN and CC distances. Based on a comparison with the results of the GED experiment and the results of high-level DLPNO-CCSD(T0) calculations, it can be recommended to use the B3LYP, TPSSh, and X3LYP functionals for studying the molecular structure of azobenzene derivatives.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/physchem4020010/s1, Figure S1: FOD plot for AB; Figure S2: Comparison of theoretical radial distribution functions f(r) of E-AB and Z-AB; Figure S3: Relative ranges of vibrational amplitudes R(l) for pairs of atom Xi and Yj (Xi, Yj = H, C, N); Figure S4: Relative ranges of vibrational corrections R(rh1 − ra) for pairs of atom Xi and Yj (Xi, Yj = H, C, N); Figure S5: Relative ranges of vibrational corrections R(re − ra) for pairs of atom Xi and Yj (Xi, Yj = H, C, N); Figure S6: Relative ranges of vibrational amplitudes R(l) for pairs of atom Xi and Yj (Xi, Yj = H, C, N); Figure S7: Relative ranges of vibrational corrections R(rh1 − ra) for pairs of atom Xi and Yj (Xi, Yj = H, C, N); Figure S8: Results of GED structural refinement for E-AB in the framework of MOCED method using starting parameters re, l, rh1 − ra obtained by different DFT calculations; Figure S9: Results of GED structural refinement for E-AB in the framework of MOCED method using starting parameters re, l, re − ra obtained by different DFT calculations; Figure S10: Results of GED structural refinement for E-AB in the framework of RM using starting parameters re, l, rh1 − ra obtained by different DFT calculations; Figure S11: Results of GED structural refinement for E-AB in the framework of RM using starting parameters re, l, re − ra obtained by different DFT calculations; Figure S12: Potential energy function of simultaneous rotation of two phenyl rings around the N1-C2 and N’1-C’2 bonds in the E-AB molecule, calculated in different approximations; Figure S13. Internuclear distances N1-N’1 (red circles) and N1-C2 (blue squares) vs. dihedral angles φ1 and φ’1 in the E-AB molecule from the B3LYP-GD3/pcseg-2 calculations; Figures S14–S16: Comparison of theoretical radial distribution functions f(r) of pseudoconformers of E-AB; Figure S17: The ratio of disagreement factors Rf as a function of torsion angles φ1 and φ’1, responsible for rotation of phenyls; Table S1. Unex Z-matrix of E-AB; Table S2: Structural parameters (Å) of E-AB according different DFT-calculations; Table S3: Relative energies of E-AB according DLPNO-CCSD(T0) calculations; Table S4: Relative energies of Z-AB according DLPNO-CCSD(T0) calculations; Table S5: Energies of Z-AB relative to the E-AB according DLPNO-CCSD(T0) calculations; Table S6: Relative energies of pseudoconformers of E-AB and vibrational frequency of phenyls rotations according DFT, MP2 and DLPNO-CCSD(T0) calculations; Table S7: Internuclear distances rg of E-AB determined by MOCED structural analyzes using starting internuclear distances re, vibrational amplitudes l and corrections re − ra from results of different DFT calculations; Table S8: Internuclear distances rg of E-AB determined by MOCED structural analyzes using starting internuclear distances re, vibrational amplitudes l and corrections rh1 − ra from results of different DFT calculations; Table S9: Internuclear distances rg and corresponding contribution of experimental GED data to parameters (w) of E-AB determined by RM structural analyzes using starting internuclear distances re, vibrational amplitudes l and corrections re − ra from results of different DFT calculations. Table S10: Internuclear distances rg and corresponding contribution of experimental GED data to parameters (w) of E-AB determined by RM structural analyzes using starting internuclear distances re, vibrational amplitudes l and corrections rh1 − ra from results of different DFT calculations; Table S11: Cartesian atomic coordinates of final semiexperimental equilibrium structure (re) of E-AB according GED method.
Author Contributions
Conceptualization, A.E.P.; methodology, A.E.P., I.Y.K., A.V.E. and Y.A.Z.; software, Y.A.Z.; validation, A.E.P.; formal analysis, A.E.P., I.Y.K. and A.V.E.; investigation, A.E.P., I.Y.K., A.V.E., M.N.Z. and Y.A.Z.; resources, Y.A.Z.; writing—original draft preparation, A.E.P., I.Y.K., M.N.Z., A.V.E. and Y.A.Z.; writing—review and editing, A.E.P., M.N.Z. and Y.A.Z.; visualization, A.E.P. and I.Y.K.; project administration, A.E.P.; funding acquisition, A.E.P. All authors have read and agreed to the published version of the manuscript.
Funding
The study was supported by the Russian Science Foundation (grant № 22-73-00314).
Data Availability Statement
Data is contained within the article and Supplementary Material.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Fedele, C.; Ruoko, T.-P.; Kuntze, K.; Virkki, M.; Priimagi, A. New tricks and emerging applications from contemporary azobenzene research. Photochem. Photobiol. Sci. 2022, 21, 1719–1734. [Google Scholar] [CrossRef] [PubMed]
- Giles, L.W.; Faul, C.F.J.; Tabor, R.F. Azobenzene isomerization in condensed matter: Lessons for the design of efficient light-responsive soft-matter systems. Mater. Adv. 2021, 2, 4152–4164. [Google Scholar] [CrossRef]
- Purkait, M.K.; Sinha, M.K.; Mondal, P.; Singh, R. (Eds.) Chapter 4—Photoresponsive Membranes. In Stimuli Responsive Polymeric Membranes; Interface Science and Technology; Elsevier: Amsterdam, The Netherlands, 2018; Volume 25, pp. 115–144. [Google Scholar] [CrossRef]
- Natansohn, A.; Rochon, P. Photoinduced Motions in Azo-Containing Polymers. Chem. Rev. 2002, 102, 4139–4176. [Google Scholar] [CrossRef] [PubMed]
- Manickasundaram, S.; Kannan, P.; Hassan, Q.M.A.; Palanisamy, P.K. Azo dye based poly(alkyloxymethacrylate)s and their spacer effect on optical data storage. J. Mater. Sci. Mater. Electron. 2008, 19, 1045–1053. [Google Scholar] [CrossRef]
- Beharry, A.A.; Woolley, G.A. Azobenzene photoswitches for biomolecules. Chem. Soc. Rev. 2011, 40, 4422–4437. [Google Scholar] [CrossRef] [PubMed]
- Mohr, G.J.; Müller, H.; Bussemer, B.; Stark, A.; Carofiglio, T.; Trupp, S.; Heuermann, R.; Henkel, T.; Escudero, D.; González, L. Design of acidochromic dyes for facile preparation of pH sensor layers. Anal. Bioanal. Chem. 2008, 392, 1411–1418. [Google Scholar] [CrossRef] [PubMed]
- Shikhaliyev, N.Q.; Kuznetsov, M.L.; Maharramov, A.M.; Gurbanov, A.V.; Ahmadova, N.E.; Nenajdenko, V.G.; Mahmudov, K.T.; Pombeiro, A.J.L. Noncovalent interactions in the design of bis-azo dyes. CrystEngComm 2019, 21, 5032–5038. [Google Scholar] [CrossRef]
- Vapaavuori, J.; Bazuin, C.G.; Priimagi, A. Supramolecular design principles for efficient photoresponsive polymer–azobenzene complexes. J. Mater. Chem. C 2018, 6, 2168–2188. [Google Scholar] [CrossRef]
- Walther, M.; Kipke, W.; Schultzke, S.; Ghosh, S.; Staubitz, A. Modification of Azobenzenes by Cross-Coupling Reactions. Synthesis 2021, 53, 1213–1228. [Google Scholar] [CrossRef]
- Concilio, S.; Sessa, L.; Petrone, A.M.; Porta, A.; Diana, R.; Iannelli, P.; Piotto, S. Structure Modification of an Active Azo-Compound as a Route to New Antimicrobial Compounds. Molecules 2017, 22, 875. [Google Scholar] [CrossRef]
- Dong, L.; Feng, Y.; Wang, L.; Feng, W. Azobenzene-based solar thermal fuels: Design, properties, and applications. Chem. Soc. Rev. 2018, 47, 7339–7368. [Google Scholar] [CrossRef] [PubMed]
- Kang, H.-C.; Lee, B.M.; Yoon, J.; Yoon, M. Synthesis and Surface-Active Properties of New Photosensitive Surfactants Containing the Azobenzene Group. J. Colloid Interface Sci. 2000, 231, 255–264. [Google Scholar] [CrossRef] [PubMed]
- Biswas, N.; Umapathy, S. Density Functional Calculations of Structures, Vibrational Frequencies, and Normal Modes of trans- and cis-Azobenzene. J. Phys. Chem. A 1997, 101, 5555–5566. [Google Scholar] [CrossRef]
- Kurita, N.; Tanaka, S.; Itoh, S. Ab Initio Molecular Orbital and Density Functional Studies on the Stable Structures and Vibrational Properties of trans- and cis-Azobenzenes. J. Phys. Chem. A 2000, 104, 8114–8120. [Google Scholar] [CrossRef]
- Fliegl, H.; Köhn, A.; Hättig, C.; Ahlrichs, R. Ab Initio Calculation of the Vibrational and Electronic Spectra of trans- and cis-Azobenzene. J. Am. Chem. Soc. 2003, 125, 9821–9827. [Google Scholar] [CrossRef] [PubMed]
- Hättig, C.; Hald, K. Implementation of RI-CC2 triplet excitation energies with an application to trans-azobenzene. Phys. Chem. Chem. Phys. 2002, 4, 2111–2118. [Google Scholar] [CrossRef]
- Briquet, L.; Vercauteren, D.P.; Perpète, E.A.; Jacquemin, D. Is solvated trans-azobenzene twisted or planar? Chem. Phys. Lett. 2006, 417, 190–195. [Google Scholar] [CrossRef]
- Duarte, L.; Fausto, R.; Reva, I. Structural and spectroscopic characterization of E- and Z-isomers of azobenzene. Phys. Chem. Chem. Phys. 2014, 16, 16919–16930. [Google Scholar] [CrossRef] [PubMed]
- Pogonin, A.E.; Kurochkin, I.Y.; Malyasova, A.S.; Ksenofontova, K.V.; Koifman, O.I. Molecular Structure and Vibrational Spectra of 4-(4-Hydroxyphenylazo)phthalonitrile: DFT Study. Macroheterocycles 2023, 16, 156–167. [Google Scholar] [CrossRef]
- Chen, P.C.; Chieh, Y.C. Azobenzene and stilbene: A computational study. J. Mol. Struct. THEOCHEM 2003, 624, 191–200. [Google Scholar] [CrossRef]
- Giricheva, N.I.; Lebedev, I.S.; Fedorov, M.S.; Bubnova, K.E.; Girichev, G.V. Structural aspects of trans–cis isomerization of azobenzene, 4,4′-azopyridine, and azoxybenzene. J. Struct. Chem. 2021, 62, 1976–1987. [Google Scholar] [CrossRef]
- De Lange, J.J.; Robertson, J.M.; Woodward, I.; Bragg, W.H. X-ray crystal analysis of trans-azobenzene. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1939, 171, 398–410. [Google Scholar] [CrossRef]
- Brown, C.J. A refinement of the crystal structure of azobenzene. Acta Crystallogr. 1966, 21, 146–152. [Google Scholar] [CrossRef]
- Bouwstra, J.A.; Schouten, A.; Kroon, J. Structural studies of the system trans-azobenzene/trans-stilbene. I. A reinvestigation of the disorder in the crystal structure of trans-azobenzene, C12H10N2. Acta Crystallogr. Sect. C 1983, 39, 1121–1123. [Google Scholar] [CrossRef]
- Harada, J.; Ogawa, K.; Tomoda, S. Molecular Motion and Conformational Interconversion of Azobenzenes in Crystals as Studied by X-ray Diffraction. Acta Crystallogr. Sect. B 1997, 53, 662–672. [Google Scholar] [CrossRef]
- Harada, J.; Ogawa, K. Invisible but Common Motion in Organic Crystals: A Pedal Motion in Stilbenes and Azobenzenes. J. Am. Chem. Soc. 2001, 123, 10884–10888. [Google Scholar] [CrossRef] [PubMed]
- Traetteberg, M.; Hillmo, I.; Hagen, K. A gas electron diffraction study of the molecular structure of trans-azobenzene. J. Mol. Struct. 1977, 39, 231–239. [Google Scholar] [CrossRef]
- Lin, M.M.; Shorokhov, D.; Zewail, A.H. Conformations and Coherences in Structure Determination by Ultrafast Electron Diffraction. J. Phys. Chem. A 2009, 113, 4075–4093. [Google Scholar] [CrossRef][Green Version]
- Tsuji, T.; Takashima, H.; Takeuchi, H.; Egawa, T.; Konaka, S. Molecular Structure and Torsional Potential of trans-Azobenzene. A Gas Electron Diffraction Study. J. Phys. Chem. A 2001, 105, 9347–9353. [Google Scholar] [CrossRef]
- Demaison, J.; Vogt, N. Molecular Structures from Gas-Phase Electron Diffraction. In Accurate Structure Determination of Free Molecules; Springer International Publishing: Cham, Switzerland, 2020; pp. 167–204. ISBN 978-3-030-60492-9. [Google Scholar]
- Chiu, N.S.; Ewbank, J.D.; Askari, M.; Schäfer, L. Molecular orbital constrained gas electron diffraction studies. J. Mol. Struct. 1979, 54, 185–195. [Google Scholar] [CrossRef]
- Kurochkin, I.Y.; Otlyotov, A.A.; Girichev, G.V.; Pogonin, A.E.; Kiselev, A.N. DFT study of molecular structure of 5,10,15,20-tetrakis(4′-halogenophenyl)porphyrins and their isomers. Izv. Vyss. Uchebnykh Zaved. Seriya Khimiya Khimicheskaya Tekhnologiya 2020, 63, 51–57. [Google Scholar] [CrossRef]
- Pogonin, A.E.; Tverdova, N.V.; Ischenko, A.A.; Rumyantseva, V.D.; Koifman, O.I.; Giricheva, N.I.; Girichev, G.V. Conformation analysis of copper(II) etioporphyrin-II by combined gas electron diffraction/mass-spectrometry methods and DFT calculations. J. Mol. Struct. 2015, 1085, 276–285. [Google Scholar] [CrossRef]
- Tverdova, N.V.; Pogonin, A.E.; Ischenko, A.A.; Rumyantseva, V.D.; Koifman, O.I.; Giricheva, N.I.; Girichev, G.V. Combined gas-phase electron diffraction/mass spectrometry and DFT study of the molecular structure of zinc(II) etioporphyrin-II. Struct. Chem. 2015, 26, 1521–1530. [Google Scholar] [CrossRef]
- Pogonin, A.E.; Postnikova, D.A.; Shagurin, A.Y.; Marfin, Y.S.; Girichev, G.V. Analysis of the sensitivity of the gas electron diffraction method to the determination of the conformational composition of phenyl and thiophenyl substituted aza-BODIPY: Theoretical study. ChemChemTech [Izv. Vyss. Uchebn. Zaved. Khim. Khim. Tekhnol.] 2022, 65, 29–37. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09, Revision D.01; Gaussian Inc.: Wallingford, CT, USA, 2009. [Google Scholar]
- Becke, A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785. [Google Scholar] [CrossRef] [PubMed]
- Grimme, S. Semiempirical GGA-type density functional constructed with a long-range dispersion correction. J. Comput. Chem. 2006, 27, 1787–1799. [Google Scholar] [CrossRef] [PubMed]
- Schmider, H.L.; Becke, A.D. Optimized density functionals from the extended G2 test set. J. Chem. Phys. 1998, 108, 9624–9631. [Google Scholar] [CrossRef]
- Boese, A.D.; Martin, J.M.L. Development of density functionals for thermochemical kinetics. J. Chem. Phys. 2004, 121, 3405–3416. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional exchange-energy approximation with correct asymptotic behavior. Phys. Rev. A 1988, 38, 3098. [Google Scholar] [CrossRef]
- Perdew, J.P. Density-functional approximation for the correlation energy of the inhomogeneous electron gas. Phys. Rev. B 1986, 33, 8822–8824. [Google Scholar] [CrossRef] [PubMed]
- Yanai, T.; Tew, D.P.; Handy, N.C. A new hybrid exchange-correlation functional using the Coulomb-attenuating method (CAM-B3LYP). Chem. Phys. Lett. 2004, 393, 51–57. [Google Scholar] [CrossRef]
- Vydrov, O.A.; Scuseria, G.E. Assessment of a long-range corrected hybrid functional. J. Chem. Phys. 2006, 125, 234109. [Google Scholar] [CrossRef] [PubMed]
- Vydrov, O.A.; Scuseria, G.E.; Perdew, J.P. Tests of functionals for systems with fractional electron number. J. Chem. Phys. 2007, 126, 154109. [Google Scholar] [CrossRef]
- Vydrov, O.A.; Heyd, J.; Krukau, A.V.; Scuseria, G.E. Importance of short-range versus long-range Hartree-Fock exchange for the performance of hybrid density functionals. J. Chem. Phys. 2006, 125, 74106. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Schultz, N.E.; Truhlar, D.G. Exchange-correlation functional with broad accuracy for metallic and nonmetallic compounds, kinetics, and noncovalent interactions. J. Chem. Phys. 2005, 123, 161103. [Google Scholar] [CrossRef]
- Zhao, Y.; Truhlar, D.G. The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: Two new functionals and systematic testing of four M06-class functionals and 12 other function. Theor. Chem. Acc. 2008, 120, 215–241. [Google Scholar] [CrossRef]
- Zhao, Y.; Truhlar, D.G. Comparative DFT Study of van der Waals Complexes: Rare-Gas Dimers, Alkaline-Earth Dimers, Zinc Dimer, and Zinc-Rare-Gas Dimers. J. Phys. Chem. A 2006, 110, 5121–5129. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Truhlar, D.G. Density Functional for Spectroscopy: No Long-Range Self-Interaction Error, Good Performance for Rydberg and Charge-Transfer States, and Better Performance on Average than B3LYP for Ground States. J. Phys. Chem. A 2006, 110, 13126–13130. [Google Scholar] [CrossRef] [PubMed]
- Adamo, C.; Barone, V. Exchange functionals with improved long-range behavior and adiabatic connection methods without adjustable parameters: The mPW and mPW1PW models. J. Chem. Phys. 1998, 108, 664–675. [Google Scholar] [CrossRef]
- Adamo, C.; Barone, V. Toward reliable density functional methods without adjustable parameters: The PBE0 model. J. Chem. Phys. 1999, 110, 6158–6170. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865, Erratum in Phys. Rev. Lett. 1997, 78, 1396. [Google Scholar] [CrossRef]
- Tao, J.; Perdew, J.P.; Staroverov, V.N.; Scuseria, G.E. Climbing the Density Functional Ladder: Nonempirical Meta--Generalized Gradient Approximation Designed for Molecules and Solids. Phys. Rev. Lett. 2003, 91, 146401. [Google Scholar] [CrossRef] [PubMed]
- Staroverov, V.N.; Scuseria, G.E.; Tao, J.; Perdew, J.P. Comparative assessment of a new nonempirical density functional: Molecules and hydrogen-bonded complexes. J. Chem. Phys. 2003, 119, 12129, Erratum in J. Chem. Phys. 2004, 121, 11507. [Google Scholar] [CrossRef]
- Van Voorhis, T.; Scuseria, G.E. A novel form for the exchange-correlation energy functional. J. Chem. Phys. 1998, 109, 400–410. [Google Scholar] [CrossRef]
- Xu, X.; Goddard, W.A. The X3LYP extended density functional for accurate descriptions of nonbond interactions, spin states, and thermochemical properties. Proc. Natl. Acad. Sci. USA 2004, 101, 2673–2677. [Google Scholar] [CrossRef] [PubMed]
- Jensen, F. Unifying general and segmented contracted basis sets. segmented polarization consistent basis sets. J. Chem. Theory Comput. 2014, 10, 1074–1085. [Google Scholar] [CrossRef] [PubMed]
- Pritchard, B.P.; Altarawy, D.; Didier, B.; Gibson, T.D.; Windus, T.L. New Basis Set Exchange: An Open, Up-to-Date Resource for the Molecular Sciences Community. J. Chem. Inf. Model. 2019, 59, 4814–4820. [Google Scholar] [CrossRef] [PubMed]
- Notes About the Jensen Basis Sets. Available online: https://www.basissetexchange.org/family_notes/jensen/ (accessed on 8 April 2024).
- Shirazi, R.G.; Pantazis, D.A.; Neese, F. Performance of density functional theory and orbital-optimised second-order perturbation theory methods for geometries and singlet–triplet state splittings of aryl-carbenes. Mol. Phys. 2020, 118, e1764644. [Google Scholar] [CrossRef]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef]
- Liakos, D.G.; Guo, Y.; Neese, F. Comprehensive Benchmark Results for the Domain Based Local Pair Natural Orbital Coupled Cluster Method (DLPNO-CCSD(T)) for Closed- and Open-Shell Systems. J. Phys. Chem. A 2020, 124, 90–100. [Google Scholar] [CrossRef] [PubMed]
- Saitow, M.; Becker, U.; Riplinger, C.; Valeev, E.F.; Neese, F. A new near-linear scaling, efficient and accurate, open-shell domain-based local pair natural orbital coupled cluster singles and doubles theory. J. Chem. Phys. 2017, 146, 164105. [Google Scholar] [CrossRef] [PubMed]
- Riplinger, C.; Neese, F. An efficient and near linear scaling pair natural orbital based local coupled cluster method. J. Chem. Phys. 2013, 138, 34106. [Google Scholar] [CrossRef] [PubMed]
- Riplinger, C.; Sandhoefer, B.; Hansen, A.; Neese, F. Natural triple excitations in local coupled cluster calculations with pair natural orbitals. J. Chem. Phys. 2013, 139, 134101. [Google Scholar] [CrossRef] [PubMed]
- Neese, F.; Wennmohs, F.; Becker, U.; Riplinger, C. The ORCA quantum chemistry program package. J. Chem. Phys. 2020, 152, 224108. [Google Scholar] [CrossRef] [PubMed]
- Dunning, T.H. Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen. J. Chem. Phys. 1989, 90, 1007–1023. [Google Scholar] [CrossRef]
- Weigend, F.; Köhn, A.; Hättig, C. Efficient use of the correlation consistent basis sets in resolution of the identity MP2 calculations. J. Chem. Phys. 2002, 116, 3175–3183. [Google Scholar] [CrossRef]
- Martin, J.M.L. Ab initio total atomization energies of small molecules—Towards the basis set limit. Chem. Phys. Lett. 1996, 259, 669–678. [Google Scholar] [CrossRef]
- Weigend, F.; Ahlrichs, R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297–3305. [Google Scholar] [CrossRef]
- Grimme, S.; Hansen, A. A Practicable Real-Space Measure and Visualization of Static Electron-Correlation Effects. Angew. Chemie Int. Ed. 2015, 54, 12308–12313. [Google Scholar] [CrossRef]
- Vishnevskiy, Y.V. UNEX Version 1.6 2023. Available online: https://unex.vishnevskiy.group/en/index.html (accessed on 23 March 2023).
- Vishnevskiy, Y.V.; Zhabanov, Y.A. New implementation of the first-order perturbation theory for calculation of interatomic vibrational amplitudes and corrections in gas electron diffraction. J. Phys. Conf. Ser. 2015, 633, 012076. [Google Scholar] [CrossRef]
- Mitzel, N.W.; Rankin, D.W.H. SARACEN—Molecular structures from theory and experiment: The best of both worlds. Dalt. Trans. 2003, 3650–3662. [Google Scholar] [CrossRef]
- Vishnevskiy, Y.V.; Abaev, M.A.; Rykov, A.N.; Gurskii, M.E.; Belyakov, P.A.; Erdyakov, S.Y.; Bubnov, Y.N.; Mitzel, N.W. Structure and Bonding Nature of the Strained Lewis Acid 3-Methyl-1-boraadamantane: A Case Study Employing a New Data-Analysis Procedure in Gas Electron Diffraction. Chem. A Eur. J. 2012, 18, 10585–10594. [Google Scholar] [CrossRef] [PubMed]
- Kochikov, I.V.; Tarasov, Y.I.; Kuramshina, G.M.; Spiridonov, V.P.; Yagola, A.G.; Strand, T.G. Regularizing algorithm for determination of equilibrium geometry and harmonic force field of free molecules from joint use of electron diffraction, vibrational spectroscopy and ab initio data with application to benzene. J. Mol. Struct. 1998, 445, 243–258. [Google Scholar] [CrossRef]
- Tikhonov, D.S.; Vishnevskiy, Y.V.; Rykov, A.N.; Grikina, O.E.; Khaikin, L.S. Semi-experimental equilibrium structure of pyrazinamide from gas-phase electron diffraction. How much experimental is it? J. Mol. Struct. 2017, 1132, 20–27. [Google Scholar] [CrossRef]
- Baše, T.; Holub, J.; Fanfrlík, J.; Hnyk, D.; Lane, P.D.; Wann, D.A.; Vishnevskiy, Y.V.; Tikhonov, D.; Reuter, C.G.; Mitzel, N.W. Icosahedral Carbaboranes with Peripheral Hydrogen–Chalcogenide Groups: Structures from Gas Electron Diffraction and Chemical Shielding in Solution. Chem. A Eur. J. 2019, 25, 2313–2321. [Google Scholar] [CrossRef] [PubMed]
- Morino, Y.; Hirota, E. Molecular Structure and Internal Rotation of Hexachloroethane, Hexachlorodisilane, and Trichloromethyl-Trichlorosilane. J. Chem. Phys. 1958, 28, 185–197. [Google Scholar] [CrossRef]
- Vishnevskiy, Y.V. UNEX User Manual. Available online: https://unex.vishnevskiy.group/files/unexdocs/manual.html (accessed on 10 March 2024).
- Lee, T.J.; Taylor, P.R. A diagnostic for determining the quality of single-reference electron correlation methods. Int. J. Quantum Chem. 1989, 36, 199–207. [Google Scholar] [CrossRef]
- Liakos, D.G.; Neese, F. Interplay of Correlation and Relativistic Effects in Correlated Calculations on Transition-Metal Complexes: The (Cu2O2)2+ Core Revisited. J. Chem. Theory Comput. 2011, 7, 1511–1523. [Google Scholar] [CrossRef]
- Jiang, W.; DeYonker, N.J.; Wilson, A.K. Multireference Character for 3d Transition-Metal-Containing Molecules. J. Chem. Theory Comput. 2012, 8, 460–468. [Google Scholar] [CrossRef]
- Chamkin, A.A.; Serkova, E.S. DFT, DLPNO-CCSD(T), and NEVPT2 benchmark study of the reaction between ferrocenium and trimethylphosphine. J. Comput. Chem. 2020, 41, 2388–2397. [Google Scholar] [CrossRef] [PubMed]
- Tikhonov, D.S.; Sharapa, D.I.; Otlyotov, A.A.; Solyankin, P.M.; Rykov, A.N.; Shkurinov, A.P.; Grikina, O.E.; Khaikin, L.S. Nitroxoline Molecule: Planar or Not? A Story of Battle between π–π Conjugation and Interatomic Repulsion. J. Phys. Chem. A 2018, 122, 1691–1701. [Google Scholar] [CrossRef] [PubMed]
- Bauer, F.; Lukas, M.A. Comparingparameter choice methods for regularization of ill-posed problems. Math. Comput. Simul. 2011, 81, 1795–1841. [Google Scholar] [CrossRef]
- Vishnevskiy, Y.V.; Schwabedissen, J.; Rykov, A.N.; Kuznetsov, V.V.; Makhova, N.N. Conformational and Bonding Properties of 3,3-Dimethyl- and 6,6-Dimethyl-1,5-diazabicyclo [3.1.0]hexane: A Case Study Employing the Monte Carlo Method in Gas Electron Diffraction. J. Phys. Chem. A 2015, 119, 10871–10881. [Google Scholar] [CrossRef]
- Hamilton, W.C. Significance tests on the crystallographic R factor. Acta Crystallogr. 1965, 18, 502–510. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).