Thermodynamic Analysis of ArxXe1-x Solid Solutions Based on Kirkwood–Buff Theory
Abstract
:1. Introduction
2. Materials and Methods
2.1. Theory
2.1.1. Kirkwood–Buff Integrals in Crystals
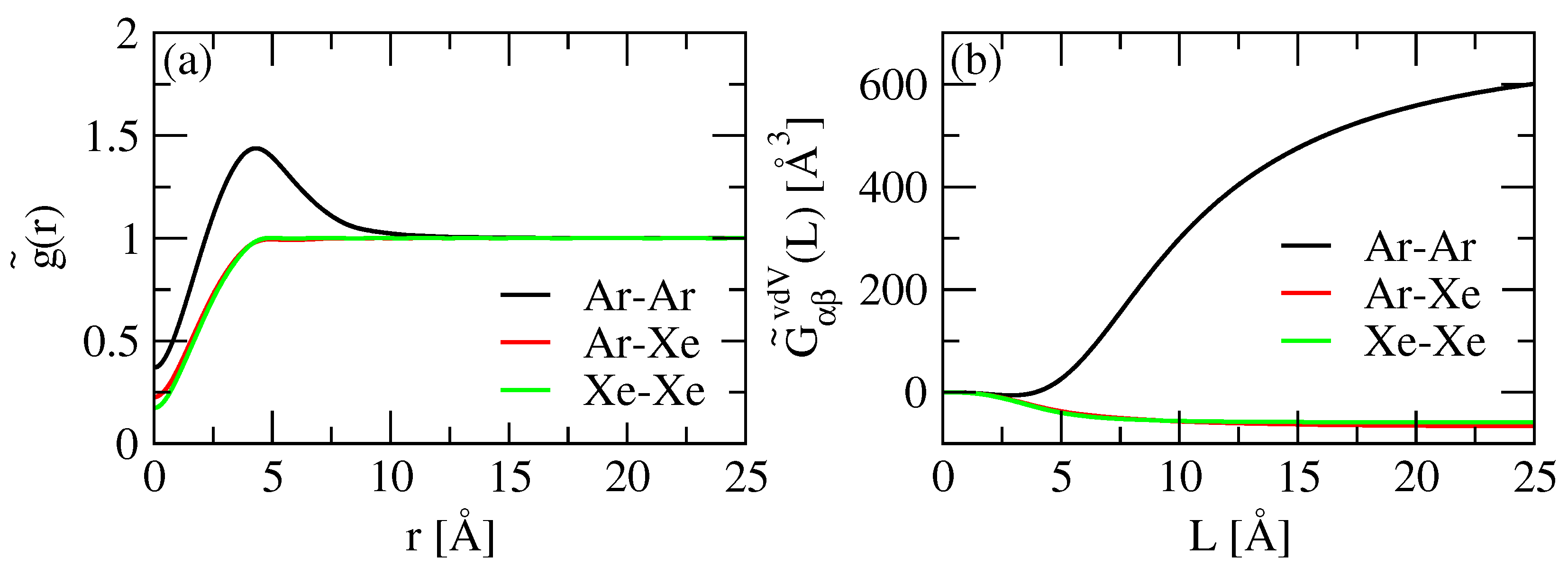
2.1.2. Convolution of the RDF
2.1.3. RDF Correction by Ganguly and van der Vegt
2.2. Monte Carlo Simulations
3. Results and Discussion
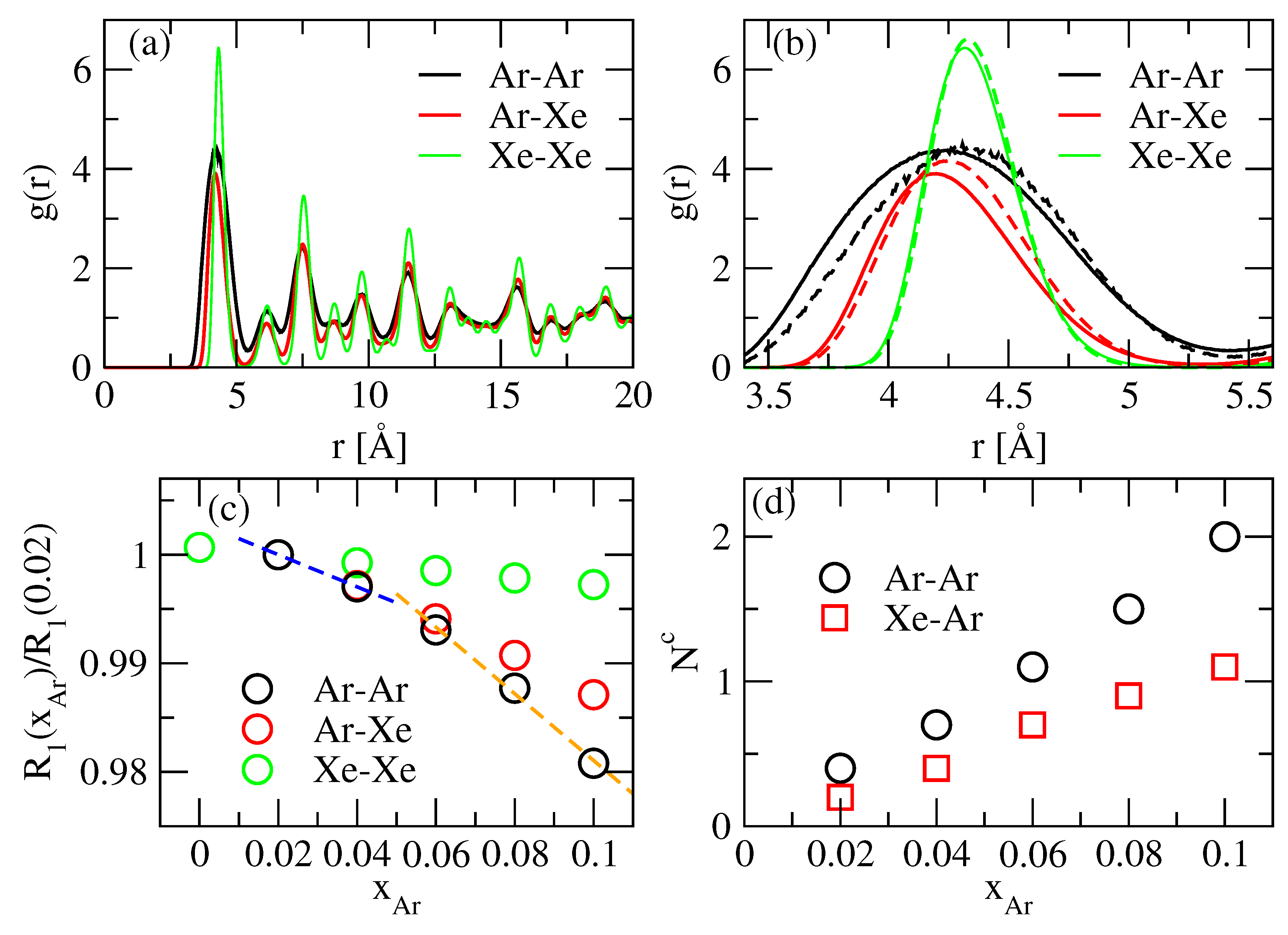
3.1. Monte Carlo Simulation
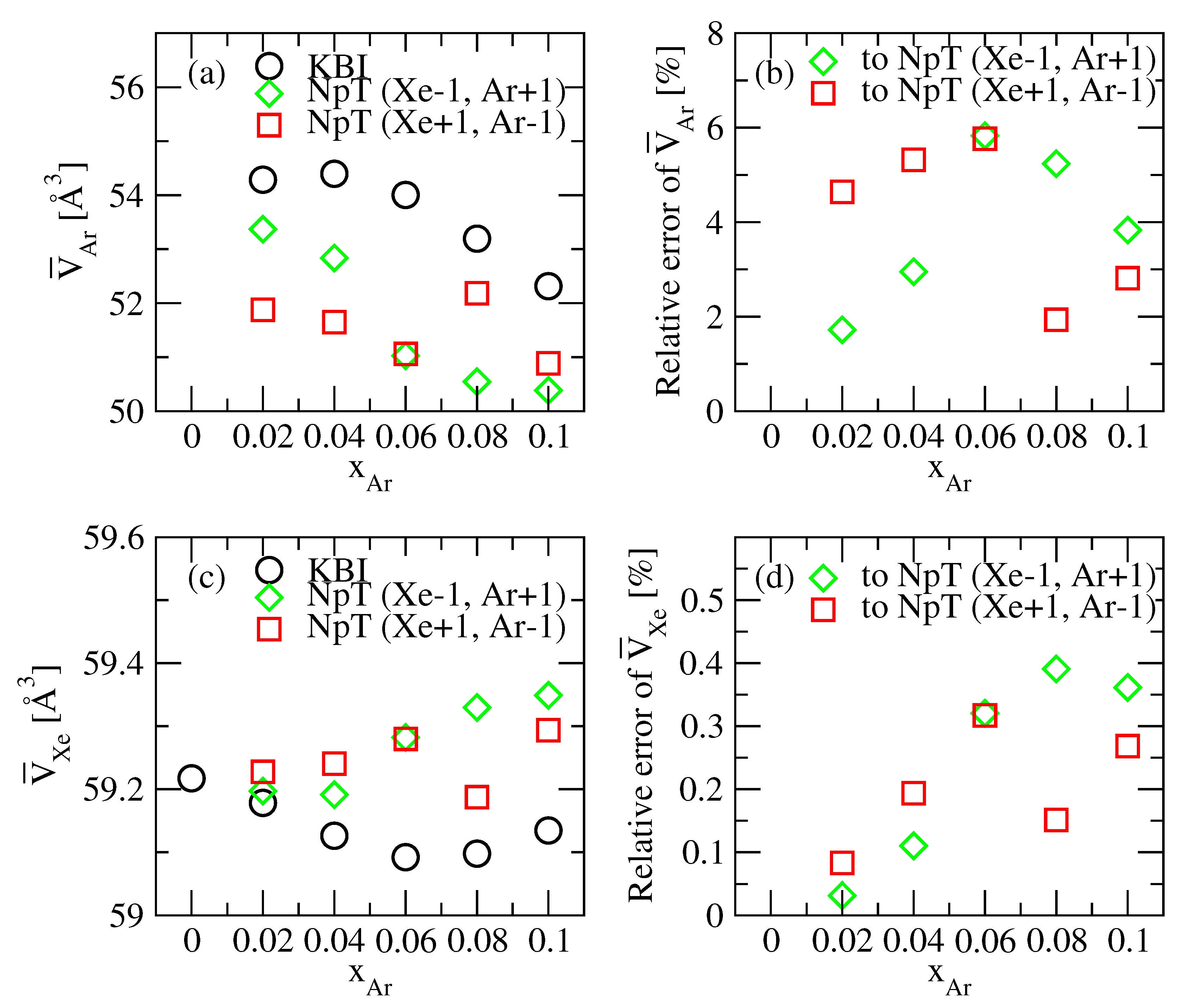
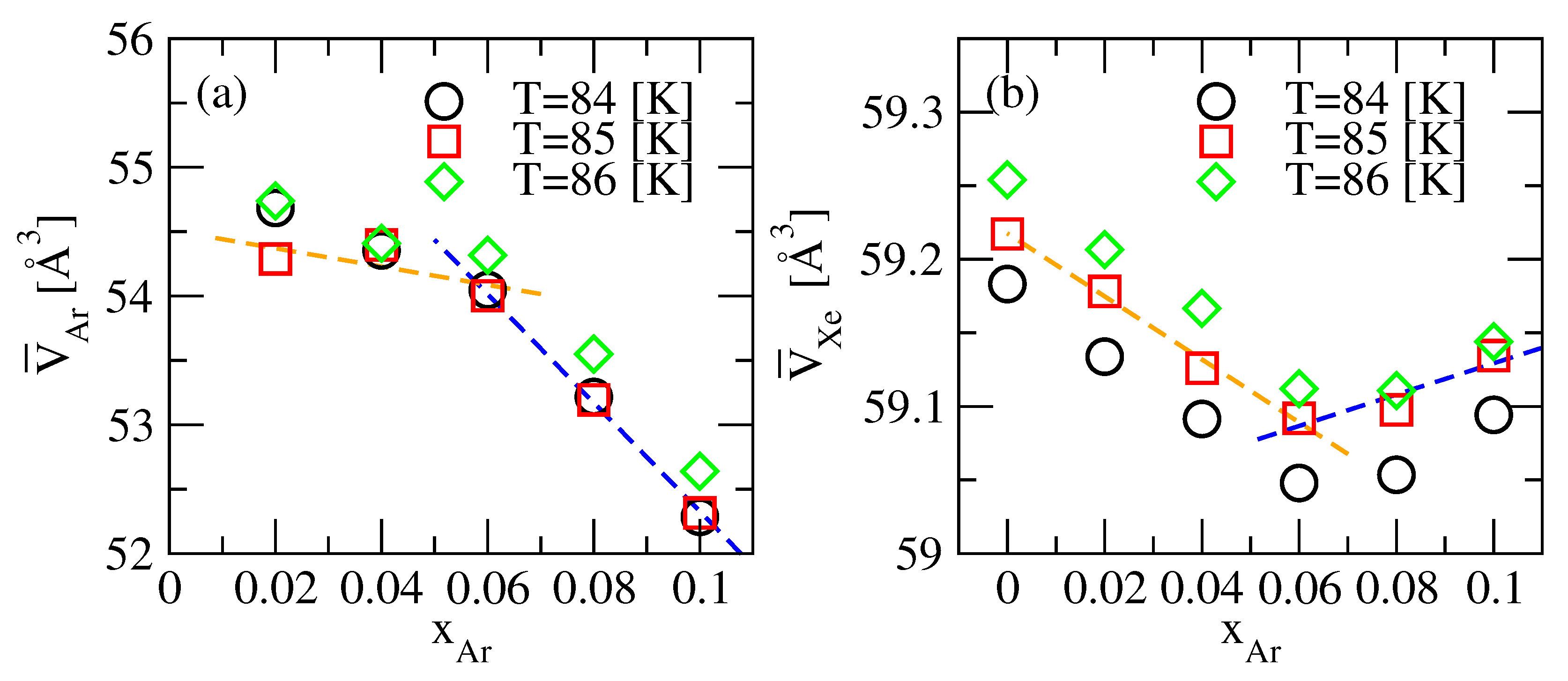
3.2. KBI and Partial Molar Volumes
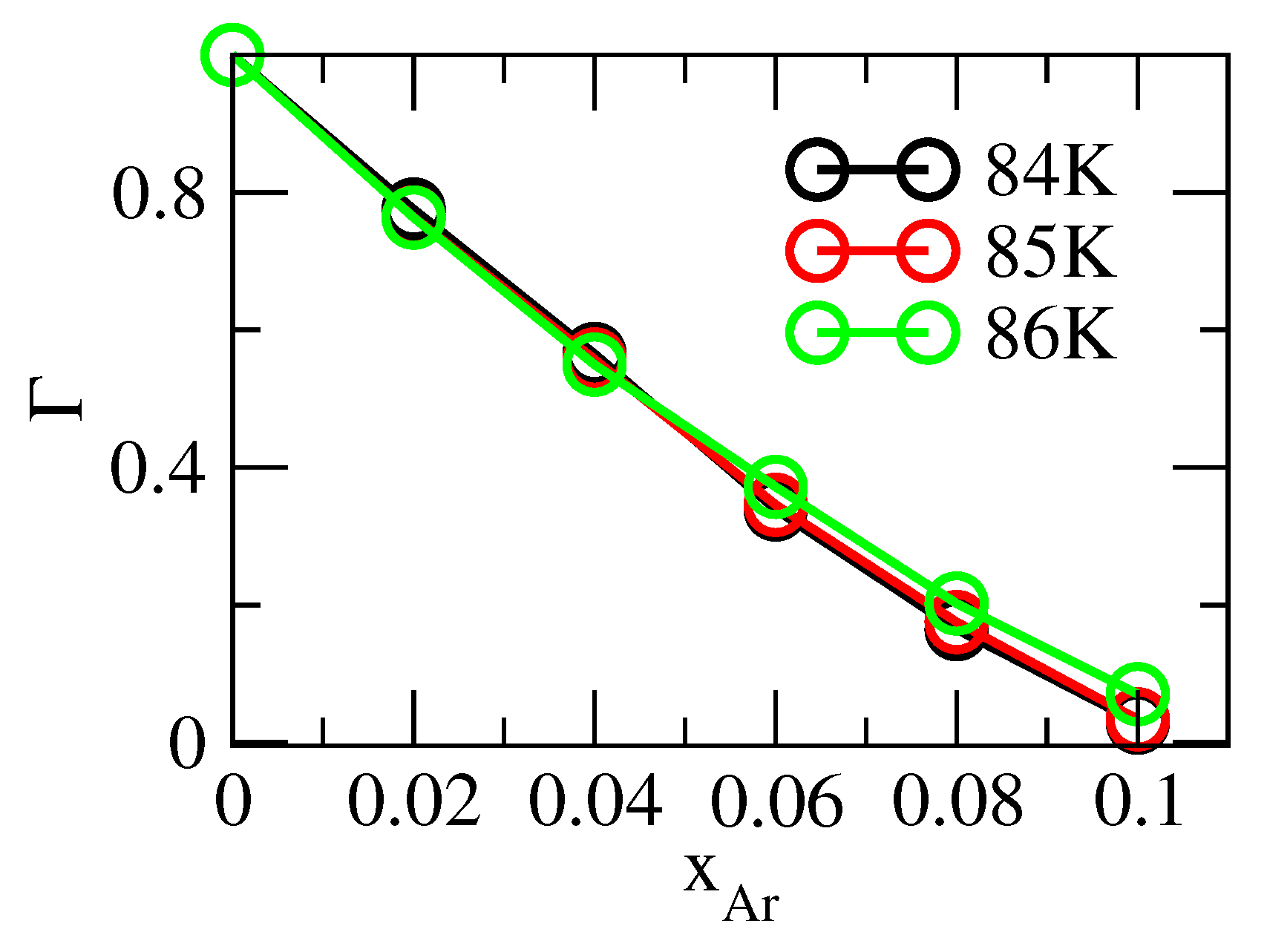
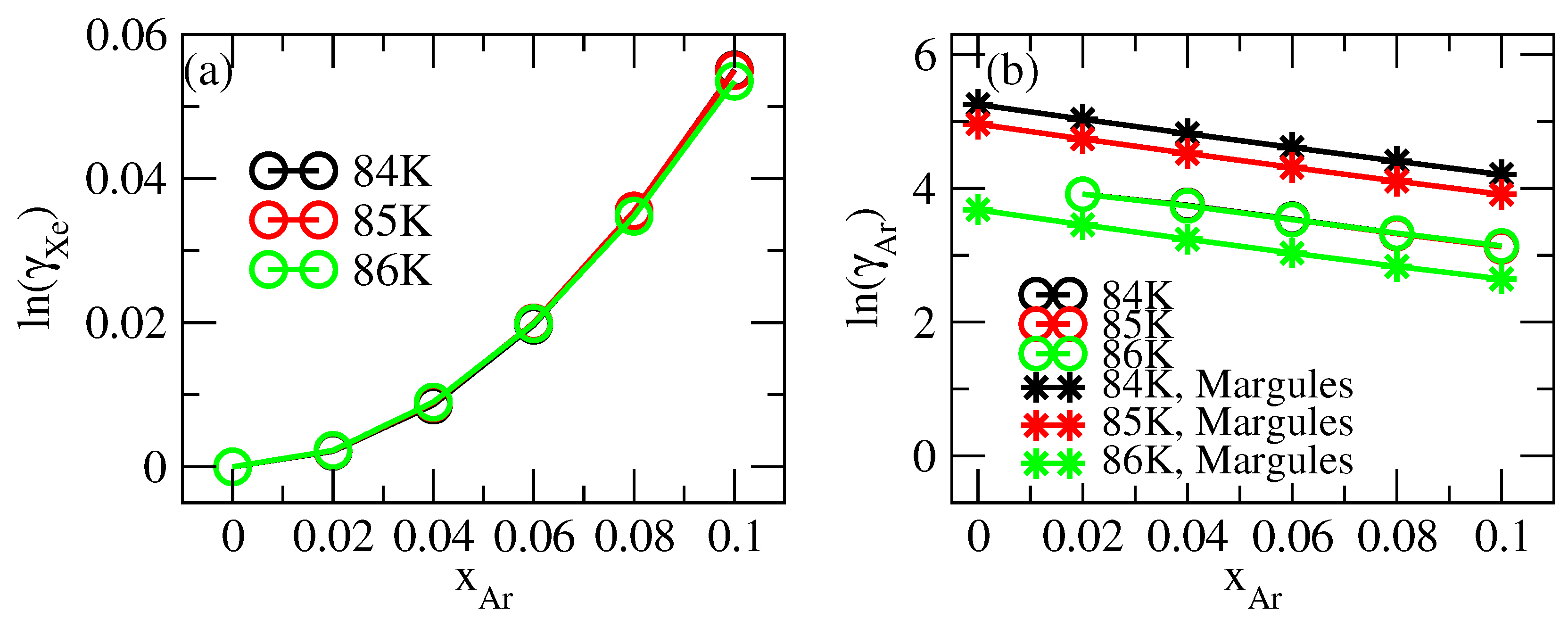
3.3. Thermodynamic Correction Factor and Chemical Potential
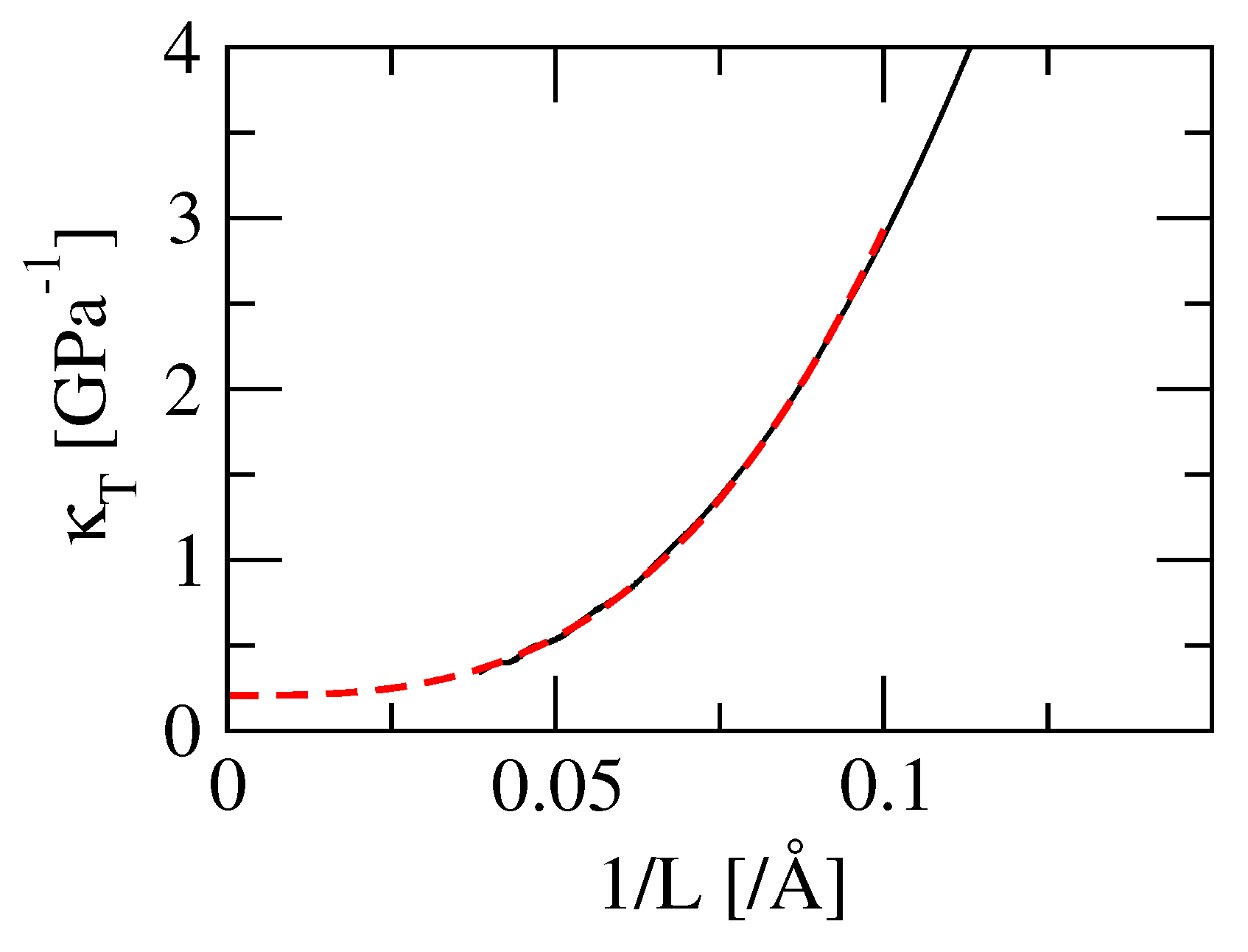
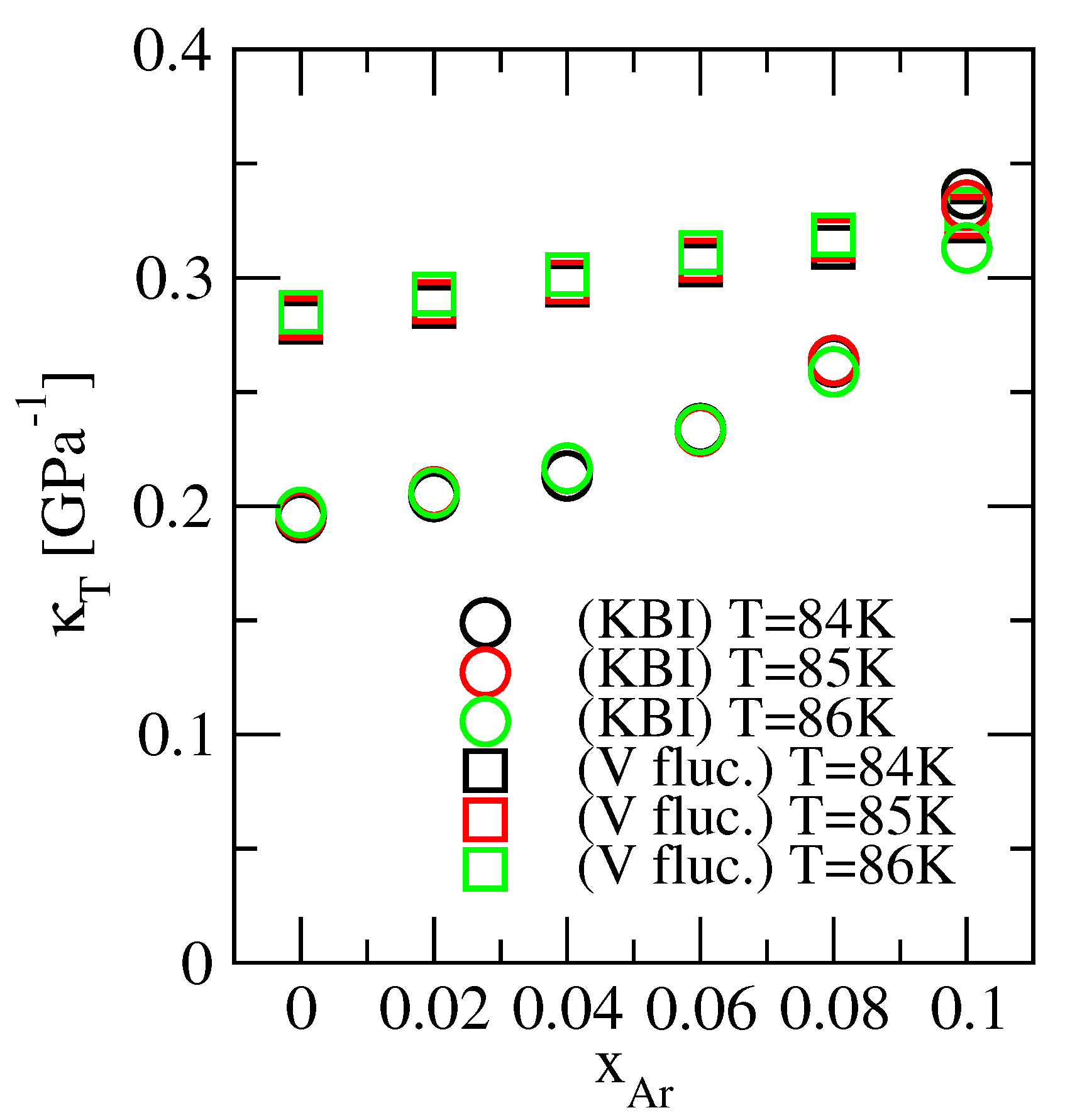
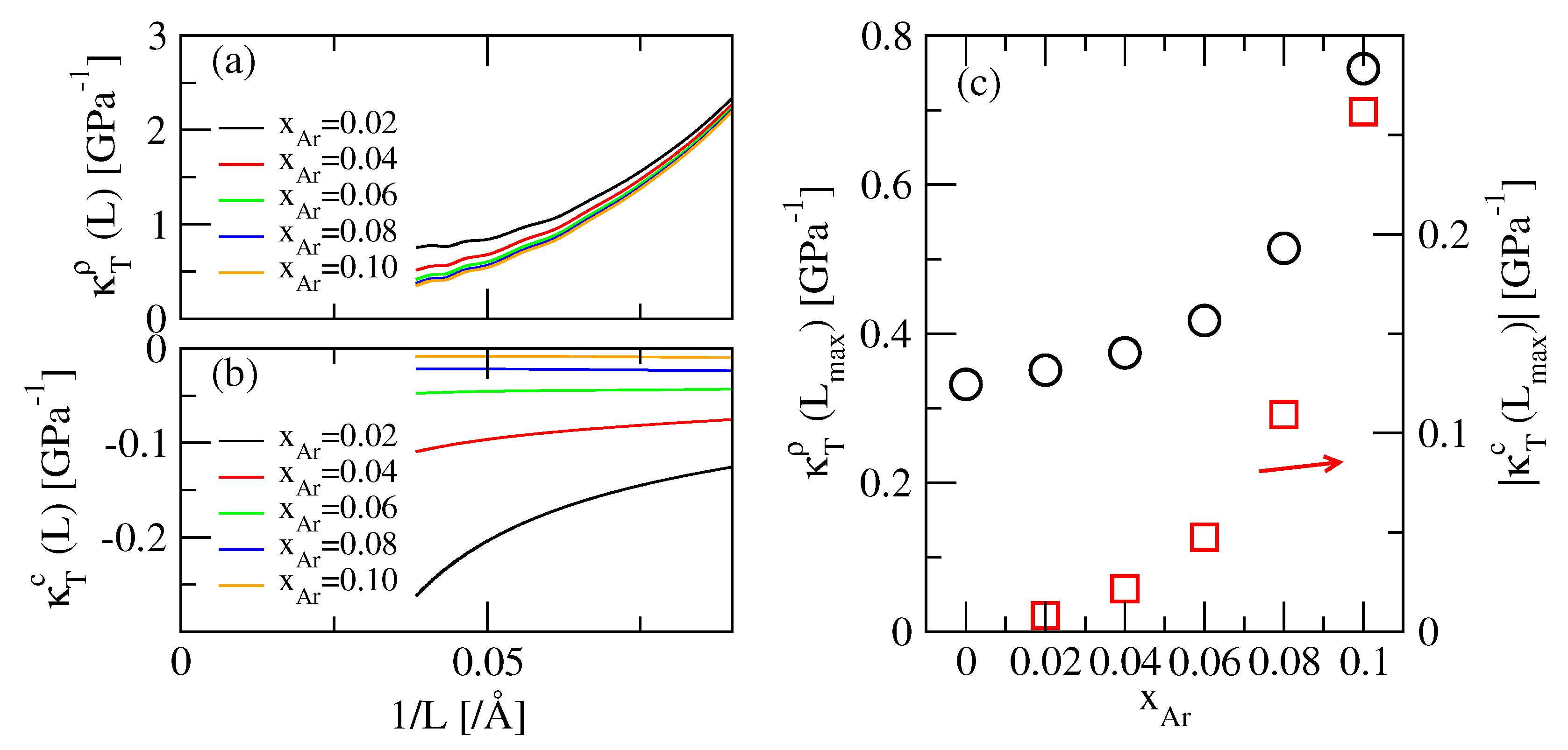
3.4. Isothermal Compressibility
4. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kirkwood, J.G.; Buff, F.P. The Statistical Mechanical Theory of Solutions. I. J. Chem. Phys. 1951, 19, 774–777. [Google Scholar] [CrossRef]
- Ben-Naim, A. Inversion of the Kirkwood–Buff theory of solutions: Application to the water–ethanol system. J. Chem. Phys. 1977, 67, 4884–4890. [Google Scholar] [CrossRef]
- Liu, X.; Martin-Calvo, A.; McGarrity, E.; Schnell, S.K.; Calero, S.; Simon, J.M.; Bedeaux, D.; Kjelstrup, S.; Bardow, A.; Vlugt, T.J.H. Fick diffusion coefficients in ternary liquid systems from equilibrium molecular dynamics simulations. Ind. Eng. Chem. Res. 2012, 51, 10247. [Google Scholar] [CrossRef]
- Fingerhut, R.; Herres, G.; Vrabec, J. Thermodynamic factor of quaternary mixtures from Kirkwood–Buff integration. Mol. Phys. 2020, 118, e1643046. [Google Scholar] [CrossRef]
- Perera, A.; Sokolić, F. Modeling nonionic aqueous solutions: The acetone-water mixture. J. Chem. Phys. 2004, 121, 11272–11282. [Google Scholar] [CrossRef]
- Ganguly, P.; van der Vegt, N.F.A. Convergence of Sampling Kirkwood–Buff Integrals of Aqueous Solutions with Molecular Dynamics Simulations. J. Chem. Theory Comput. 2013, 9, 1347–1355. [Google Scholar] [CrossRef]
- Collell, J.; Galliero, G. Determination of the thermodynamic correction factor of fluids confined in nano-metric slit pores from molecular simulation. J. Chem. Phys. 2014, 140, 194702. [Google Scholar] [CrossRef]
- Fingerhut, R.; Vrabec, J. Kirkwood–Buff integration: A promising route to entropic properties? Fluid Phase Equilibria 2019, 485, 270–281. [Google Scholar] [CrossRef] [Green Version]
- Kobayashi, T.; Reid, J.E.S.J.; Shimizu, S.; Fyta, M.; Smiatek, J. The properties of residual water molecules in ionic liquids: A comparison between direct and inverse Kirkwood–Buff approaches. Phys. Chem. Chem. Phys. 2017, 19, 18924–18937. [Google Scholar] [CrossRef] [Green Version]
- Dawass, N.; Krüger, P.; Schnell, S.; Simon, J.M.; Vlugt, T.J.H. Kirkwood–Buff integrals from molecular simulation. Fluid Phase Equilibria 2019, 486, 21–36. [Google Scholar] [CrossRef]
- Proffen, T.; Billinge, S.J.L.; Egami, T.; Louca, D. Structural analysis of complex materials using the atomic pair distribution function—A practical guide. Z. Kristallogr. Cryst. Mater. 2003, 218, 132–143. [Google Scholar] [CrossRef]
- Billinge, S.J.L.; Levin, I. The Problem with Determining Atomic Structure at the Nanoscale. Science 2007, 316, 561–565. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Miyaji, M.; Radola, B.; Simon, J.M.; Krüger, P. Extension of Kirkwood–Buff theory to solids and its application to the compressibility of fcc argon. J. Chem. Phys. 2021, 154, 164506. [Google Scholar] [CrossRef] [PubMed]
- Krüger, P. Validity of the compressibility equation and Kirkwood–Buff theory for crystalline matter. Phys. Rev. E 2021, 103, L061301. [Google Scholar] [CrossRef] [PubMed]
- Krüger, P.; Schnell, S.K.; Bedeaux, D.; Kjelstrup, S.; Vlugt, T.J.H.; Simon, J.M. Kirkwood–Buff Integrals for Finite Volumes. J. Phys. Chem. Lett. 2013, 4, 235–238. [Google Scholar] [CrossRef] [PubMed]
- Campestrini, M.; Stringari, P.; Arpentinier, P. Solid–liquid equilibrium prediction for binary mixtures of Ar, O2, N2, Kr, Xe, and CH4 using the LJ-SLV-EoS. Fluid Phase Equilibria 2014, 379, 139–147. [Google Scholar] [CrossRef] [Green Version]
- Krüger, P. Ensemble averaged Madelung energies of finite-volumes and surfaces. Phys. Rev. B 2020, 101, 205423. [Google Scholar] [CrossRef]
- Dawass, N.; Krüger, P.; Schnell, S.K.; Bedeaux, D.; Kjelstrup, S.; Simon, J.M.; Vlugt, T.J.H. Finite-size effects of Kirkwood–Buff integrals from molecular simulations. Mol. Simul. 2018, 44, 599–612. [Google Scholar] [CrossRef]
- Krüger, P.; Vlugt, T.J.H. Size and shape dependence of finite-volume Kirkwood–Buff integrals. Phys. Rev. E 2018, 97, 051301. [Google Scholar] [CrossRef] [Green Version]
- Dawass, N.; Krüger, P.; Simon, J.M.; Vlugt, T.J.H. Kirkwood–Buff integrals of finite systems: Shape effects. Mol. Phys. 2018, 116, 1573–1580. [Google Scholar] [CrossRef] [Green Version]
- Santos, A. Finite-size estimates of Kirkwood–Buff and similar integrals. Phys. Rev. E 2018, 98, 063302. [Google Scholar] [CrossRef] [Green Version]
- Cortes-Huerto, R.; Kremer, K.; Potestio, R. Communication: Kirkwood–Buff integrals in the thermodynamic limit from small-sized molecular dynamics simulations. J. Chem. Phys. 2016, 145, 141103. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mick, J.R.; Soroush Barhaghi, M.; Jackman, B.; Rushaidat, K.; Schwiebert, L.; Potoff, J.J. Optimized Mie potentials for phase equilibria: Application to noble gases and their mixtures with n-alkanes. J. Chem. Phys. 2015, 143, 114504. [Google Scholar] [CrossRef] [PubMed]
- Lorentz, H.A. Ueber die Anwendung des Satzes vom Virial in der kinetischen Theorie der Gase. Ann. Physik 1881, 248, 127–136. [Google Scholar] [CrossRef] [Green Version]
- Berthelot, D. Sur le mélange des gaz. Compt. Rendus 1898, 126, 1703–1706. [Google Scholar]
- Purton, J.; Crabtree, J.; Parker, S. DL_MONTE: A general purpose program for parallel Monte Carlo simulation. Mol. Simul. 2013, 39, 1240–1252. [Google Scholar] [CrossRef]
- Brukhno, A.V.; Grant, J.; Underwood, T.L.; Stratford, K.; Parker, S.C.; Purton, J.A.; Wilding, N.B. DL_MONTE: A multipurpose code for Monte Carlo simulation. Mol. Simul. 2019, 47, 131–151. [Google Scholar] [CrossRef] [Green Version]
- Primorac, T.; Pozar, M.; Sokolić, F.; Zoranić, L. The influence of binary mixtures’ structuring on the calculation of Kirkwood–Buff integrals: A molecular dynamics study. J. Mol. Liq. 2021, 324, 114773. [Google Scholar] [CrossRef]
- Manzhelii, V.G.; Prokhvatilov, A.I.; Minchina, I.Y.; Yantsevich, L.D. Handbook of Binary Solutions of Cryocrystals; Begell House: New York, NY, USA, 1996. [Google Scholar]
- Yantsevich, L.D.L.; Prokhvatilov, A.I.; Barylnik, A.S. Phase diagrams of Ar-Xe, Kr-Xe and Kr-CO binary alloys. Fiz. Nizk. Temp. 1996, 22, 218–221. [Google Scholar]
- Bhatia, A.B.; Thornton, D.E. Structural Aspects of the Electrical Resistivity of Binary Alloys. Phys. Rev. B 1970, 2, 3004–3012. [Google Scholar] [CrossRef]

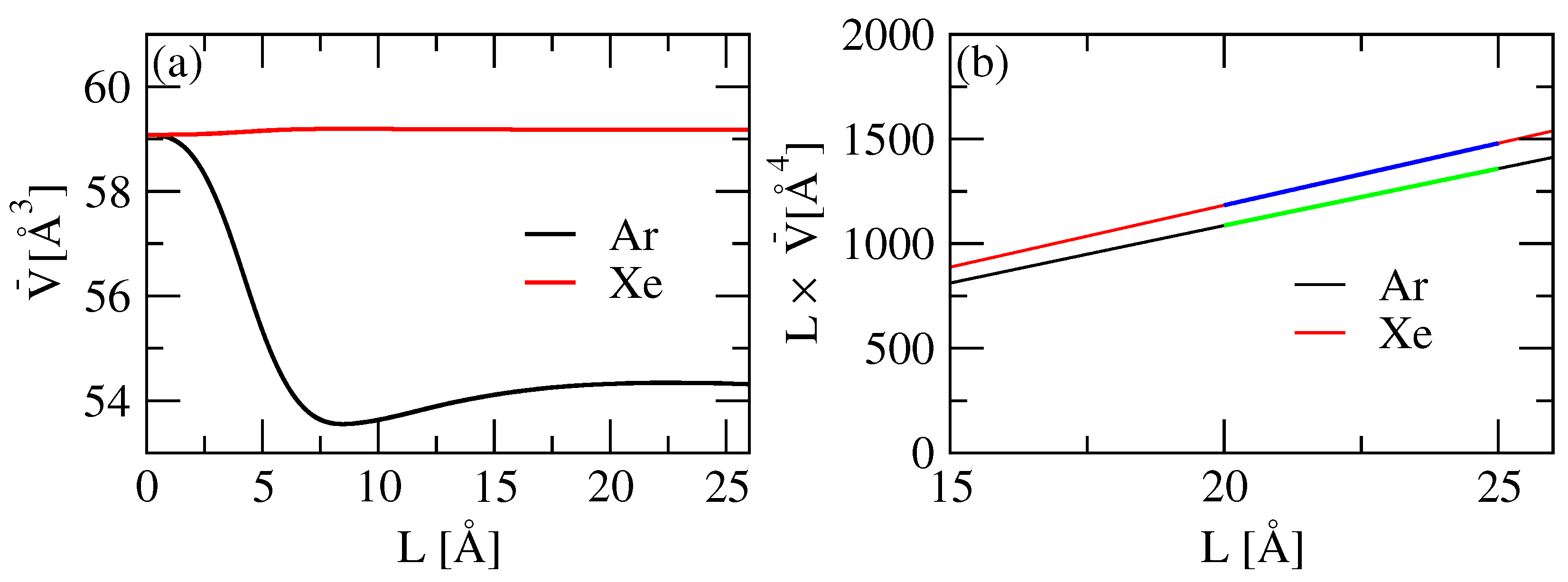



| Atom | (K) | (Å) | |
|---|---|---|---|
| Ar | 122.10 | 3.405 | 13 |
| Xe | 243.80 | 3.964 | 14 |
| T (K) | (Å) | (Å) | (Å) | (Å) | (GPa) | (GPa) | ||
|---|---|---|---|---|---|---|---|---|
| 84 | 0 | 0.01690 | - | - | −58.96 | 0.1950 | 0.2804 | 1.00 |
| 85 | 0 | 0.01689 | - | - | −58.99 | 0.1960 | 0.2824 | 1.00 |
| 86 | 0 | 0.01688 | - | - | −59.02 | 0.1973 | 0.2849 | 1.00 |
| 84 | 0.02 | 0.01694 | 0.7936 | −0.7045 | −58.68 | 0.2042 | 0.2873 | 0.775 |
| 85 | 0.02 | 0.01693 | 0.8471 | −0.7092 | −58.72 | 0.2063 | 0.2896 | 0.764 |
| 86 | 0.02 | 0.01692 | 0.8507 | −0.7157 | −58.72 | 0.2058 | 0.2930 | 0.763 |
| 84 | 0.04 | 0.01698 | 1.047 | −0.9630 | −57.41 | 0.2132 | 0.2967 | 0.565 |
| 85 | 0.04 | 0.01697 | 1.082 | −0.9769 | −57.38 | 0.2166 | 0.2981 | 0.557 |
| 86 | 0.04 | 0.01696 | 1.120 | −0.9913 | −57.37 | 0.2167 | 0.3014 | 0.549 |
| 84 | 0.06 | 0.01702 | 1.768 | −1.602 | −52.85 | 0.2340 | 0.3057 | 0.339 |
| 85 | 0.06 | 0.01701 | 1.712 | −1.567 | −53.11 | 0.2328 | 0.3078 | 0.346 |
| 86 | 0.06 | 0.01700 | 1.524 | −1.466 | −53.69 | 0.2335 | 0.3112 | 0.372 |
| 84 | 0.08 | 0.01707 | 3.430 | −3.258 | −37.82 | 0.2631 | 0.3134 | 0.165 |
| 85 | 0.08 | 0.01706 | 3.175 | −3.055 | −39.48 | 0.2638 | 0.3167 | 0.175 |
| 86 | 0.08 | 0.01705 | 2.656 | −2.667 | −42.43 | 0.2588 | 0.3188 | 0.202 |
| 84 | 0.10 | 0.01712 | 18.12 | −18.39 | 116.3 | 0.3367 | 0.3250 | 0.0288 |
| 85 | 0.10 | 0.01711 | 15.50 | −15.81 | 90.86 | 0.3318 | 0.3270 | 0.0335 |
| 86 | 0.10 | 0.01710 | 7.101 | −7.597 | 10.54 | 0.3131 | 0.3300 | 0.0700 |
| T (K) | (Å) | (Å) | (Å) | (Å) | (Å) | (Å) | |
|---|---|---|---|---|---|---|---|
| 84 | 0 | - | - | - | 59.18 | - | - |
| 85 | 0 | - | - | - | 59.22 | - | - |
| 86 | 0 | - | - | - | 59.25 | - | - |
| 84 | 0.02 | 54.68 | - | - | 59.13 | - | - |
| 85 | 0.02 | 54.29 | 51.88 | 53.37 | 59.18 | 59.22 | 59.20 |
| 86 | 0.02 | 54.74 | - | - | 59.21 | - | - |
| 84 | 0.04 | 54.36 | - | - | 59.09 | - | - |
| 85 | 0.04 | 54.40 | 51.65 | 52.84 | 59.13 | 59.24 | 59.19 |
| 86 | 0.04 | 54.41 | - | - | 59.17 | - | - |
| 84 | 0.06 | 54.05 | - | - | 59.05 | - | - |
| 85 | 0.06 | 54.00 | 51.06 | 51.03 | 59.09 | 59.28 | 59.28 |
| 86 | 0.06 | 54.32 | - | - | 59.11 | - | - |
| 84 | 0.08 | 53.22 | - | - | 59.05 | - | - |
| 85 | 0.08 | 53.19 | 52.18 | 50.55 | 59.10 | 59.19 | 59.33 |
| 86 | 0.08 | 53.55 | - | - | 59.11 | - | - |
| 84 | 0.10 | 52.29 | - | - | 59.09 | - | - |
| 85 | 0.10 | 52.32 | 50.88 | 50.38 | 59.13 | 59.29 | 59.35 |
| 86 | 0.10 | 52.64 | - | - | 59.14 | - | - |
| Temperature | 84 (K) | 85 (K) | 86 (K) |
|---|---|---|---|
| b | 5.54457 | 5.63663 | 5.76786 |
| c | −0.58653 | −1.35139 | −4.17325 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Miyaji, M.; Simon, J.-M.; Krüger, P. Thermodynamic Analysis of ArxXe1-x Solid Solutions Based on Kirkwood–Buff Theory. Physchem 2022, 2, 191-206. https://doi.org/10.3390/physchem2020014
Miyaji M, Simon J-M, Krüger P. Thermodynamic Analysis of ArxXe1-x Solid Solutions Based on Kirkwood–Buff Theory. Physchem. 2022; 2(2):191-206. https://doi.org/10.3390/physchem2020014
Chicago/Turabian StyleMiyaji, Masafumi, Jean-Marc Simon, and Peter Krüger. 2022. "Thermodynamic Analysis of ArxXe1-x Solid Solutions Based on Kirkwood–Buff Theory" Physchem 2, no. 2: 191-206. https://doi.org/10.3390/physchem2020014
APA StyleMiyaji, M., Simon, J.-M., & Krüger, P. (2022). Thermodynamic Analysis of ArxXe1-x Solid Solutions Based on Kirkwood–Buff Theory. Physchem, 2(2), 191-206. https://doi.org/10.3390/physchem2020014







