Anomalous Diffusion and Surface Effects on the Electric Response of Electrolytic Cells
Abstract
:1. Introduction
2. The Geometry of the Cell and Conservation Laws
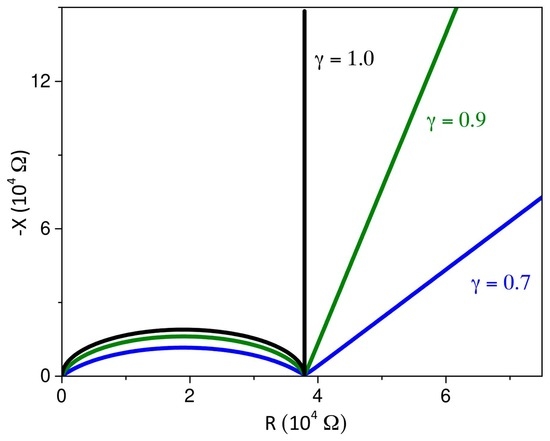
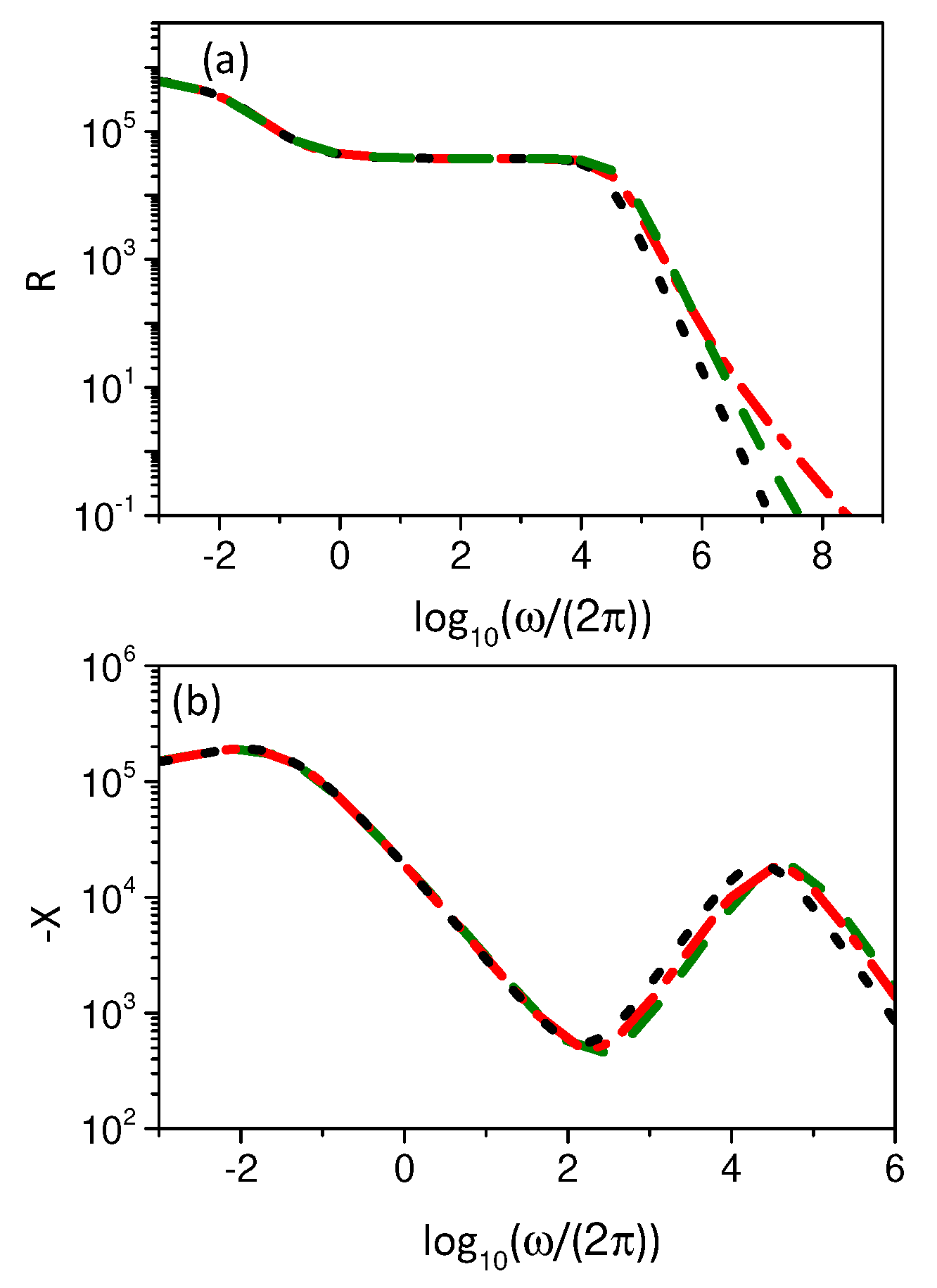
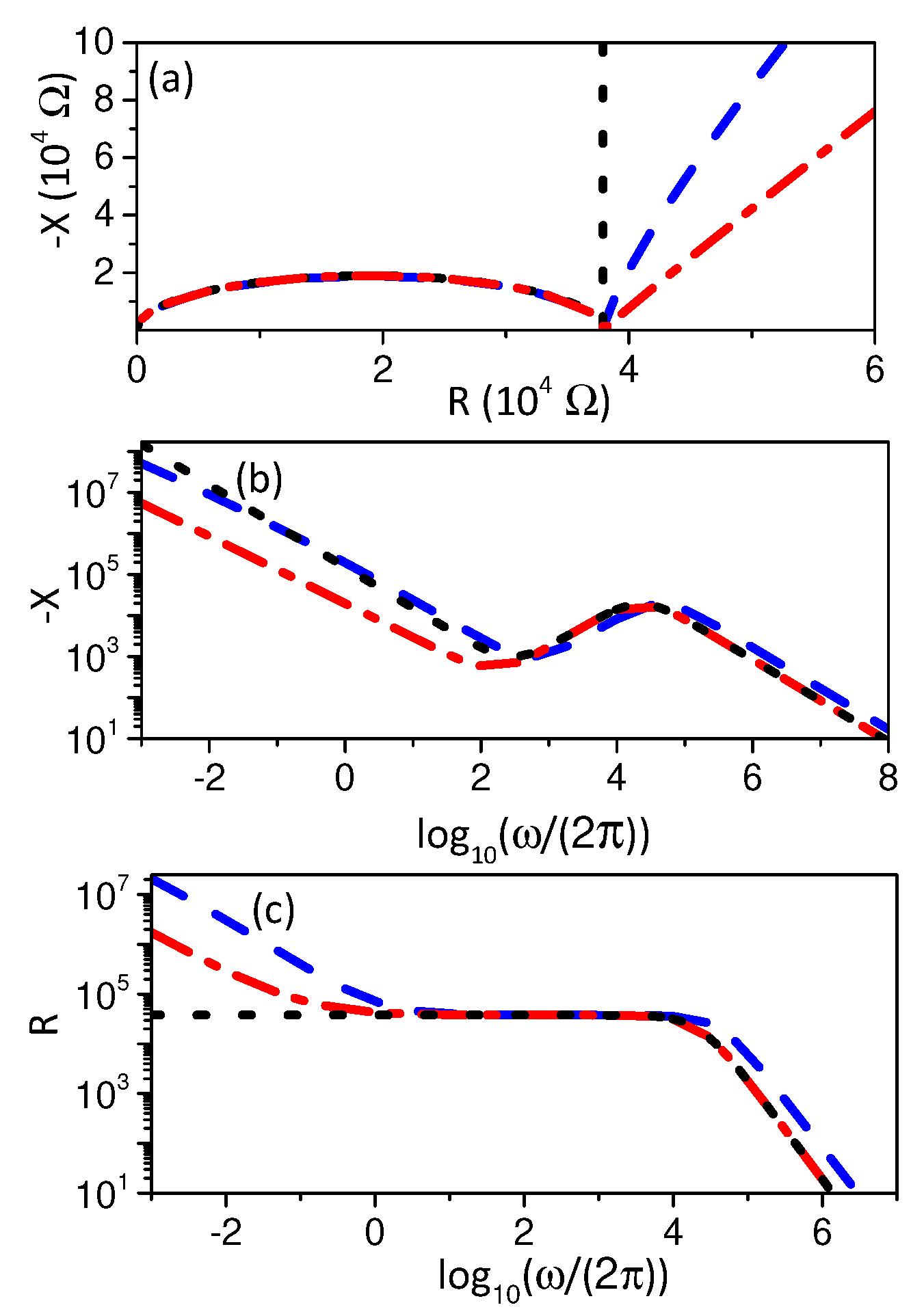
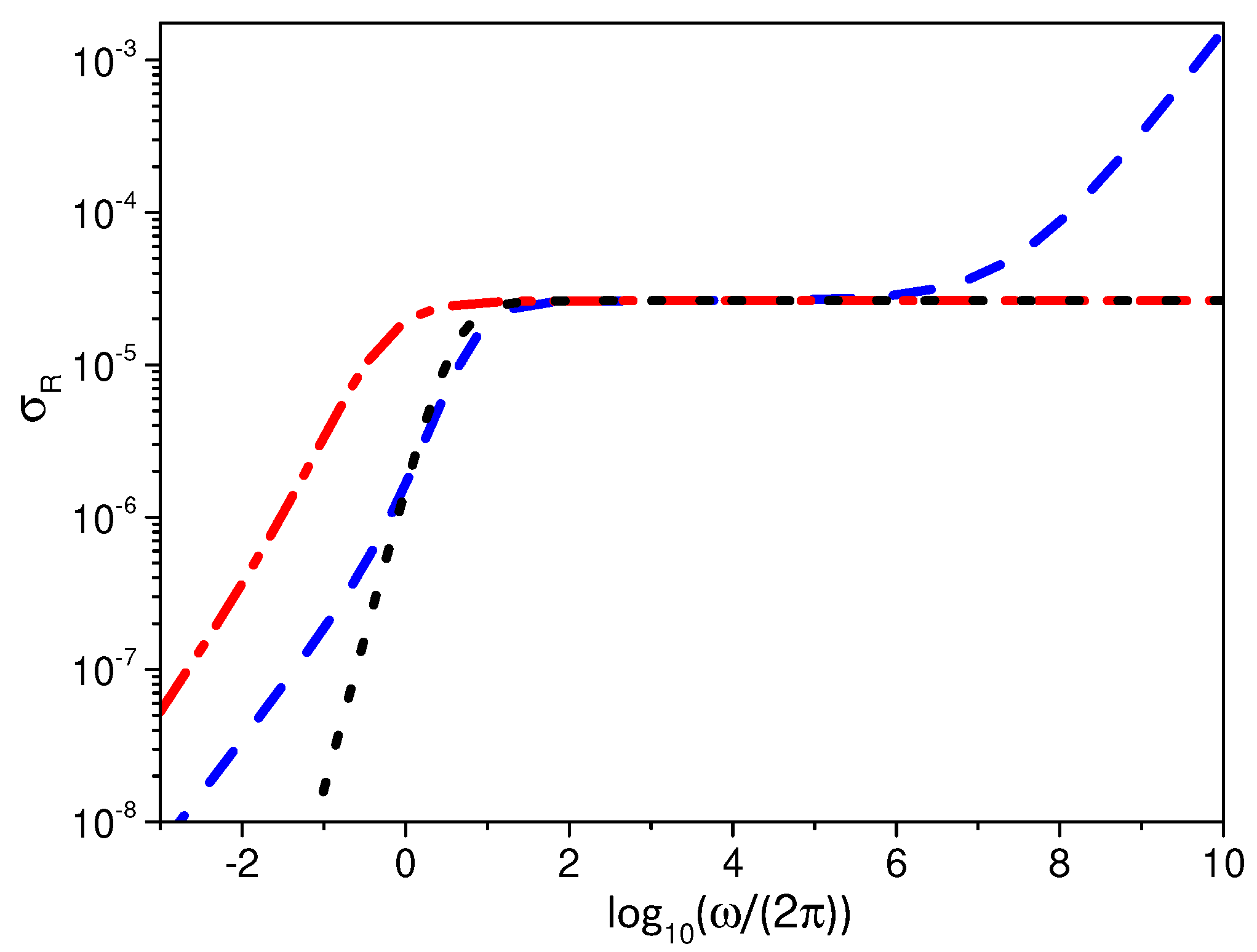
3. Electrical Impedance
3.1. Boundary Condition: Perfect Blocking Electrodes
3.2. Boundary Condition: Integrodifferential Conditions
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Macdonald, J.R.; Johnson, W.B. Fundamental of impedance spectroscopy. In Impedance Spectroscopy, Theory, Experiment, and Applications; Barsoukov, E., Macdonald, J.R., Eds.; Wiley: New York, NY, USA, 2005; pp. 1–26. [Google Scholar]
- Orazem, M.E.; Tribollet, B. Electrochemical Impedance Spectroscopy; Wiley: New York, NY, USA, 2008. [Google Scholar]
- Sidebottom, D.L. Colloquium: Understanding ion motion in disordered solids from impedance spectroscopy scaling. Rev. Mod. Phys. 2009, 81, 999. [Google Scholar] [CrossRef]
- Macdonald, J.R. Theory of ac space–charge polarization effects in photoconductors, Semiconductors, and Electrolytes. Phys. Rev. 1953, 92, 4–17. [Google Scholar] [CrossRef]
- Trukhan, E.M. Dispersion of the dielectric constant of heterogeneous systems. Sov. Phys. Solid State (Engl. Transl.) 1963, 4, 2560. [Google Scholar]
- Basu, T.; Goswami, M.M.; Middya, T.R.; Tarafdar, S. Morphology and Ion-Conductivity of Gelatin-LiClO4 Films: Fractional Diffusion Analysis. J. Phys. Chem. B 2012, 116, 11362–11369. [Google Scholar] [CrossRef]
- Basu, T.; Giri, A.; Tarafdar, S.; Das, S. Electrical impedance response of gamma irradiated gelatin based solid polymer electrolytes analyzed using a generalized calculus formalism. J. Electroanal. Chem. 2015, 755, 52–62. [Google Scholar] [CrossRef] [Green Version]
- Majumdar, S.; Ray, R.; Sen, P. Anomalous intra diffusive behavior of chitosan/PVDF solid polymer electrolytes and the enhancement of effective specific capacitance with nanostructured spinel MnCoFeO4 electrode in solid-state supercapacitors. Electrochim. Acta 2021, 385, 138295. [Google Scholar] [CrossRef]
- L’vov, P.E.; Sibatov, R.T.; Yavtushenko, I.O.; Kitsuk, E.P. Time-Fractional Phase Field Model of Electrochemical Impedance. Fractal Fract. 2021, 5, 191. [Google Scholar] [CrossRef]
- Barbero, G.; Evangelista, L.R.; Lenzi, E.K. Time-Fractional Approach to the Electrochemical Impedance: The Displacement Current. arXiv 2022, arXiv:2201.00731. [Google Scholar]
- Lelidis, I.; Barbero, G. Role of the displacement current on Warburg-type behavior. Phys. Rev. E 2017, 95, 052604. [Google Scholar] [CrossRef]
- Borukhov, I.; Andelman, D.; Orlandi, H. Steric Effects in Electrolytes: A Modified Poisson-Boltzmann Equation. Phys. Rev. Lett. 1997, 79, 435–438. [Google Scholar] [CrossRef] [Green Version]
- Kornyshev, A.A. Double-Layer in Ionic Liquids: Paradigm Change? J. Phys. Chem. B 2007, 111, 5545–5557. [Google Scholar] [CrossRef] [PubMed]
- Ochoa-Tapia, J.A.; Valdes-Parada, F.J.; Alvarez-Ramirez, J. A fractional-order Darcy’s law. Physica A 2007, 374, 1–14. [Google Scholar] [CrossRef]
- Carcione, J.M.; Sanchez-Sesma, F.J.; Luzón, F.; Gavilán, J.J.P. Theory and simulation of time-fractional fluid diffusion in porous media. J. Phys. A 2013, 46, 345501. [Google Scholar] [CrossRef]
- Zhou, H.W.; Yang, S. Fractional derivative approach to non-Darcian flow in porous media. J. Hydrol. 2018, 566, 910–918. [Google Scholar] [CrossRef]
- Prakasha, D.G.; Veeresha, P.; Singh, J. Fractional approach for equation describing the water transport in unsaturated porous media with Mittag-Leffler kernel. Front. Phys. 2019, 7, 193. [Google Scholar] [CrossRef] [Green Version]
- Metzler, R.; Klafter, J. The random walk’s guide to anomalous diffusion: A fractional dynamics approach. Phys. Rep. 2000, 339, 1–77. [Google Scholar] [CrossRef]
- Chechkin, A.V.; Gorenflo, R.; Sokolov, I.M. Retarding subdiffusion and accelerating superdiffusion governed by distributed-order fractional diffusion equations. Phys. Rev. E 2002, 66, 046129. [Google Scholar] [CrossRef] [Green Version]
- Mainardi, F.; Pagnini, G.; Gorenflo, R. Some aspects of fractional diffusion equations of single and distributed order. App. Math. Comp. 2007, 187, 295–305. [Google Scholar] [CrossRef] [Green Version]
- Li, H.; Zheng, K.; Yang, J.; Zhao, J. Anomalous Diffusion Inside Soft Colloidal Suspensions Investigated by Variable Length Scale Fluorescence Correlation Spectroscopy. ACS Omega 2020, 5, 11123–11130. [Google Scholar] [CrossRef]
- Chepizhko, O.; Peruani, F. Diffusion, subdiffusion, and trapping of active particles in heterogeneous media. Phys. Rev. Lett. 2013, 111, 160604. [Google Scholar] [CrossRef] [Green Version]
- O’Shaughnessy, B.; Procaccia, I. Analytical solutions for diffusion on fractal objects. Phys. Rev. Lett. 1985, 54, 455. [Google Scholar] [CrossRef] [PubMed]
- Bogolyubov, A.N.; Potapov, A.A.; Rehviashvili, S.S. An approach to introducing fractional integro-differentiation in classical electrodynamics. Mosc. Univ. Phys. Bull. 2009, 64, 365–368. [Google Scholar] [CrossRef]
- Stefański, T.P.; Gulgowski, J. Formulation of time-fractional electrodynamics based on Riemann-Silberstein vector. Entropy 2021, 23, 987. [Google Scholar] [CrossRef] [PubMed]
- Barbero, G.; Macdonald, J.R. Transport process of ions in insulating media in the hyperbolic diffusion regime. Phys. Rev. E 2010, 81, 051503. [Google Scholar] [CrossRef] [Green Version]
- Tateishi, A.A.; Ribeiro, H.V.; Lenzi, E.K. The role of fractional time-derivative operators on anomalous diffusion. Front. Phys. 2017, 5, 52. [Google Scholar] [CrossRef] [Green Version]
- Lenzi, E.K.; Evangelista, L.R.; Barbero, G. Fractional diffusion equation and impedance spectroscopy of electrolytic cells. J. Phys. Chem. B 2009, 113, 11371–11374. [Google Scholar] [CrossRef]
- Scher, H.; Lax, M. Stochastic transport in a disordered solid. I. Theory. Phys. Rev. B 1973, 7, 4491–4502. [Google Scholar] [CrossRef]
- Scher, H.; Lax, M. Stochastic transport in a disordered solid. II. Impurity conduction. Phys. Rev. B 1973, 7, 4502–4519. [Google Scholar] [CrossRef]
- Evangelista, L.R.; Lenzi, E.K. Fractional Diffusion Dquations and Anomalous Diffusion; Cambridge University Press: Cambridge, UK, 2018. [Google Scholar]
- Lenzi, E.K.; de Paula, J.L.; Silva, F.R.G.B.; Evangelista, L.R. A connection between anomalous Poisson-Nernst-Planck model and equivalent circuits with constant phase elements. J. Phys. Chem. C 2013, 117, 23685–23690. [Google Scholar] [CrossRef]
- Lenzi, E.K.; Evangelista, L.R.; Taghizadeh, L.; Pasterk, D.; Zola, R.S.; Sandev, T.; Heitzinger, C.; Petreska, I. Reliability of Poisson–Nernst–Planck anomalous models for impedance spectroscopy. J. Phys. Chem. B 2019, 123, 7885–7892. [Google Scholar] [CrossRef]
- Ciuchi, F.; Mazzulla, A.; Scaramuzza, N.; Lenzi, E.K.; Evangelista, L.R. Fractional diffusion equation and the electrical impedance: Experimental evidence in liquid-crystalline cells. J. Phys. Chem. C 2012, 116, 8773–8777. [Google Scholar] [CrossRef]
- Evangelista, L.R.; Lenzi, E.K.; Barbero, G.; Macdonald, J.R. On the equivalence between specific adsorption and kinetic equation descriptions of the admittance response in electrolytic cells. J. Chem. Phys. 2013, 138, 114702. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Friauf, R.J. Polarization effects in the ionic conductivity of silver bromide. J. Chem. Phys. 1954, 22, 1329–1338. [Google Scholar] [CrossRef]
- Jorcin, J.; Orazem, M.E.; Pébére, N.; Tribollet, B. CPE analysis by local electrochemical impedance spectroscopy. Electrochim. Acta 2006, 51, 1473–1479. [Google Scholar] [CrossRef]
- Lenzi, E.K.; Zola, R.S.; Ribeiro, H.V.; Vieira, D.S.; Ciuchi, F.; Mazzulla, A.; Scaramuzza, N.; Evangelista, L.R. Ion motion in electrolytic cells: Anomalous diffusion evidences. J. Phys. Chem. B 2017, 121, 2882–2886. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Scarfone, A.M.; Barbero, G.; Evangelista, L.R.; Lenzi, E.K. Anomalous Diffusion and Surface Effects on the Electric Response of Electrolytic Cells. Physchem 2022, 2, 163-178. https://doi.org/10.3390/physchem2020012
Scarfone AM, Barbero G, Evangelista LR, Lenzi EK. Anomalous Diffusion and Surface Effects on the Electric Response of Electrolytic Cells. Physchem. 2022; 2(2):163-178. https://doi.org/10.3390/physchem2020012
Chicago/Turabian StyleScarfone, Antonio M., Giovanni Barbero, Luiz R. Evangelista, and Ervin K. Lenzi. 2022. "Anomalous Diffusion and Surface Effects on the Electric Response of Electrolytic Cells" Physchem 2, no. 2: 163-178. https://doi.org/10.3390/physchem2020012
APA StyleScarfone, A. M., Barbero, G., Evangelista, L. R., & Lenzi, E. K. (2022). Anomalous Diffusion and Surface Effects on the Electric Response of Electrolytic Cells. Physchem, 2(2), 163-178. https://doi.org/10.3390/physchem2020012