Abstract
Almandine garnet has received considerable amounts of interest due to its application in manufacturing and engineering processes. Defect processes, Fe-ion diffusion pathways, and promising dopants on the Al, Fe, and Si sites are examined using classical pair potential simulations in almandine garnet. The cation antisite (Al–Si) defect cluster is the most favourable defect, highlighting the cation disorder in this material. A three-dimensional long-range Fe-ion diffusion pathway with an activation energy of 0.44 eV suggests that the ionic conductivity in this material is high. The most favourable isovalent dopants on the Fe, Al, and Si sites were found to be the Mn, Ga, and Ge, respectively. Subvalent doping of Ga on the Si site is a favourable process to increase the Fe content in this material.
1. Introduction
Almandine garnet (Fe3Al2Si3O12) is a nesosilicate mineral found in metamorphic rocks, such as mica schists, amphibolites, granulites, granites, aplites, and granitic pegmatite [1,2,3]. It is generally found as a mixture of other minerals, such as pyrope (Mg3Al2Si3O12) and spessartine (Mn3Al2Si3O12) [4]. A trace amount of impurities, such as Zn, Sc, Cr, V, Zr, and Co has also been found in this material [1]. The deposits of almandine garnet are extensively distributed geographically in regions, such as Alaska, Germany, Norway, India, Sri Lanka, and Australia [3,5,6].
Almandine garnet has many industrial and research applications. Transparent almandine garnet is a very popular gemstone that is used to make jewellery [3]. It is also a good abrasive for sandblasting [7], surface grinding [8], and water jet cutting [9]. Furthermore, it is used as a reinforcement material to enhance the physical, chemical, and mechanical properties of alloys [10].
Several experimental studies [11,12,13,14,15] have been carried out on almandine garnet to measure its enthalpy of formation [16], examine its cation diffusion [17], study the effects of chemical weathering [18], and determine the temperature-dependent disordered configurations [19]. An experimental work carried out by Jain et al. [10] indicates that the metal matrix composite reinforced with almandine garnet enhances its mechanical property and corrosion resistance than that in the parental Ni alloy. The resultant composite is expected to be suitable for aerospace gas turbine applications [10]. Electrical conductivities of almandine garnet, pyrope, and their mixed composites were measured using complex impedance spectroscopy by Romano et al. [20]. Substitution of Fe on the Mg site enhances electrical conductivity and there is a smooth change in the activation energies with the composition at 10 GPa [20]. The surface of almandine garnet has been recently considered for the adsorption of seawater ions, such as Na+, Ca2+, and Mg2+ [8]. The reactivity of the irradiated surface of almandine garnet was examined by Hsiao et al. [21] and it was found that the irradiation reduced the coordination state of the cations and enhanced the reactivity. The presence of an appreciable amount of Fe3+ ions was determined in almandine garnet by Woodland et al. [22] and it was concluded that iron in aluminous garnets should be present in the ferric state. In order to identify garnet species including almandine garnet, Li et al. [23], used spectroscopic techniques and discovered a correlation between the chemical composition and spectroscopy [vibrational and Raman (or IR)].
Though there are many experimental studies available in the literature, only a few theoretical studies on this material have been reported [24,25]. Borinski et al. [24] used a numerical method together with experimental data to analyse the diffusion behaviour of Fe and Mg in almandine–pyrope-rich garnets. The quantum mechanical simulation of IR and Raman spectra of the almandine garnet was reported by Ferrari et al. [25], showing a good agreement between calculated wavenumbers and corresponding experimental values. Density functional theory-based calculations were performed by Nobes et al. [26] to compare the structural and mechanical properties of almandine garnet with available experimental data. This study further considered examining the correlation between the compressibility and size of the divalent cation.
A fundamental understanding of intrinsic and extrinsic defects in almandine garnet is useful to optimise its performance for future applications in various industries. Atomistic simulations, based on the classical pair potentials, can provide valuable information about defect processes, self-diffusion, and promising dopants. This simulation technique has been successfully used to model crystalline materials and has provided experiments with distinctive understanding and extrapolation [27,28,29,30,31,32,33]. To the best of our knowledge, there is no simulation study on the defects, diffusion, and dopant reported for almandine garnet available in the literature.
In this study, we report the results of intrinsic defect processes, Fe2+ ion diffusion pathways, together with the activation energies and solutions of MO (M = Co, Mn, Ni, Mg, Zn, Sr, and Ba), M2O3 (M = Ga, In, Sc, Y, Gd, and La) and MO2 (M = Ge, Ti, Sn, Zr, and Ce) in almandine garnet.
2. Computational Methods
The classical pair potential method, as implemented in the GULP (General Utility Lattice Program) package (version 3.4.1) [34], was employed to calculate the formation energies of intrinsic defects, Fe ion diffusion pathways, and solution of divalent, trivalent, and tetravalent dopants. The classical Born model of an ionic crystal lattice is assumed in this method. All systems were considered as crystalline solids and interactions between ions were modelled using long-range attraction (Coulomb) and short-range (Pauli repulsion and van der Waals attraction) forces. Buckingham potentials (see Table 1) [35,36] were used to describe the short-range interactions.

Table 1.
Buckingham potential parameters [35,36] were used in the classical simulations of Fe3Al2Si3O12. Two-body [Φij (rij) = Aij exp (−rij/ρij) − Cij/rij6], where A, ρ, and C are parameters that were selected to reproduce the experimental crystal structure of Fe3Al2Si3O12. The values of Y and K represent the shell charges and spring constants. A very large spring constant means there is no shell charge and the atom is treated as a core.
Full geometry optimization (cell parameters and ionic positions) was performed using the Broyden–Fletcher–Goldfarb–Shanno (BFGS) [37] algorithm. The lattice relaxation of the point defects and the migrating ions was investigated using the Mott–Littleton method [38]. Fe ion diffusion pathways were calculated, considering two adjacent Fe vacancy sites as the initial and final configurations. The activation energy of migration is determined and presented as the local maximal energy along this diffusion path. The current methodology treats ions as spherical shapes with full charge at the dilute limit. Therefore, it is expected that calculated defect energies will be overestimated. However, the relative energy trend will be consistent [39]. The current methodology has been previously used to reproduce the experimentally observed Li-ion migration pathway in LiFePO4 [40,41] and the presence of the Ca2+ ion on the Ba site in barite [42].
3. Results and Discussion
3.1. Crystal Structure of Almandine Garnet
The crystal structure of almandine garnet is cubic (space group Ia3d) with experimental lattice parameters, a = b = c = 11.507 Å and α = β = γ = 90° [43]. Its three-dimensional network framework consists of octahedral AlO6 and tetrahedral SiO4 units connected via their corners (see Figure 1). First, the experimentally observed crystal structure was allowed to relax completely (both atomic positions and lattice constants) to validate the quality of the potentials used in this study. The calculated lattice parameters were compared with corresponding experimental values. There is an excellent agreement between the calculated equilibrium lattice constants and those observed in the experiment (see Table 2).
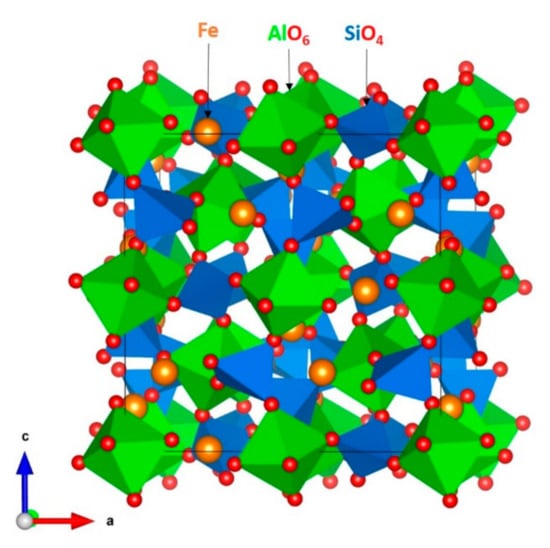
Figure 1.
The crystal structure of the almandine garnet.

Table 2.
Calculated and experimental lattice parameters of almandine garnet.
3.2. Intrinsic Defects
A series of isolated point defects (vacancy and interstitial) were generated, and their formation energies were calculated. These energies were then combined to calculate the formation energies of Frenkel, Schottky, and antisite defects. These defect processes are useful in understanding the electrochemical and diffusion properties of a material. The antisite defect was calculated in two different forms, namely isolated and cluster. In the isolated form, defects were considered separately, and their energies were combined. Defects were considered in the same supercell in the cluster form. The following equations represent the reactions involving these defects as written using Kröger–Vink notation [44]:
The defect energies are reported in Figure 2. The most favourable defect is the Al–Si antisite defect cluster, indicating that a small amount of cation mixing will be present. The antisite defect cluster has been found in many oxide materials [45,46,47]. Other antisite defect cluster energies are lower than the Frenkel and Schottky defect energies. However, they are possible only at high temperatures. In all antisite defect clusters, energies are lower than their corresponding isolated forms. This is due to the aggregation of isolated defects forming a cluster with exoergic binding energy. The Fe Frenkel defect energy is 2.23 eV/defect. This defect is important, as it can facilitate the formation of Fe vacancies and vacancy-assisted Fe diffusion. The O Frenkel is higher by 0.34 eV than the Fe Frenkel. Both Fe and O Frenkel defects can occur only at high temperatures. Other Frenkel and Schottky defect processes are highly endoergic, and they will not take place at normal temperatures.
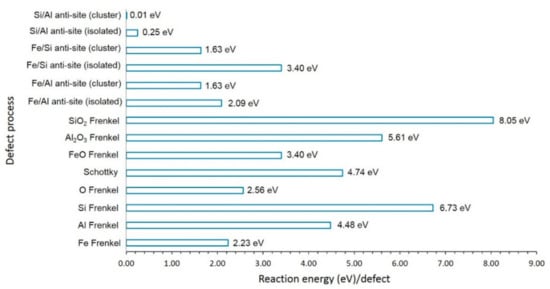
Figure 2.
Energies of intrinsic defect processes.
3.3. Fe Ion Migration
The diffusion properties comparatively determine the performance of a material. The diffusion of Fe-ions in this material can be of interest in the application of abrasives. Materials exhibiting long-range Fe-ion diffusion with low activation energy can influence their electrochemical performance.
Atomistic simulations based on the classical pair potentials can provide beneficial evidence on diffusion pathways and activation energies. The present practice has been efficaciously applied to various ionic materials to compute migration pathways together with activation energies [48,49,50].
We have identified a promising local Fe–Fe hoping distance of 3.52 Å. Both linear and curve pathways were considered. The activation energy (1.83 eV) calculated for the linear pathway is higher than that calculated for the curved pathway (0.44 eV) (see Figure 3). Fe ion moves in all directions, forming a three-dimensional pathway. The low activation of Fe ion diffusion means that the ionic conductivity in this material is high. We have considered a range of other pathways with longer Fe–Fe hoping distances greater than 5.00 Å, but these were all found to have prohibitively high migration barriers (>4.50 eV).
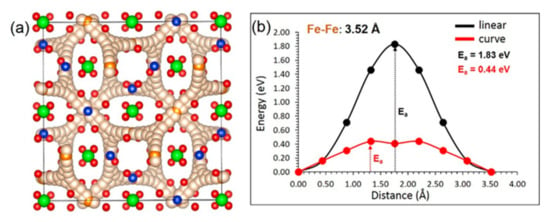
Figure 3.
(a) Three-dimensional Fe-ion migration pathway and (b) energy profile diagram showing activation energies for both linear and curved pathways.
3.4. Solution of Dopants
A variety of dopants were considered for screening and predicting promising dopants that can be verified experimentally. Appropriate charge-compensating defects and lattice energies were introduced to calculate solution energies. Buckingham potentials used for dopant oxides are provided in the electronic supplementary data (see Table S1).
3.4.1. Divalent Dopants
First, divalent dopants (M = Co, Mn, Ni, Mg, Zn, Ca, Sr and Ba) were considered on the Fe site. The following equation was used to calculate the solution energy:
The results reveal that the most favourable dopant (−0.08 eV) is calculated for Mn on the Fe site (see Figure 4). This indicates that almandine garnet prefers to form an almandine–spessartine mixed phase. The solution energy calculated for Ca is lower by 0.04 eV than that calculated for Mn. As both Ca and Mn exhibit exothermic solution energies, there is a necessity for experimental verification. Solution energies calculated for Ni, Mg, Co, Zn, Mn, Ca, and Sr range between −0.08 eV and 0.28 eV. This is partly due to the ionic radius of Fe2+ (0.92 Å) being closer to those dopants (0.69 Å–1.12 Å). The solution energy calculated for Ba is extremely positive (3.50 eV) due to its larger ionic radius (1.42 Å).
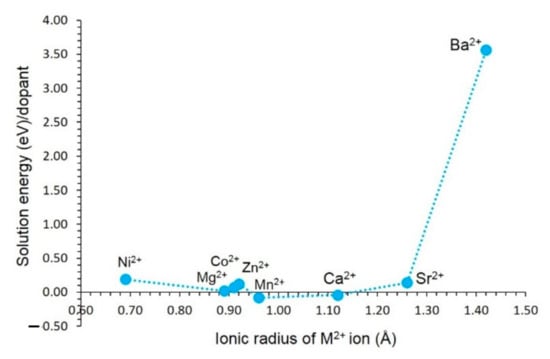
Figure 4.
Solution energy of MO (M = Ni, Co, Mn, Mg, Zn, Ca, Sr, and Ba) with respect to the M2+ ionic radius.
3.4.2. Trivalent Dopants
A range of trivalent dopants was considered on the Al site. The following reaction equation explains the doping process.
Figure 5 reports the solution energies. The most favourable dopant is Ga. Its solution energy is −0.11 eV. The preference of Ga is partly due to the ionic radius of Al3+ (0.54 Å) being closer to the ionic radius of Ga3+ (0.62 Å). Solution energy gradually increases with increasing ionic radius. Solution energy calculated for La is 3.31 eV, suggesting that this dopant is highly unlikely to substitute under normal conditions. The possible experimental composition that can be synthesised is Fe3 (Al1-xGax)2Si3O12.
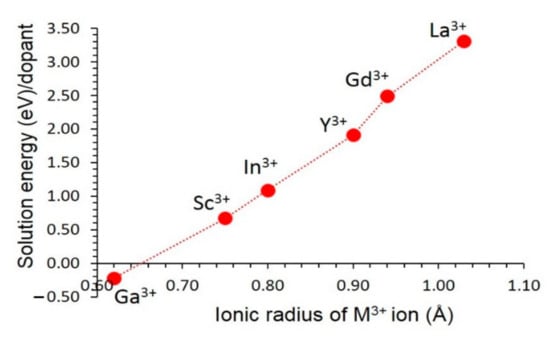
Figure 5.
Solution energy of M2O3 (M = Ga, Sc, In, Y, Gd, and La) with respect to the M3+ ionic radius.
Trivalent doping on the Si site can generate Fe interstitials as charge-compensating defects, as defined by the following equation. This is an efficient way of introducing additional Fe2+ in the lattice to increase the Fe2+ ion intercalation process in this material.
The most favourable solution energy dopant is the Ga3+ although its solution energy is 2.69 eV (see Figure 6). This doping process should be carried out at high temperatures. Solution energy increases with increasing ionic radius. The most unfavourable dopant is the La3+. This is partly due to the larger ionic radius of La3+ than that of the other dopant ions.
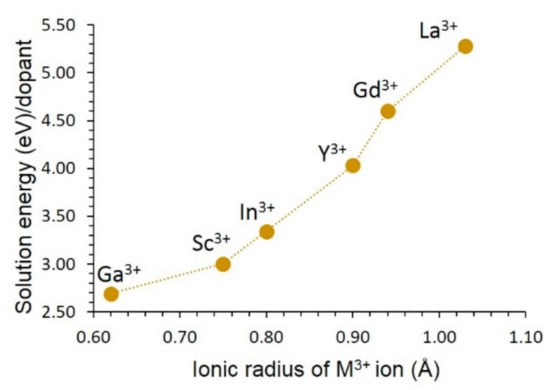
Figure 6.
Solution energy of M2O3 (M = Ga, Sc, In, Y, Gd, and La) with respect to the M3+ ionic radius (charge compensation: Fe interstitial according to Equation (17)).
3.4.3. Tetravalent Dopants
Finally, tetravalent cations were substituted on the Si site. This doping process required no charge-compensating defects, as written by the following reaction equation.
The Ge4+ ion is the most thermodynamically favourable dopant for this process (see Figure 7), with a solution energy of 0.57 eV. This is due to the ionic radius of Ge4+ (0.39 Å), closer to that of Si4+ (0.26 Å). The possible doped composition that would be worth trying experimentally is Fe3Al2(Si1-xGex)3O12 (x = 0.0 < x < 1.0). Solution energy then gradually increases with the increasing ionic radius. The largest endoergic solution energy (5.00 eV) is calculated for Ce4+. The doping of Ce4+ requires high temperatures.
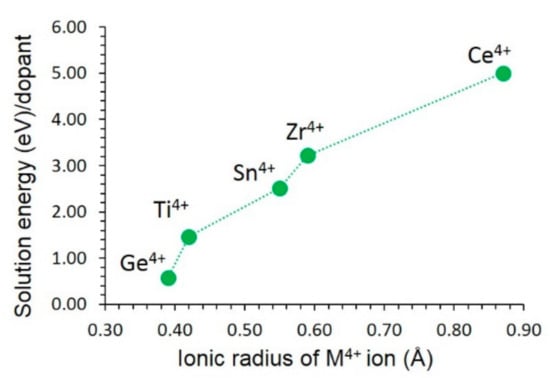
Figure 7.
Solution energy of MO2 with respect to the M4+ ionic radius in Fe3Al2Si3O12.
4. Conclusions
In this work, the use of modelling materials based on the classical potential simulations allowed us to examine the defect chemistry, Fe ion diffusion pathways, and the solution of dopants. The lowest energy defect process is the Al–Si antisite cluster, suggesting that a small amount of cation intermixing is possible in this material. The diffusion of Fe2+ ions is three-dimensional and fast with an activation energy of 0.44 eV. The isovalent candidate dopants on the Fe, Al, and Si are Mn, Ga, and Ge, respectively. A possible strategy for increasing the Fe2+ ions in this material is by doping Ga on the Si site. The main objective of the present investigation is to motivate further experimental and theoretical studies.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/physchem2010004/s1, Table S1: Buckingham potential parameters used in the classical simulations of Fe3Al2Si3O12.
Author Contributions
Computation, J.L.S. and N.K.; writing, J.L.S. and N.K.; analysis and editing, S.G. and N.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Acknowledgments
Computational facilities were provided by the Imperial College London and the University of Jaffna.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Sultana, N. Trace Elements in Almandine Garnet, Vemireddipalle Area, Krishna District, Andhra Pradesh, India. Int. J. Sci. Res. Sci. Technol. 2019, 6, 184–187. [Google Scholar] [CrossRef]
- Yu, M.; Xia, Q.-X.; Zheng, Y.-F.; Zhao, Z.-F.; Chen, Y.-X.; Chen, R.-X.; Luo, X.; Li, W.-C.; Xu, H. The composition of garnet in granite and pegmatite from the Gangdese orogen in southeastern Tibet: Constraints on pegmatite petrogenesis. Am. Miner. 2021, 106, 265–281. [Google Scholar] [CrossRef]
- Sultana, N.; Podila, S.P. Almandine Gemstone—A review. Int. J. Recent Sci. Res. 2018, 9, 29204–29209. [Google Scholar]
- Geiger, C.A.; Feenstra, A. Molar volumes of mixing of almandine-pyrope and almandine-spessartine garnets and the crystal chemistry and thermodynamic-mixing properties of the aluminosilicate garnets. Am. Miner. 1997, 82, 571–581. [Google Scholar] [CrossRef]
- Čopjaková, R.; Sulovský, P.; Paterson, B.A. Major and trace elements in pyrope–almandine garnets as sediment provenance indicators of the Lower Carboniferous Culm sediments, Drahany Uplands, Bohemian Massif. Lithos 2005, 82, 51–70. [Google Scholar] [CrossRef]
- Sajeev, K.; Osanai, Y. Thermal gradients in the Sri Lankan granulite terrane: A garnet-biotite thermometric approach. J. Metamorph. Geol. 2005, 23, 383–397. [Google Scholar] [CrossRef]
- Usman, K.R.; Hainin, M.R.; Satar, M.K.I.M.; Warid, M.N.M.; Usman, A.; Al-Saffar, Z.H.; Bilema, M.A. A comparative assessment of the physical and microstructural properties of waste garnet generated from automated and manual blasting process. Case Stud. Constr. Mater. 2021, 14, e00474. [Google Scholar] [CrossRef]
- Poon, J.; Madden, D.C.; Wood, M.H.; van Tol, R.; Sonke, H.; Clarke, S.M. Surface Chemistry of Almandine Garnet. J. Phys. Chem. C 2020, 124, 5099–5117. [Google Scholar] [CrossRef]
- Stewart, H.A. Stock Removal Rates for Aluminium Oxide-Coated and Garnet-Coated Abrasive Belts. For. Prod. J. 1978, 28, 29–31. [Google Scholar]
- Jain, M.; Purushotham, G. Effect of Almandine on Microstructure and Corrosion properties of Nickel super alloy (K500) Composite for Aerospace Gas Turbine Application. IOP Conf. Ser. Mater. Sci. Eng. 2018, 376, 012051. [Google Scholar] [CrossRef]
- Chinner, G.A.; Clifford, T.N.; Nicolaysen, L.O.; Burger, A.J. Almandine in Thermal Aureoles. J. Pet. 1962, 3, 316–341. [Google Scholar] [CrossRef]
- Stone, M. The Significance of Almandine Garnets in the Lundy and Dartmoor Granites. Miner. Mag. 1988, 52, 651–658. [Google Scholar] [CrossRef]
- Guinel, M.J.-F.; Norton, M.G. The origin of asterism in almandine-pyrope garnets from Idaho. J. Mater. Sci. 2006, 41, 719–725. [Google Scholar] [CrossRef]
- Koziol, A.M.; Bohlen, S.R. Solution properties of almandine-pyrope garnet as determined by phase equilibrium experiments. Am. Mineral. 1992, 77, 765–773. [Google Scholar]
- Li, B.; Ge, J.; Zhang, B. Diffusion in garnet: A review. Acta Geochim. 2018, 37, 19–31. [Google Scholar] [CrossRef] [Green Version]
- Woodland, A.B.; Wood, B.J. Electrochemical measurement of the free energy of almandine (Fe3Al2Si3O12) garnet. Geochim. Cosmochim. Acta 1989, 53, 2277–2282. [Google Scholar] [CrossRef]
- Freer, R. An experimental measurement of cation diffusion in almandine garnet. Nature 1979, 280, 220–222. [Google Scholar] [CrossRef]
- Price, J.; Bryan-Ricketts, D.S.; Anderson, D.; Velbel, M.A. Weathering of Almandine Garnet: Influence of Secondary Minerals on the Rate-Determining Step, and Implications for Regolith-Scale Al Mobilization. Clays Clay Miner. 2013, 61, 34–56. [Google Scholar] [CrossRef]
- Quartieri, S.; Antonioli, G.; Artioli, G.; Geiger, C.; Lottici, P. Temperature Dependence of Disorder and Correlation Effects in the Almandine X-Site. J. Phys. IV Fr. 1997, 7, C2-1157–C2-1158. [Google Scholar] [CrossRef]
- Romano, C.; Poe, B.T.; Kreidie, N.; McCammon, C.A. Electrical conductivities of pyrope-almandine garnets up to 19 GPa and 1700 °C. Am. Miner. 2006, 91, 1371–1377. [Google Scholar] [CrossRef]
- Hsiao, Y.-H.; La Plante, E.C.; Krishnan, N.M.A.; Dobbs, H.A.; Le Pape, Y.; Neithalath, N.; Bauchy, M.; Israelachvili, J.N.; Sant, G.N. Role of Electrochemical Surface Potential and Irradiation on Garnet-Type Almandine’s Dissolution Kinetics. J. Phys. Chem. C 2018, 122, 17268–17277. [Google Scholar] [CrossRef]
- Woodland, A.B.; Droop, G.; O’Neill, H.S.C. Almandine-rich garnet from near Collobrieres, southern France, and its petrological significance. Eur. J. Mineral. 1995, 7, 187–194. [Google Scholar] [CrossRef]
- Li, W.; Zheng, J.; Pei, J.; Xu, X.; Chen, T. Correlations between Garnet Species and Vibration Spectroscopy: Isomorphous Substitution Implications. Crystals 2022, 12, 104. [Google Scholar] [CrossRef]
- Borinski, S.A.; Hoppe, U.; Chakraborty, S.; Ganguly, J.; Bhowmik, S.K. Multicomponent diffusion in garnets I: General theoretical considerations and experimental data for Fe–Mg systems. Contrib. Miner. Pet. 2012, 164, 571–586. [Google Scholar] [CrossRef]
- Ferrari, A.M.; Valenzano, L.; Meyer, A.; Orlando, R.; Dovesi, R. Quantum-Mechanical ab Initio Simulation of the Raman and IR Spectra of Fe3Al2Si3O12 Almandine. J. Phys. Chem. A 2009, 113, 11289–11294. [Google Scholar] [CrossRef] [PubMed]
- Nobes, R.; Akhmatskaya, E.; Milman, V.; Winkler, B.; Pickard, C. Structure and properties of aluminosilicate garnets and katoite: An ab initio study. Comput. Mater. Sci. 2000, 17, 141–145. [Google Scholar] [CrossRef]
- Kuganathan, N.; Kordatos, A.; Anurakavan, S.; Iyngaran, P.; Chroneos, A. Li3SbO4 lithium-ion battery material: Defects, lithium ion diffusion and tetravalent dopants. Mater. Chem. Phys. 2019, 225, 34–41. [Google Scholar] [CrossRef]
- Kuganathan, N.; Ganeshalingam, S.; Chroneos, A. Defects, Dopants and Lithium Mobility in Li9V3(P2O7)3(PO4)2. Sci. Rep. 2018, 8, 8140. [Google Scholar] [CrossRef]
- Kuganathan, N.; Chroneos, A. Na3V(PO4)2 cathode material for Na ion batteries: Defects, dopants and Na diffusion. Solid State Ion. 2019, 336, 75–79. [Google Scholar] [CrossRef] [Green Version]
- Devanathan, R.; Weber, W.; Singhal, S.; Gale, J. Computer simulation of defects and oxygen transport in yttria-stabilized zirconia. Solid State Ion. 2006, 177, 1251–1258. [Google Scholar] [CrossRef] [Green Version]
- Pandey, R.; Gale, J.D.; Sampath, S.K.; Recio, J.M. Atomistic Simulation Study of Spinel Oxides: Zinc Aluminate and Zinc Gallate. J. Am. Ceram. Soc. 1999, 82, 3337–3341. [Google Scholar] [CrossRef]
- Williford, R.E.; Weber, W.J.; Devanathan, R.; Gale, J.D. Effects of Cation Disorder on Oxygen Vacancy Migration in Gd2Ti2O7. J. Electroceram. 1999, 3, 409–424. [Google Scholar] [CrossRef]
- Henson, N.J.; Cheetham, A.K.; Gale, J.D. Computational Studies of Aluminum Phosphate Polymorphs. Chem. Mater. 1996, 8, 664–670. [Google Scholar] [CrossRef]
- Gale, J.D.; Rohl, A.L. The General Utility Lattice Program (GULP). Mol. Simul. 2003, 29, 291–341. [Google Scholar] [CrossRef]
- Kuganathan, N.; Islam, M.S. Li2MnSiO4 Lithium Battery Material: Atomic-Scale Study of Defects, Lithium Mobility, and Trivalent Dopants. Chem. Mater. 2009, 21, 5196–5202. [Google Scholar] [CrossRef]
- Lewis, G.V.; Catlow, C.R.A. Potential models for ionic oxides. J. Phys. C Solid State Phys. 1985, 18, 1149–1161. [Google Scholar] [CrossRef]
- Gale, J.D. GULP: A computer program for the symmetry-adapted simulation of solids. J. Chem. Soc. Faraday Trans. 1997, 93, 629–637. [Google Scholar] [CrossRef]
- Mott, N.F.; Littleton, M.J. Conduction in polar crystals. I. Electrolytic conduction in solid salts. Trans. Faraday Soc. 1938, 34, 485–499. [Google Scholar] [CrossRef]
- Grimes, R.W.; Busker, G.; McCoy, M.A.; Chroneos, A.; Kilner, J.A.; Chen, S.-P. The Effect of Ion Size on Solution Mechanism and Defect Cluster Geometry. Ber. Bunsenges. Phys. Chem. 1997, 101, 1204–1210. [Google Scholar] [CrossRef]
- Fisher, C.A.J.; Prieto, V.M.H.; Islam, M.S. Lithium Battery Materials LiMPO4 (M = Mn, Fe, Co, and Ni): Insights into Defect Association, Transport Mechanisms, and Doping Behavior. Chem. Mater. 2008, 20, 5907–5915. [Google Scholar] [CrossRef]
- Nishimura, S.-I.; Kobayashi, G.; Ohoyama, K.; Kanno, R.; Yashima, M.; Yamada, A. Experimental visualization of lithium diffusion in LixFePO4. Nat. Mater. 2008, 7, 707–711. [Google Scholar] [CrossRef] [PubMed]
- Wahid, F.A.; Thomson, G.B.; Graham, G.M.; Jackson, R.A. A computational study of the effect of doping divalent cations in barite. J. Mater. Chem. 2002, 12, 3799–3802. [Google Scholar] [CrossRef]
- Prandl, W. Die magnetische Struktur und die Atomparameter* des Almandins Al2Fe3(SiO4)3. Z. Krist.-Cryst. Mater. 1971, 134, 333–343. [Google Scholar] [CrossRef]
- Kröger, F.A.; Vink, H.J. Relations between the Concentrations of Imperfections in Crystalline Solids. In Solid State Physics; Seitz, F., Turnbull, D., Eds.; Academic Press: Cambridge, MA, USA, 1956; Volume 3, pp. 307–435. [Google Scholar]
- Devaraju, M.K.; Truong, Q.D.; Hyodo, H.; Sasaki, Y.; Honma, I. Synthesis, characterization and observation of antisite defects in LiNiPO4 nanomaterials. Sci. Rep. 2015, 5, 11041. [Google Scholar] [CrossRef] [Green Version]
- Politaev, V.V.; Petrenko, A.A.; Nalbandyan, V.B.; Medvedev, B.S.; Shvetsova, E.S. Crystal structure, phase relations and electrochemical properties of monoclinic Li2MnSiO4. J. Solid State Chem. 2007, 180, 1045–1050. [Google Scholar] [CrossRef]
- Nytén, A.; Abouimrane, A.; Armand, M.; Gustafsson, T.; Thomas, J.O. Electrochemical performance of Li2FeSiO4 as a new Li-battery cathode material. Electrochem. Commun. 2005, 7, 156–160. [Google Scholar] [CrossRef]
- Quinzeni, I.; Fujii, K.; Bini, M.; Yashima, M.; Tealdi, C. Na+ diffusion mechanism and transition metal substitution in tunnel-type manganese-based oxides for Na-ion rechargeable batteries. Mater. Adv. 2022, 3, 986–997. [Google Scholar] [CrossRef]
- Ward, R.E.; Freeman, C.L.; Dean, J.S.; Sinclair, D.C.; Harding, J.H. Using Metadynamics to Obtain the Free Energy Landscape for Cation Diffusion in Functional Ceramics: Dopant Distribution Control in Rare Earth-Doped BaTiO3. Adv. Funct. Mater. 2020, 30, 1905077. [Google Scholar] [CrossRef]
- Fisher, C.; Matsubara, H. Oxide ion diffusion along grain boundaries in zirconia: A molecular dynamics study. Solid State Ion. 1998, 113–115, 311–318. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).