Vibrational Analysis of Benziodoxoles and Benziodazolotetrazoles
Abstract
1. Introduction
2. Computational and Experimental Methods
3. Results/Discussion
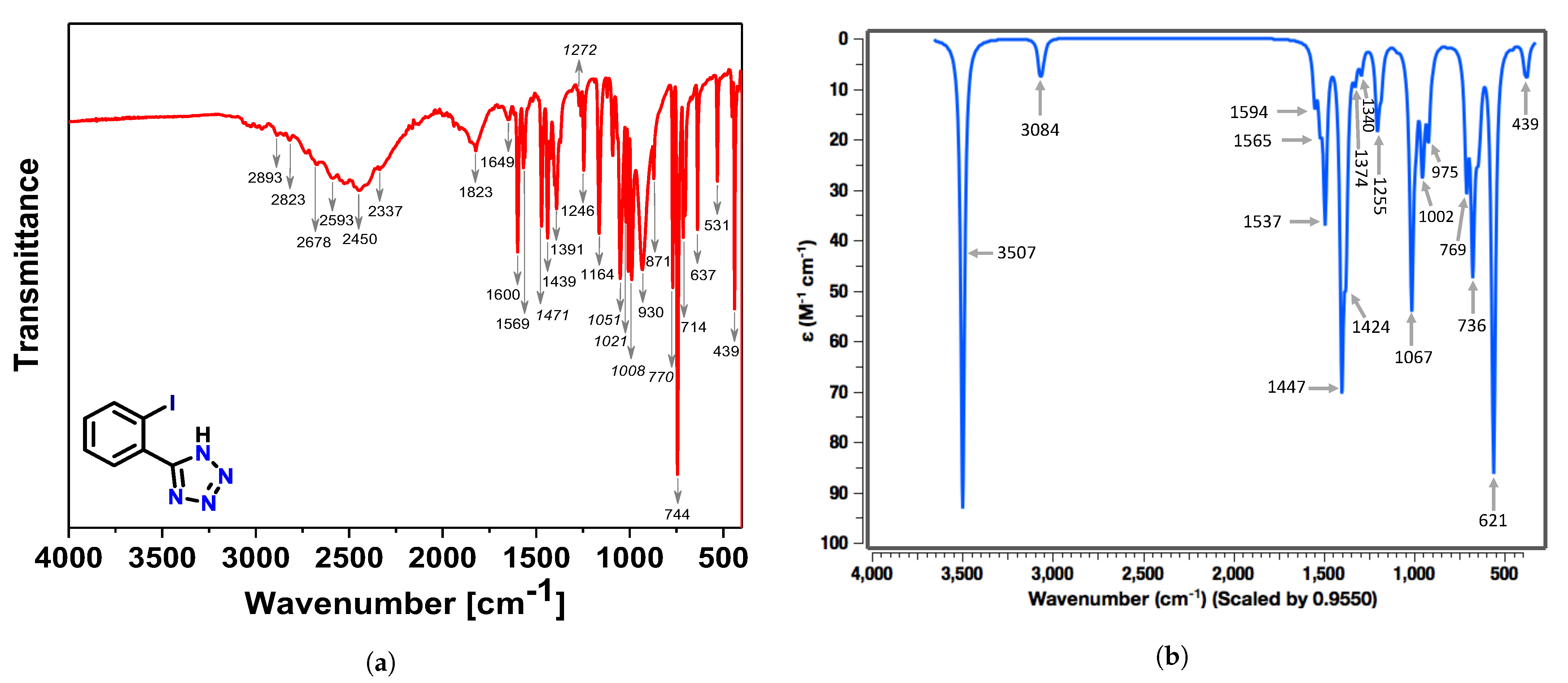
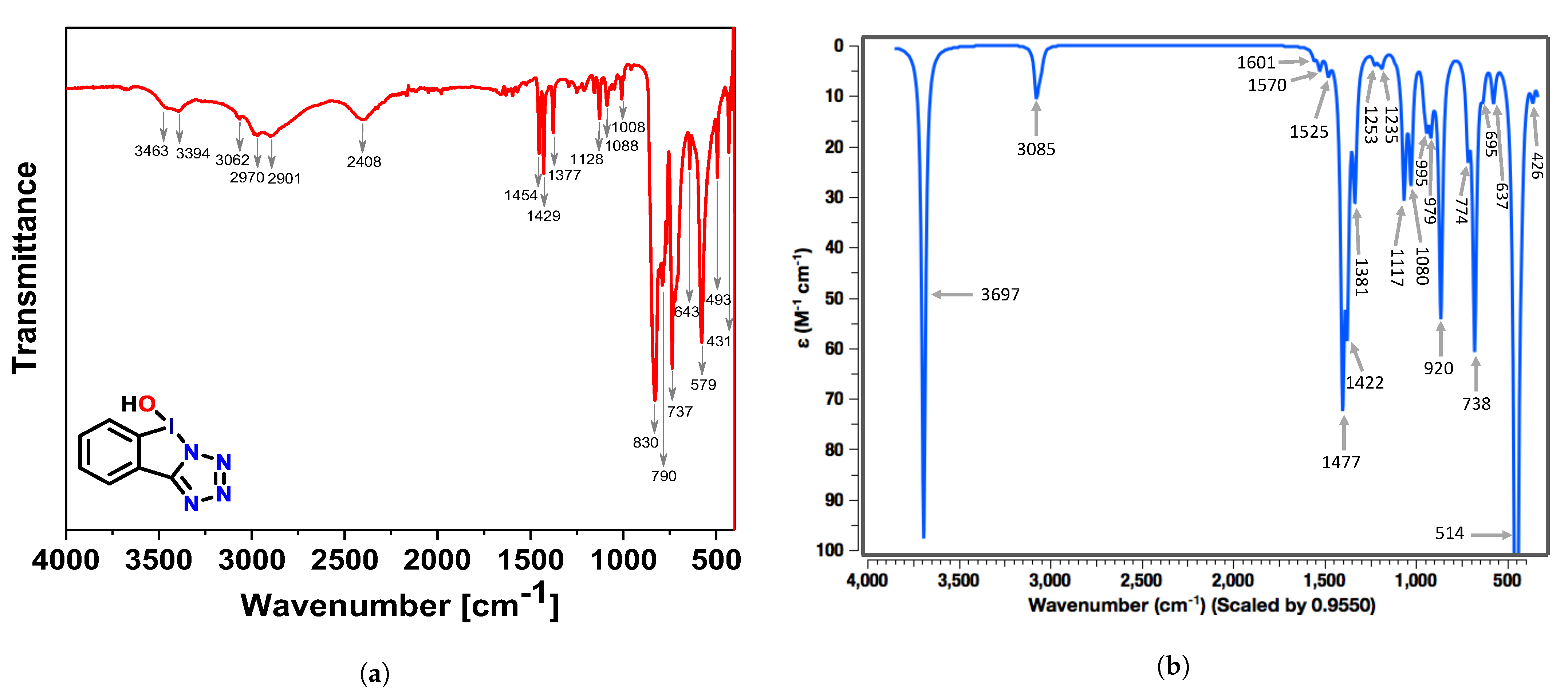
3.1. Experimental and Theoretical IR-Spectra
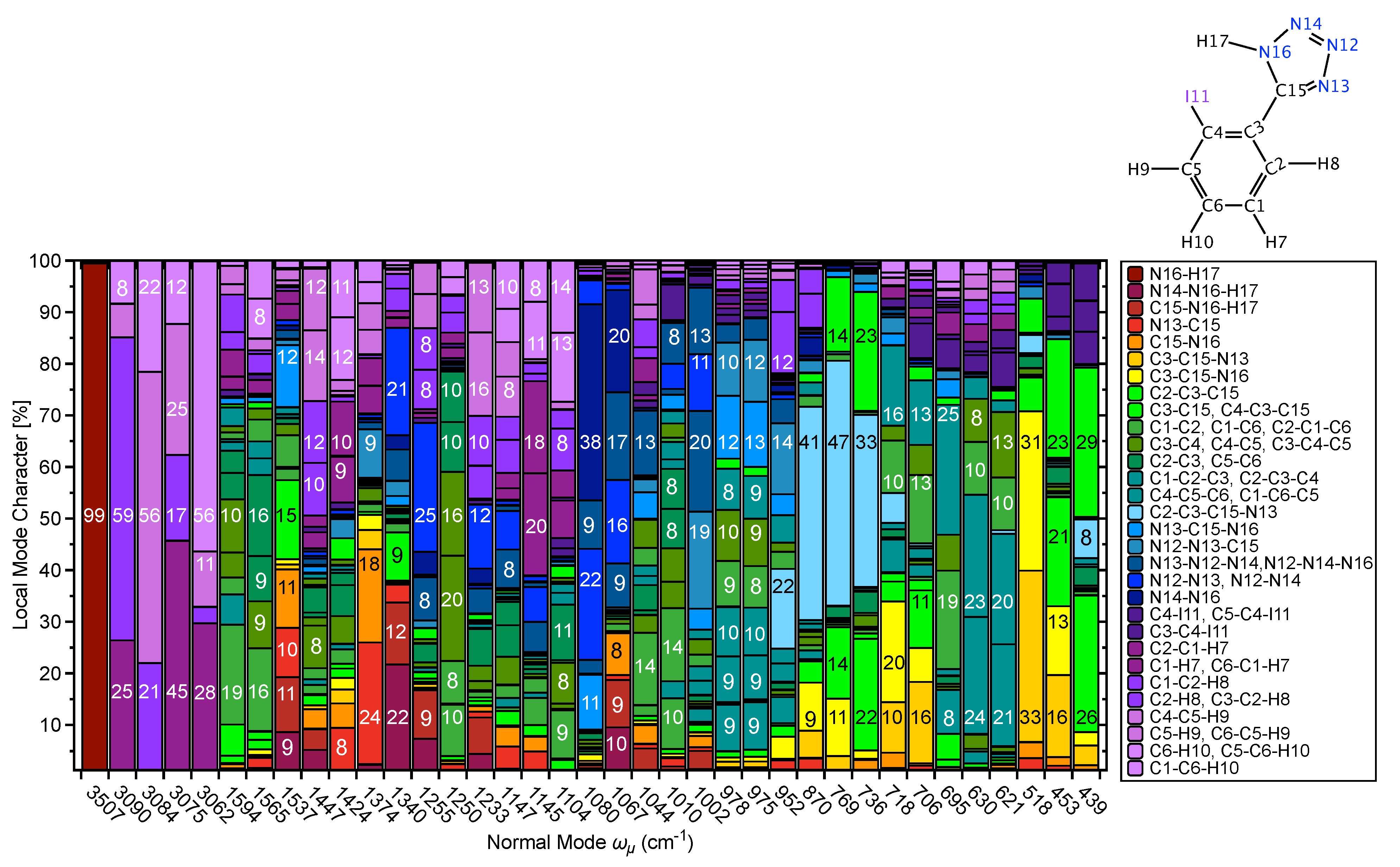
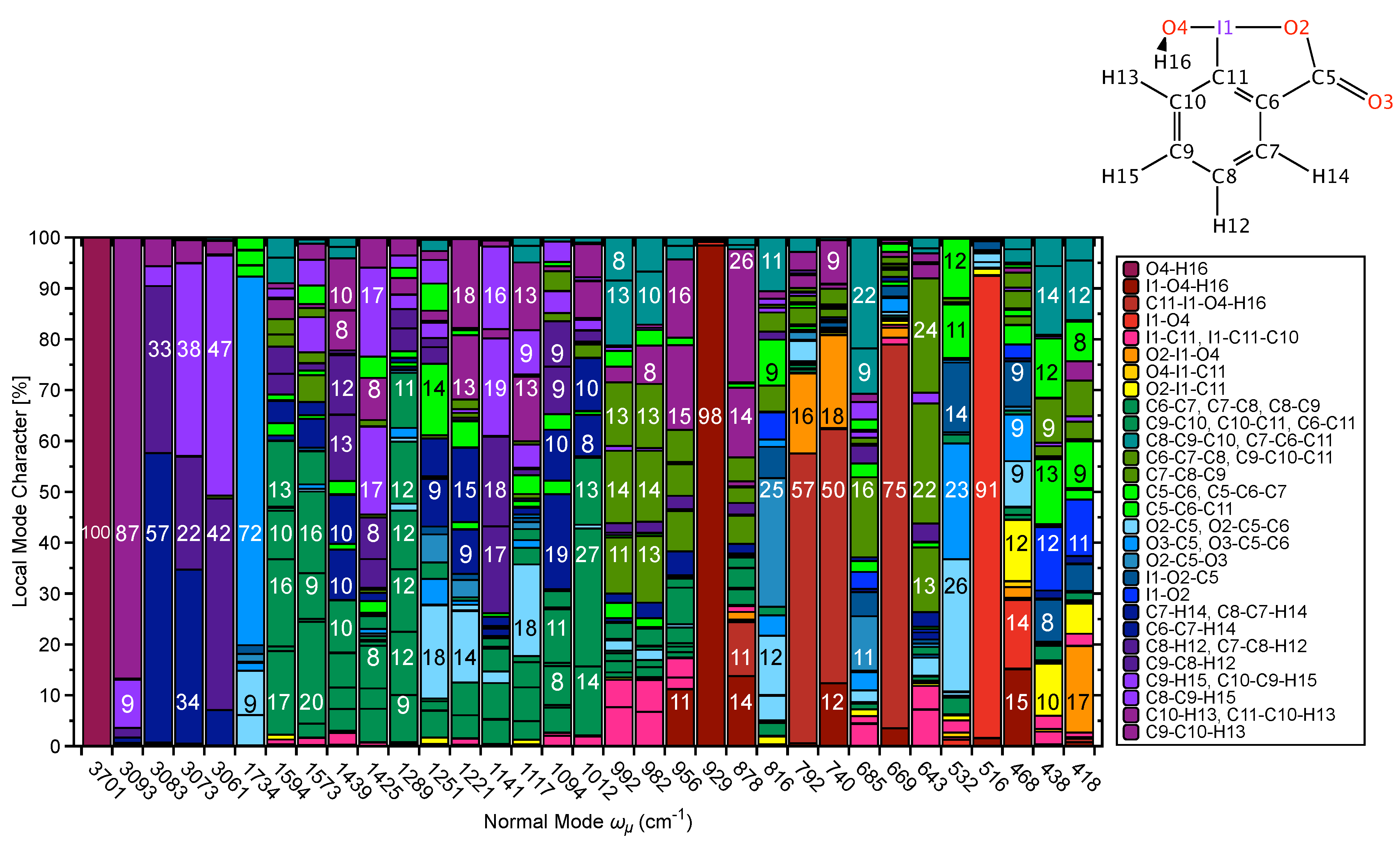
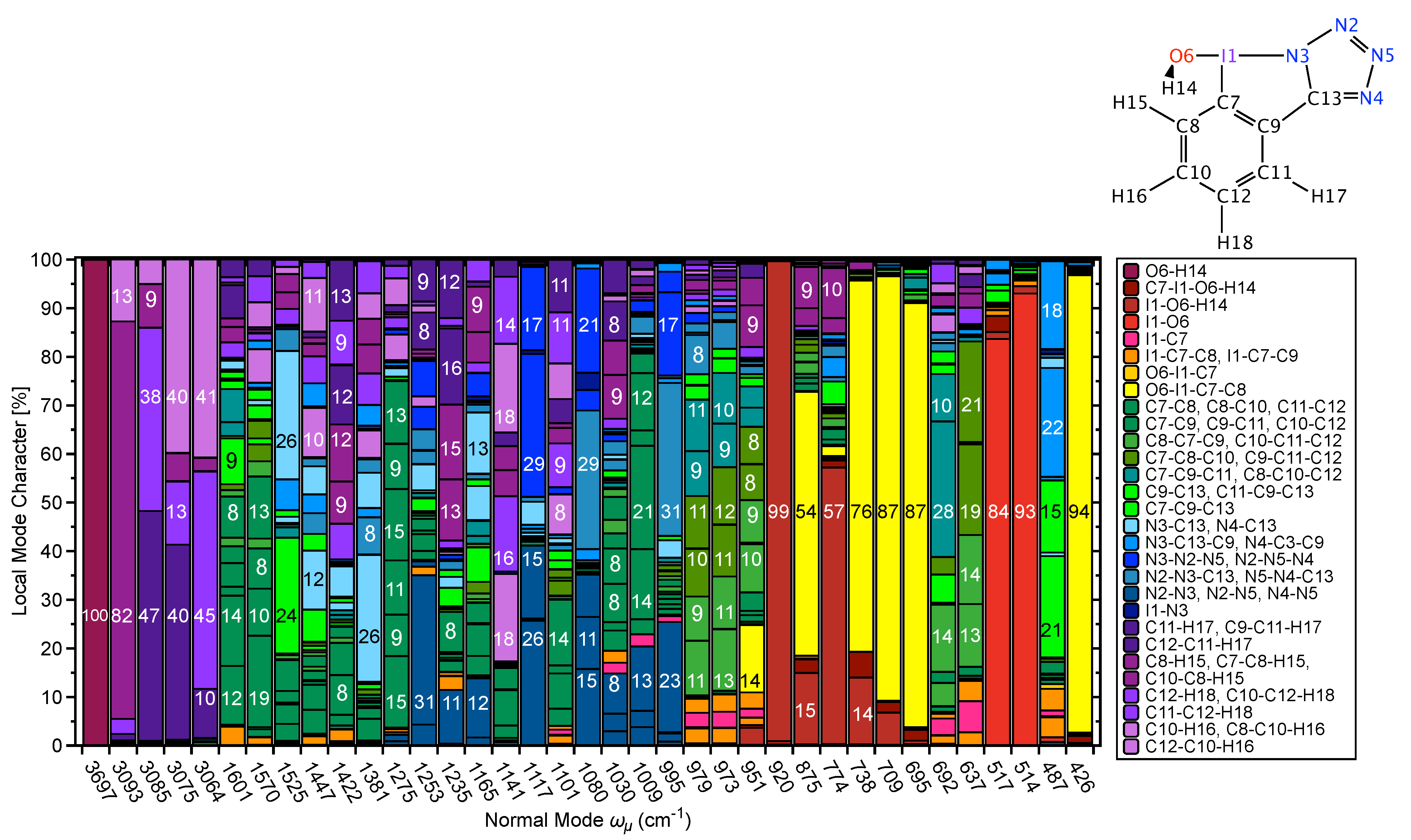
CNM Analysis
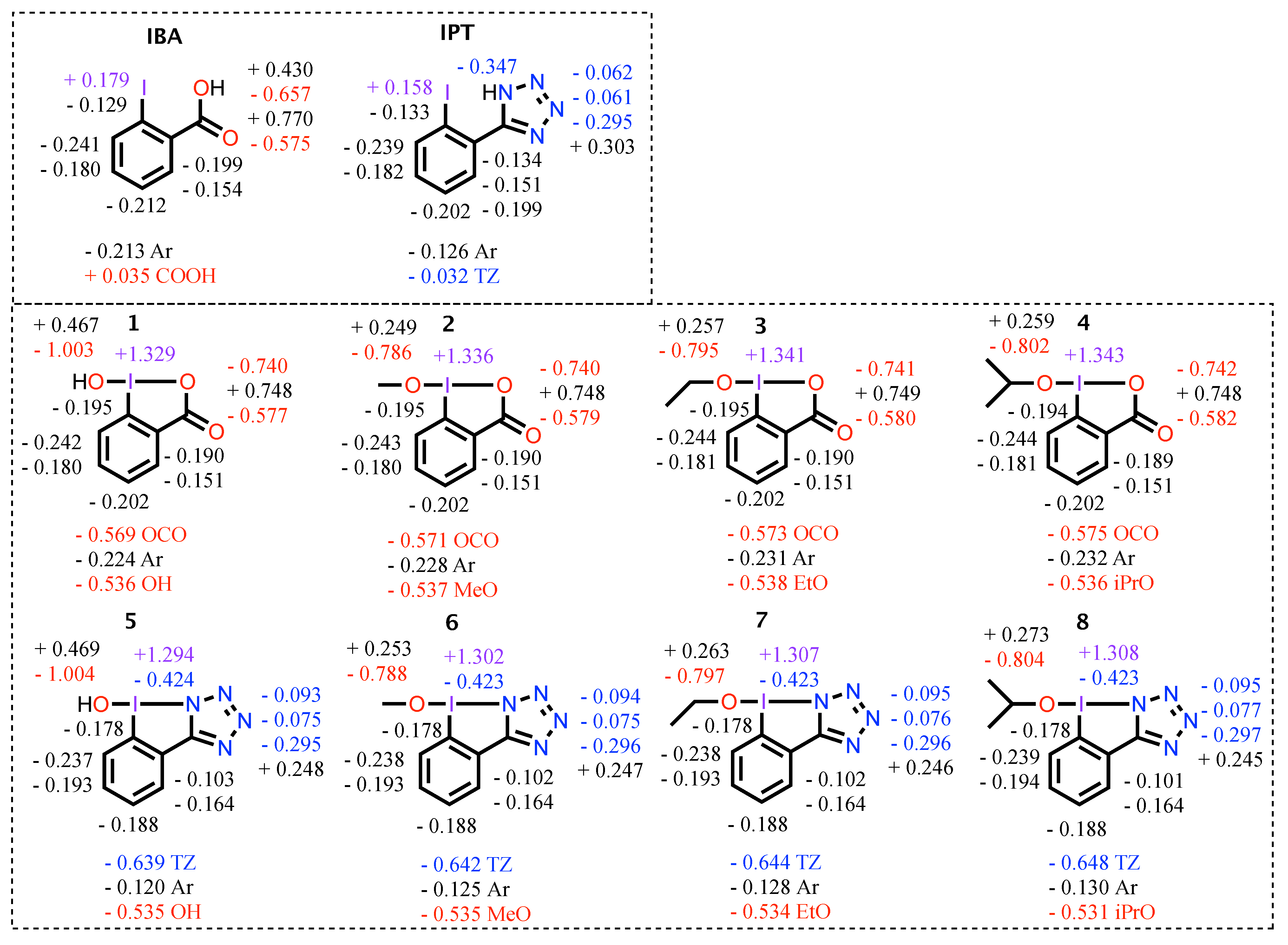
3.2. NBO Analysis
3.3. LVM and QTAIM Analyses
4. Conclusions and Outlook
- The TZ groups in BIATs 5–8 are more capable electron withdrawing groups compared to the OCO groups in BIOs 1–4
- Compared to BIATs 5–8, BIOs 1–4 have Ar rings nearly two times more negative in charge, iodine atoms with positive in charges, and stronger I−C and I−O (hydroxyl/alkoxy) bonds
- The weakest bonds in this work are the I−N bonds
- The 3c-4e L−I−L bond angles of BIATs 5–8 are up to 2.5 larger compared to the analogous bonds in BIOs 1–4
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| 3c-4e | 3-Center 4-Electron |
| Ar | Ortho-Disubstituted Benzene |
| BIAT | Benziodazolotetrazole |
| BIO | Alkoxybenziodoxole |
| CNM | Characterization of Normal Modes |
| CT | Charge Transfer |
| DFT | Density Functional Theory |
| exp | Experimental |
| HV | Hypervalent |
| HVI | Hypervalent Iodine |
| IBA | 2-Iodobenzoic Acid |
| IPT | 5-(2-Iodophenyl)tetrazole |
| L | Ligand |
| LVM | Local Vibrational Mode |
| MAE | Mean Absolute Error |
| NBO | Natural Bond Orbital |
| OCO | Carboxyl/Carboxylate Ester |
| RCN4− | Tetrazolate |
| RCO2− | Carboxylate |
| RMSE | Root Mean Square Error |
| theor | Theoretical |
| TZ | Tetrazole |
References
- Varvoglis, A. Organic Compounds of Polycoordinated Iodine; Wiley-VCH: Weinheim, Germany, 1992; p. 414. ISBN 0471188255. [Google Scholar]
- Willgerodt, C. Die Organischen Verbindungen mit Mehrwertigem Jod; Ferdinand Enke: Stuttgart, Germany, 1914; p. 266. ISBN 978-0526136322. [Google Scholar]
- Varvoglis, A. Hypervalent Iodine in Organic Synthesis; Academic Press: San Diego, CA, USA, 1997; p. 223. ISBN 0-12-714975-9. [Google Scholar]
- Wirth, T. Hypervalent Iodine Chemistry: Modern Developments in Organic Synthesis; Springer: Berlin, Germany, 2003; p. 264. ISBN 978-3-540-44107-6. [Google Scholar]
- Zhdankin, V.V. Hypervalent Iodine Chemistry: Preparation, Structure and Synthetic Applications of Polyvalent Iodine Compounds; Wiley: Chichester, UK, 2014; p. 468. ISBN 9781118341032. [Google Scholar]
- Yoshimura, A.; Zhdankin, V.V. Advances in Synthetic Applications of Hypervalent Iodine Compounds. Chem. Rev. 2016, 116, 3328–3435. [Google Scholar] [CrossRef] [PubMed]
- Zhdankin, V.V. Hypervalent iodine compounds: Reagents of the future. Arkivoc 2020, iv, 1–11. [Google Scholar] [CrossRef]
- Zhdankin, V.V. Benziodoxole-Based Hypervalent Iodine Reagents in Organic Synthesis. Curr. Org. Synth. 2005, 2, 121–145. [Google Scholar] [CrossRef]
- Bamberger, J.; Ostler, F.; Mancheno, O.G. Frontiers in Halogen and Chalcogen-Bond Donor Organocatalysis. ChemCatChem 2019, 11, 5198–5211. [Google Scholar] [CrossRef]
- Vaish, A.; Tsarevsky, N.V. Hypervalent Iodine Compounds in Polymer Science and Technology. In Main Group Strategies towards Functional Organic Materials; Baumgartner, T., Jaekle, F., Eds.; Wiley: Chichester, UK, 2018; pp. 483–514. [Google Scholar] [CrossRef]
- Musher, J.I. The Chemistry of Hypervalent Molecules. Angew. Chem. Int. Ed. 1969, 8, 54–68. [Google Scholar] [CrossRef]
- Pimentel, G.C. The Bonding of Trihalide and Bifluoride Ions by the Molecular Orbital Method. J. Chem. Phys. 1951, 19, 446–448. [Google Scholar] [CrossRef]
- Hach, R.J.; Rundle, R.E. The Structure of Tetramethylammonium Pentaiodide. J. Am. Chem. Soc. 1951, 73, 4321–4324. [Google Scholar] [CrossRef]
- Munzarova, M.L.; Hoffmann, R. Electron-Rich Three-Center Bonding: Role of s,p Interactions across the p-Block. J. Am. Chem. Soc. 2002, 124, 4787–4795. [Google Scholar] [CrossRef]
- Durrant, M.C. A quantitative definition of hypervalency. Chem. Sci. 2015, 6, 6614–6623. [Google Scholar] [CrossRef]
- Kalemosa, A.; Ariyarathnab, I.R.; Khanb, S.N.; Miliordosb, E.; Mavridis, A. Hypervalency and the chemical bond. Comput. Theoret. Chem. 2019, 1153, 65–74. [Google Scholar] [CrossRef]
- Crabtree, R.H. Hypervalency, secondary bonding and hydrogen bonding: Siblings under the skin. Chem. Soc. Rev. 2017, 46, 1720–1729. [Google Scholar] [CrossRef]
- Kupwade, R.V. A Concise Review of Hypervalent Iodine with Special Reference to Dess- Martin Periodinane. Mini-Rev. Org. Chem. 2020, 17, 946-1–946-12. [Google Scholar] [CrossRef]
- Yannacone, S.; Oliveira, V.; Verma, N.; Kraka, E. A Continuum from Halogen Bonds to Covalent Bonds: Where Do λ3 Iodanes Fit? Inorganics 2019, 7, 47. [Google Scholar] [CrossRef]
- Varvoglis, A. Aryliodine(III) Dicarboxylates. Chem. Soc. Rev. 1981, 10, 377. [Google Scholar] [CrossRef]
- Waser, J. Benziodoxol(on)e Reagents as Tools in Organic Synthesis: The Background behind the Discovery at the Laboratory of Catalysis and Organic Synthesis. Synlett 2016, 27, 2761–2773. [Google Scholar] [CrossRef]
- Ostrovskii, V.A.; Koldobskii, G.I.; Trifonov, R.E. Tetrazoles. In Comprehensive Heterocyclic Chemistry III; Katritzky, A.R., Ramsden, C.A., Scriven, E.F.V., Taylor, R.J.K., Eds.; Elsevier: Oxford, UK, 2008; pp. 257–423. [Google Scholar] [CrossRef]
- Kumar, R.; Vaish, A.; Runčevski, T.; Tsarevsky, N.V. Hypervalent Iodine Compounds with Tetrazole Ligands. J. Org. Chem. 2018, 83, 12496–12506. [Google Scholar] [CrossRef] [PubMed]
- Vaish, A.; Sayala, K.D.; Tsarevsky, N.V. N-Heterocycle (Tetrazole)-Stabilized Pseudocyclic λ3-Iodane: Synthesis and Reactivity. Tetrahedron Lett. 2019, 60, 150995. [Google Scholar] [CrossRef]
- Kumar, R.; Sayala, K.D.; Camdzic, L.L.; Siegler, M.; Vaish, A.; Tsarevsky, N. Heterocyclic Hypervalent Iodine(III) Compounds with Fused Benziodazole and Tetrazole Rings (I-Substituted Tetrazolo[1,5-b][1,2]Benziodazoles). ChemRxiv 2020. [Google Scholar] [CrossRef]
- Wang, T.; Gao, H.; Shreeve, J.M. Functionalized Tetrazole Energetics: A Route to Enhanced Performance. Z. Anorg. Allg. Chem. 2021, 647, 157–191. [Google Scholar] [CrossRef]
- Singh, R.P.; Verma, R.D.; Meshri, D.T.; Shreeve, J.M. Energetic Nitrogen-Rich Salts and Ionic Liquids. Angew. Chem. Int. Ed. 2006, 45, 3584–3601. [Google Scholar] [CrossRef] [PubMed]
- Trifonov, R.E.; Ostrovskii, V.A. Protolytic Equilibria in Tetrazoles. Russ. J. Org. Chem. 2006, 42, 1585–1605. [Google Scholar] [CrossRef]
- Wani, M.Y.; Silva, M.R.; Krishnakumar, B.; Kumar, S.; Al-Bogami, A.S.; Aqlan, F.M.; Sobral, A.J.F.N. Catalytic Synthesis of 5-Substituted Tetrazoles: Unexpected Reactions and Products. J. Heterocycl. Chem. 2019, 56, 1613–1621. [Google Scholar] [CrossRef]
- Koch, E.C. High Explosives, Propellants, Pyrotechnics; DeGruyter: Boston, MA, USA, 2021. [Google Scholar]
- Dosch, D.E.; Reichel, M.; Born, M.; Klapötke, T.M.; Karaghiosoff, K. Investigation of Structure-Property Relationships of Three Nitroaromatic Compounds: 1-Fluoro-2,4,6-Trinitrobenzene, 2,4,6-Trinitrophenyl Methanesulfonate, and 2,4,6-Trinitrobenzaldehyde. Cryst. Growth Des. 2020, 21, 243–248. [Google Scholar] [CrossRef]
- Li, J. Relationships for the Impact Sensitivities of Energetic C-Nitro Compounds Based on Bond Dissociation Energy. J. Phys. Chem. B 2010, 114, 2198–2202. [Google Scholar] [CrossRef] [PubMed]
- Li, J. A Quantitative Relationship for the Shock Sensitivities of Energetic Compounds based on X−NO2 (X = C, N, O) Bond Dissociation Energy. J. Hazard. Mater. 2010, 180, 768–772. [Google Scholar] [CrossRef] [PubMed]
- Luo, Y.R. Comprehensive Handbook of Chemical Bond Energies; Taylor and Francis: Boca Raton, FL, USA, 2007. [Google Scholar]
- Morse, M.D. Predissociation measurements of bond dissociation energies. Acc. Chem. Res. 2018, 52, 119–126. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, Q.; Vo, T.T.; Parrish, D.A.; Shreeve, J.M. Energetic Salts with π-Stacking and Hydrogen-Bonding Interactions Lead the Way to Future Energetic Materials. J. Am. Chem. Soc. 2015, 137, 1697–1704. [Google Scholar] [CrossRef] [PubMed]
- Cremer, D.; Kraka, E. From Molecular Vibrations to Bonding, Chemical Reactions, and Reaction Mechanism. Curr. Org. Chem. 2010, 14, 1524–1560. [Google Scholar] [CrossRef]
- Kalescky, R.; Kraka, E.; Cremer, D. Are Carbon-Halogen Double and Triple Bonds Possible? Int. J. Quantum Chem. 2014, 114, 1060–1072. [Google Scholar] [CrossRef]
- Kalescky, R.; Zou, W.; Kraka, E.; Cremer, D. Quantitative Assessment of the Multiplicity of Carbon-Halogen Bonds: Carbenium and Halonium Ions with F, Cl, Br, and I. J. Phys. Chem. A 2014, 118, 1948–1963. [Google Scholar] [CrossRef]
- Oliveira, V.; Kraka, E.; Cremer, D. Quantitative Assessment of Halogen Bonding Utilizing Vibrational Spectroscopy. Inorg. Chem. 2016, 56, 488–502. [Google Scholar] [CrossRef] [PubMed]
- Setiawan, D.; Sethio, D.; Cremer, D.; Kraka, E. From Strong to Weak NF Bonds: On the Design of a New Class of Fluorinating Agents. Phys. Chem. Chem. Phys. 2018, 20, 23913–23927. [Google Scholar] [CrossRef] [PubMed]
- Sethio, D.; Oliveira, V.; Kraka, E. Quantitative Assessment of Tetrel Bonding Utilizing Vibrational Spectroscopy. Molecules 2018, 23, 2763. [Google Scholar] [CrossRef] [PubMed]
- Grant, D.J.; Matus, M.H.; Switzer, J.R.; Dixon, D.A.; Francisco, J.S.; Christe, K.O. Bond Dissociation Energies in Second-Row Compounds. J. Phys. Chem. A 1966, 112, 3145–3156. [Google Scholar] [CrossRef] [PubMed]
- Konkoli, Z.; Cremer, D. A New Way of Analyzing Vibrational Spectra. I. Derivation of Adiabatic Internal Modes. Int. J. Quantum Chem. 1998, 67, 1–9. [Google Scholar] [CrossRef]
- Konkoli, Z.; Larsson, J.A.; Cremer, D. A New Way of Analyzing Vibrational Spectra. II. Comparison of Internal Mode Frequencies. Int. J. Quantum Chem. 1998, 67, 11–27. [Google Scholar] [CrossRef]
- Konkoli, Z.; Cremer, D. A New Way of Analyzing Vibrational Spectra. III. Characterization of Normal Vibrational Modes in terms of Internal Vibrational Modes. Int. J. Quantum Chem. 1998, 67, 29–40. [Google Scholar] [CrossRef]
- Konkoli, Z.; Larsson, J.A.; Cremer, D. A New Way of Analyzing Vibrational Spectra. IV. Application and Testing of Adiabatic Modes within the Concept of the Characterization of Normal Modes. Int. J. Quantum Chem. 1998, 67, 41–55. [Google Scholar] [CrossRef]
- Cremer, D.; Larsson, J.A.; Kraka, E. New Developments in the Analysis of Vibrational Spectra on the Use of Adiabatic Internal Vibrational Modes. In Theoretical and Computational Chemistry; Parkanyi, C., Ed.; Elsevier: Amsterdam, The Netherlands, 1998; pp. 259–327. [Google Scholar]
- Kraka, E.; Zou, W.; Tao, Y. Decoding Chemical Information from Vibrational Spectroscopy Data: Local Vibrational Mode Theory. WIREs Comput. Mol. Sci. 2020, 10, e1480. [Google Scholar] [CrossRef]
- Klapötke, T.M. Chemistry of High-Energy Materials, 5th ed.; DeGruyter: Boston, MA, USA, 2019. [Google Scholar]
- Kettner, M.A.; Klapötke, T.M. New Energetic Polynitrotetrazoles. Chem. Eur. J. 2015, 21, 3755–3765. [Google Scholar] [CrossRef]
- Köhler, J.; Meyer, R.; Homburg, A. Explosivstoffe; Wiley: Weinheim, Germany, 2008. [Google Scholar]
- Becke, A.D. Density-Functional Thermochemistry. III. The Role of Exact Exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- Becke, A.D. A New Mixing of Hartree-Fock and Local Density-Functional Theories. J. Chem. Phys. 1993, 98, 1372–1377. [Google Scholar] [CrossRef]
- Becke, A.D. Density-Functional Thermochemistry. V. Systematic Optimization of Exchange-Correlation Functionals. J. Chem. Phys. 1997, 107, 8554–8560. [Google Scholar] [CrossRef]
- Salomon, O.; Reiher, M.; Hess, B.A. Assertion and Validation of the Performance of the B3LYP Functional for the First Transition Metal Row and the G2 Test Set. J. Chem. Phys. 2002, 117, 4729–4737. [Google Scholar] [CrossRef]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A Consistent and Accurate Ab Initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef] [PubMed]
- Grimme, S.; Ehrlich, S.; Goerigk, L. Effect of the Damping Function in Dispersion Corrected Density Functional Theory. J. Comput. Chem. 2011, 32, 1456–1465. [Google Scholar] [CrossRef]
- Zhao, Y.; Truhlar, D.G. The M06 Suite of Density Functionals for Main Group Thermochemstry, Thermochemical Kinetics, Noncovalent Interactions, Excited States, and Transition Elements: Two New Functionals and Systematic Testing of Four M06-Class Functionals and 12 Other Functionals. Theor. Chem. Acc. 2007, 120, 215–241. [Google Scholar]
- Chai, J.D.; Head-Gordon, M. Long-Range Corrected Hybrid Density Functionals with Damped Atom-Atom Dispersion Corrections. Phys. Chem. Chem. Phys. 2008, 10, 6615–6620. [Google Scholar] [CrossRef]
- Dunning, T.H. Gaussian Basis Sets for use in Correlated Molecular Calculations. I. The Atoms Boron through Neon and Hydrogen. J. Chem. Phys. 1989, 90, 1007–1023. [Google Scholar] [CrossRef]
- Kendall, R.A.; Dunning, T.H.; Harrison, R.J. Electron Affinities of the First-Row Atoms Revisited. Systematic Basis Sets and Wave Functions. J. Chem. Phys. 1992, 96, 6796–6806. [Google Scholar] [CrossRef]
- Woon, D.E.; Dunning, T.H. Gaussian Basis Sets for use in Correlated Molecular Calculations. III. The Atoms Aluminum through Argon. J. Chem. Phys. 1993, 98, 1358–1371. [Google Scholar] [CrossRef]
- Woon, D.E.; Dunning, T.H. Gaussian Basis Sets for use in Correlated Molecular Calculations. IV. Calculation of Static Electrical Response Properties. J. Chem. Phys. 1994, 100, 2975–2988. [Google Scholar] [CrossRef]
- Peterson, K.A. Systematically Convergent Basis Sets with Relativistic Pseudopotentials. I. Correlation Consistent Basis Sets for the Post-d Group 13-15 Elements. J. Chem. Phys. 2003, 119, 11099–11112. [Google Scholar] [CrossRef]
- Peterson, K.A.; Figgen, D.; Goll, E.; Stoll, H.; Dolg, M. Systematically Convergent Basis Sets with Relativistic Pseudopotentials. II. Small-Core Pseudopotentials and Correlation Consistent Basis Sets for the Post-d Group 16-18 Elements. J. Chem. Phys. 2003, 119, 11113–11123. [Google Scholar] [CrossRef]
- Schäfer, A.; Horn, H.; Ahlrichs, R. Fully optimized contracted Gaussian basis sets for atoms Li to Kr. J. Chem. Phys. 1992, 97, 2571–2577. [Google Scholar] [CrossRef]
- Schäfer, A.; Huber, C.; Ahlrichs, R. Fully optimized contracted Gaussian basis sets of triple zeta valence quality for atoms Li to Kr. J. Chem. Phys. 1994, 100, 5829–5835. [Google Scholar] [CrossRef]
- Weigend, F.; Ahlrichs, R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297. [Google Scholar] [CrossRef]
- Weigend, F. Accurate Coulomb-fitting basis sets for H to Rn. Phys. Chem. Chem. Phys. 2006, 8, 1057–1065. [Google Scholar] [CrossRef]
- Heinen, F.; Engelage, E.; Cramer, C.J.; Huber, S.M. Hypervalent Iodine(III) Compounds as Biaxial Halogen Bond Donors. J. Am. Chem. Soc. 2020, 142, 8633–8640. [Google Scholar] [CrossRef]
- Sibert III, E.L. Modeling vibrational anharmonicity in infrared spectra of high frequency vibrations of polyatomic molecules. J. Chem. Phys. 2019, 150, 090901. [Google Scholar] [CrossRef]
- Morse, M.D. Clusters of Transition-Metal Atoms. Chem. Rev. 1986, 86, 1049–1109. [Google Scholar] [CrossRef]
- Byrd, E.F.C.; Sherrill, C.D.; Head-Gordon, M. The Theoretical Prediction of Molecular Radical Species: A Systematic Study of Equilibrium Geometries and Harmonic Vibrational Frequencies. J. Phys. Chem. A 2001, 105, 9736–9747. [Google Scholar] [CrossRef]
- Coolidge, M.B.; Marlin, J.E.; Stewart, J.J.P. Calculations of Molecular Vibrational Frequencies using Semiempirical Methods. J. Comput. Chem. 1991, 12, 948–952. [Google Scholar] [CrossRef]
- Galabov, B.; Yamaguchi, Y.; Remington, R.B.; Schaefer, H.F. High Level Ab Initio Quantum Mechanical Predictions of Infrared Intensities. J. Phys. Chem. A 2002, 106, 819–832. [Google Scholar] [CrossRef]
- Halls, M.D.; Velkovski, J.; Schlegel, H.B. Harmonic Frequency Scaling Factors for Hartree-Fock, S-VWN, B-LYP, B3-LYP, B3-PW91 and MP2 with the Sadlej pVTZ Electric Property Basis Set. Theor. Chem. Acc. 2001, 105, 413–421. [Google Scholar] [CrossRef]
- Irikura, K.K.; Johnson, R.D.; Kacker, R.N. Uncertainties in Scaling Factors for Ab Initio Vibrational Frequencies. J. Phys. Chem. A 2005, 109, 8430–8437. [Google Scholar] [CrossRef]
- Scott, A.P.; Radom, L. Harmonic Vibrational Frequencies: An Evaluation of Hartree-Fock, Møller-Plesset, Quadratic Configuration Interaction, Density Functional Theory, and Semiempirical Scale Factors. J. Phys. Chem. 1996, 100, 16502–16513. [Google Scholar] [CrossRef]
- Shefter, E.; Wolf, W. Crystal and Molecular Structure of 1,3Dihydro-1-hydroxy-3-oxo-1,2-benziodoxole. Nature 1964, 203, 512–513. [Google Scholar] [CrossRef]
- Shefter, E.; Wolf, W. Crystal and Molecular Structure of 1,3Dihydro-1-hydroxy-3-oxo-1,2-benziodoxole. J. Pharm. Sci. 1965, 54, 104–107. [Google Scholar] [CrossRef]
- Gräfenstein, J.; Cremer, D. Efficient DFT integrations by locally augmented radial grids. J. Chem. Phys. 2007, 127, 164113. [Google Scholar] [CrossRef]
- Huang, Y.; Chang, C.; Yuan, J.; Zhao, Z. High-Harmonic and Terahertz Spectroscopy (HATS): Methods and Applications. Appl. Sci. 2019, 9, 853. [Google Scholar] [CrossRef]
- Wu, G. Vibrational Spectroscopy; De Gruyter: Berlin, Germany, 2019. [Google Scholar]
- Smith, E.; Dent, G. Modern Raman Spectroscopy: A Practical Approach; Wiley: New York, NY, USA, 2019. [Google Scholar]
- Wilson, E.B.; Decius, J.C.; Cross, P.C. Molecular Vibrations; McGraw-Hill: New York, NY, USA, 1955. [Google Scholar]
- Wilson, E.B., Jr. A Method of Obtaining the Expanded Secular Equation for the Vibration Frequencies of a Molecule. J. Chem. Phys. 1939, 7, 1047–1052. [Google Scholar] [CrossRef]
- Woodward, L.A. Introduction to the Theory of Molecular Vibrations and Vibrational Spectroscopy; Oxford University Press: Oxford, UK, 1972. [Google Scholar]
- Quack, M. Spectra and Dynamics of Coupled Vibrations in Polyatomic Molecules. Annu. Rev. Phys. Chem. 1990, 41, 839–874. [Google Scholar] [CrossRef]
- Halonen, L. Local Mode Vibrations in Polyatomic Molecules. In Advances in Chemical Physics; Prigogine, I., Rice, S., Eds.; Wiley: New York, NY, USA, 1998; Volume 104, pp. 41–179. [Google Scholar]
- Jensen, P. An introduction to the theory of local mode vibrations. Mol. Phys. 2000, 98, 1253–1285. [Google Scholar] [CrossRef]
- Zou, W.; Cremer, D. C2 in a Box: Determining its Intrinsic Bond Strength for the X1Σ+g Ground State. Chem. Eur. J. 2016, 22, 4087–4097. [Google Scholar] [CrossRef]
- Oomens, J.; Kraka, E.; Nguyen, M.K.; Morton, T.M. Structure, Vibrational Spectra, and Unimolecular Dissociation of Gaseous 1-Fluoro-1-phenethyl Cations. J. Phys. Chem. A 2008, 112, 10774–10783. [Google Scholar] [CrossRef] [PubMed]
- Zou, W.; Kalescky, R.; Kraka, E.; Cremer, D. Relating Normal Vibrational Modes to Local Vibrational Modes: Benzene and Naphthalene. J. Mol. Model. 2012, 19, 2865–2877. [Google Scholar] [CrossRef] [PubMed]
- Kalescky, R.; Kraka, E.; Cremer, D. Identification of the Strongest Bonds in Chemistry. J. Phys. Chem. A 2013, 117, 8981–8995. [Google Scholar] [CrossRef]
- Kalescky, R.; Kraka, E.; Cremer, D. Description of Aromaticity with the Help of Vibrational Spectroscopy: Anthracene and Phenanthrene. J. Phys. Chem. A 2013, 118, 223–237. [Google Scholar] [CrossRef] [PubMed]
- Kalescky, R.; Kraka, E.; Cremer, D. New Approach to Tolman’s Electronic Parameter Based on Local Vibrational Modes. Inorg. Chem. 2013, 53, 478–495. [Google Scholar] [CrossRef]
- Humason, A.; Zou, W.; Cremer, D. 11,11Dimethyl-1,6-methano[10]annulene-An Annulene with an Ultralong CC Bond or a Fluxional Molecule? J. Phys. Chem A. 2014, 119, 1666–1682. [Google Scholar] [CrossRef] [PubMed]
- Sethio, D.; Lawson Daku, L.M.; Hagemann, H.; Kraka, E. Quantitative Assessment of B−B−B, B−Hb−B, and B−Ht Bonds: From BH3 to B12H122−. ChemPhysChem 2019, 20, 1967–1977. [Google Scholar] [CrossRef]
- Makoś, M.Z.; Freindorf, M.; Sethio, D.; Kraka, E. New Insights into Fe-H2 and Fe-H− Bonding of a [NiFe] Hydrogenase Mimic–A Local Vibrational Mode Study. Theor. Chem. Acc. 2019, 138, 76. [Google Scholar] [CrossRef]
- Makoś, M.Z.; Zou, W.; Freindorf, M.; Kraka, E. Metal-Ring Interactions in Actinide Sandwich Compounds: A Combined Normalized Elimination of the Small Component and Local Vibrational Mode Study. Mol. Phys. 2020, 118, e1768314. [Google Scholar] [CrossRef]
- Verma, N.; Tao, Y.; Zou, W.; Chen, X.; Chen, X.; Freindorf, M.; Kraka, E. A Critical Evaluation of Vibrational Stark Effect (VSE) Probes with the Local Vibrational Mode Theory. Sensors 2020, 20, 2358. [Google Scholar] [CrossRef]
- Freindorf, M.; Kraka, E. Critical Assessment of the FeC and CO Bond strength in Carboxymyoglobin–A QM/MM Local Vibrational Mode Study. J. Mol. Model. 2020, 26, 281-1–281-15. [Google Scholar] [CrossRef] [PubMed]
- Kraka, E.; Freindorf, M. Characterizing the Metal Ligand Bond Strength via Vibrational Spectroscopy: The Metal Ligand Electronic Parameter (MLEP). In Topics in Organometallic Chemistry–New Directions in the Modeling of Organometallic Reactions; Lledós, A., Ujaque, G., Eds.; Springer: Berlin/Heidelberg, Germany, 2020; Volume 67, pp. 1–43. [Google Scholar]
- Freindorf, M.; Kraka, E.; Cremer, D. A Comprehensive Analysis of Hydrogen Bond Interactions Based on Local Vibrational Modes. Int. J. Quantum Chem. 2012, 112, 3174–3187. [Google Scholar] [CrossRef]
- Kalescky, R.; Zou, W.; Kraka, E.; Cremer, D. Local Vibrational Modes of the Water Dimer–Comparison of Theory and Experiment. Chem. Phys. Lett. 2012, 554, 243–247. [Google Scholar] [CrossRef]
- Kalescky, R.; Kraka, E.; Cremer, D. Local Vibrational Modes of the Formic Acid Dimer–The Strength of the Double H-Bond. Mol. Phys. 2013, 111, 1497–1510. [Google Scholar] [CrossRef]
- Kraka, E.; Freindorf, M.; Cremer, D. Chiral Discrimination by Vibrational Spectroscopy Utilizing Local Modes. Chirality 2013, 25, 185–196. [Google Scholar] [CrossRef]
- Setiawan, D.; Kraka, E.; Cremer, D. Description of Pnicogen Bonding with the help of Vibrational Spectroscopy-The Missing Link between Theory and Experiment. Chem. Phys. Lett. 2014, 614, 136–142. [Google Scholar] [CrossRef]
- Setiawan, D.; Kraka, E.; Cremer, D. Strength of the Pnicogen Bond in Complexes Involving Group VA Elements N, P, and As. J. Phys. Chem. A 2014, 119, 1642–1656. [Google Scholar] [CrossRef]
- Setiawan, D.; Kraka, E.; Cremer, D. Hidden Bond Anomalies: The Peculiar Case of the Fluorinated Amine Chalcogenides. J. Phys. Chem. A 2015, 119, 9541–9556. [Google Scholar] [CrossRef] [PubMed]
- Kraka, E.; Setiawan, D.; Cremer, D. Re-Evaluation of the Bond Length-Bond Strength Rule: The Stronger Bond Is not Always the Shorter Bond. J. Comp. Chem. 2015, 37, 130–142. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Dai, H.; Yan, H.; Zou, W.; Cremer, D. B-H π Interaction: A New Type of Nonclassical Hydrogen Bonding. J. Am. Chem. Soc. 2016, 138, 4334–4337. [Google Scholar] [CrossRef]
- Setiawan, D.; Cremer, D. Super-Pnicogen Bonding in the Radical Anion of the Fluorophosphine Dimer. Chem. Phys. Lett. 2016, 662, 182–187. [Google Scholar] [CrossRef]
- Oliveira, V.; Kraka, E.; Cremer, D. The Intrinsic Strength of the Halogen Bond: Electrostatic and Covalent Contributions Described by Coupled Cluster Theory. Phys. Chem. Chem. Phys. 2016, 18, 33031–33046. [Google Scholar] [CrossRef]
- Tao, Y.; Zou, W.; Jia, J.; Li, W.; Cremer, D. Different Ways of Hydrogen Bonding in Water–Why Does Warm Water Freeze Faster than Cold Water? J. Chem. Theory Comput. 2017, 13, 55–76. [Google Scholar] [CrossRef]
- Oliveira, V.; Cremer, D. Transition from Metal-Ligand Bonding to Halogen Bonding Involving a Metal as Halogen Acceptor: A Study of Cu, Ag, Au, Pt, and Hg Complexes. Chem. Phys. Lett. 2017, 681, 56–63. [Google Scholar] [CrossRef]
- Oliveira, V.; Cremer, D.; Kraka, E. The Many Facets of Chalcogen Bonding: Described by Vibrational Spectroscopy. J. Phys. Chem. A 2017, 121, 6845–6862. [Google Scholar] [CrossRef] [PubMed]
- Oliveira, V.; Kraka, E. Systematic Coupled Cluster Study of Noncovalent Interactions Involving Halogens, Chalcogens, and Pnicogens. J. Phys. Chem. A 2017, 121, 9544–9556. [Google Scholar] [CrossRef] [PubMed]
- Zou, W.; Zhang, X.; Dai, H.; Yan, H.; Cremer, D.; Kraka, E. Description of an Unusual Hydrogen Bond Between Carborane and a Phenyl Group. J. Organometal. Chem. 2018, 856, 114–127. [Google Scholar] [CrossRef]
- Lyu, S.; Beiranvand, N.; Freindorf, M.; Kraka, E. Interplay of Ring Puckering and Hydrogen Bonding in Deoxyribonucleosides. J. Phys. Chem. A 2019, 123, 7087–7103. [Google Scholar] [CrossRef]
- Oliveira, V.P.; Marcial, B.L.; Machado, F.B.C.; Kraka, E. Metal-Halogen Bonding Seen through the Eyes of Vibrational Spectroscopy. Materials 2020, 13, 55. [Google Scholar] [CrossRef] [PubMed]
- Tao, Y.; Qiu, Y.; Zou, W.; Nanayakkara, S.; Yannacone, S.; Kraka, E. In Situ Assessment of Intrinsic Strength of X-I⋯OA Type Halogen Bonds in Molecular Crystals with Periodic Local Vibrational Mode Theory. Molecules 2020, 25, 1589. [Google Scholar] [CrossRef]
- Yannacone, S.; Sethio, D.; Kraka, E. Quantitative Assessment of Intramolecular Hydrogen Bonds in Neutral Histidine. Theor. Chem. Acc. 2020, 139, 125-1–125-10. [Google Scholar] [CrossRef]
- Martins, J.; Quintino, R.P.; Politi, J.R.S.; Sethio, D.; Gargano, R.; Kraka, E. Computational Analysis of Vibrational Frequencies and Rovibrational Spectroscopic Constants of Hydrogen Sulfide Dimer using MP2 and CCSD(T). Spectrochim. Acta A 2020, 239, 118540-1–118540-9. [Google Scholar] [CrossRef]
- Yannacone, S.; Freindorf, M.; Tao, Y.; Zou, W.; Kraka, E. Local Vibrational Mode Analysis of π-Hole Interactions between Aryl Donors and Small Molecule Acceptors. Crystals 2020, 10, 556. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian16 Revision B.01; Gaussian Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Zou, W.; Tao, Y.; Freindorf, M.; Makoś, M.Z.; Verma, N.; Kraka, E. Local Vibrational Mode Analysis (LModeA); Computational and Theoretical Chemistry Group (CATCO), Southern Methodist University: Dallas, TX, USA, 2020. [Google Scholar]
- Reed, A.E.; Curtiss, L.A.; Weinhold, F. Intermolecular Interactions from a Natural Bond Orbital, Donor-Acceptor Viewpoint. Chem. Rev. 1988, 88, 899–926. [Google Scholar] [CrossRef]
- Weinhold, F.; Landis, C.R. Valency and Bonding: A Natural Bond Orbital Donor-Acceptor Perspective; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Weinhold, F.; Landis, C.R.; Glendening, E.D. What is NBO Analysis and How is it Useful? Int. Rev. Phys. Chem. 2016, 35, 39–440. [Google Scholar] [CrossRef]
- Keith, T.A. AIMAll (Version 17.11.14). 2017. Available online: aim.tkgristmill.com (accessed on 12 May 2021).
- Cremer, D.; Kraka, E. Chemical Bonds without Bonding Electron Density? Does the Difference Electron-Density Analysis Suffice for a Description of the Chemical Bond? Angew. Chem. Int. Ed. 1984, 23, 627–628. [Google Scholar] [CrossRef]
- Cremer, D.; Kraka, E. A Description of the Chemical Bond in Terms of Local Properties of Electron Density and Energy. Croat. Chem. Acta 1984, 57, 1259–1281. [Google Scholar]
- Kraka, E.; Cremer, D. Chemical Implication of Local Features of the Electron Density Distribution. In Theoretical Models of Chemical Bonding. The Concept of the Chemical Bond; Maksic, Z.B., Ed.; Springer: Berlin/Heidelberg, Germany, 1990; Volume 2, pp. 453–542. [Google Scholar]
- Kraszkiewicz, L.; Skulski, L. Optimized syntheses of iodylarenes from iodoarenes, with sodium periodate as the oxidant. Part II. Arkivoc 2003, 2003, 120–125. [Google Scholar] [CrossRef]
- Origin(Pro) 9.1.0 (64 bit); OriginLab Corporation: Northampton, MA, USA, 2013.
- Kaczmarek, J.; Grzonka, Z. Substituent Effects in Infrared Absorption Spectra of 5-Phenyltetrazoles. Pol. J. Chem. 1980, 54, 1297–1300. [Google Scholar]
- Matveeva, N.A.; Sushko, N.I.; Makarevich, N.I.; Gaponik, P.N.; Ivashkevich, O.A.; Koren, A.O. Substituent Effects in Infrared Absorption Spectra of 5-Phenyltetrazoles. Zh. Prikl. Spektrosk. 1992, 57, 442–450. [Google Scholar]
- Rogachev, A.Y.; Hoffmann, R. Iodine (I2) as a Janus-Faced Ligand in Organometallics. J. Am. Chem. Soc. 2013, 135, 3262–3275. [Google Scholar] [CrossRef] [PubMed]
- Boyer, J.H.; Miller, E.J. The Tetrazole-Azidoazomethine Equilibrium. J. Am. Chem. Soc. 1959, 81, 4671–4673. [Google Scholar] [CrossRef]
- Henry, R.A.; Finnegan, W.G.; Lieber, E. Kinetics of the Isomerization of Substituted 5-Aminotetrazoles. J. Am. Chem. Soc. 1955, 77, 2264–2270. [Google Scholar] [CrossRef]
- Lieber, E.; Rao, C.N.R.; Chao, T.S.; Ramachandran, J. Relative Acidities of 5-(Substituted Phenyl)amino-4-phenyl-1,2,3-triazoles. J. Org. Chem. 1958, 23, 1916–1918. [Google Scholar] [CrossRef]
- Sanderson, R. Polar Covalence; Academic Press: New York, NY, USA, 1983. [Google Scholar]
- Courtois, B. Découverte d’une substance nouvelle dans le varech. Ann. Chim. 1813, 88, 304–310. [Google Scholar]
- Silberrad, O. IX.–The Constitution of Nitrogen Iodide. J. Chem. Soc. Trans. 1905, 87, 55–66. [Google Scholar] [CrossRef][Green Version]
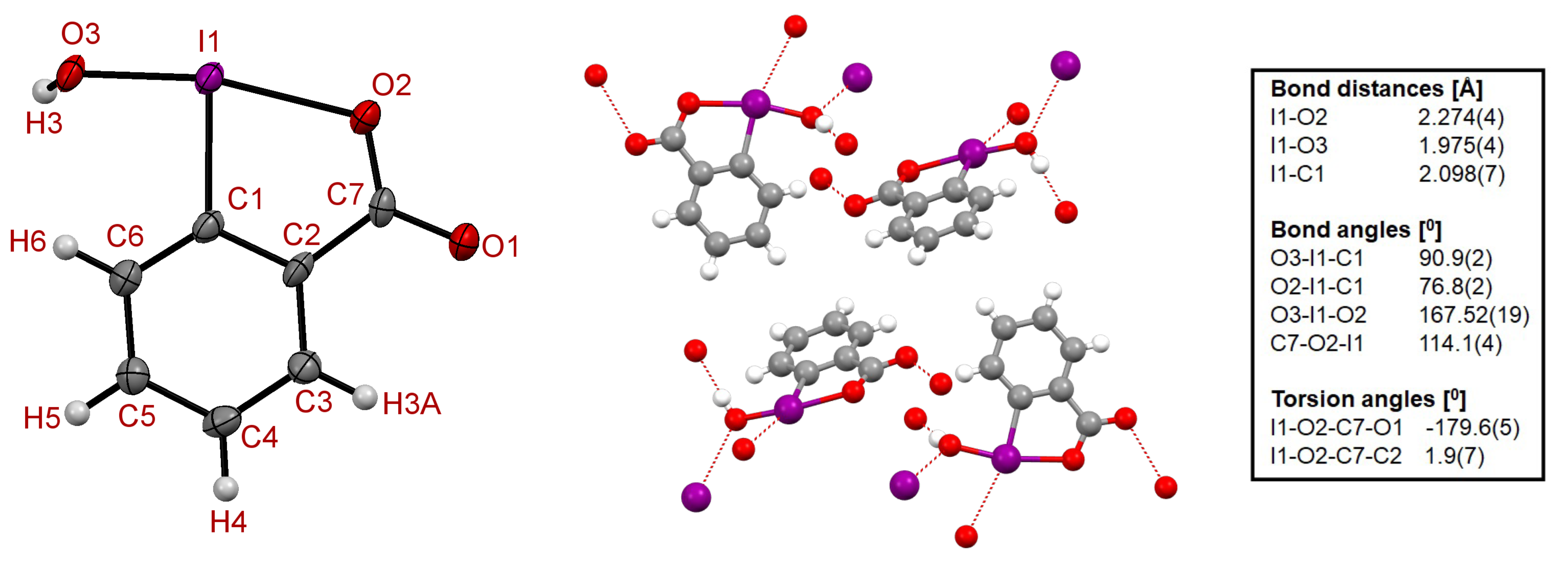



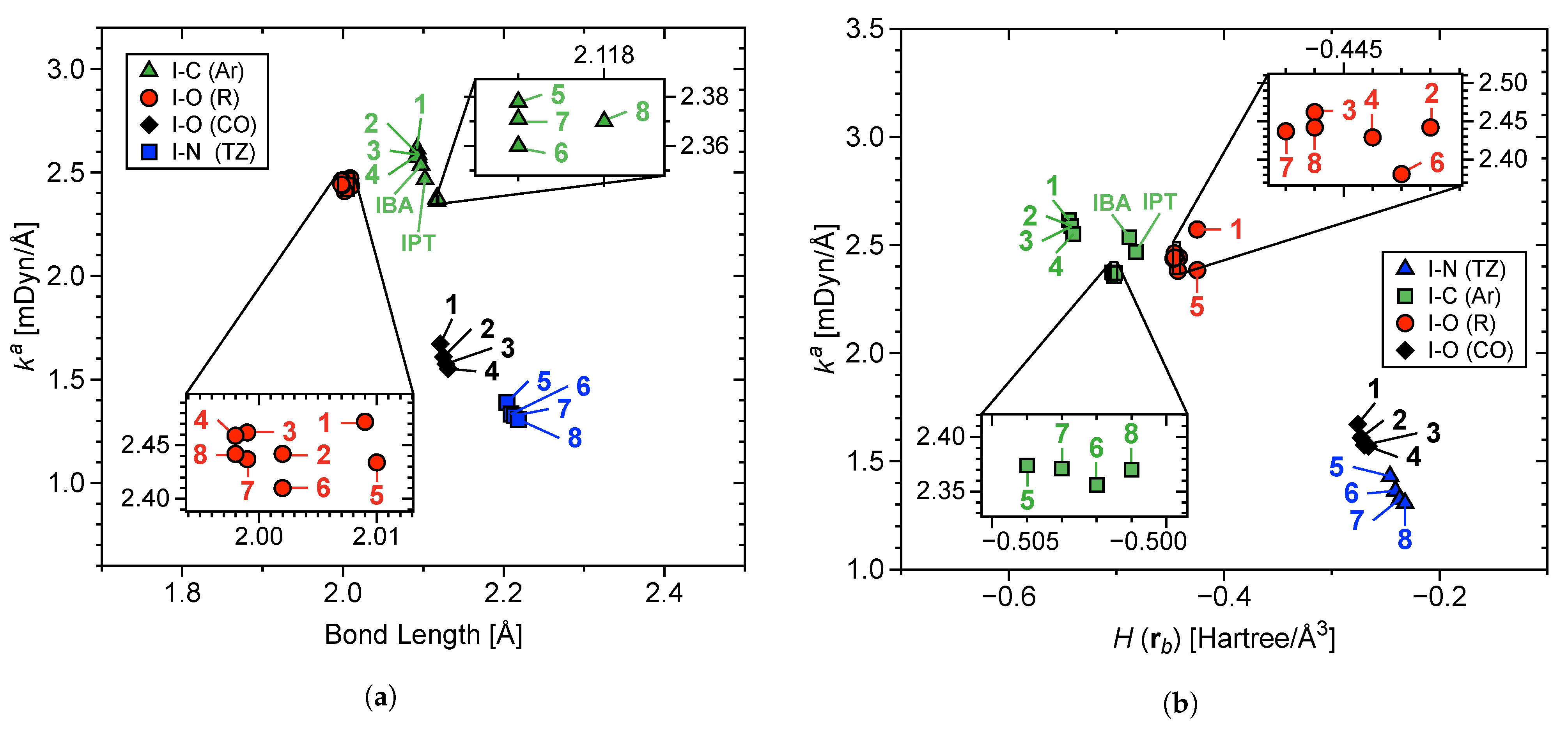
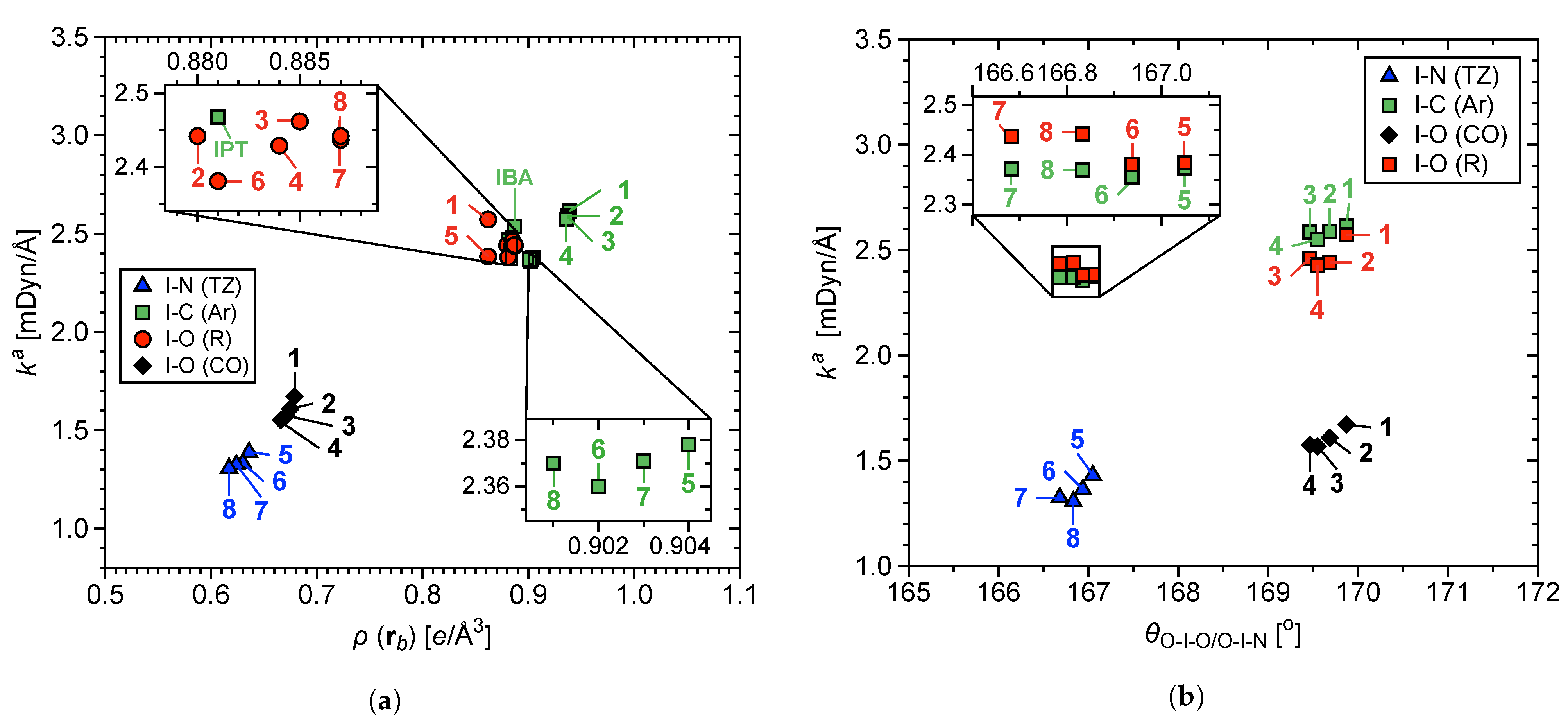
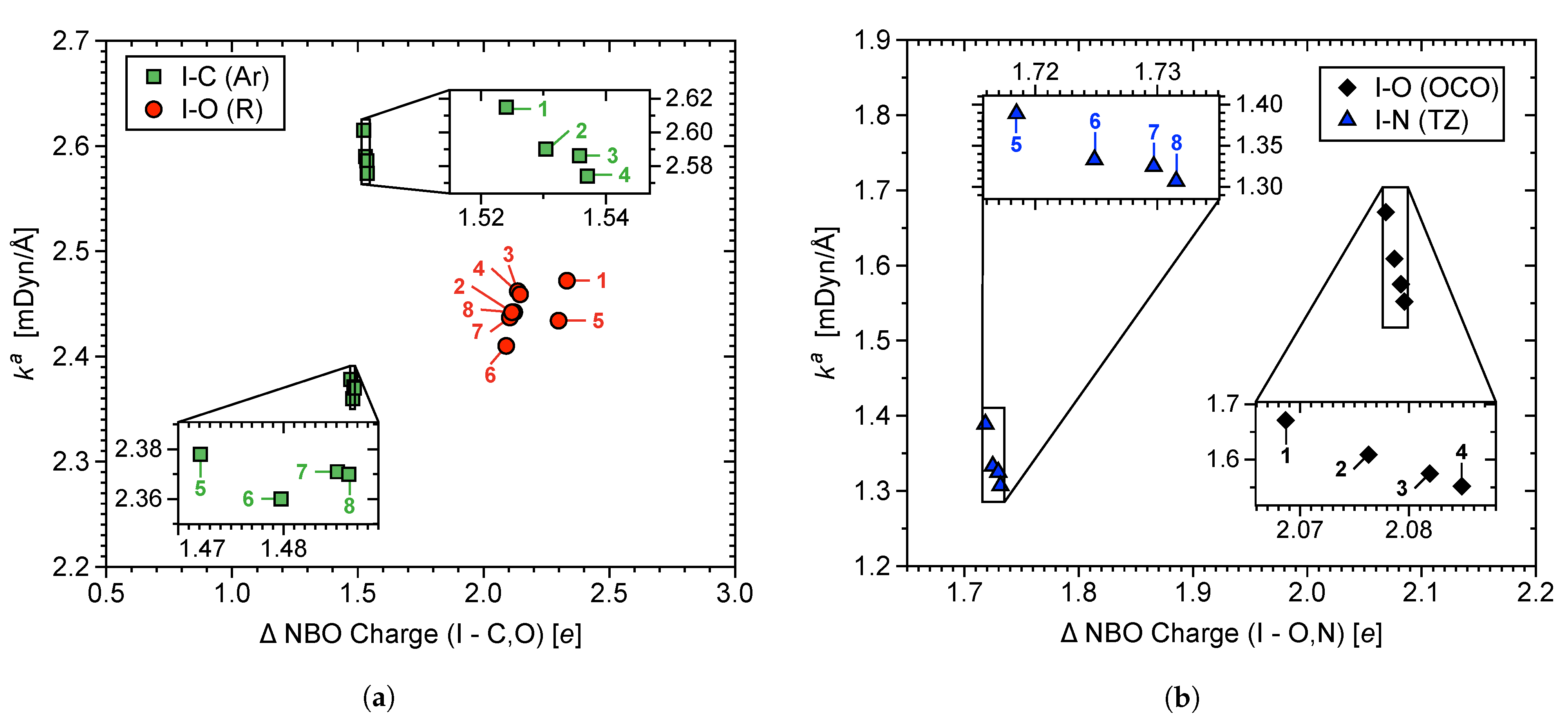
| Parameter | exp | B97X-D | B3LYP | M06-2X | |||
|---|---|---|---|---|---|---|---|
| acpVTZ | TZVP | acpVTZ | TZVP | acpVTZ | TZVP | ||
| R (I−C) | 2.098 | 2.100 | 2.091 | 2.125 | 2.116 | 2.095 | 2.087 |
| R (I−OR) | 1.975 | 2.023 | 2.009 | 2.054 | 2.040 | 2.016 | 2.004 |
| R (I−OCO) | 2.274 | 2.131 | 2.121 | 2.160 | 2.150 | 2.124 | 2.113 |
| (O−I−O) | 167.5 | 169.7 | 169.8 | 169.9 | 170.0 | 169.1 | 169.3 |
| (C−I−OR) | 90.9 | 91.1 | 91.1 | 91.5 | 91.5 | 90.5 | 90.4 |
| (C−I−OCO) | 76.8 | 78.6 | 78.8 | 78.3 | 78.5 | 78.7 | 78.9 |
| (O−C−O−I) | 179.6 | 179.0 | 178.8 | 179.1 | 179.0 | 178.8 | 178.7 |
| (C−C−O−I) | −1.9 | −1.2 | −1.4 | −1.0 | −1.2 | −1.3 | −1.5 |
| Model Chemistry | % Error (Average) | MAE | Standard Deviation | RMSE |
|---|---|---|---|---|
| B97X-D/acpVTZ-PP | 1.81 | 16.44 | 21.13 | 26.35 |
| B97X-D/TZVP | 1.50 | 12.99 | 16.25 | 20.48 |
| B3LYP/acpVTZ-PP | 1.89 | 17.31 | 18.38 | 24.91 |
| B3LYP/TZVP | 2.11 | 19.06 | 17.67 | 25.69 |
| B3LYP/TZVPP | 2.12 | 18.82 | 19.02 | 26.41 |
| B3LYP-D3/acpVTZ-PP | 1.86 | 16.95 | 18.09 | 24.46 |
| B3LYP-D3/TZVP | 2.07 | 18.54 | 17.57 | 25.24 |
| B3LYP-D3/TZVPP | 2.05 | 18.00 | 19.10 | 25.89 |
| B3LYP-D3BJ/acpVTZ-PP | 1.77 | 16.38 | 17.73 | 23.81 |
| B3LYP-D3BJ/TZVP | 1.80 | 16.95 | 16.37 | 23.28 |
| B3LYP-D3BJ/TZVPP | 1.97 | 17.76 | 18.26 | 25.15 |
| M06-2X/acpVTZ-PP | 1.45 | 13.61 | 16.13 | 20.80 |
| M06-2X/TZVP | 2.17 | 22.04 | 17.25 | 27.72 |
| # | Bond | R | Atom | Charge | ||||
|---|---|---|---|---|---|---|---|---|
| IBA | I−C4 | 2.097 | 2.536 | 626.6 | 0.887 | −0.488 | C4 | −0.199 |
| - | - | - | - | - | - | I | +0.179 | |
| IPT | I−C4 | 2.102 | 2.468 | 618.1 | 0.881 | −0.482 | C4 | −0.134 |
| - | - | - | - | - | - | I | +0.158 | |
| 1 | I−O2 | 2.121 | 1.671 | 446.8 | 0.679 | −0.276 | O2 | −0.740 |
| I−O4 | 2.009 | 2.472 | 543.4 | 0.862 | −0.425 | O4 | −1.003 | |
| I−C | 2.092 | 2.615 | 636.3 | 0.939 | −0.544 | C11 | −0.195 | |
| - | - | - | - | - | - | I | +1.329 | |
| 2 | I−O2 | 2.125 | 1.609 | 438.4 | 0.675 | −0.273 | O2 | −0.740 |
| I−O4 | 2.002 | 2.442 | 540.1 | 0.880 | −0.442 | O4 | −0.786 | |
| I−C | 2.093 | 2.590 | 633.2 | 0.937 | −0.542 | C11 | −0.195 | |
| - | - | - | - | - | - | I | +1.336 | |
| 3 | I−O2 | 2.128 | 1.575 | 433.8 | 0.671 | −0.270 | O2 | −0.741 |
| I−O4 | 1.999 | 2.462 | 542.4 | 0.885 | −0.446 | O4 | −0.795 | |
| I−C | 2.093 | 2.586 | 632.7 | 0.937 | −0.542 | C11 | −0.195 | |
| - | - | - | - | - | - | I | +1.341 | |
| 4 | I−O2 | 2.131 | 1.552 | 430.6 | 0.666 | −0.266 | O2 | −0.742 |
| I−O4 | 1.998 | 2.459 | 542.1 | 0.884 | −0.444 | O4 | −0.802 | |
| I−C | 2.093 | 2.574 | 631.3 | 0.936 | −0.540 | C11 | −0.194 | |
| - | - | - | - | - | - | I | +1.343 | |
| 5 | I−N | 2.204 | 1.389 | 432.3 | 0.636 | −0.246 | N3 | −0.424 |
| I−O | 2.010 | 2.434 | 539.2 | 0.862 | −0.425 | O6 | −1.004 | |
| I−C | 2.117 | 2.378 | 606.8 | 0.904 | −0.504 | C7 | −0.178 | |
| - | - | - | - | - | - | I | +1.294 | |
| 6 | I−N | 2.209 | 1.333 | 428.5 | 0.630 | −0.241 | N3 | −0.423 |
| I−O | 2.002 | 2.410 | 533.4 | 0.881 | −0.443 | O6 | −0.788 | |
| I−C | 2.117 | 2.360 | 603.9 | 0.902 | −0.502 | C7 | −0.178 | |
| - | - | - | - | - | - | I | +1.302 | |
| 7 | I−N | 2.213 | 1.325 | 422.3 | 0.624 | −0.237 | N3 | −0.423 |
| I−O | 1.999 | 2.437 | 539.7 | 0.887 | −0.447 | O6 | −0.797 | |
| I−C | 2.117 | 2.371 | 605.9 | 0.903 | −0.503 | C7 | −0.178 | |
| - | - | - | - | - | - | I | +1.307 | |
| 8 | I−N | 2.218 | 1.307 | 419.5 | 0.617 | −0.232 | N3 | −0.423 |
| I−O | 1.998 | 2.442 | 540.2 | 0.887 | −0.446 | O6 | −0.804 | |
| I−C | 2.118 | 2.370 | 605.7 | 0.901 | −0.501 | C7 | −0.178 | |
| - | - | - | - | - | - | I | +1.308 |
| # | R | Atom | Charge | Atom | Charge | Charge | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| IBA | 1.4950 | 4.408 | 626.6 | 1.8291 | −1.6880 | C12 (OCO) | 0.7700 | C3 (Ar) | −0.1991 | 0.9691 |
| IPT | 1.4690 | 4.468 | 618.1 | 1.8679 | −1.7820 | C15 (TZ) | 0.3025 | C3 (Ar) | −0.1343 | 0.4368 |
| 1 | 1.5033 | 4.123 | 1080.0 | 1.7951 | −1.6272 | C5 (OCO) | 0.7478 | C6 (Ar) | −0.1903 | 0.9380 |
| 2 | 1.5037 | 4.120 | 1079.6 | 1.7935 | −1.6246 | C5 (OCO) | 0.7482 | C6 (Ar) | −0.1902 | 0.9385 |
| 3 | 1.5042 | 4.104 | 1077.4 | 1.7920 | −1.6222 | C5 (OCO) | 0.7486 | C6 (Ar) | −0.1897 | 0.9382 |
| 4 | 1.5042 | 4.109 | 1078.1 | 1.7920 | −1.6222 | C5 (OCO) | 0.7484 | C6 (Ar) | −0.1891 | 0.9375 |
| 5 | 1.4489 | 5.587 | 1257.1 | 1.9489 | −1.9120 | C13 (TZ) | 0.2483 | C9 (Ar) | −0.1026 | 0.3509 |
| 6 | 1.4489 | 5.579 | 1256.2 | 1.9487 | −1.9116 | C8 (TZ) | 0.2467 | C4 (Ar) | −0.1023 | 0.3490 |
| 7 | 1.4488 | 5.588 | 1257.3 | 1.9486 | −1.9114 | C13 (TZ) | 0.2459 | C9 (Ar) | −0.1019 | 0.3477 |
| 8 | 1.4489 | 5.583 | 1256.7 | 1.9494 | −1.9127 | C12 (TZ) | 0.2448 | C8 (Ar) | −0.1012 | 0.3461 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yannacone, S.; Sayala, K.D.; Freindorf, M.; Tsarevsky, N.V.; Kraka, E. Vibrational Analysis of Benziodoxoles and Benziodazolotetrazoles. Physchem 2021, 1, 45-68. https://doi.org/10.3390/physchem1010004
Yannacone S, Sayala KD, Freindorf M, Tsarevsky NV, Kraka E. Vibrational Analysis of Benziodoxoles and Benziodazolotetrazoles. Physchem. 2021; 1(1):45-68. https://doi.org/10.3390/physchem1010004
Chicago/Turabian StyleYannacone, Seth, Kapil Dev Sayala, Marek Freindorf, Nicolay V. Tsarevsky, and Elfi Kraka. 2021. "Vibrational Analysis of Benziodoxoles and Benziodazolotetrazoles" Physchem 1, no. 1: 45-68. https://doi.org/10.3390/physchem1010004
APA StyleYannacone, S., Sayala, K. D., Freindorf, M., Tsarevsky, N. V., & Kraka, E. (2021). Vibrational Analysis of Benziodoxoles and Benziodazolotetrazoles. Physchem, 1(1), 45-68. https://doi.org/10.3390/physchem1010004