Probabilistic Evaluation of Flexural Demand in RC Beams Through Monte Carlo Simulation
Abstract
1. Introduction
2. Methods
2.1. Definition of the Structural Model
- Real projects executed in Lima.
- Current Peruvian codes (E.060: Reinforced Concrete; E.020: Loads).
- Best practices in regional structural design.
2.2. Identification of Random Variables
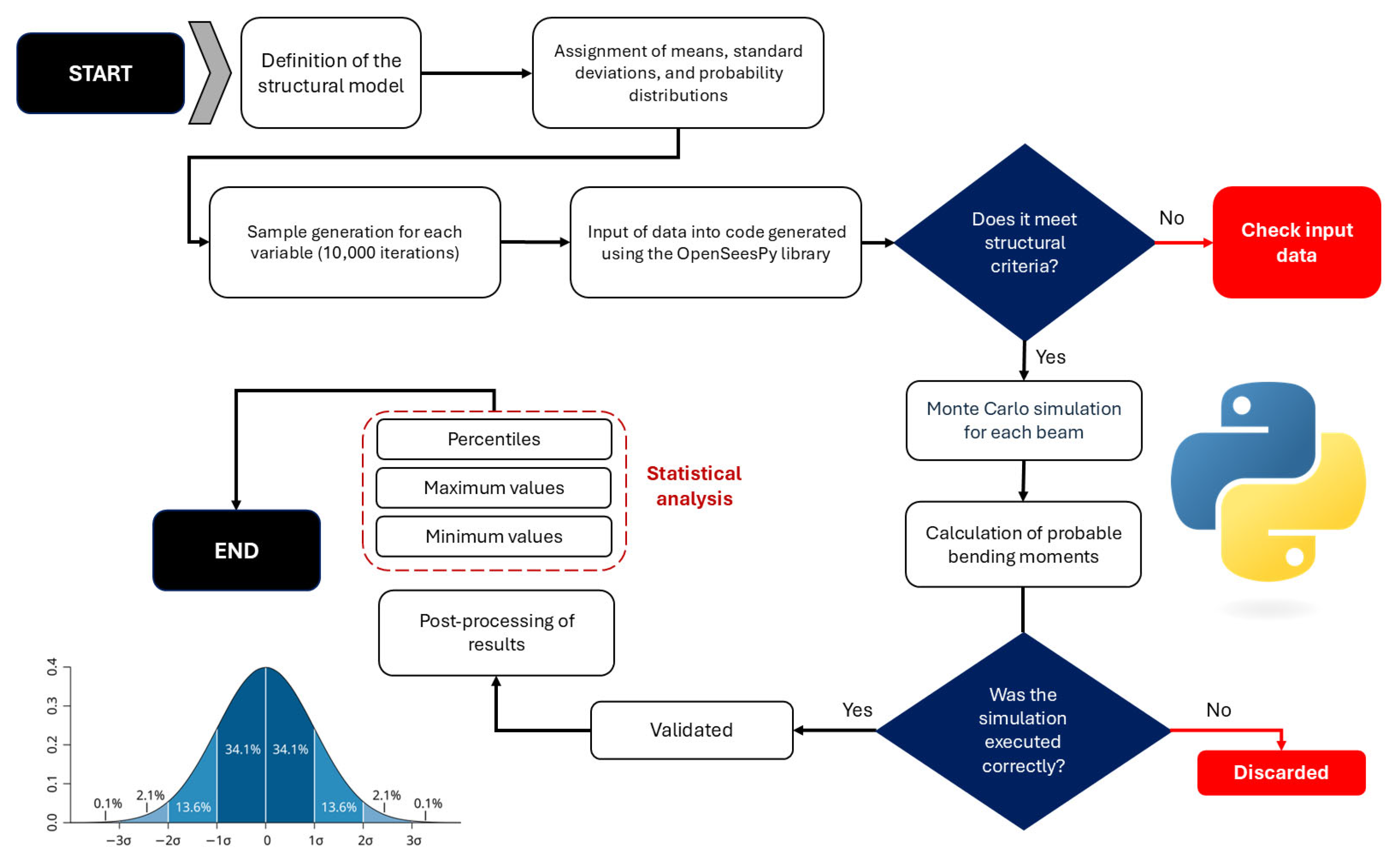
2.3. Monte Carlo Simulation
2.4. Processing and Analysis of Results
3. Results
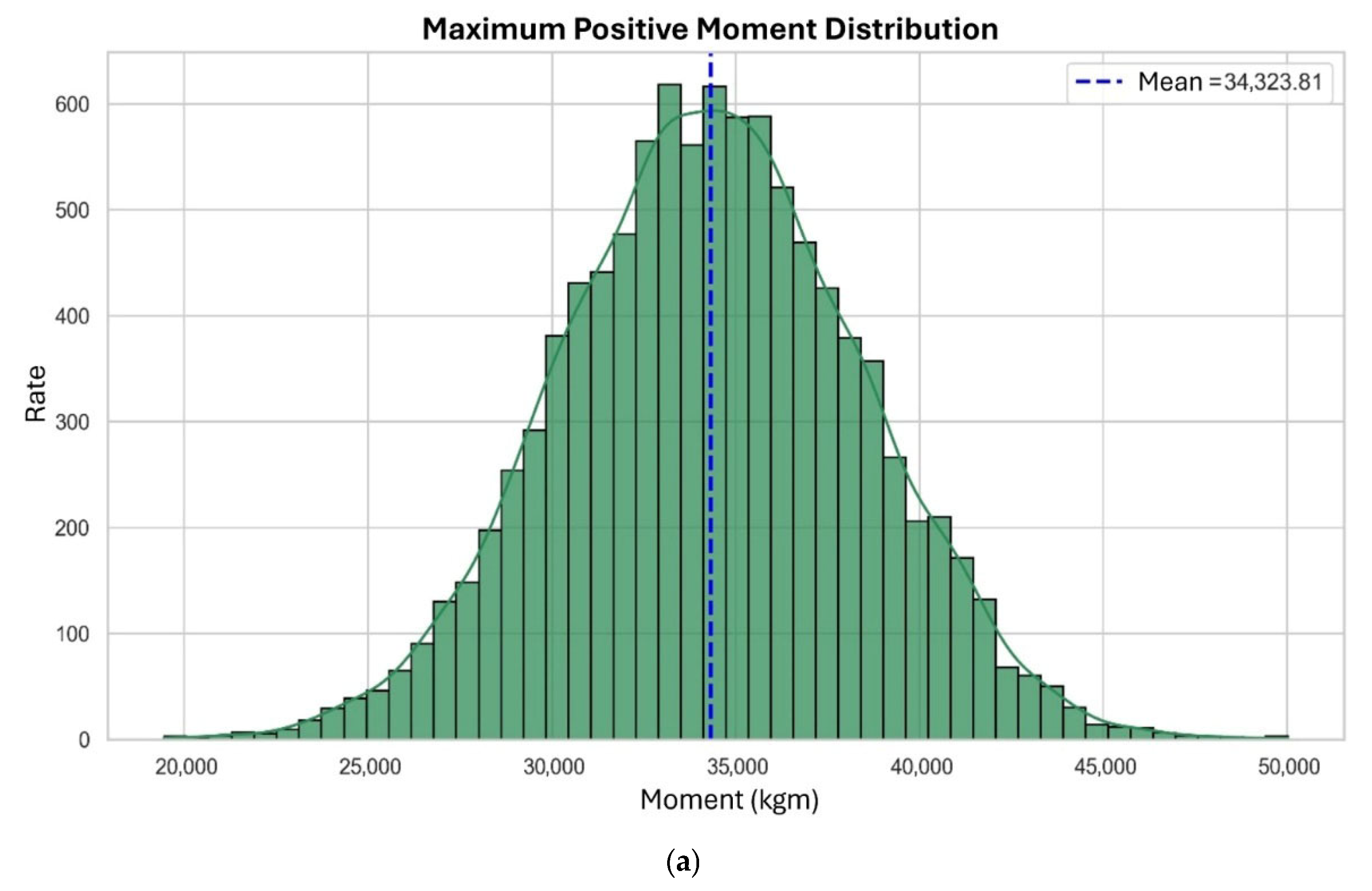
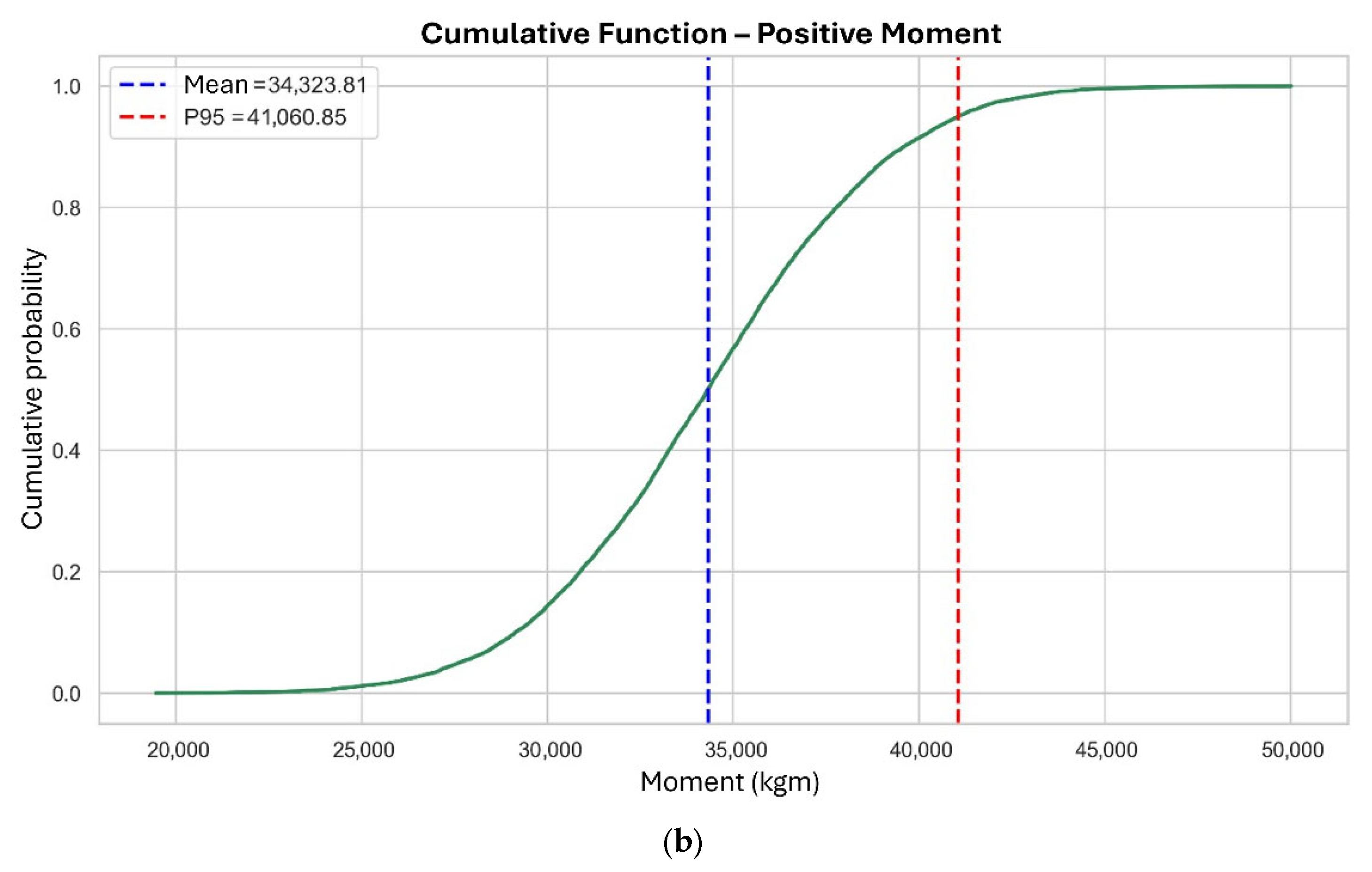
3.1. Positive Bending Moments
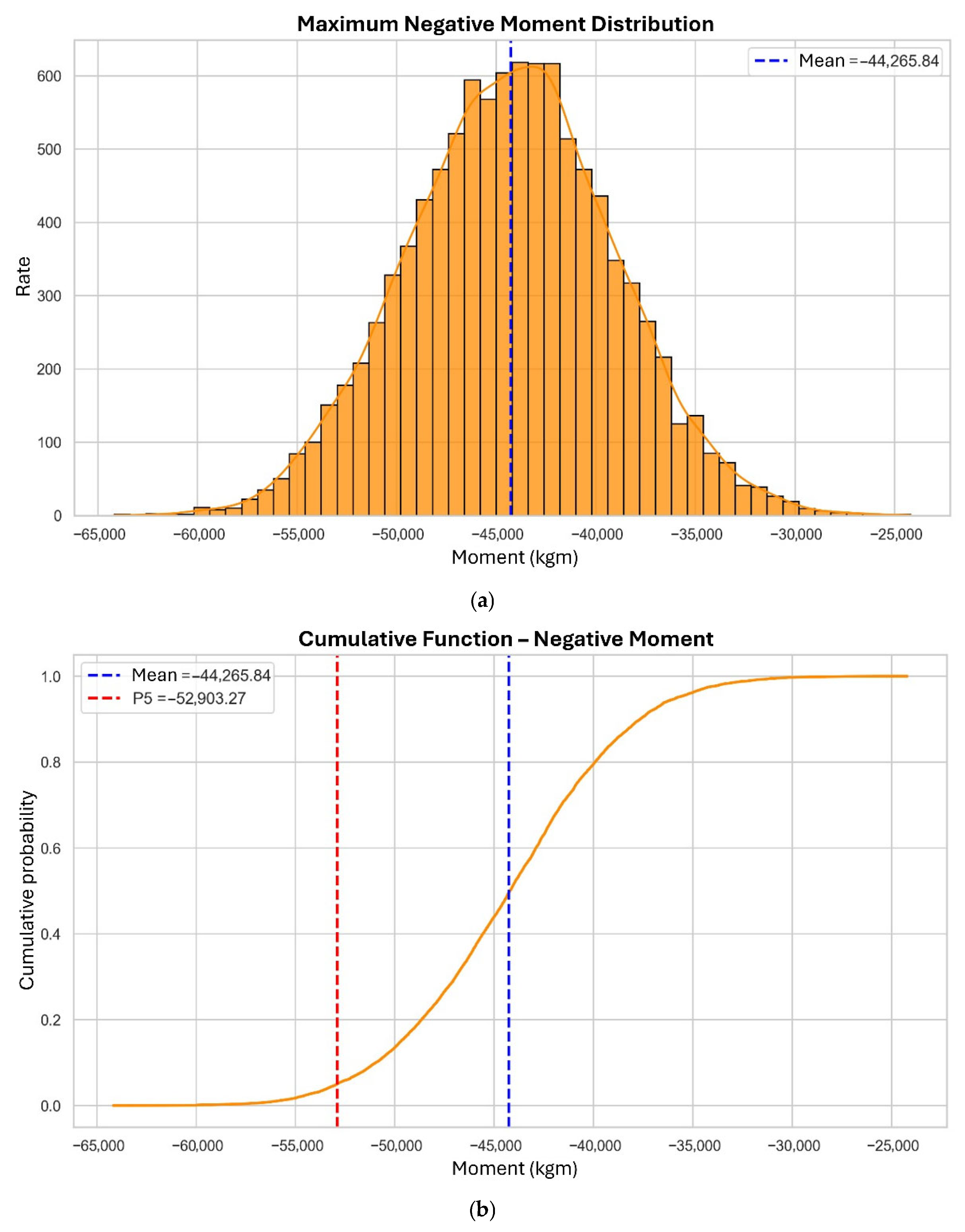
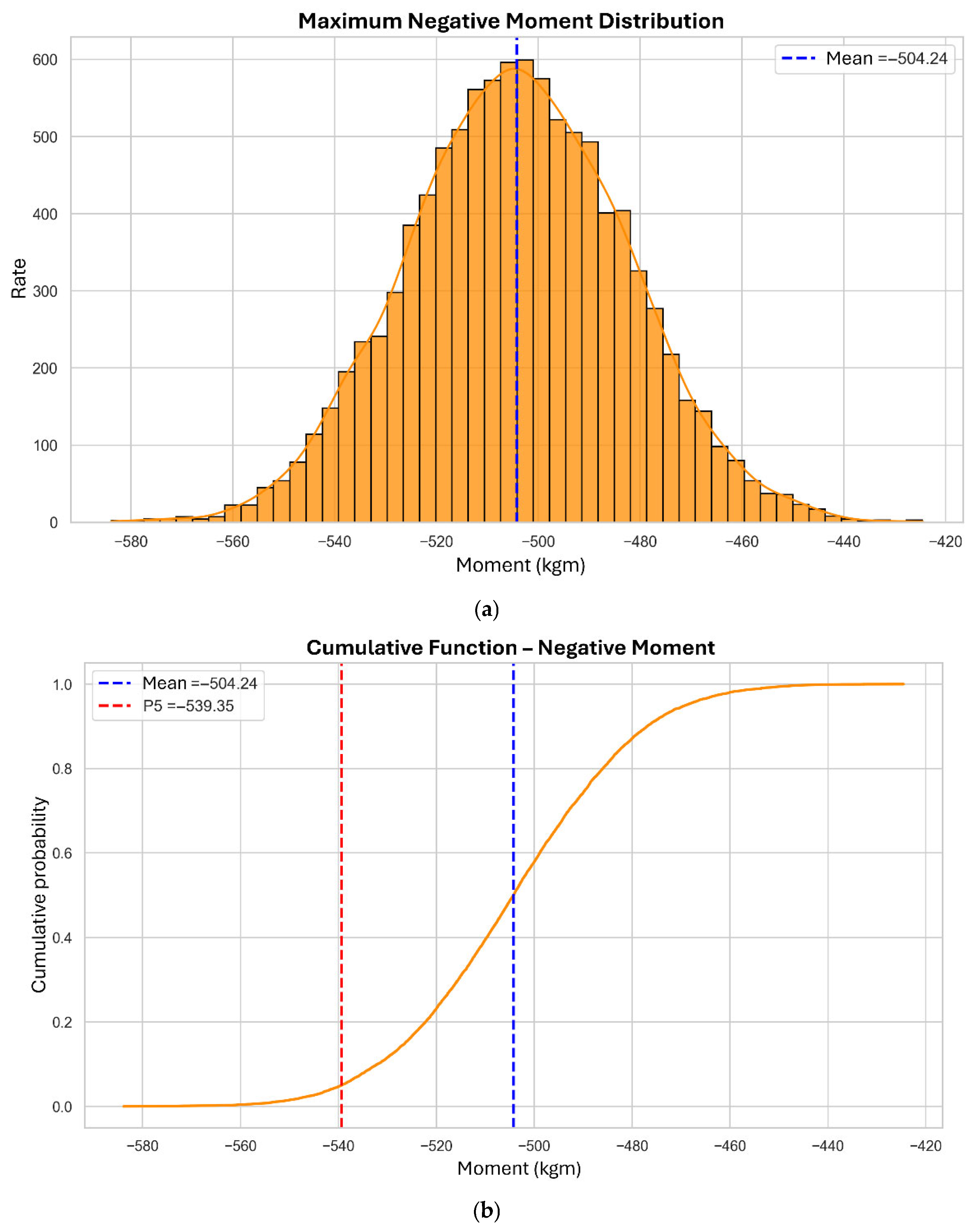
3.2. Negative Bending Moments
3.2.1. Comparison of Deterministic and Probabilistic Values
3.2.2. Primary Beams
3.2.3. Secondary Beams
3.3. Comparative Reinforcement Demand Under Deterministic and Probabilistic Moments
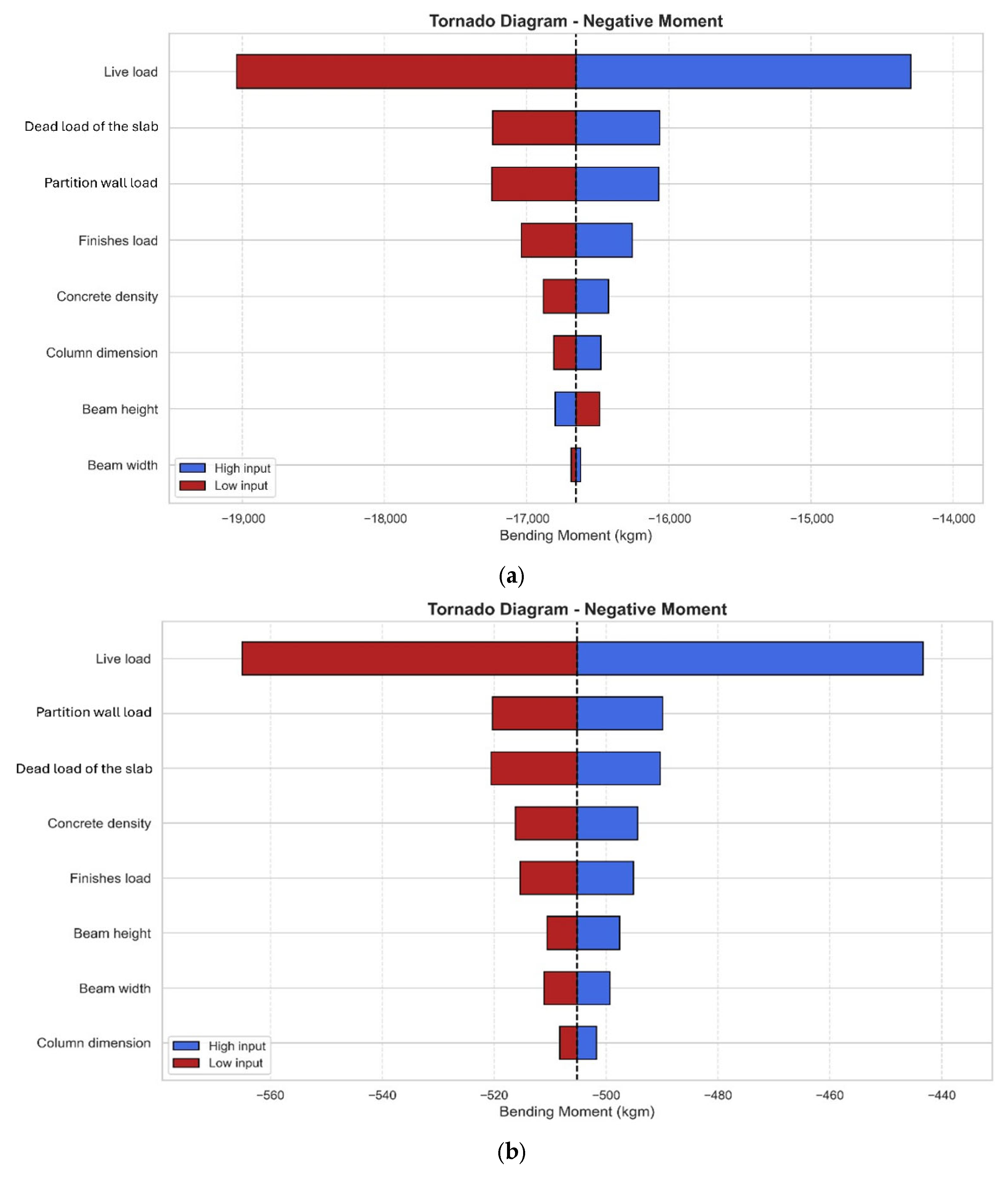
4. Discussion of Results
4.1. Research Gaps and Contributions
4.2. Study Limitations
4.3. Future Research
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Steenbergen, R.D.J.M.; Vrouwenvelder, A.C.W.M. The JCSS probabilistic model Code, future developments. Struct. Saf. 2024, 113, 102540. [Google Scholar] [CrossRef]
- Ribeiro, L.d.R.; Kroetz, H.M.; Parisi, F.; Beck, A.T. Optimal risk-based design of reinforced concrete beams against progressive collapse. Eng. Struct. 2024, 300, 117158. [Google Scholar] [CrossRef]
- American Concrete Institute. Building Code Requirements for Structural Concrete and Commentary (ACI 318-19); American Concrete Institute: Farmington Hills, MI, USA, 2019. [Google Scholar]
- Jahani, E.; Shayanfar, M.A.; Barkhordari, M.A. A new adaptive importance sampling Monte Carlo method for structural reliability. KSCE J. Civ. Eng. 2012, 17, 210–215. [Google Scholar] [CrossRef]
- Scherer, M.; Titello, E.P.; Morsch, I.B.; Real, M.d.V.; Filho, A.C. Comparison of two FORM methodologies for reinforced concrete beams under flexure. Lat. Am. J. Solids Struct. 2021, 18, e402. [Google Scholar] [CrossRef]
- Associação Brasileira de Normas Técnicas. NBR 6118:2014–Projeto de Estruturas de Concreto–Procedimento; ABNT: Rio de Janeiro, Brazil, 2014. [Google Scholar]
- Ramezanianpour, A.A.; Miyamoto, A. Concrete Carbonation Modelling and Monte Carlo Simulation Method for Uncertainty Analysis of Stochastic Front Depth. Yamaguchi Univ. Fac. Eng. Res. Rep. 2000, 50, 149–152. [Google Scholar]
- Ahsana, P.V.; Rao, K.B.; Anoop, M.B. Stochastic analysis of flexural strength of RC beams subjected to chloride induced corrosion. Mater. Res. 2015, 18, 1224–1241. [Google Scholar] [CrossRef]
- Zhou, S.; Zhang, J.; Zhang, Q.; Chen, W. Uncertainty theory-based structural reliability analysis and design optimization under epistemic uncertainty. Appl. Sci. 2022, 12, 2846. [Google Scholar] [CrossRef]
- Li, Z.; Liu, X.; Kou, D.; Hu, Y.; Zhang, Q.; Yuan, Q. Probabilistic models for the shear strength of RC deep beams. Appl. Sci. 2023, 13, 4853. [Google Scholar] [CrossRef]
- Nunes, J.H.C.; Junior, E.T.d.L.; de Lima, F.B. Reliability Analysis of Serviceability Limit States of Beams in a Benchmark Reinforced Concrete Building. XLV Ibero-Latin American Congress on. Comput. Methods Eng. 2024, 6, 10428. [Google Scholar]
- Félix, E.F.; Falcão, I.d.S.; dos Santos, L.G.; Carrazedo, R.; Possan, E. A Monte Carlo-based approach to assess the reinforcement depassivation probability of RC structures: Simulation and analysis. Buildings 2023, 13, 993. [Google Scholar] [CrossRef]
- Kim, S.H.; Boldoo, T.; Kim, D.Y.; Chu, I.; Woo, S.K. Probabilistic Moment Capacity Models of Reinforced Concrete Slab Members for Underground Box Culverts. Appl. Sci. 2021, 11, 8520. [Google Scholar] [CrossRef]
- Blagojevic’, P.; Blagojevic’, N.; Kukaras, D. Flexural Behavior of Steel Fiber Reinforced Concrete Beams: Probabilistic Numerical Modeling and Sensitivity Analysis. Appl. Sci. 2021, 11, 9591. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, J.; Chen, H. Reliability Analysis of Flexural Capacity of Reinforced Concrete Beams Using Monte Carlo Simulation. Materials 2022, 15, 4155. [Google Scholar]
- Szép, J.; Habashneh, M.; Lógó, J.; Movahedi Rad, M. Reliability assessment of reinforced concrete beams under elevated temperatures: A probabilistic approach using finite element and physical models. Sustainability 2023, 15, 6077. [Google Scholar] [CrossRef]
- Kolo, D.N.; Aguwa, J.I.; Tsado, T.Y.; Abdullahi, M.; Yusuf, A.; Oritola, S.F. Reliability studies on reinforced concrete beam subjected to bending forces with natural stone as coarse aggregate. Asian J. Civ. Eng. 2021, 22, 485–491. [Google Scholar] [CrossRef]
- Taj, S.; Karthik, B.M.; Mamatha, N.R.; Rakesh, J. Prediction of reliability index and probability of failure for reinforced concrete beam subjected to flexure. Int. J. Adv. Res. Arts Sci. Eng. Manag. (IJARASEM) 2019, 6, 1–6. [Google Scholar]
- Costa, L.G.L.; Santiago, W.C.; Beck, A.T. Probabilistic models for live loads in buildings: Critical review, comparison to Brazilian design standards and calibration of partial safety factors. Rev. IBRACON Estrut. Mater. 2023, 16, e16204. [Google Scholar] [CrossRef]
- Kamin’ski, M.; Błon’ski, R. Analytical and numerical reliability analysis of certain Pratt steel truss. Appl. Sci. 2022, 12, 2901. [Google Scholar] [CrossRef]
- Tytarenko, R.; Khmil, R.; Blikharskyy, Y.; Katunský, D.; Popovych, V. Development of a Model for Assessing the Reliability of RC Beams Strengthened Under 50% of ULS Load Using Monte Carlo Simulation. Lect. Notes Civ. Eng. 2024, 604, 553–562. [Google Scholar]
- Ministerio de Vivienda, Construcción y Saneamiento. Reglamento Nacional de Edificaciones: Norma E.020 Cargas; Ministerio de Vivienda, Construcción y Saneamiento: Lima, Perú, 2006.
- Ministerio de Vivienda, Construcción y Saneamiento. Reglamento Nacional de Edificaciones: Norma E.060 Concreto Armado; Ministerio de Vivienda, Construcción y Saneamiento: Lima, Perú, 2020.

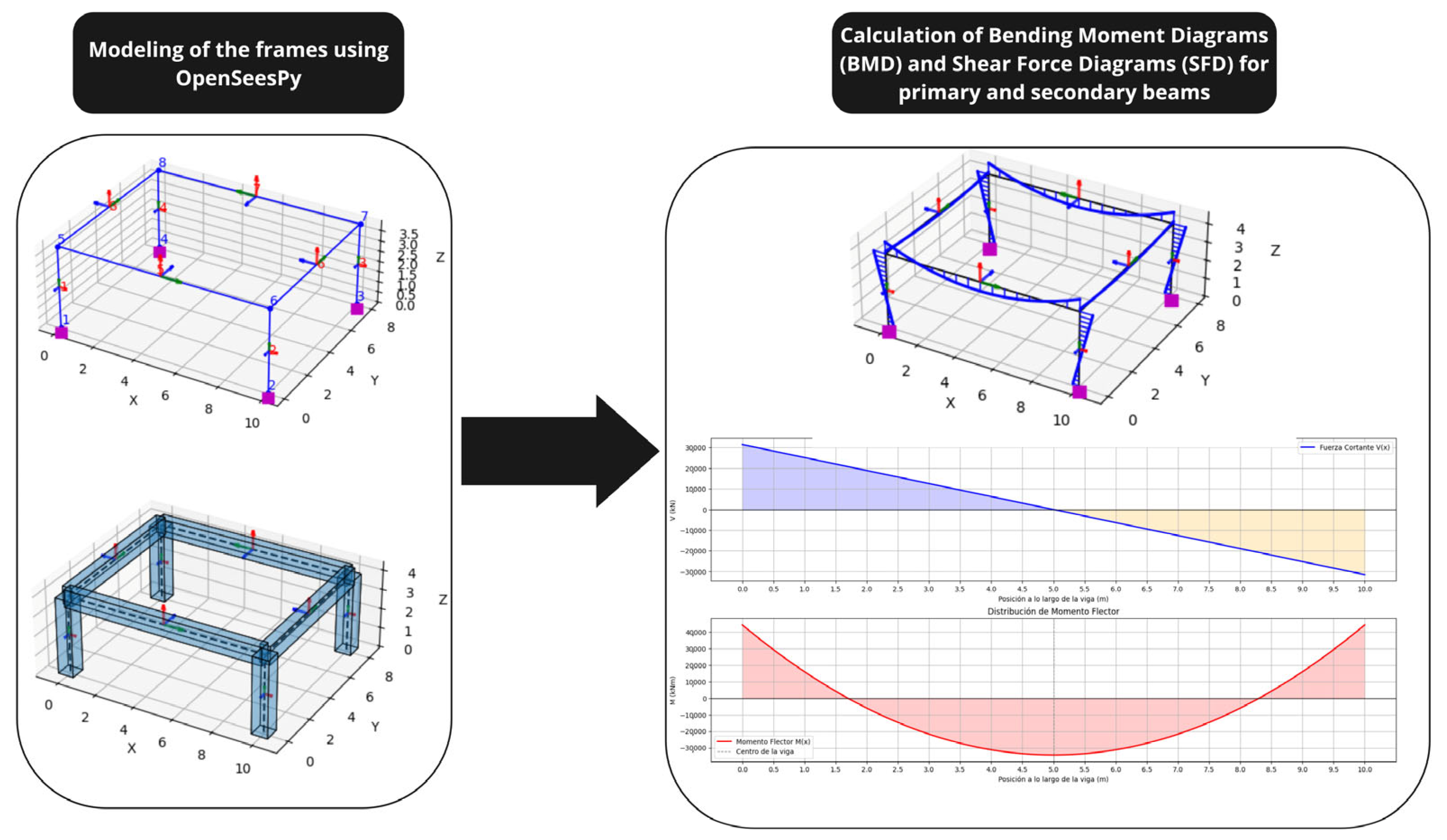
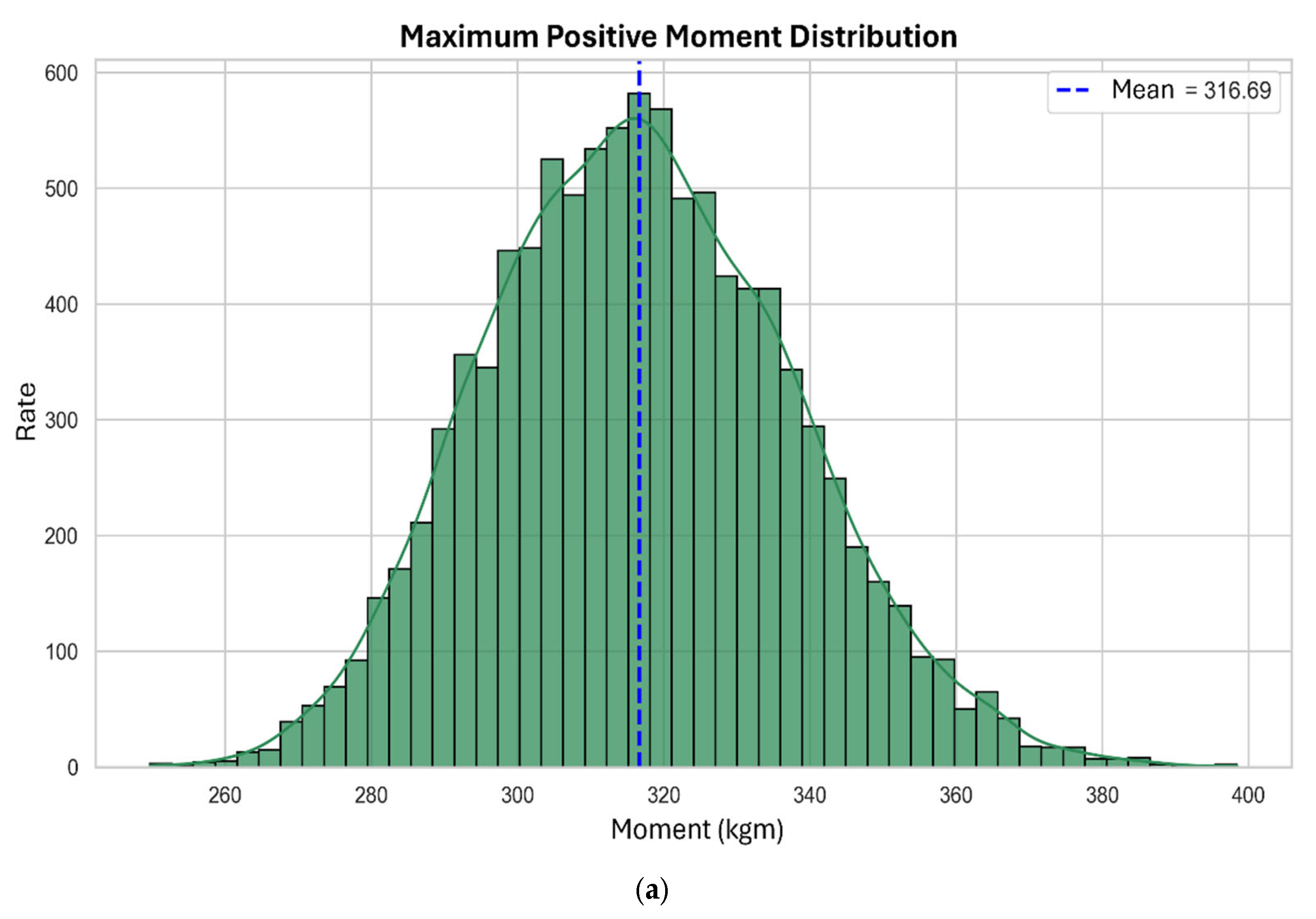
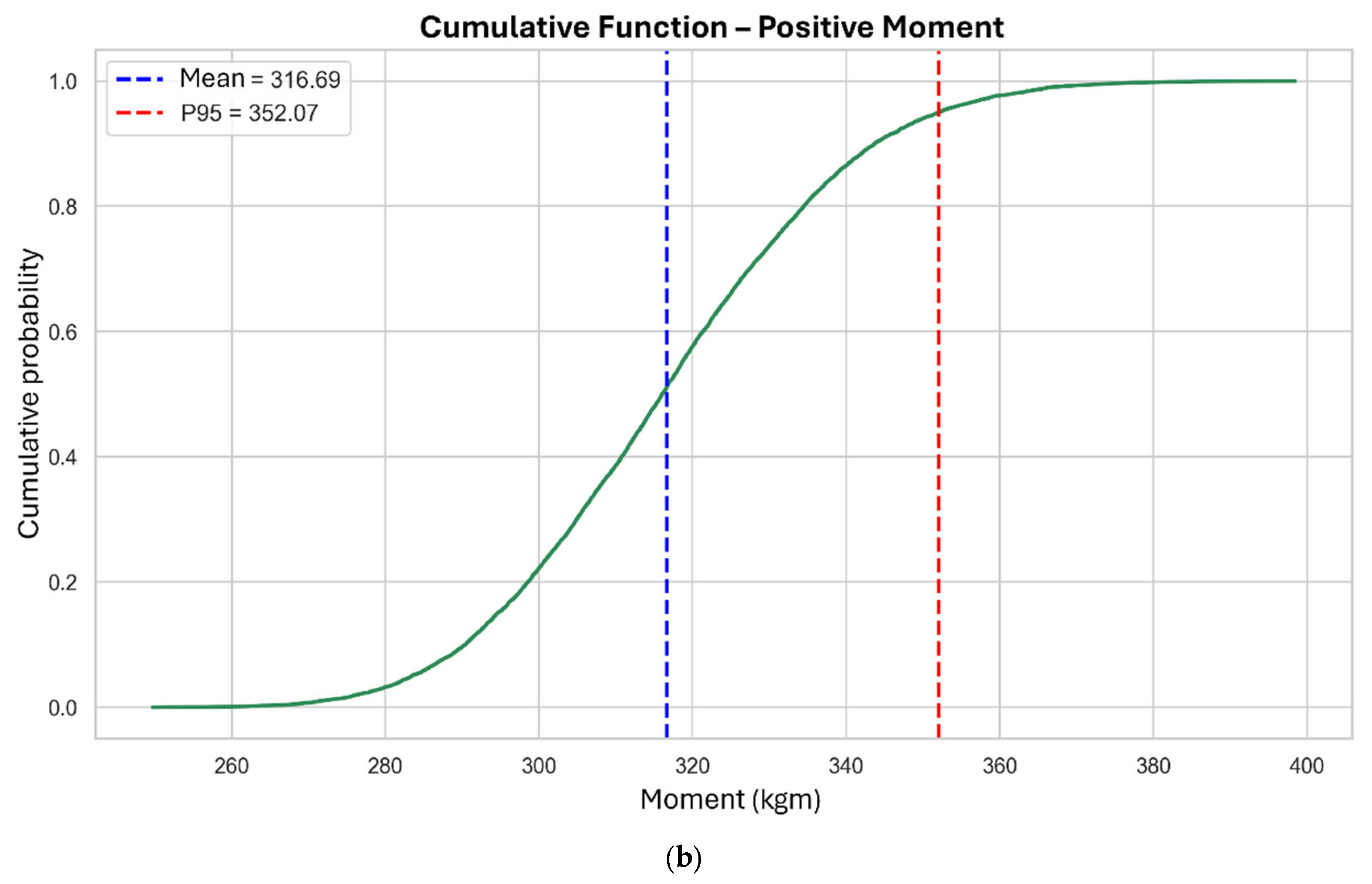
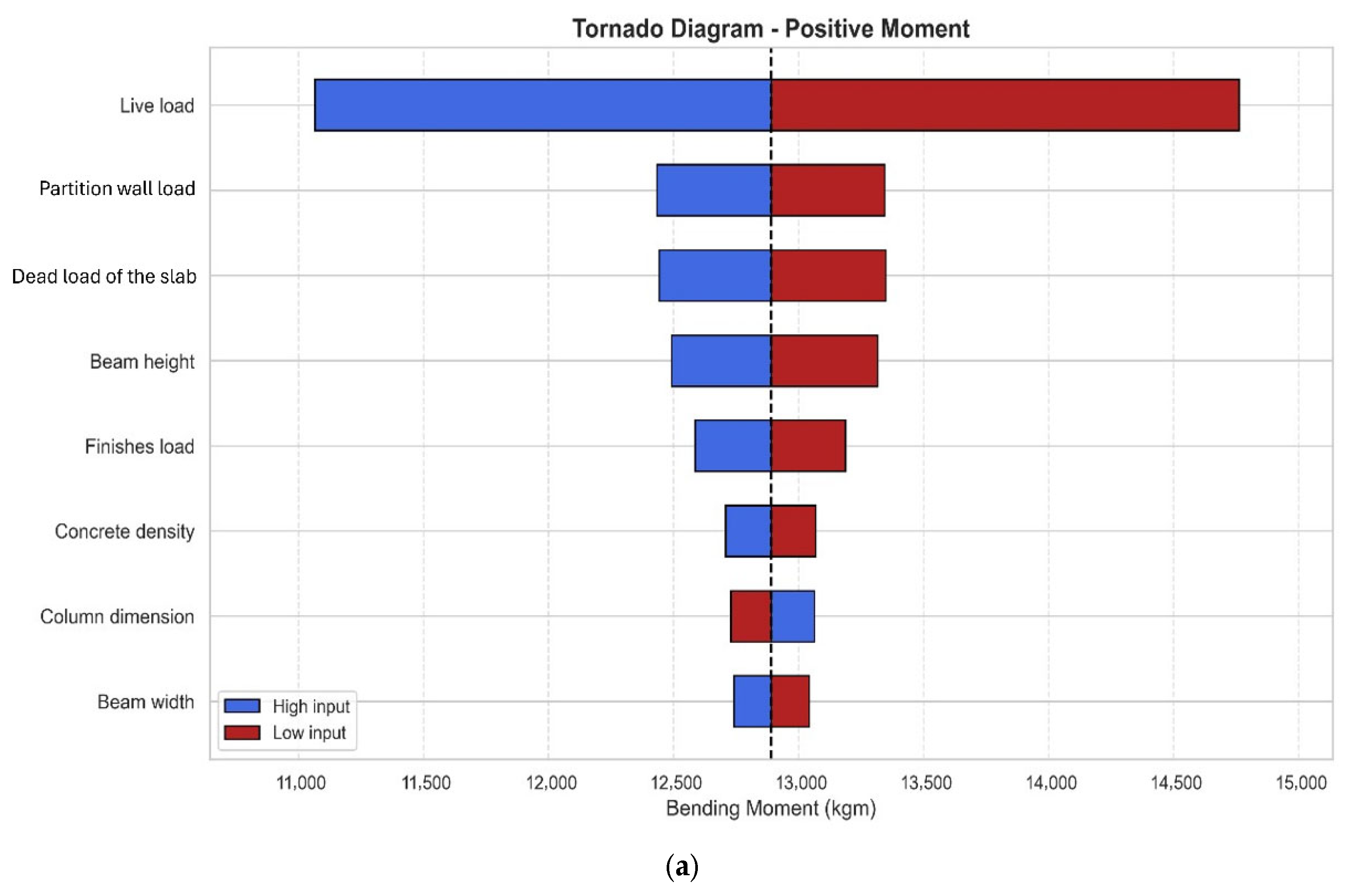
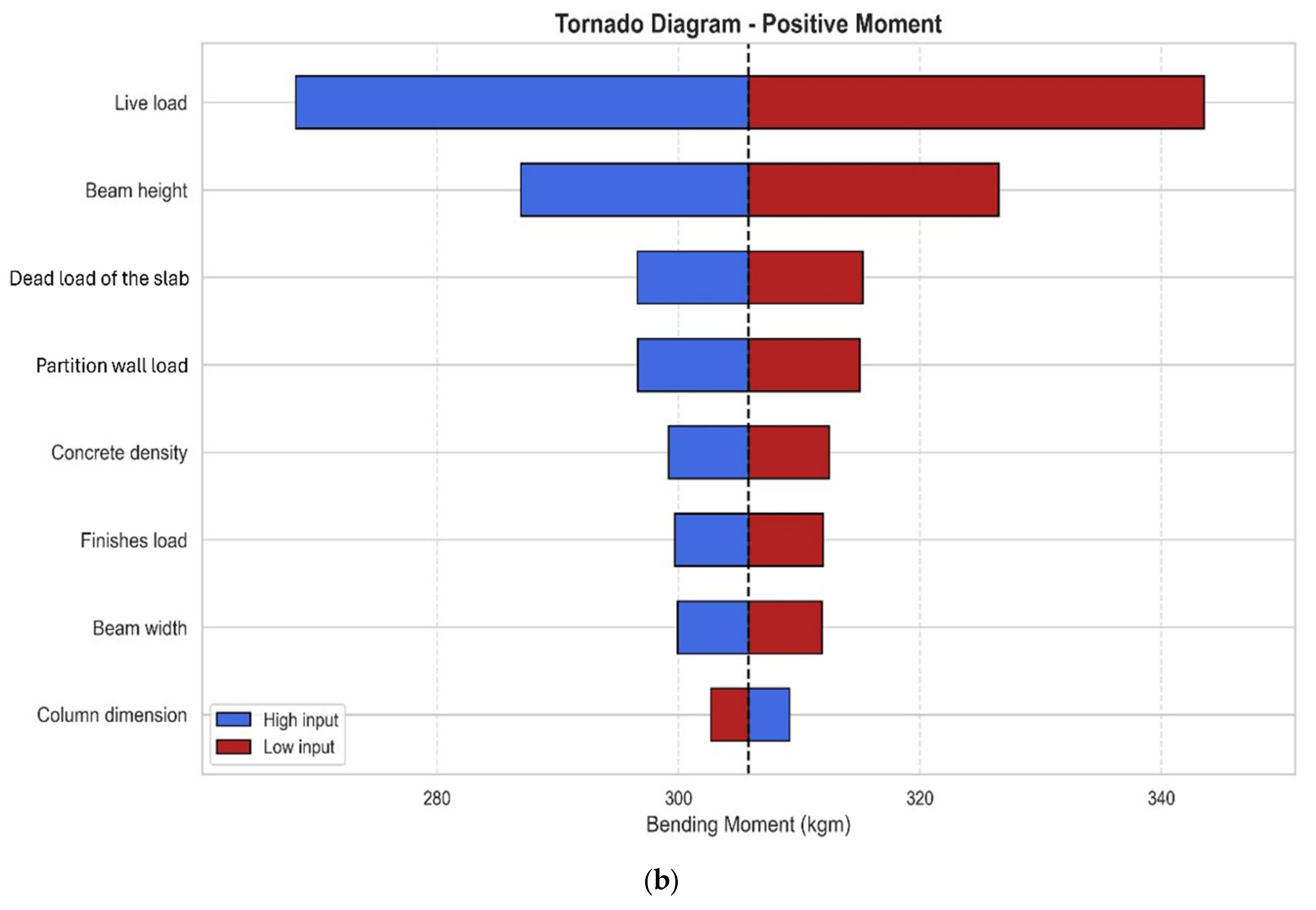
| Frame | Column Height (m) | Column (cm) | Secondary Beam (cm) | Primary Beam (cm) | Secondary Span (m) | Primary Span (m) |
|---|---|---|---|---|---|---|
| 1 | 3.00 | 45 × 45 | 25 × 30 | 30 × 45 | 3.0 | 4.5 |
| 2 | 3.00 | 50 × 50 | 25 × 35 | 30 × 50 | 3.5 | 5.0 |
| 3 | 3.30 | 55 × 55 | 25 × 35 | 35 × 55 | 4.0 | 6.0 |
| 4 | 3.30 | 55 × 55 | 25 × 40 | 35 × 60 | 4.5 | 6.5 |
| 5 | 3.50 | 65 × 65 | 30 × 45 | 40 × 65 | 5.0 | 7.0 |
| 6 | 3.50 | 65 × 65 | 30 × 50 | 40 × 70 | 5.5 | 7.5 |
| 7 | 3.70 | 70 × 70 | 35 × 55 | 45 × 75 | 6.0 | 8.0 |
| 8 | 3.70 | 70 × 70 | 35 × 60 | 45 × 80 | 6.5 | 8.5 |
| 9 | 3.90 | 75 × 75 | 40 × 65 | 50 × 85 | 7.0 | 9.0 |
| 10 | 3.90 | 80 × 80 | 40 × 70 | 50 × 90 | 8.0 | 10.0 |
| Variable (Unit) | Distribution | Parameters |
|---|---|---|
| Beam width (m) | Triangular | min = b − 0.02, max = b + 0.02 |
| Beam height (m) | Triangular | min = h − 0.05, max = h + 0.05 |
| Column side (m) | Triangular | min = a − 0.02, max = a + 0.02 |
| Concrete density (kg/m3) | Normal | µ = 2400, σ = 120 |
| Slab dead load (kg/m2) | Normal | µ = 300, σ = 30 |
| Live load (kg/m2) | Normal | µ = 250, σ = 100 |
| Finish load (kg/m2) | Normal | µ = 100, σ = 20 |
| Partition wall load (kg/m2) | Normal | µ = 150, σ = 30 |
| Number of Simulations | Mean | Relative Differences with Respect to 10,000 | 95th Percentile (P95) | Relative Differences with Respect to 10,000 |
|---|---|---|---|---|
| 1000 | 13,009.91 | 0.34 | 15,651.80 | 0.13 |
| 5000 | 12,998.06 | 0.43 | 15,615.16 | 0.37 |
| 10,000 | 13,054.20 | 0.00 | 15,672.41 | 0.00 |
| 50,000 | 13,020.53 | 0.26 | 15,652.02 | 0.13 |
| 100,000 | 13,031.31 | 0.18 | 15,658.25 | 0.09 |
| Frame | Main Beams | Secondary Beams | ||
|---|---|---|---|---|
| P50 (kg·m) | P95 (kg·m) | P50 (kg·m) | P95 (kg·m) | |
| 1 | 2596.75 | 3161.50 | 316.73 | 351.46 |
| 2 | 3560.23 | 4315.54 | 449.89 | 495.28 |
| 3 | 5949.05 | 7174.10 | 564.39 | 616.55 |
| 4 | 8109.72 | 9831.12 | 772.85 | 844.88 |
| 5 | 10,068.59 | 12,081.64 | 1074.78 | 1171.74 |
| 6 | 13,054.20 | 15,672.41 | 1402.08 | 1527.24 |
| 7 | 16,603.52 | 19,920.73 | 1935.07 | 2107.61 |
| 8 | 20,824.01 | 24,981.35 | 2446.75 | 2670.98 |
| 9 | 25,723.45 | 30,675.43 | 3269.21 | 3560.50 |
| 10 | 34,396.31 | 41,044.93 | 4393.33 | 4774.12 |
| Frame | Main Beams | Secondary Beams | ||
|---|---|---|---|---|
| P50 (kg·m) | P95 (kg·m) | P50 (kg·m) | P95 (kg·m) | |
| 1 | −3090.40 | −3719.69 | −504.12 | −539.95 |
| 2 | −4569.24 | −5503.59 | −731.45 | −781.66 |
| 3 | −7711.45 | −9276.79 | −979.14 | −1046.49 |
| 4 | −9826.77 | −11,787.37 | −1285.72 | −1373.83 |
| 5 | −13,583.08 | −16,224.02 | −1835.83 | −1963.19 |
| 6 | −16,709.78 | −19,990.22 | −2311.35 | −2466.98 |
| 7 | −21,134.30 | −25,215.49 | −3127.09 | −3340.29 |
| 8 | −25,175.70 | −30,052.25 | −3807.73 | −4065.95 |
| 9 | −31,024.77 | −36,862.13 | −5005.26 | −5343.13 |
| 10 | −44,345.52 | −52,686.07 | −6954.30 | −7436.24 |
| Frame | Deterministic (kg·m) | Probabilistic P95 (kg·m) | Variation (%) |
|---|---|---|---|
| 1 | 2594.31 | 3161.50 | 21.86 |
| 2 | 3547.26 | 4315.54 | 21.66 |
| 3 | 5944.56 | 7174.10 | 20.68 |
| 4 | 8095.36 | 9831.12 | 21.44 |
| 5 | 10,057.93 | 12,081.64 | 20.12 |
| 6 | 13,021.96 | 15,672.41 | 20.35 |
| 7 | 16,606.45 | 19,920.73 | 19.96 |
| 8 | 20,806.74 | 24,981.35 | 20.06 |
| 9 | 25,734.65 | 30,675.43 | 19.20 |
| 10 | 34,331.85 | 41,044.93 | 19.55 |
| Frame | Deterministic (kg·m) | Probabilistic P95 (kg·m) | Variation (%) |
|---|---|---|---|
| 1 | −3090.55 | −3719.69 | 20.36 |
| 2 | −4562.07 | −5503.59 | 20.64 |
| 3 | −7719.65 | −9276.79 | 20.17 |
| 4 | −9829.22 | −11,787.37 | 19.92 |
| 5 | −13,588.90 | −16,224.02 | 19.39 |
| 6 | −16,696.45 | −19,990.22 | 19.73 |
| 7 | −21,141.70 | −25,215.49 | 19.27 |
| 8 | −25,187.88 | −30,052.25 | 19.31 |
| 9 | −31,065.87 | −36,862.13 | 18.66 |
| 10 | −44,310.12 | −52,686.07 | 18.90 |
| Frame | Deterministic (kg·m) | Probabilistic P95 (kg·m) | Variation (%) |
|---|---|---|---|
| 1 | 316.17 | 351.46 | 11.16 |
| 2 | 449.60 | 495.28 | 10.16 |
| 3 | 563.90 | 616.55 | 9.34 |
| 4 | 772.65 | 844.88 | 9.35 |
| 5 | 1074.16 | 1171.74 | 9.08 |
| 6 | 1400.59 | 1527.24 | 9.04 |
| 7 | 1933.30 | 2107.61 | 9.02 |
| 8 | 2442.65 | 2670.98 | 9.35 |
| 9 | 3268.74 | 3560.50 | 8.93 |
| 10 | 4391.41 | 4774.12 | 8.71 |
| Frame | Deterministic (kg·m) | Probabilistic P95 (kg·m) | Variation (%) |
|---|---|---|---|
| 1 | −505.00 | −539.95 | 6.92 |
| 2 | −732.40 | −781.66 | 6.73 |
| 3 | −979.95 | −1046.49 | 6.79 |
| 4 | −1287.58 | −1373.83 | 6.70 |
| 5 | −1836.79 | −1963.19 | 6.88 |
| 6 | −2312.22 | −2466.98 | 6.69 |
| 7 | −3127.78 | −3340.29 | 6.79 |
| 8 | −3807.60 | −4065.95 | 6.79 |
| 9 | −5008.97 | −5343.13 | 6.67 |
| 10 | −6957.83 | −7436.24 | 6.88 |
| Frame | Deterministic (kg·cm) | Probabilistic (kg·cm) | As1 (cm2) | As2 (cm2) | Variation (%) |
|---|---|---|---|---|---|
| 1 | −3090.55 | −3719.69 | 2.14 | 2.59 | 21.03 |
| 2 | −4562.07 | −5503.59 | 2.81 | 3.41 | 21.35 |
| 3 | −7719.65 | −9276.79 | 4.29 | 5.18 | 20.75 |
| 4 | −9829.22 | −11,787.37 | 4.97 | 6.00 | 20.72 |
| 5 | −13,588.90 | −16,224.02 | 6.29 | 7.56 | 20.19 |
| 6 | −16,696.45 | −19,990.22 | 7.14 | 8.61 | 20.59 |
| 7 | −21,141.70 | −25,215.49 | 8.37 | 10.05 | 20.07 |
| 8 | −25,187.88 | −30,052.25 | 9.31 | 11.17 | 19.98 |
| 9 | −31,065.87 | −36,862.13 | 10.75 | 12.83 | 19.35 |
| 10 | −44,310.12 | −52,686.07 | 14.55 | 17.45 | 19.93 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Llanos, D.; Huerta, A.; Huisa, J.; Ariza Flores, V. Probabilistic Evaluation of Flexural Demand in RC Beams Through Monte Carlo Simulation. Constr. Mater. 2025, 5, 72. https://doi.org/10.3390/constrmater5040072
Llanos D, Huerta A, Huisa J, Ariza Flores V. Probabilistic Evaluation of Flexural Demand in RC Beams Through Monte Carlo Simulation. Construction Materials. 2025; 5(4):72. https://doi.org/10.3390/constrmater5040072
Chicago/Turabian StyleLlanos, Diego, Aracely Huerta, Jairsinho Huisa, and Victor Ariza Flores. 2025. "Probabilistic Evaluation of Flexural Demand in RC Beams Through Monte Carlo Simulation" Construction Materials 5, no. 4: 72. https://doi.org/10.3390/constrmater5040072
APA StyleLlanos, D., Huerta, A., Huisa, J., & Ariza Flores, V. (2025). Probabilistic Evaluation of Flexural Demand in RC Beams Through Monte Carlo Simulation. Construction Materials, 5(4), 72. https://doi.org/10.3390/constrmater5040072






