Thermal Performance of Lightweight Earth: From Prediction to Optimization through Multiscale Modeling
Abstract
1. Introduction
2. Material Description
2.1. Lightweight Earths
2.2. Earth-Based Binder
2.3. Plant-Aggregates
2.4. Earth-Based Materials Incorporating Plant Aggregates
3. Methodology
3.1. Mean-Field Homogenization (MFH) Methods: Double-Inclusion and Mori-Tanaka Models
3.2. Challenges in Homogenization
3.3. Particulate Orientation
3.4. Particulate Thermal Conductivity Tensor
3.5. Representative Volume Element (RVE)
3.6. Overall Study Strategy
4. Application, Validation and Optimization
4.1. Modeling Input Data
4.1.1. Particulate Thermal Conductivity
4.1.2. Binder Thermal Conductivity
4.1.3. Volume Fractions
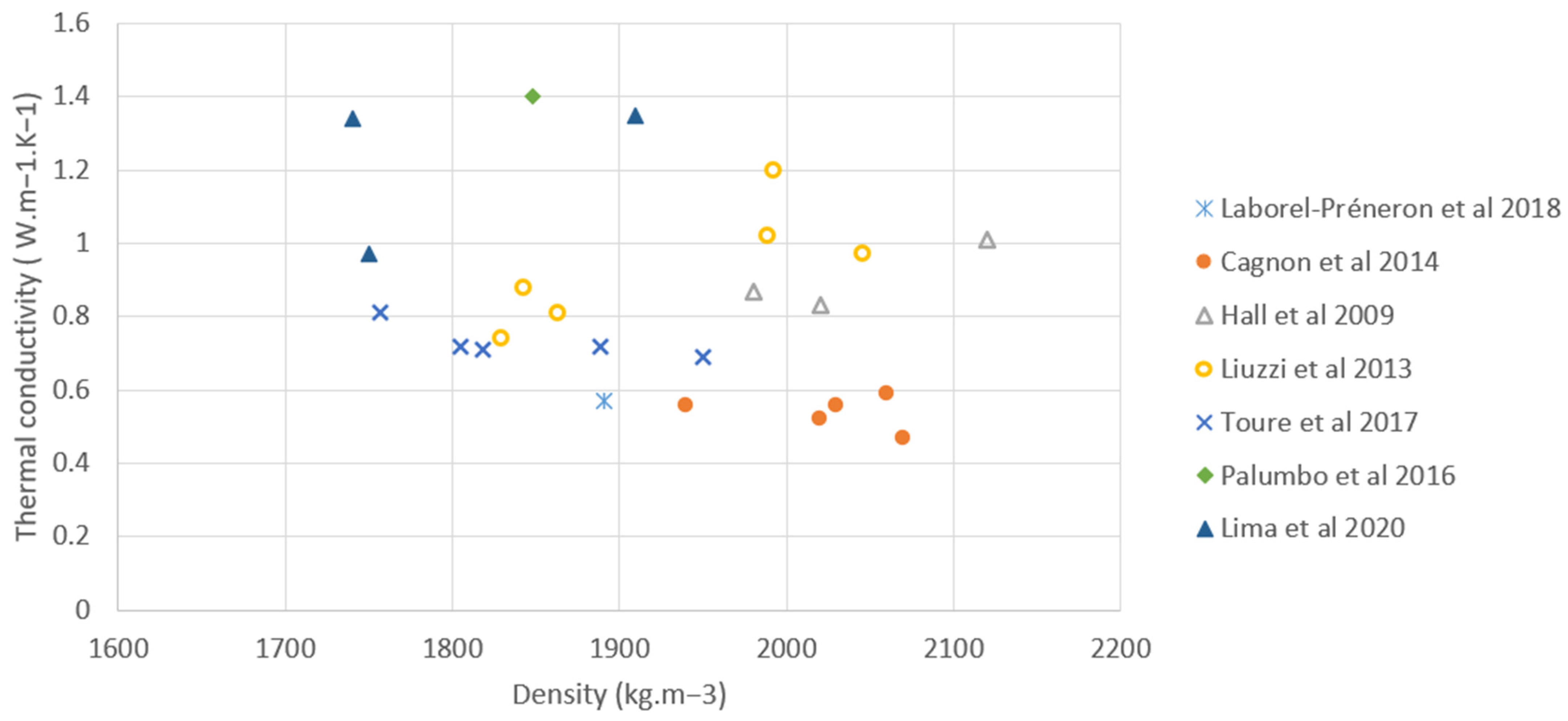
4.2. Validation
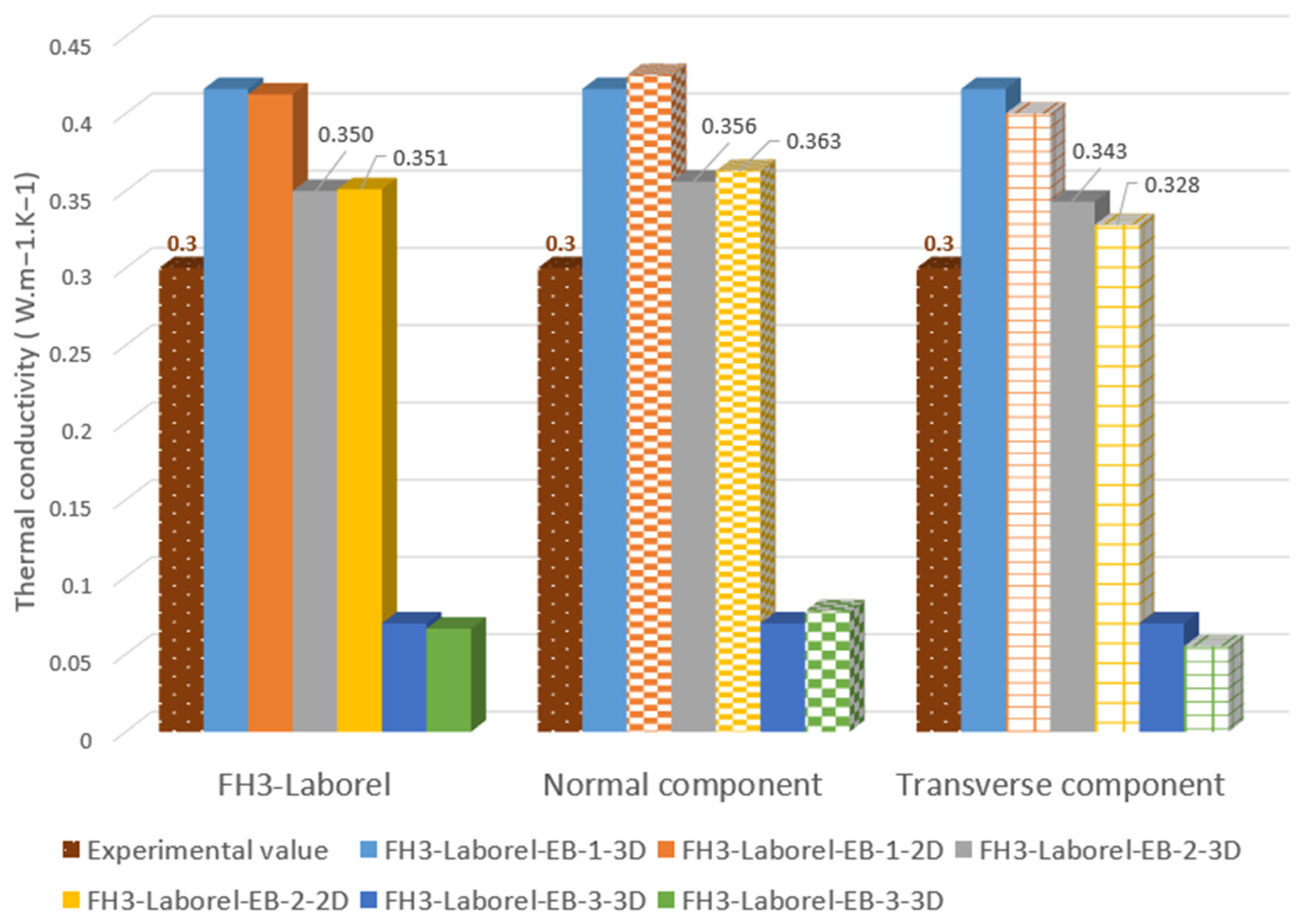
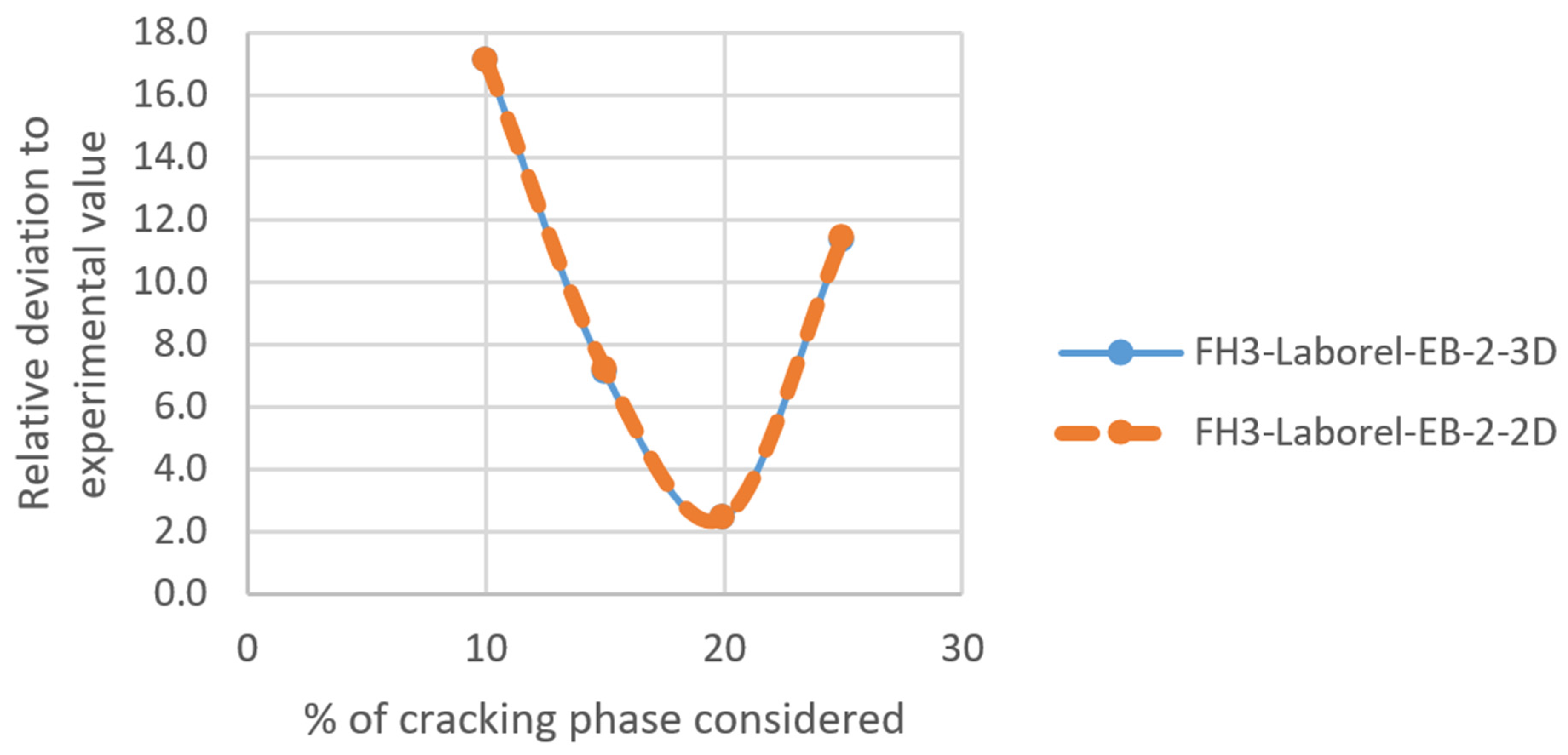
4.2.1. Fine-Based Composites
- FH3-Laborel composite
- FH6-Laborel composite
- -
- Models only considering the raw earth matrix and aggregates overestimate the effective thermal conductivity of lightweight earth by almost 50%.
- -
- Models based on the double inclusion scheme underestimate the experimental value by an average of 60%.
4.2.2. Clay-Based Composites
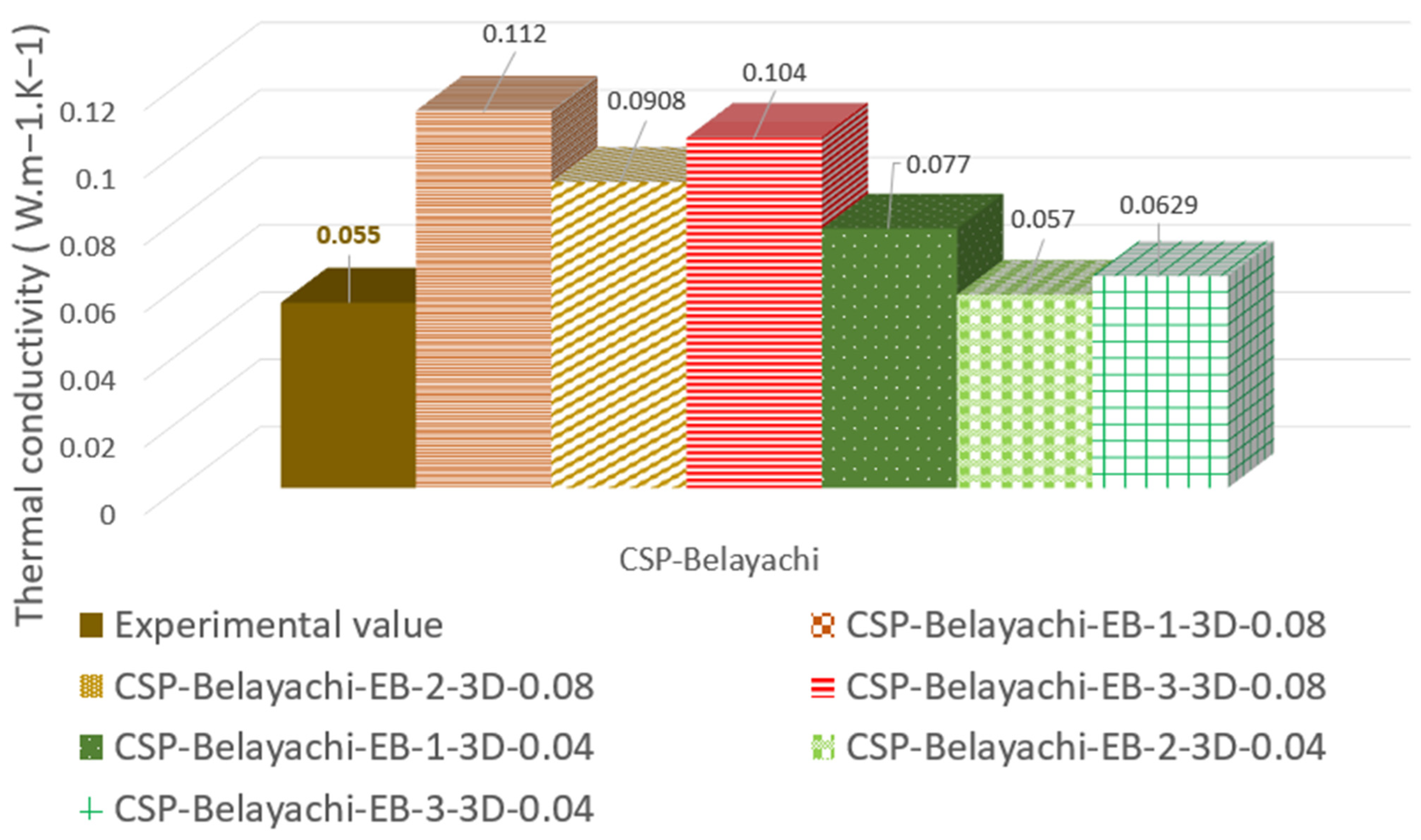
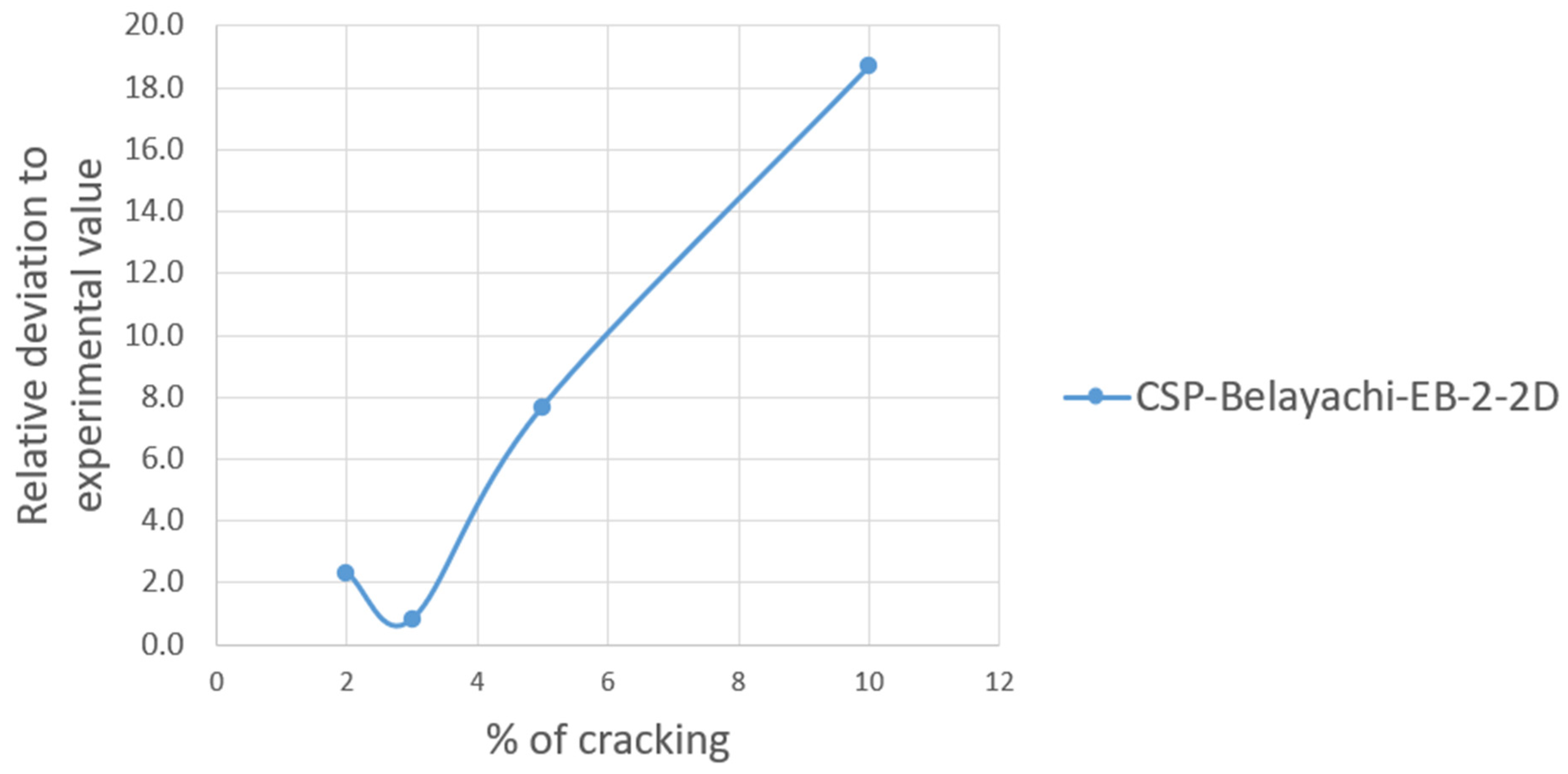
- CSP-Belayachi
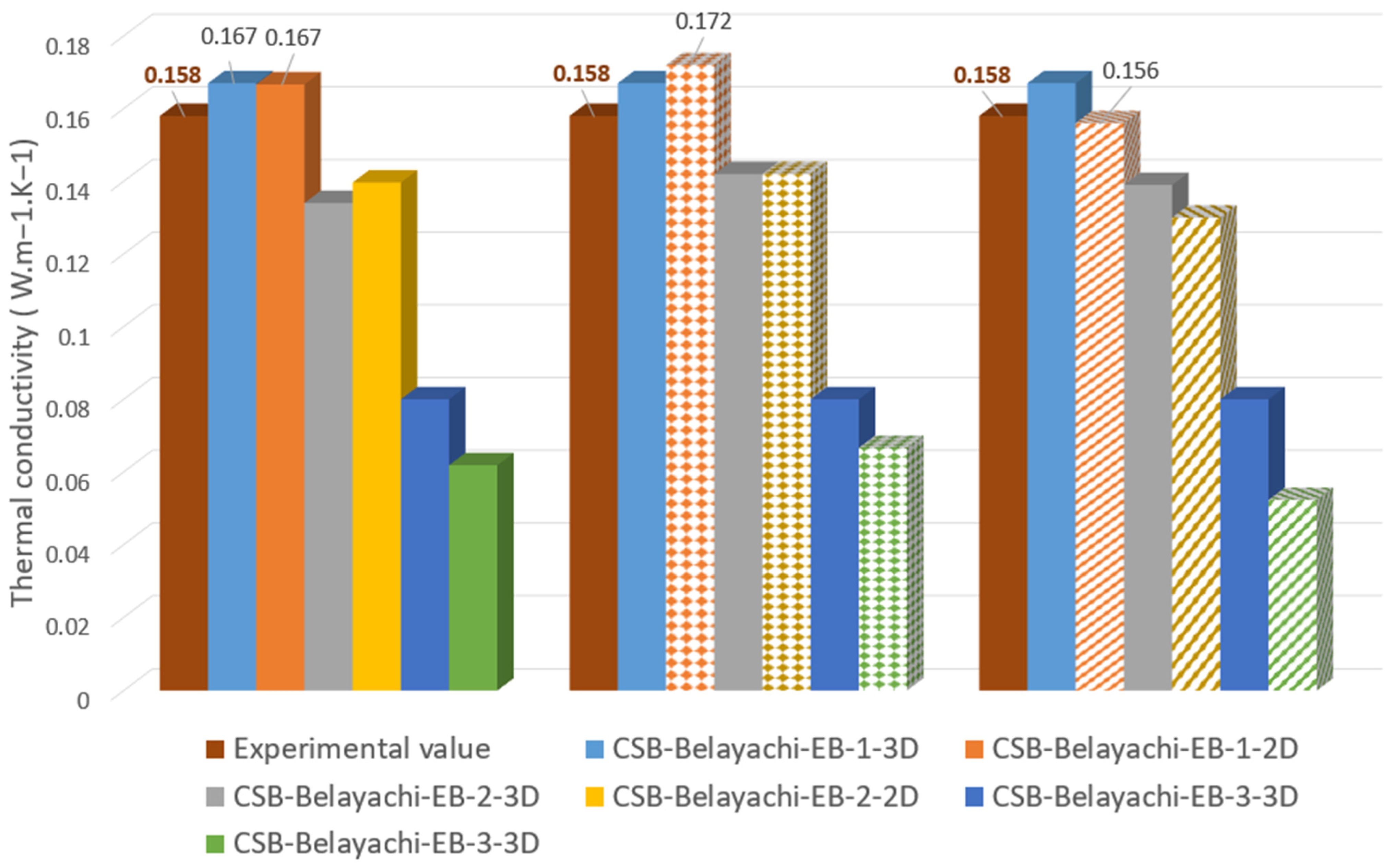
- CSB-Belayachi
4.3. Optimization Criteria
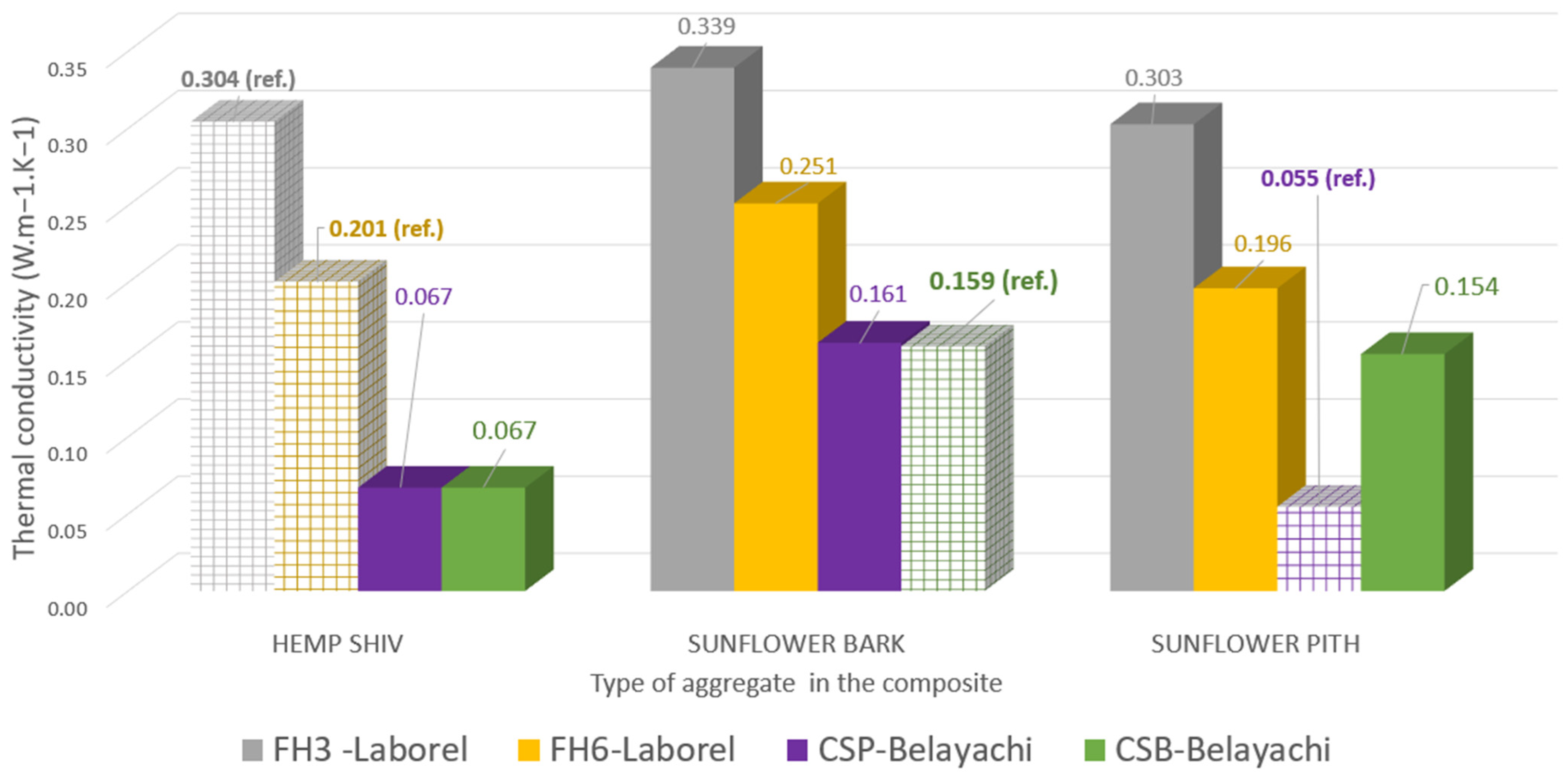
4.3.1. Influence of Aggregate Type on Thermal Properties
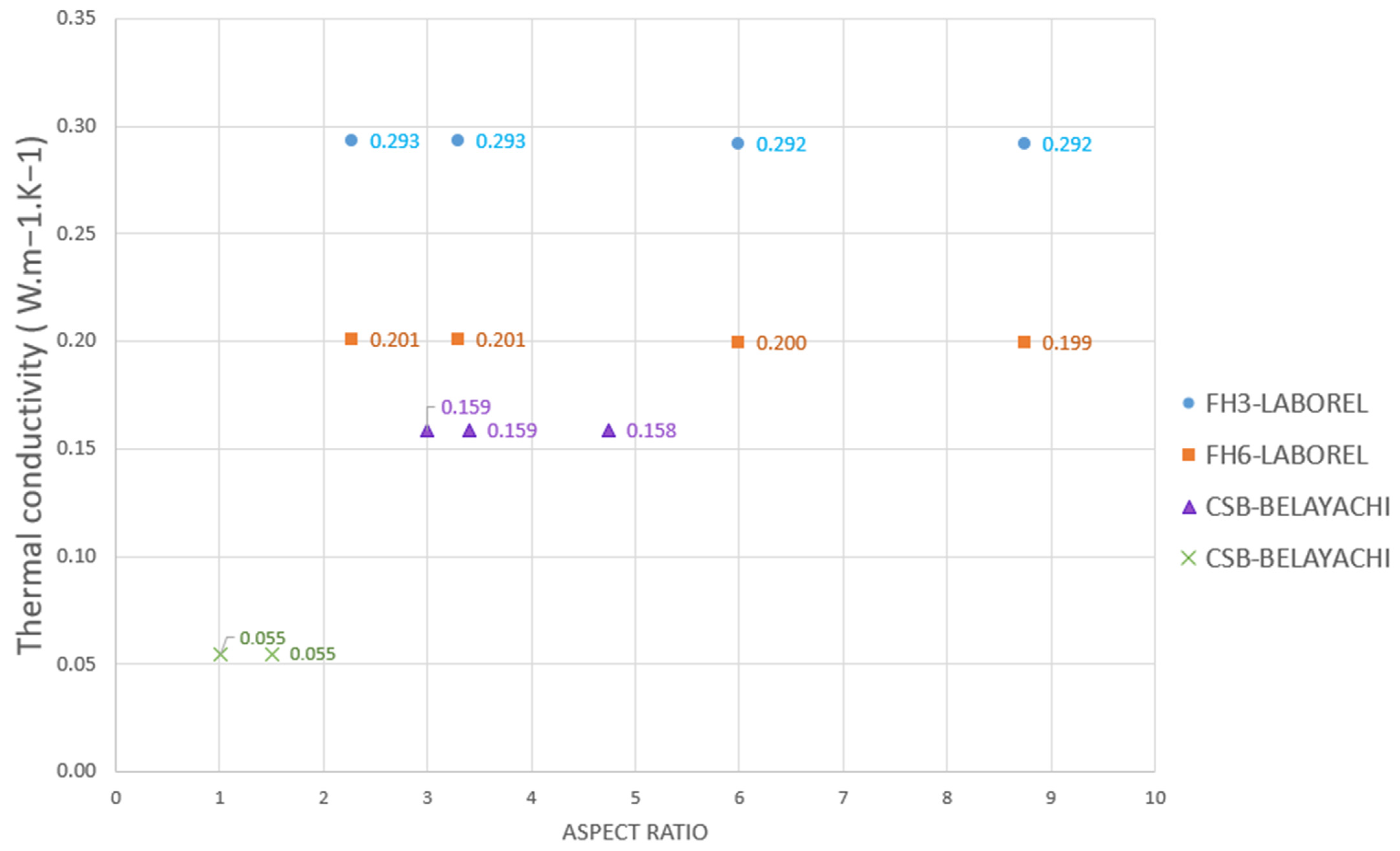
4.3.2. Influence of Aspect Ratio Variation on Thermal Conductivity
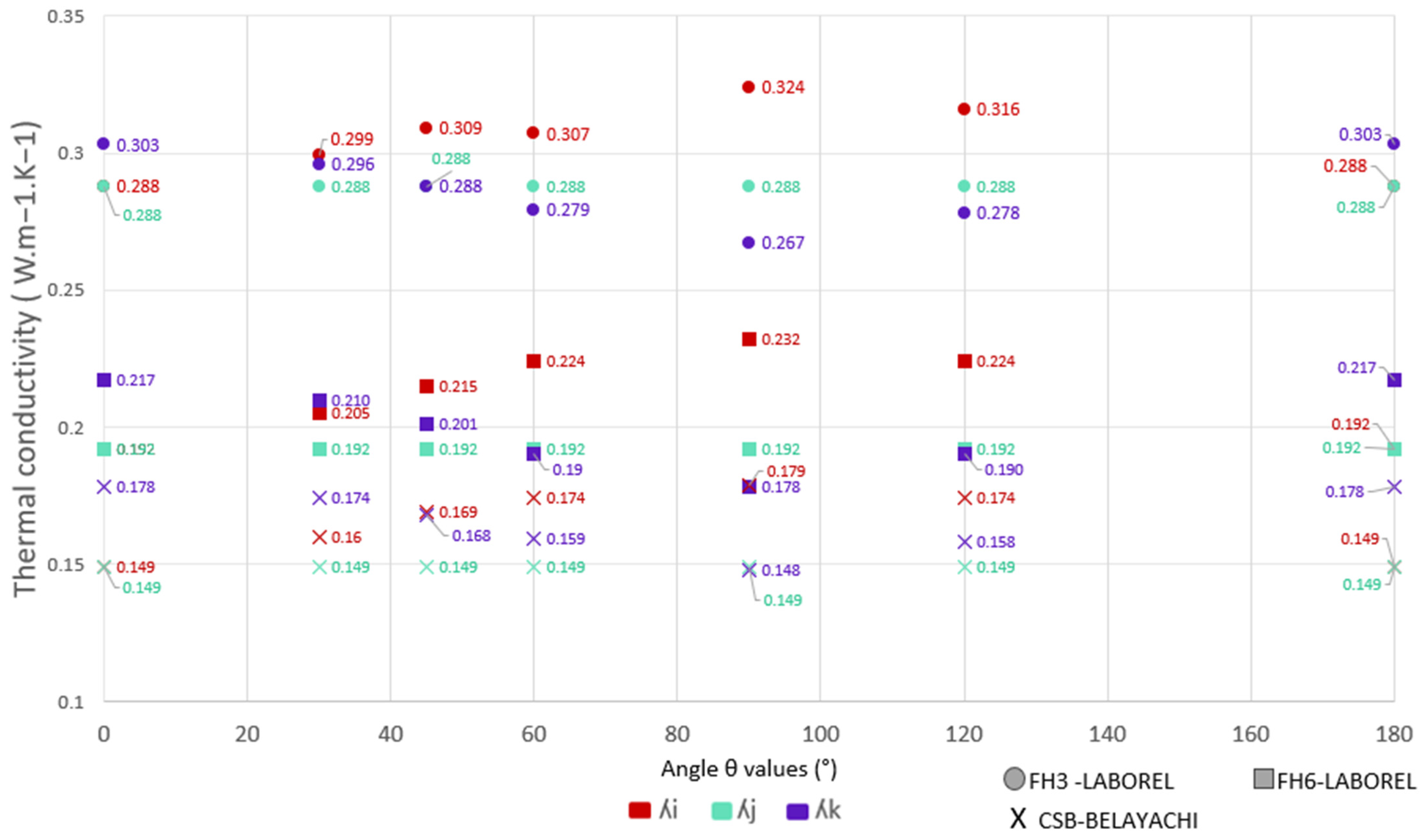
4.3.3. Influence of Preferential Orientation on Thermal Behavior
5. Results
5.1. Initial Modeling
5.2. Influence of Aggregate Type on Thermal Conductivity
5.3. Effect of Aggregate Shape on Thermal Conductivity
5.4. Impact of Aggregate Orientation on Thermal Conductivity
6. Conclusions
6.1. Relevance of Methods Used
6.2. Optimization of Formulations
6.3. Future Outlooks
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Latin symbols | |
| Thermal conductivity tensor | |
| Concentration tensor | |
| Interaction tensor | |
| Thermal conductivity tensor of the inclusion i and the matrix 0. | |
| Thermal conductivity tensor of the matrix 0 | |
| Depolarization tensor | |
| Volume fraction of r phase | |
| Volume of r phase | |
| Greek symbols | |
| λ | Thermal conductivity (W/(mK)) |
| Kronecker symbol | |
| Superscripts | |
| MT | Mori-Tanaka scheme |
| EB | Earth-based |
| Subscripts | |
| r | r-th phase |
| m | Earth-based binder |
| i,j,k | Reference to the Cartesian coordinate space vector base |
| tot | Total |
| hom | Homogeneous materials |
| T | Parallel to the compaction (for the earth composites) or fiber axis (for aggregates) |
| N | Perpendicular to the compaction (for earth composites) or fiber axis (for aggregates) |
| Abbreviations | |
| RVE | Representative Volume Element |
| FWAS | Quarry fines from aggregate washing processing |
| FH3 | Composite with FWAS and hemp shiv |
| FH6 | Composite with FWAS and hemp shiv |
| CSP | Composite with clay and sunflower pith |
| CSB | Composite with clay and sunflower bark |
References
- Lagouin, M. Caractérisation et Optimisation Multiphysiques d’une Paroi Bicouche bio et Géosourcée. These de Doctorat, Université Toulouse III, Toulouse, France, 2020. Available online: https://www.theses.fr/2020TOU30258 (accessed on 1 October 2022).
- RILEM. BEC: Bio-Stabilised Earth-Based Construction: Performance-Approach for Better Resilience. Available online: https://www.rilem.net/groupe/bec-bio-stabilised-earth-based-construction-performance-approach-for-better-resilience-447 (accessed on 4 April 2024).
- Fabbri, A.; Morel, J.C.; Aubert, J.-E.; Bui, Q.-B.; Gallipoli, D.; Ventura, A.; Reddy, V.B.V.; Hamard, E.; Pele-Peltier, A.; Abhilash, H.N. An overview of the remaining challenges of the RILEM TC 274-TCE, testing and characterisation of earth-based building materials and elements. RILEM Tech. Lett. 2021, 6, 150–157. [Google Scholar] [CrossRef]
- Rosa Latapie, S.; Abou-Chakra, A.; Sabathier, V. Bibliometric Analysis of Bio- and Earth-Based Building Materials: Current and Future Trends. Constr. Mater. 2023, 3, 474–508. [Google Scholar] [CrossRef]
- Anglade, E.; Sellier, A.; Aubert, J.-E.; Papon, A. An Experimental Study on Clay and Sand Mixes to Develop a Non-Linear Homogenized Model for Earth Construction Materials. Constr. Technol. Archit. 2022, 1, 293–302. [Google Scholar] [CrossRef]
- Mori, T.; Tanaka, K. Average stress in matrix and average elastic energy of materials with misfitting inclusions. Acta Metall. 1973, 21, 571–574. [Google Scholar] [CrossRef]
- Hori, M.; Nemat-Nasser, S. Double-inclusion model and overall moduli of multi-phase composites. Mech. Mater. 1993, 14, 189–206. [Google Scholar] [CrossRef]
- Laborel-Préneron, A.; Magniont, C.; Aubert, J.-E. Hygrothermal properties of unfired earth bricks: Effect of barley straw, hemp shiv and corn cob addition. Energy Build. 2018, 178, 265–278. [Google Scholar] [CrossRef]
- Gomes, M.I.; Faria, P.; Gonçalves, T.D. Earth-based mortars for repair and protection of rammed earth walls. Stabilization with mineral binders and fibers. J. Clean. Prod. 2018, 172, 2401–2414. [Google Scholar] [CrossRef]
- Laborel-Préneron, A.; Aubert, J.-E.; Magniont, C.; Maillard, P.; Poirier, C. Effect of Plant Aggregates on Mechanical Properties of Earth Bricks. J. Mater. Civ. Eng. 2017, 29, 04017244. [Google Scholar] [CrossRef]
- Gasnier, H. Construire en Terres D’Excavation, un Enjeu pour la Ville Durable. Ph.D. Thesis, Université Grenoble Alpes, Saint-Martin-d’Hères, France, 2019. Available online: https://theses.hal.science/tel-02165900 (accessed on 4 April 2024).
- Wang, L.; Lenormand, H.; Zmamou, H.; Leblanc, N. Effect of variability of hemp shiv on the setting of lime hemp concrete. Ind. Crop. Prod. 2021, 171, 113915. [Google Scholar] [CrossRef]
- Laborel-Préneron, A.; Magniont, C.; Aubert, J.-E. Characterization of Barley Straw, Hemp Shiv and Corn Cob as Resources for Bioaggregate Based Building Materials. Waste Biomass Valori. 2018, 9, 1095–1112. [Google Scholar] [CrossRef]
- Lagouin, M.; Magniont, C.; Sénéchal, P.; Moonen, P.; Aubert, J.-E.; Laborel-préneron, A. Influence of types of binder and plant aggregates on hygrothermal and mechanical properties of vegetal concretes. Constr. Build. Mater. 2019, 222, 852–871. [Google Scholar] [CrossRef]
- Magniont, C.; Escadeillas, G.; Coutand, M.; Oms-Multon, C. Use of plant aggregates in building ecomaterials. Eur. J. Environ. Civ. Eng. 2012, 16, 17–33. [Google Scholar] [CrossRef]
- Arufe, S.; Hellouin de Menibus, A.; Leblanc, N.; Lenormand, H. Physico-chemical characterisation of plant particles with potential to produce biobased building materials. Ind. Crop. Prod. 2021, 171, 113901. [Google Scholar] [CrossRef]
- Ratsimbazafy, H.H.; Laborel-Preneron, A.; Magniont, C.; Evon, P. A review of the multi-physical characteristics of plant aggregates and their effects on the properties of plant-based concrete. Recent Prog. Mater. 2021, 3, 1–69. [Google Scholar] [CrossRef]
- Rosa Latapie, S.; Lagouin, M.; Sabathier, V.; Abou-Chakra, A. From aggregate to particleboard: A new multi-scale model approach to thermal conductivity in bio-based materials. J. Build. Eng. 2023, 78, 107664. [Google Scholar] [CrossRef]
- Brouard, Y.; Belayachi, N.; Hoxha, D.; Ranganathan, N.; Méo, S. Mechanical and hygrothermal behavior of clay—Sunflower (Helianthus annuus) and rape straw (Brassica napus) plaster bio-composites for building insulation. Constr. Build. Mater. 2018, 161, 196–207. [Google Scholar] [CrossRef]
- Belayachi, N.; Ismail, B.; Broard, Y. Propriétés effectives thermiques d’un bio-composite à base de tournesol. Acad. J. Civ. Eng. 2022, 40, 240–243. [Google Scholar] [CrossRef]
- de Menibus, A.H.; Basco, C.; Degrave-Lemeurs, M.; Colinart, T.; Glé, P.; Hamard, E.; Lecompte, T.; Lenormand, H.; Meunier, M.; Vinceslas, T. Étude des bétons biosourcés à base de terre crue et de chanvre dans le cadre du projet ECO-TERRA. Acad. J. Civ. Eng. 2018, 36, 25–28. [Google Scholar] [CrossRef]
- Eshelby, J.D. The Determination of the Elastic Field of an Ellipsoidal Inclusion, and Related Problems. Proc. R. Soc. Lond. Ser. A 1957, 241, 376–396. [Google Scholar] [CrossRef]
- Collet, F.; Chamoin, J.; Pretot, S.; Lanos, C. Comparison of the hygric behaviour of three hemp concretes. Energy Build. 2013, 62, 294–303. [Google Scholar] [CrossRef]
- Bluhm, J.; De Boer, R. The Volume Fraction Concept in the Porous Media Theory. ZAMM—J. Appl. Math. Mech./Z. Für Angew. Math. Mech. 1997, 77, 563–577. [Google Scholar] [CrossRef]
- Bennai, F.; El Hachem, C.; Abahri, K.; Belarbi, R. Microscopic hydric characterization of hemp concrete by X-ray microtomography and digital volume correlation. Constr. Build. Mater. 2018, 188, 983–994. [Google Scholar] [CrossRef]
- Rosa Latapie, S.; Sabathier, V.; Abou-Chakra, A. Bio-based building materials: A prediction of insulating properties for a wide range of agricultural by-products. J. Build. Eng. 2024, 86, 108867. [Google Scholar] [CrossRef]
- Rosa Latapie, S.; Lagouin, M.; Douk, N.; Sabathier, V.; Abou-Chakra, A. Multiscale Modelling of Bio-composites: Towards Prediction of Their Thermal Conductivity Based on Adequate Knowledge of Their Constituents. In Bio-Based Building Materials; Amziane, S., Merta, I., Page, J., Eds.; RILEM Bookseries; Springer Nature: Cham, Switzerland, 2023; pp. 841–858. [Google Scholar] [CrossRef]
- Huang, G.; Abou-Chakra, A.; Geoffroy, S.; Absi, J. A Multi-Scale Numerical Simulation on Thermal Conductivity of Bio-Based Construction Materials. Constr. Mater. 2022, 2, 148–165. [Google Scholar] [CrossRef]
- Palumbo, M.; McGregor, F.; Heath, A.; Walker, P. The influence of two crop by-products on the hygrothermal properties of earth plasters. Build. Environ. 2016, 105, 245–252. [Google Scholar] [CrossRef]
- Cagnon, H.; Aubert, J.E.; Coutand, M.; Magniont, C. Hygrothermal properties of earth bricks. Energy Build. 2014, 80, 208–217. [Google Scholar] [CrossRef]
- Toure, P.M.; Sambou, V.; Faye, M.; Thiam, A. Mechanical and thermal characterization of stabilized earth bricks. Energy Procedia 2017, 139, 676–681. [Google Scholar] [CrossRef]
- Lima, J.; Faria, P.; Santos Silva, A. Earth Plasters: The Influence of Clay Mineralogy in the Plasters’ Properties. Int. J. Archit. Herit. 2020, 14, 948–963. [Google Scholar] [CrossRef]
- Hall, M.; Allinson, D. Analysis of the hygrothermal functional properties of stabilised rammed earth materials. Build. Environ. 2009, 44, 1935–1942. [Google Scholar] [CrossRef]
- Liuzzi, S.; Hall, M.R.; Stefanizzi, P.; Casey, S.P. Hygrothermal behaviour and relative humidity buffering of unfired and hydrated lime-stabilised clay composites in a Mediterranean climate. Build. Environ. 2013, 61, 82–92. [Google Scholar] [CrossRef]
- Liu, L.; He, H.; Dyck, M.; Lv, J. Modeling thermal conductivity of clays: A review and evaluation of 28 predictive models. Eng. Geol. 2021, 288, 106107. [Google Scholar] [CrossRef]
- Barnaure, M.; Bonnet, S.; Poullain, P. Earth buildings with local materials: Assessing the variability of properties measured using non-destructive methods. Constr. Build. Mater. 2021, 281, 122613. [Google Scholar] [CrossRef]
- Saad, M.; Sabathier, V.; Turatsinze, A. Natural Fibers vs. Synthetic Fibers Reinforcement: Effect on Resistance of Mortars to Impact Loads. In Construction Technologies and Architecture; Trans Tech Publications Ltd.: Bäch, Switzerland, 2022; p. 102. [Google Scholar] [CrossRef]
- Sáez-Pérez, M.P.; Brümmer, M.; Durán-Suárez, J.A. A review of the factors affecting the properties and performance of hemp aggregate concretes. J. Build. Eng. 2020, 31, 101323. [Google Scholar] [CrossRef]
- Williams, J.; Lawrence, M.; Walker, P. The influence of constituents on the properties of the bio-aggregate composite hemp-lime. Constr. Build. Mater. 2018, 159, 9–17. [Google Scholar] [CrossRef]
- Fehrmann, J.; Belleville, B.; Ozarska, B.; Gutowski, W.S.; Wilson, D. Influence of particle granulometry and panel composition on the physico-mechanical properties of ultra-low-density hemp hurd particleboard. Polym. Compos. 2023, 44, 7363–7383. [Google Scholar] [CrossRef]
- Achour, C.; Remond, S.; Belayachi, N. Swelling and shrinkage of plant aggregates: Experimental and treatment effect. Ind. Crop. Prod. 2023, 203, 117173. [Google Scholar] [CrossRef]
- Ghanem, R.; Soize, C.; Mehrez, L.; Aitharaju, V. Probabilistic learning and updating of a digital twin for composite material systems. Int. J. Numer. Methods Eng. 2022, 123, 3004–3020. [Google Scholar] [CrossRef]
- Duprat, F.; Vu, N.T.; Sellier, A. Accelerated carbonation tests for the probabilistic prediction of the durability of concrete structures. Constr. Build. Mater. 2014, 66, 597–605. [Google Scholar] [CrossRef]
- Biedermann, A.; Taroni, F. Bayesian networks and probabilistic reasoning about scientific evidence when there is a lack of data. Forensic Sci. Int. 2006, 157, 163–167. [Google Scholar] [CrossRef]

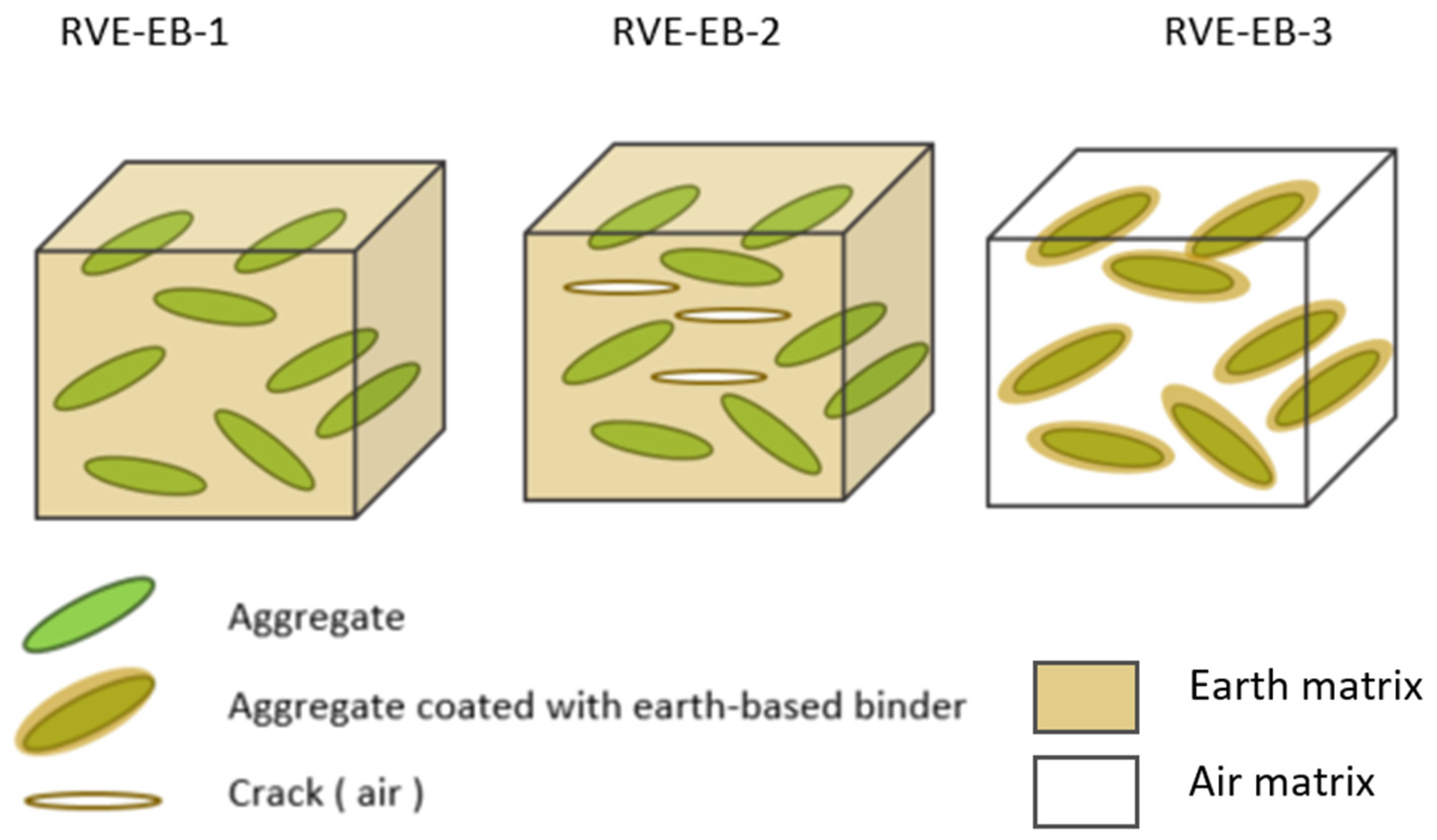





| Earth Composite | Reference | Binder/Aggregate | Density (kg·m−3) | Volume Fraction of the Aggregate | Porosity of the Composite (%) | Thermal Conductivity (W·m−1·K−1) | Measurement Conditions |
|---|---|---|---|---|---|---|---|
| FH3-Laborel | Laborel Préneron et al. 2018 [8] | FWAS/Hemp shiv | 1519 ± 38 | 0.22 | / | 0.30 ± 0.01 | 25 °C, dry state |
| FH6-Laborel | FWAS/Hemp shiv | 1271 ± 16 | 0.37 | / | 0.20 ± 0.01 | ||
| CSP-Belayachi | Brouard et al. 2018 [19] Belayachi et al. 2022 [20] | Clay/Sunflower Pith | 235 | / | 90 | 0.055 | Dry state |
| CSB-Belayachi | Clay/Sunflower Bark | 714 | / | 64 | 0.158 |
| Lightweight Earth | Binder (%) | Aggregate (%) | Water (%) |
|---|---|---|---|
| FH3-Laborel | / | 3 | 17 |
| FH6-Laborel | / | 6 | 20 |
| Binder/Aggregate Weight Ratio | Water/Binder Weight Ratio | Aggregate/Clay Volume Ratio | |
| CSP-Belayachi | 2.4 | 1 | 26 |
| CSB-Belayachi | 2.4 | 1 | 4.7 |
| Reference | Type of Aggregate | Calculation Method in Reference of Rosa Latapie et al., 2023 [27,28,29,30,31] | Modeled Particulate Thermal Conductivity (W·m−1·K−1) | |
|---|---|---|---|---|
| λT | λN | |||
| Laborel-Préneron et al., 2018 [10] | Hemp shiv | From measurement on bulk particles | 0.044 | 0.066 |
| Brouard et al., 2022 [19] | Sunflower pith | λiso = 0.08 | ||
| Sunflower bark | 0.045 | 0.068 | ||
| Earth-Based Binder | Aggregate | ||||||
|---|---|---|---|---|---|---|---|
| Composite | Density (kg·m−3) | Thermal Conductivity (W·m−1·K−1) | Particulate Density (kg·m−3) | Particulate Thermal Conductivity (W·m−1·K−1) | Volume Fraction | Aspect Ratio | |
| λT | λN | ||||||
| FH3-Laborel | 1891 (FWAS) | 0.57 ± 0.03 | 248 | 0.044 | 0.066 | 0.22 | 3.3 |
| FH6-Laborel | 0.37 | ||||||
| CSP-Belayachi | 900 (clay) | 0.27 | 56 | λN = λT = 0.08 or 0.04 | 0.79 | 1 | |
| CSB-Belayachi | 425 | 0.045 | 0.068 | 0.39 | 3.4 | ||
| Earth-Based Materials | ||||
|---|---|---|---|---|
| Composite | FH3-Laborel | FH6-Laborel | CSP-Belayachi | CSB-Belayachi |
| Model type | EB-2-2D | EB-2-2D | EB-3-3D | EB-1-2D |
| Calibrated value | 18% cracking | 24% cracking | 15% coating | / |
| λcomposite [W·m−1·K−1] | 0.3 | 0.2 | 0.055 | 0.158 |
| [W·m−1·K−1] | 0.304 | 0.201 | 0.055 | 0.159 |
| Relative deviation | 3% | 1% | 1% | 1% |
| Earth-Based Materials | |||
|---|---|---|---|
| Composite | FH3-Laborel | FH6-Laborel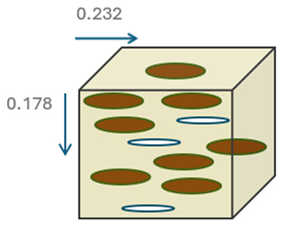 | CSB-Belayachi |
| λmax/λmin | 1.2 | 1.3 | 1.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rosa Latapie, S.; Sabathier, V.; Abou-Chakra, A. Thermal Performance of Lightweight Earth: From Prediction to Optimization through Multiscale Modeling. Constr. Mater. 2024, 4, 543-565. https://doi.org/10.3390/constrmater4030029
Rosa Latapie S, Sabathier V, Abou-Chakra A. Thermal Performance of Lightweight Earth: From Prediction to Optimization through Multiscale Modeling. Construction Materials. 2024; 4(3):543-565. https://doi.org/10.3390/constrmater4030029
Chicago/Turabian StyleRosa Latapie, Séverine, Vincent Sabathier, and Ariane Abou-Chakra. 2024. "Thermal Performance of Lightweight Earth: From Prediction to Optimization through Multiscale Modeling" Construction Materials 4, no. 3: 543-565. https://doi.org/10.3390/constrmater4030029
APA StyleRosa Latapie, S., Sabathier, V., & Abou-Chakra, A. (2024). Thermal Performance of Lightweight Earth: From Prediction to Optimization through Multiscale Modeling. Construction Materials, 4(3), 543-565. https://doi.org/10.3390/constrmater4030029





