Optimizing Lumber Densification for Mitigating Rolling Shear Failure in Cross-Laminated Timber (CLT)
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Methodology for Densification
2.3. Bending Test Procedure
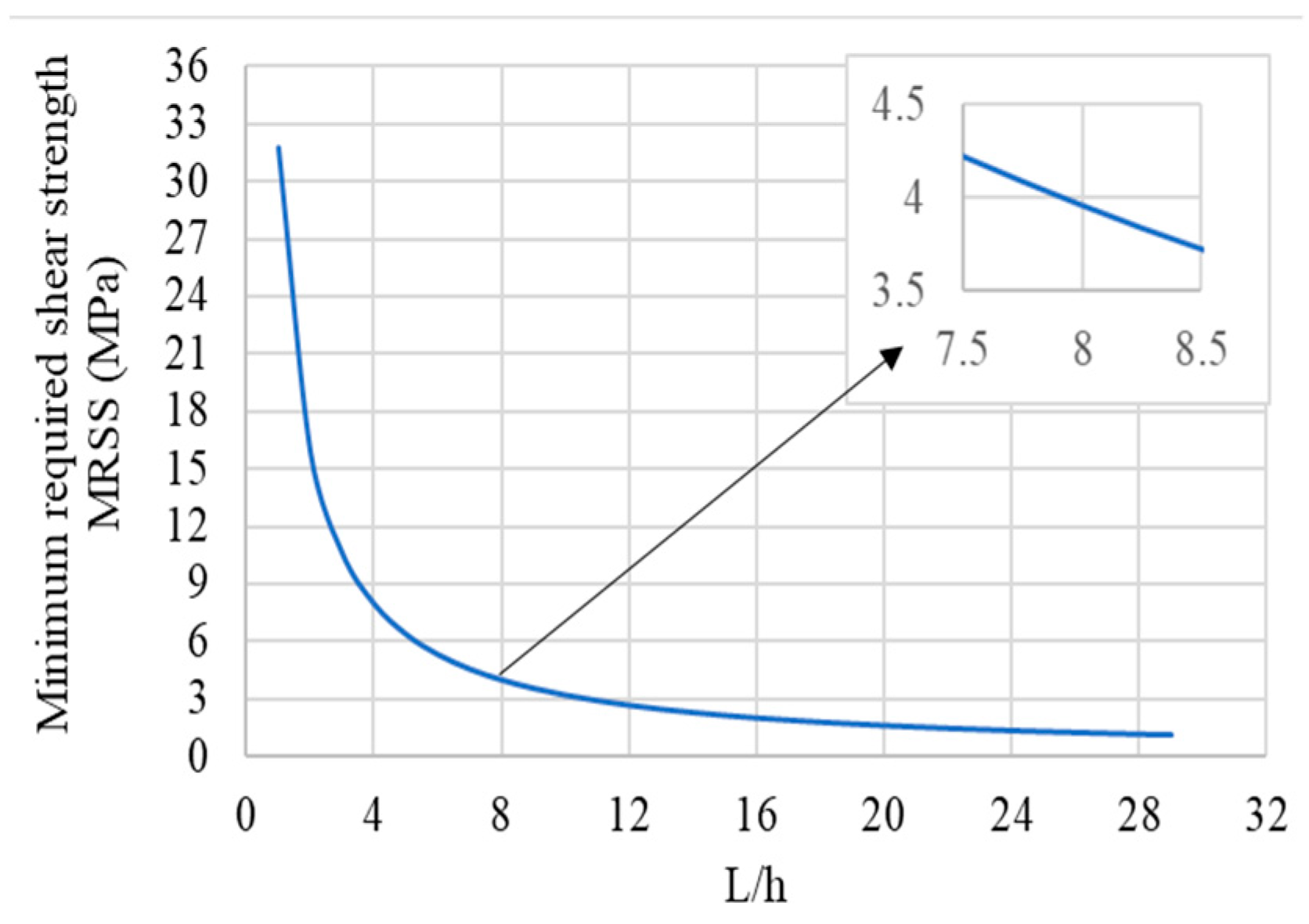
2.4. Required Densification to Meet MRSS
3. Results
3.1. Shear Strength Assessment of Non-Densified Lumber
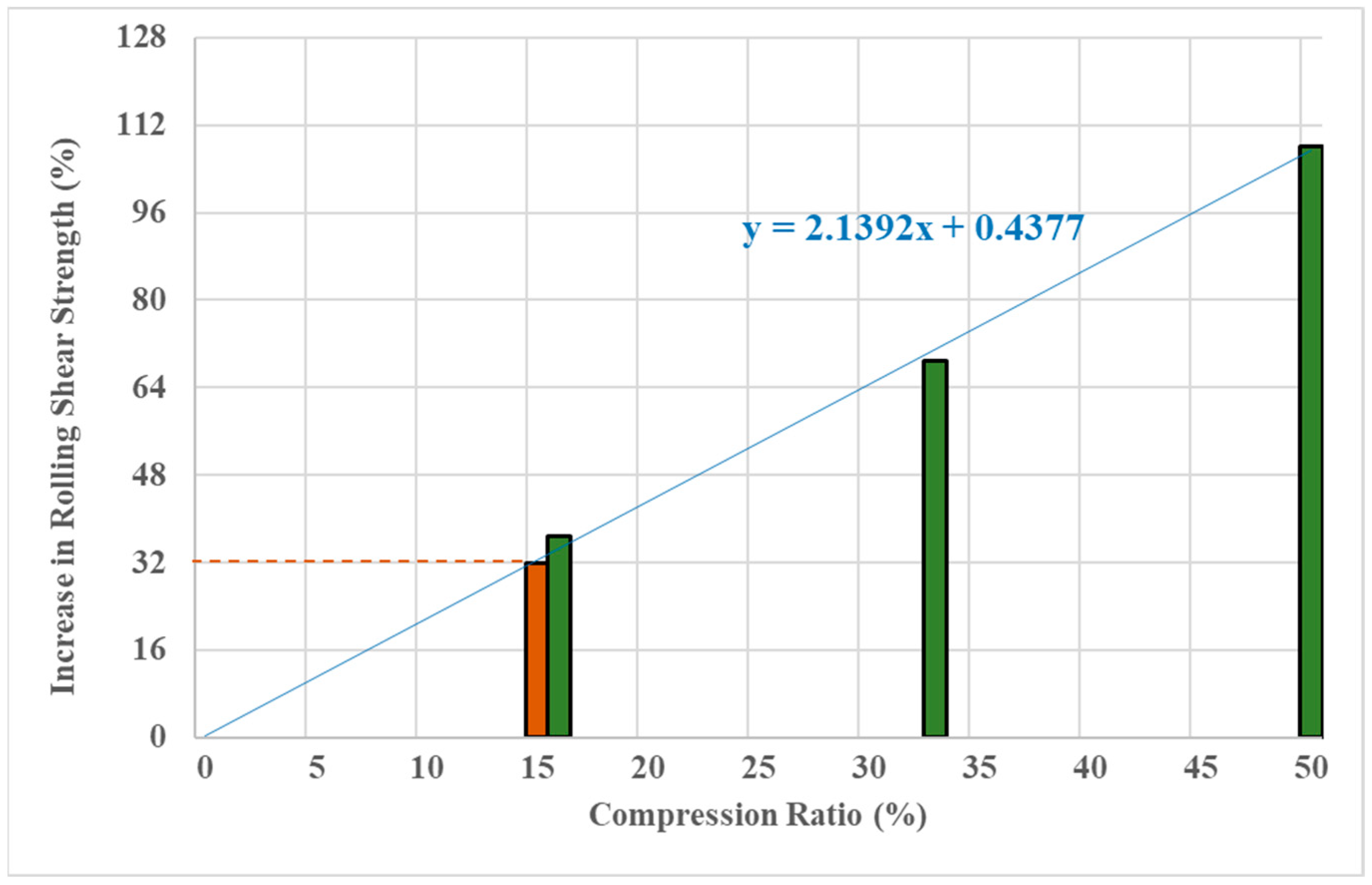
3.2. Effect of Densification on Failure Mode and Rolling Shear Strength
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kawaai, Y.; Takanashi, R.; Ishihara, W.; Ohashi, Y.; Sawata, K.; Sasaki, T. Out-of-plane shear strength of cross-laminated timber made of Japanese Larch (Larix kaempferi) with various layups and spans. J. Wood Sci. 2023, 69, 33. [Google Scholar] [CrossRef]
- Brandner, R.; Flatscher, G.; Ringhofer, A.; Schickhofer, G.; Thiel, A. Cross laminated timber (CLT): Overview and development. Eur. J. Wood Wood Prod. 2016, 74, 331–351. [Google Scholar] [CrossRef]
- Kumar, C.; Li, X.; Subhani, M.; Shanks, J.; Dakin, T.; McGavin, R.L.; Ashraf, M. A Review of Factors Influencing Rolling Shear in CLT and Test Methodology. J. Test Eval. 2022, 50, 1634–1656. [Google Scholar] [CrossRef]
- Forest Products Laboratory (US). Wood Handbook: Wood as an Engineering Material; General Technical Report FPL-GTR-282; Department of Agriculture, Forest Service, Forest Products Laboratory: Madison, WI, USA, 2021.
- Ehrhart, T.; Brandner, R. Rolling shear: Test configurations and properties of some European soft- and hardwood species. Eng. Struct. 2018, 172, 554–572. [Google Scholar] [CrossRef]
- Aicher, S.; Christian, Z.; Hirsch, M. Rolling shear modulus and strength of beech wood laminations. Holzforschung 2016, 70, 773–781. [Google Scholar] [CrossRef]
- Li, M.; Dong, W.; Lim, H. Influence of Lamination Aspect Ratios and Test Methods on Rolling Shear Strength Evaluation of Cross-Laminated Timber. J. Mater. Civ. Eng. 2019, 31, 04019310. [Google Scholar] [CrossRef]
- Gui, T.; Cai, S.; Wang, Z.; Zhou, J. Influence of aspect ratio on rolling shear properties of fast-grown small diameter eucalyptus lumber. J. Renew. Mater. 2020, 8, 1053–1066. [Google Scholar] [CrossRef]
- Nero, R.; Christopher, P.; Ngo, T. Investigation of rolling shear properties of cross-laminated timber (CLT) and comparison of experimental approaches. Constr. Build. Mater. 2022, 316, 125897. [Google Scholar] [CrossRef]
- Pradhan, S.; Entsminger, D.E.; Mohammadabadi, M.; Ragon, K.; Nkeuwa, W.N. The effects of densification on rolling shear performance of southern yellow pine cross-laminated timber. Constr. Build. Mater. 2023, 392, 132024. [Google Scholar] [CrossRef]
- Zhou, Y.; Shen, Z.; Li, H.; Lu, Y.; Wang, Z. Study on in-plane shear failure mode of cross-laminated timber panel. J. Wood Sci. 2022, 68, 36. [Google Scholar] [CrossRef]
- Dong, W.; Wang, Z.; Zhou, J.; Gong, M. Experimental study on bending properties of cross-laminated timber-bamboo composites. Constr. Build. Mater. 2021, 300, 124313. [Google Scholar] [CrossRef]
- Kumar, C.; Faircloth, A.; Shanks, J.; McGavin, R.L.; Li, X.; Ashraf, M.; Subhani, M. Investigating Factors Influencing Rolling Shear Performance of Australian CLT Feedstock. Forests 2023, 14, 711. [Google Scholar] [CrossRef]
- Bendtsen, B.A. Rolling shear characteristics of nine structural softwoods. For. Prod. J. 1976, 26, 51–56. [Google Scholar]
- Li, M. Evaluating rolling shear strength properties of cross-laminated timber by short-span bending tests and modified planar shear tests. J. Wood Sci. 2017, 63, 331–337. [Google Scholar] [CrossRef]
- Fellmoser, P.; Blaß, H.J. Influence of rolling shear modulus on strength and stiffness of structural bonded timber elements. In Proceedings of the CIB-W18 Meeting, Edinburgh, UK, 31 August–3 September 2004. [Google Scholar]
- Dumail, J.-F.; Olofsson, K.; Salmén, L. An Analysis of Rolling Shear of Spruce Wood by the Iosipescu Method. Holzforschung 2000, 54, 420–426. [Google Scholar] [CrossRef]
- Aicher, S.; Dill-Langer, G. Basic considerations to rolling shear modulus in wooden boards. Otto-Graf-J. 2000, 11, 157. [Google Scholar]
- Sretenovic, A.; Müller, U.; Gindl, W. Comparison of the in-plane shear strength of OSB and plywood using five point bending and EN 789 steel plate test methods. Eur. J. Wood Wood Prod. 2005, 63, 160–164. [Google Scholar] [CrossRef]
- Xu, B.-H.; Zhang, S.-D.; Zhao, Y.-H.; Bouchaïr, A. Rolling Shear Properties of Hybrid Cross-Laminated Timber. J. Mater. Civ. Eng. 2021, 33, 04021159. [Google Scholar] [CrossRef]
- Li, Q.; Wang, Z.; Liang, Z.; Li, L.; Gong, M.; Zhou, J. Shear properties of hybrid CLT fabricated with lumber and OSB. Constr. Build. Mater. 2020, 261, 120504. [Google Scholar] [CrossRef]
- Li, H.; Wang, B.J.; Wang, L.; Wei, Y. An experimental and modeling study on apparent bending moduli of cross-laminated bamboo and timber (CLBT) in orthogonal strength directions. Case Stud. Constr. Mater. 2022, 16, e00874. [Google Scholar] [CrossRef]
- Wang, Z.; Fu, H.; Gong, M.; Luo, J.; Dong, W.; Wang, T.; Chui, Y.H. Planar shear and bending properties of hybrid CLT fabricated with lumber and LVL. Constr. Build. Mater. 2017, 151, 172–177. [Google Scholar] [CrossRef]
- Wang, Z.; Gong, M.; Chui, Y.-H. Mechanical properties of laminated strand lumber and hybrid cross-laminated timber. Constr. Build. Mater. 2015, 101, 622–627. [Google Scholar] [CrossRef]
- Bahmanzad, A.; Clouston, P.L.; Arwade, S.R.; Schreyer, A.C. Shear Properties of Eastern Hemlock with Respect to Fiber Orientation for Use in Cross Laminated Timber. J. Mater. Civ. Eng. 2020, 32, 04020165. [Google Scholar] [CrossRef]
- Buck, D.; Wang, X.A.; Hagman, O.; Gustafsson, A. Bending properties of Cross Laminated Timber (CLT) with a 45° alternating layer configuration. Bioresources 2016, 11, 4633–4644. [Google Scholar] [CrossRef]
- Chui, Y.H. Simultaneous evaluation of bending and shear moduli of wood and the influence of knots on these parameters. Wood Sci. Technol. 1991, 25, 125–134. [Google Scholar] [CrossRef]
- Cao, Y.; Street, J.; Mitchell, B.; To, F.; DuBien, J.; Seale, R.D.; Shmulsky, R. Effect of knots on horizontal shear strength in southern yellow pine. BioResources 2018, 13, 4509–4520. [Google Scholar] [CrossRef]
- Tabarsa, T.; Chui, Y.H. Effects of hot-pressing on properties of white spruce. For. Prod. J. 1997, 47, 71. [Google Scholar]
- Navi, P.; Girardet, F. Effects of thermo-hydro-mechanical treatment on the structure and properties of wood. Holzforschung 2000, 54, 287–293. [Google Scholar] [CrossRef]
- Rassam, G.; Ghofrani, M.; Taghiyari, H.R.; Jamnani, B.; Khajeh, M.A. Mechanical performance and dimensional stability of nano-silver impregnated densified spruce wood. Eur. J. Wood Wood Prod. 2012, 70, 595–600. [Google Scholar] [CrossRef]
- Kuai, B.; Wang, Z.; Gao, J.; Tong, J.; Zhan, T.; Zhang, Y.; Lu, J.; Cai, L. Development of densified wood with high strength and excellent dimensional stability by impregnating delignified poplar by sodium silicate. Constr. Build. Mater. 2022, 344, 128282. [Google Scholar] [CrossRef]
- Pelit, H.; Yorulmaz, R. Influence of densification on mechanical properties of thermally pretreated spruce and poplar wood. Bioresources 2019, 14, 9739–9754. [Google Scholar] [CrossRef]
- Ulker, O.; Imirzi, O.; Burdurlu, E. The Effect of Densification Temperature on Some Physical and Mechanical Properties of Scots Pine (Pinus sylvestris L.). Bioresources 2012, 7, 5581–5592. [Google Scholar] [CrossRef]
- Yu, H.; Hse, C.Y.; Jiang, Z. Effect of PF impregnation and surface densification on the mechanical properties of small-scale wood laminated poles. In Proceedings of the Conference on Advanced Biomass Science and Technology for Bio-Based Products, Beijing, China, 23–25 May 2007; Hse, C.-Y., Jiang, Z., Kuo, M.-L., Eds.; Chinese Academy of Forestry, People’s Republic of China: Beijing, China, 2009; pp. 357–363. [Google Scholar]
- Pradhan, S.; Entsminger, E.D.; Mohammadabadi, M.; Ragon, K. Influence of densification on structural performance and failure mode of CLT under bending load. Bioresources 2024, 19, 2342–2352. [Google Scholar] [CrossRef]



| S. No | Sample ID | Pmax (N) | P/Δ (N/mm) | Apparent Modulus of Elasticity, Eapp (MPa) | Rolling Shear Strength, τmax (MPa) |
|---|---|---|---|---|---|
| 1 | ND1 | 50,483 | 6896.85 | 8488.62 | 2.68 |
| 2 | ND2 | 62,048.6 | 7674.77 | 9435.65 | 3.22 |
| 3 | ND3 | 58,211.7 | 9300.82 | 11,587.4 | 3.06 |
| 4 | ND4 | 61,821.4 | 7420.48 | 9000.71 | 3.2 |
| 5 | ND5 | 67,046.5 | 7699.46 | 9506.11 | 3.48 |
| 6 | ND6 | 44,366.8 | 6951.67 | 8772.12 | 2.41 |
| Average | 57,329.7 | 7657.34 | 9465.1 | 3 | |
| COV | 13% | 10% | 11% | 12% | |
| S. No | Sample ID | P/Δ (N/mm) | Pmax (N) | Modulus of Rupture (MPa) | Apparent Modulus of Elasticity, (MPa) | Maximum Shear Stress, (MPa) | Failure Mode |
|---|---|---|---|---|---|---|---|
| 1 | D1 | 8738.31 | 83,548.35 | 45.08 | 10,205.05 | 4.24 | Tensile |
| 2 | D2 | 8276.33 | 78,239.92 | 42.21 | 9583.99 | 3.97 | Tensile |
| 3 | D3 | 8456.71 | 90,446.67 | 49.95 | 10,102.93 | 4.68 | Tensile |
| 4 | D4 | 9403.62 | 96,728.70 | 52.08 | 10,915.23 | 4.90 | Tensile |
| 5 | D5 | 9476.47 | 87,517.13 | 47.30 | 11,072.67 | 4.44 | Horizontal Shear |
| 6 | D6 | 9367.37 | 88,425.19 | 48.09 | 11,068.69 | 4.50 | Tensile |
| Average | 8953.13 | 87,484.33 | 47.45 | 10,491.43 | 4.45 | ||
| COV | 5% | 7% | 7% | 5% | 7% | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pradhan, S.; Mohammadabadi, M.; Seale, R.D.; Thati, M.; Entsminger, E.D.; Nkeuwa, W.N. Optimizing Lumber Densification for Mitigating Rolling Shear Failure in Cross-Laminated Timber (CLT). Constr. Mater. 2024, 4, 342-352. https://doi.org/10.3390/constrmater4020019
Pradhan S, Mohammadabadi M, Seale RD, Thati M, Entsminger ED, Nkeuwa WN. Optimizing Lumber Densification for Mitigating Rolling Shear Failure in Cross-Laminated Timber (CLT). Construction Materials. 2024; 4(2):342-352. https://doi.org/10.3390/constrmater4020019
Chicago/Turabian StylePradhan, Suman, Mostafa Mohammadabadi, Roy Daniel Seale, Manikanta Thati, Edward D. Entsminger, and William Nguegang Nkeuwa. 2024. "Optimizing Lumber Densification for Mitigating Rolling Shear Failure in Cross-Laminated Timber (CLT)" Construction Materials 4, no. 2: 342-352. https://doi.org/10.3390/constrmater4020019
APA StylePradhan, S., Mohammadabadi, M., Seale, R. D., Thati, M., Entsminger, E. D., & Nkeuwa, W. N. (2024). Optimizing Lumber Densification for Mitigating Rolling Shear Failure in Cross-Laminated Timber (CLT). Construction Materials, 4(2), 342-352. https://doi.org/10.3390/constrmater4020019





