Monotonic and Cyclic Seismic Analyses of Old-Type RC Columns with Short Lap Splices
Abstract
1. Introduction
- A closed form solution of bond equations governing the behavior of lap-spliced bars of an RC column was developed considering nonlinearity in the bond–slip law.
- The latter was embedded in a Windows-based software program for fiber-based, distributed nonlinearity analysis of prismatic frame elements undergoing lateral sway such as would occur during an earthquake.
- Moment, shear, and axial load interaction were considered in calculating the resistance curve for RC columns that underwent flexure shear or purely shear-dominated modes of failure, and the distinct contributions of the many contributing sources of column deformation (curvature, shear angle, axial elongation, lap splice slip) were illustrated through the developed algorithm.
- The proposed analytical model can also solve the column state of stress under full cyclic load reversals for flexure-dominated response conditions of RC columns with deficient lap splices at the base of the column.
2. Materials and Methods
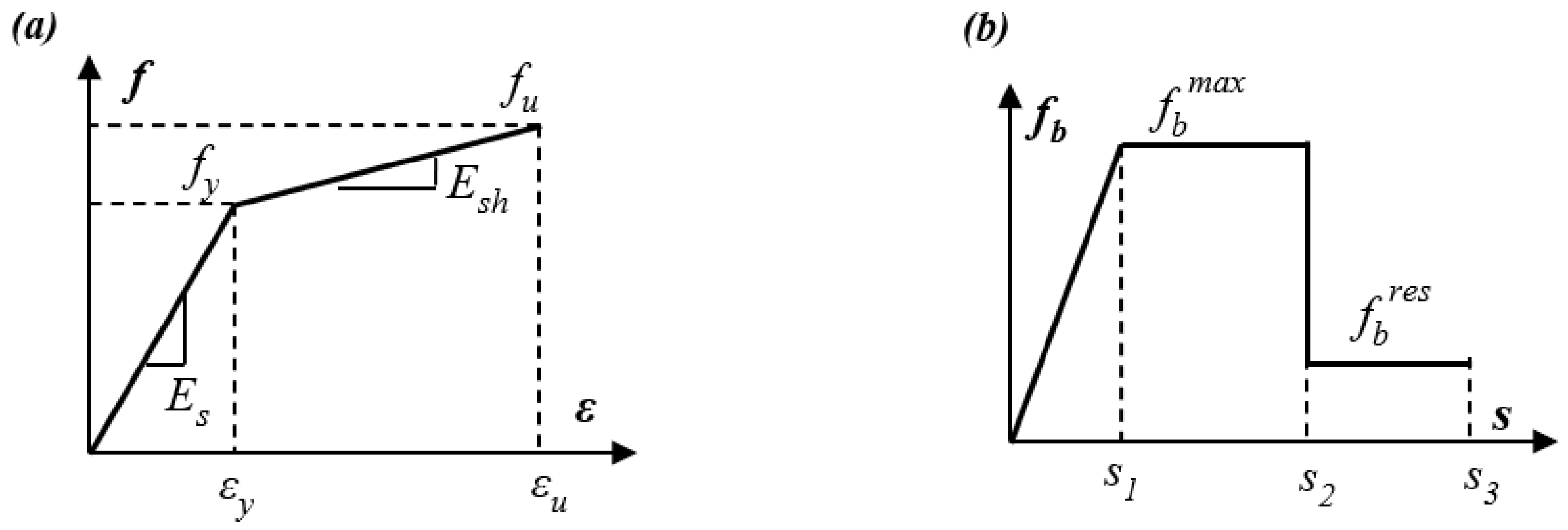
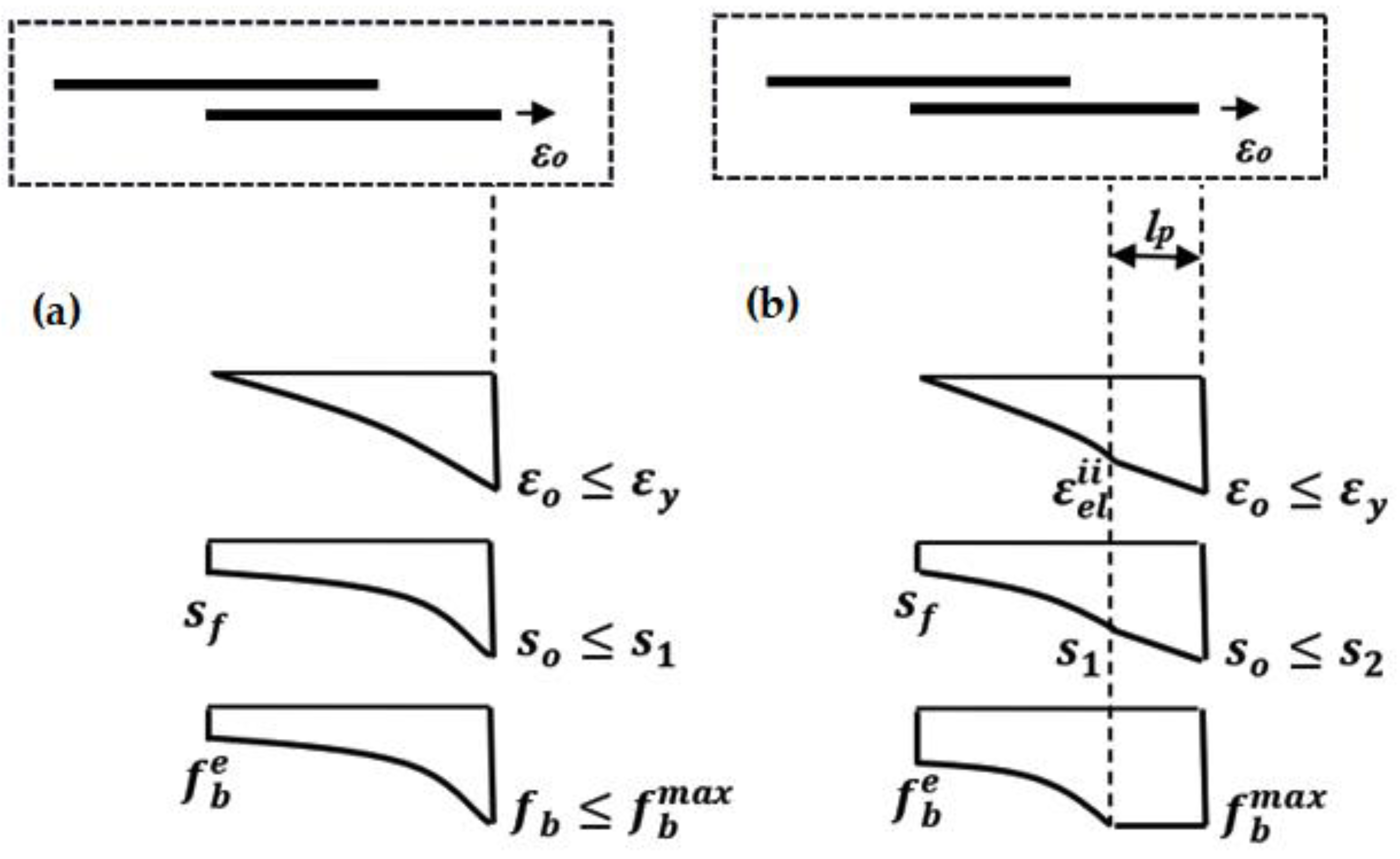
2.1. Bond–Slip Distribution along the Lap Splice of a Linear Elastic Bar
- 1.
- The distributions of bar strain, slip, and bond stress across the length (for ) are determined under the assumption that fb(s) = fbmax remains constant. Consequently, the bar stress and strain change linearly with distance over the segment lp where bond plastification occurs:
- 2.
- For the distributions of bar strain, slip and bond stress over the remaining lap splice length (which is still in the elastic range), (for ), these are obtained from the elastic solution Equations (9)–(11):
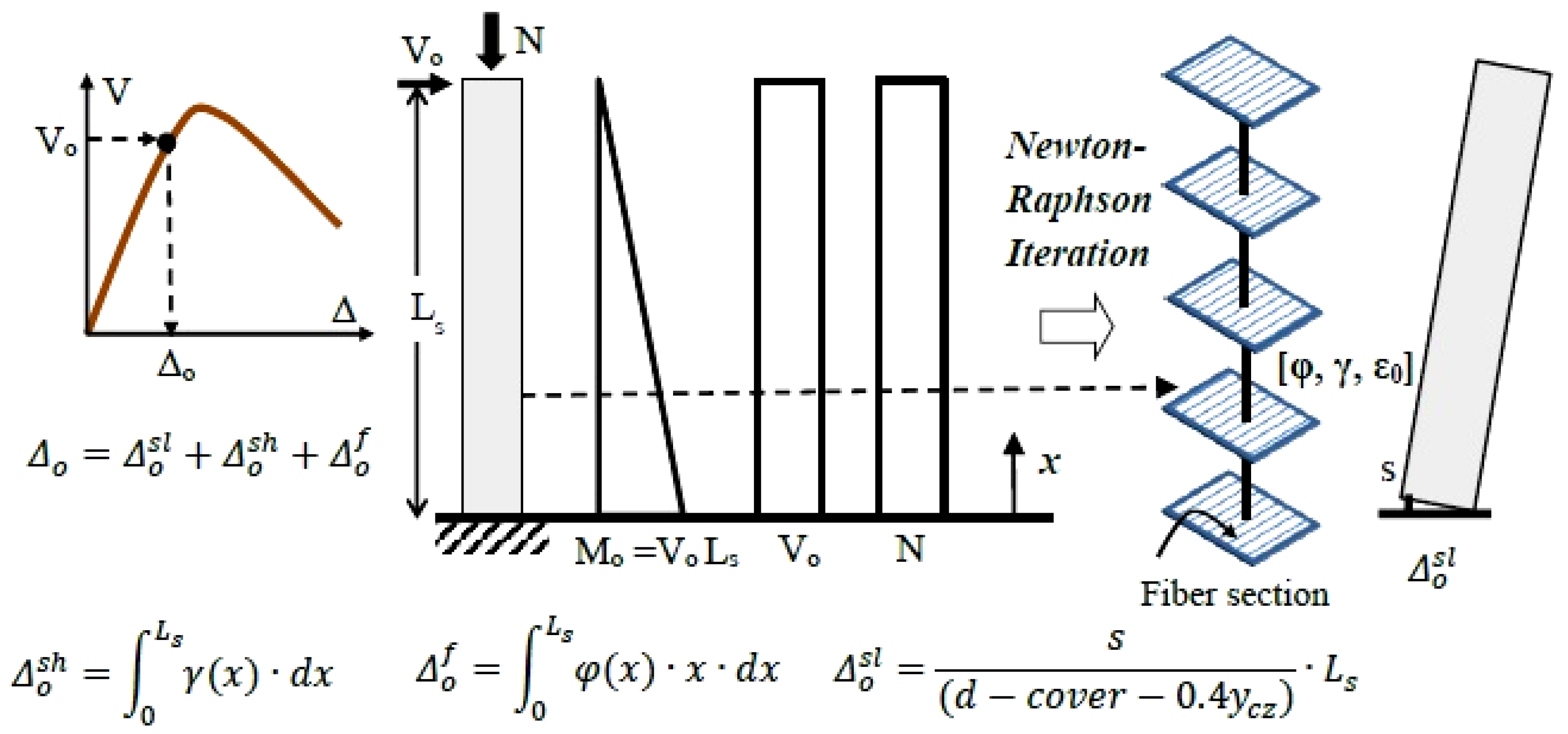
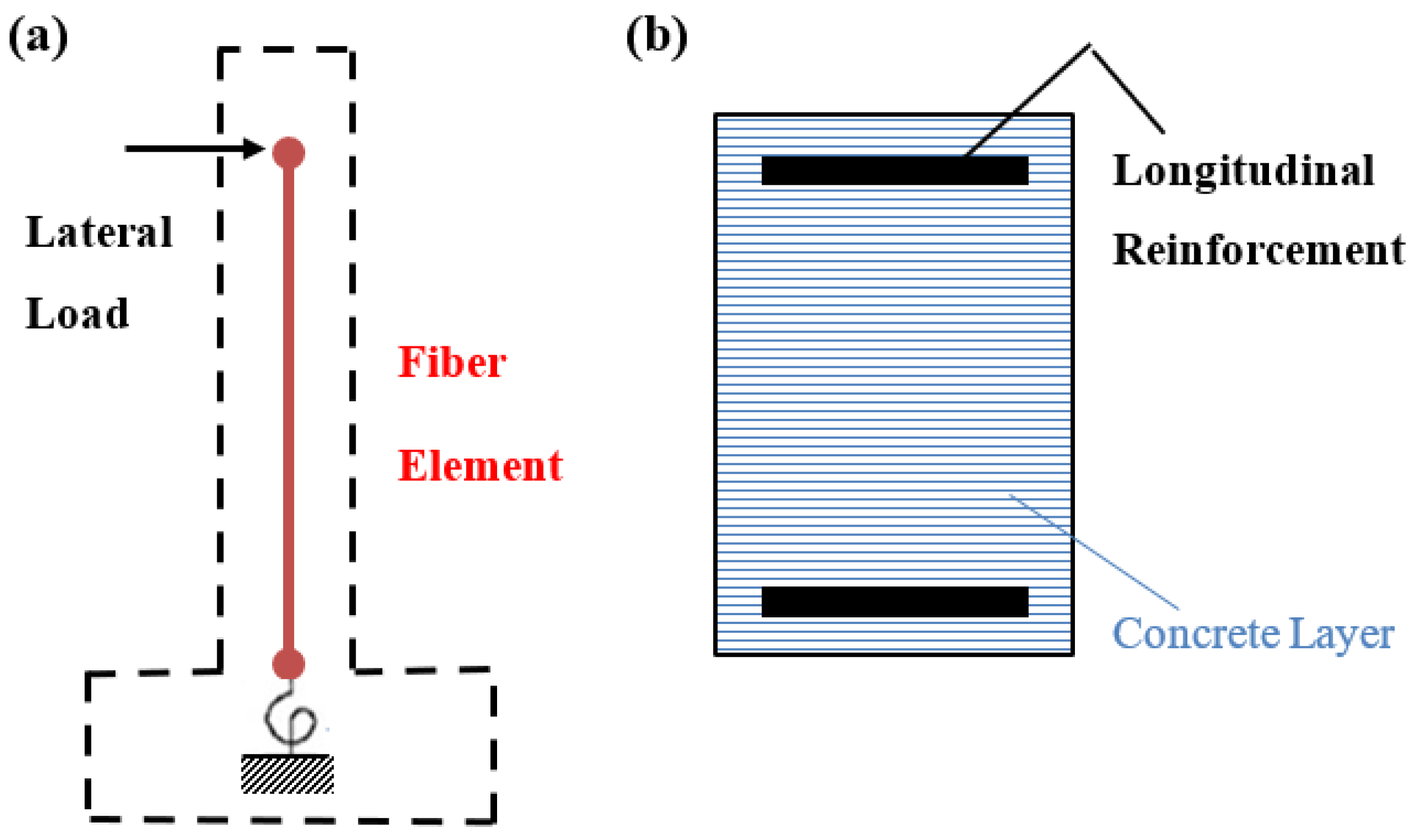
2.2. Analytical Model for Monotonic and Cyclic Seismic Analyses
2.2.1. Pushover Seismic Analysis
2.2.2. Cyclic Seismic Analysis
3. Results
4. Discussion
5. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Melek, M.; Wallace, J.W. Cyclic behavior of columns with short lap splices. Struct. J. 2004, 101, 802–811. [Google Scholar]
- Cho, J.Y.; Pincheira, J.A. Inelastic analysis of reinforced concrete columns with short lap splices subjected to reversed cyclic loads. ACI Mater. J. 2006, 103, 280. [Google Scholar]
- Chail, Y.H.; Priestley, M.N.; Seible, F. Seismic retrofit of circular bridge columns for enhanced flexural performance. Struct. J. 1991, 88, 572–584. [Google Scholar]
- Sun, Z.; Priestley, M.J.N.; Seible, F. Diagnostics and Retrofit of Rectangular Bridge Columns for Seismic Loads; Department of Applied Mechanics and Engineering Sciences, University of California: San Diego, CA, USA, 1993. [Google Scholar]
- Reyes, O.; Pincheira, J.A. R/C columns with lap splices subjected to earthquake. In ASCE Structures Congress; ASCE: Reston, VA, USA, 1999; pp. 369–372. [Google Scholar]
- Tariverdilo, S.; Farjadi, A.; Barkhordary, M. Fragility curves for reinforced concrete frames with lap-spliced columns. Int. J. Eng. Trans. A Basics 2009, 22, 213. [Google Scholar]
- Zhang, Y.; Tien, I. Methodology for regularization of force-based elements to model reinforced concrete columns with short lap splices. ASCE J. Eng. Mech. 2020, 146, 04020073. [Google Scholar] [CrossRef]
- Tastani, S.P.; Brokalaki, E.; Pantazopoulou, S.J. State of Bond along Lap-Splices. ASCE J. Struct. Eng. 2015, 141, 04015007. [Google Scholar] [CrossRef]
- Megalooikonomou, K.G. Modeling the Behavior of Shear-Critical Reinforced Concrete Columns under Lateral Loads. Ph.D. Thesis, Department of Civil and Environmental Engineering, Faculty of Engineering, University of Cyprus, Nicosia, Cyprus, December 2019. [Google Scholar] [CrossRef]
- Megalooikonomou, K.G. Seismic Assessment and Retrofit of Reinforced Concrete Columns, 1st ed.; Cambridge Scholars Publishing: Newcastle upon Tyne, UK, 2019; p. 387. [Google Scholar]
- Megalooikonomou, K.G. PHAETHON: Software for Analysis of Shear-Critical Reinforced Concrete Columns. Mod. Appl. Sci. 2018, 12, 1–22. [Google Scholar] [CrossRef][Green Version]
- Megalooikonomou, K.G.; Tastani, S.P.; Pantazopoulou, S.J. Effect of Yield Penetration on Column Plastic Hinge Length. Eng. Struct. 2018, 156, 161–174. [Google Scholar] [CrossRef]
- Tassios, T.P.; Yannopoulos, P.J. Analytical studies on reinforced concrete members under cyclic loading based on bond-slip relationships. ACI Mater. J. 1981, 78, 206–216. [Google Scholar]
- Filippou, F.; Popov, E.; Bertero, V. Modeling of R/C joints under cyclic excitations. ASCE J. Struct. Eng. 1983, 109, 2666–2684. [Google Scholar] [CrossRef]
- Vecchio, F.J.; Collins, M.P. The modified compression field theory for reinforced concrete elements subjected to shear. ACI J. Proc. 1986, 83, 219–231. [Google Scholar]
- Vecchio, F.J.; Collins, M.P. Predicting the Response of Reinforced Concrete Beams Subjected to Shear Using Modified Compression Field Theory. ACI Struct. J. 1988, 85, 258–268. [Google Scholar]
- Bentz, E.C. Sectional Analysis of Reinforced Concrete Members. Ph.D Thesis, Department of Civil Engineering, University of Toronto, Toronto, ON, Canada, 2000. [Google Scholar]
- Elwood, K.J.; Moehle, J.P. Axial Capacity Model for Shear-Damaged Columns. ACI Struct. J. 2005, 102, 578–587. [Google Scholar]
- Filippou, F.C.; Fenves, G.L. Methods of analysis for earthquake-resistant structures. In Earthquake Engineering: From Engineering Seismology to Performance-Based Engineering; Bozorgnia, Y., Bertero, V.V., Eds.; CRC Press: Boca Raton, FL, USA, 2004. [Google Scholar]
- Filippou, F.C.; Constantinides, M. FEDEAS Lab—Getting Started Guide and Simulation Examples, NEESgrid Report 2004-22 and SEMM Report 2004-05. 2004. Available online: https://fedeas.net/ (accessed on 10 February 2024).
- Mathworks. MATLAB: User’s Guide (R2018b); Mathworks: Portola Valley, CA, USA, 2018. [Google Scholar]
- Spacone, E.; Filippou, F.C.; Taucer, F.F. Fibre beam–column model for non-linear analysis of R/C frames: Part, I. Formulation. Earthq. Eng. Struct. Dyn. 1996, 25, 711–725. [Google Scholar] [CrossRef]
- Mander, J.B.; Priestley, M.J.N.; Park, R. Theoretical stress-strain model for confined concrete. J. Struct. Eng. ASCE 1988, 114, 1804–1826. [Google Scholar] [CrossRef]
- Menengotto, M.; Pinto, E. Method of Analysis for Cyclically Loaded Reinforced Concrete Plane Frames Including Changes in Geometry and Non-elastic Behavior of Elements under Combined Normal Force and Bending. In Proceedings of the IABSE Symposium on Resistance and Ultimate Deformability of Structures Acted on by Well-Defined Repeated Loads, Final Report, Lisbon, Portugal; 1973; pp. 15–22. [Google Scholar]
- Karsan, I.D.; Jirsa, J.O. Behavior of concrete under compressive loadings. J. Struct. Div. 1969, 95, 2543–2564. [Google Scholar] [CrossRef]
- Popovics, S. A numerical approach to the complete stress-strain curves for concrete. Cem. Concr. Res. 1973, 3, 583–599. [Google Scholar] [CrossRef]
- Richart, F.E.; Brandtzaeg, A.; Brown, R.L. A study of the failure of concrete under combined compressive stresses. In Engineering Experiment Station Bulletin No. 185; University of Illinois: Urbana, IL, USA, 1928. [Google Scholar]
- Lynn, A.C.; Moehle, J.P.; Mahin, S.A.; Holmes, W.T. Seismic Evaluation of Existing Reinforced Concrete Columns. Earthq. Spectra 1996, 12, 715–739. [Google Scholar] [CrossRef]
- Megalooikonomou, K.G.; Beligiannis, G.N. Random Forests Machine Learning Applied to PEER Structural Performance Experimental Columns Database. Appl. Sci. 2023, 13, 12821. [Google Scholar] [CrossRef]
- Elwood, K.J.; Moehle, J.P. Drift Capacity of Reinforced Concrete Columns with Light Transverse Reinforcement. Earthq. Spectra 2005, 21, 71–89. [Google Scholar] [CrossRef]
- Panagiotakos, T.B.; Fardis, M.N. Deformations of reinforced concrete members at yielding and ultimate. ACI Struct. J. 2001, 98, 135–148. [Google Scholar]
- Priestley, M.J.N.; Seible, F.; Calvi, M. Seismic Design and Retrofit of Bridges; J. Wiley & Sons Inc.: New York, NY, USA, 1996. [Google Scholar]
- Pujol, S.; Ramirez, J.A.; Sozen, M.A. Drift Capacity of Reinforced Concrete Columns Subjected to Cyclic Shear Reversals; Seismic Response of Concrete Bridges, SP-187; American Concrete Institute: Farmington Hills, MI, USA, 1999; pp. 255–274. [Google Scholar]
- Sezen, H.; Moehle, J.P. Seismic Tests of Concrete Columns with Light Transverse Reinforcement. ACI Struct. J. 2006, 103, 842–849. [Google Scholar]
- Kim, C.; Park, H.; Eom, T. Effects of type of bar lap splice on reinforced concrete columns subjected to cyclic loading. ACI Struct. J. 2019, 116, 183–194. [Google Scholar] [CrossRef]
- Lee, C.S.; Han, S.W. Cyclic behaviour of lightly-reinforced concrete columns with short lap splices subjected to unidirectional and bidirectional loadings. Eng. Struct. 2019, 189, 373–384. [Google Scholar] [CrossRef]
- Seifi, A.; Hosseini, A.; Marefat, M.S.; Khanmohammadi, M. Seismic retrofitting of old-type RC columns with different lap splices by NSM GFRP and steel bars. Struct. Des. Tall Spec. Build. 2018, 27, e1413. [Google Scholar] [CrossRef]
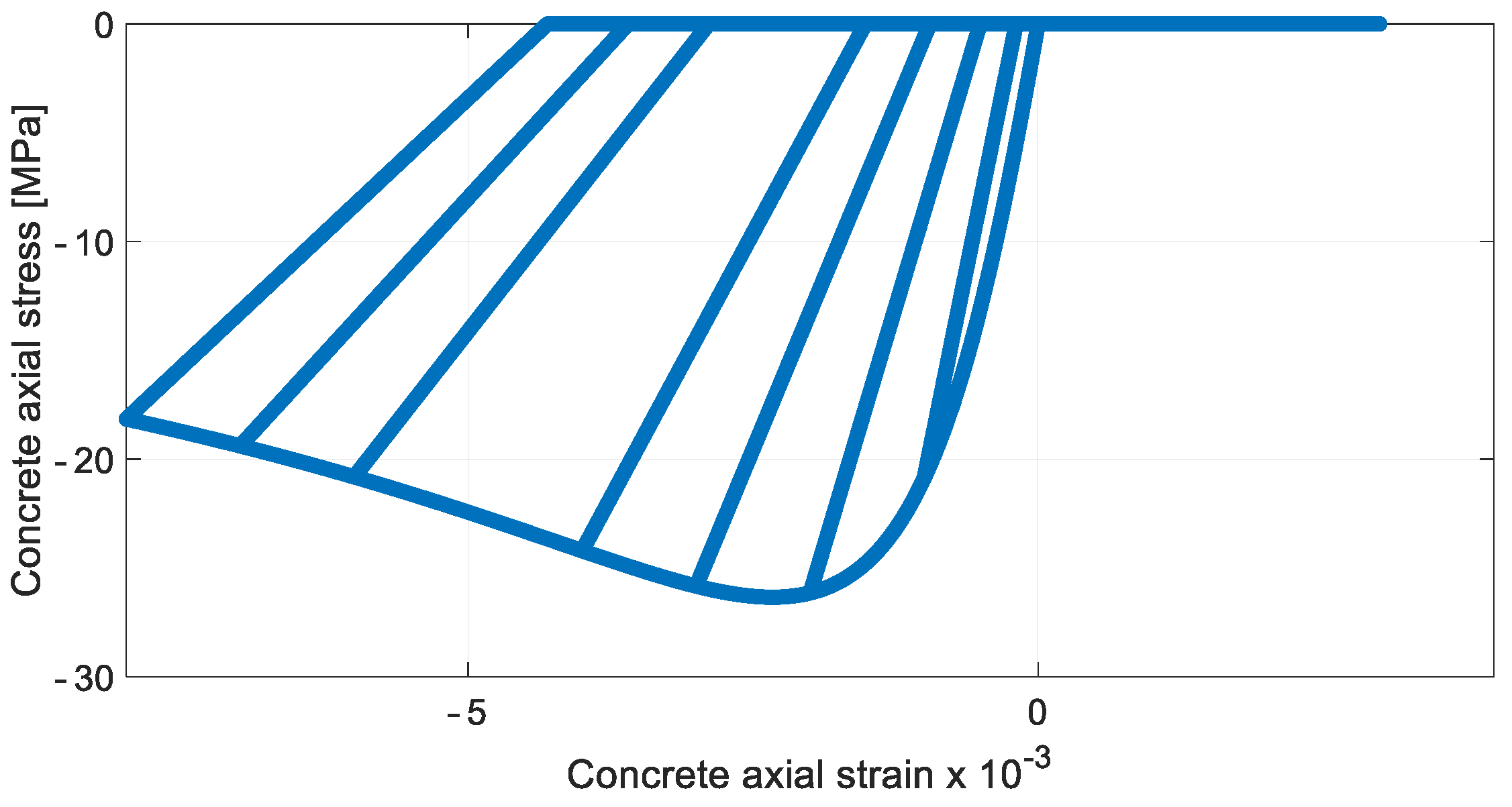


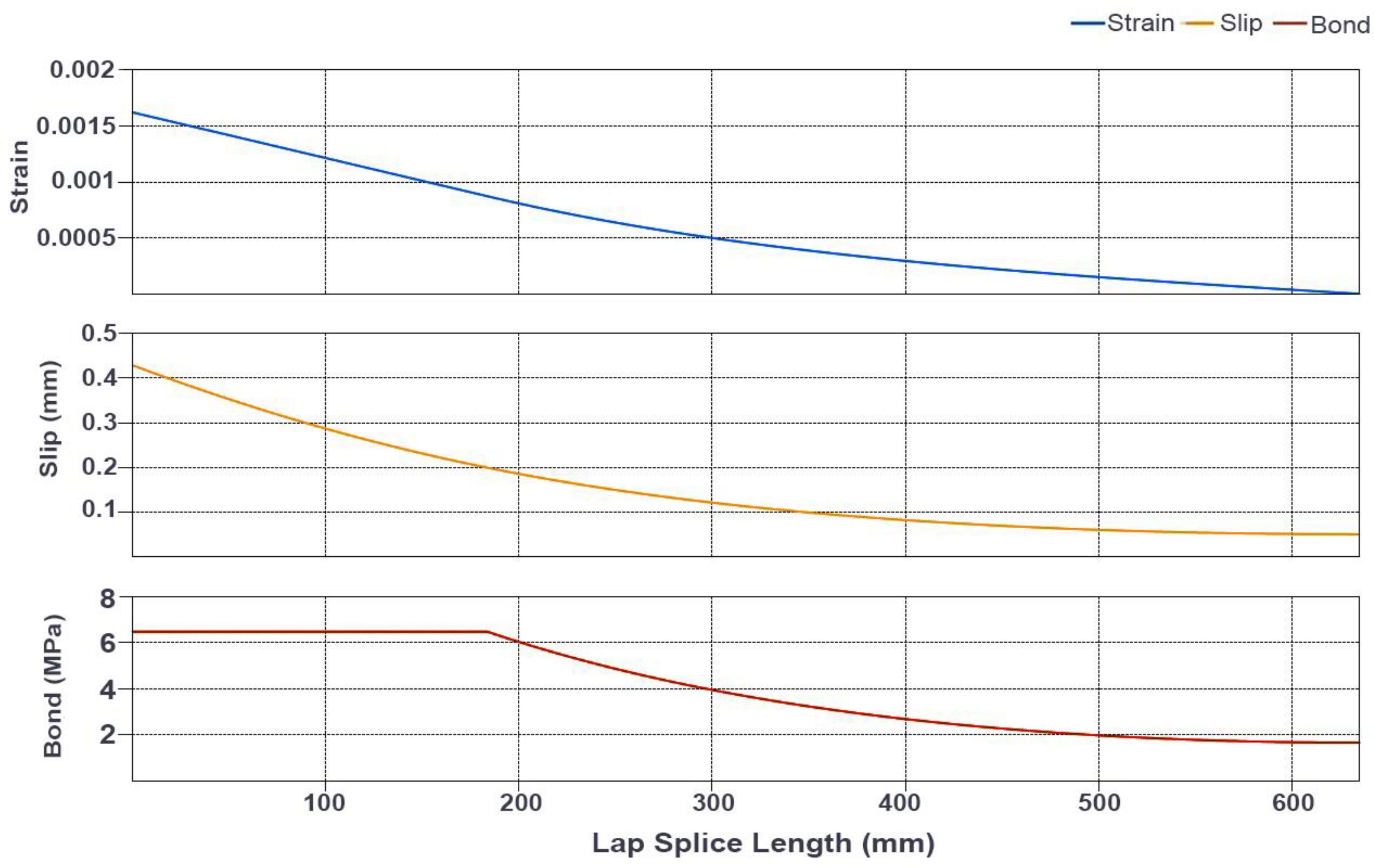

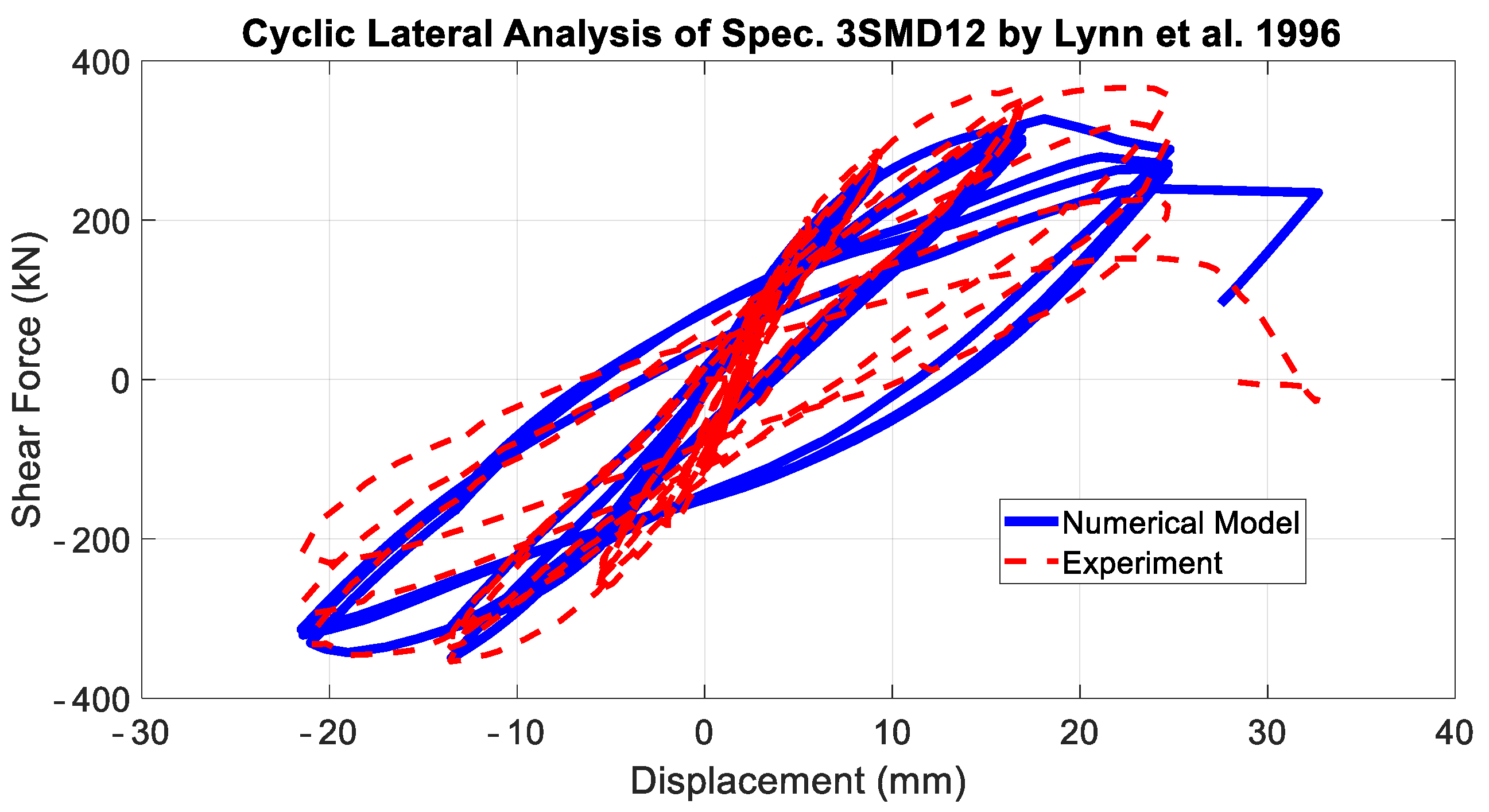
| Case | Axial Load (kN) | Width (mm)–Depth (mm) | Shear Span (mm)– Lap Splice Length (mm) | Clear Cover (mm) | Concrete Strength (MPa) | Number–Diameter (mm)–Reinforcing Ratio of Longitudinal Bars | Yielding–Ultimate Strength of Long. Bars (MPa) | Yielding Strength (MPa)–Spacing (mm)–Diameter (mm)–Ratio of Transv. Reinf. |
|---|---|---|---|---|---|---|---|---|
| Lynn et al. (1996) [28]–(Spec. 3SLH18) | 503 | 457.2 457.2 | 1473.2 635 | 38.1 | 26.9 | 8 31.75 0.0303 | 330.96 496 | 399.91 457.2 9.525 0.00082 |
| Lynn et al. (1996) [28]–(Spec. 3SMD12) | 1512 | 457.2 457.2 | 1473.2 635 | 38.1 | 25.5 | 8 31.75 0.0303 | 330.96 496 | 399.91 304.8 9.525 0.0021 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Megalooikonomou, K.G. Monotonic and Cyclic Seismic Analyses of Old-Type RC Columns with Short Lap Splices. Constr. Mater. 2024, 4, 329-341. https://doi.org/10.3390/constrmater4020018
Megalooikonomou KG. Monotonic and Cyclic Seismic Analyses of Old-Type RC Columns with Short Lap Splices. Construction Materials. 2024; 4(2):329-341. https://doi.org/10.3390/constrmater4020018
Chicago/Turabian StyleMegalooikonomou, Konstantinos G. 2024. "Monotonic and Cyclic Seismic Analyses of Old-Type RC Columns with Short Lap Splices" Construction Materials 4, no. 2: 329-341. https://doi.org/10.3390/constrmater4020018
APA StyleMegalooikonomou, K. G. (2024). Monotonic and Cyclic Seismic Analyses of Old-Type RC Columns with Short Lap Splices. Construction Materials, 4(2), 329-341. https://doi.org/10.3390/constrmater4020018





