Abstract
Concrete and other semi-brittle materials are pressure sensitive. Their resistance to shear depends on the confining pressure acting normal to the shear plane. This behaviour is modelled using experimentally calibrated failure criteria, such as the Mohr–Coulomb failure surface. Pressure sensitivity is also strongly evident in fibre-reinforced, strain-hardening cementitious composites (SHCC), despite the internal confinement these materials possess on account of their fibre content. However, because of the great range and variety of mixes used in such materials, no general failure criteria have yet been proposed. In this paper, the pressure-sensitive shear strength of SHCC containing short discontinuous PVA fibres is modelled with a three-parameter failure criterion. The parameters of the criterion are calibrated to the experimental results obtained from several tests that combine shear and normal pressure. These include uniaxial tension and compression, split tests, triaxial compression, and a series of push-off tests with and without reinforcement crossing the shear sliding plane. The calibration of the failure criterion explicitly accounted for the magnitude of internal confinement which is generated in the cementitious matrix in response to fibre tension. The criterion is appropriate for general purpose analysis of the stress state of SHCC, but most importantly it is used to assess the SHCC contribution to the shear strength of structural elements.
1. Introduction
Cracking limits the strength and service life of concrete structural members unless reinforcement is available. The flexural strength of reinforced concrete (RC) members is provided by longitudinal reinforcement. In the general mechanics framework of structural concrete members, reinforced concrete is treated as a continuum. Reinforcement is considered smeared and fully bonded to concrete. This allows assuming the definition of continuous (smeared) principal strain and stress [1]; therefore, this approximation is only possible in the presence of adequate shear reinforcement. To mitigate diagonal tension cracking and dislocation in the web of structural members, hoops and stirrups are routinely used in design. But reinforcement congestion, particularly in critical regions (beam–column joints, plastic hinges, and coupling beams), coupled with additional considerations such as labour intensity, cost, and the susceptibility of stirrups to corrosion underscore the need for a more effective option. Alternative forms of reinforcement, such as distributed fibres, have been used for several decades to supplement the mechanisms related to the absorption of energy of concrete through cracking. The concept of using short fibres as reinforcement and partial rebar replacement to alleviate congestion has only become possible with the introduction of strain-hardening cementitious composites (SHCC). These are cementitious materials that can sustain large tensile strains after cracking without a loss of tensile strength. This type of property cannot be obtained without the use of a pertinent type and volumetric ratio of fibres in the cementitious mix. In the remainder of this paper, the term SHCC is used to refer to fibre-reinforced materials with a post-cracking strain-hardening response in tension.
Fibre-reinforced concrete (FRC) was first patented in 1874 [2]. Today, various fibre geometries and material types are used in FRC (e.g., steel (S), silicon (Si), carbon (C), ceramics (Ce), glass (G), nylon (Ny), polypropylene (PP), polyethylene (PE), and polyvinyl alcohol (PVA)). The strain-hardening ductility in FRC is only possible if: (a) an adequate number of fibres intersects the crack surface at an equivalent angle of 90°, and (b) the embedded fibres develop an adequate bond strength with controlled slip along their anchorage length, so that multiple cracking may occur throughout the length of the members [3]. As a rule of thumb, the fibres can only mitigate the effect of flaws and discontinuities that do not exceed a fraction of the fibre length. Flaws include microcracks which the fibres may intercept before they coalesce to crack lengths that exceed the range of action of the fibre used. Coarse aggregates also disturb the stress transfer between fibres and the cementitious matrix. This is why only a strain-softening response in tension is observed in conventional FRCs. In these materials, at least pea-gravel size aggregates are combined with longer and larger diameter fibres. Therefore, a smaller number of fibres per unit area crosses the planes of cracks and the response is marked by strain softening, and a moderate amount of residual toughness after cracking. This limitation is removed in SHCC materials through pertinent aggregate gradation. For example, the maximum aggregate size used is less than 1/10th of the typical fibre length, the fibre diameters are fine so that the fibre aspect ratio is at least equal 65, whereas the number of fibres crossing a unit area of the matrix is at least 0.30/1 mm2. So, although the matrix of SHCC resembles that of a mortar, the high tensile and compressive strengths of these materials classify them into the category of concrete. SHCCs are ideal for innovative design and retrofit applications in RC construction on account of the large tensile strain that can be developed after cracking without the loss of tensile strength.
Some design codes have recently developed specifications for the introduction of ultra-high performance concrete reinforced with steel fibres in design practice ([4,5]). However, many of these specifications are still informative provisions (i.e., not enforced). But the lower strength SHCCs that are made with synthetic or natural fibres have yet to be addressed in retrofit manuals and design codes. A primary reason is that the selection of options among non-metallic fibres is vast, whereas the experimental database contains mostly tests that were conducted using different fractions of such fibres. This leads to fragmentation of the available results that are needed to support the derivation of design provisions. Nevertheless, the available evidence illustrates conclusively the efficacy of PVA and PE fibres in controlling crack propagation and enabling the development of significant tensile deformation capacity [3,6,7]. The resilience of the SHCC materials to post-cracking stresses is particularly relevant in design problems where concrete tension is relied upon. One such example is shear design: the concrete contribution term, Vc, is correlated to the diagonal tension failure of concrete in the critical section (ACI 318-19 [8]; and Eurocode 2 2004 [9]). For example, considering the tensile cracking strength of concrete equal to (or 6 in the state of pure shear (which is considered to occur at the neutral axis of a flexural member), the maximum shear stress, vc, equals the principal tensile strength, . The corresponding shear force associated with the formation of diagonal tension cracks taken over the depth d and width bw of the cross section is estimated from or (ACI 318-19 [8]). Therefore, the average shear strength over the cross section is taken at about 1/3 of the tensile strength of the material.
For complex states of stress, a variety of models in the form of “failure criteria” are known in the literature, describing the combination of stresses’ values that lead to shear failure. As an example, consider a sliding plane with a unit normal vector, , where a pressure occurs normal to a sliding plane. The shear strength of concrete, , which can be developed on the sliding plane increases with an increasing magnitude of . This property is known as the pressure-sensitivity of concrete and is characteristic of many semi-brittle materials such as rock or mortar. Pressure may be the result of either external or internal confinement. Despite the differences of SHCC materials from concrete, they too are pressure-sensitive. In this context, a primary difference from normal concrete is that strain-hardening concrete is internally confined, due to the presence of fibres. This intrinsic internal confining pressure is added on to any other form of confining stress that is generated by the applied loads.
Several experimental studies have been conducted to examine the performance of SHCC in retrofitting applications. Fewer studies deal with the development of constitutive models to predict the mechanical response of these materials [10,11,12,13,14,15,16,17,18,19]. The approach taken is to carry out material characterization tests so as to provide adequate data for the calibration of SHCC-specific failure criteria. Jiang et al. [10] carried out a series of 21 triaxial tests on confined cylinders of SHCC reinforced with PVA fibres at a volumetric ratio of 2%. The results were used to derive a confinement model and the compression meridian of a failure criterion. It is noted that in all cases a strongly linear relationship between normal compressive strength and the external confining pressures was reported. Wu et al. [12] adopted the RHT plasticity model of LS-DYNA [20,21], which was developed for UHPC, to describe the evolution of damage, the strain rate, and the strain-hardening/softening response of SHCC materials. Wilson et al. [22] used ANSYS’ microplane model [23] to simulate the flexural behaviour of SHCC beam elements in order to capture the experimental response up to peak load. Krahl et al. [14] used a similar approach to model UHPC beam specimens with the damage plasticity model of Abaqus [24]. They reported reduced damage with a higher fibre content, a behaviour that is reflected by failure criteria with meridians that are nearly linear for cases with higher fibre contents—as in the previous case, the response was reproduced up to the peak point. Liao et al. [13] studied the effect of fibre content and normal stress on shear strength. The SHCC material considered different volumetric ratios of PE fibres (0%, 0.5% and 1.5%). Tests were conducted on 100 mm cubes under combined compression-shear loading. A failure criterion was obtained based on these data, which illustrated a nearly linear relationship between shear and normal stress on the sliding plane. A different approach using a hypoelastic stress strain model had been used by Hung and Li [15]. In that study, an orthotropic rotating crack model with coincident principal stress and strain axes was used. Uniaxial stress–strain models were used to describe the behaviour along the principal axes.
In the present work, the contribution to shear of SHCC materials reinforced with synthetic fibres is evaluated through a broad collection of tests conducted under different states of stress, using PVA-fibre-reinforced SHCC material. Additionally, to align with the goals of environmentally sustainable development, the mortar matrix of the tested SHCC contained a great amount of fly ash, approximately in the order of 60% replacement of cement. Note that fly ash is an industrial waste with pozzolanic properties, usually used to improve the rheology properties of the fresh mix and the final strength of the material [25,26,27]. To support the calibration of a failure criterion that describes the combination of shear stress and normal pressure leading to material failure, the stresses were decomposed into deviatoric and hydrostatic components. Various types of tests were conducted to provide data for the calibration of the failure criterion, including shear push-off tests with and without reinforcement crossing the sliding plane. SHCC push-off specimens of two different sizes were tested to assess the sensitivity of the shear response to size effect. The proposed failure criterion is a much-needed tool for the practical design of SHCC members to shear but also in the finite element analysis of structural components made of SHCC.
2. Background for the Model of the Failure Envelope of SHCC
2.1. Three-Parameter Failure Model of Concrete
The pressure sensitivity of the shear strength of conventional concrete is expressed by the shape of the failure surface, , which is a function of the stress invariants (I1, J2, and J3) to maintain symmetry with respect to the principal stresses, . The most familiar failure criterion is a three-parameter envelope that is smooth and convex and is known as a three-parameter criterion as depicted by Equation (1) (Bresler–Pister criterion [28], also reported in Chen [29]):
where the parameters a, b, and c are acquired from common tests conducted on concrete samples. Usually, the experimental results used for this purpose are: (i) the uniaxial tension test to measure the material tensile strength, ; (ii) the uniaxial compression test to obtain the compressive strength, ; and (iii) a biaxial compression test under equal stresses in two orthogonal axes to obtain the corresponding biaxial compression strength, . The terms and are the octahedral normal and shear stresses. These are defined as:
where is the angle of similarity (also known as the Lode angle, [29]); in the case of the shear meridian, (. The invariants in Equation (2) are defined as:
For conventional concrete, it is ; also, the uniaxial compression test and the biaxial compression, , . Based on these, the coefficients from (1) are calculated in Equation (4) below.
2.2. Internal Confinement of SHCC—Effect on the State of Stress
SHCC materials differ from conventional concrete in that they respond to any form of tensile deformation including lateral dilation by mobilizing an internal passive confinement that is exerted by the fibres. Figure 1a depicts a rectangular elementary sample of SHCC material, subjected to a state of pure shear stress. The shear distortion causes tension in one of the diagonals of the element which, after the cracking of the matrix, places any fibre reinforcement crossing the crack path into tension. The free body diagram of the part of the body to the left of an arbitrary section A-A reveals the presence of the fibre stresses, σf, acting along the random orientation of fibres intersecting the plane of the section (black arrows in Figure 1b). These stresses produce a resultant force in the direction normal to the A-A section, which is then maintained in equilibrium along the x-axis with the help of a lateral confining pressure, σc,f (shown by red arrows in Figure 1b) Similarly, in Figure 1c, the behaviour of a circular unconfined column of SHCC is depicted: compression normal to the circular section causes lateral expansion (dilation) of the cross section, thereby placing the randomly distributed fibres in tension. The free body equilibrium of a column slice cut along the diameter reveals the fibre stresses which are tensile; the equilibrium of actions in the horizontal direction requires the presence of a compressive lateral pressure, σc,f, as in the case of common confinement by external jacketing
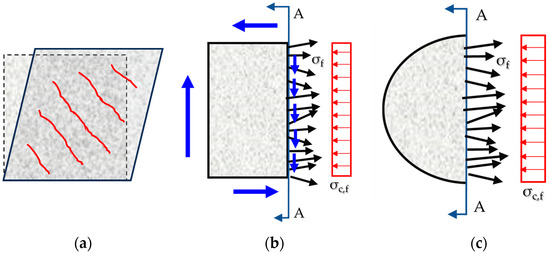
Figure 1.
(a) Conventional concrete element under pure shear. (b) internal confining pressure in an SHCC element under pure shear, due to the mobilization of fibres in the element’s plane; (c) internal confining pressure in a SHCC cylinder compressed axially due to the mobilization of fibres normal to the load to restrain dilation.
The magnitude of the internal confining pressure, σc,f, depends on the number of fibres crossing an arbitrary plane:
where is the stress of the i-th fibre crossing the plane A-A (see Figure 1b), is the angle of inclination of the i-th fibre with respect to the horizontal, and Nf is the total number of fibres crossing the A-A plane. The internal confining stress, , which results from the action of the fibres, is obtained from Equation (5b):
The term represents the average fibre stress in the cross-section A-A, and is the characteristic number of fibres crossing a unit area (1 mm2) of a matrix reinforced by a volumetric ratio Vf of fibres. This is equal to [3]:
where df is the fibre diameter. Thus, for Vf = 1%, and df = 0.1 mm, it is estimated that 1 fibre crosses every 1.6 mm2. The length of the fibre, Lf, is also critical, as it determines the load-bearing capacity of a single fibre after cracking, and from there the post-cracking resistance of the SHCC. Considering that the maximum anchored length is Lf/2, and the mean value at any plane is half of that, it follows that the maximum value of is limited by the development capacity of the fibre:
In Equation (6a), is the bond strength between the surface of the fibres and the surrounding cementitious matrix. Therefore, after cracking, the tensile strength of the material, , is ideally obtained from:
where is a fibre orientation factor (for random distribution, this is taken as 0.5 (CSA-S6, Annex 8 [30]). Thus, the post-cracking resistance of the material depends on the length-to-diameter ratio of the fibre, Lf/df. Note that longer and thinner fibres are needed to ensure the hardening response (where ). After substitution in Equation (5b), the internal confining pressure of concrete is also obtained as . Therefore, the internal confining pressure cannot exceed (in absolute magnitude) the tensile strength of the material after cracking.
To avoid any uncertainties associated with the bond strength, , Georgiou and Pantazopoulou [31] measured the internal confining pressure experimentally, , and confirmed the above theoretical finding, i.e., they found it approximately the same as the tensile strength of SHCC, . This is also consistent with the French National addition to Eurocode 2 [4], related to the design of fibre-reinforced concrete, which recognizes explicitly the presence of an intrinsic confining pressure, and sets it conservatively equal to 0.8. Based on this discussion and the preceding Section 2.1, it is concluded that in stress analysis, and for random fibre distribution, an isotropic confining pressure (compressive) may be considered to act in the SHCC material equal in magnitude to
3. Materials and Methods
3.1. Experimental Methodology
To adapt Equation (1) as a failure criterion to SHCC, the model needs to be recalibrated to experimental results obtained from SHCC tests to determine the pertinent values of the model coefficients. In this effort, the internal confining pressure defined in Section 2.2 needs be accounted for in the stress analysis of the various specimen forms and stress states considered. For the needs of the investigation, a series of uncracked push-off specimens were tested, having the geometry depicted in Figure 2. Push-off specimens were used to assess the mechanics of shear stress transfer across a sliding failure plane [32,33,34]. The most common form of the push-off test setup simulates the state of pure shear across an interface (Figure 2a). In this test, the vertical failure plane is guided—by means of the horizontal notches—to align with the applied load. By adjusting the depth of the notch, the failure plane is guided to occur at an angle relative to the x-axis, as depicted by the red jagged line. In this manner, the failure plane is inclined to the axis of loading and by designing this, a sliding plane is formed that is subjected to the simultaneous action of normal compression and shear stresses (Figure 2b,c). Further modification of the push-off specimen was developed where a combination of normal tension and shear stresses occurs on the failure plane [34]; (in this case the failure plane’s angle to the x-axis is negative (Figure 2d)).
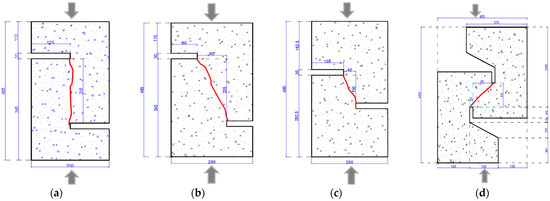
Figure 2.
Dimensions and layout of the push-off specimens: (a) pure shear stress (PSS); (b) shear compression A (SCA); (c) shear compression B (SCB); (d) shear tension (ST).
The parameters of the experimental study were: (1) The mix design: two cases were considered, i.e., the plain cementitious matrix and the fibre-reinforced matrix, in order to calculate the influence of the fibre reinforcement in the shear strength of SHCC. A comparison was made for push-off specimens in pure shear (PSS). (2) The influence of steel rebar reinforcement crossing the shear plane: again, the comparison was made using PSS specimens containing either fibre-reinforced or plain cementitious matrices. (3) The effect of combined normal stress on the shear strength of SHCC: in this group of fibre-reinforced specimens, the failure plane is guided by the design of the notch depth, to develop at an angle relative to the applied load (Figure 2, the specimen identification code for this category is CS when the combined stress normal to the guided shear plane is compressive, and TS if tensile). Two different sizes (full and half scale) of specimens were used in this part of the investigation to evaluate the effect of size on shear strength (since, in the absence of steel reinforcement, the shear strength is only dependent on the SHCC material’s tensile strength). Two identical specimens were tested for each parameter combination, except for the specimen group that also made comparisons with an unreinforced or/and fibreless case, in which three identical specimens were tested to anticipate possible brittle failures.
A total of six push-off specimen groups were tested as outlined in Table 1; listed are the specimen identification code (ID), the material, amount of reinforcement and the angle α of the intended shear plane with respect to the x-axis, the length of the shear plane R, and the scale and number of specimens tested for each parameter combination. The small letter S in the denomination of the specimen ID code refers to short (i.e., half scale) specimens. The code R refers to reinforced specimens (i.e., having stirrups crossing the failure plane). It is noted that the cases modelled in Figure 2 are under planar loading; thus, scaling only refers to the planar dimensions of the specimens. The out-of-plane thickness was 100 mm in all cases to mitigate the out-of-plane instability during the tests and to minimize the wall effects on the fibre distribution in casting the small specimens.

Table 1.
Geometry of push-off specimens 1.
Instrumentation included linear potentiometers (LPs) to measure the dislocation of the specimen in the shear plane, in the x and y directions. Specimens were tested using displacement control, with a mm/s displacement rate of the loading piston. It is noted that no collapse or loss of integrity was reported in the SHCC (i.e., in the fibre-reinforced specimens) even in the post-peak range of the load-displacement envelope.
In addition to the push-off tests listed above, a number of auxiliary tests for the characterization of the properties of the three mix designs used for the preparation of the push-off specimens were performed. These tests were conducted in identical triplicates and included: (1) uniaxial tension, (2) uniaxial compression, (3) split cylinder tests, and (4) flexural modulus tests (i.e., four-point bending tests on beams without steel reinforcement). The results from these tests are summarized in brief in the following sections. Peak values are followed by the post-peak localization of damage during the tests; thus, these values are used in the calibration of the failure criterion for SHCC. Direct tension tests were conducted on double-T dog-bone specimens of Mix B (Figure 3a) at a displacement rate of 0.0025 mm/s. The double-T specimen cross section over the central gauge length of 100 mm was 25 × 50 mm2 [3]. Uniaxial compression tests were performed under displacement control measuring both axial and circumferential deformation at the cylinder mid-height to quantify the lateral expansion (phenomenological Poisson’s ratio).

Figure 3.
Typical failure patterns observed in the SHCC material characterization tests: (a) direct tension; (b) uniaxial compression; (c) cylinder splitting; (d) four-point bending.
Cylinder splitting is an accepted test for indirect measurement of the tensile strength of conventional concrete [35]. For SHCC, it can be used to determine the tensile strength at cracking; however, results beyond that point in the case of the tension-hardening response may only be seen in a qualitative light. The reason is that owing to the deformability of the material, bearing action develops under the loading roller, resulting in the formation of vertical compression struts between the multiple cracks that open parallel to the loading axis [3]. Similar disclaimers are valid for all other forms of indirect tension tests. In the present study, splitting tests were conducted under displacement control of the loading plate at a constant stroke rate of 0.50 mm/min. SHCC cylinder specimens were 100 mm in diameter and 100 mm in length. Lateral extension of the horizontal diameter of the split SHCC cylinder was obtained by horizontally placed LVDTs. Four-point flexural tests were also conducted at a rate of 3 μm/sec on beam specimens having a cross section of 100 mm × 100 mm, and spans of 100 mm or 200 mm between the loading points to indirectly measure the strain-hardening properties of the SHCC.
3.2. Mix Design and Materials
Three types of mixes were used in the experimental investigation, by considering two different types of PVA fibres, and by also testing specimens comprising the matrix without fibres (referred to as Plain in Table 1) to investigate their contribution. The three mix designs are given as weight ratios in Table 2 for all the materials, except for the fibres, where their proportion is given as the volume fraction, Vf. Silica sand (containing at least 95% of Si) with a maximum grain size of 300 μm was used in all cases. Type F Fly ash (FA) was used for cement replacement. This type of FA has pozzolanic properties, with a particle size of less than 50 microns [36]. Dry densified silica fume and ground granulated blast furnace slag were used to enhance the compressive strength of the ternary mixes.

Table 2.
Push-off specimen mix design.
Two different types of PVA fibres (Kurallon K-II) were used; both were 12 mm long but were differentiated in diameter (100 dtex in Mix A and 39 dtex in Mix B, respectively). Nominal mechanical characteristics of the fibres are given in Table 3. For the specimens with rebars crossing the shear plane, reinforcement comprised 6 mm diameter bars with experimentally obtained properties as listed in Table 4. Plain and unreinforced specimens (i.e., when no internal steel was provided) were strengthened locally with carbon FRP strips to prevent flexural failure outside the study region, along the horizontal cross sections that extended from the notches. The strips placed vertically were 50 mm wide and were chemically anchored on both sides of the potential flexural crack.

Table 3.
Properties of different PVA fibres.

Table 4.
Properties of reinforced bars used in the push-off specimens.
4. Experimental Results
4.1. Material Characterization Test Results
The failure patterns from the characterization tests are depicted in Figure 3, revealing the beneficial contribution of the fibres. The behaviour of the SHCC specimens was marked by the formation of multiple cracking after the first initial crack that appears in the cementitious matrix. The increase in strength due to the transfer of stress through the crack is initiated by the elongation and pullout of fibres. This is evident in all modes of failure, from uniaxial tension (Figure 3a) to compression (Figure 3b). In the tests under uniaxial compression, multiple cracking developed on the lateral surface of the cylinders, but the specimens maintained their integrity (no delamination was observed up until the end of the experiment). First, cracking was observed when the load in the ascending branch was at 70% of the peak. Several cracks developed beyond that point, gradually increasing in number and width up to the peak load. After localization of cracking into a few major cracks (beyond the peak), a gradual reduction in strength occurred, at a rate much slower than what is known for conventional concrete. Fibres crossing the cracked planes appeared stretched, pulled, or ruptured. In the case of the splitting cylinder test, even though the maximum stress was concentrated at one diametric plane of the specimen, in the case of the SHCC mixes, multiple cracks appeared over a band of approximately 20 mm (Figure 3c). The cracks were oriented normal to the horizontal diameter of the cylinder, indicating strain-hardening characteristics in the post-cracking response, as compared to the specimens of the fibreless mix which experienced sudden failure past the first cracking. A ductile response marked by multiple crack formation, deflection hardening, and great energy dissipation capacity was also observed in the flexural beam tests. Cracks formed normal to the longitudinal axis of the specimens and were concentrated between the central load points (constant moment region) (Figure 3d).
Figure 4 plots the sample results obtained from the SHCC and plain mix stress–strain and load-deformation diagrams from the various material tests. For the uniaxial tension, after the first crack, multiple cracking appeared on the specimen within the critical section (Figure 4a), with the tensile strength gradually increasing with a mild hardening slope, exhibiting characteristics of an elastic–plastic response curve, up to a tensile strain of 0.01. The tensile cracking strength ranged between 2.5 to 3.5 MPa, whereas the ultimate tensile strength varied between 3.0 and 4.0 MPa. The flexural strength behaviour is plotted in Figure 4d. The same trend of higher flexural values is observed, while the tensile strength of the Plain mix that failed in a brittle manner was only one-quarter of that of the mixes that included fibres.
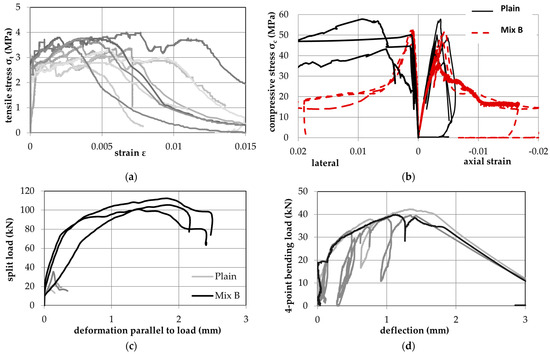
Figure 4.
Sample results from the material tests: (a) direct tension results: tension stress-strain curves; (b) compression stress-axial strain-lateral strain; (c) split cylinder test load vs. horizontal extension; (d) four-point bending load-deflection.
Average values of the mechanical properties obtained from all the material tests are summarized in Table 5. The tensile strength of SHCC obtained from the splitting tests corresponds to the onset of cracking. As depicted in Figure 3c and Figure 4c, multiple cracking occurred in the splitting region, leading to significant energy dissipation prior to the collapse of the specimen; however, this is not entirely attributable to the tension-hardening of the SHCC. Indeed, after cracking and with increasing bearing action of the loading plates, local crushing occurred under the plates. Therefore, a part of the load transfer occurred through compression struts forming parallel to the cracks. The uniaxial compressive response is plotted in Figure 5b; the compressive strengths obtained in all cases were in the range of 50–60 MPa. Lateral strain plots highlight the precipitous lateral expansion of the plain material after strength attainment. The magnitudes of lateral strain in the post-peak envelope of the SHCC specimens were more controlled, indicating the effective confining action of the fibres.

Table 5.
Summary of compression and tension tests on the different mixes.
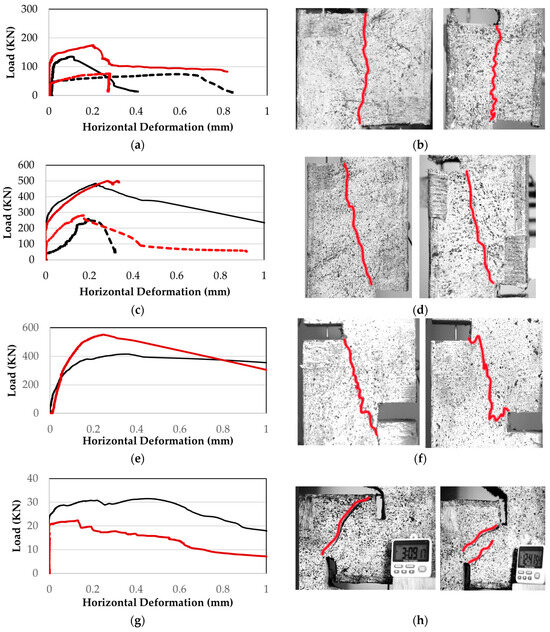
Figure 5.
Load-horizontal deformation diagrams of push-off tests with various shear plane inclination angles and corresponding failure cracks: (a,b) pure shear; (c,d) shear compression A; (e,f) shear compression B; (g,h) shear tension.
4.2. Push-off Test Results
4.2.1. Variation in Shear Plane
The load-lateral deformation response curves of the push-off specimens for varying shear plane angles are plotted in Figure 5, accompanied by photos of the observed crack patterns. The peak load resistance of the specimens increased with the increasing angle of the shear plane due to the higher contribution of the compressive stresses, imparted by the angle of failure. All the specimens developed the peak load at a lateral deformation of 0.2 mm irrespective of the angle of the sliding plane. Also, the post-peak softening part of the response was steeper for the lower absolute magnitude of compressive stress. In fact, the pure shear specimens—both full and half scale—developed a significant amount of degradation in the resistance curves following the occurrence of cracking along the shear plane. In the case of the shear tension specimens (ST), the response was very ductile, and it was marked by the formation of multiple cracks. The response was controlled by gradual fibre pullout following the widening of the main crack and the gradual degradation of the load resistance.
4.2.2. Effect of Reinforcement Crossing the Failure Plane (Fibres and Stirrups)
The load-lateral deformation response curves of all the push-off specimens, containing either fibres or steel reinforcement across the shear plane are summarized in Figure 6 (top). Crack patterns near failure are depicted in Figure 6 (bottom). The unreinforced PSP specimens (without fibres or stirrups) failed in a brittle manner immediately after cracking. Specimens with the same plain matrix but reinforced with bars crossing the shear plane (PSP-R) were dominated by the action of the reinforcement. After cracking and due to the absence of aggregates, the friction on the shear plane was minimal and the full shear load was transferred through the dowel action of the steel bars. When fibres were added in the matrix (PSB), the gradual formation of several cracks occurred prior to the peak load which was followed by crack localization. Despite the loss of resistance, the material maintained its integrity, exhibiting an almost elastic–plastic load-deformation response curve. The load obtained in this case was of the same order or higher than that of the fibreless matrix reinforced with 6Φ6 (S300) crossing the shear plane; however, the behaviour was much more ductile. Cracks in the fibre- and steel-reinforced specimens (PSB-R) were steeper than in unreinforced SHFRCC specimens (PSB). Cracks were points of dislocation of the horizontal stirrups crossing the shear plane, highlighting the dowel action that was developed in the bars. The localized damage and dislocation extended to the right and left of the shear plane over a total width of about 60 mm, without delamination of the SHCC specimen. The load carrying capacity was not increased in the case of the reinforced SHCC specimens over that of the otherwise identical plain reinforced case. Thus, in both cases, the ultimate strength was controlled by the fibres. However, the extent of visible damage in the two cases was starkly different (see Figure 6g,h).
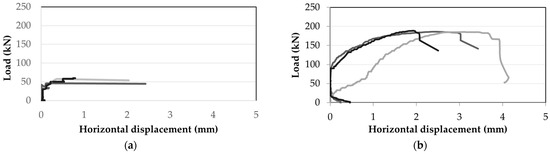
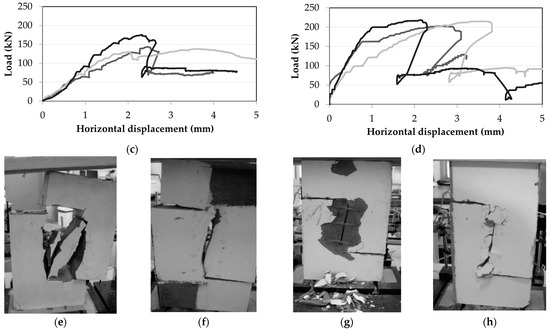
Figure 6.
Load-horizontal deformation diagrams of push-off tests with/without fibres and reinforcement bars: (a,e) PSP; (b,f) PSB; (c,g) PSP-R; (d,h) PSB-R.
5. Calculation and Analysis of the Shear Failure Stress
The shear strength of SHCC in relation to the magnitude of normal stresses σn acting on the shear plane was developed by determining the τn-σn interaction curve of the SHCC corresponding to a Mohr–Coulomb failure model. Here, the subscript on the normal and shear stress refers to the normal to the plane of sliding, , see Figure 7a. The components of the load normal to the shear plane, , (shown in red in Figure 7a,b) and parallel to the shear plane, , (shown in blue in Figure 7a,b) were derived, with α being the inclination/slope angle of the shear plane measured with reference to the horizontal plane, α = tan−1(H/L), where H is the vertical distance and L the horizontal distance between notches.
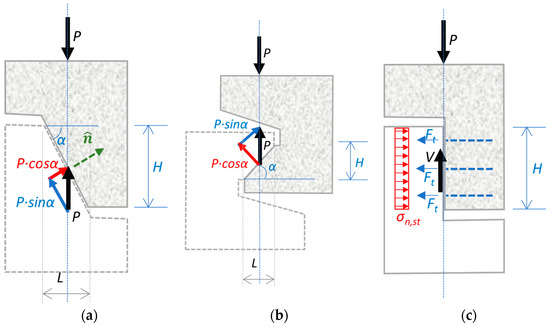
Figure 7.
Calculation of normal and shear stress along the failure plane for different angle α: (a) compression shear; (b) shear tension; (c) pure shear in a specimen with horizontal stirrups.
The stresses on the shear failure surface were obtained by the normal and shear load components, divided by the shear plane’s area (R∙t) according to Equation (7). In Equation (7), t is equal to the depth of the specimen and R = (H2 + L2)1/2 is the length of the sliding plane (Figure 8, Table 1):
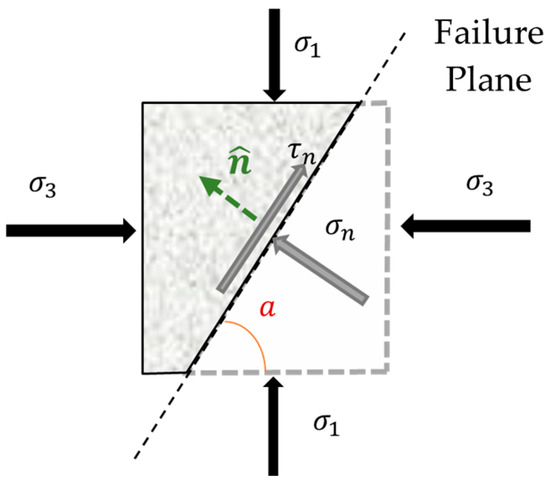
Figure 8.
Failure plane in push-off with angle α.
The subscript n refers to the sliding plane; σn is normal, and τn is parallel to the sliding plane. Calculated values are listed in Table 6. Figure 8c represents the example of a push-off specimen under plain shear. For the sake of generality, the example containing horizontal stirrups is depicted. If Ft,i is the tension force developing in each stirrup layer that is crossing the sliding plane, then the normal pressure σn,st that is clamping the plane of sliding (which was vertical for all reinforced push-off specimens) is calculated as:
where m is the total number of stirrup layers within the notch distance H. For example, for perimeter stirrups, with two stirrup legs having a total area At (i.e., considering both stirrup cross sections) intersecting the sliding plane per layer, the peak value of Ft,i is equal to Atfy, where fy is the yield strength of the steel rebars.

Table 6.
Normal and shear stresses from tests (compression positive).
Other than the pressures exerted by stirrups or by the applied loads as per Figure 7, an important feature of SHCC is the presence of internal confinement generated by the fibres as discussed in Section 2.2. The internal confining pressure is a passive action, which ought to be considered in resolving the stress state within the SHCC. In the remainder, where either compressive or tensile stress was actively applied externally in any specific direction, then the value of the stress in direction parallel to the imposed action was taken equal to the minimum value from among the confining pressure and the applied active pressure; however, in any other direction, the rise of the passive normal stress σn,f was taken into consideration for extracting the principal stresses for the various experiments conducted in the present work (whether they were push-off tests, uniaxial compression tests that generate lateral passive confinement, etc.). For consistency with Section 2.1, the passive confining pressure was taken as equal to the splitting strength at the onset of the cracking of the material, fcr,split, in the opposite direction. When both stirrup reinforcement and fibre reinforcement were present, then the sum of these two passively generated confining pressures was used in the remainder of the calculations (see term σconf in Table 6).
Figure 9 plots the normal vs. shear stress pairs that acted on the shear plane at the peak response, as listed in Table 6. As shown in the last column of the table, the total confining stress σconf acting normal to the shear plane was obtained as the sum of the internal confining pressures, provided by three different possible sources (depending on the specimen form): (a) the fibres, σc,f; (b) the normal acting pressure by the applied load, σn; and (c) any stirrups that cross the vertical (shear) plane, σn,st. A first conclusion is that no size effect is evident, from the average values of geometrically similar, full, and half-scale specimens. The absence of a clear effect of size in the experimental results of the present study is consistent with reports by other investigators who studied the size effect on shear of UHPC [37,38]. In these experimental studies, it was found that the size effect was substantially limited by even small amounts of fibres and could be entirely mitigated for materials that exhibit a robust tension-hardening response.
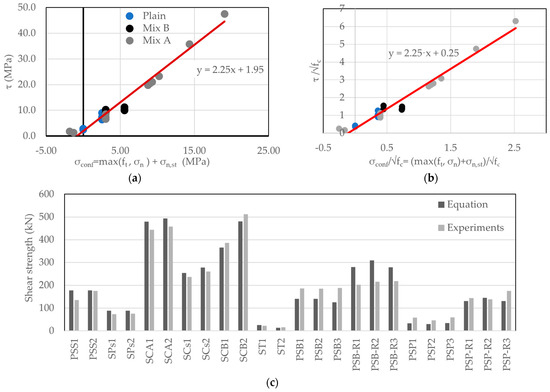
Figure 9.
(a) Shear and normal stresses from test of specimens and the Mohr–Coulomb failure criterion; (b) the same terms normalized with supporting Equation (10); (c) comparison of experimental results with calculations of Equation (10).
All the results are following a clear nearly linear correlation, a failure surface. The failure surface has the characteristics of a frictional material with no cap. A Mohr–Coulomb-type failure surface assumes that the limiting shearing stress is dependent on the normal stress in the same plane as follows:
In Equation (9), c is the cohesion and φ is the internal friction angle. Using the above frictional/cohesive model in combination with the experimental data of the push-off tests, the characteristic values of these parameters were obtained as c = 1.95 MPa and φ = 65.92°.
The shear and normal stress values plotted in Figure 9a are normalized with respect to the , which is considered a multiple of the tensile strength for cement-based composites as explained in the introduction; therefore, the shear strength of a cross section with fibres, axial load, and rebars acting on or crossing the shear plane is determined from Equation (10). The calculated value from Equation (10) for each individual specimen is plotted against the experimental peak value in Figure 9c. The graph indicates that all specimens having either normal stresses acting on the shear plane and internal fibre confinement, or cases where confinement is provided by stirrups without fibres, are all organized by a single expression for the limiting shear strength of the failure plane.
6. Discussion: A Three-Parameter Failure Criterion for SHCC
A failure criterion for SHCC composites is the envelope of the three invariant stress combinations that define the attainment of peak response which heralds the onset of post-peak damage. With the use of this limiting boundary, it is possible to establish the incremental stress–strain relationship for SHCC in the plastic range. While the friction/cohesion Mohr/Coulomb model developed in the preceding section could be used for this purpose, while also being practical for design, it has a few disadvantages when used in a numerical context (e.g. finite element context): these are (a) the failure surfaces are planar, intersecting each other at sharp corners; and (b) the derivation did not consider the intermediate principal stress [29]. In the present investigation, the intermediate stress is set equal to the internal confinement secured by the fibres. Thus, the general stress tensor that is used for derivation of the failure criterion is as follows:
Τo maintain the symmetry of the failure criterion with respect to the principal axes, the octahedral stresses τoct and σoct, which are invariant combinations of I1 and J2, were used (see Equation (2)), while the influence of J3 or θ was neglected. As a starting point, the relationship between the octahedral stresses which was calibrated for normal concrete (Equation (1)) was considered and correlated with the available experimental database for SHCC developed for the needs of the present work. All the material characterization tests conducted by the authors [27,31,39] were included in the calibration along with the push-off results of this study, to increase the range of the testbed supporting the derivation of the failure criterion. In total, a collection of results from more than 60 experiments were used, which included: uniaxial tension, uniaxial compression, splitting, push-off, and confined cylinders in compression with the use of carbon and glass FRP jackets in various layers. The relations between the octahedral stresses are approximated by a quadratic parabola, as per Equation (1) [28,29] (normal stresses σc were positive when tensile and the value of fc always positive). The parameters a, b, and c are established by curve-fitting of the available experimental test data. The equations that were used to derive the octahedral stresses of the experimental set were given in Section 2.1. The complete set of octahedral stresses of all the experiments are plotted in Figure 10a, while in Figure 10b the experimental values are normalized by the compressive strength of the material, and they are fitted with the parabola shown with the black line. The equation of the parabola has the following form:
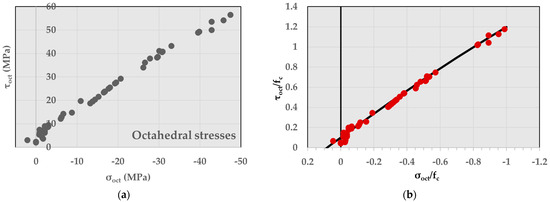
Figure 10.
(a) Octahedral stresses from the experimental dataset; (b) meridian of the failure surface: normalized octahedral stresses and the failure criterion (Equation (12)).
The coefficient of determination R2 = 0.993 shows a very good fit of the model to the data. The mean absolute error is MAE = 0.0225, showing that the average absolute error between the experimental results and the model prediction is very low. Also, the mean squared error is MSE = 0.0008. It is noted that only the third variable, c, is dramatically different from that describing the failure criterion of regular concrete. This implies that the nonlinearity of the envelope which is owing to the second-order term (curving of the meridian for high compressive stresses due to plastification and damage under high compressive stresses) is much less obvious here. Therefore, the so-called upper cap of the plasticity, if it exists in the case of SHCC, occurs at a much higher limit beyond the test range of the present study. It is noted that this result is consistent with observations reported by other researchers who have studied the constitutive behaviour of SHCC [10,11,12,13,14,15,16,17,18,19]. In all cases found in the literature, the failure criteria were nearly linear, indicating the damage control effected by the presence of fibres in SHCC, which differentiates its constitutive response from regular concrete where damage is an essential variable of the plasticity formulations used in the concrete damage plasticity model of Abaqus [24] and the RHT in LS-Dyna [21].
7. Conclusions
The attractive properties of strain-hardening cementitious materials in tension have led to a rapid growth in their use in high-performance construction and experimentation in innovative technologies (such as the area of precast concrete elements, ranging from Accelerated Bridge Construction (ABC) to architectural cladding for building envelopes). The tensile ductility and toughness of SHCC materials also render them ideal in the field of retrofitting for jacketing applications, replacement of damaged concrete in plastic hinge regions, deck overlays, and additive manufacturing. The characterization of SHCC material failure is needed to develop a constitutive model that can be used to analyse complete structural components. Because of the great range of available SHCC mixes (owing to the variety of synthetic fibres and constituents in the cementitious matrix), the constitutive behaviour under complex stress states, apart from uniaxial tension and uniaxial compression, is not yet fully understood or described in the form of failure criteria.
In this study, the mechanisms of shear resistance of SHCC were studied using a range of different tests that were intended to produce tension-related shear failure under different normal stress states. In this manner, failure criteria were derived and calibrated against the experiments. The primary findings of the investigation are as follows:
- SHCC with tension-hardening behaviour exhibits a nearly linear increase in shear resistance with increasing normal compressive stress acting on the plane of sliding.
- Damage in the form of dilation and crack opening is limited by the fibres and the fine and dense aggregate structure of the SHCC material. Also, it reduces with an increasing volumetric ratio of fibres, which also prolongs the range of tension-hardening behaviour of the composite.
- The pressure sensitivity which is inherent to all cementitious materials is also observed in SHCC. This refers to the dependence of the shear strength of the material to the normal clamping pressures that are acting on the shear plane by means of externally applied load, reinforcement, and by the internal confinement of the material which is owing to the distributed fibres embedded in the matrix.
- In the present work, the mechanisms of shear resistance of SHCC were studied using a range of different tests intended to produce tension-related shear failure under different normal stress states.
- The results were used to calibrate a Mohr–Coulomb-type shear-normal stress failure model that predicts the contribution of SHCC to the shear strength of a structural component (Equation (10)). Without the use of steel reinforcement or external load, this comprises the contributions of the matrix concrete and the fibres, as follows: where A is the shear area.
- The internal angle of friction was estimated at slightly over 60°, which is needed in structural components to define the crack plane with respect to the transverse axis of a member failing in shear and normal compression (e.g., in a column, this corresponds to an angle of 30° with respect to the longitudinal axis).
- The failure envelope, expressed in terms of stress invariants, was also derived to be used as an experimentally calibrated generalized failure criterion for SHCC materials in numerical modelling. The new failure criterion, which accounts for the internal confinement imparted by the fibres, shows an almost negligible contribution of the nonlinear term which is characteristic of conventional concrete. This underscores the damage control imparted by the fibres, thereby producing an almost linear meridian between octahedral stresses, and it is an exceptional feature of SHCC that sets it apart from plain concrete.
Author Contributions
Conceptualization, A.G. and S.P.; methodology, S.P.; formal analysis, A.G. and S.P.; investigation, N.E. and A.G.; data curation, A.G. and S.P.; writing—original draft preparation, A.G. and S.P.; writing—review and editing, A.G. and S.P.; supervision, S.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to future research publications related to the subject.
Acknowledgments
The work presented in this study was conducted in the laboratories of the first and third author; the second author was supported by the NSERC-Discovery Grant of the third author and by the fellowship of Lassonde School of Engineering at York University.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Vecchio, F.J.; Collins, M.P. Compression Response of Cracked Reinforced Concrete. J. Struct. Eng. 1993, 119, 29–41. [Google Scholar] [CrossRef]
- Balaguru, P.N.; Shah, S.P. Fiber Reinforced Cement Composites; McGraw-Hill: New York, NY, USA, 1992. [Google Scholar]
- Georgiou, A.V.; Pantazopoulou, S.J. Effect of Fiber Length and Surface Characteristics on the Mechanical Properties of Cementitious Composites. Constr. Build. Mater. 2016, 125, 1216–1228. [Google Scholar] [CrossRef]
- NF P 18-710; French Standard (AFNOR): National Addition to Eurocode 2, Design of Concrete Structures: Specific Rules for Ultra-High Performance FRC. AFNOR: Paris, France, 2016.
- CSA International. Canadian Highway Bridge Design Code, Section 16: Fibre-Reinforced Structures, Annex 8; CSA International: Toronto, ON, Canada, 2020. [Google Scholar]
- Li, V.; Kanda, T. Innovations Forum: Engineered Cementitious Composites for Structural Applications. Concr. Int. 1998, 10, 66–69. [Google Scholar] [CrossRef]
- Paegle, I.; Fischer, G. Evaluation of Standardized Test Methods to Characterize Fiber Reinforced Cement Composites. In Proceedings of the 8th RILEM International Symposium on Fiber Reinforced Concrete: Challenges and Opportunities (BEFIB 2012), Guimarães, Portugal, 19–21 September 2012; Barros, J., Ed.; RILEM Publications S.A.R.L.: Bagneux Cedex, France, 2012; pp. 9–16. [Google Scholar]
- ACI Committee 318. Building Code Requirements for Reinforced Concrete (ACI 318-71); American Concrete Institute: Detroit, MI, USA, 1971. [Google Scholar]
- EN 1992-1-2; Eurocode 2: Design of Concrete Structures—Part 1–2: General Rules—Structural Fire Design. European Committee for Standardization: Brussels, Belgium, 2004.
- Jiang, X.; Li, Q.; Yin, X.; Xu, S. Investigation on Triaxial Compressive Mechanical Properties of Ultra High Toughness Cementitious Composites with High Strain Capacity. Cem. Concr. Res. 2023, 170, 107185. [Google Scholar] [CrossRef]
- Jang, H.O.; Lee, H.S.; Cho, K.; Kim, J. Numerical and Experimental Analysis of the Shear Behavior of Ultrahigh-Performance Concrete Construction Joints. Adv. Mater. Sci. Eng. 2018, 2018, 6429767. [Google Scholar] [CrossRef]
- Wu, P.; Xu, S.; Li, Q.; Zhou, F.; Al-Mansour, A.; Zhao, X. A Plasticity-Based Dynamic Constitutive Model for Ultra High Toughness Cementitious Composites. Int. J. Impact Eng. 2022, 161, 104086. [Google Scholar] [CrossRef]
- Liao, Q.; Su, Y.; Yu, J.; Yu, K. Compression-Shear Performance and Failure Criteria of Seawater Sea-Sand Engineered Cementitious Composites with Polyethylene Fibers. Constr. Build. Mater. 2022, 345, 128386. [Google Scholar] [CrossRef]
- Krahl, P.A.; Carrazedo, R.; El Debs, M.K. Mechanical Damage Evolution in UHPFRC: Experimental and Numerical Investigation. Eng. Struct. 2018, 170, 63–77. [Google Scholar] [CrossRef]
- Hung, C.C.; Li, S.H. Three-Dimensional Model for Analysis of High Performance Fiber Reinforced Cement-Based Composites. Compos. Part B Eng. 2013, 45, 1441–1447. [Google Scholar] [CrossRef]
- Chen, M.; Pei, C. Influence of Different Kinds of Steel Fibers on Flexural Behavior of Ultra-High Performance Concrete Beam by AnSYS. In Proceedings of the 5th International Conference on Machinery, Materials and Computing Technology (ICMMCT 2017), Taiyuan, China, 14–16 April 2017; pp. 1–6. [Google Scholar]
- Menetrey, P.; Willam, K.J. Triaxial Failure Criterion for Concrete and Its Generalization. ACI Struct. J. 1995, 92, 311–318. [Google Scholar]
- Ralli, Z.G.; Genikomsou, A.S.; Pantazopoulou, S.J. Comparative Evaluation of Nonlinear F.E.A. Inverse Analysis of Tensile Properties of UHPFRC. In Proceedings of the Fib Symposium 2021, Lisbon, Portugal, 14–16 June 2021; pp. 563–573. [Google Scholar]
- Riedel, W.; Mayrhofer, C.; Thoma, K.; Stolz, A. Engineering and Numerical Tools for Explosion Protection of Reinforced Concrete. Int. J. Prot. Struct. 2010, 1, 85–102. [Google Scholar] [CrossRef]
- Riedel, W.; Thoma, K.; Hiermaier, S. Penetration of Reinforced Concrete by BETA-B-500, Numerical Analysis Using a New Macroscopic Concrete Model for Hydrocodes. In Proceedings of the International Symposium on the Interaction of the Effects of Munitions with Structures (ISIEMS), Berlin, Germany, 17–20 May 1999; pp. 315–322. [Google Scholar]
- Riedel, W. 10 Years RHT: A Review of Concrete Modelling and Hydrocode Applications. In Predictive Modeling of Dynamic Processes: A Tribute to Professor Klaus Thoma; Hiermaier, S., Ed.; Springer: New York, NY, USA, 2009; pp. 143–165. [Google Scholar]
- Wilson, W.; O’Flaherty, T. Finite Element Analysis of Ultra High Performance Fibre Reinforced Concrete Beams Using Microplane Modelling. In Proceedings of the Fibre Reinforced Concrete: Improvements and Innovations, RILEM-Fib International Symposium on FRC, Valencia, Spain, 18–20 November 2020; pp. 1–10. [Google Scholar]
- ANSYS. ANSYS® AUTODYN 2022 R2 Release 2022; ANSYS: Canonsburg, PA, USA, 2022. [Google Scholar]
- Smith, M. ABAQUS/Standard User’s Manual; Dassault Systèmes: Vélizy-Villacoublay, France, 2009. [Google Scholar]
- Ferraris, C.F.; Obla, K.H.; Hill, R. The Influence of Mineral Admixtures on the Rheology of Cement Paste and Concrete. Cem. Concr. Res. 2001, 31, 245–255. [Google Scholar] [CrossRef]
- Thomas, M.D.A. Optimizing the Use of Fly Ash in Concrete; Portland Cement Association: Skokie, IL, USA, 2007. [Google Scholar]
- Georgiou, A.V. Characterization of the Structural Performance of Strain Hardening Fiber Reinforced Cementitious Composites. Ph.D. Thesis, University of Cyprus, Nicosia, Cyprus, 2017. [Google Scholar]
- Bresler, B.; Pister, K.S. Strength of Concrete under Combined Stresses. ACI J. Proc. 1958, 551, 321–345. [Google Scholar]
- Chen, W.F. Plasticity in Reinforced Concrete; McGraw-Hill: New York, NY, USA, 1982. [Google Scholar]
- CSA International. Canadian Highway Bridge Design Code—Annex 8.1 Fibre Reinforced Concrete (New Edition); CSA International: Toronto, ON, Canada, 2018. [Google Scholar]
- Georgiou, A.V.; Pantazopoulou, S.J. Experimental Investigation on the Confining Effect of Fibers in SHFRCC. Compos. Struct. 2018, 202, 29–37. [Google Scholar] [CrossRef]
- Mattock, A.H.; Hawkins, N.M. Shear Transfer in Reinforced Concrete. ACI J Proc. 1969, 66, 735–744. [Google Scholar]
- Walraven, J.C.; Reinhardt, H.W. Theory and Experiments on the Mechanical Behaviour of Cracks in Plain and Reinforced Concrete Subjected to Shear Loading; Delft University Press: Delft, The Netherlands, 1981; Volume 26, pp. 1–64. [Google Scholar]
- Foster, R.M.; Morley, C.T.; Lees, J.M. Modified Push-Off Testing of an Inclined Shear Plane in Reinforced Concrete Strengthened with CFRP Fabric. J. Compos. Constr. 2016, 20, 04015061. [Google Scholar] [CrossRef]
- ASTM C496/C496M; Standard Test Method for Splitting Tensile Strength of Cylindrical Concrete Specimens. ASTM International: West Conshohocken, PA, USA, 2006; Volume 06, pp. 1–5.
- ASTM C618; Standard Specification for Coal Fly Ash and Raw or Calcined Natural Pozzolan for Use in Concrete. ASTM International: West Conshohocken, PA, USA, 2008; Volume 04, pp. 1–6.
- Cucuzza, R.; Aloisio, A.; Accornero, F.; Marinelli, A.; Bassoli, E.; Marano, G.C. Size-Scale Effects and Modelling Issues of Fibre-Reinforced Concrete Beams. Constr. Build. Mater. 2023, 392, 131727. [Google Scholar] [CrossRef]
- Minelli, F.; Conforti, A.; Cuenca, E.; Plizzari, G. Are Steel Fibres Able to Mitigate or Eliminate Size Effect in Shear? Mater. Struct. 2014, 47, 459–473. [Google Scholar] [CrossRef]
- Georgiou, A.V.; Pantazopoulou, S.J. Experimental and Analytical Investigation of the Shear Behavior of Strain Hardening Cementitious Composites. Struct. Eng. Mech. 2019, 72, 781–792. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).