A Critical Comparison of Correlations for Rapid Estimation of Subgrade Stiffness in Pavement Design and Construction
Abstract
1. Introduction
2. Methodology
2.1. General Description
2.2. Literature Review on MR-CBR Correlations
2.3. Laboratory Procedure
2.4. Definition of Pavement Design Parameters
3. Results and Discussion
3.1. Laboratory Procedure
3.1.1. Physical Properties
3.1.2. Mechanical Properties
3.2. Determination of Resilient Modulus MR
3.3. Sensitivity Analysis
4. Conclusions
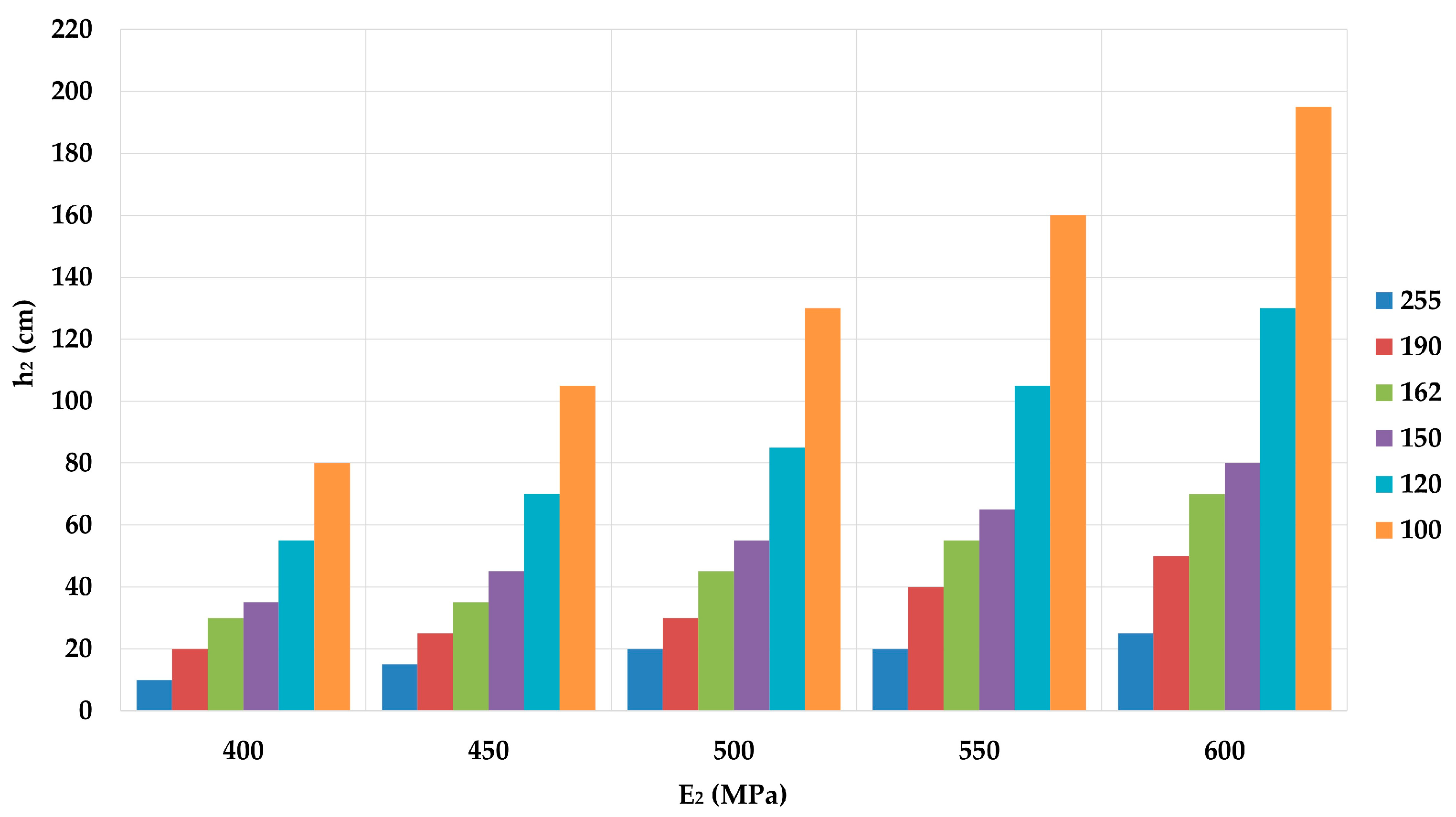
- In general, the thickness of the unbound granular layer (h2) increases when the modulus of elasticity (E2) increases, assuming a constant value of the resilient modulus (MR). In addition, h2 also increases when MR decreases at a constant value of E2. The observed discrepancies between the results are probably due to the inadequacy of the MR-CBR correlation for the soil material studied. For example, the values of MR for the Paterson et al. [32] and Powell et al. [33] correlations are of the same order of magnitude, but there are variations in the h2 values due to the suitability of the first correlation for a comparatively higher quality material;
- From all correlations, it can be deduced that as MR decreases, lower values of E2 are required to ensure lower values of h2, taking into account a combination of economical construction and minimum compaction effort;
- According to the correlation of Green and Hall [31], the requirement of high-quality unbound material for the construction layer (base/sub-base) makes construction uneconomical despite the low thickness h2 required, while for lower values of E2, h2 is extremely low for a total layer thickness;
- The correlations of Heukelom and Foster [29] and Heukelom and Klomp [30] appear to be similarly applicable to the soil sample studied, since similar thicknesses of the design layer occur for the same values of E2. However, due to the different limitations of each correlation, the values of h2 may produce a conservative or overpredicted solution, respectively;
- As for the Hopkins et al. [34] correlation, h2 has a wide range of acceptable values, namely 25 to 40 cm, which refers to a medium-high range of E2 values of 450–550 MPa;
- Based on the current findings, the Hopkins et al. [34] correlation assumes an appropriate overall thickness of the base and sub-base layers. In this context, low values of h2 are required for correspondingly low values of E2. This is considered to be the optimum combination for an economical structure, since a lower compaction effort may be required incidentally. However, considering also the limitations of each correlation, the correlation of Heukelom and Foster [29] seems to be an acceptable solution too.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- NCHRP. Guide for Mechanistic–Empirical Design of New and Rehabilitated Structures; NCHRP Report 01–37A; National Cooperative Highway Research Program: Washington, DC, USA, 2010. [Google Scholar]
- Sagar, C.P.; Badiger, M.; Mamatha, K.H.; Dinesh, S.V. Prediction of CBR using dynamic cone penetrometer index, Mater. Today Proc. 2022, 60, 223–228. [Google Scholar] [CrossRef]
- Seed, H.B.; Chan, C.K.; Lee, C.E. Resilience characteristics of subgrade soils and their relation to fatigue failures in asphalt pavements. In Proceedings of the International Conference on the Structural Design of Asphalt Pavements, Ann Arbor, MI, USA, 20–24 August 1962; pp. 77–113. [Google Scholar]
- SETRA. Conception et Dimensionnement des Structures de Chaussée; SETRA-LCPC: Paris, France, 1994; ISBN 2-7208-7010-2. [Google Scholar]
- American Association of State Highway and Transportation Officials (AASHTO). A Policy on Geometric Design of Highways and Streets; The Association: Washington, DC, USA, 2004; ISBN 13 9781560512639. [Google Scholar]
- Austroads. Pavement Design: A Guide to the Structural Design of Road Pavements; ARRB Transport Research Ltd.: Sydney, NSW, Australia, 2004. [Google Scholar]
- Brown, S.F. Soil mechanics in pavement engineering. Geotechnique 1996, 46, 383–426. [Google Scholar] [CrossRef]
- Arshad, M. Development of a Correlation between the Resilient Modulus and CBR Value for Granular Blends Containing Natural Aggregates and RAP/RCA Materials. Adv. Mater. Sci. Eng. 2019, 2019, 8238904: 1–8238904: 16. [Google Scholar] [CrossRef]
- Khalid, R.A.; Ahmad, N.; Arshid, M.U.; Zaidi, S.B.; Maqsood, T.; Hamid, A. Performance evaluation of weak subgrade soil under increased surcharge weight. Constr. Build. Mater. 2022, 318, 126131. [Google Scholar] [CrossRef]
- Hight, D.W.; Stevens, M.G.H. An analysis of the California Bearing Ratio test in saturated clays. Geotechnique 1982, 32, 315–322. [Google Scholar] [CrossRef]
- Fleming, P.R.; Rogers, C.D.F. Assessment of pavement foundations during construction. Proc. Inst. Civ. Eng.-Transp. 1995, 111, 105–115. [Google Scholar] [CrossRef]
- Brown, S.F.; O’Reilly, M.P.; Loach, S.C. The relationship between California Bearing Ratio and elastic stiffness for compacted clays. Gr. Eng. 1996, 23, 27–31. [Google Scholar]
- Hossain, S.; Dickerson, G.; Weaver, C. Comparative Study of VTM and AASHTO Test Method for CBR. VDOT: Co Materials Division. 2005. Available online: https://www.virginiadot.org/business/resources/bu-mat-cbr-report.pdf (accessed on 23 January 2023).
- Kumar, P.; Dilip, D.; Babu, G.L.S. Critical appraisal of correlations between CBR and subgrade modulus. Indian Highw. 2014, 75, 15–24. [Google Scholar]
- Mendoza, C.; Caicedo, B. Elastoplastic framework of relationships between CBR and Young’s modulus for fine grained materials. Transp. Geotech. 2019, 21, 100280. [Google Scholar] [CrossRef]
- Garg, N.; Larkin, A.; Brar, H. A comparative subgrade evaluation using CBR, vane shear, light weight deflectometer, and resilient modulus tests. In Proceedings of the 8th International Conference on the Bearing Capacity of Roads, Railways and Airfields, Champaign, IL, USA,, 29 June–2 July 2009; CRC Press: Boca Raton, FL, USA, 2009; pp. 57–64. [Google Scholar]
- Dione, A.; Fall, M.; Berthaud, Y.; Benboudjama, F.; Michou, A. Implementation of resilient modulus–CBR relationship in mechanistic pavement design. Sci. Appliquées Et De L’ingénieur 2014, 1, 65–71. [Google Scholar]
- Kwon, J.; Kim, S.-H.; Tutumluer, E.; Wayne, M.H. Characterization of unbound aggregate materials considering physical and morphological properties. Int. J. Pavement Eng. 2017, 18, 303–308. [Google Scholar] [CrossRef]
- El-Ashwah, A.S.; Awed, A.M.; El-Badawy, S.M.; Gabr, A.R. A new approach for developing resilient modulus master surface to characterize granular pavement materials and subgrade soils. Constr. Build. Mater. 2019, 194, 372–385. [Google Scholar] [CrossRef]
- Chu, X.; Dawson, A.; Thom, N. Prediction of resilient modulus with consistency index for fine-grained soils. Transp. Geotech. 2021, 31, 100650. [Google Scholar] [CrossRef]
- Lim, S.M.; Yao, K.; Jin, D.; Albadri, W.M.; Liu, X. Influence of matric suction on resilient modulus and CBR of compacted Ballina clay. Constr. Build. Mater. 2022, 359, 129482. [Google Scholar] [CrossRef]
- George, V.; Kumar, A. Effect of soil parameters on modulus of resilience based on portable falling weight deflectometer tests on lateritic sub-grade soils. Int. J. Geotech. Eng. 2017, 14, 55–61. [Google Scholar] [CrossRef]
- Dhar, S.; Hussain, M. The strength and microstructural behavior of lime stabilized subgrade soil in road construction. Int. J. Geotech. Eng. 2021, 15, 471–483. [Google Scholar] [CrossRef]
- Jiang, X.; Gabrielson, J.; Titi, H.; Huang, B.; Bai, Y.; Polaczyk, P.; Hu, W.; Zhang, M.; Xiao, R. Field investigation and numerical analysis of an inverted pavement system in Tennessee, USA. Constr. Build. Mater. 2022, 35, 100759. [Google Scholar] [CrossRef]
- Jiang, X.; Titi, H.; Ma, Y.; Polaczyk, P.; Zhang, M.; Gabrielson, J.; Bai, Y.; Huang, B. Evaluating the performance of inverted pavement structure using the accelerated pavement test (APT). Constr. Build. Mater. 2022, 346, 128489. [Google Scholar] [CrossRef]
- Yoder, E.J.; Witczak, M.W. Principles of Pavement Design, 2nd ed.; John Wiley & Sons: New York, NY, USA, 1975; ISBN 0471977802. [Google Scholar]
- Hveem, F.N. Pavement deflections and fatigue failures. Highw. Res. Board Bull. 1955, 114, 43–87. [Google Scholar]
- Abukhettala, M.; Fall, M. Geotechnical characterization of plastic waste materials in pavement subgrade applications. Transp. Geotech. 2021, 27, 100472. [Google Scholar] [CrossRef]
- Heukelom, W.; Foster, C.R. Dynamic Testing of Pavement. J. Soil Mech. Found. Div. 1960, 86, 1–28. [Google Scholar] [CrossRef]
- Heukelom, W.; Klomp, A.J.G. Dynamic testing as a means of controlling pavements during and after construction. In Proceedings of the International Conference on the Structural Design of Asphalt Pavements, Ann Arbor, MI, USA, 20–24 August 1962; Volume 203, pp. 495–510. [Google Scholar]
- Green, J.L.; Hall, J.W. Non- Destructive Vibratory Testing of Airport Pavement: Experimental Tests Results and Development of Evaluation Methodology and Procedure; Report no FAA-RD-73-205; Federal Aviation Administration: Washington, DC, USA, 1975. [Google Scholar]
- Paterson, W.D.L.; Maree, J.H. An Interim Mechanistic Procedure for the Structural Design Pavements; Technical Report RP/5/78; National Institute for Transport and Road Research: Pretoria, South Africa, 1978. [Google Scholar]
- Powell, W.D.; Potter, J.F.; Mayhew, H.C.; Nunn, M.E. The Structural Design of Bituminous Roads; Transport and Road Research Laboratory (TRRL) Report 1115; TRRL: Berkshire, UK, 1984. [Google Scholar]
- Hopkins, T.C. Bearing Capacity Analyses of Pavements; Research Report KTC-91-8; Kentucky Transportation Center: Lexington, KY, USA, 1991. [Google Scholar]
- EN 933-2; Test for Geometrical Properties of Aggregates-Part 2: Determination of Particle Size Distribution–Test Sieves, Nominal Size of Apertures. European Committee Standardization: Brussels, Belgium, 2020.
- ASTM D2487-17E01; Standard Practice for Classification of Soils for Engineering Purposes (Unified Soil Classification System). American Society for Testing and Material (ASTM) International: West Conshohocken, PA, USA, 2020.
- EN 13286-2; Unbound and Hydraulically Bound Mixtures-Part 2: Test Methods for Laboratory Reference Density and Water Content. European Committee Standardization: Brussels, Belgium, 2011.
- EN 13286-47; Unbound and Hydraulically Bound Mixtures–Part 47: Test Method for Determination of California Bearing Ratio, Immediate Bearing Index and Linear Swelling. European Committee Standardization: Brussels, Belgium, 2021.
- Huang, Y.H. Pavement Analysis and Design; Pearson Education, Inc.: Hoboken, NJ, USA, 2004; ISBN 0131424739. [Google Scholar]
- Shell. International Petroleum Company Limited, Shell Pavement Design Manual: Asphalt Pavements and Overlays for Road Traffic; Shell: London, UK, 1978. [Google Scholar]
- Nassiri, S.; Shafiee, M.H.; Khan, M.R.H.; Bayat, A. Evaluation of variation in unbound layers’ moduli and its effect on pavement design. Int. J. Geotech. Eng. 2015, 9, 140–149. [Google Scholar] [CrossRef]
- Dormon, E.M.; Metcalf, C.T. Design curves for flexible pavements based on layered system theory. Highw. Res. Rec. 1965, 71, 69–84. [Google Scholar]
- Brown, S.F.; Pappin, J.W. Modeling of Granular Materials in Pavements. Trans. Res. Rec. 1985, 1022, 45–51. [Google Scholar]
- Uzan, J. Characterization of granular material. Trans. Res. Rec. 1985, 1022, 52–59. [Google Scholar]
- Moffat, M.A.; Jameson, G.W. Characterization of Granular Material and Development of a Subgrade Strain Criterion; Report WD R98-005; Australian Road Research (ARRB): Victoria, BC, USA, 1998. [Google Scholar]
- Salt, G.; Stevens, D. Modular Ratios for Unbound Granular Pavement Layers. 2006. Available online: https://www.semanticscholar.org/paper/Modular-ratios-for-unbound-granular-pavement-layers-Salt-Stevens/1566fb5ba97c7f2ee54268139aecef833e5434cf (accessed on 23 January 2023).



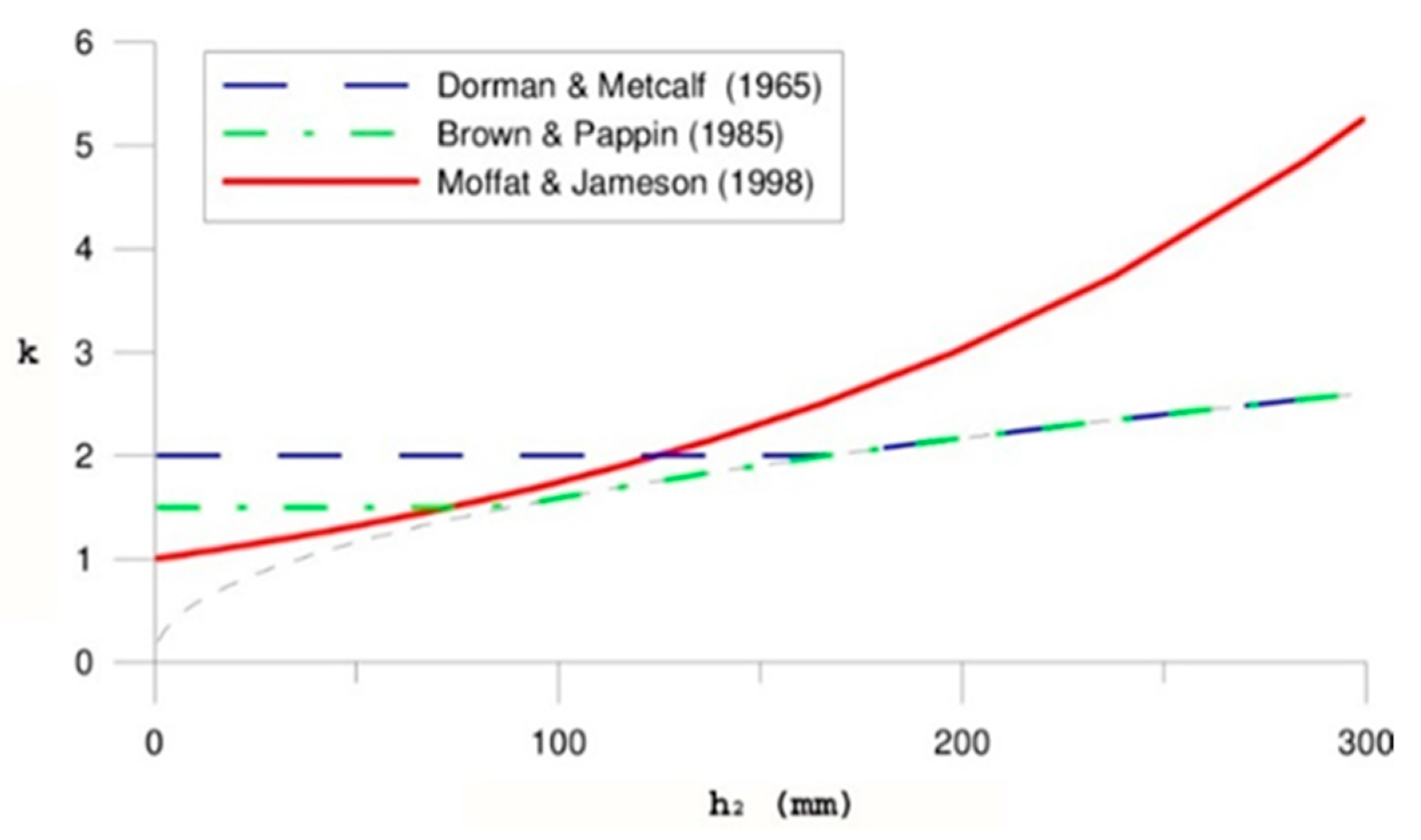

| Reference | Equation | |
|---|---|---|
| Heukelom and Foster [29] | (13) | |
| Dormon and Metcalf [42] | (14) | |
| Brown and Pappin [43] | (15) | |
| Properties | Sample Soil |
|---|---|
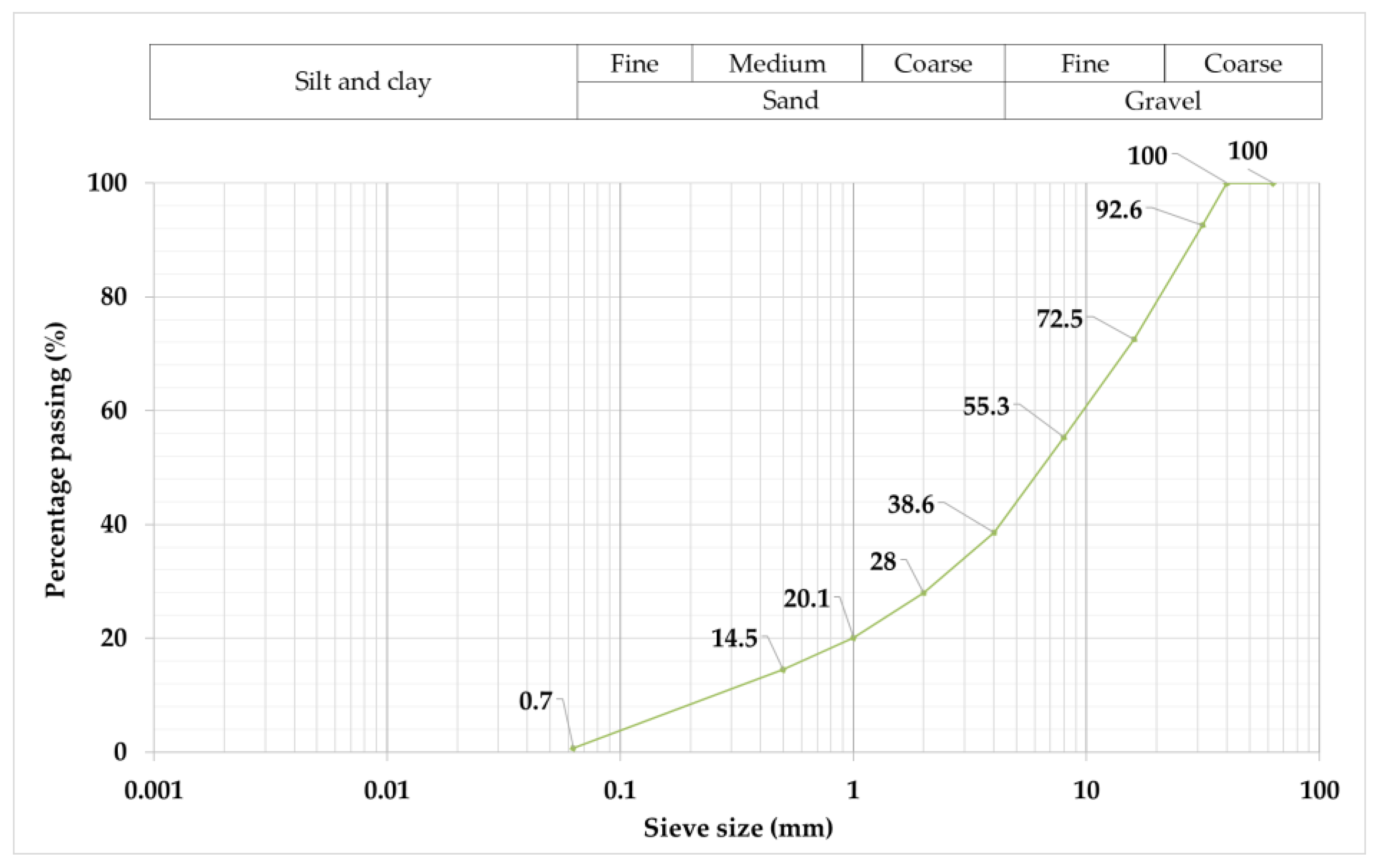
| d10 (mm) | 0.2 |
| d30 (mm) | 2.2 |
| d60 (mm) | 10 |
| Coefficient of uniformity (Cu) | 4.5 |
| Coefficient of curvature (Cc) | 2.4 |
| Optimum moisture content (%) | 6.5 |
| Maximum dry density (kg/m3) | 2240 |
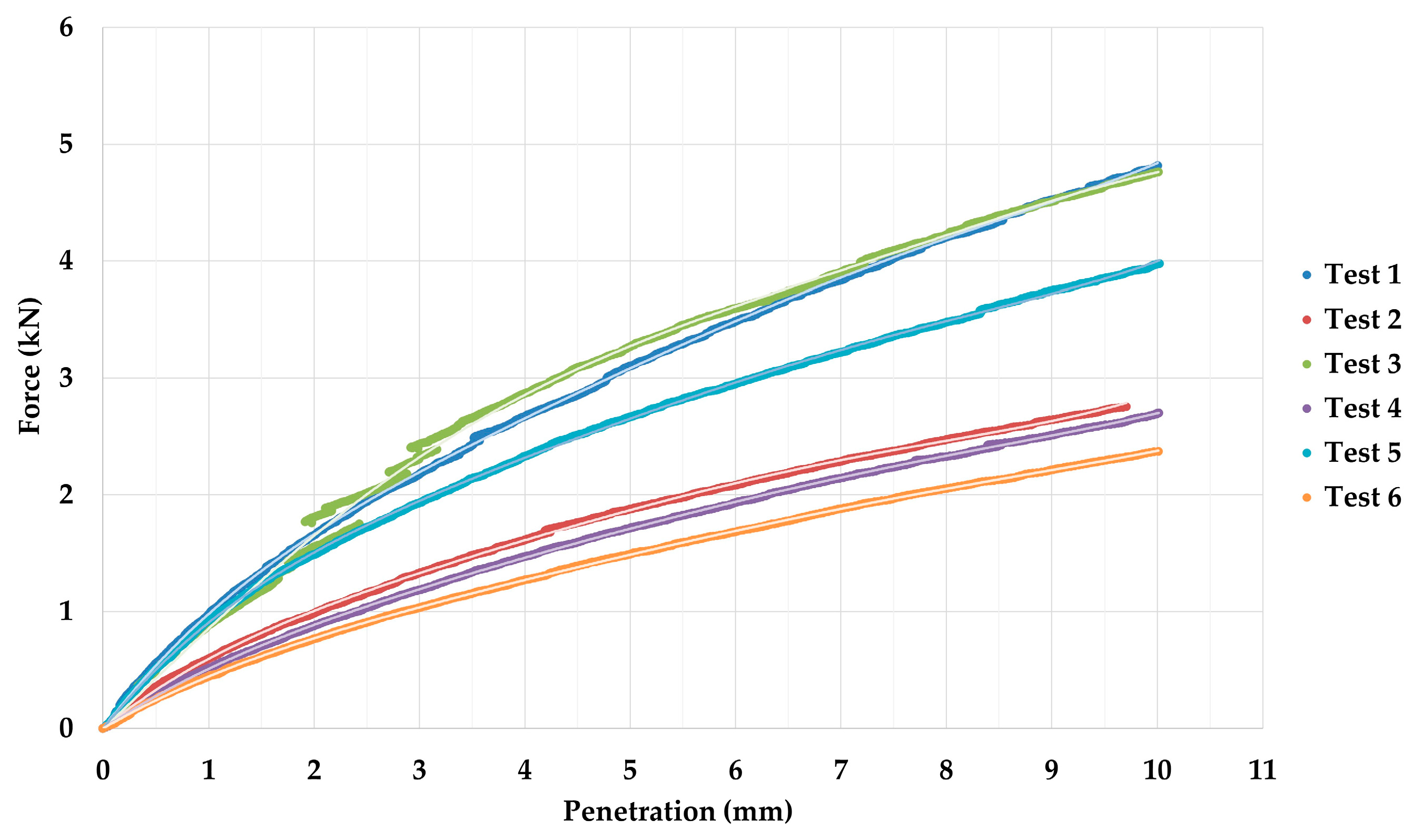
| No. Test | Standard Penetration (mm) | Applied Forces (kN) | CBR (%) |
|---|---|---|---|
| 1 | 2.50 | 1.95 | 14.77 |
| 5.00 | 3.10 | 15.50 | |
| 2 | 2.50 | 1.18 | 8.94 |
| 5.00 | 1.87 | 9.35 | |
| 3 | 2.50 | 2.03 | 15.38 |
| 5.00 | 3.28 | 16.40 | |
| 4 | 2.50 | 1.05 | 7.95 |
| 5.00 | 1.73 | 8.65 | |
| 5 | 2.50 | 1.75 | 13.26 |
| 5.00 | 2.65 | 13.25 | |
| 6 | 2.50 | 0.92 | 6.97 |
| 5.00 | 1.49 | 7.45 |
| Reference | Correlation |
|---|---|
| Heukelom and Foster [29] | |
| Heukelom and Klomp [30] | |
| Green and Hall [31] | |
| Paterson et al. [32] | |
| Powell et al. [33] | |
| Hopkins et al. [34] |
| Correlation | MR (MPa) |
|---|---|
| Green and Hall [31] | 255 |
| Hopkins et al. [34] | 190 |
| Heukelom and Foster [29] | 162 |
| Heukelom and Klomp [30] | 150 |
| Paterson et al. [32] | 120 |
| Powell et al. [33] | 100 |
| Correlation | Green and Hall [31] | Hopkins et al. [34] | Heukelom and Foster [29] | Heukelom and Klomp [30] | Paterson et al. [32] | Powell et al. [33] | |
|---|---|---|---|---|---|---|---|
| MR (MPa) | 255 | 190 | 162 | 150 | 120 | 100 | |
| K | |||||||
| E2 (MPa) | 400 | 1.57 | 2.10 | 2.47 | 2.67 | 3.32 | 4.02 |
| 450 | 1.76 | 2.36 | 2.78 | 3 | 3.74 | 4.52 | |
| 500 | 1.96 | 2.62 | 3.09 | 3.33 | 4.15 | 5.02 | |
| 550 | 2.16 | 2.88 | 3.40 | 3.67 | 4.57 | 5.52 | |
| 600 | 2.35 | 3.14 | 3.70 | 4 | 4.98 | 6.02 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Plati, C.; Tsakoumaki, M. A Critical Comparison of Correlations for Rapid Estimation of Subgrade Stiffness in Pavement Design and Construction. Constr. Mater. 2023, 3, 127-142. https://doi.org/10.3390/constrmater3010009
Plati C, Tsakoumaki M. A Critical Comparison of Correlations for Rapid Estimation of Subgrade Stiffness in Pavement Design and Construction. Construction Materials. 2023; 3(1):127-142. https://doi.org/10.3390/constrmater3010009
Chicago/Turabian StylePlati, Christina, and Maria Tsakoumaki. 2023. "A Critical Comparison of Correlations for Rapid Estimation of Subgrade Stiffness in Pavement Design and Construction" Construction Materials 3, no. 1: 127-142. https://doi.org/10.3390/constrmater3010009
APA StylePlati, C., & Tsakoumaki, M. (2023). A Critical Comparison of Correlations for Rapid Estimation of Subgrade Stiffness in Pavement Design and Construction. Construction Materials, 3(1), 127-142. https://doi.org/10.3390/constrmater3010009






