Experimental Investigation on the Compressive Stress-Sensing Ability of Steel Fiber-Reinforced Cement-Based Composites under Varying Temperature Conditions
Abstract
1. Introduction
2. Experimental Details
2.1. Materials
2.2. Electrical Properties Characterization and Testing Configuration
2.3. Stress-Sensing Capacity
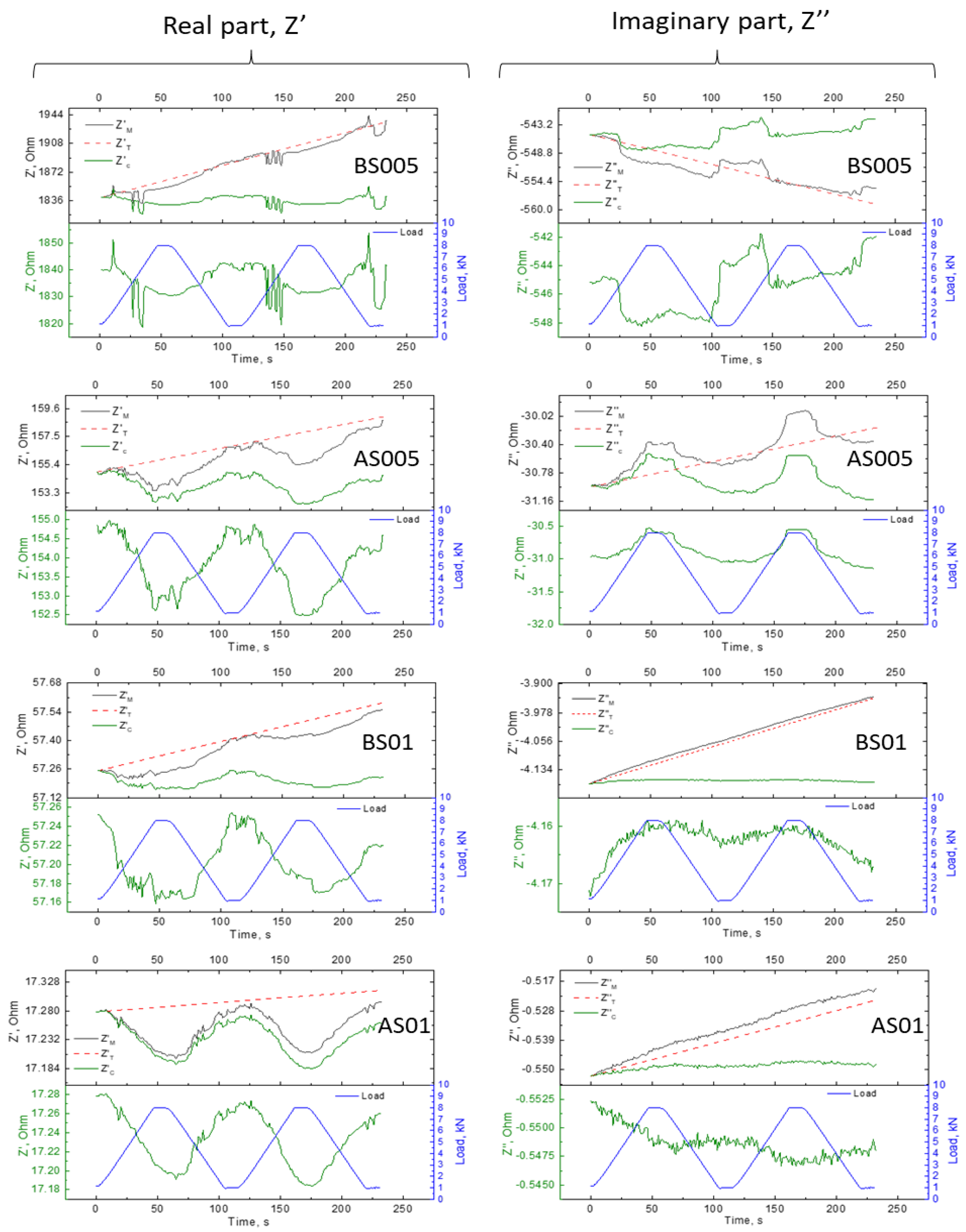
3. Results and Discussion
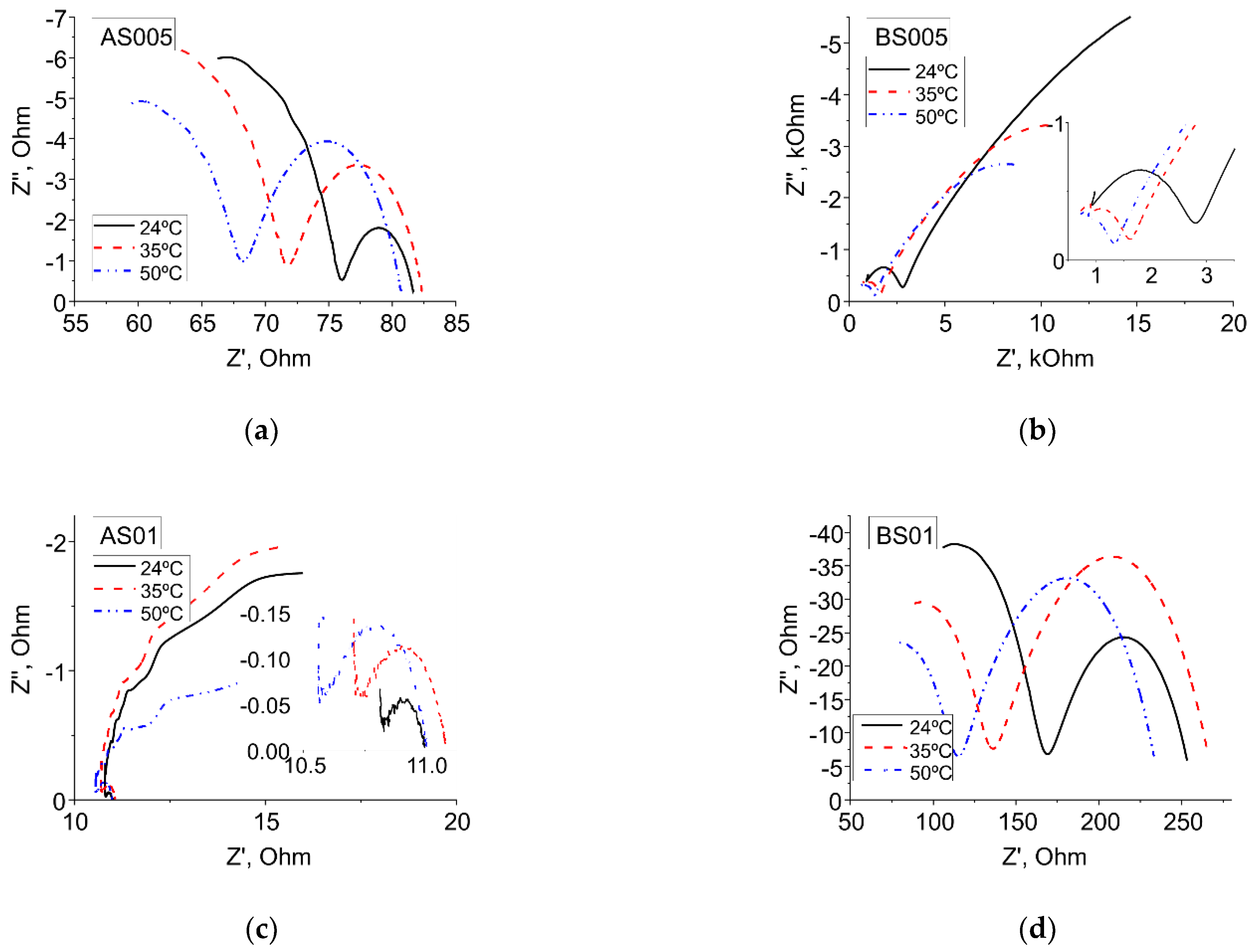
3.1. Electrical Impedance Spectroscopy Characterization
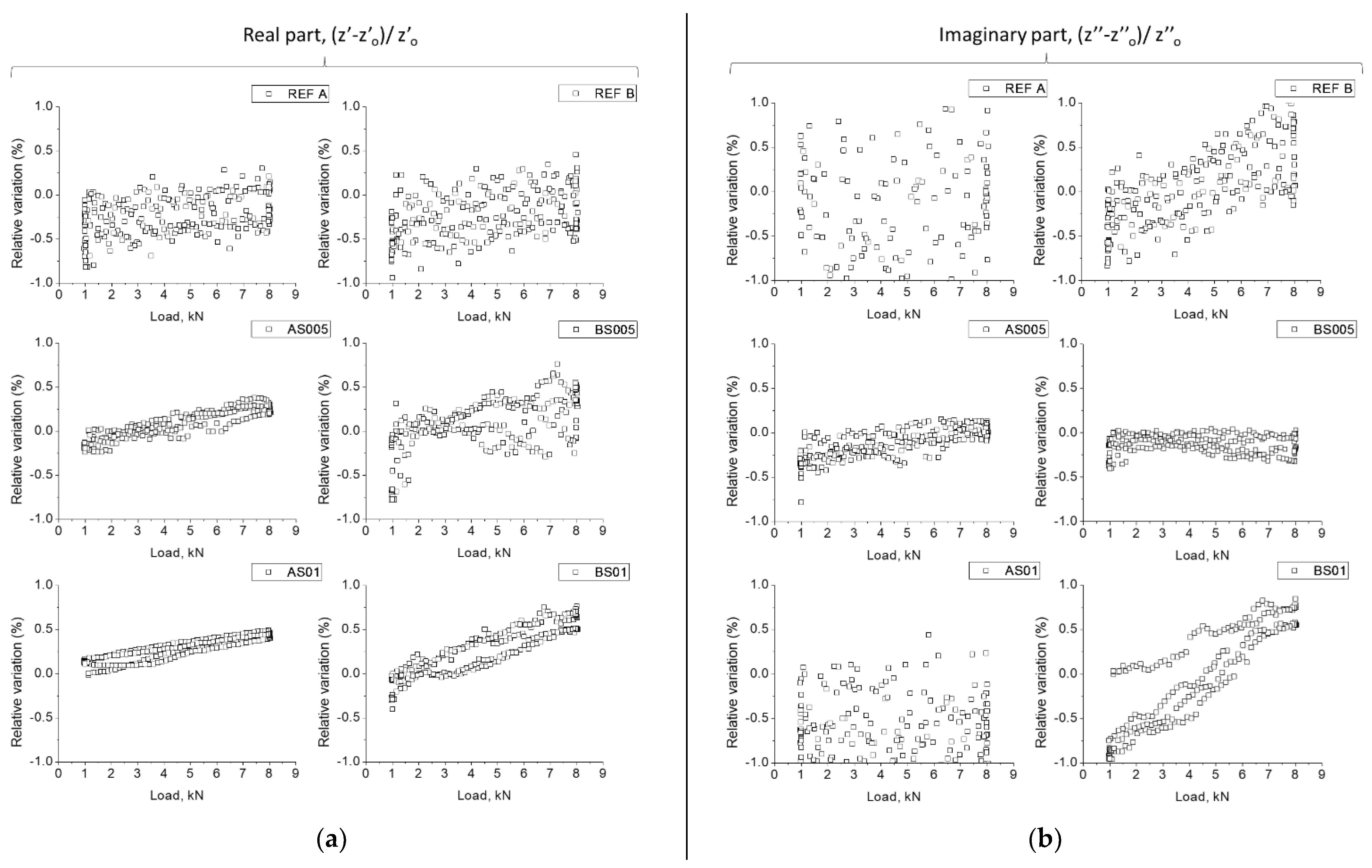
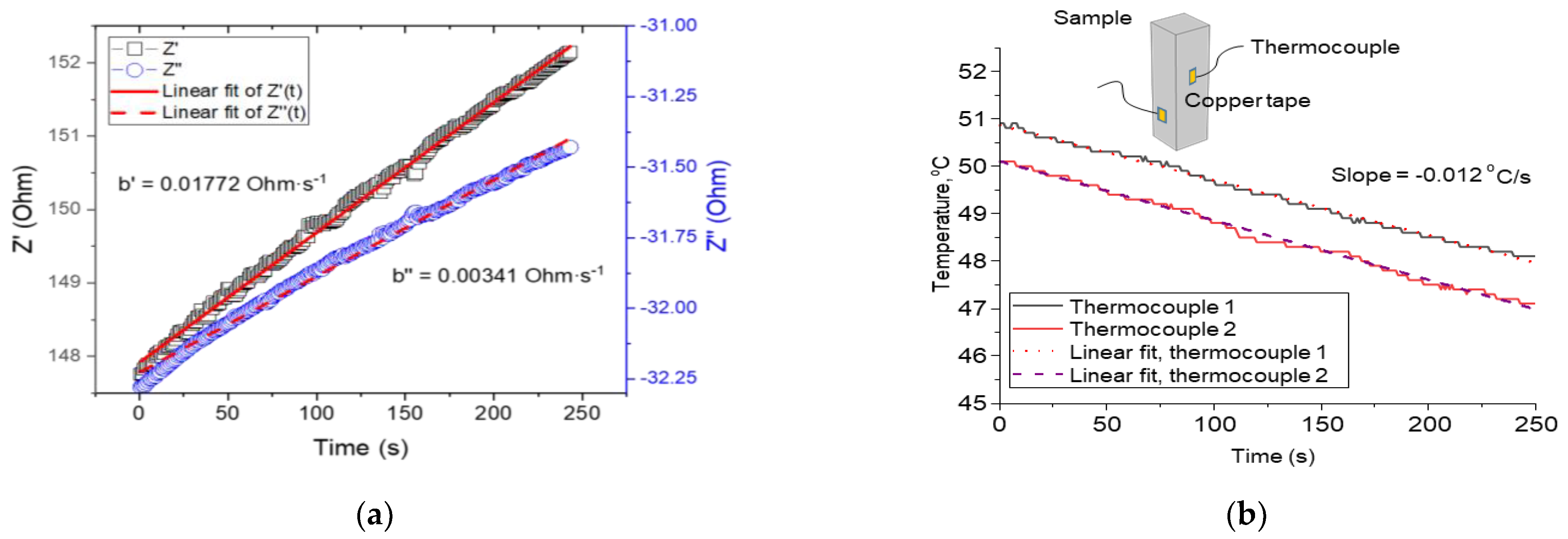
3.2. Stress-Sensing Capacity and Influence of Varying Sample Temperature
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chen, P.W.; Chung, D.D.L. Concrete as a new strain stress sensor. Compos. Part B Eng. 1996, 27, 11–23. [Google Scholar] [CrossRef]
- Carmona, F.; Canet, R.; Delhaes, P. Piezoresistivity of heterogeneous solids. J. Appl. Phys. 1987, 61, 2550–2557. [Google Scholar] [CrossRef]
- Banthia, N.; Djeridane, S.; Pigeon, M. Electrical resistivity of carbon and steel micro-fiber reinforced cements. Cem. Concr. Res. 1992, 22, 804–814. [Google Scholar] [CrossRef]
- Chen, P.-W.; Chung, D.D.L. Carbon fiber reinforced concrete for smart structures capable of non-destructive flaw detection. Smart Mater. Struct. 1993, 2, 22–30. [Google Scholar] [CrossRef]
- Chung, D.D.L. A critical review of piezoresistivity and its application in electrical-resistance-based strain sensing. J. Mater. Sci. 2020, 55, 15367–15396. [Google Scholar] [CrossRef]
- Dong, W.; Li, W.; Tao, Z.; Wang, K. Piezoresistive properties of cement-based sensors: Review and perspective. Constr. Build. Mater. 2019, 203, 146–163. [Google Scholar] [CrossRef]
- Han, B.; Wang, Y.; Dong, S.; Zhang, L.; Ding, S.; Yu, X.; Ou, J. Smart concretes and structures: A review. J. Intell. Mater. Syst. Struct. 2015, 26, 1303–1345. [Google Scholar] [CrossRef]
- Han, B.; Yu, X.; Ou, J. Self-Sensing Concrete in Smart Structures; Elsevier: Amsterdam, The Netherlands, 2014. [Google Scholar] [CrossRef]
- Downey, A.; D’Alessandro, A.; Baquera, M.; García-Macías, E.; Rolfes, D.; Ubertini, F.; Laflammea, S.; Castro-Triguero, R. Damage detection, localization and quantification in conductive smart concrete structures using a resistor mesh model. Eng. Struct. 2017, 148, 924–935. [Google Scholar] [CrossRef]
- Bontea, D.-M.; Chung, D.D.L.; Lee, G.C. Damage in carbon fiber-reinforced concrete, monitored by electrical resistance measurement. Cem. Concr. Res. 2000, 30, 651–659. [Google Scholar] [CrossRef]
- Hou, T.-C.; Lynch, J.P. Conductivity-based strain monitoring and damage characterization of fiber reinforced cementitious structural components. Proc. SPIE 2005, 5765, 419–429. [Google Scholar] [CrossRef]
- Peled, A.; Torrents, J.M.; Mason, T.O.; Shah, S.P.; Garboczi, E.J. Electrical impedance spectra to monitor damage during tensile loading of cement composites. ACI Mater. J. 2001, 98, 313–322. [Google Scholar] [CrossRef]
- Li, M.; Lin, V.W.J.; Lynch, J.P.; Li, V.C. Carbon Black Engineered Cementitious Composites—Mechanical and Electrical Characterization. In SP-292: Structural Health Monitoring Technologies; American Concrete Institute: Farmington Hills, MI, USA, 2013; Volume 292, pp. 59–73. [Google Scholar] [CrossRef]
- Gupta, S.; Gonzalez, J.G.; Loh, K.J. Self-sensing concrete enabled by nano-engineered cement-aggregate interfaces. Struct. Health Monit. 2017, 16, 309–323. [Google Scholar] [CrossRef]
- Downey, A.; D’Alessandro, A.; Ubertini, F.; Laflamme, S. Automated crack detection in conductive smart-concrete structures using a resistor mesh model. Meas. Sci. Technol. 2018, 29, 035107. [Google Scholar] [CrossRef]
- Laflamme, S.; D’Alessandro, A.; Castro-Triguero, R.; Downey, A.; Garcia-Macias, E.; Ubertini, F. Continuous and embedded solutions for SHM of concrete structures using changing electrical potential in self-sensing cement-based composites. In Nondestructive Characterization and Monitoring of Advanced Materials, Aerospace, and Civil Infrastructure; SPIE: Bellingham, WA, USA, 2017; Volume 101691G. [Google Scholar] [CrossRef]
- Konsta-Gdoutos, M.S.; Aza, C.A. Self sensing carbon nanotube (CNT) and nanofiber (CNF) cementitious composites for real time damage assessment in smart structures. Cem. Concr. Compos. 2014, 53, 162–169. [Google Scholar] [CrossRef]
- Han, B.; Yu, X.; Kwon, E. A self-sensing carbon nanotube/cement composite for traffic monitoring. Nanotechnology 2009, 20, 445501. [Google Scholar] [CrossRef]
- Shi, Z.Q.; Chung, D.D.L. Carbon fiber-reinforced concrete for traffic monitoring and weighing in motion. Cem. Concr. Res. 1999, 29, 435–439. [Google Scholar] [CrossRef]
- Ranade, R.; Zhang, J.; Lynch, J.P.; Li, V.C. Influence of micro-cracking on the composite resistivity of Engineered Cementitious Composites. Cem. Concr. Res. 2014, 58, 1–12. [Google Scholar] [CrossRef]
- Ding, S.; Wang, Y.-W.W.; Ni, Y.-Q.Q.; Han, B. Structural modal identification and health monitoring of building structures using self-sensing cementitious composites. Smart Mater. Struct. 2020, 29, 055013. [Google Scholar] [CrossRef]
- D’Alessandro, A.; Birgin, H.B.; Ubertini, F. Carbon Microfiber-Doped Smart Concrete Sensors for Strain Monitoring in Reinforced Concrete Structures: An Experimental Study at Various Scales. Sensors 2022, 22, 6083. [Google Scholar] [CrossRef]
- D’Alessandro, A.; Ubertini, F.; García-Macías, E.; Castro-Triguero, R.; Downey, A.; Laflamme, S.; Meoni, A.; Materazzi, A.L. Static and Dynamic Strain Monitoring of Reinforced Concrete Components through Embedded Carbon Nanotube Cement-Based Sensors. Shock Vib. 2017, 2017, 3648403. [Google Scholar] [CrossRef]
- Ubertini, F.; Materazzi, A.L.; D’Alessandro, A.; Laflamme, S. Natural frequencies identification of a reinforced concrete beam using carbon nanotube cement-based sensors. Eng. Struct. 2014, 60, 265–275. [Google Scholar] [CrossRef]
- Monteiro, A.O.; Cachim, P.B.; Costa, P.M.F.J. Self-sensing piezoresistive cement composite loaded with carbon black particles. Cem. Concr. Compos. 2017, 81, 59–65. [Google Scholar] [CrossRef]
- Ferdiansyah, T.; Turatsinze, A.; Balayssac, J. Design and characterization of self-sensing steel fiber reinforced concrete. MATEC Web Conf. 2018, 199, 11008. [Google Scholar] [CrossRef][Green Version]
- Nguyen, D.L.; Lam, M.N.-T.; Kim, D.J.; Song, J. Direct tensile self-sensing and fracture energy of steel-fiber-reinforced concretes. Compos. Part B Eng. 2020, 183, 107714. [Google Scholar] [CrossRef]
- Wen, S.; Chung, D.D.L. A comparative study of steel- and carbon-fibre cement as piezoresistive strain sensors. Adv. Cem. Res. 2003, 15, 119–128. [Google Scholar] [CrossRef]
- Han, B.G.; Han, B.Z.; Ou, J.P. Experimental study on use of nickel powder-filled Portland cement-based composite for fabrication of piezoresistive sensors with high sensitivity. Sens. Actuators A Phys. 2009, 149, 51–55. [Google Scholar] [CrossRef]
- Dinesh, A.; Suji, D.; Pichumani, M. Electro-mechanical investigations of steel fiber reinforced self-sensing cement composite and their implications for real-time structural health monitoring. J. Build. Eng. 2022, 51, 104343. [Google Scholar] [CrossRef]
- Yoo, D.Y.; You, I.; Lee, S.J. Electrical properties of cement-based composites with carbon nanotubes, graphene, and graphite nanofibers. Sensors 2017, 17, 1064. [Google Scholar] [CrossRef]
- Yoo, D.Y.; You, I.; Zi, G.; Lee, S.J. Effects of carbon nanomaterial type and amount on self-sensing capacity of cement paste. Meas. J. Int. Meas. Confed. 2019, 134, 750–761. [Google Scholar] [CrossRef]
- Han, B.; Ou, J. Embedded piezoresistive cement-based stress/strain sensor. Sens. Actuators A Phys. 2007, 138, 294–298. [Google Scholar] [CrossRef]
- Lee, S.H.; Kim, S.; Yoo, D.Y. Hybrid effects of steel fiber and carbon nanotube on self-sensing capability of ultra-high-performance concrete. Constr. Build. Mater. 2018, 185, 530–544. [Google Scholar] [CrossRef]
- Ding, Y.; Liu, G.; Hussain, A.; Pacheco-Torgal, F.; Zhang, Y. Effect of steel fiber and carbon black on the self-sensing ability of concrete cracks under bending. Constr. Build. Mater. 2019, 207, 630–639. [Google Scholar] [CrossRef]
- Lee, S.Y.; Le, H.V.; Kim, D.J. Self-stress sensing smart concrete containing fine steel slag aggregates and steel fibers under high compressive stress. Constr. Build. Mater. 2019, 220, 149–160. [Google Scholar] [CrossRef]
- Loamrat, K.; Sappakittipakorn, M.; Sukontasukkul, P.; Banthia, N. Effect of Carbon Fiber and Graphite Powder on Resistivity of Cement-based Sensor under Compression. KMUTNB Int. J. Appl. Sci. Technol. 2014, 7, 29–35. [Google Scholar] [CrossRef]
- Toutanji, H.A.; El-Korchi, T.; Katz, R.N. Strength and reliability of carbon-fiber-reinforced cement composites. Cem. Concr. Compos. 1994, 16, 15–21. [Google Scholar] [CrossRef]
- ACI Committee 544. Report on the Physical Properties and Durability of Fiber-Reinforced Concrete; American Concrete Institute: Farmington Hills, MI, USA, 2010. [Google Scholar]
- Bentur, A.; Mindess, S. Fibre Reinforced Cementitious Composites, 2nd ed.; Taylor & Francis Group: London, UK; New York, NY, USA, 2007. [Google Scholar]
- Paul, S.C.; van Zijl, G.P.A.G.; Šavija, B. Effect of Fibers on Durability of Concrete: A Practical Review. Materials 2020, 13, 4562. [Google Scholar] [CrossRef]
- Reza, F.; Batson, G.B.; Yamamuro, J.A.; Lee, J.S. Volume Electrical Resistivity of Carbon Fiber Cement Composites. ACI Mater. J. 2001, 98, 25–35. [Google Scholar]
- Chang, C.; Song, G.; Gao, D.; Mo, Y.L. Temperature and mixing effects on electrical resistivity of carbon fiber enhanced concrete. Smart Mater. Struct. 2013, 22, 035021. [Google Scholar] [CrossRef]
- Chacko, R.M.; Banthia, N.; Mufti, A.A. Carbon-fiber-reinforced cement-based sensors. Can. J. Civ. Eng. 2007, 34, 284–290. [Google Scholar] [CrossRef]
- del Moral, B.; Baeza, F.J.; Navarro, R.; Galao, O.; Zornoza, E.; Vera, J.; Farcas, C.; Garcés, P. Temperature and humidity influence on the strain sensing performance of hybrid carbon nanotubes and graphite cement composites. Constr. Build. Mater. 2021, 284, 122786. [Google Scholar] [CrossRef]
- Ou, J.; Han, B. Piezoresistive cement-based strain sensors and self-sensing concrete components. J. Intell. Mater. Syst. Struct. 2009, 20, 329–336. [Google Scholar] [CrossRef]
- Song, X.H.; Zheng, L.X.; Li, Z.Q. Temperature Compensation in Deformation Testing for Smart Concrete Structures. Key Eng. Mater. 2009, 326–328, 1503–1506. [Google Scholar] [CrossRef]
- Cabeza, M.; Merino, P.; Nóvoa, X.R.; Sánchez, I. Electrical effects generated by mechanical loading of hardened Portland cement paste. Cem. Concr. Compos. 2003, 25, 351–356. [Google Scholar] [CrossRef]
- Sánchez, I.; Nóvoa, X.R.; de Vera, G.; Climent, M.A. Microstructural modifications in Portland cement concrete due to forced ionic migration tests. Study by impedance spectroscopy. Cem. Concr. Res. 2008, 38, 1015–1025. [Google Scholar] [CrossRef]
- Cabeza, M.; Merino, P.; Miranda, A.; Nóvoa, X.R.; Sanchez, I. Impedance spectroscopy study of hardened Portland cement paste. Cem. Concr. Res. 2002, 32, 881–891. [Google Scholar] [CrossRef]
- Tumidajski, P.J. Electrical conductivity of Portland cement mortars. Cem. Concr. Res. 1996, 26, 529–534. [Google Scholar] [CrossRef]
- Mason, T.O.; Campo, M.A.; Hixson, A.D.; Woo, L.Y. Impedance spectroscopy of fiber-reinforced cement composites. Cem. Concr. Compos. 2002, 24, 457–465. [Google Scholar] [CrossRef]
- Torrents, J.; Mason, T.; Garboczi, E. Impedance spectra of fiber-reinforced cement-based composites: A modeling approach. Cem. Concr. Res. 2000, 30, 585–592. [Google Scholar] [CrossRef]
- Allam, H.; Duplan, F.; Clerc, J.P.; Amziane, S.; Burtschell, Y. About electrical resistivity variation during drying and improvement of the sensing behavior of carbon fiber-reinforced smart concrete. Constr. Build. Mater. 2020, 264, 120699. [Google Scholar] [CrossRef]
- Allam, H.; Duplan, F.; Amziane, S.; Burtschell, Y. Assessment of manufacturing process efficiency in the dispersion of carbon fibers in smart concrete by measuring AC impedance. Cem. Concr. Compos. 2021, 127, 104394. [Google Scholar] [CrossRef]
- Berrocal, C.G.; Hornbostel, K.; Geiker, M.R.; Löfgren, I.; Lundgren, K.; Bekas, D.G. Electrical resistivity measurements in steel fibre reinforced cementitious materials. Cem. Concr. Compos. 2018, 89, 216–229. [Google Scholar] [CrossRef]
- Berrocal, C.; Lundgren, K.; Löfgren, I. Influence of Steel Fibres on Corrosion of Reinforcement in Concrete in Chloride Environments: A Review. In Proceedings of the 7th International Conference Fibre Concrete 2013 Proceedings, Paris, France, 2–4 September 2013. [Google Scholar]
- EN 197-1:2012; Cement—Composition, Specifications and Conformity Criteria for Common Cements. CEN: Brussels, Belgium, 2012.
- EN 196-1:2016; Methods of Testing Cement. Part 1: Determination of Strength. CEN: Brussels, Belgium, 2016.
- Hixson, A.D.; Woo, L.Y.; Campo, M.A.; Mason, T.O.; Garboczi, E.J. Intrinsic conductivity of short conductive fibers in composites by impedance spectroscopy. J. Electroceram. 2001, 7, 189–195. [Google Scholar] [CrossRef]
- Woo, L.Y.; Wansom, S.; Ozyurt, N.; Mu, B.; Shah, S.P.; Mason, T.O. Characterizing fiber dispersion in cement composites using AC-Impedance Spectroscopy. Cem. Concr. Compos. 2005, 27, 627–636. [Google Scholar] [CrossRef]
- Keddam, M.; Takenouti, H.; Nóvoa, X.R.; Andrade, C.; Alonso, C. Impedance measurements on cement paste. Cem. Concr. Res. 1997, 27, 1191–1201. [Google Scholar] [CrossRef]
- McCarter, W.J.J. A parametric study of the impedance characteristics of cement-aggregate systems during early hydration. Cem. Concr. Res. 1994, 24, 1097–1110. [Google Scholar] [CrossRef]
- Princigallo, A.; van Breugel, K.; Levita, G. Influence of the aggregate on the electrical conductivity of Portland cement concretes. Cem. Concr. Res. 2003, 33, 1755–1763. [Google Scholar] [CrossRef]
- Xu, G.; Beaudoin, J.J.; Jolicoeur, C.; Pagé, M. The effect of a polynaphthalene sulfonate superplasticizer on the contribution of the interfacial transition zone to the electrical resistivity of mortars containing silica and limestone fine aggregate. Cem. Concr. Res. 2000, 30, 683–691. [Google Scholar] [CrossRef]
- Xu, G.; Beaudoin, J.J. Effect of polycarboxylate superplasticizer on contribution of interfacial transition zone to electrical conductivity of Portland cement mortars. ACI Mater. J. 2000, 97, 418–424. [Google Scholar]
- Zhang, M.Q.; Zeng, H.M.; Wang, H.F.; Yao, X. An equivalent circuit model for electric conductive polymer composites. Adv. Compos. Lett. 1993, 2, 096369359300200. [Google Scholar] [CrossRef]
- Almuhammadi, K.; Bera, T.K.; Lubineau, G. Electrical impedance spectroscopy for measuring the impedance response of carbon-fiber-reinforced polymer composite laminates. Compos. Struct. 2017, 168, 510–521. [Google Scholar] [CrossRef]
- Torrents, J.M.; Mason, T.O.; Peled, A.; Shah, S.P.; Garboczi, E.J. Analysis of the impedance spectra of short conductive fiber-reinforced composites. J. Mater. Sci. 2001, 36, 4003–4012. [Google Scholar] [CrossRef]
- Solgaard, A.O.S.; Geiker, M.; Edvardsen, C.; Küter, A. Observations on the electrical resistivity of steel fibre reinforced concrete. Mater. Struct. 2014, 47, 335–350. [Google Scholar] [CrossRef]
- Chiarello, M.; Zinno, R. Electrical conductivity of self-monitoring CFRC. Cem. Concr. Compos. 2005, 27, 463–469. [Google Scholar] [CrossRef]
- Baeza, F.J.; Chung, D.D.L.; Zornoza, E.; Andión, L.G.; Garcés, P. Triple percolation in concrete reinforced with carbon fiber. ACI Mater. J. 2010, 107, 396–402. [Google Scholar]
- Castellote, M.; Andrade, C.; Alonso, M.C. Standardization, to a Reference of 25 °C, of Electrical Resistivity for Mortars and Concretes in Saturated or Isolated Conditions. ACI Mater. J. 2003, 99, 119–127. [Google Scholar]
- Spragg, R.P.; Castro, J.; Nantung, T.; Paredes, M.; Weiss, J. Variability Analysis of the Bulk Resistivity Measured Using Concrete Cylinders. Adv. Civ. Eng. Mater. 2012, 1, 104596. [Google Scholar] [CrossRef]
- Chung, D.D.L.; Wang, Y. Capacitance-based stress self-sensing in cement paste without requiring any admixture. Cem. Concr. Compos. 2018, 94, 255–263. [Google Scholar] [CrossRef]
- García-Macías, E.; D’Alessandro, A.; Castro-Triguero, R.; Pérez-Mira, D.; Ubertini, F. Micromechanics modeling of the uniaxial strain-sensing property of carbon nanotube cement-matrix composites for SHM applications. Compos. Struct. 2017, 163, 195–215. [Google Scholar] [CrossRef]
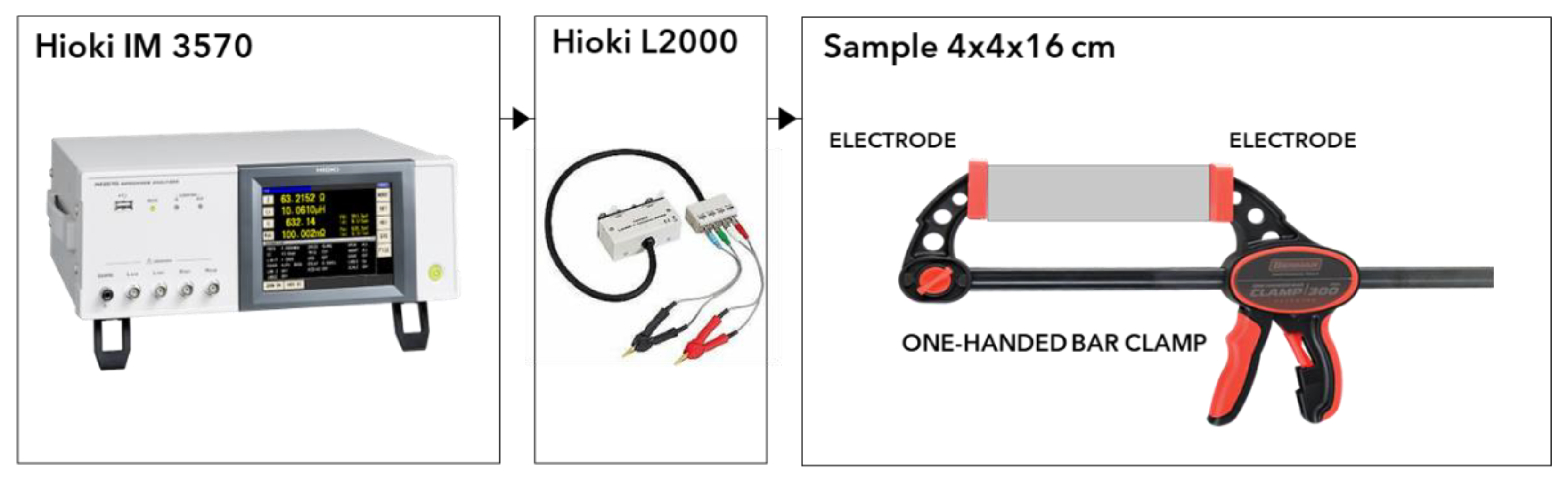





| Mortar | W/C | Aggregate Volume Fraction | Fiber Volume Fraction |
|---|---|---|---|
| REF A | 0.40 | 0.6 | - |
| AS005 | 0.05% | ||
| AS01 | 0.10% | ||
| REF B | 0.4 | - | |
| BS005 | 0.05% | ||
| BS01 | 0.10% |
| Sample | T, °C | Equivalent Circuit Parameters | Cusp Values | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| R1, Ohm | T1, SP1 Ohm−1 (×10−4) | P1 | R2, Ohm | T2, SP2 Ohm−1 (×10−8) | P2 | Rcomposite, Ohm | Frequency, Hz | |||
| AS005 | 1 | 24 | 5.8 | 6.6 | 0.70 | 76.04 | 1.6 | 0.67 | 76.0 | 81.8 |
| 2 | 3.8 | 10.0 | 0.70 | 57.32 | 1.8 | 0.68 | 57.3 | 61.1 | ||
| 3 | 5.3 | 7.39 | 0.70 | 75.75 | 1.5 | 0.67 | 75.7 | 81.1 | ||
| 1 | 35 | 10.6 | 2.27 | 0.71 | 71.92 | 3.3 | 0.63 | 71.9 | 82.5 | |
| 2 | 7.1 | 3.3 | 0.71 | 54.19 | 3.6 | 0.64 | 54.2 | 61.3 | ||
| 3 | 9.4 | 2.6 | 0.71 | 71.43 | 2.9 | 0.63 | 71.4 | 80.8 | ||
| 1 | 50 | 12.3 | 1.7 | 0.72 | 68.52 | 7.3 | 0.58 | 68.5 | 80.8 | |
| 2 | 8.4 | 2.5 | 0.71 | 52.37 | 7.8 | 0.59 | 52.4 | 60.8 | ||
| 3 | 11.4 | 1.9 | 0.71 | 69.07 | 6.1 | 0.59 | 69.1 | 80.5 | ||
| AS01 (*) | 1 | 24 | 0.2 | 190.3 | 0.67 | 10.82 | 0.3 | 0.89 | 10.8 | 11.0 |
| 2 | 0.3 | 87.7 | 0.69 | 14.67 | 0.9 | 0.79 | 14.7 | 15.0 | ||
| 3 | 0.5 | 60.5 | 0.69 | 16.99 | 1.8 | 0.75 | 17.0 | 17.5 | ||
| 1 | 35 | 0.4 | 47.8 | 0.70 | 10.72 | 0.7 | 0.84 | 10.7 | 11.1 | |
| 2 | 0.7 | 23.0 | 0.71 | 14.47 | 3.2 | 0.71 | 14.5 | 15.2 | ||
| 3 | 0.9 | 16.1 | 0.72 | 16.63 | 10 | 0.63 | 16.6 | 17.5 | ||
| 1 | 50 | 0.4 | 32.7 | 0.71 | 10.58 | 5.1 | 0.68 | 10.6 | 11.0 | |
| 2 | 0.8 | 16.0 | 0.73 | 14.24 | 27 | 0.56 | 14.2 | 15.0 | ||
| 3 | 1.1 | 12.1 | 0.72 | 16.30 | 62 | 0.50 | 16.3 | 17.4 | ||
| BS005 | 1 | 24 | 18114 | 0.1 | 0.61 | 2801 | 4.0 | 0.57 | 2801 | 20,915 |
| 2 | 8545 | 0.1 | 0.58 | 4052 | 0.7 | 0.65 | 4052 | 12,597 | ||
| 3 | 4100 | 0.1 | 0.56 | 2402 | 0.6 | 0.68 | 2402 | 6502 | ||
| 1 | 35 | 12503 | 0.1 | 0.59 | 1576 | 1.4 | 0.64 | 1576 | 14,079 | |
| 2 | 10096 | 0.1 | 0.58 | 2577 | 0.6 | 0.69 | 2577 | 12,673 | ||
| 3 | 4509 | 0.1 | 0.53 | 1681 | 0.4 | 0.72 | 1681 | 6190 | ||
| 1 | 50 | 10168 | 0.1 | 0.58 | 1295 | 1.2 | 0.66 | 1295 | 11,463 | |
| 2 | 6835 | 0.1 | 0.58 | 1868 | 0.6 | 0.68 | 1868 | 8703 | ||
| 3 | 4509 | 0.1 | 0.53 | 1681 | 0.3 | 0.72 | 1681 | 6190 | ||
| BS01 | 1 | 24 | 90.1 | 1.2 | 0.62 | 168.2 | 3.9 | 0.67 | 168.2 | 258.3 |
| 2 | 357.1 | 0.6 | 0.60 | 324.4 | 2.2 | 0.69 | 324.4 | 681.5 | ||
| 3 | 174.9 | 0.8 | 0.62 | 250.6 | 2.5 | 0.68 | 250.6 | 425.5 | ||
| 1 | 35 | 135.6 | 0.7 | 0.62 | 135.5 | 5.3 | 0.65 | 135.5 | 271.1 | |
| 2 | 449.1 | 0.5 | 0.60 | 235.5 | 2.3 | 0.69 | 235.5 | 684.6 | ||
| 3 | 265.0 | 0.4 | 0.61 | 206.2 | 3.0 | 0.68 | 206.2 | 471.2 | ||
| 1 | 50 | 123.5 | 0.7 | 0.62 | 114.8 | 5.9 | 0.65 | 114.8 | 238.3 | |
| 2 | 397.7 | 0.4 | 0.60 | 195 | 2.6 | 0.69 | 195.0 | 592.7 | ||
| 3 | 221.0 | 0.5 | 0.61 | 167.2 | 3.4 | 0.67 | 167.2 | 388.2 | ||
| Sample | Initial Temperature, °C | b′, Ohm·s−1 (×10−4) | b″, Ohm·s−1 (×10−4) | |
|---|---|---|---|---|
| AS005 | 1 | 35 | 3.82 | 3.61 |
| 2 | 4.81 | 5.10 | ||
| 3 | 5.40 | 5.19 | ||
| 1 | 50 | 12.4 | 16.1 | |
| 2 | 12.7 | 9.84 | ||
| 3 | 16.8 | 14.1 | ||
| AS01 | 1 | 35 | -- | 0.20 |
| 2 | -- | 0.31 | ||
| 3 | -- | 0.47 | ||
| 1 | 50 | -- | 0.81 | |
| 2 | -- | 0.90 | ||
| 3 | 1.50 | 1.27 | ||
| BS005 | 1 | 35 | 3516.2 | −0.02 |
| 2 | 9817.7 | −0.13 | ||
| 3 | 7765.0 | −0.19 | ||
| 1 | 50 | 5622.2 | −588.4 | |
| 2 | 7043.6 | −475.3 | ||
| 3 | 5165.0 | −537.4 | ||
| BS01 | 1 | 35 | 83.1 | 16.6 |
| 2 | 228.2 | 10.4 | ||
| 3 | 141.8 | 25.7 | ||
| 1 | 50 | 177.2 | 34.1 | |
| 2 | 473.4 | 21.5 | ||
| 3 | 333.5 | 38.5 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Eiras, J.N.; Duplan, F.; Payan, C. Experimental Investigation on the Compressive Stress-Sensing Ability of Steel Fiber-Reinforced Cement-Based Composites under Varying Temperature Conditions. Constr. Mater. 2022, 2, 258-275. https://doi.org/10.3390/constrmater2040017
Eiras JN, Duplan F, Payan C. Experimental Investigation on the Compressive Stress-Sensing Ability of Steel Fiber-Reinforced Cement-Based Composites under Varying Temperature Conditions. Construction Materials. 2022; 2(4):258-275. https://doi.org/10.3390/constrmater2040017
Chicago/Turabian StyleEiras, Jesús N., François Duplan, and Cédric Payan. 2022. "Experimental Investigation on the Compressive Stress-Sensing Ability of Steel Fiber-Reinforced Cement-Based Composites under Varying Temperature Conditions" Construction Materials 2, no. 4: 258-275. https://doi.org/10.3390/constrmater2040017
APA StyleEiras, J. N., Duplan, F., & Payan, C. (2022). Experimental Investigation on the Compressive Stress-Sensing Ability of Steel Fiber-Reinforced Cement-Based Composites under Varying Temperature Conditions. Construction Materials, 2(4), 258-275. https://doi.org/10.3390/constrmater2040017






