Response of Well-Graded Gravel–Rubber Mixtures in Triaxial Compression: Application of a Critical State-Based Generalized Plasticity Model

Abstract

The reuse of rubber inclusions obtained from End-of-Life Tires (ELTs) offers both environmental and technical benefits in civil engineering applications, reducing landfill disposal and enhancing the dynamic properties of geomaterials. The use of well-graded Gravel–Rubber Mixtures (wgGRMs), produced by blending well-graded gravel with granulated rubber, has been investigated for use in different geotechnical applications. The percentage of rubber inclusions included in wgGRMs significantly modifies the mechanical response of these mixtures, influencing stiffness, strength, dilatancy and dynamic properties. Due to the material heterogeneity (i.e., stiff gravel and soft rubber), the effective implementation of wgGRMs requires the development of constitutive models that can capture the non-linear stress–strain response of wgGRMs subjected to representative in situ loading conditions. In this study, a critical state-based generalized plasticity model is presented and tailored for wgGRMs. Calibration is performed using experimental data from isotropically consolidated drained triaxial tests on wgGRMs with different rubber contents. It is shown that the model accurately reproduces key features observed experimentally, including post-peak strain softening, peak strength variation, and volumetric changes across different confining pressure levels and rubber content fractions. This model represents a useful tool for predicting the behavior of wgGRMs in engineering practice, supporting the reuse of ELT-derived rubber.

1. Introduction

The disposal of End-of-Life Tires (ELTs) remains a pressing environmental challenge. Currently, approximately 1.5 billion ELTs are generated globally each year—equating to around 17 million tons of waste rubber [1,2]. Global ELT management statistics indicate that most ELTs are directed towards recovery pathways with clearly defined end uses, primarily material recovery (42% of total ELTs) and energy recovery (15%), while a smaller share—around 2%—is utilized in civil engineering applications and backfilling [3]. This framework underscores both the opportunities and constraints of current ELT valorization approaches, while emphasizing the need to enhance ELT recycling practices—particularly within civil engineering applications.

Recent research has investigated and characterized soil–rubber mixtures (SoRMs), produced by blending shredded/crumb rubber from ELTs with granular soils (mainly sand and/or gravel), for civil engineering applications. These geomaterials find use as lightweight fills [4,5], retaining wall backfill [6], drainage layers [7,8,9], and geotechnical seismic isolation systems [10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27], taking advantage of rubber’s excellent durability, low density, and enhanced damping properties [28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44]. Experimental studies reveal that SoRMs exhibit a distinct mechanical behavior compared to pure granular soils, depending on the parent soil and granulated rubber properties and test conditions [28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44]. Among the SoRMs, Gravel–Rubber Mixtures (GRMs), produced by blending granulated rubber from ELTs with poorly graded gravel, exhibit a general reduction in stiffness with partial replacement of gravel with rubber inclusions, accompanied by a transition in mechanical response from strain-softening to strain-hardening behavior. The volumetric response also varies depending on rubber content: mixtures with low rubber content often exhibit dilation, while those with higher rubber content tend to show contractive behavior [28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44]. Additionally, rubber inclusions improve energy dissipation under both monotonic and cyclic loading [18,24,45,46,47,48,49,50,51,52,53]. However, poorly graded gravel demands precise particle size selection, increasing time and cost requirements—making well-graded gravel a more practical choice for GRM production. Well-graded Gravel–Rubber Mixtures (wgGRMs) show excellent performance in both static and cyclic conditions, in terms of strength and energy dissipation capacity [54,55]. The mechanical response of wgGRMs is overall similar to that observed for other GRMs, especially in terms of stress–strain (strength) response, whereas they show a more contractive behavior compared to GRMs [54,55].

The effective implementation of GRMs and wgGRMs in engineering practice requires developing and integrating constitutive models that adequately describe the non-linear stress–strain response of materials subjected to representative in situ loading conditions. In geotechnical numerical modeling, a balance must be struck between computational efficiency and the level of sophistication in soil representation [56,57,58,59,60,61]. As stress–strain demands grow, the constitutive model must incorporate greater complexity—accounting for nonlinearity, plasticity, and hardening–softening behavior [62]. Increased model sophistication inevitably entails a larger set of parameters to be determined, making thorough and accurate calibration an essential step. Fiamingo et al. [63] have made a first step in this direction, investigating the capability of the Hardening Soil model with small-strain stiffness (HS-small) [64,65], which is present in many commonly used finite element (FE) codes, to reproduce the behavior of GRMs under static conditions. Results from FE simulation of isotropically consolidated drained monotonic triaxial tests (TxCD) [63] highlight that HS-small can capture the mechanical behavior of mixtures with volumetric rubber content (VRC) up to 45%, with material hardening and compressive behavior. However, the HS-small model is not able to describe the post-peak softening response that is associated with the material dilatancy, which in GRMs has typically been observed for VRC of less than 60% (gravel-like materials and dual mixtures [44]).

To address this issue, this study presents the first application of a critical-state-based generalized plasticity model [62,66] to wgGRMs, capable of reproducing their behavior over a wide range of confining pressures and rubber contents while accurately capturing post-peak hardening/softening responses. The model parameters are determined from experimental results obtained through TxCD tests on wgGRMs [54] with different VRC. By optimizing these parameters, the model successfully captures the principal experimentally observed behaviors, including strain-softening response, variations in peak strength, and volumetric changes across a range of confining pressures and VRC.

The contribution of this study is threefold. First, it adapts the critical state-based generalized plasticity framework, previously applied to other granular materials [62], for the first time to wgGRMs. Second, it moves beyond the experimental characterization of wgGRMs [54] by providing a predictive constitutive model. Third, and most critically, it resolves the key limitation of the HS-small model identified in Fiamingo et al. [63] by accurately capturing the post-peak softening response, thereby offering a more physically consistent framework for predicting the mechanical behavior of wgGRMs across a wide range of stress states and rubber contents. The model calibrated in this study provides a robust predictive framework for assessing the mechanical behavior of wgGRMs in geotechnical engineering applications. By enabling more accurate performance evaluation under varying stress conditions and material compositions, it supports the sustainable reuse of ELT-derived rubber in civil infrastructure, thereby contributing to resource conservation and waste reduction initiatives.

2. Characteristics of Well-Graded Gravel Rubber Mixtures (wgGRMs)

Laboratory tests on wgGRM specimens with VRC of 0, 25, 40, and 100% (hereafter indicated as wgGRM 100/0, wgGRM 75/25, wgGRM 60/40, and wgGRM 0/100, respectively) were performed by the authors to investigate their physical properties and mechanical behavior in static, dynamic, and cyclic conditions [54,55,56]. In this study, the TxCD test results [54] for wgGRM 100/0, wgGRM 75/25, and wgGRM 60/40 are further examined to calibrate the critical state-based generalized plasticity model parameters (Section 3.2). In the following sections, the main physical and mechanical properties, and critical state characteristics of the wgGRMs are briefly reported for comprehensiveness.

2.1. Physical Properties

The sandy gravel used in the mixtures was obtained from a quarry located near Christchurch City, New Zealand. In accordance with ASTM D2487-17 [67], the material is classified as well-graded gravel (GW). The particle size distribution comprises approximately 55% gravel, 43% sand, and 2% non-plastic fines. Shredded rubber derived from ELTs was commercially available in New Zealand as crumb rubber (tire chips and granulated rubber) and is free from steel reinforcement. It can be classified as granulated rubber according to ASTM D6270-17 [68]. The particle size distribution curves for the pure well-graded gravel (wgGRM 100/0) and pure granulated rubber (wgGRM 0/100) are shown in Figure 1a. The wgGRM 100/0 has a mean grain size of D_50,G = 5.78 mm, a uniformity coefficient (C_u,G) of approximately 27, and a curvature coefficient (C_c,G) of 2.18. The wgGRM 0/100 has a mean grain size of D_50,R = 5.35 mm, an approximate C_u,R of 1.94, and C_c,G of 1.46. The mixtures are characterized by a particle size ratio or aspect ratio (AR) of D_50,R/D_50,G ≈ 1, which ensures satisfactory strength and low compressibility [30,69], as well as minimal leaching characteristics [70,71].

The specific gravities of well-graded gravel (G_s,G = 2.67) and rubber (G_s,R = 1.15) [54] were determined according to NZS 4402 [72]. The variation in maximum and minimum void ratios (e_max and e_min) with VRC, evaluated according to ASTM D4254-16 [73] and ASTM D698-12 [74], respectively, is shown in Figure 1b. A continuous increase in e_max and e_min with increasing VRC is observed, as no distinct skeleton packing develops due to the similar sizes of rubber and gravel particles (AR ≈ 1). Specifically, as VRC increases, the rubber inclusions replace the gravel grains in the mixtures [30].

2.2. Mechanical Properties

TxCD tests were performed on homogeneous specimens at a degree of compaction (D_c) of 95% by using the under-compaction method [75]. Furthermore, 3% water by weight was introduced to generate suction, providing apparent cohesion that prevented rubber segregation. The saturation procedure involved three sequential methods: CO₂ percolation, water percolation, and the application of 250 kPa back-pressure. The isotropically consolidated specimens were then brought to effective confining pressures (p₀′) of 30, 60, and 100 kPa. These confinement levels simulate the field stress conditions for which wgGRMs are employed as lightweight backfills and geotechnical seismic isolation systems. Finally, specimens were sheared at a constant axial strain rate of 0.25%/min. More details about materials, specimen preparation, testing conditions, and test results on wgGRMs are reported in Fiamingo et al. [54].

Typical TxCD test results for wgGRM 100/0, wgGRM 0/100, and wgGRM 60/40 at p₀′ of 30, 60, and 100 kPa are reported in Figure 2, Figure 3 and Figure 4. The selected rubber percentage (0, 100, and 40%) describes the characteristic response of three distinct behavioral domains: gravel-like behavior, in which interparticle interactions among gravel particles dominate; rubber-like behavior, in which interactions among rubber inclusions are predominant; and transitional behavior, where both gravel and rubber fractions contribute significantly to load transfer [44,54].

Deviatoric stress–deviatoric strain (q-ε_q) relationships and volumetric strain–deviatoric strain (ε_v-ε_q) responses observed for wgGRM 100/0, wgGRM 0/100, and wgGRM 60/40 (initial void ratio, e₀ = 0.299–0.554; measured at the end of isotropic consolidation) are shown in Figure 2a,b, Figure 3a,b and Figure 4a,b. The wgGRM 100/0 exhibits a pronounced peak in deviatoric stress followed by post-peak softening behavior across all p₀′ levels (Figure 2a). Peak stress increases with p₀′ (Figure 2a) due to enhanced particle interlocking. In terms of volumetric response (Figure 2b), the higher p₀′ produces more contractive behavior, as gravel grains are forced to roll over one another and pack in a denser configuration, limiting dilation. In contrast, the wgGRM 0/100 displays an almost linear stress–strain relationship without a distinct peak shear stress (Figure 3a), i.e., strain-hardening behavior, along with a fully contractive response (Figure 3b), irrespective of the p₀′ level. The wgGRM 60/40 exhibits strain-hardening behavior across all p₀′ values (Figure 4a). In terms of volumetric response (Figure 4b), it shows contractive behavior. Minor dilation occurs at large deviatoric strains, with the onset strain decreasing as p₀′ is reduced. At low p₀′ levels, the less-compressed rubber fraction deforms less than the rigid gravel, facilitating particle sliding and rearrangement rather than deformation.

Moreover, the results indicate that at a deviatoric strain (ε_q) of approximately 20%, the wgGRM 100/0 reaches a state where deformation progresses continuously while maintaining a constant applied stress and constant volume (Figure 2b). This ultimate condition is generally referred to as the critical state, denoting the limiting condition in soil mechanics at which soil sustains indefinite shear deformation without any further variation in stress or volumetric response [76,77,78]. This condition is not clearly achieved for wgGRM 0/100 and wgGRM 60/40 (Figure 3b and Figure 4b). However, as for the wgGRM 60/40, it was possible to extrapolate the data point for the critical state condition to a “most probable” value as reported in Fiamingo et al. [54].

The critical state condition is represented by the Critical State Line (CSL) in Figure 2c,d, Figure 3c,d and Figure 4c,d, through both deviatoric stress–effective mean stress (q-p′) and void ratio–effective mean stress (e-p′) plots. Based on experimental and extrapolated data, the slope of the CSL (denoted as M_css) in the q-p′ plot was evaluated for wgGRM 100/0 and wgGRM 60/40, equal to 1.63 and 1.49, respectively (Figure 2c and Figure 4c). More specifically, for wgGRMs 60/40, the extrapolation was performed considering the data point to a “most probable” value, according to a well-established procedure adopted by many researchers [79,80,81,82,83]. Through this procedure, it is possible to determine the values of the void ratio and stress ratio at the critical state, as discussed in Fiamingo et al. [54]. As for the e-p′ paths, the void ratio for wgGRM 100/0 remains essentially constant between the consolidation and failure states at p₀′ = 30 and 60 kPa. In contrast, a slight reduction in void ratio is observed at p₀′ = 100 kPa (Figure 2d). For the wgGRM 100/0, the critical state is ultimately reached, accompanied by an increase in void ratio indicative of dilative behavior. Conversely, for the wgGRM 0/100, the void ratio decreases for all the confining pressures, indicating a full contractive behavior (Figure 3d). Regarding the wgGRM 60/40, the void ratio evolution shows a pronounced decrease (contractive behavior) from consolidation to failure, followed by minimal or negligible dilation as the mixture response approaches the critical state (Figure 4d).

In summary, the test results indicate that the critical state is not clearly achieved for wgGRM 0/100 and wgGRM 60/40. For wgGRM 0/100, the material behaves as a continuum of highly compressible, elastic particles. The deformation mechanism is dominated by the continuous volumetric compression of the rubber particles themselves, rather than the sliding and rolling of rigid grains typical of soils. A true critical state, where volume remains constant, may not exist in the classical sense for a pure granular rubber assembly under the stresses applied; it may require larger strains to achieve a state where compression ceases. For wgGRM 60/40, the soft rubber particles shield the gravel particles from forming a strong, persistent force chain network. The deformable rubber matrix absorbs the strain, preventing the gravel from rearranging into a stable, constant-volume configuration.

2.3. Insights into the Potential Critical State Behavior of wgGRMs

Based on experimental and extrapolated data [54], a potential evaluation of the critical state conditions for the different wgGRMs was performed. The CSL was additionally characterized using the model proposed by Li and Wang [54], wherein the void ratio at the critical state (e_cs) is defined by Equation (1):

$$e_{\mathrm{c}\mathrm{s}}=e-\lambda {\left({\displaystyle \frac{p_0^{\prime }}{p_{\mathrm{r}\mathrm{e}\mathrm{f}}}}\right)}^{1-n}$$

(1)

where λ is the slope of the CSL in the plane (p′/p_ref)¹⁻ⁿ-e, p_ref is the reference confining pressure (taken as 100 kPa), and n is a material constant (for an assemblage of granules with isotropic structure, a value of 0.3 is suggested [84]).

Figure 5 shows the trends obtained for wgGRM 100/0, wgGRM 75/25, and wgGRM 60/40, considering p₀′ equal to 30, 60, and 100 kPa. The resulting linear relationships exhibit comparable slopes, with an average value of approximately λ = 0.15.

As discussed in Fiamingo et al. [54], a critical state surface (CSS) [35] can be defined for wgGRMs in the p′-e-VRC space (Figure 6a) using Equation (2):

$$e_{\mathrm{c}\mathrm{s}}\left({\mathrm{f}}_{\mathrm{V}\mathrm{R}\mathrm{C}}\right)=e_{\mathsf{\Gamma }}\left({\mathrm{f}}_{\mathrm{V}\mathrm{R}\mathrm{C}}\right)-{\lambda }^{*}\left(f_{\mathrm{V}\mathrm{R}\mathrm{C}}\right)\ln p^{\prime }$$

(2)

being e_Γ and λ^* functions of VRC (f_VRC). More specifically, e_Γ is evaluated from the material coefficients for each mixture with different VRC, and it can be expressed by Equation (3):

$$e_{\mathsf{\Gamma }}\left(f_{\mathrm{V}\mathrm{R}\mathrm{C}}\right)=0.0001{\left(VRC\right)}^2-0.006\left(VRC\right)+0.833$$

(3)

λ^* is the slope of the CSS in the p′-e-VRC space (equal to the mean slope of all the CSLs in the p′-e plane, equal to 0.092).

The CSS can also be described in the p′-q-VRC space (Figure 6b) using Equation (4):

$$q_{\mathrm{c}\mathrm{s}}\left(f_{\mathrm{V}\mathrm{R}\mathrm{C}}\right)={M_{\mathrm{c}\mathrm{s}\mathrm{s}}}^{*}\left(f_{\mathrm{V}\mathrm{R}\mathrm{C}}\right)p^{\prime }$$

(4)

being q_cs and M_css^* functions of VRC (f_VRC). More specifically, q_cs is the deviatoric stress at the critical stress, and M_css^* is the slope of the CSS into the plane p′-q, evaluated considering the M_css of each stress path. It can be expressed according to Equation (5):

$${M_{\mathrm{c}\mathrm{s}\mathrm{s}}}^{*}\left(f_{\mathrm{V}\mathrm{R}\mathrm{C}}\right)=-0.0002{\left(VRC\right)}^2+0.0068\left(VRC\right)+1.63$$

(5)

Figure 6 confirms a good agreement between the CSS obtained by Equations (2) and (4), and the corresponding test data. Hence, a CSS can be defined for describing the stress–strain behavior and volumetric change of wgGRMs over a wide range of stress conditions and VRC.

3. Constitutive Model

The generalized plasticity framework [85,86,87] has proven to be highly effective in describing the mechanical response of sands and soils, particularly under both monotonic and cyclic conditions. In the generalized plasticity models, the yield surface, plastic potential, and hardening laws are not explicitly defined; instead, direction vectors are utilized.

Several studies in the literature have proposed the use of a model based on generalized plasticity and the critical state concept to characterize the mechanical behavior of coarse-grained materials [66,88]. In particular, Chiaro et al. [62] demonstrated that a critical state surface generalized plasticity model can effectively capture the stress–strain response and volumetric behavior of granular waste materials, such as coal wash and basic oxygen steel slag mixtures, across a wide range of stress conditions. In this framework, as previously introduced, a critical-state-based generalized plasticity model is adopted and specifically calibrated for wgGRMs to reproduce their behavior over a wide range of confining pressures and rubber contents. In the following sections, the fundamental equations of the constitutive model and the calibration process of the model parameters are discussed.

3.1. Fundamental Equations

The critical-state-based generalized plasticity model for wgGRMs is formulated for axisymmetric triaxial loading conditions (σ₂′ = σ₃′ and ε₂ = ε₃). Under this assumption, the stress and strain invariants are expressed as

$$\mathsf{\sigma }=\left\{\begin{array}{c}q\\ p\prime \end{array}\right\}=\left\{\begin{array}{c}{\sigma }_2\prime -{\sigma }_3\prime \\ \left({\sigma }_1\prime +2{\sigma }_3\prime \right)/3\end{array}\right\}$$

(6)

$$\epsilon =\left\{\begin{array}{c}{\epsilon }_{\mathrm{q}}\\ {\epsilon }_{\mathrm{v}}\end{array}\right\}=\left\{\begin{array}{c}2\left({\epsilon }_1-{\epsilon }_3\right)/3\\ {\epsilon }_1+2{\epsilon }_3\end{array}\right\}$$

(7)

The major and minor principal stresses and strains are denoted by σ₁′, σ₃′, ε₁, and ε₃, respectively.

The elastoplastic relationship is written in matrix form as:

$$\left\{\mathrm{d}\sigma \right\}={\mathbf{M}}^{\mathrm{e}\mathrm{p}}\left\{\mathrm{d}\epsilon \right\}$$

(8)

$$\left\{\begin{array}{c}\mathrm{d}q\\ {\mathrm{d}p}^{\prime }\end{array}\right\}=\left({\mathbf{M}}^{\mathrm{e}}-{\displaystyle \frac{{\mathbf{M}}^{\mathrm{e}}{\mathbf{m}}_{\mathrm{g}}{\mathbf{n}}_{\mathrm{f}}^{\mathrm{T}}{\mathbf{M}}^{\mathrm{e}}}{\mathrm{H}+{\mathbf{n}}_{\mathrm{f}}^{\mathrm{T}}{\mathbf{M}}^{\mathrm{e}}{\mathbf{m}}_{\mathrm{g}}}}\right)\left\{\begin{array}{c}{\mathrm{d}\epsilon }_{\mathrm{q}}\\ \mathrm{d}{\epsilon }_{\mathrm{v}}\end{array}\right\}$$

(9)

where (dσ) and (dε) are the stress and strain increment, M^e and M^ep are the elastic and elastoplastic stiffness matrices, m_g is the plastic flow direction vector, n_f is the loading direction vector, and H is the plastic modulus.

For strain-controlled drained triaxial loading investigated in this paper (where dε_q is prescribed and dp′ = dq/3), the governing equations become:

$$\mathrm{d}q=\left({\displaystyle \frac{3GH+3GK{\mathrm{m}}_{\mathrm{v}}{\mathrm{n}}_{\mathrm{v}}}{H+3G{\mathrm{m}}_{\mathrm{q}}{\mathrm{n}}_{\mathrm{q}}+K{\mathrm{m}}_{\mathrm{v}}{\mathrm{n}}_{\mathrm{v}}}}\right)\mathrm{d}{\epsilon }_{\mathrm{q}}-\left({\displaystyle \frac{3GK{\mathrm{m}}_{\mathrm{q}}{\mathrm{n}}_{\mathrm{v}}}{H+3G{\mathrm{m}}_{\mathrm{q}}{\mathrm{n}}_{\mathrm{q}}+K{\mathrm{m}}_{\mathrm{v}}{\mathrm{n}}_{\mathrm{v}}}}\right)\mathrm{d}{\epsilon }_{\mathrm{v}}$$

(10)

$$\mathrm{d}{\epsilon }_{\mathrm{v}}={\displaystyle \frac{G}{K}}\left({\displaystyle \frac{H+K{\mathrm{m}}_{\mathrm{v}}{\mathrm{n}}_{\mathrm{v}}-3K{\mathrm{m}}_{\mathrm{v}}{\mathrm{n}}_{\mathrm{q}}}{H+3G{\mathrm{m}}_{\mathrm{q}}{\mathrm{n}}_{\mathrm{q}}+G{\mathrm{m}}_{\mathrm{q}}{\mathrm{n}}_{\mathrm{v}}}}\right)\mathrm{d}{\epsilon }_{\mathrm{q}}$$

(11)

with G and K being shear and bulk moduli, respectively. The vectors m_q, m_v, and n_q, n_v represent components of m_g and n_f.

In the next sections, the major constituents of the model, such as elasticity, dilatancy, plastic flow direction, and plastic modulus, are described.

3.1.1. Elastic and Plastic Strains

The model assumes that both elastic and plastic strains develop for any given stress increment; thus, no purely elastic domain exists. Plastic strains are obtained as the difference between total and elastic strains. Elastic strains are evaluated using conventional elasticity theory [89]:

$$\mathrm{d}{\epsilon }_{\mathrm{q}}^{\mathrm{p}}=\mathrm{d}{\epsilon }_{\mathrm{q}}-\mathrm{d}{\epsilon }_{\mathrm{q}}^{\mathrm{e}}=\mathrm{d}{\epsilon }_{\mathrm{q}}-\mathrm{d}q/3G$$

(12)

$$\mathrm{d}{\epsilon }_{\mathrm{v}}^{\mathrm{p}}=\mathrm{d}{\epsilon }_{\mathrm{v}}-\mathrm{d}{\epsilon }_{\mathrm{v}}^{\mathrm{e}}=\mathrm{d}{\epsilon }_{\mathrm{v}}-\mathrm{d}{p}^{\prime }/K$$

(13)

where G and K are derived as

$$G={\displaystyle \frac{3\left(1-2\mathsf{\nu }\right)}{2\left(1+\mathsf{\nu }\right)}}K$$

(14)

$$K={\displaystyle \frac{\left(1+e\right)}{\mathsf{\kappa }}}{p}^{\prime }$$

(15)

Here, ν is the Poisson’s ratio and κ is the swelling–recompression index.

3.1.2. Stress–Dilatancy Relationship (Flow Rule)

The volumetric response during drained shearing is captured through a stress–dilatancy relation, which links plastic strain increments (d_g = dε^p_v/dε^p_q) to stress ratio (η = q/p′):

$$d_{\mathrm{g}}={\xi }_{\mathrm{g}}\left[{M_{\mathrm{c}\mathrm{s}\mathrm{s}}}^{*}\mathrm{e}\mathrm{x}\mathrm{p}\left({\mu }_{\mathrm{g}}{\psi }^{\mathrm{*}}\right)-\eta \right]$$

(16)

where ξ_g and μ_g are dilatancy constants, and ψ^* is the state parameter, according to Been and Jefferies [90]. It should be emphasized that Equation (11) represents an extension of the linear stress–dilatancy relationship introduced by Manzari and Dafalias [91], and it complies with the critical state surface (CSS) and phase transformation (PT) conditions, where volumetric strain is equal to zero for ψ = 0 and for η = M_css^* exp(ξ_g ψ*), respectively. Equation (16) expresses the dilatancy law: it links volumetric strain increment to shear strain increment, showing that whether the mixture contracts or dilates depends not only on stress ratio but also on its state relative to the critical state surface. Dilatancy (d_g) becomes zero at the critical state (η = M_css^*) and at the phase transformation (PT) state (η ≠ M_css^*), where soil shifts from contractive to dilative behavior.

3.1.3. Plastic Flow (Loading Direction)

Generalized plasticity does not require explicit yield or plastic potential surfaces, requiring the use of the plastic flow direction and loading direction vectors. The non-associate flow rule was adopted. Plastic flow direction (m_g) and loading direction (n_f) vectors are defined in triaxial space as

$${\mathbf{m}}_{\mathrm{g}}=\left\{\begin{array}{c}{\mathrm{m}}_{\mathrm{q}}=1/\sqrt{1+d_{\mathrm{g}}^2}\\ {\mathrm{m}}_{\mathrm{v}}=d_{\mathrm{g}}/\sqrt{1+d_{\mathrm{g}}^2}\end{array}\right\}$$

(17)

$${\mathbf{n}}_{\mathrm{f}}=\left\{\begin{array}{c}{\mathrm{n}}_{\mathrm{q}}=1/\sqrt{1+d_{\mathrm{f}}^2}\\ {\mathrm{n}}_{\mathrm{v}}=d_{\mathrm{f}}/\sqrt{1+d_{\mathrm{f}}^2}\end{array}\right\}$$

(18)

The loading direction vector d_f is expressed as

$$d_{\mathrm{f}}={\xi }_{\mathrm{f}}\left[{\eta }_{\mathrm{f}}\mathrm{e}\mathrm{x}\mathrm{p}\left({\mu }_{\mathrm{f}}{\psi }^{\mathrm{*}}\right)-\eta \right]$$

(19)

where ξ_f, η_f, and μ_f are plastic potential constants.

Equation (19) defines the plastic loading direction, which governs how shear loading is partitioned into shear and volumetric plastic strains, describing the degree of coupling between shear deformation and volume change; a mechanism strongly influenced by particle shape and the presence of rubber inclusions.

3.1.4. Plastic Modulus

The hardening/softening response is governed by the plastic modulus H:

$$H=h_0\left({\displaystyle \frac{{{\eta }_{\mathrm{p}\mathrm{k}}}^{*}}{\eta }}-1\right){\left[1-{\displaystyle \frac{\left({\xi }_{\mathrm{f}}-1\right)}{{\xi }_{\mathrm{f}}}}\left({\displaystyle \frac{\eta }{{\eta }_{\mathrm{f}}}}\right)\right]}^4\sqrt{{\displaystyle \frac{p^{\prime }}{p_{\mathrm{a}\mathrm{t}\mathrm{m}}}}}$$

(20)

with:

$${{\eta }_{pk}}^{*}={M_{\mathrm{c}\mathrm{s}\mathrm{s}}}^{*}\mathrm{e}\mathrm{x}\mathrm{p}\left({-\mu }_{\mathrm{p}\mathrm{k}}{\psi }^{\mathrm{*}}\right)$$

(21)

where h₀ and μ_pk are hardening material constants, η_pk^* is the virtual peak stress ratio, and p_atm is the atmospheric pressure (=100 kPa). Equation (20) defines the plastic modulus, which sets the rate at which the material’s resistance to shear stress changes as deformation progresses. It was proposed by Li and Dafalias [92] and modified by Ling and Yang [66]. It is important to highlight that the difference between η and η_pk^* governs the plastic modulus H. Accordingly, H takes a positive value (indicating hardening) when η_pk^* > η, a negative value (indicating softening) when η_pk^* < η, and becomes zero (corresponding to peak failure) when η_pk^* = η.

3.2. Calibration and Determination of Model Parameters

To enable the practical application of the proposed constitutive model, it is necessary to establish an explicit set of 11 material parameters that adequately represent the behavior of wgGRMs under different stress states. They are the elastic parameters (κ and ν), and parameters related to the critical state surface (e_Γ, λ^*, M_css^*), dilatancy (ξ_g, μ_g), loading direction (ξ_f, μ_f), and plastic modulus (h₀, μ_pk).

Table 1. Parameters of the proposed model for wgGRMs.

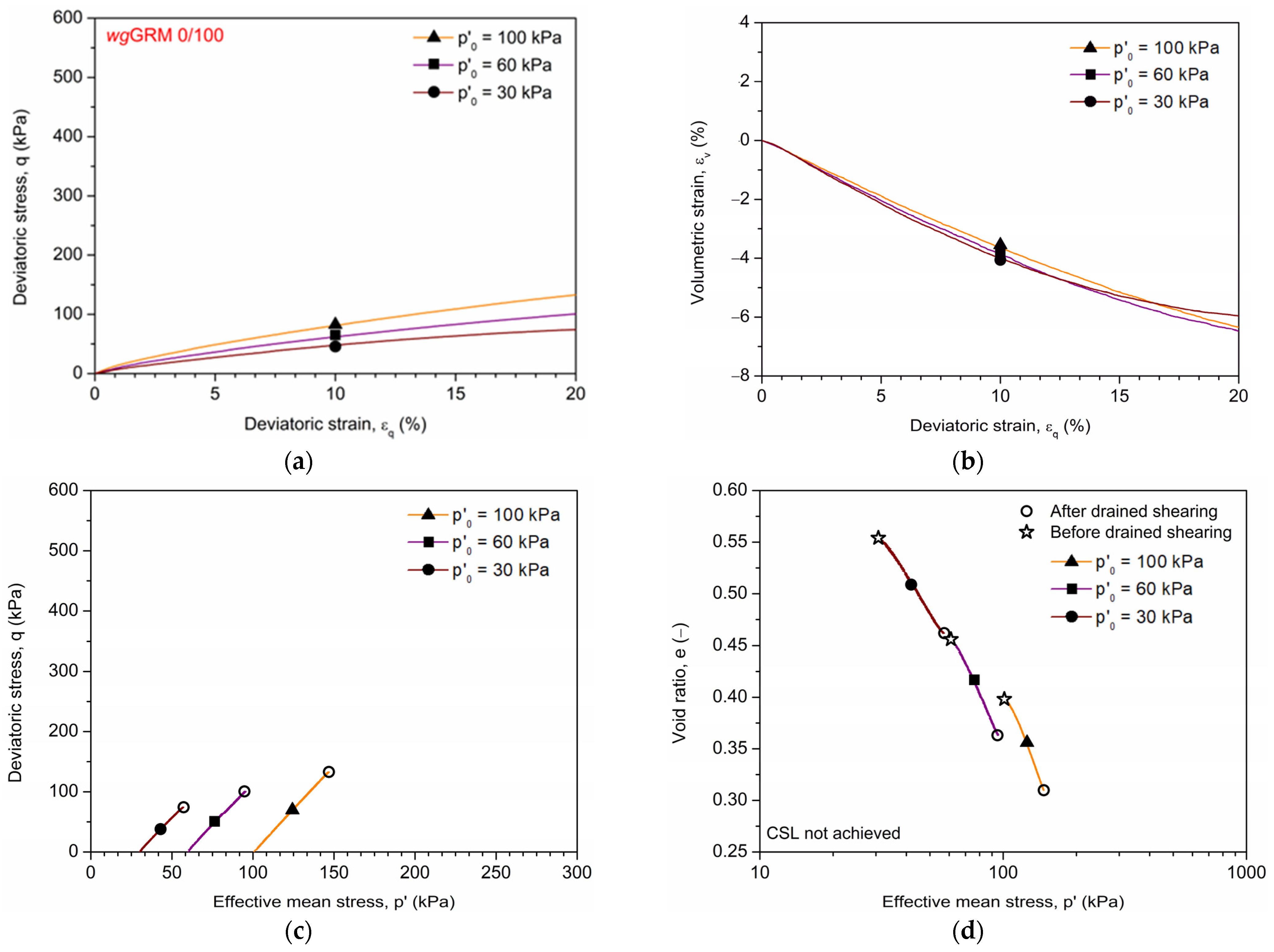
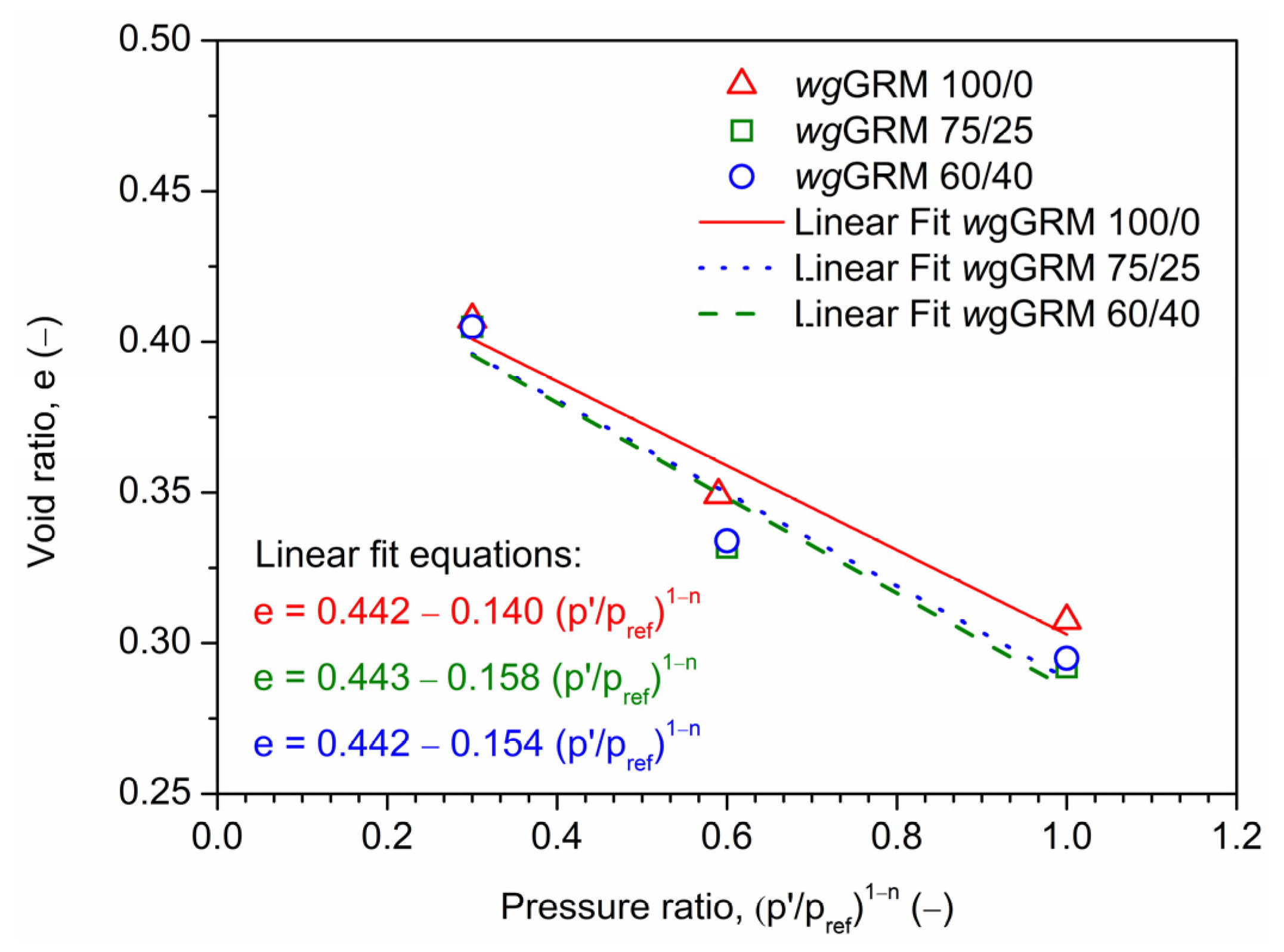
Soil Parameter	wgGRM 100/0			wgGRM 75/25			wgGRM 60/40
Confining Pressure, p0′ (kPa)	100	60	30	100	60	30	100	60	30
Elastic
κ (−)	0.00180	0.00256	0.00182	0.00923	0.01023	0.00844	0.02137	0.01596	0.01064
ν (−)	0.35			0.40			0.42
Critical State Surface (CSS)
eΓ (−)	0.833			0.762			0.791
λ* (−)	0.092			0.092			0.092
Mcss* (−)	1.625			1.494			1.348
Dilatancy
ξg (−)	0.7			1.1			1.2
μg (−)	7	5	4		6		6
Loading Direction
ξf (−)	0.7			1.1			1.2
μf (−)	2			2			2
Plastic Modulus
h0 (kPa)	2500	4000	10,000	1800			1200
μpk (−)	28	18	12	14	10	9	14	10	9

reports the values of the model parameters calibrated for each mixture.

Table 2. Equations for the model parameters proposed for wgGRMs.

Soil Parameter	Confining Pressure, p′0 (kPa)
	100	60	30
Elastic
κ (−)	10−5(VRC)2 − 2(VRC)10−5 + 0.002	2 × 10−6(VRC)2 − 3(VRC)10−4 + 0.003	−3 × 10−6(VRC)2 + 3(VRC)10−4 + 0.003
ν (−)	−2 × 10−5(VRC)2 + 0.0024(VRC) + 0.35
Critical State Surface (CSS)
eΓ (−)	0.0001(VRC)2 − 0.006(VRC) + 0.833
λ* (−)	0.092
Mcss* (−)	−0.0002(VRC)2 + 0.0068(VRC) + 1.63
Dilatancy
ξg (−)	−0.0002(VRC)2 + 0.022(VRC) + 0.7
μg (−)	0.001(VRC)2 − 0.07(VRC) + 7	−0.001(VRC)2 + 0.07(VRC) + 5	−0.002(VRC)2 + 0.13(VRC) + 4
Loading Direction
ξf (−)	−0.0002(VRC)2 + 0.022(VRC) + 0.7
μf (−)	2
Plastic Modulus
h0 (kPa)	−0.3(VRC)2 − 20.5(VRC) + 2500	1.2(VRC)2 − 118(VRC) + 4000	7.2(VRC)2 − 508(VRC) + 10,000
μpk (−)	0.014(VRC)2 − 0.91(VRC) + 28	0.008(VRC)2 − 0.52(VRC) + 18	0.003(VRC)2 − 0.2(VRC) + 12

reports the equations obtained for each parameter as a function of VRC. As previously introduced, the model was calibrated against the results of TxCD tests [54], covering a range of VRC = 0–40% (wgGRM 100/0, wgGRM 75/25, and wgGRM 60/40), e₀ = 0.299–0.554, p₀′ = 30–100 kPa.

Regarding the elastic properties, the swelling–recompression index (κ) was evaluated from Equations (14) and (15), considering the q-ε_q curves. Poisson’s ratio (ν) was back-calculated from the test results, and found to be equal to 0.35, 0.40, and 0.42 for wgGRM 100/0, wgGRM 75/25, and wgGRM 60/40, respectively.

The critical state parameters were defined according to the data reported in Section 2.3, resulting in:

• The critical void ratio at p′ = 1 kPa: e_Γ(f_VRC) = 0.0001(VRC)² − 0.006(VRC) + 0.833
• The slope of the CSS in the e-p′ plane: λ^* = 0.092 (constant)
• The slope of CSS in the q-p′ plot: M^*css(f_VRC) = −0.0002(VRC)² + 0.0068(VRC) + 1.63

Dilatancy parameters were obtained by matching the experimental stress–dilatancy trends for each mixture. The parameter ξ_g was obtained by plotting the d_g−(M_css^*−η) data for each mixture, as in Chiaro et al. [62]. The parameter μ_g was defined by evaluating Equation (16) at the PT state, obtaining:

$$d_{\mathrm{g}}=0\to \left[{M_{\mathrm{c}\mathrm{s}\mathrm{s}}}^{*}\mathrm{e}\mathrm{x}\mathrm{p}\left({\mu }_{\mathrm{g}}{\psi }^{\mathrm{*}}\right)-\eta \right]=0\to {\mu }_{\mathrm{g}}={\displaystyle \frac{1}{{{\psi }_{\mathrm{p}\mathrm{t}}}^{*}}}\ln \left({\displaystyle \frac{{\eta }_{\mathrm{p}\mathrm{t}}}{{M_{\mathrm{c}\mathrm{s}\mathrm{s}}}^{*}}}\right)$$

(22)

where η_pt and ψ_pt^* are the values of η and ψ^* at the PT state, respectively.

As for the loading direction parameters, the value of ξ_f was fixed equal to ξ_g, according to Manzanal et al. [88]. Instead, the value of μ_f was defined by matching the shape of the ε_v-ε_q relationship.

Finally, the plastic modulus parameter h₀ was defined by matching the shape of the q-ε_q curves, while μ_pk was defined by evaluating Equation (21) at the peak of the deviatoric stress, obtaining:

$$H=0\to {M_{\mathrm{c}\mathrm{s}\mathrm{s}}}^{*}\mathrm{e}\mathrm{x}\mathrm{p}\left({-\mu }_{\mathrm{p}\mathrm{k}}{\psi }^{\mathrm{*}}\right)=0\to {\mu }_{\mathrm{p}\mathrm{k}}={\displaystyle \frac{1}{{{\psi }_{\mathrm{p}\mathrm{k}}}^{*}}}\ln \left({\displaystyle \frac{{M_{\mathrm{c}\mathrm{s}\mathrm{s}}}^{*}}{{\eta }_{\mathrm{p}\mathrm{k}}}}\right)$$

(23)

where η_pk and ψ_pk^* are the values of η and ψ^* at the peak of the deviatoric stress, respectively. Figure 7 shows a schematic flowchart that summarizes the key steps of the calibration process for the proposed critical-state-based generalized plasticity model.

From the calibration of model parameters—particularly the dilatancy-related soil parameters—it emerges that ξ_g increases with VRC, regardless of confining pressure (a similar trend is observed for the loading direction parameter μ_f). For μ_g, a dependency on p₀′ is observed only in the case of wgGRM 100/0, where μ_g decreases as p₀′ decreases. In contrast, for mixtures with VRC > 0 (wgGRM 75/25 and wgGRM 60/40), μ_g remains constant across all investigated values of p₀′ and VRC. With respect to the loading direction parameter μ_f, a constant value can be assigned for all tested mixtures and confining pressures. For the plastic modulus parameters, h₀ shows a dependency on p₀′ only in the wgGRM 100/0 mixture, where it increases as p₀′ decreases, as shown in Figure 8. For mixtures with VRC > 0, h₀ remains constant. Conversely, μ_pk decreases with decreasing p₀′ across all investigated mixtures.

4. Simulation Results

The comparison between the experimental results and the model predictions highlights the model’s strong capability to reproduce the mechanical response of wgGRMs with varying effective confining pressures and rubber contents. The comparison is performed considering the TxCD tests [54], carried out on wgGRM 100/0, wgGRM 75/25, and wgGRM 60/40 at p₀′ = 30, 60, and 100 kPa.

For the wgGRM 100/0 (Figure 9a,b), the model accurately captures the peak of deviatoric stress and post-peak softening, particularly when p₀′ = 30 and 60 kPa, as well as the dilative behavior observed experimentally.

As for the mixtures with VRC = 25% (wgGRM 75/25), the model accurately predicts the peak of deviatoric stress and its reduction for ε_q ≥ 15% (Figure 9c). As for the volumetric response, the contractive behavior and tendency toward lower volumetric dilation are both well captured (Figure 9d). At VRC = 40% (wgGRM 60/40), the model successfully describes the experimentally observed post-peak strength reduction, enhanced ductility and contractive behavior (Figure 9e,f). Across all mixtures, the influence of p₀′ is consistently well captured, with the model reproducing both the increase in strength and the shift from dilative to more contractive behavior at higher pressures.

Figure 10a,b compare the experimental and numerical prediction of the stress ratio–dilatancy ratio (η-D) responses at p₀′ = 30, 60, and 100 kPa for wgGRM 75/25 and wgGRM 60/40, respectively.

Considering the experimental results, it is worth noting that the stress–dilatancy curves for wgGRMs exhibit a characteristic “downward hook” where the stress ratio at the PT is slightly higher than at the critical state—a feature also reported in other soil–rubber mixtures [38,82]. At the beginning of shearing, the soft rubber particles are significantly more compressible than the gravel. Under shear, these rubber particles deform and compress, filling the voids between the gravel grains. This process dominates the initial volumetric response, leading to contractive behavior. As shearing continues and the rubber particles are compressed to a denser state, the stiff gravel skeleton begins to bear an increasing proportion of the load. Once the gravel-to-gravel contacts become the primary load-bearing mechanism, the mixture starts to exhibit dilatant behavior. This marks the PT: the stress ratio at this point is high because a substantial shear stress was required to first compress the rubber and engage the full strength of the gravel skeleton. The final, steady-state Critical State is reached when the continuous shear deformation no longer causes volume change. At this state, the stress ratio is lower than at the PT because the internal structure has achieved a stable configuration where the compressibility of the rubber and the dilatancy of the gravel are in balance under continuous shear.

The constitutive model demonstrates a high degree of accuracy in replicating the fundamental stress-dilatancy behavior observed in the experiments. More specifically, the model accurately reproduces the peak stress ratio for both mixtures at all confining pressures. In addition, it reproduces and predicts the experimental trend where the dilatancy ratio (D) increases to a maximum following the peak stress and then gradually decreases towards a critical state (where D ≈ 0 and η remain constant) at large shear strains. A critical validation point is the model’s ability to predict the stress ratio at which the volumetric behavior transitions from contractive (negative D, volumetric compression) to dilative (positive D, volumetric expansion).

5. Discussion

The simulation results in Figure 9 and Figure 10 validate the robust predictive capabilities of the proposed critical state-based generalized plasticity model. This represents a significant advancement over recent efforts, such as the HS-small model by Fiamingo et al. [63], which, while effective for high-rubber-content mixtures (VRC ≥ 45%), fails to capture the post-peak softening response in mixtures with a dominant gravel skeleton. In contrast, the calibrated model, through its incorporation of critical-state physics and a state-dependent plastic modulus (Equations (20) and (21)), inherently captures both the peak strength and the subsequent softening as the material dilates toward the critical state. This physical consistency is crucial for safer numerical predictions, as models that neglect softening risk overestimating post-peak strength. Additionally, the calibrated model offers a superior prediction of stress-dependent dilatancy, which is essential for accurately evaluating settlement and deformation.

Minor discrepancies, such as in the precise prediction of the dilation onset strain at low confining pressures, can be attributed to micro-mechanical mechanisms not explicitly captured by the macroscopic constitutive framework. At these low confinement levels, the behavior is highly sensitive to the local arrangement of particles and the evolution of force chains. The model approximates the homogenized response, but it cannot replicate the instantaneous, micro-scale rearrangements where a few gravel particles, initially in a stable configuration, suddenly slip or roll past each other, triggering dilation earlier than predicted. These micro-mechanical complexities become more pronounced at low stresses, where the confining pressure is insufficient to suppress localized instabilities.

The generalized plasticity framework achieves high accuracy for monotonic loading—accurately describing nonlinearity, dilatancy, and peak/softening behavior—without the complexity of explicitly defining yield surfaces. This makes it more straightforward to calibrate and implement for practicing engineers, while remaining rooted in the robust critical state theory.

The results align with and extend the general understanding of gravel–rubber mixture behavior derived from experimental studies. The transition from a distinct peak and dilatant response (wgGRM 100/0) to a more ductile, strain-hardening, and contractive response (wgGRM 60/40) with increasing VRC has been consistently reported for GRMs [31,44,51]. More importantly, the calibrated model parameters provide quantitative insight into this transition. The successful calibration of the model against this well-established experimental backdrop reinforces its validity and its ability to encapsulate the underlying mechanics of these complex composite materials.

Within the generalized plasticity framework, the model calibrated by Chiaro et al. [62] for coal wash and steel slag mixtures provides a valuable benchmark for the calibration of the constitutive model. While the mathematical structure is similar, the calibrated parameters for wgGRMs are different. For example, specific trends and values of ξ_g and μ_g for wgGRMs differ from those proposed in Chiaro et al. [62], reflecting the unique role of the highly compressible rubber inclusions. The continuous functions established for the critical state parameters e_Γ and M*_css with respect to VRC (Equations (3) and (5)) are a key contribution, providing a unified framework that allows designers to predict the behavior of any mixture composition within a single, consistent model. This moves beyond the characterization of a single mixture and enables robust material optimization for specific engineering applications, thereby facilitating the sustainable reuse of end-of-life tires in geotechnical practice.

6. Conclusions

This study presents and calibrates—for the first time—a critical state-based generalized plasticity model specifically tailored for well-graded Gravel–Rubber Mixtures (wgGRMs).

The previous generalized plasticity models proposed in the literature were developed and calibrated for conventional geomaterials like sands, and waste materials like coal wash and steel slag. The significant improvement here is the successful application to wgGRMs, which are characterized by a strong contrast between the stiffness of gravel grains and that of rubber inclusions. This required complete recalibration and demonstrated the framework’s robustness in capturing behaviors driven by this unique material heterogeneity. The calibration was performed using experimental data from isotropically consolidated drained monotonic triaxial tests on wgGRMs with varying volumetric rubber content (VRC) and effective confining pressures. The outcomes of this study allow for several important conclusions to be drawn.

The experimental results highlight that the inclusion of rubber significantly modifies the mechanical behavior of well-graded gravel. Mixtures with low or no rubber content exhibit a strain-softening response and dilative volumetric tendencies at lower confining pressures, while higher rubber contents promote strain-hardening behavior accompanied by predominantly contractive volumetric responses. These distinct transitions underscore the importance of accurately capturing the combined effects of gravel skeleton interaction and rubber particle deformability within a constitutive framework.

The proposed critical state-based generalized plasticity model demonstrated good predictive capabilities in reproducing these experimentally observed behaviors. Compared to the Hardening Soil with Small Strain Stiffness (HS-small) constitutive model, which has recently been adopted in FE numerical tools to reproduce the mechanical behavior of poorly graded gravel–rubber mixtures, the CSL-based generalized plasticity model can reproduce the softening effects associated with material dilatancy. More specifically, the model is able to:

• describe the peak stress and post-peak softening in wgGRMs;
• capture the progressive reduction in strength and enhanced ductility with increasing VRC;
• reproduce the shift from dilative to contractive responses with increasing confining pressure;
• predict the stress–dilatancy relationships and the transition from contractive to dilative phases, aligning closely with observed critical state conditions.

These findings confirm that the model is both flexible and robust in describing the non-linear stress–strain and volumetric responses of wgGRMs. By offering a physically consistent representation of material behavior, it can provide reliable input for advanced numerical analyses in geotechnical practice.

From a broader perspective, the study contributes to the sustainable management of End-of-Life Tires (ELTs). The validated constitutive model supports the safe and effective use of wgGRMs in a range of civil engineering applications, such as lightweight embankments, retaining wall backfills, drainage systems, and geotechnical seismic isolation foundations. In all these contexts, performance depends heavily on the accurate characterization of stress–strain response and volumetric change under different stress paths, which the present model successfully delivers.

Ultimately, this research presents several avenues for future exploration. At present, the characterization of wgGRMs is based only on consolidated drained triaxial tests. The established dilatancy relationship—which describes the material’s volumetric behavior—could be adopted to estimate the development of pore water pressures under undrained conditions, effectively modeling them as a “mirror-effect” to the volumetric strains [93]. Further developments are required to extend its applicability to cyclic and dynamic loading conditions, which are critical for earthquake engineering and long-term performance assessments. Additional investigations carried out on large-sized specimens will also be valuable in addressing potential scale effects and ensuring model applicability at the field level. The adoption of the Discrete Element Method (DEM) modeling would explicitly investigate particle-scale interactions and provide quantitative insights to refine macroscopic behavior, in a similar manner done by Chew et al. [44] for GRMs in direct shear tests. Finally, a critical next step is the implementation of this constitutive model within finite element (FE) software. This will enable the upscaling of the material behavior characterized in this study to perform non-linear dynamic analyses of full-scale geotechnical systems. A primary application would be the performance assessment of geotechnical seismic isolation (GSI) foundations utilizing wgGRMs, allowing for the quantitative evaluation of their effectiveness in reducing seismic forces on structures.