Monotonic Behaviour and Physical Characteristics of Silty Sands with Kaolinite Clay
Abstract
1. Introduction
1.1. Research Overview
1.2. Void Ratio and Relative Density for Sands
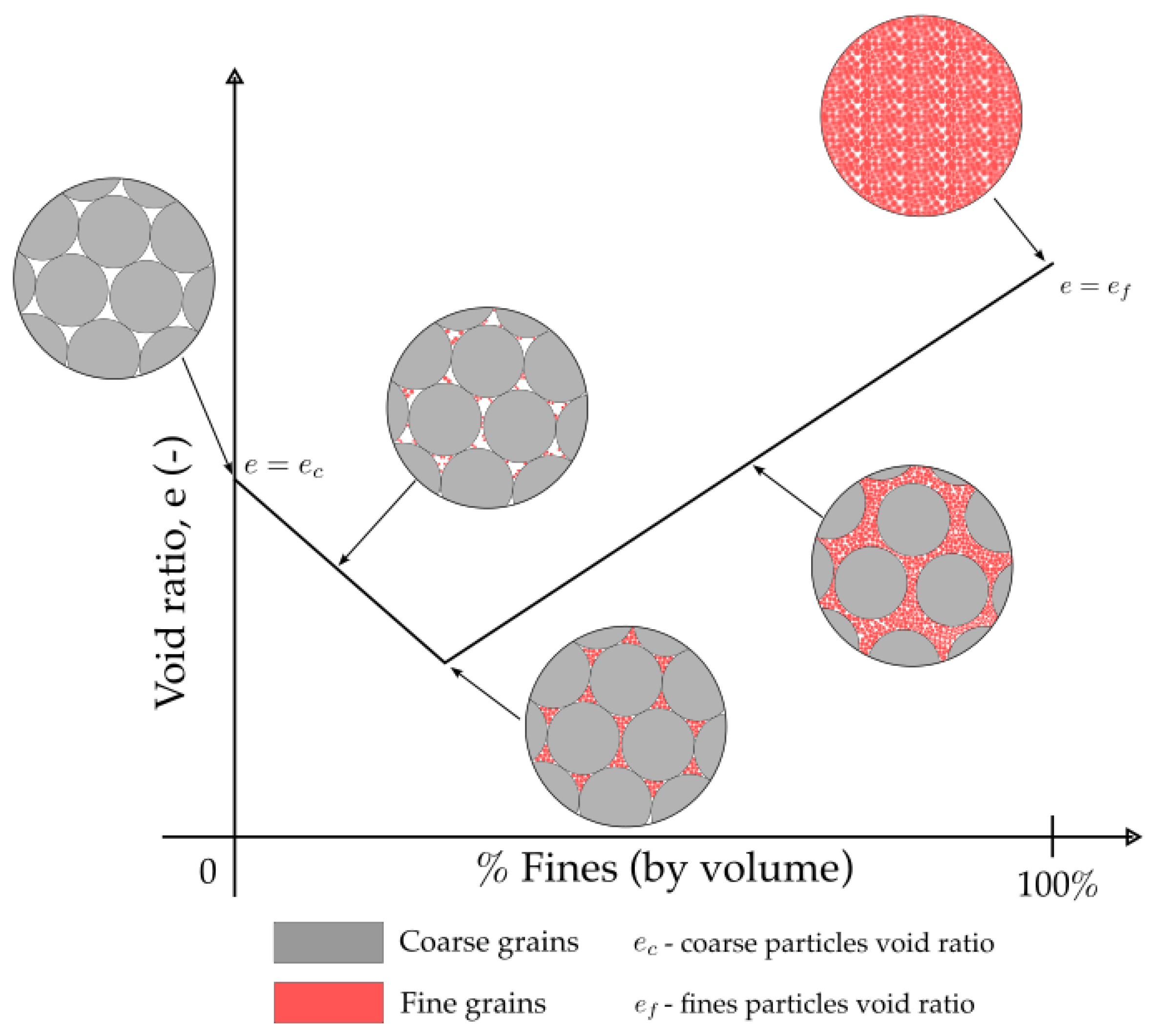
1.3. Equivalent Void Ratio and Relative Density for Silty Sands
1.4. Alternative Void Ratios
2. Methodology
2.1. Silty Sand Mixtures
2.2. Physical Property Determination
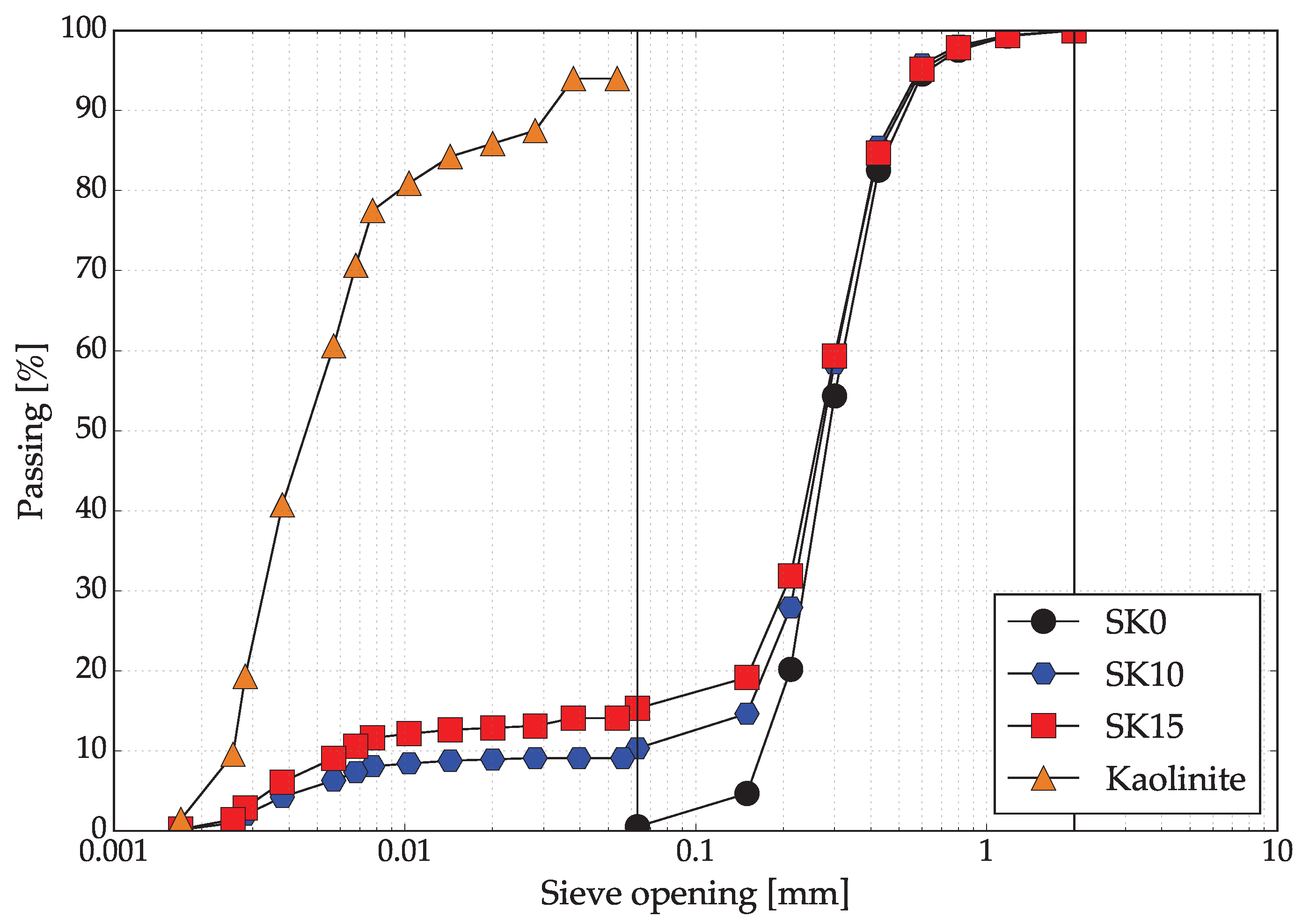
2.2.1. Specific Gravity, Granulometric Analysis
2.2.2. Conventional Minimum and Maximum Void Ratio Determination
2.2.3. Alternative Minimum and Maximum Void Ratio Determination
2.3. Monotonic Compression
2.3.1. Triaxial Testing System
2.3.2. Sample Preparation Method
2.3.3. Triaxial Testing Program
3. Results and Discussion
3.1. Conventional Minimum and Maximum Void Ratio
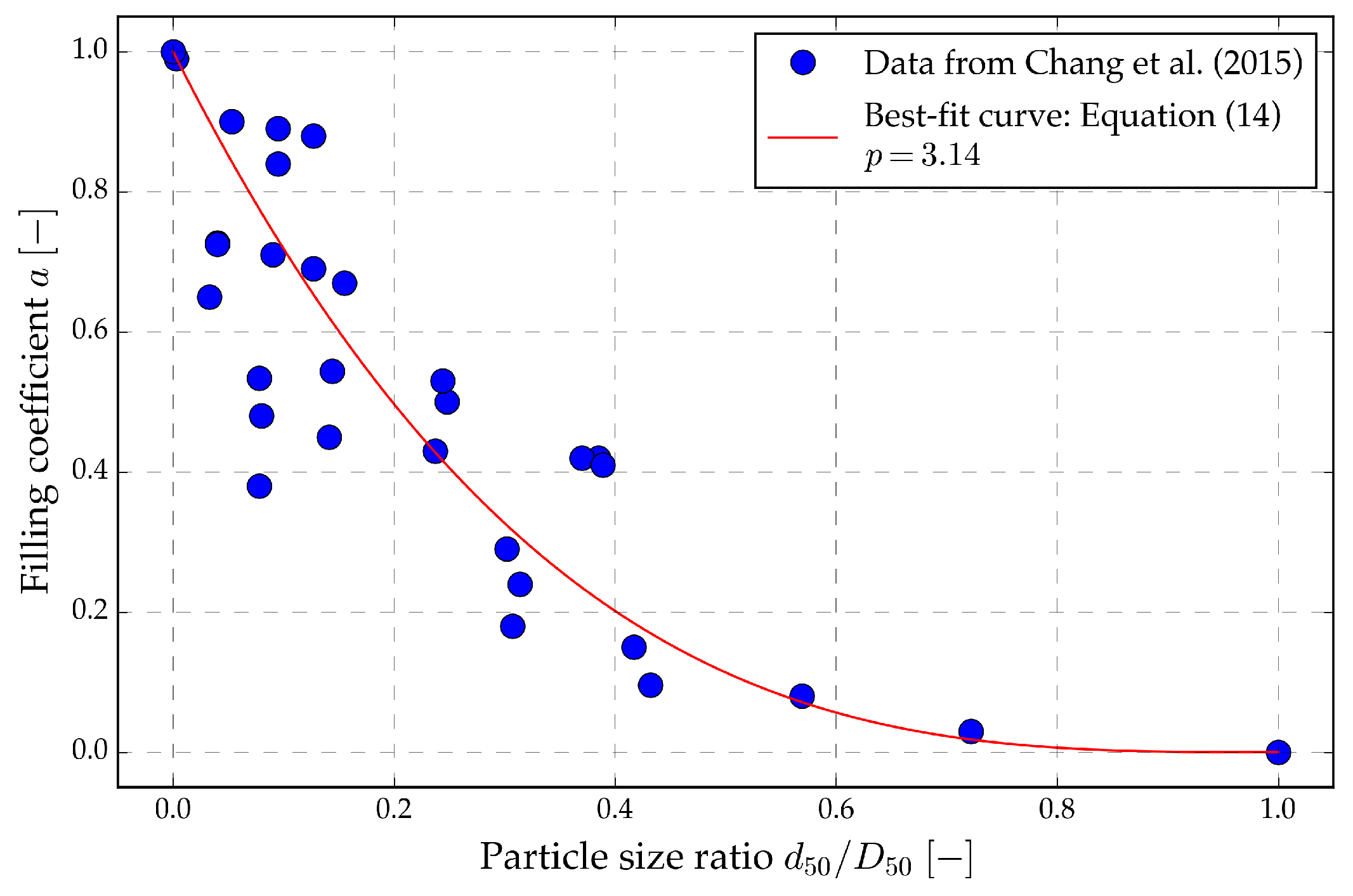
3.2. Alternative Minimum and Maximum Void Ratios
3.3. Sample Preparation
3.4. Physical Characteristics of Clayey and Silty Sands with Clay Minerals
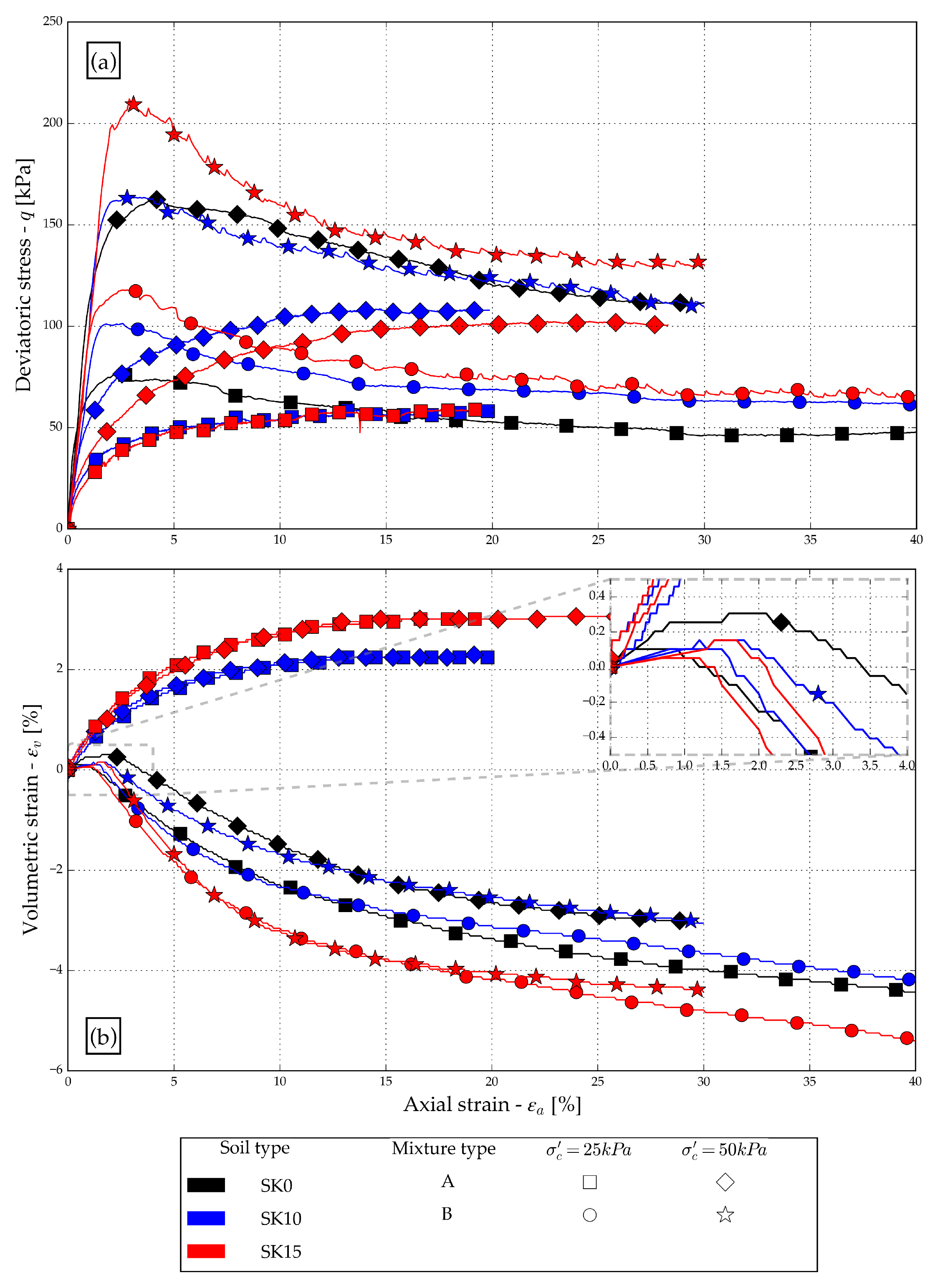
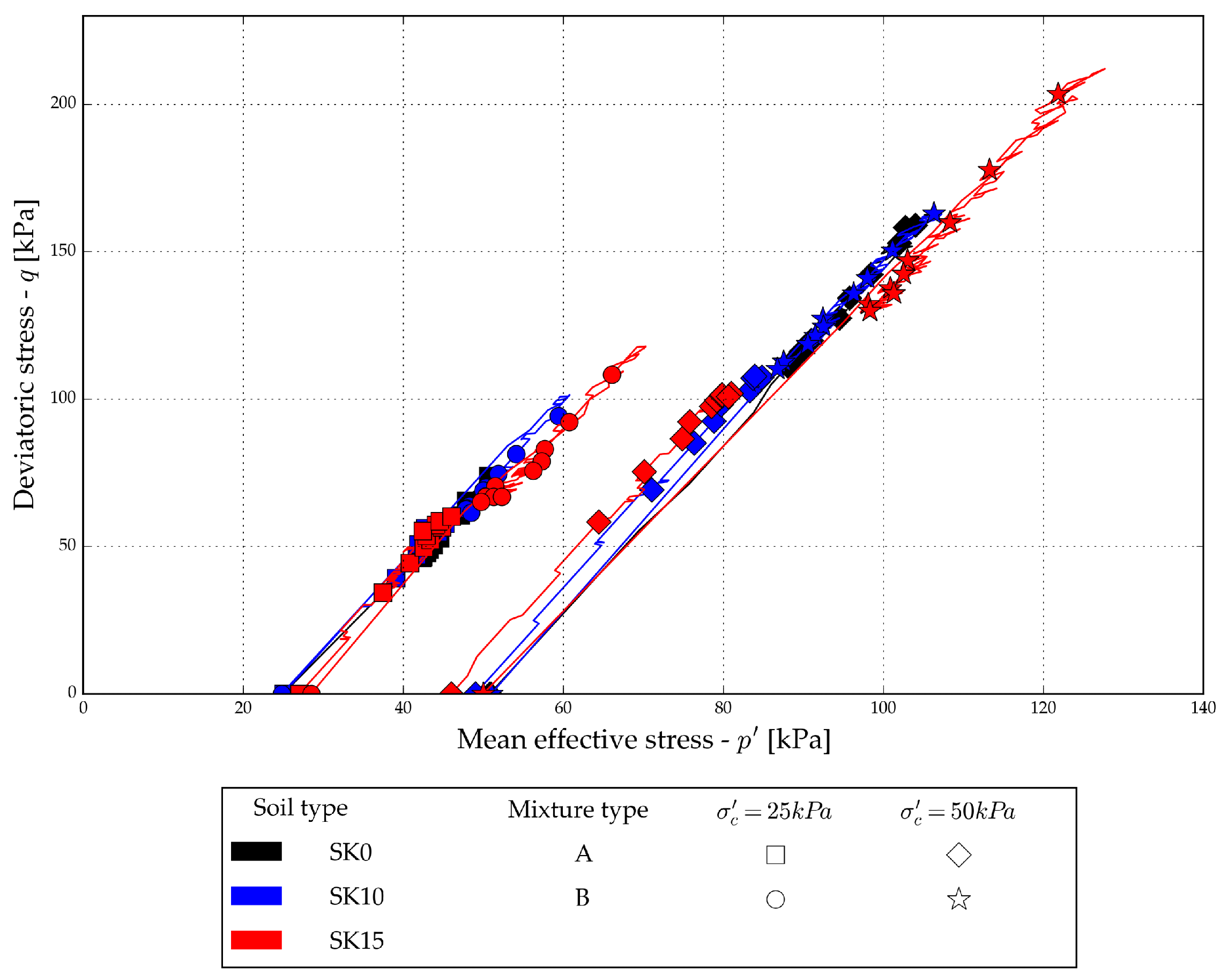
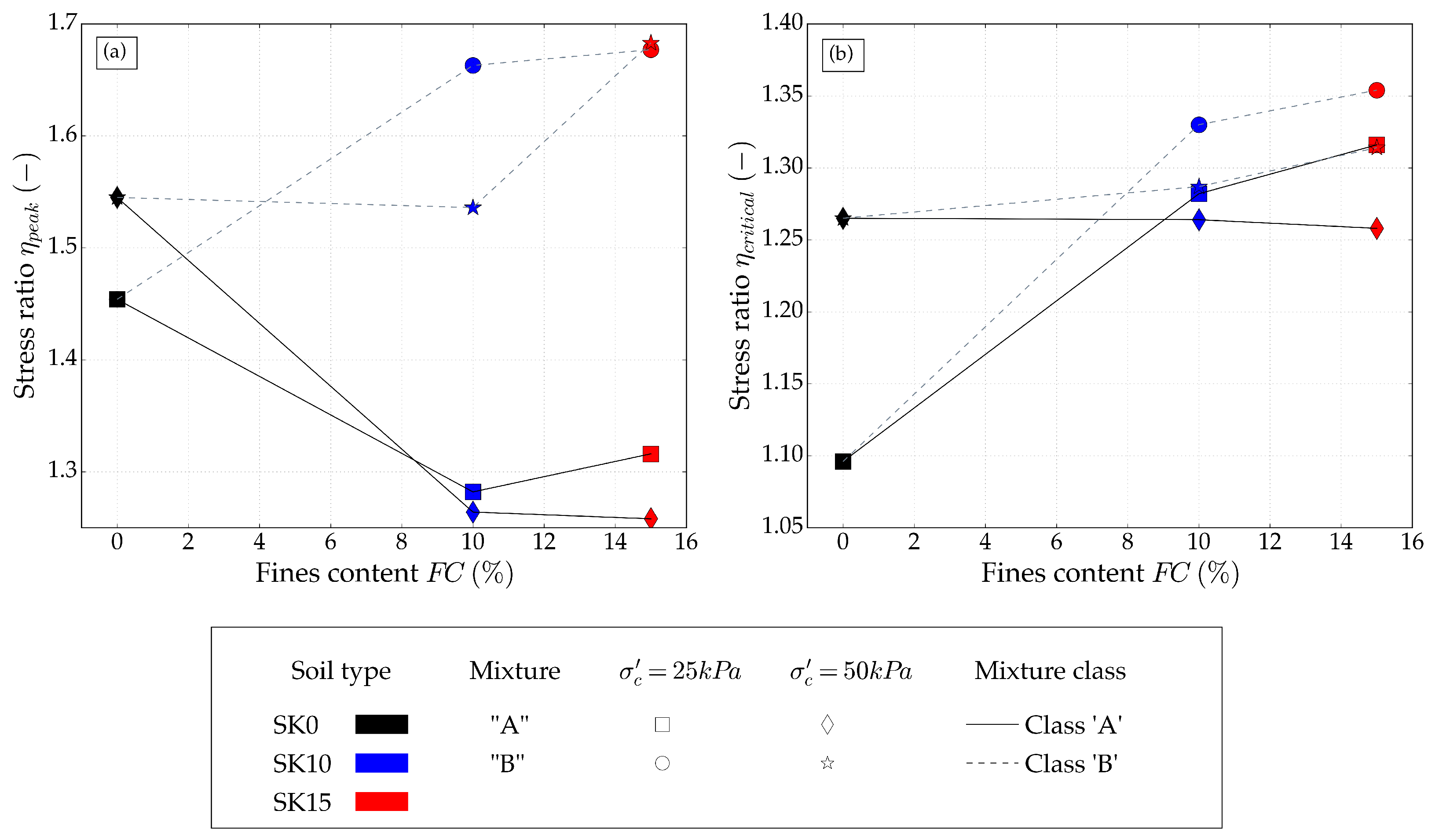
3.5. Drained Compression Tests
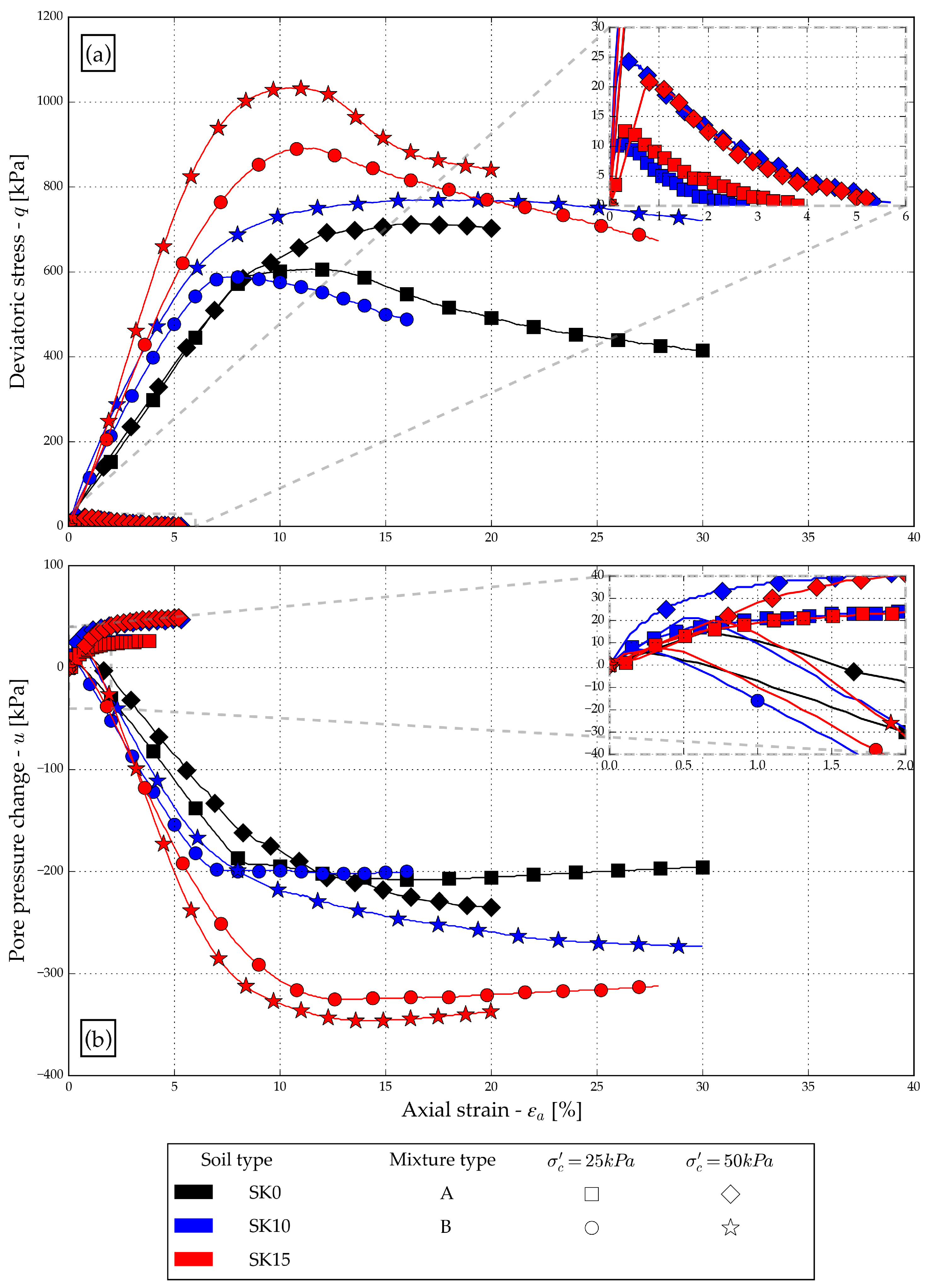
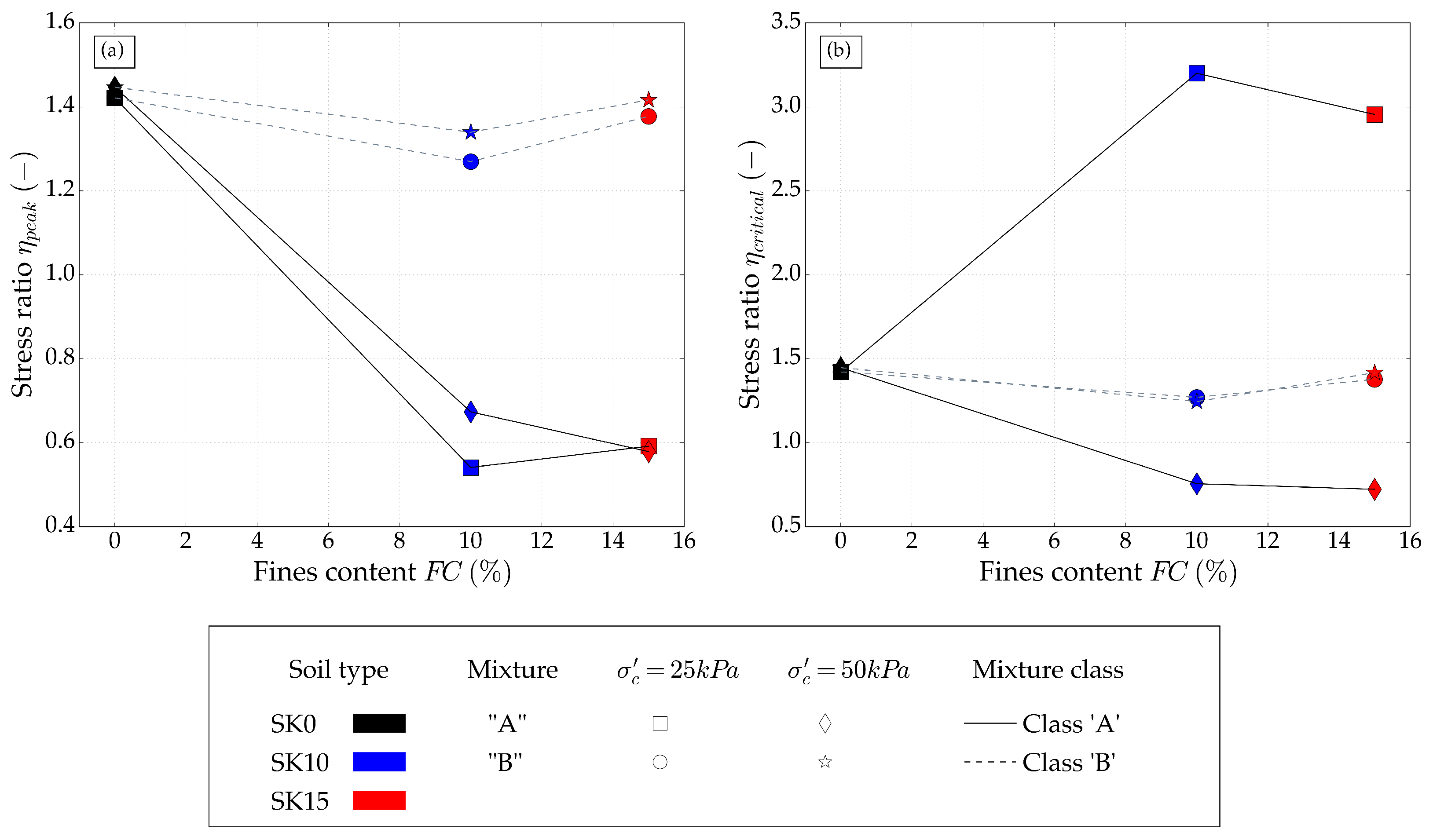
3.6. Undrained Compression Tests
4. Conclusions
4.1. Void Ratio Determination Methods
4.2. Drained Compression Tests
4.3. Undrained Compression Tests
4.4. Physical Characteristics of Clayey and Silty Sands with Clay Minerals
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| CSL | Critical State Line |
| SSL | Steady State Line |
| ISL | Instability State Line |
| LVDT | Linear variable differential transducer |
References
- Lade, P.V.; Liggio, C.D.; Yamamuro, J.A. Effects of Non-Plastic Fines on Minimum and Maximum Void Ratios of Sand. Geotech. Test. J. 1998, 21, 336–347. [Google Scholar] [CrossRef]
- Thevanayagam, S. Effect of Fines and Confining Stress on Undrained Shear Strength of Silty Sands. J. Geotech. Geoenviron. Eng. 1998, 124, 479–491. [Google Scholar] [CrossRef]
- Yang, J.; Wei, L.M.; Dai, B.B. State Variables for Silty Sands: Global Void Ratio or Skeleton Void Ratio? Soils Found. 2015, 55, 99–111. [Google Scholar] [CrossRef]
- Phan, V.T.A.; Hsiao, D.H. Undrained Behavior and Shear Strength of Clean Sand Containing Low-Plastic Fines. IOP Conf. Ser. Earth Environ. Sci. 2018, 143, 12020. [Google Scholar] [CrossRef]
- Rabbi, A.T.M.Z.; Rahman, M.M.; Cameron, D.A. The Relation between the State Indices and the Characteristic Features of Undrained Behaviour of Silty Sand. Soils Found. 2019, 59, 801–813. [Google Scholar] [CrossRef]
- Othman, B.A.; Marto, A.; Uzuoka, R.; Ueda, K.; Satar, M.H.M. Liquefaction Resistance of Sand-Kaolin Mixtures: Effect of Sand Sizes. IOP Conf. Ser. Earth Environ. Sci. 2022, 1103, 12026. [Google Scholar] [CrossRef]
- Tafili, M.; Knittel, L.; Gauger, V.; Wichtmann, T.; Stutz, H.H. Experimental Study on Monotonic to High-Cyclic Behaviour of Sand-Silt Mixtures. Acta Geotech. 2024, 19, 4227–4240. [Google Scholar] [CrossRef]
- Derakhshandi, M.; Rathje, E.M.; Hazirbaba, K.; Mirhosseini, S.M. The Effect of Plastic Fines on the Pore Pressure Generation Characteristics of Saturated Sands. Soil Dyn. Earthq. Eng. 2008, 28, 376–386. [Google Scholar] [CrossRef]
- Lade, P.V.; Yamamuro, J.A.; Liggio, C.D.J. Effects of Fines Content on Void Ratio, Compressibility, and Static Liquefaction of Silty Sand. Geomech. Eng. 2009, 1, 1–15. [Google Scholar] [CrossRef]
- Monkul, M.M.; Yamamuro, J.A. Influence of silt size and content on liquefaction behavior of sands. Can. Geotech. J. 2011, 48, 931–942. [Google Scholar] [CrossRef]
- Yang, J.; Wei, L.M. Collapse of Loose Sand with the Addition of Fines: The Role of Particle Shape. Géotechnique 2012, 62, 1111–1125. [Google Scholar] [CrossRef]
- Sarkar, D.; Goudarzy, M.; König, D.; Wichtmann, T. Influence of particle shape and size on the threshold fines content and the limit index void ratios of sands containing non-plastic fines. Soils Found. 2020, 60, 621–633. [Google Scholar] [CrossRef]
- Mitchell, J.K.; Soga, K. Fundamentals of Soil Behavior, 3rd ed.; Wiley: Hoboken, NJ, USA, 2005. [Google Scholar]
- Holtz, R.D.; Kovacs, W.D.; Sheahan, T.C. An Introduction to Geotechnical Engineering; Pearson: London, UK, 2011. [Google Scholar]
- Cheng, Z.; Wang, J.; Xu, D.; Fan, X. DEM study on the micromechanical behaviour of sand-clay mixtures. Powder Technol. 2024, 435, 119400. [Google Scholar] [CrossRef]
- Thevanayagam, S.; Martin, G.R. Liquefaction in silty soils—Screening and remediation issues. Soil Dyn. Earthq. Eng. 2002, 22, 1035–1042. [Google Scholar] [CrossRef]
- Rahman, M.M.; Lo, S.R.; Gnanendran, C.T. On Equivalent Granular Void Ratio and Steady State Behaviour of Loose Sand with Fines. Can. Geotech. J. 2008, 45, 1439–1456. [Google Scholar] [CrossRef]
- Rahman, M.M.; Lo, S.R. Undrained Behavior of Sand-Fines Mixtures and Their State Parameter. J. Geotech. Geoenviron. Eng. 2014, 140, 4014036. [Google Scholar] [CrossRef]
- Karimian, A.; Hassanlourad, M. Undrained monotonic shear behaviour of loose sand-silt soil mixture. Int. J. Geotech. Eng. 2020, 14, 919–929. [Google Scholar] [CrossRef]
- Prodan, M.V.; Peranić, J.; Pajalić, S.; Arbanas, Ž. Physical Modelling of Rainfall-Induced Sandy and Clay-Like Slope Failures. Adv. Mater. Sci. Eng. 2023, 2023, 3234542. [Google Scholar] [CrossRef]
- Arbanas, Ž.; Peranić, J.; Jagodnik, V.; Prodan, M.V.; Čeh, N. Remedial Measures Impact on Slope Stability and Landslide Occurrence in Small-Scale Slope Physical Model in 1 g Conditions. In Progress in Landslide Research and Technology, Volume 2 Issue 2, 2023; Alcántara-Ayala, I., Željko, A., Huntley, D., Konagai, K., Arbanas, S.M., Mikoš, M., Ramesh, M.V., Sassa, K., Sassa, S., Tang, H., et al., Eds.; Springer Nature: Cham, Switzerland, 2023; pp. 197–220. [Google Scholar] [CrossRef]
- D4253-16, A; Test Methods for Maximum Index Density and Unit Weight of Soils Using a Vibratory Table. ASTM International: West Conshohocken, PA, USA, 2016.
- D4254-16, A; Standard Test Methods for Minimum Index Density and Unit Weight of Soils and Calculation of Relative Density. ASTM International: West Conshohocken, PA, USA, 2016.
- Mijic, Z.; Bray, J.D.; Riemer, M.F.; Cubrinovski, M.; Rees, S.D. Test Method for Minimum and Maximum Densities of Small Quantities of Soil. Soils Found. 2021, 61, 533–540. [Google Scholar] [CrossRef]
- Chang, C.S.; Wang, J.Y.; Ge, L. Modeling of Minimum Void Ratio for Sand–Silt Mixtures. Eng. Geol. 2015, 196, 293–304. [Google Scholar] [CrossRef]
- Chang, C.S.; Wang, J.Y.; Ge, L. Maximum and Minimum Void Ratios for Sand-Silt Mixtures. Eng. Geol. 2016, 211, 7–18. [Google Scholar] [CrossRef]
- Goudarzy, M.; Sarkar, D.; Lieske, W.; Wichtmann, T. Influence of plastic fines content on the liquefaction susceptibility of sands: Monotonic loading. Acta Geotech. 2022, 17, 1719–1737. [Google Scholar] [CrossRef]
- Gobbi, S.; Reiffsteck, P.; Lenti, L.; d’Avila, M.P.S.; Semblat, J.F. Liquefaction triggering in silty sands: Effects of non-plastic fines and mixture-packing conditions. Acta Geotech. 2022, 17, 391–410. [Google Scholar] [CrossRef]
- Thevanayagam, S.; Mohan, S. Intergranular State Variables and Stress–Strain Behaviour of Silty Sands. Géotechnique 2000, 50, 1–23. [Google Scholar] [CrossRef]
- Polito, C.P. Models for Estimating Coefficients for the Prediction of Maximum and Minimum Index Void Ratios for Mixtures of Sand and Non-Plastic Silt. Technical report, Engineering. Preprints 2023, 2023091306. [Google Scholar] [CrossRef]
- Marušić, D.; Jagodnik, V. Atterberg Limits Determination and Soil Classification Using Fall Cone Device on the Silty Sands and Sandy Silts. Int. J. Geotech. Eng. 2025, 19, 78–87. [Google Scholar] [CrossRef]
- D854-14, A; Standard Test Methods for Specific Gravity of Soil Solids by Water Pycnometer. Technical Report; ASTM: West Conshohocken, PA, USA, 2014.
- 17892-4:2016; Geotechnical Research and Testing—Laboratory Soil Testing—Part 4: Particle Size Analysis (in Croatian). ISO: Zagreb, Croatia, 2016.
- Jagodnik, V.; Arbanas, Ž. Cyclic Behaviour of Uniform Sand in Drained and Undrained Conditions at Low Confining Stress in Small-Scale Landslide Model. Sustainability 2022, 14, 12797. [Google Scholar] [CrossRef]
- Sridharan, A.; Nagaraj, H.; Prakash, K. Determination of the Plasticity Index from Flow Index. Geotech. Test. J. 1999, 22, 175–181. [Google Scholar] [CrossRef]
- Fleureau, J.M.; Verbrugge, J.C.; Huergo, P.J.; Correia, A.G.; Kheirbek-Saoud, S. Aspects of the behaviour of compacted clayey soils on drying and wetting paths. Can. Geotech. J. 2002, 39, 1341–1357. [Google Scholar] [CrossRef]
- Jagodnik, V.; Kraus, I.; Ivanda, S.; Arbanas, Ž. Behaviour of Uniform Drava River Sand in Drained ConditionA Critical State Approach. Appl. Sci. 2020, 10, 5733. [Google Scholar] [CrossRef]
- Lade, P.V. Triaxial Testing of Soils; Wiley: Hoboken, NJ, USA, 2016. [Google Scholar] [CrossRef]
- D7181-20, A; Standard Test Method for Consolidated Drained Triaxial Compression Test for Soils. ASTM: West Conshohocken, PA, USA, 2020.
- D4767-11, A; Standard Test Method for Consolidated Undrained Triaxial Compression Test for Cohesive Soils. ASTM: West Conshohocken, PA, USA, 2020.
- Ladd, R.S. Preparing Test Specimens Using Undercompaction. Geotech. Test. J. 1978, 1, 16–23. [Google Scholar] [CrossRef]
- Water Supply and Drainage Utility Company, Rijeka. Water Quality and Testing (in Croatian); Water Supply and Drainage Utility Company: Rijeka, Croatia, 2025. [Google Scholar]
- Won, J.; Park, J.; Kim, J.; Jang, J. Impact of Particle Sizes, Mineralogy and Pore Fluid Chemistry on the Plasticity of Clayey Soils. Sustainability 2021, 13, 11741. [Google Scholar] [CrossRef]
- Skempton, A.W. The Pore–Pressure Coefficients A and B. Géotechnique 1954, 4, 143–147. [Google Scholar] [CrossRef]
- Andrade, F.; Al-Qureshi, H.; Hotza, D. Measuring the plasticity of clays: A review. Appl. Clay Sci. 2011, 51, 1–7. [Google Scholar] [CrossRef]
- Murthy, T.G.; Loukidis, D.; Carraro, J.A.H.; Prezzi, M.; Salgado, R. Undrained Monotonic Response of Clean and Silty Sands. Géotechnique 2007, 57, 273–288. [Google Scholar] [CrossRef]







| Soil Type | Sand (S) [%] | Kaolinite (K) [%] |
|---|---|---|
| Modland (SK0) | 100 | 0 |
| SK10 | 90 | 10 |
| SK15 | 85 | 15 |
| Kaolinite (SK100) | 0 | 100 |
| Soil Type | Specific Gravity () | (mm) | (mm) | (mm) | Liquid Limit (%) | Plastic Limit (%) |
|---|---|---|---|---|---|---|
| SK0 | 2.70 | 0.1713 | 0.2888 | N/A | N/A | N/A |
| SK10 | 2.69 | 0.0535 | 0.2757 | N/A | N/A | N/A |
| SK15 | 2.67 | 0.0063 | 0.2701 | N/A | N/A | N/A |
| SK100 | 2.60 | 0.0026 | N/A | 0.0047 | 53 | 30 |
| Test ID | Soil Type | Mixture Type | Relative Density, [%] | Effective Mean Confining Stress, [kPa] | Test Type |
|---|---|---|---|---|---|
| 050_SK0_DR_EFF25 | SK0 | N/A | 80 | 25 | CID |
| 041_SK0_DR_EFF50 | SK0 | N/A | 80 | 50 | CID |
| 015_SK10_A_DR_EFF25 | SK10 | A | 80 | 25 | CID |
| 021_SK10_A_DR_EFF50 | SK10 | A | 80 | 50 | CID |
| 018_SK15_A_DR_EFF25 | SK15 | A | 80 | 25 | CID |
| 012_SK15_A_DR_EFF50 | SK15 | A | 80 | 50 | CID |
| 049_SK10_B_DR_EFF25 | SK10 | B | 80 | 25 | CID |
| 046_SK10_B_DR_EFF50 | SK10 | B | 80 | 50 | CID |
| 048_SK15_B_DR_EFF25 | SK15 | B | 80 | 25 | CID |
| 047_SK15_B_DR_EFF50 | SK15 | B | 80 | 50 | CID |
| 042_SK0_UND_EFF25 | SK0 | N/A | 80 | 25 | CIU |
| 034_SK0_UND_EFF50 | SK0 | N/A | 80 | 50 | CIU |
| 016_SK10_A_UND_EFF25 | SK10 | A | 80 | 25 | CIU |
| 020_SK10_A_UND_EFF50 | SK10 | A | 80 | 50 | CIU |
| 007_SK15_A_UND_EFF25 | SK15 | A | 80 | 25 | CIU |
| 054_SK15_A_UND_EFF50 | SK15 | A | 80 | 50 | CIU |
| 043_SK10_B_UND_EFF25 | SK10 | B | 80 | 25 | CIU |
| 035_SK10_B_UND_EFF50 | SK10 | B | 80 | 50 | CIU |
| 044_SK15_B_UND_EFF25 | SK15 | B | 80 | 25 | CIU |
| 045_SK15_B_UND_EFF50 | SK15 | B | 80 | 50 | CIU |
| Specimen Type | Void Ratios | Present Research | Previous Research [20,21] |
|---|---|---|---|
| SK0 | 0.641 | 0.641 | |
| 0.911 | 0.911 | ||
| SK10 | 0.596 | 0.647 | |
| 1.022 | 1.121 | ||
| SK15 | 0.64 | 0.544 | |
| 1.128 | 1.43 | ||
| SK100 | 0.78 | - | |
| 1.378 | - |
| Filling Coefficient | Mean Grain Size Ratio | Power Fit Parameter p | Filling Constant | Filling Constant |
|---|---|---|---|---|
| 0.957 | 0.014 | 3.14 | 1.156 | 0.170 |
| Soil Type | Void Ratio | B-Mixtures | A-Mixture |
|---|---|---|---|
| SK10 | 0.479 | 0.596 | |
| 0.724 | 1.022 | ||
| SK15 | 0.399 | 0.64 | |
| 0.631 | 1.128 |
| Soil Type | Mixture Type | Initial Void Ratio, [-] | Relative Density, [%] |
|---|---|---|---|
| SK10 | A | 0.684 | 16 |
| B | 0.536 | 114 | |
| SK15 | A | 0.738 | N/A |
| B | 0.456 | 138 |
| Initial Conditions | Peak State Values | Critical State Values | ||||
|---|---|---|---|---|---|---|
| Test ID | Initial Void Ratio, [-] | Confining Mean Effective Stress, [kPa] | Stress Ratio at Peak, [-] | Void Ratio at Critical State, [-] | Stress Ratio at Critical State, [-] | Mean Effective Stress at Critical State [kPa] |
| 050_SK0_DR_EFF25 | 0.695 | 25 | 1.454 | 0.758 | 1.096 | 42.55 |
| 041_SK0_DR_EFF50 | 0.695 | 50 | 1.545 | 0.732 | 1.265 | 88.17 |
| 015_SK10_A_DR_EFF25 | 0.681 | 25 | 1.282 | 0.639 | 1.282 | 43.65 |
| 021_SK10_A_DR_EFF50 | 0.681 | 50 | 1.264 | 0.633 | 1.264 | 84.68 |
| 018_SK15_A_DR_EFF25 | 0.738 | 25 | 1.316 | 0.682 | 1.316 | 44.53 |
| 012_SK15_A_DR_EFF50 | 0.738 | 50 | 1.258 | 0.669 | 1.258 | 80.95 |
| 049_SK10_B_DR_EFF25 | 0.522 | 25 | 1.663 | 0.571 | 1.330 | 50.33 |
| 046_SK10_B_DR_EFF50 | 0.522 | 50 | 1.536 | 0.562 | 1.287 | 89.32 |
| 048_SK15_B_DR_EFF25 | 0.436 | 25 | 1.677 | 0.505 | 1.354 | 54.69 |
| 047_SK15_B_DR_EFF50 | 0.436 | 50 | 1.683 | 0.506 | 1.314 | 99.63 |
| Test ID | Initial Void Ratio, [-] | Effective Mean Confining Stress, [kPa] | Void Ratio After Consolidation, [-] | Void Ratio at Crtitical State, [-] | Mean Effective Stress at Crtitical State, [kPa] | State Parameter, [-] |
|---|---|---|---|---|---|---|
| 050_SK0_DR_EFF25 | 0.695 | 25 | 0.691 | 0.758 | 42.55 | −0.067 |
| 041_SK0_DR_EFF50 | 0.695 | 50 | 0.681 | 0.732 | 88.17 | −0.051 |
| 015_SK10_A_DR_EFF25 | 0.681 | 25 | 0.677 | 0.639 | 43.65 | 0.038 |
| 021_SK10_A_DR_EFF50 | 0.681 | 50 | 0.67 | 0.633 | 84.62 | 0.037 |
| 018_SK15_A_DR_EFF25 | 0.738 | 25 | 0.734 | 0.682 | 44.53 | 0.052 |
| 012_SK15_A_DR_EFF50 | 0.738 | 50 | 0.722 | 0.669 | 80.95 | 0.053 |
| 049_SK10_B_DR_EFF25 | 0.523 | 25 | 0.52 | 0.571 | 50.33 | −0.051 |
| 046_SK10_B_DR_EFF50 | 0.523 | 50 | 0.519 | 0.562 | 89.32 | −0.043 |
| 048_SK15_B_DR_EFF25 | 0.445 | 25 | 0.443 | 0.505 | 54.69 | −0.062 |
| 047_SK15_B_DR_EFF50 | 0.445 | 50 | 0.443 | 0.506 | 99.63 | −0.063 |
| Initial Condition | Undrained Instability State | Steady State | ||||
|---|---|---|---|---|---|---|
| Test ID | Void Ratio [-] | Confining Mean Effective Stress, [kPa] | Mean Effective Stress, [kPa] | Deviatoric Stress, [kPa] | Mean Effective Stress, [kPa] | Deviatoric Stress, [kPa] |
| 042_SK0_UND_EFF25 | 0.695 | 25 | 425.68 | 605.05 | 425.68 | 605.05 |
| 034_SK0_UND_EFF50 | 0.695 | 50 | 435.49 | 630.03 | 435.49 | 630.03 |
| 016_SK10_A_UND_EFF25 | 0.681 | 25 | 19.52 | 10.56 | 0.05 | 0.16 |
| 020_SK10_A_UND_EFF50 | 0.681 | 50 | 36.11 | 24.23 | 4.01 | 3.03 |
| 007_SK15_A_UND_EFF25 | 0.738 | 25 | 21.17 | 12.52 | 0.22 | 0.65 |
| 054_SK15_A_UND_EFF50 | 0.738 | 50 | 35.93 | 20.79 | 2.63 | 1.9 |
| 043_SK10_B_UND_EFF25 | 0.523 | 25 | 383.14 | 486.42 | 383.14 | 486.42 |
| 035_SK10_B_UND_EFF50 | 0.523 | 50 | 574.56 | 769.69 | 579.28 | 720.83 |
| 044_SK15_B_UND_EFF25 | 0.445 | 25 | 647.11 | 891.32 | 647.11 | 891.32 |
| 045_SK15_B_UND_EFF50 | 0.445 | 50 | 729.41 | 1033.24 | 729.41 | 1033.24 |
| Test ID | Initial Void Ratio, [-] | Effective Mean Confining Stress, [kPa] | Void Ratio After Consolidation, [-] | Mean Effective Stress at Steady State, [kPa] |
|---|---|---|---|---|
| 042_SK0_UND_EFF25 | 0.695 | 25 | 0.695 | 425.68 |
| 034_SK0_UND_EFF50 | 0.695 | 50 | 0.695 | 435.49 |
| 016_SK10_A_UND_EFF25 | 0.681 | 25 | 0.678 | 0.05 |
| 020_SK10_A_UND_EFF50 | 0.681 | 50 | 0.678 | 4.01 |
| 007_SK15_A_UND_EFF25 | 0.738 | 25 | 0.736 | 0.22 |
| 054_SK15_A_UND_EFF50 | 0.738 | 50 | 0.736 | 2.63 |
| 043_SK10_B_UND_EFF25 | 0.523 | 25 | 0.522 | 383.14 |
| 035_SK10_B_UND_EFF50 | 0.523 | 50 | 0.518 | 579.28 |
| 044_SK15_B_UND_EFF25 | 0.445 | 25 | 0.443 | 647.11 |
| 045_SK15_B_UND_EFF50 | 0.445 | 50 | 0.44 | 729.41 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Marušić, D.; Jagodnik, V. Monotonic Behaviour and Physical Characteristics of Silty Sands with Kaolinite Clay. Geotechnics 2025, 5, 70. https://doi.org/10.3390/geotechnics5040070
Marušić D, Jagodnik V. Monotonic Behaviour and Physical Characteristics of Silty Sands with Kaolinite Clay. Geotechnics. 2025; 5(4):70. https://doi.org/10.3390/geotechnics5040070
Chicago/Turabian StyleMarušić, Davor, and Vedran Jagodnik. 2025. "Monotonic Behaviour and Physical Characteristics of Silty Sands with Kaolinite Clay" Geotechnics 5, no. 4: 70. https://doi.org/10.3390/geotechnics5040070
APA StyleMarušić, D., & Jagodnik, V. (2025). Monotonic Behaviour and Physical Characteristics of Silty Sands with Kaolinite Clay. Geotechnics, 5(4), 70. https://doi.org/10.3390/geotechnics5040070






