Numerical Modeling of Expansive Soil Behavior Using an Effective Stress-Based Constitutive Relationship for Unsaturated Soils

Abstract

Previous studies have extensively applied the generalized consolidation theory, which incorporates a two-stress state variable framework, to predict the volumetric behavior of unsaturated expansive soils under varying mechanical stress and matric suction. A key requirement for this approach is a constitutive surface that links the soil void ratio to both net stress and matric suction. A large number of fitting parameters are typically needed to accurately fit a two-variable void ratio surface equation to laboratory test data. In this study, a single-stress state variable framework was adopted to describe the void ratio as a function of effective stress for unsaturated soils. The proposed approach was applied to fit void ratio–effective stress constitutive curves to laboratory test data for two different expansive clays. Additionally, a finite element model coupling variably saturated flow and stress–strain analysis was developed to simulate the volume change behavior of expansive clay subjected to moisture fluctuations. The model utilizes suction stress to compute the effective stress field and incorporates the dependency of soil modulus on volumetric water content based on the proposed void ratio–effective stress relationship. The developed numerical model was validated against a benchmark problem in which a layer of Regina expansive clay was subjected to a constant infiltration rate. The results demonstrate the effectiveness of the proposed model in simulating expansive soil deformations under varying moisture conditions over time.

1. Introduction

Numerical methods equipped with constitutive relationships for unsaturated soil mechanics formulation, in particular, have become essential tools in geotechnical engineering for modeling the highly nonlinear and coupled hydro-mechanical processes that govern the behavior of expansive soils. These methods enable detailed predictions of soil movement and stress changes under variable climatic and loading conditions, which are often impractical to capture through the conventional numerical methods.

Several analytical and numerical methods have been developed to predict the volume change behavior of unsaturated expansive soils under environmental and mechanical loadings. These methods typically utilize a constitutive law that relates soil state variables (i.e., water content, matric suction, or mechanical stress) to volume change [1,2]. Adem and Vanapalli [3] reviewed various approaches for predicting the long-term volume change in expansive soils and classified them into three categories:

• Consolidation theory-based methods: These methods analyze transient water flow and soil volume change by applying the coupled consolidation theory of unsaturated soils. They incorporate volume change constitutive models, including elastic formulations (e.g., [4,5]) and elastoplastic models (e.g., [6]).
• Water content-based methods: These approaches relate soil movement due to environmental variations over time to changes in water content rather than matric suction (e.g., [2,7]). Unlike coupled models, these methods focus solely on soil movement resulting from moisture fluctuations.
• Suction-based methods: These techniques assess soil movements in response to environmental changes by estimating or predicting variations in matric suction (e.g., [8,9]).

The increasing reliance on numerical modeling in expansive soil research is evident from a broad body of literature proposing various constitutive relationships and computational frameworks to capture the behavior of unsaturated soils. These models range from simple one-dimensional approaches to sophisticated numerical models.

Vu and Fredlund [4,10] introduced an elasticity-based model for unsaturated expansive soils to simulate nonlinear stress–strain behavior, incorporating the coefficient of compressibility as a function of net normal stress and matric suction. They applied two-stress state constitutive relationships initially proposed by Fredlund and Morgenstern [11]. Vu and Fredlund [4,10] evaluated their model using both coupled and uncoupled approaches across multiple examples and found that the results from the uncoupled analysis closely align with those from the coupled analysis.

Ito and Hu [12] developed a coupled numerical model to predict the hydraulic and mechanical behavior of Regina expansive clay. In their approach, the initial and final matric suction values predicted by the hydraulic model were used as input stress conditions for a separate displacement model. This displacement model incorporated two elastic moduli: one corresponding to net normal stress and the other to suction. Their findings showed that the model produced results in good agreement with field observations.

Later, Ito et al. [13] introduced a two-stage, two-dimensional finite element model to simulates wetting-induced deformations in expansive soils. Their approach incorporated a coupled soil–atmosphere model for seepage analysis and a suction-based displacement model to capture expansive soil behavior using normal stress and matric suction. The simulations were conducted using the general partial differential equation solver FlexPDE software (version 7.07, PDE Solutions Inc., Spokane, WA, USA). They validated their model against field monitoring data reported by Hu et al. [14].

Adem and Vanapalli [9] proposed a simple method for predicting the time-dependent vertical movements of unsaturated expansive soils.

This approach, known as the Modulus of Elasticity-Based Method (MEBM), integrates the constitutive relationship for unsaturated soils developed by Fredlund and Morgenstern [11] with the VADOSE/W software (version 7.11, GEO-SLOPE International, Ltd., Calgary, AB, Canada) [15]—a finite element model capable of simulating variably saturated flow with an implemented soil–atmosphere boundary condition. Adem and Vanapalli [3] later enhanced this framework by incorporating a semi-empirical method originally proposed by [16] to estimate the modulus of elasticity for unsaturated expansive soils, thereby improving the model’s predictive capability for soil movement over time [3,9,17].

Karunarathne et al. [18] developed a numerical model to estimate ground movements in expansive soils at two sites in Melbourne, Australia. They utilized VADOSE/W [15] software to simulate soil moisture variations due to climatic factors, and the predicted soil moisture values were subsequently used in FLAC3D software (version 5.0, Itasca Consulting Group, Inc., Minneapolis, MI, USA) to model ground movements. The unsaturated hydraulic conductivity function in the flow model was estimated using the Fredlund–Xing method [19]. The formulations in the FLAC software were based on the assumption of isotropic free swelling behavior, where linear swelling strain is related to changes in moisture content through a linear expansion coefficient. The initial soil suction profile was estimated by converting the field measured volumetric water content profile using the laboratory-measured soil–water characteristic curve (SWCC). The model was employed to assess long-term variations in ground movements due to climatic conditions. Model validation was conducted by comparing field-measured and model-predicted volumetric water content values.

Zhang et al. [20] used the HYDRUS 2D software (Version 2.1, PC-Progress, Groton, MA, USA) package [21] to simulate one year of water infiltration into a road embankment. They generated climate-specific matric suction profiles using HYDRUS 2D and applied them to compute pavement vertical movements using [22] suction-based constitutive law, which relates soil layer height changes to variations in suction. Through a series of sensitivity analyses, Zhang et al. [20] demonstrated that initial moisture conditions and hydraulic conductivity have the most significant influence on pavement vertical movement, whereas the evaporation rate has minimal impact. Their findings also indicated that under an extreme rainfall event, vertical movement could double compared to normal conditions.

Despite advances in the numerical modeling of the volume change behavior of expansive soils, challenges remain in accurately defining the stress state and stiffness characteristics under unsaturated conditions. Consequently, the development of simplified yet effective numerical frameworks that reduce complexity while retaining predictive capability remains a priority.

Previous consolidation theory-based numerical models have employed a two-stress state variable approach, where the soil constitutive law is defined based on net normal stress and matric suction. This approach requires two sets of constitutive parameters to predict the response of expansive soils to both mechanical and environmental loadings. For instance, in elasticity-based methods within the two-stress state framework, the relevant material properties include the elastic modulus with respect to net normal stress and the elastic modulus with respect to suction stress.

In this study, an unsaturated soil mechanics framework based on a single-stress state variable was adopted. The framework integrates suction stress—a novel variable—into Terzaghi’s effective stress concept. This approach was used to describe the relationship between the void ratio and effective stress in unsaturated soils. The proposed constitutive relationship was then used to define a variable stiffness model, capturing the dependency of the soil elastic modulus on volumetric water content. This elastic modulus equation was integrated into a two-dimensional finite element model, which combines transient variably saturated seepage analysis with effective stress–strain analysis. The finite element model utilizes suction stress to compute the effective stress field as a single-stress state variable. The developed numerical model was applied to a benchmark problem, simulating a partially paved Regina expansive clay surface subjected to a constant infiltration rate for 175 days. The results were compared with findings from previous studies, including those by [9,10,23,24].

2. Background and Theoretical Framework

To analyze how expansive soils respond to water variations induced by climatic factors, a hydro-mechanical modeling approach is typically employed. This involves coupling a time-dependent variably saturated seepage model with a mechanical strain–stress model. The seepage model must incorporate a soil–atmosphere boundary, while the mechanical model requires an unsaturated soil mechanics framework. Since the mechanical properties of expansive soils are highly dependent on water content, an appropriate constitutive model is essential for accurately simulating volumetric deformation behavior. The volume change characteristics of expansive soils can be described using constitutive relationships that link deformation state variables (e.g., void ratio, e) to the relevant stress state variable(s).

2.1. Two-Stress State Constitutive Surface

The two-stress state approach, which utilizes net normal stress and matric suction, has been widely applied to describe the volume change and shear strength behavior of soils. In this framework, soil volume can change due to variations in both mechanical stress and matric suction. Consequently, the constitutive relationships must be expressed as a constitutive surface within the void ratio–net normal stress–matric suction space.

Several mathematical models have been proposed in the literature to describe the void ratio constitutive surface. Fredlund and Hasan [25] suggested that this surface can be linearized over a wide range of stresses by applying a logarithmic transformation to the stress state variables, as represented by the following equation:

$$e=a+b\log \left(\sigma -u_a\right)+c\log \left(u_a-u_w\right)$$

(1)

where $a$, $b$, and $c$ are equation constants, $u_a$ is the pore-air pressure, $u_w$ is the pore-water pressure, $\sigma -u_a$ is the net total stress, and $u_w-u_a$ is the matric suction.

Lloret and Alonso [26] examined various mathematical formulations to describe the volume change constitutive surface of unsaturated soils under different loading conditions. By comparing the best-fitting models to experimental data from different soil types, they proposed the following equations:

$$e=a^{*}+b^{*}\log \left(\sigma -u_a\right)+c^{*}\log \left(u_a-u_w\right)+d^{*}log\left(\sigma -u_a\right)\log \left(u_a-u_w\right)$$

(2)

where $a^{*}$, $b^{*}$, $c^{*}$, and $d^{*}$ are equation constants.

Fredlund [27] proposed the following equation for an overconsolidated soil:

$$e=a^{\#}+b^{\#}ln\left[1+{\left({\displaystyle \frac{\sigma }{c^{\#}}}\right)}^2\right]+d^{\#}ln\left[1+{\left({\displaystyle \frac{\sigma }{f}}\right)}^2\right]$$

(3)

where $a^{\#}=a_1+a_2\left(u_a-u_w\right),b^{\#}=b_1+b_2\ln \left(u_a-u_w\right),d^{\#}=d_1+d_2\ln \left(u_a-u_w\right)$, and $a_1$, $a_2$, $b_1$, $b_2$, $c^{\#}$, $d_1$, $d_2$, and $f$ are eight fitting parameters.

Vu [28] evaluated six different mathematical equations to define a void ratio constitutive surface for Regina clay. The following six-parameter equation was shown to provide an optimal constitutive surface:

$$e=a^{~}+b^{~}log\left[{\displaystyle \frac{1+c^{~}\left(\sigma -u_a\right)+d^{~}(u_a-u_w)}{1+f^{~}\left(\sigma -u_a\right)+g\left(\right(u_a-u_w)}}\right]$$

(4)

where $a^{~}$, $b^{~}$, $c^{~}$, $d^{~}$, $f^{~}$, and $g$ are equation constants. Vu [28] proposed $a^{~}$ = 1.183, $b^{~}$ = −0.283, $c^{~}$ = 0.015, $d^{~}$ = 0.045, $f^{~}$ = 0, and $g$ = 0.00534 for Regina clay using laboratory test data obtained from a series of free swell oedometer and constant matric suction consolidation tests.

A constitutive surface can be simplified to a plane by assuming a linear relationship between the state variables. If the void ratio is linearly related to the logarithm of net stress and the logarithm of matric suction, the resulting plane constitutive surface can be expressed using the following equation:

$${\displaystyle \frac{{\sigma }_m-u_a}{{10}^{\left(\frac{e^{\daleth }-b^{\daleth }}{a^{\daleth }}\right)}}}+{\displaystyle \frac{u_a-u_w}{{10}^{\left(\frac{e^{\daleth }-d^{\daleth }}{c^{\daleth }}\right)}}}=1$$

(5)

where $a^{\daleth }$, $b^{\daleth }$, $c^{\daleth }$, and $d^{\daleth }$ are equation constants. However, the constant void ratio curve for the void ratio constitutive surface does not necessarily have to be a straight line. Zhang [5] suggested that a quadratic constant void ratio curve could provide a more accurate representation of soil volume change behavior. Based on this assumption, Zhang [5] proposed the following mathematical expression for the void ratio constitutive surface:

$$\left({\sigma }_m-u_a\right){10}^{\left[y_{\mathrm{n}\mathrm{t}-}{b}_{\mathrm{n}\mathrm{t}}\ln \left({\displaystyle \frac{a_{\mathrm{n}\mathrm{t}}}{e-x_{\mathrm{n}\mathrm{t}}}}-1\right)\right]}+\left(u_a-u_w\right){10}^{[y_{\mathrm{m}\mathrm{s}}-b_{\mathrm{m}\mathrm{s}}\ln \left({\displaystyle \frac{a_{\mathrm{m}\mathrm{s}}}{e-x_{\mathrm{m}\mathrm{s}}}}-1\right)]}=1$$

(6)

where $a_{\mathrm{n}\mathrm{t}}$, $b_{\mathrm{n}\mathrm{t}}$, $x_{\mathrm{n}\mathrm{t}}$, and $y_{\mathrm{n}\mathrm{t}}$ are fitting parameters associated with the first term (net total stress), and $a_{\mathrm{m}\mathrm{s}}$, $b_{\mathrm{m}\mathrm{s}}$, $x_{\mathrm{m}\mathrm{s}}$, and $y_{\mathrm{m}\mathrm{s}}$ are fitting parameters corresponding to the second term (matric suction). Zhang [5] used the above equation to establish the constitutive surface for an expansive clay from a site at Arlington, Texas, in the United States. The regression parameters proposed by [5] to fit the equation to the available laboratory testing data are presented in

Table 1. Regression parameters for Arlington (Texas) expansive clay, Zhang [5].

	Regression Parameters
net total stress term	$a_{nt}=$ 0.6641	$b_{nt}=$ −0.6811	$x_{nt}=$ 3.3957	$y_{nt}=$ 0.1731
matric suction term	$a_{ms}=$ 0.3604	$b_{ms}=$ −0.5073	$x_{ms}=$ 2.7015	$y_{ms}=$ 0.4740

.

The reviewed literature suggests that most mathematical equations proposed for the void ratio surface require between three and eight constants to achieve the best fit to experimental data. In general, a larger number of fitting parameters improves the accuracy of constitutive relationships in representing experimental results. However, an excessive number of parameters can lead to a loss of physical interpretability of the equations [26].

2.2. Effective Stress Equation Based on Suction Stress

Effective stress is a fundamental stress state variable widely used to evaluate soil strength and simulate soil deformation behavior within the classical soil mechanics framework. Bishop [29] extended Terzaghi’s effective stress principle to apply to unsaturated soil conditions, as shown in the following equation:

$${\sigma }^{\prime }=\left(\sigma -u_a\right)-\chi \left(u_w-u_a\right)$$

(7)

where $u_a$ is the pore-air pressure, $u_w$ is the pore-water pressure, $\sigma -u_a$ is the net total stress, and $u_w-u_a$ is the matric suction. $\chi$ is a scaling parameter depending on the degree of soil saturation with the constraints of being zero when soil is completely dry and being unity when soil is fully saturated. The single-valued effective stress equation described above has been found to be insufficient for accurately representing both volume change and shear strength behavior [30,31]. Early attempts to develop a single-stress state variable for unsaturated soil conditions were later succeeded by the two-stress state variable approach [32,33].

Despite its widespread use, the two-stress state variable approach has a significant practical limitation: it cannot be applied within the framework of classical mechanics, which considers effective stress as the sole governing stress state variable for soil behavior [34]. Additionally, ensuring a smooth transition from unsaturated to saturated conditions in elasto-plastic models presents another challenge when using this approach [30].

To address these limitations, several researchers have proposed modified effective stress formulations for unsaturated soils (e.g., [30,35,36,37,38,39,40]). In this study, the single-stress state variable approach proposed by Lu et al. [34] was adopted to compute effective stress. The time-dependent changes in water content were used to capture variations in effective stress, which in turn were used to simulate the volumetric behavior of expansive soils.

Lu and Likos [38] extended the pioneering work by Bishop [29], to define a new stress variable called suction stress (${\sigma }^s$) within the context of Terzaghi’s effective stress equation as follows:

$${\sigma }^{\prime }=(\sigma -u_a)-{\sigma }^s$$

(8)

Lu et al. [34] proposed a closed-form expression for suction stress for the full range of matric suction:

$${\sigma }^s=-(u_a-u_w)\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}(u_a-u_w)\le 0$$

(9)

$${\sigma }^s={\displaystyle \frac{(u_a-u_w)}{{\left(1+{\left[\alpha (u_a-u_w)\right]}^n\right)}^{\left(n-1\right)/n}}}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}(u_a-u_w)\ge 0$$

(10)

where $\alpha$ and $n$ are the parameters used to define the soil–water characteristic curve (SWCC) of a soil using van Genuchten’s [41] equation.

3. Proposed Single-Stress State Constitutive Relationship

The relationship between the void ratio (e) and the logarithm of effective stress (σ’) has been widely used for saturated soils. For unsaturated soil conditions, laboratory tests to assess soil deformation behavior are typically conducted under controlled net total stress and controlled matric suction separately. However, the single-stress state framework discussed in the previous section suggests that the volume change behavior of an unsaturated soil can be represented using a void ratio–effective stress relationship, incorporating SWCC parameters.

In this study, a simple approach was adopted to investigate a unique relationship between void ratio and effective stress for two expansive soils: Texas expansive clay, as reported by [5], and Regina expansive clay, as reported by [28]. To achieve this, the void ratio for each expansive soil was computed using Equation (4) for Regina expansive clay and Equation (5) for Texas expansive clay, based on a dataset of net stress–matric suction values. The effective stress corresponding to each combination of net stress and matric suction was then determined using Equations (8)–(10), resulting in a dataset of effective stress–void ratio values for each soil.

To compute effective stress, the parameters α and n (as per Equation (9)) must first be determined. This was accomplished by fitting van Genuchten’s equation [41] to the SWCC data for each soil. RETC software (Version: 6.01, PC-Progress, Groton, MA, USA) [42] was used to obtain soil–water characteristic parameters for both expansive clays, as summarized in

Table 2. SWCC parameters α and n.

	α (1/kPa)	n
Regina Expansive Clay	1.2350	1.10
Texas Expansive Clay	0.0029	1.27

.

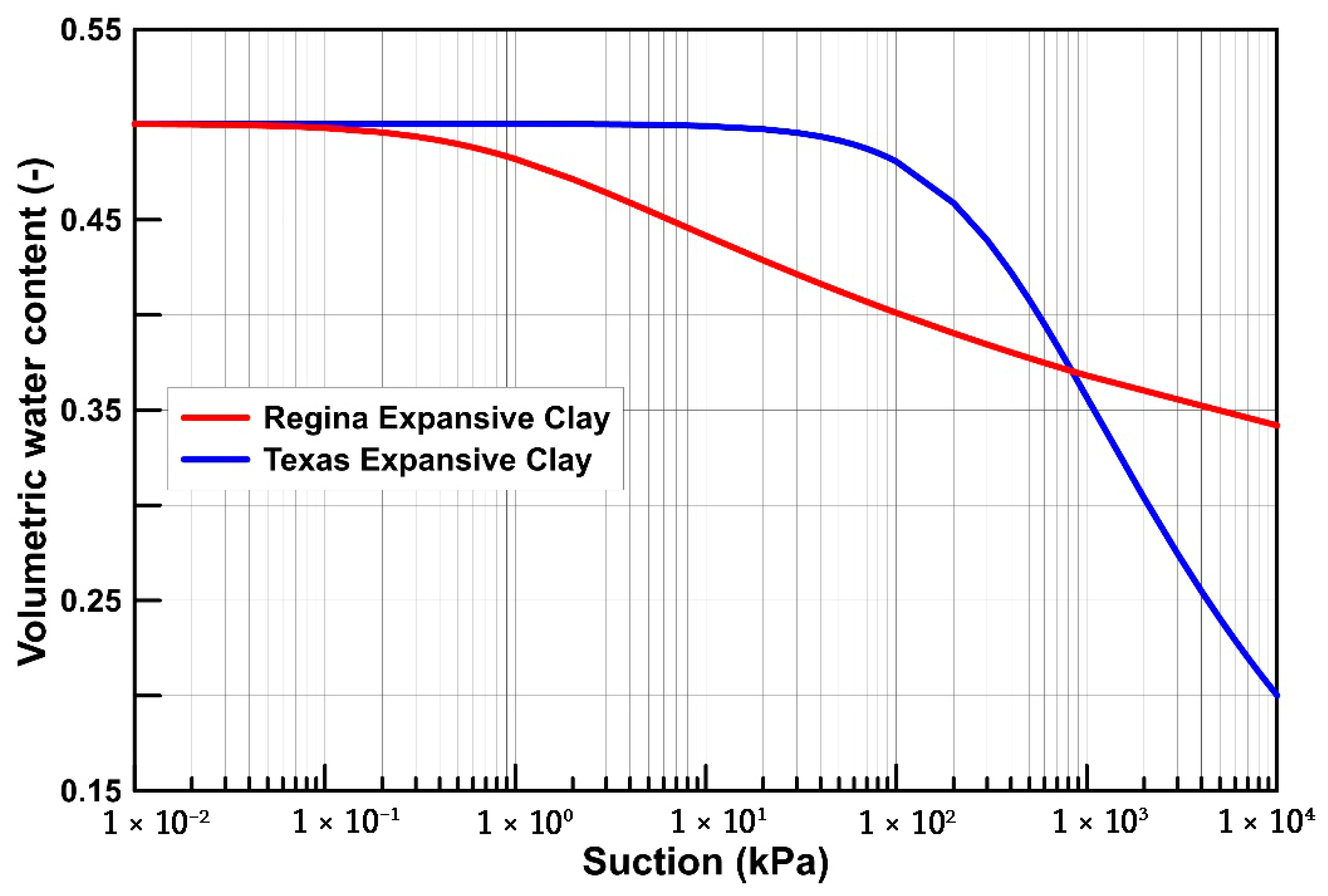
The SWCC curves for these two soils are presented in Figure 1.

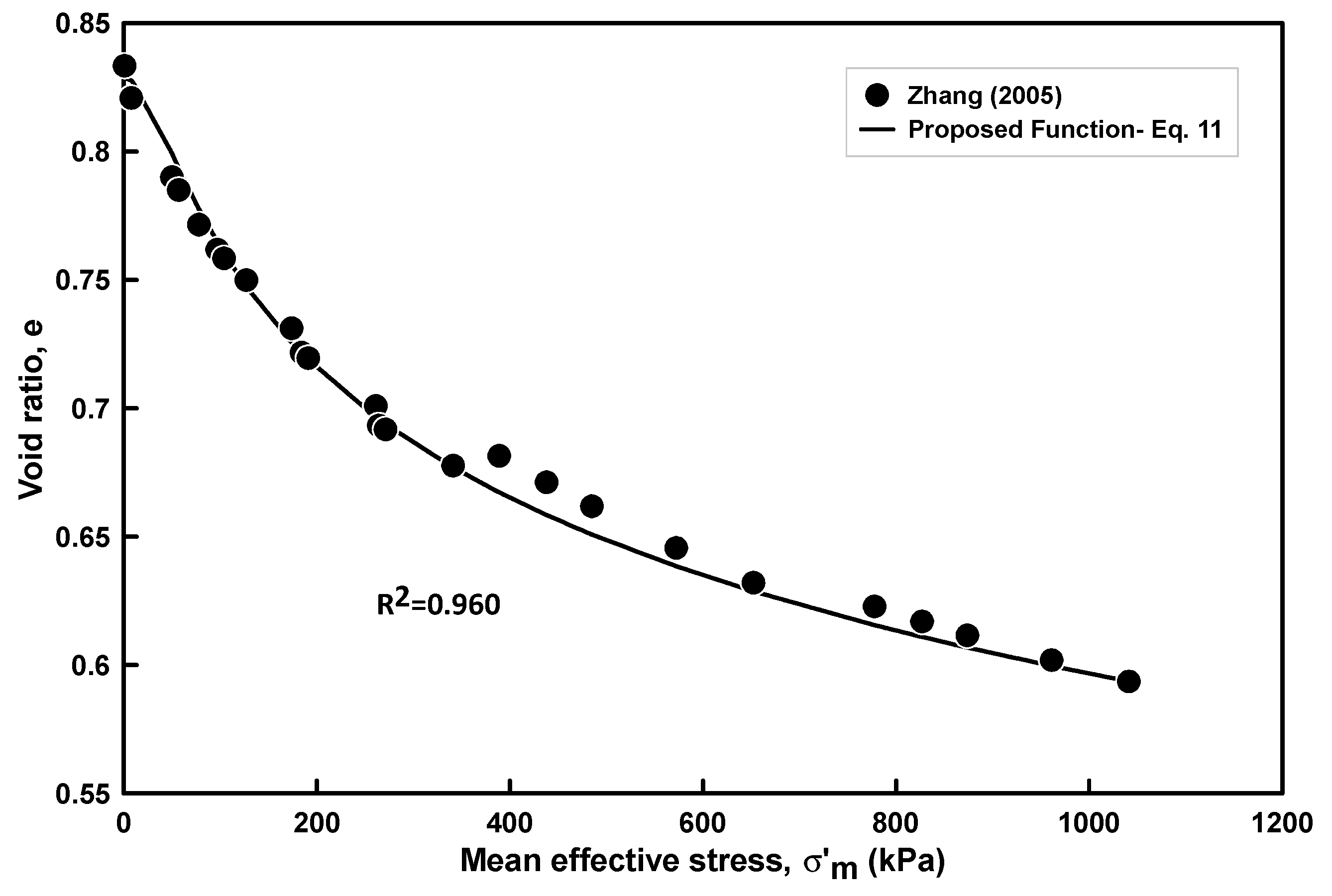
The above-mentioned approach converts a void ratio constitutive surface in $e-\sigma -(u_a-u_w)$ space into a void ratio constitutive curve in $e-\sigma \prime$ space. Figure 2 and Figure 3 depict the results obtained, illustrating the changes in void ratio concerning the mean effective stress for Regina expansive clay and Texas expansive clay, respectively. The curve-fitting process for the acquired data was performed using MATLAB R2019a. (The MathWorks, Inc., Natick, MA, USA). The following equation was used to characterize the relationship between void ratio variations and changes in mean effective stress:

$$e=A+B ln\left[1+{({\displaystyle \frac{{{\sigma }_m}^{\prime }}{C}})}^2\right]$$

(11)

where $A$, $B$, and $C$ are equation constants, and ${{\sigma }_m}^{\prime }$ is the mean effective stress.

The fitted curves for these two expansive clays are shown in Figure 2 and Figure 3, and the fitting parameters are presented in

Table 3. Regression parameters for two expansive clays in this study.

	$\mathit{A}$	$\mathit{B}$	$\mathit{C}$	${\mathit{R}}^2$	$\mathit{M}\mathit{S}\mathit{E}$	$\mathit{R}\mathit{M}\mathit{S}\mathit{E}$
Regina Clay	1.183	−0.032	8.475	0.960	1.79 × 10−4	0.0134
Texas Clay	0.829	−0.038	45.697	0.993	4.76 × 10−5	0.0069

.

The regression model performance was validated using several regression indices including R-Squared (R²), mean square error (MSE), and root mean square error (RMSE). The obtained values for these indices are presented in Table 3.

The best-fit curve for the relationship between the void ratio and mean effective stress was obtained using three fitting parameters in Equation (11). In comparison, Equation (4) required six fitting parameters for Regina expansive clay, while Equation (6) required eight fitting parameters for Texas expansive clay. However, the proposed suction stress-based approach simplifies the constitutive void ratio–effective stress relationship by utilizing Equation (11), which involves only three fitting parameters ($A$, $B$, and $C$) along with two physically meaningful parameters ($\alpha$ and $n$) derived from van Genuchten’s SWCC model.

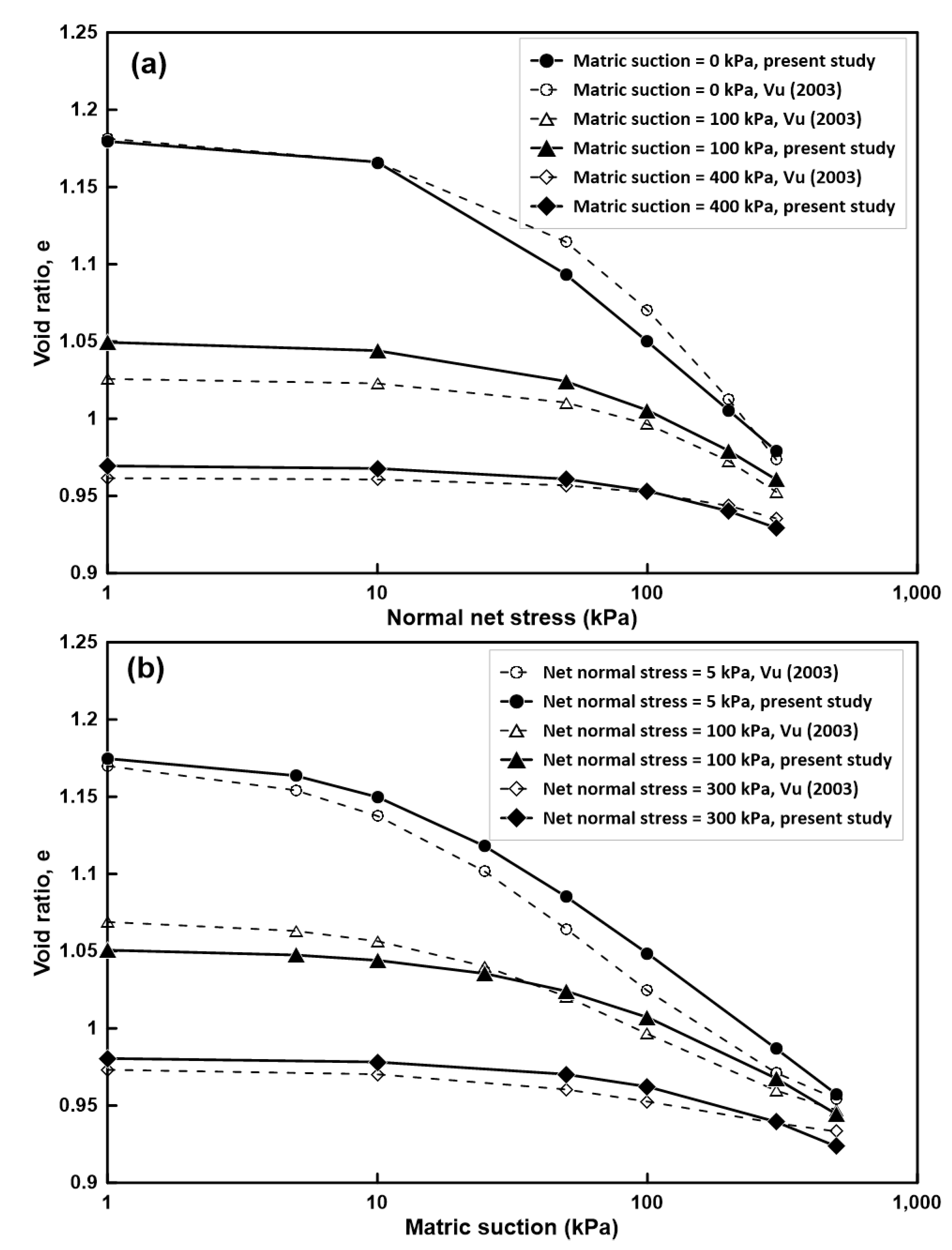
The proposed approach was utilized to reproduce the two-stress state void ratio constitutive relationships by generating a series of single-stress state constitutive relationships while keeping the normal net stress or matric suction constant. A comparison of the original and simulated void ratio curves is presented in Figure 4 and Figure 5 for Regina clay and Texas clay, respectively.

The results presented in these figures demonstrate that the effective stress-based method can approximate the two-stress state constitutive surface with a high degree of accuracy, while requiring fewer fitting parameters for the two expansive clays analyzed in this study.

For Regina clay, the maximum variation in void ratio is less than 5%, whereas for Texas clay, the predicted curves exhibit excellent agreement, with a void ratio difference of less than 2% at the same matric suction and net normal stress values.

4. Numerical Model

In this study, HYDRUS (2D/3D) version 3.04.0140 [21], in combination with the Slope Cube module [43], was used to simulate two-dimensional transient fields of soil moisture, matric suction, suction stress, total and effective stresses, and deformation.

HYDRUS 2D is a finite element software that numerically solves a modified form of Richards’ equation to model water flow in variably saturated soils. The Slope Cube module extends HYDRUS by computing stresses and deformations resulting from transient variably saturated flow analysis. Originally developed to assess landslide initiation and locations under rainfall conditions, Slope Cube is an effective stress-based finite element module capable of simulating soil deformations due to variations in the suction stress field, as described in the previous section. Additionally, the module incorporates a power-law equation to account for elastic modulus variations with soil moisture.

The pore-pressure distribution, influenced by infiltration, is updated at each time step through seepage analysis using HYDRUS 2D. This updated information is then utilized by the Slope Cube module to compute suction stress, the effective stress field, and the resulting soil deformations.

4.1. Variably Saturated Flow Analysis

HYDRUS 2D numerically solves the Richards’ equation for saturated–unsaturated water flow through porous medium. The two-dimensional form of Richards’ equation is given as follows [44]:

$${\displaystyle \frac{\partial \theta }{\partial t}}={\displaystyle \frac{\partial }{\partial x}}\left[K(h)({\displaystyle \frac{\partial h}{\partial x}})\right]+{\displaystyle \frac{\partial }{\partial z}}\left[K(h)({\displaystyle \frac{\partial h}{\partial z}}+1)\right]+S_w$$

(12)

where $\theta$ is the volumetric water content (${\displaystyle \frac{m^3}{m^3}}$), $t$ is time, $K\left(h\right)$ is the unsaturated hydraulic conductivity (m/s), $h$ is the soil water matric head (m), and $S_w$ is a source (positive) or sink (negative) term that represents the volume of water added or removed per unit time from a unit volume of soil ($m^3{m}^{-3}{s}^{-1})$.

The equation assumes that the air phase remains at atmospheric pressure and has a negligible influence on the liquid flow process. Richards’ equation is a highly nonlinear partial differential equation, with analytical solutions only possible under simplified initial and boundary conditions. Additionally, the equation assumes that the soil is rigid and incompressible [45,46].

The solution of Richards’ equation requires the relationship between volumetric water content $\left(\theta \right)$ and matric suction ($h$), as well as the relationship between hydraulic conductivity (K) and matric suction ($h$). The relationship between volumetric water content and matric suction is called the soil–water characteristic curve (SWCC), and the relationship between hydraulic conductivity and matric suction is called the hydraulic conductivity function (HCF).

The soil–water characteristic curve (SWCC) is the fundamental soil hydraulic function, providing a framework for explaining most aspects of unsaturated soil behavior. Numerous mathematical models have been developed to describe the SWCC, each with varying degrees of accuracy (e.g., [19,41,47]). In this study, the widely used [41] model was adopted:

$$\theta ={\theta }_r+({\theta }_s-{\theta }_r){\left[{\displaystyle \frac{1}{1+{\left(\alpha \left|h\right|\right)}^n}}\right]}^{(1-{\displaystyle \frac{1}{n}})}$$

(13)

This equation describes the relationship between soil volumetric water content and matric suction ($h$) for a given saturated water content (${\theta }_s$) and residual water content (${\theta }_r$). There are also two empirical coefficients α and n in this function, which are related to the air entry value and pore-size distribution of the soil.

In unsaturated soils, hydraulic conductivity is significantly influenced by changes in both the void ratio and the degree of saturation [48]. Since the degree of saturation can be expressed as a function of matric suction, the hydraulic conductivity can also be described as a function of matric suction and the void ratio. The hydraulic conductivity function (HCF) can be determined through direct measurement, indirect computation, or by estimating it using the soil–water characteristic curve (SWCC) and saturated hydraulic conductivity. Various HCF models have been proposed in the literature to describe the hydraulic behavior of unsaturated soils (e.g., [19,41,49,50,51]). van Genuchten [41] derived a predictive equation for the unsaturated hydraulic conductivity function by applying [52] statistical pore-size distribution model. This model is expressed as follows:

$${\displaystyle \frac{K\left(h\right)}{K_{sat}}}={\mathsf{\Theta }}^p{\left[1-{(1-{\mathsf{\Theta }}^{{\displaystyle \frac{1}{m}}})}^m\right]}^2,\mathsf{\Theta }={\displaystyle \frac{\theta -{\theta }_r}{{\theta }_s-{\theta }_r}},m=1-{\displaystyle \frac{1}{n}}$$

(14)

where $K\left(h\right)$ is the hydraulic conductivity (m/s), $K_{sat}$ is the saturated hydraulic conductivity (m/s), $p$ is a constant set to 0.5, and $n$ is a fitting parameter of SWCC. This equation is used in this study.

4.2. Stress–Strain Analysis

The calculation of the effective stress field and soil displacements requires a mechanical model. In unsaturated soils, a two-stress state variable mechanical model is formulated as an extension of the equations used for saturated soils, incorporating net normal stress and matric suction as independent stress state variables. However, in the effective stress-based framework adopted in this study, the mechanical model computes soil stresses and displacements by treating suction stress as a component of effective stress.

Strains are defined by the first derivatives of displacements as follows:

$${\epsilon }_{ij}={\displaystyle \frac{1}{2}}\left(u_{i,j}+u_{j,i}\right)\hspace{1em}\hspace{1em}i,j=\mathrm{1,2},3$$

(15)

where ${\epsilon }_{ij}$ is component of the small strain tensor in the $i-j$ direction, $u_i$ is displacement component in the $i$ direction, and $u_{i,j}$ is partial derivative of the displacement component $u_i$ with respect to the spatial coordinate $x_j$.

In the elasticity form, stresses and strains are related by Hook’s law through the introduction of material’s elastic properties:

$${\sigma \prime }_{ij}={\displaystyle \frac{2G\mu }{1-2\mu }}{\epsilon }_{kk}{\delta }_{ij}+2G{\epsilon }_{ij}\hspace{1em}\hspace{1em}i,j,k=\mathrm{1,2},3$$

(16)

where ${\sigma \prime }_{ij}$ is component of the effective stress tensor in the $i-j$ direction, ${\delta }_{ij}$ is the identity tensor (Kronecker delta), $\mu$ is the Poisson’s ratio reflecting the change in the normal strain in a specific direction due to the change in a unit strain orthogonal to it, and $G$ is the shear modulus reflecting the change in shear stress due to the change in a unit shear strain.

Under the equilibrium conditions, at any point within the medium, the force and momentum balance in both the horizontal and vertical directions should be satisfied. The equilibrium equations are given in index notation as

$${\sigma }_{ji,j}+f_i=0\hspace{1em}\hspace{1em}i,j=\mathrm{1,2},3$$

(17)

where $f_i$ is the body force vector in direction $i$.

The unified effective stress equation (Equation (8)) can be written in index form as

$${\sigma }_{ij}^{\prime }={\sigma }_{ij}-{\sigma }^s{\delta }_{ij}\hspace{1em}\hspace{1em}i,j=\mathrm{1,2},3$$

(18)

Implementing the effective stress Equation (18) into Equation (17) yields

$${\sigma \prime }_{ji,j}+{\sigma }_{,i}^s+f_i=0\hspace{1em}\hspace{1em}i,j=\mathrm{1,2},3$$

(19)

Equations (15), (16), and (19) include the equations required to compute the unknown variables (e.g., displacements) in an elastic medium. In the two-dimensional case, this involves eight equations with eight variables (three total stress, three strains, and two displacements). The numerical solution of these equations is implemented in the Slope Cube FE code with proper boundary conditions for displacements and stresses.

4.3. Soil Variable Stiffness

In this study, a mathematical model was developed to relate the variation in the void ratio and effective stress change based on available soil constitutive data in terms of two stress variables, i.e., net total stress (${\sigma }_{nt})$ and matric suction ($h)$.

Assuming that the void ratio is defined as a function of net total stress and soil suction, i.e., $e=f({\sigma }_{nt},h)$, the differential of this function is given by

$$de={\displaystyle \frac{\partial f}{\partial {\sigma }_{nt}}}d{\sigma }_{nt}+{\displaystyle \frac{\partial f}{\partial h}}dh$$

(20)

The single-stress state approach suggests that the void ratio can be defined as a function of the effective stress that is identified as $e=g\left({\sigma }^{\prime }\right)$ in this study. Similarly, the deferential of this function can be expanded as follows:

$$de={\displaystyle \frac{\partial g}{\partial \acute{\sigma }}}d\acute{\sigma }={\displaystyle \frac{\partial g}{\partial \acute{\sigma }}}(d{\sigma }_{nt}-d{\sigma }_s)$$

(21)

The change in net normal stress, where the soil is subject solely to climate variables or light loads such as pavements or light buildings, is typically minimal. Therefore, one can assume that the soil deformation is largely due to changes in matric suction. In this study, the net normal stress is assumed constant in the development of the mathematical model ($d{\sigma }_{nt}=0)$. This assumption has been considered in the previous studies (e.g., [9]). Therefore, Equations (20) and (21) reduce to the following equations:

$$de={\displaystyle \frac{\partial f}{\partial h}}dh$$

(22)

$$de=-{\displaystyle \frac{\partial g}{\partial \acute{\sigma }}}d{\sigma }_s$$

(23)

The above equations can be combined to obtain an equation for the change in a void ratio with respect to matric suction at a given total net stress:

$${\displaystyle \frac{de}{d\acute{\sigma }}}=-{\displaystyle \frac{\partial f}{\partial h}}\times {\displaystyle \frac{1}{\frac{d{\sigma }_s}{dh}}}$$

(24)

The first derivative of suction stress with respect to matric suction is given by the following [34]:

$${\displaystyle \frac{d{\sigma }_s}{dh}}=-{\displaystyle \frac{1}{{\left(1+{\left[\alpha h\right]}^n\right)}^{\frac{n-1}{n}}}}+{\displaystyle \frac{\left(n-1\right){\left[\alpha h\right]}^n}{{\left(1+{\left[\alpha h\right]}^n\right)}^{\frac{2n-1}{n}}}}$$

(25)

In this study, Equation (24) was used to calculate the soil deformation modulus for the effective stress–strain analysis.

Several previous studies have employed elastic moduli to simulate the heave behavior of expansive soils. In general, a linear elasticity formulation can be applied incrementally, using small stress and strain increments, to model the nonlinear stress–strain behavior of soil [28]. Within the two-stress state framework, originally proposed by Fredlund and Morgenstern [11], two elastic moduli are typically used to calculate soil deformations resulting from changes in net normal stress and matric suction. However, in an effective stress-based approach, the coefficient of volume change ($m_v$) with respect to effective stress variations can be considered as follows:

$$m_v={\displaystyle \frac{1}{1+e_0}}{\displaystyle \frac{de}{d\acute{\sigma }}}$$

(26)

For the K0-loading condition, the coefficient of volume change is related to the elastic modulus as follows:

$$E={\displaystyle \frac{(1+\mu )(1-2\mu )}{(1-\mu )m_v}}$$

(27)

where $\mu$ is the soil Poisson’s ratio.

The dependency of elastic modulus on effective stress is well established for saturated soils. Under unsaturated conditions, previous experimental studies have confirmed that the elastic modulus is also influenced by soil volumetric water content (e.g., [53,54,55]. It has been observed that the elastic modulus of a soil can increase by several orders of magnitude as it transitions from fully saturated to dry conditions, due to soil water retention mechanisms such as adsorption and capillarity [56].

In this study, Equations (24), (26), and (27) were used to evaluate the variation in the elastic modulus with matric suction at a given net total stress level. The soil–water characteristic curve (SWCC), modeled using van Genuchten’s [41] equation, was employed to compute the elastic modulus variation as a function of volumetric water content.

Several semi-empirical models have been proposed in the literature to predict the variation in elastic modulus with soil volumetric water content or matric suction under unsaturated conditions (e.g., [16,53,56,57]). In this study, the following power law equation, which expresses soil elastic modulus as a function of volumetric water content, was implemented in the numerical analysis:

$$E\left(\theta \right)=E_{dry}+\left(E_{sat}-E_{dry}\right){\left({\displaystyle \frac{\theta -{\theta }_d}{{\theta }_w-{\theta }_d}}\right)}^l$$

(28)

where $E\left(\theta \right)$ is the elastic modulus; $E\left(\theta \right)=E_{dry}$ for the drying state when $\theta ={\theta }_d$ usually measured at the residual saturation state; $E\left(\theta \right)=E_{sat}$ for the wetting state, when $\theta ={\theta }_w$ is usually measured at the fully saturated state; and $l$ is an empirical parameter.

5. Case Study

5.1. Problem Statement

Figure 6 illustrates a 5 m thick layer of Regina expansive clay, partially covered by an impervious layer. The uncovered section of the ground surface is subjected to a constant infiltration rate of 1.73 mm/s. The initial matric suction is assumed to be uniform throughout the depth, with a value of 400 kPa. The hydraulic boundary conditions are also depicted in Figure 6.

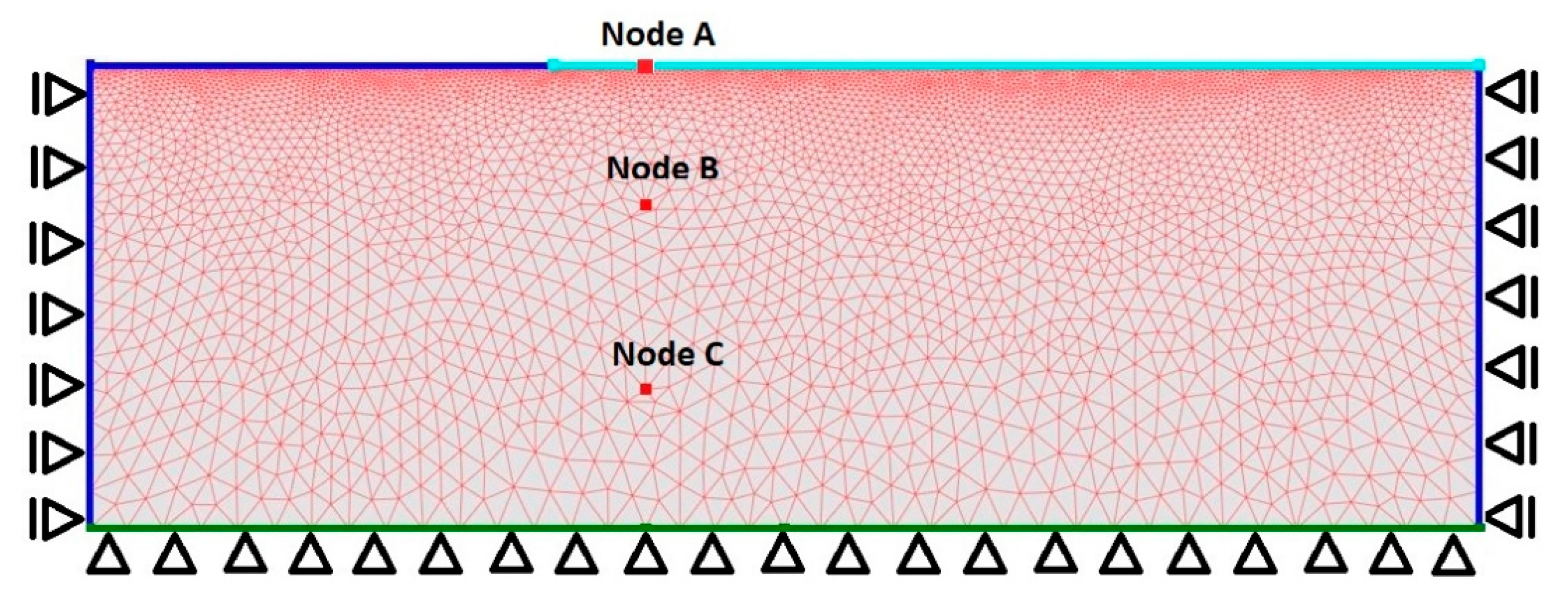
The finite element stress–strain analysis was performed with the left and right boundaries allowed to move freely in the vertical direction, while the bottom boundary was constrained in both vertical and horizontal directions. Figure 7 presents the finite element mesh and mechanical boundary conditions used in this study. The finite element model consists of 10,124 triangular elements, with a finer mesh generated near the unpaved surfaces to ensure adequate resolution within the infiltration zone. This case was originally simulated by Vu [28] and has been referenced in subsequent studies (e.g., [3,10]). The developed numerical model was used to simulate soil moisture variations over a 175-day period. More details can be found in [1].

5.2. Regina Clay Parameters

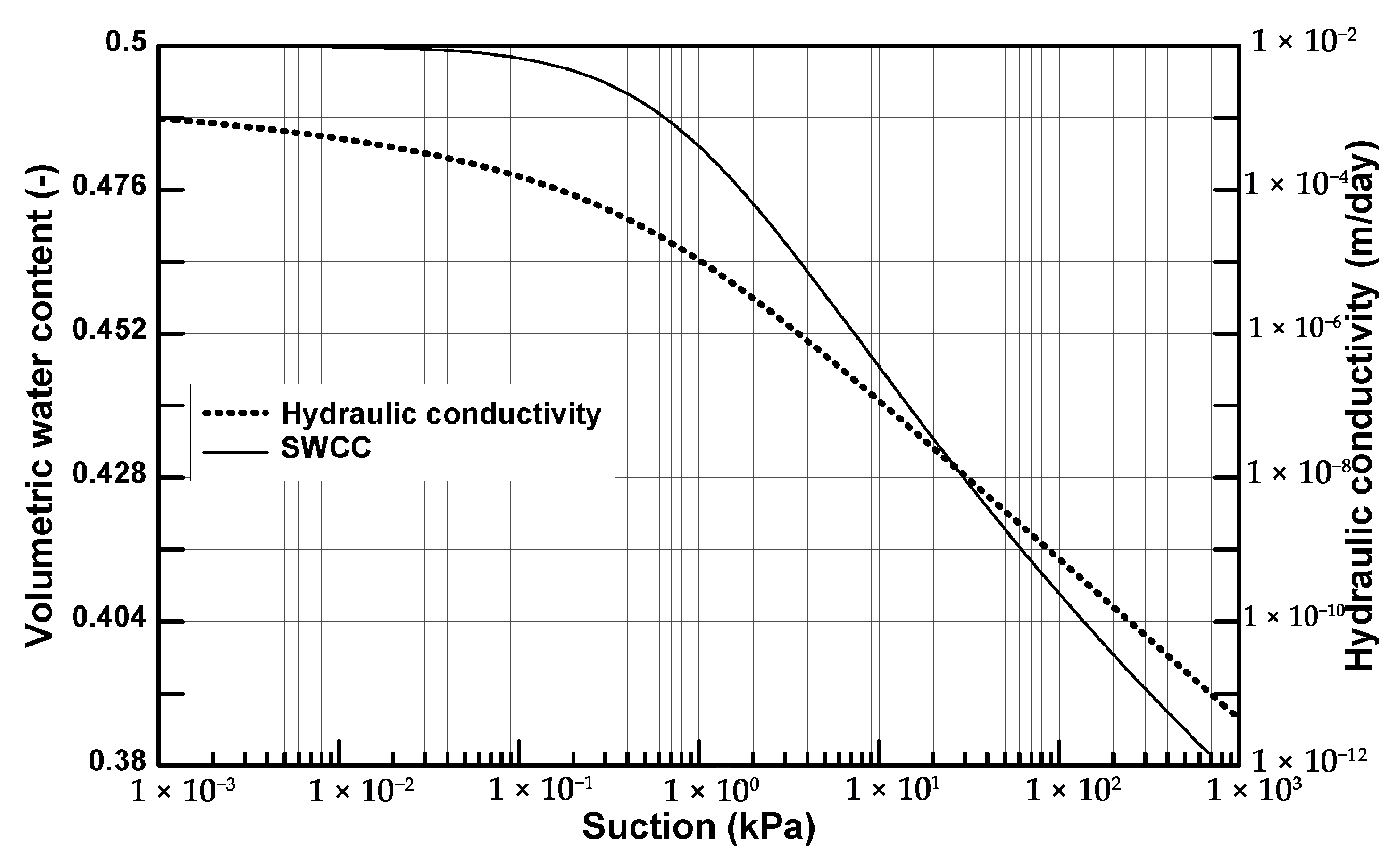
Figure 8 shows the soil–water characteristic curve (SWCC) and unsaturated hydraulic conductivity function (HCF) for Regina clay, obtained from [28,58]. The HYDRUS Cube module utilizes α and n parameters based on the SWCC curve using the mathematical model suggested by van Genuchten [41] to calculate the suction stress. These parameters are required to calculate suction stress using Equation (10).

The soil elastic moduli for dry and saturated conditions used in this study are presented in

Table 4. Elastic parameters of Regina clay estimated from the analysis of void ratio versus soil moisture data in this study.

${\mathit{E}}_{\mathit{d}\mathit{r}\mathit{y} }\left(\mathit{M}\mathit{P}\mathit{a}\right)$	${\mathit{E}}_{\mathit{s}\mathit{a}\mathit{t} }\left(\mathit{M}\mathit{P}\mathit{a}\right)$	$\mathit{l}$	$\mathit{\mu }$
51.2	0.32	0.11	0.4

.

These values were obtained from the best-fit power low curve matched to the calculated elastic modulus versus soil moisture data for the range of matric suction between 0 and 400 kPa. It should be noted that the saturated elastic modulus for Regina clay, as estimated by Adem [59], is 1.1 MPa, which is greater than the value used in this study.

Table 5. Regina clay—physical parameters used in this study (adopted from Vu [28]).

Initial Void Ratio, ${\mathit{e}}_0$	Specific Gravity, ${\mathit{G}}_{\mathit{s}}$	Total Unit Weight, ${\mathsf{\gamma }}_{\mathit{t}}$ (kN/m3)
0.955	2.83	17.27

presents the physical parameters used for Regina clay in this study.

5.3. Results and Discussion

The variation in matric suction distribution, as well as horizontal and vertical soil deformation profiles, was computed under 175 days’ infiltration of the unpaved ground surface using the HYDRUS Cube module.

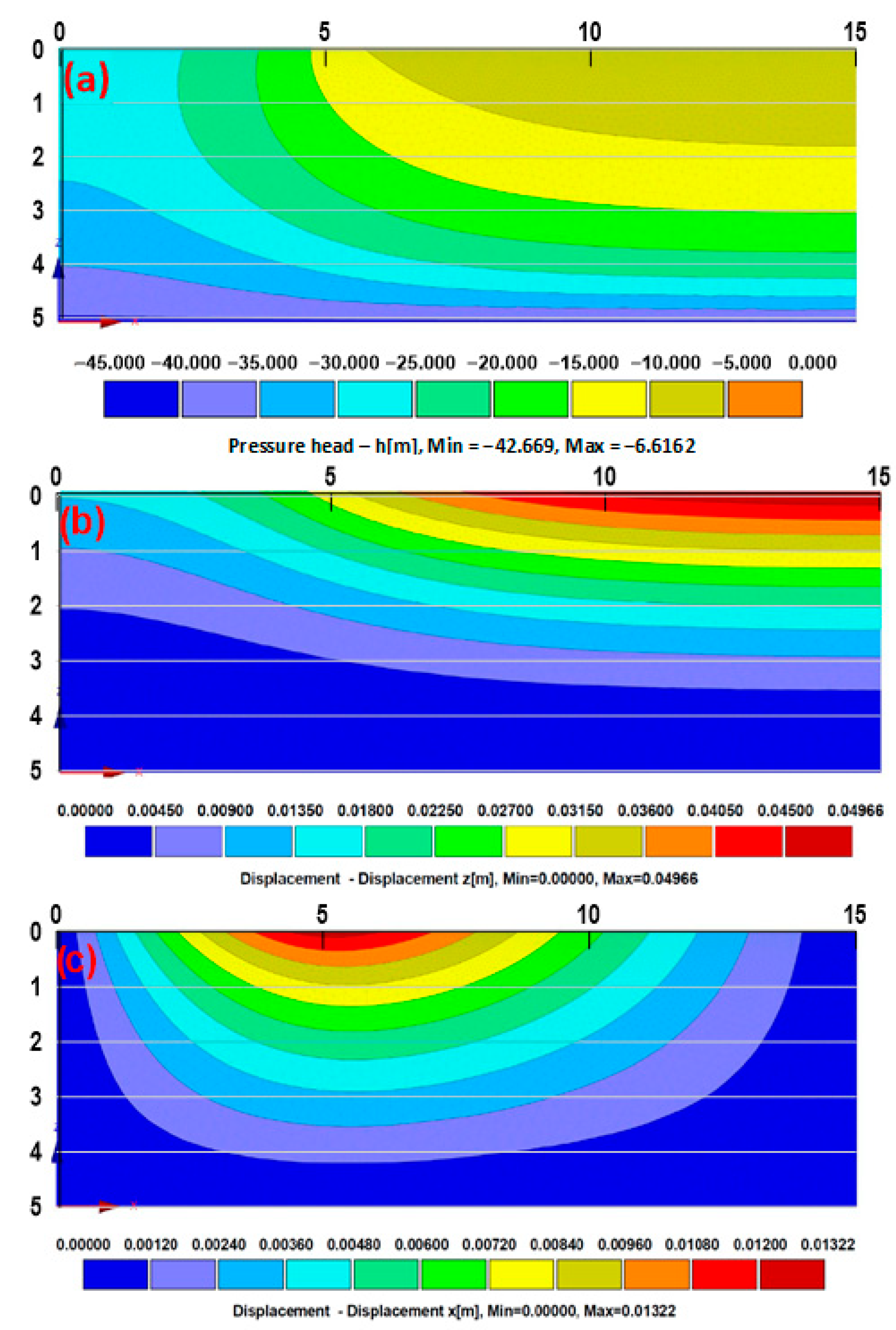
Figure 9a–c illustrate the distribution of the matric suction head and vertical and horizontal deformations at the day 175. The infiltration process led to a reduction in matric suction from its initial value of 400 kPa (40.78 m) to approximately 6 m near the unpaved ground surface. As expected, this decrease in matric suction resulted in soil heaving. After 175 days, the maximum heave reached approximately 50 mm, occurring at the farthest right side of the domain along the ground surface. In addition to heaving, the asymmetric infiltration conditions induced lateral movements in the expansive soil. The numerical results indicate that the maximum horizontal deformation at the corner of the paved area is approximately 13 mm. These findings, when compared to those reported by Vu [28] in Figures 6.84, 6.89, and 6.90, show good agreement. For example, the maximum and minimum vertical displacement values of 50 mm and 10 mm, respectively, are consistent in both studies. Similarly, the distribution of horizontal displacement magnitude and its location are also very similar.

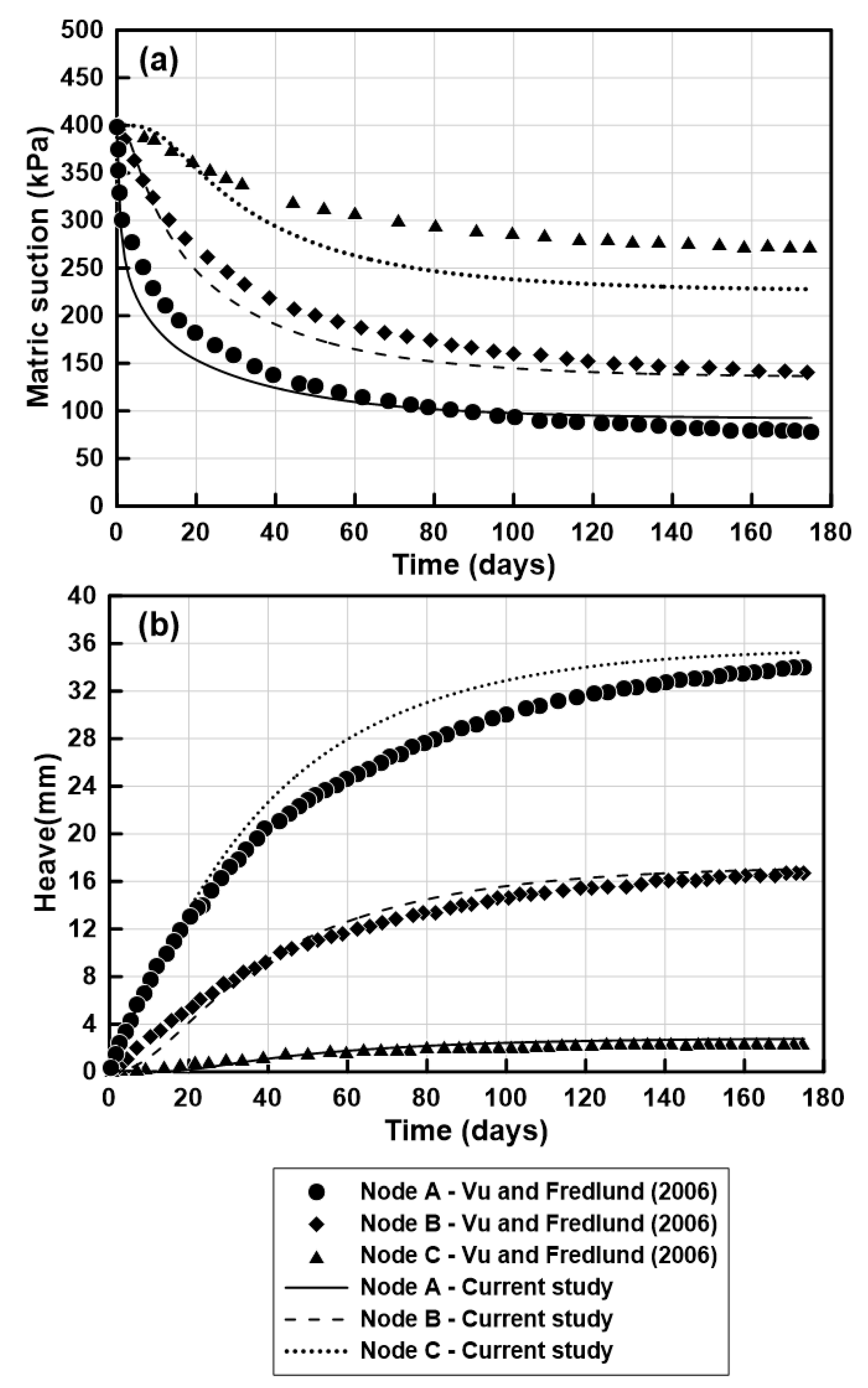
Figure 10a,b illustrate the comparison of predicted matric suction and heave at the three locations (nodes A, B, and C) over time using the developed numerical model and the results obtained by [10] using a coupled approach. The observation nodes A, B, and C are located 1 m away from the paved area at depths of 0, 1.5 m and 3.5 m, respectively. Although the anticipated matric suction at node C is approximately 20% less than that reported by [10], the matric suction compares well at shallower depths (nodes A and B).

To further quantify this comparison, the relative differences between the proposed model and the results were evaluated at key locations and times. For example, at node A (surface), the maximum heave predicted by the current study at 175 days is approximately 36 mm, compared to 34 mm reported by [10], resulting in a relative difference of about 5.9%. At node B (1.5 m depth), the difference is less than 5%. For the heave profile along the ground surface (Figure 11b), the maximum heave at 175 days is about 50 mm for the current study and 47 mm for [10], corresponding to a relative difference of approximately 6.4%. 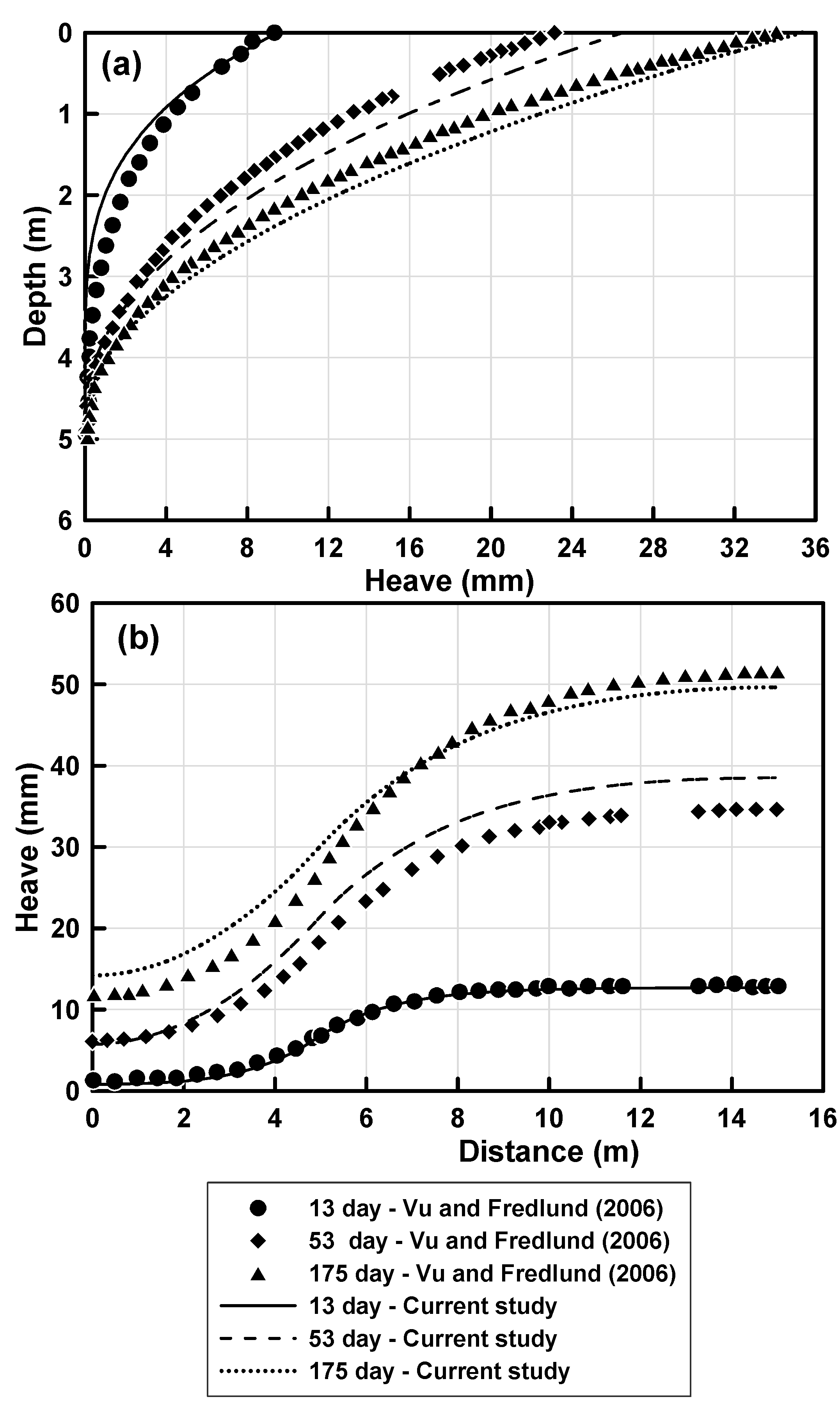Similarly, the heave profile with depth (Figure 11a) at 13 days shows a difference of about 6.3% at 2 m depth (17 mm vs. 16 mm).

The results in Figure 11a,b, which present the heave profile with depth and the ground surface heave at three different time intervals (day 13, day 53, and day 175), confirm the good agreement between the two studies despite the use of different unsaturated soil mechanics formulations. The relative differences in predicted heave values are generally within 10%, indicating strong consistency in both magnitude and distribution. Additionally, the results show that more than 75% of the total heave occurs within the first 53 days, consistent with the trends reported by [10]. These quantitative and qualitative comparisons demonstrate that the developed numerical model provides reliable predictions of both matric suction and heave, closely matching the established results in the literature.

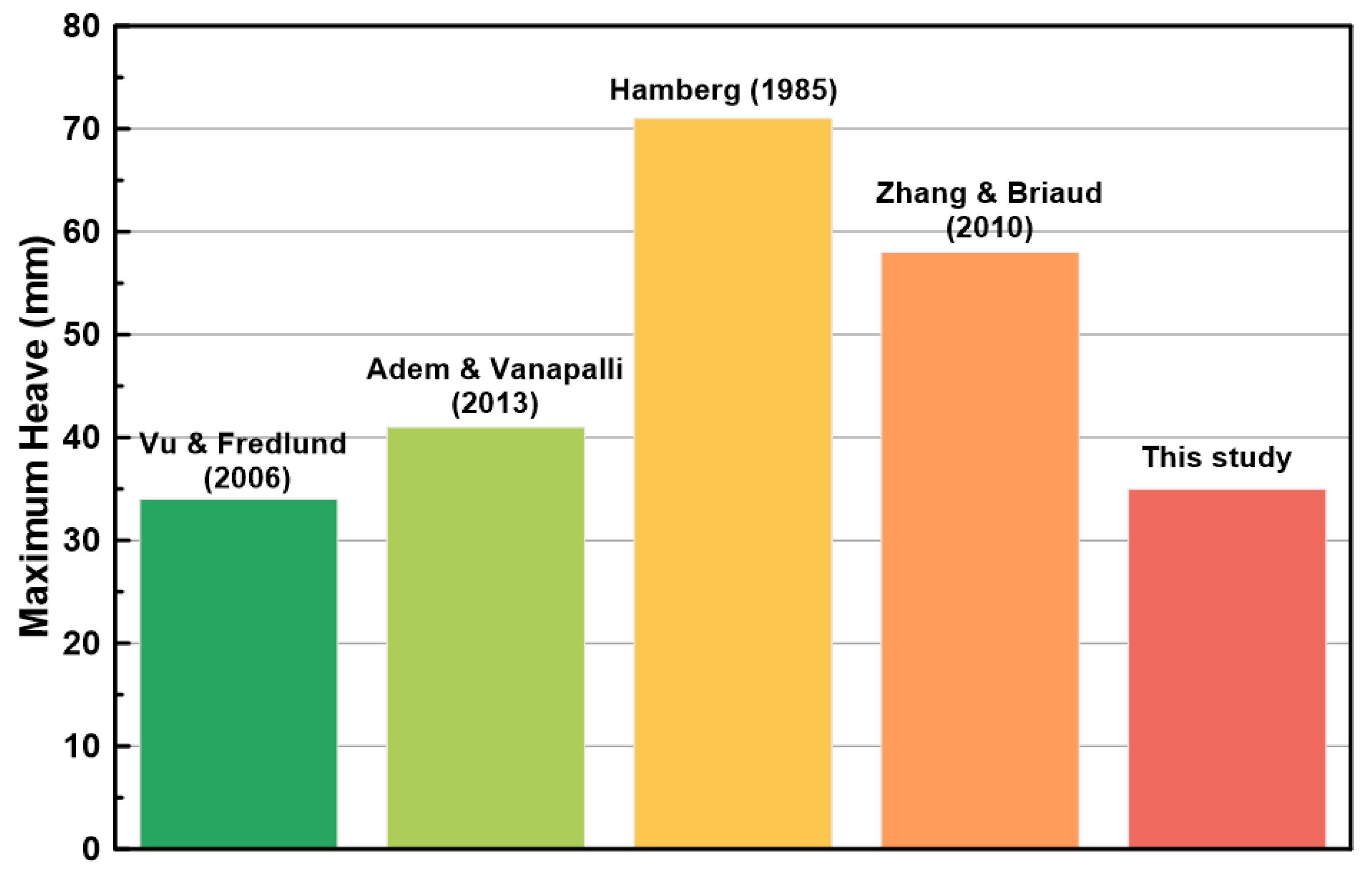
Adem and Vanapalli [9] carried out a comparison study for estimating the heave for the same benchmark problem using three different methods: [24,25] and MEBM. Figure 12 presents a summary of the maximum heave at the ground surface (node A) after 175 days using these three methods and the results obtained from effective stressed based analysis in this study. It should be noted that these three methods consider one dimensional heave, whereas the numerical model of Vu and Fredlund [10] and the numerical model developed in the current study include two-dimensional deformation analysis. And results from the current study compare better to Vu and Fredlund [10] by using fewer fitting parameters.

6. Concluding Remarks

In this study, a single-stress state variable framework was adopted to describe the void ratio as a function of effective stress for unsaturated soils. The proposed approach was applied to fit single-variable void ratio curves to laboratory test data for two expansive soils, i.e., Regina expansive clay and Texas expansive clay, across a range of mechanical stress and matric suction conditions. A logarithmic function with three constant parameters was chosen to evaluate the relationship between the void ratio and mean effective stress under unsaturated conditions. The constitutive relationships for both expansive clays were derived through curve fitting, and the accuracy of the fitted curves was assessed using regression indices.

The results demonstrate that the effective stress-based method can approximate the two-stress state constitutive data with a high degree of accuracy, while requiring fewer fitting parameters for the two expansive clays examined in this study. The proposed approach suggests that a void ratio–effective stress constitutive curve can effectively describe unsaturated soil behavior under mechanical and environmental loading, similar to how conventional consolidation theory applies to saturated soils.

A two-dimensional finite element analysis was conducted to simulate transient variably saturated seepage flow and estimate soil deformations under environmental loading, using the proposed effective stress–strain framework. The effective stress field was continuously updated based on variations in suction stress, which is a function of matric suction and the soil–water characteristic curve (SWCC). To incorporate the influence of the void ratio on elastic modulus, a mathematical approach was applied to derive the elastic modulus from the void ratio constitutive surface data. A power-law equation was then used to account for the dependency of the soil modulus on the volumetric water content. The developed numerical model was applied to simulate the behavior of a Regina expansive clay layer, partially covered by an impervious pavement, where the uncovered ground surface was subjected to a constant infiltration rate over a 175-day period. The results indicate that the proposed model effectively captures expansive soil deformations under changing moisture conditions. Unlike existing one-dimensional methods, the proposed model can simulate the two-dimensional distribution of the matric suction head and both vertical and horizontal soil deformations over time, which are critical for assessing differential movements.

The numerical results align well with those reported by Vu and Fredlund [10], while utilizing fewer fitting parameters. However, the limitations of the proposed approach should be further evaluated across a broader range of expansive soils, and additional comparative case studies are needed to assess its general applicability including materials with strong suction-dependent behavior. Further validation of the model against a range of soil–atmosphere interactions, including precipitation and evaporation, under long-term climate data and climate change considerations, is part of ongoing research.