A Review of Soil Constitutive Models for Simulating Dynamic Soil–Structure Interaction Processes Under Impact Loading
Abstract
1. Introduction
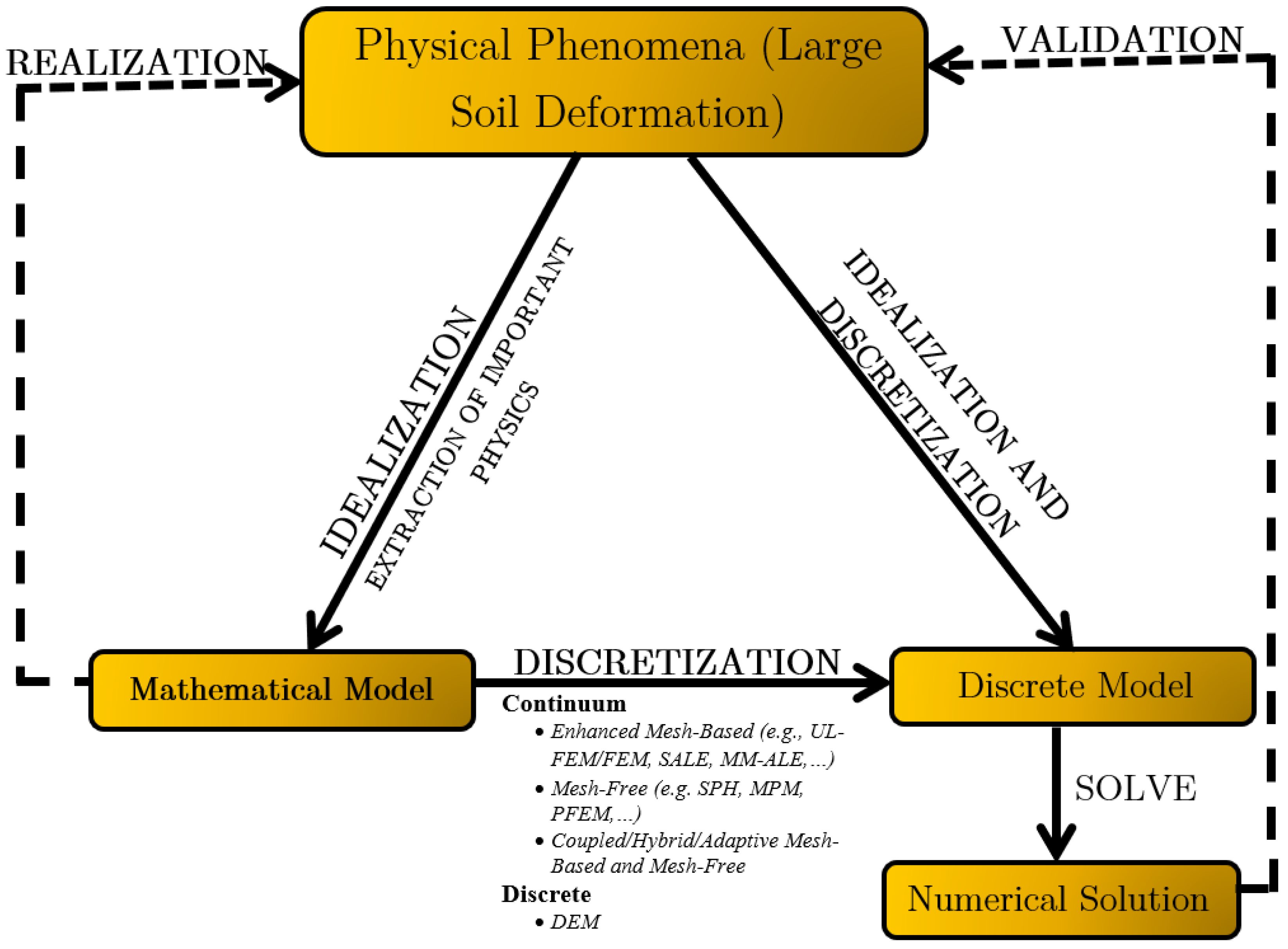
1.1. Numerical Methods for Simulating Dynamic Impact Soil-Structure Interaction Processes
1.2. Soils in Crash Testing of Barrier Systems
1.3. Scope, Objectives, and Contribution of the Study
2. Elastic Models
2.1. Hypoelastic Model
2.2. Biot Hysteretic Model
2.3. Advantages and Limitations of Elastic Soil Models
3. Simple Elastoplastic Models
3.1. Soil and Foam Model
3.2. Soil and Foam Failure Model
3.3. Pseudo-Tensor Model
3.4. Advantages and Limitations of Simple Elastoplastic Soil Models
4. Elastoplastic Models
4.1. General Elastoplasticity Framework
4.2. Soil Concrete Model
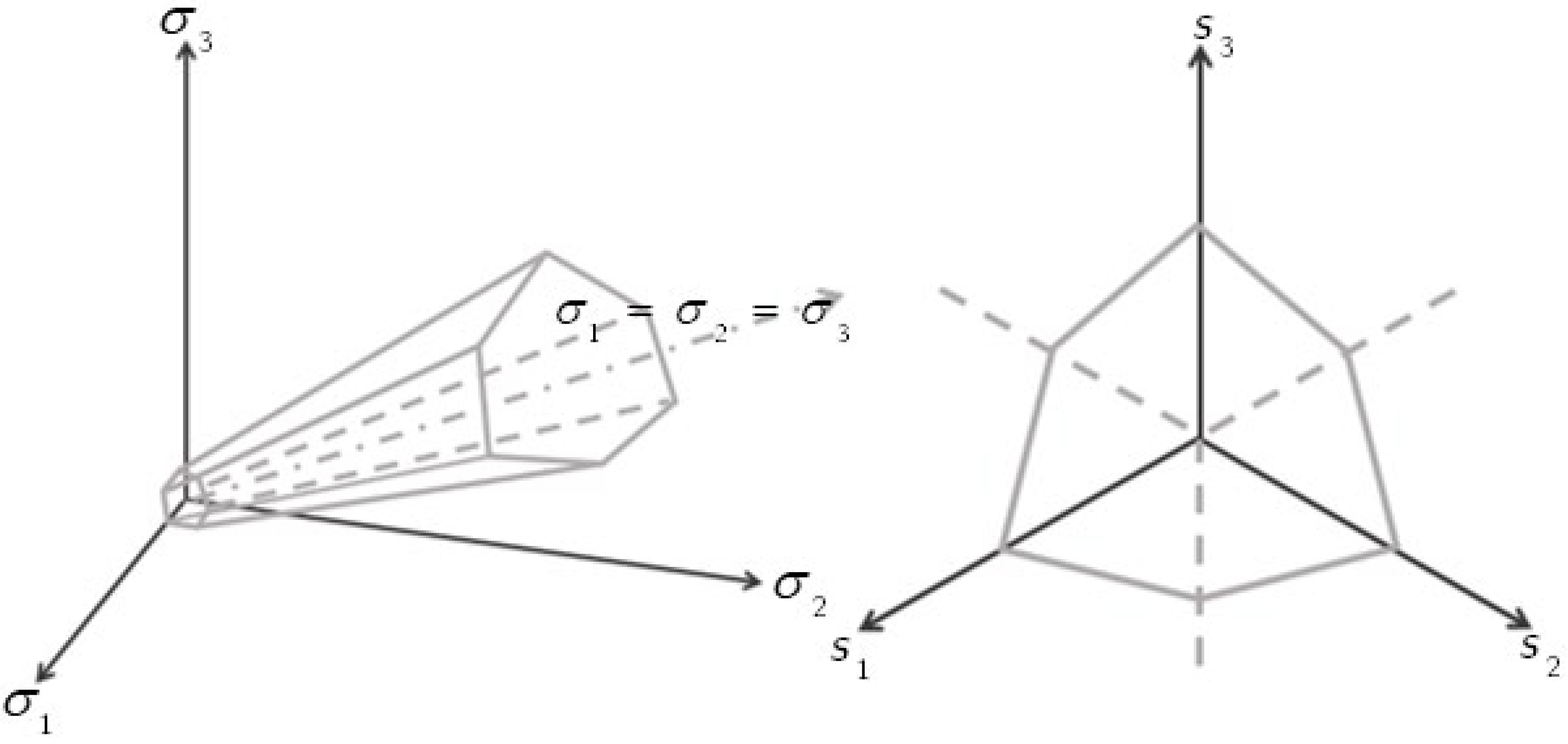
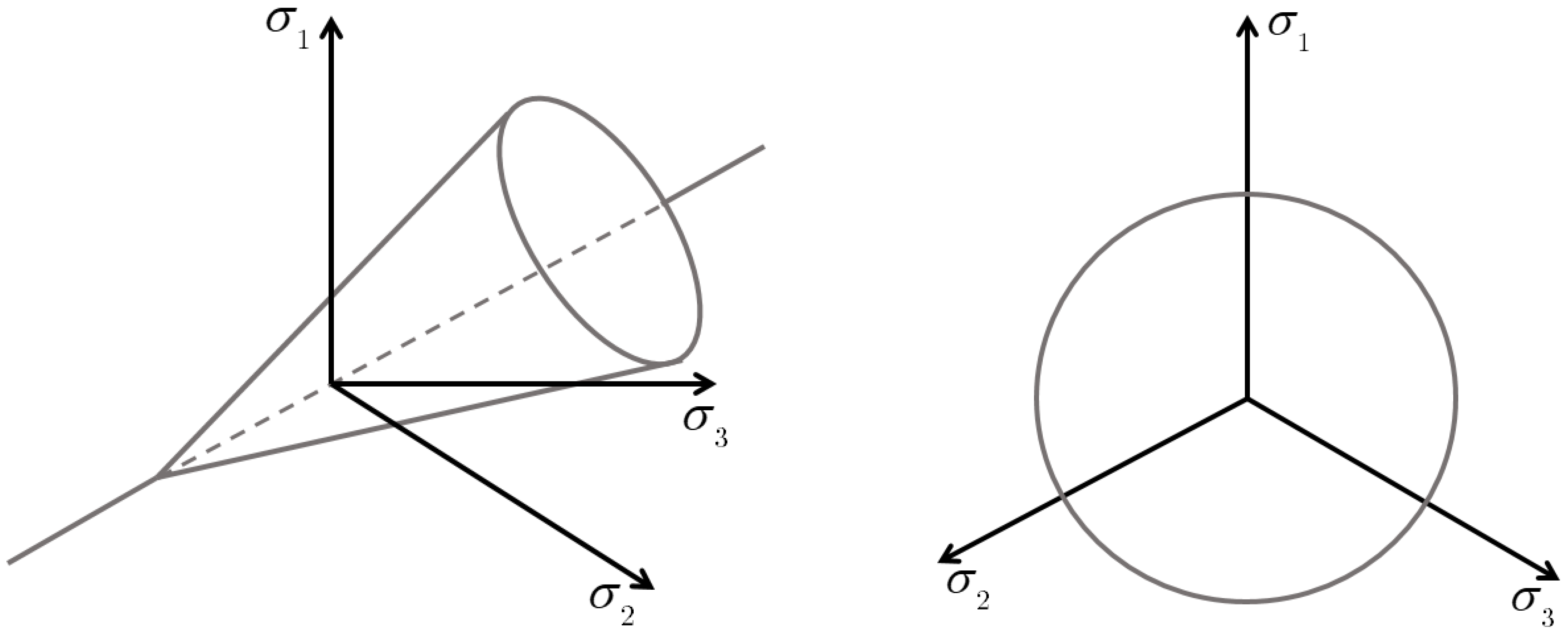
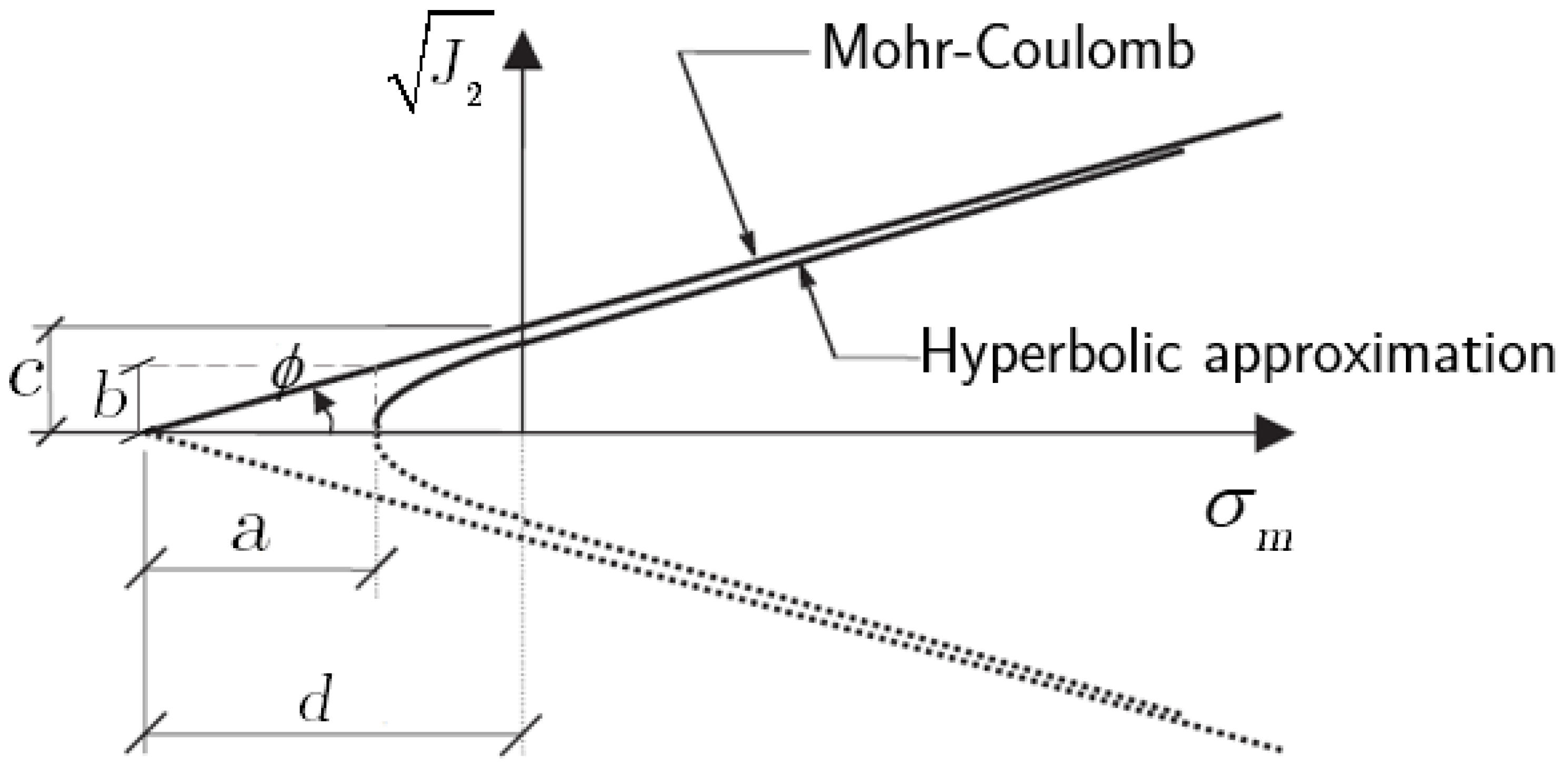
4.3. Mohr–Coulomb
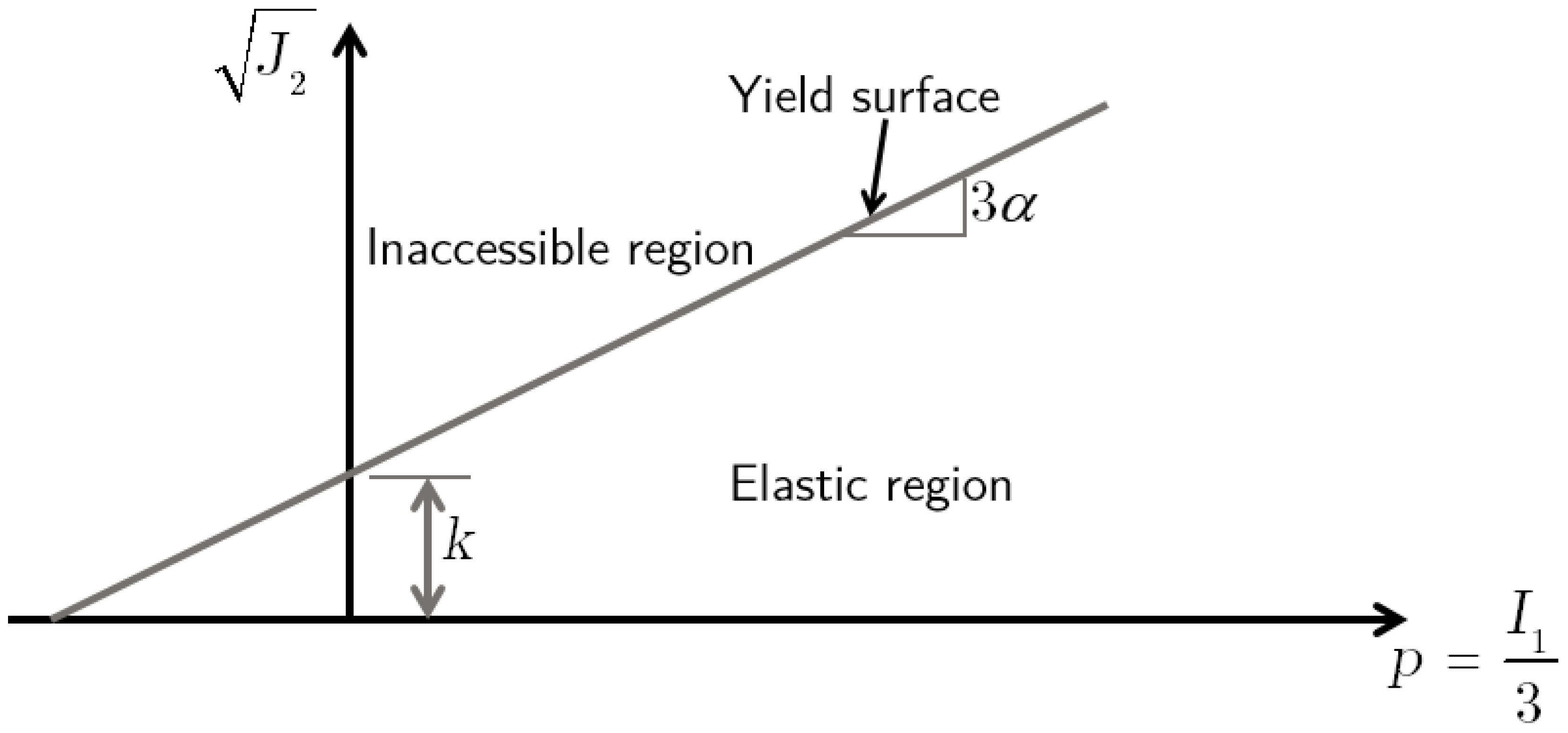
4.4. Drucker Prager Model
4.5. Jointed Rock Model
4.6. Advantages and Limitations of Elastoplastic Soil Models
5. Elasto-Viscoplastic Model
5.1. FHWA Model
5.1.1. Elastic Response
5.1.2. Yield Condition
5.1.3. Flow Rule
5.1.4. Strain Softening
5.1.5. Viscoplastic Regularization
5.2. Model Capabilities and Limitations
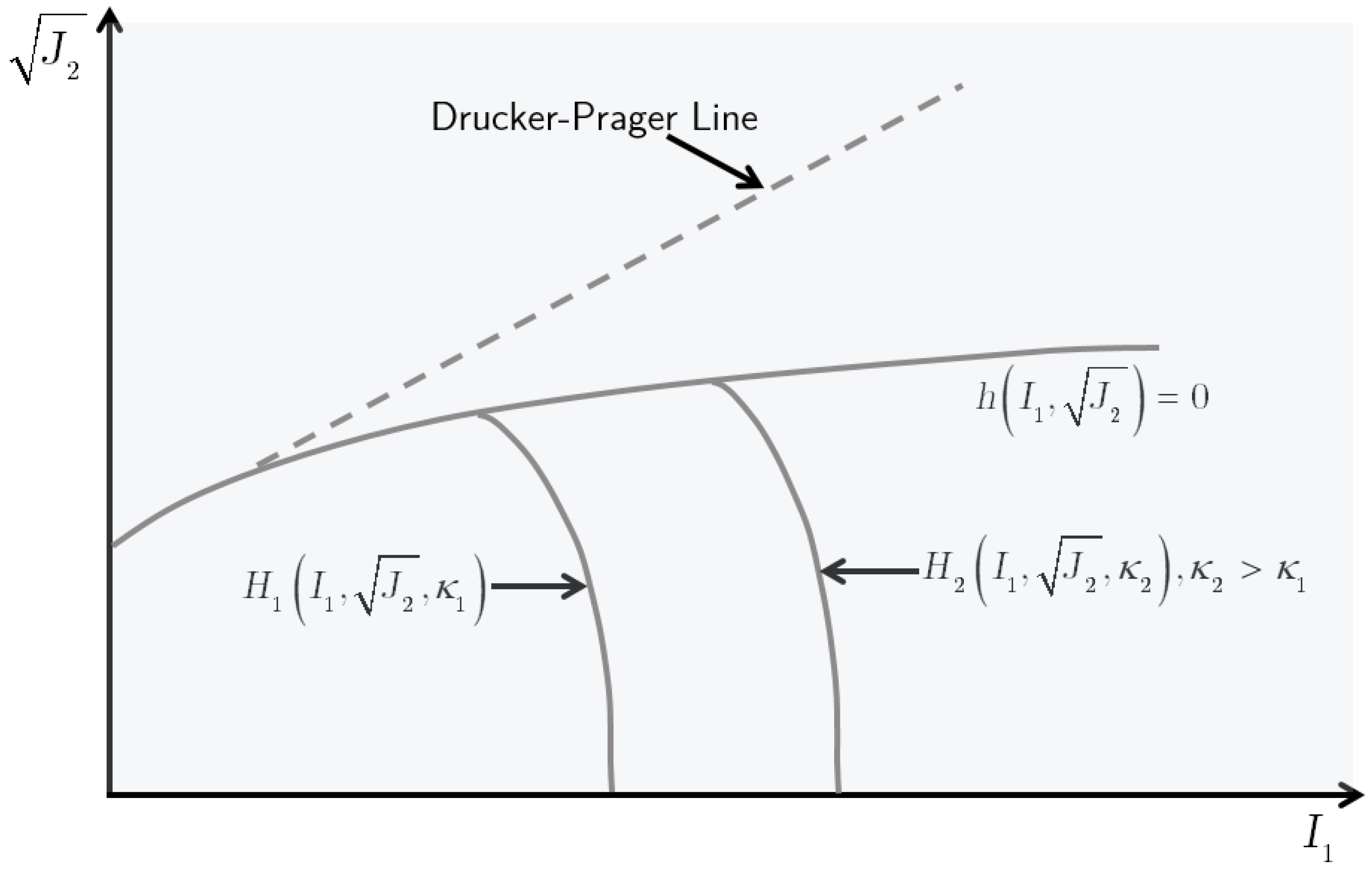
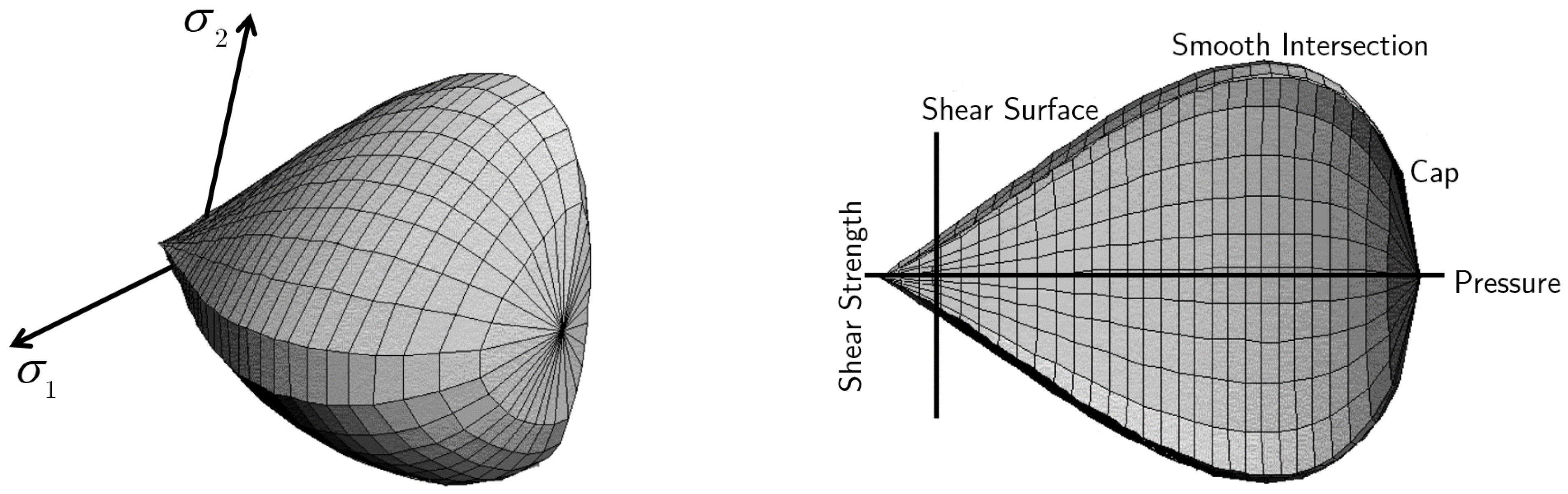
6. Cap Models
6.1. Fundamentals of Cap Models
6.2. Geologic Cap Model
6.3. Schwer Murray Cap Model
6.4. Advantages and Limitations of Cap Soil Models
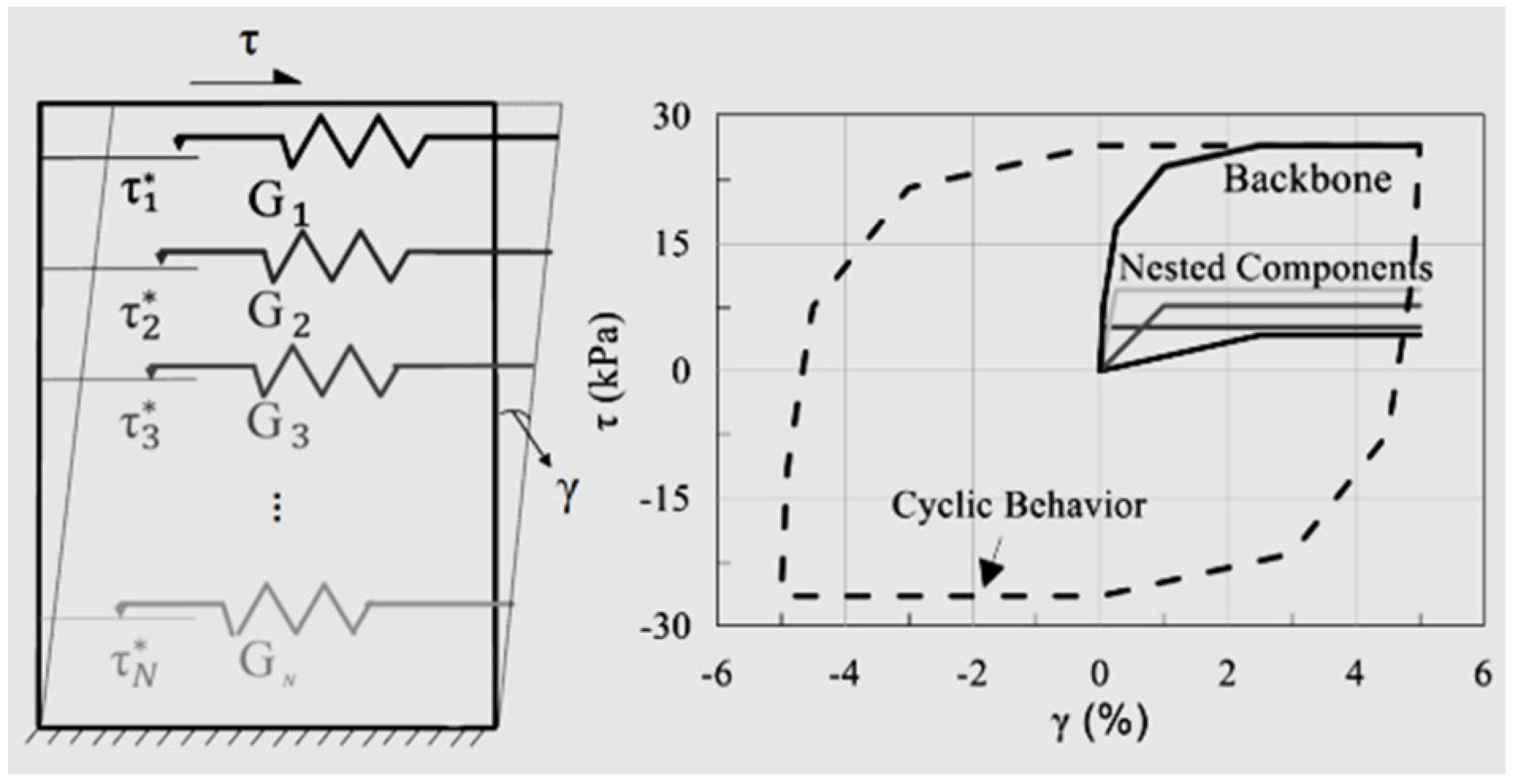
7. Nested Surface Models
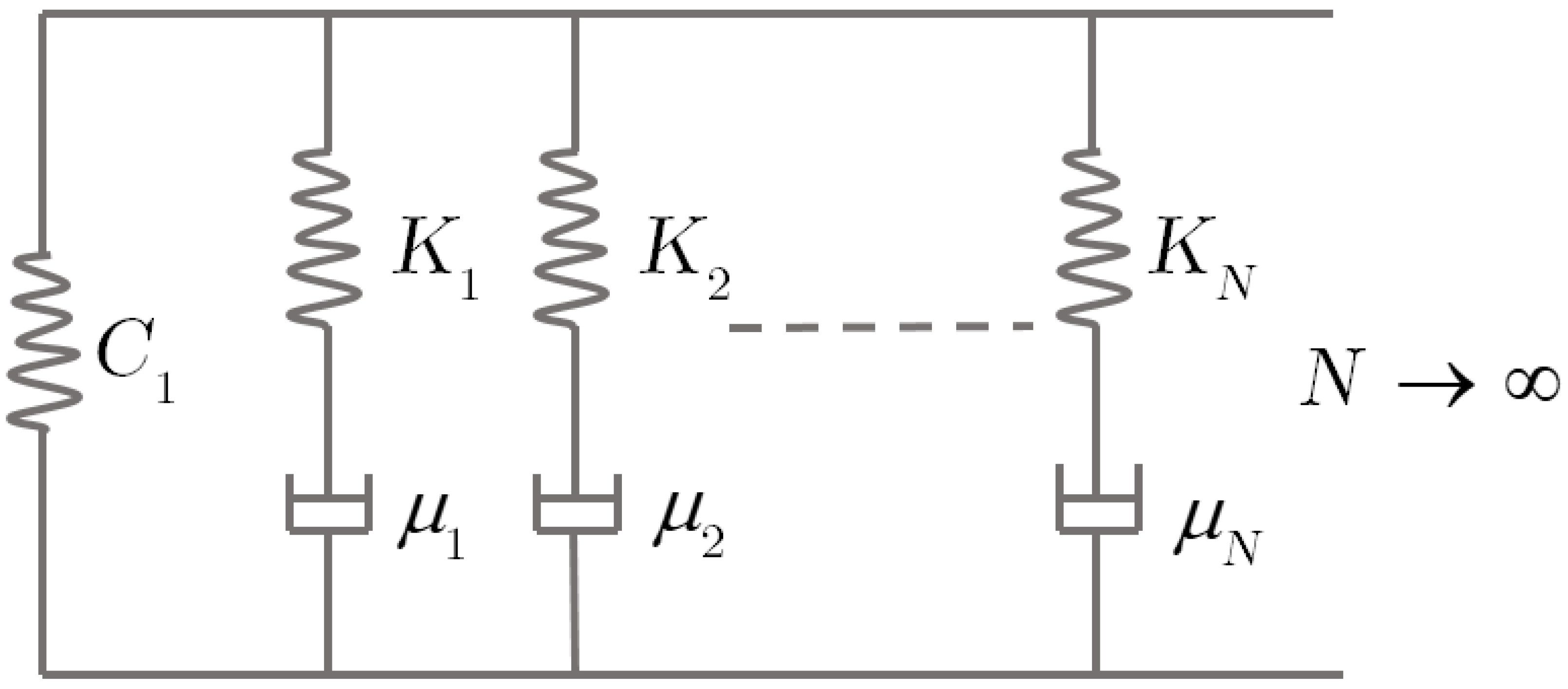
7.1. Hysteretic Soil Model
7.2. Soil Brick Model
7.3. Advantages and Limitations of Nested Surface Soil Models
8. Evaluation of Soil Constitutive Models
8.1. Comprehensive Constitutive Models
8.2. Intermediate Capability Models
8.3. Foundational Yield Models
9. Summary and Future Research Directions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| s1, s2, s3 | Axes in the deviatoric plane |
| αij | Back-stress tensor |
| K | Bulk modulus |
| α, γ, β, θ | Calibration parameters |
| L(κ) | Cap base boundary |
| Fc | Cap function |
| κ | Cap hardening parameter |
| X | Cap shape function |
| Fc(I1, κ) | Cap smoothing function |
| X(κ) | Cap upper boundary |
| a0, a1, ..., a11 | Coefficients dependent on stress invariants |
| c | Cohesion |
| p0 | Cut-off pressure |
| D | Damage evolution equation |
| ξ | Damage initiation criterion |
| ξ0 | Damage initiation threshold |
| ∂f/∂σpφ, ∂f/∂σβφ | Derivatives of f for the consistency condition |
| φs | Deviatoric part of the yield function |
| γ | Deviatoric shear strain |
| Deviatoric strain rate tensor | |
| sij | Deviatoric stress tensor components |
| ψ | Dilation angle |
| Fd | Dominant excitation frequency in Hz |
| α | Drucker–Prager parameter |
| k | Drucker–Prager parameter related to cohesion |
| Effective plastic volumetric strain | |
| Effective strain rate | |
| Effective stress tensor | |
| η | Effective viscosity parameter |
| Elastic deviatoric strain rate | |
| Elastic strain rate tensor | |
| σijtrial | Elastic trial stress tensor |
| R | Ellipticity parameter |
| a0, a1, a2 | Empirical fitting parameters for Drucker–Prager modification |
| Equivalent deviatoric stress | |
| β | Exponential decay constant related to frequency |
| Ei(x) | Exponential integral function |
| I1 | First invariant of the stress tensor |
| a0 = λ | First Lamé constant |
| i, j | Free indices in tensor notation |
| K(θ) | Function related to stress state and friction angle |
| ∂g/∂σpφ | General gradient term in plastic flow |
| ∂f/∂σpφ | General gradient term in stress space |
| Γ(I1, J2, J3, κ, αij) | General yield function |
| a, b | Geometric parameters of a hyperbolic surface (axes) |
| d | Geometric parameters of the hyperbola (intercept) |
| ∂g/∂σij | Gradient of plastic potential |
| ∂f/∂σij | Gradient of the yield function |
| ∂φs/∂sij | Gradient of φs with respect to deviatoric stress |
| ∂φs/∂p | Gradient of φs with respect to pressure |
| σφ | Hydrostatic stress |
| η | Hysteretic damping coefficient |
| dεij | Incremental strain tensor |
| dσij | Incremental stress |
| dεκκ | Incremental volumetric strain |
| X0 | Initial cap location |
| x | Integration variable in exponential integral |
| φ | Internal friction angle |
| δij | Kronecker delta |
| θ | Lode angle |
| Γ2(θ) | Lode angle-dependent scaling function |
| W, D1, D2 | Material constants for cap hardening |
| Y | Material viscosity parameter |
| Dmax | Maximum pressure-dependent damage |
| σm | Mean stress |
| p | Mean stress |
| R, α, γ, β, θ | Model parameters for elliptical cap smoothing |
| G(pref), K(pref) | Moduli at reference pressure |
| f1, f2, f3 | Mohr–Coulomb yield functions for each stress plane |
| g1, g2, g3 | Non-associated plastic potential functions |
| ∂f/∂I1, ∂f/∂√J2, ∂f/∂κ | Partial derivatives of yield function |
| φpeak | Peak friction angle |
| Plastic deviatoric strain rate | |
| Plastic multiplier | |
| Plastic part of the strain rate | |
| g | Plastic potential function |
| εpp, εpφ | Plastic strain components |
| Spq, Epq | Plastic strain components in index notation |
| Plastic volumetric strain | |
| ν | Poisson’s ratio |
| K(p) | Power-law relationship for bulk modulus |
| G(p) | Power-law relationship for shear modulus |
| φp | Pressure part of the yield function |
| τγ(p) | Pressure-dependent yield stress |
| σ1, σ2, σ3 | Principal stresses |
| Rate of change in the deviatoric yield function | |
| Rate of change in mean pressure | |
| Rate of yield function | |
| pref | Reference pressure used for normalization |
| CR(t) | Relaxation modulus (function of time) |
| μi | Relaxation time of the dashpot in the Maxwell element |
| φres | Residual friction angle |
| Cijkl | Response function in the hypoelastic model |
| J2 | Second invariant of deviatoric stress |
| a1 | Second Lamé constant (shear modulus) |
| e | Shape parameter controlling the deviatoric surface shape (0.5 < e ≤ 1.0) |
| G | Shear modulus |
| Fs | Shear surface yield function |
| C1 | Stiffness constant of spring in the Biot model |
| Ki | Stiffness of spring in the Maxwell element |
| (ξ) | Strain rate history at time ξ |
| Strain rate tensor | |
| εij | Strain tensor |
| σij(t) | Stress at time t |
| Stress rate tensor | |
| σij | Stress tensor |
| ζ | Stress update weighting parameter |
| G(σφ), K(σφ) | Stress-dependent shear and bulk moduli |
| J3 | Third invariant of the deviatoric stress tensor |
| Δt | Time step |
| τ | Total deviatoric stress |
| Trace of stress rate tensor | |
| Trace of stress tensor (σxx + σγγ + σzz) | |
| N | Transition function constant |
| σijvp | Viscoplastic interpolated stress tensor |
| n | Viscosity exponent |
| Gf | Void formation energy (strain energy at full damage) |
| V | Volume of the element |
| f | Yield function |
| τγ(pref) | Yield stress at reference pressure |
| τγ | Yield stress for each layer |
| τ1*, τ2*, … τn* | Yield stress thresholds of each plastic layer |
| E | Young’s modulus |
References
- Yosef, T.Y.; Faller, R.K.; Fang, C.; Kim, S. Modeling dynamics of laterally impacted piles in gravel using erosion method. Geotechnics 2023, 3, 1251–1278. [Google Scholar] [CrossRef]
- Beppu, M.; Miwa, K.; Itoh, M.; Katayama, M.; Ohno, T. Damage evaluation of concrete plates by high-velocity impact. Int. J. Impact Eng. 2008, 35, 1419–1426. [Google Scholar] [CrossRef]
- Nyström, U.; Gylltoft, K. Numerical studies of the combined effects of blast and fragment loading. Int. J. Impact Eng. 2009, 36, 995–1005. [Google Scholar] [CrossRef]
- Riedel, W.; Kawai, N.; Kondo, K. Numerical assessment for impact strength measurements in concrete materials. Int. J. Impact Eng. 2009, 36, 283–293. [Google Scholar] [CrossRef]
- Tu, Z.; Lu, Y. Modifications of RHT material model for improved numerical simulation of dynamic response of concrete. Int. J. Impact Eng. 2010, 37, 1072–1082. [Google Scholar] [CrossRef]
- Tu, Z.; Lu, Y. Evaluation of typical concrete material models used in hydrocodes for high dynamic response simulations. Int. J. Impact Eng. 2009, 36, 132–146. [Google Scholar] [CrossRef]
- Farnam, Y.; Mohammadi, S.; Shekarchi, M. Experimental and numerical investigations of low velocity impact behavior of high-performance fiber-reinforced cement based composite. Int. J. Impact Eng. 2010, 37, 220–229. [Google Scholar] [CrossRef]
- Teng, T.; Chu, Y.; Chang, F.; Shen, B.; Cheng, D. Development and validation of numerical model of steel fiber reinforced concrete for high-velocity impact. Comput. Mater. Sci. 2008, 42, 90–99. [Google Scholar] [CrossRef]
- Wang, Z.; Konietzky, H.; Huang, R. Elastic–plastic-hydrodynamic analysis of crater blasting in steel fiber reinforced concrete. Theor. Appl. Fract. Mech. 2009, 52, 111–116. [Google Scholar] [CrossRef]
- Zhou, X.; Hao, H. Mesoscale modelling and analysis of damage and fragmentation of concrete slab under contact detonation. Int. J. Impact Eng. 2009, 36, 1315–1326. [Google Scholar] [CrossRef]
- Coughlin, A.; Musselman, E.; Schokker, A.; Linzell, D. Behavior of portable fiber reinforced concrete vehicle barriers subject to blasts from contact charges. Int. J. Impact Eng. 2010, 37, 521–529. [Google Scholar] [CrossRef]
- Luccioni, B.; Aráoz, G.; Labanda, N. Defining Erosion Limit for Concrete. Int. J. Prot. Struct. 2013, 4, 315–340. [Google Scholar] [CrossRef]
- Frank, R.; Lazarus, R. Mixed Lagrangian-Eulerian Method. Methods Comput. Phys. 1964, 3, 47–67. [Google Scholar]
- Trulio, J. Theory and structure of the AFTON codes. In Report AFWL-TR-66-19; Air Force Weapons Laboratory, Kirtland Air Force Base: Newbury Park, California, NM, USA, 1966. [Google Scholar]
- Hirt, C.; Amsden, A.; Cook, J. An arbitrary Lagrangian-Eulerian computing method for all flow speeds. J. Comput. Phys. 1974, 14, 227–253. [Google Scholar] [CrossRef]
- Belytschko, T.; Kennedy, J. Computer models for subassembly simulation. Nucl. Eng. Des. 1978, 49, 17–38. [Google Scholar] [CrossRef]
- Donea, J.; Giuliani, S.; Halleux, J.; Granet, P.; Hamon, P.; Permezel, P. Response of fast-reactor core subassemblies to pressure transients. Nucl. Eng. Des. 1982, 68, 153–174. [Google Scholar] [CrossRef]
- Hughes, T.; Liu, W.; Zimmermann, T. Lagrangian-Eulerian finite element formulation for incompressible viscous flows. Comput. Methods Appl. Mech. Eng. 1981, 29, 329–349. [Google Scholar] [CrossRef]
- Huétink, J.; Vreede, P.; van der Lugt, J. Progress in mixed Eulerian-Lagrangian finite element simulation of forming processes. Int. J. Numer. Methods Eng. 1990, 30, 1441–1457. [Google Scholar] [CrossRef]
- Liu, W.; Belytschko, T.; Chang, H. An arbitrary lagrangian-eulerian finite element method for path-dependent materials. Comput. Methods Appl. Mech. Eng. 1986, 58, 227–245. [Google Scholar] [CrossRef]
- Liu, W.; Chang, H.; Chen, J.; Belytschko, T. Arbitrary lagrangian-eulerian petrov-galerkin finite elements for nonlinear continua. Comput. Methods Appl. Mech. Eng. 1988, 68, 259–310. [Google Scholar]
- Ramaswamy, B.; Kawahara, M. Arbitrary Lagrangian-Eulerian finite element method for unsteady, convective, incompressible viscous free surface fluid flow. Int. J. Numer. Methods Fluids 1987, 7, 1053–1075. [Google Scholar] [CrossRef]
- Benson, D. An efficient, accurate, simple ale method for nonlinear finite element programs. Comput. Methods Appl. Mech. Eng. 1989, 72, 305–350. [Google Scholar] [CrossRef]
- Rodríguez-Ferran, A.; Casadei, F.; Huerta, A. ALE stress update for transient and quasistatic processes. Int. J. Numer. Methods Eng. 1998, 43, 241–262. [Google Scholar] [CrossRef]
- Rodríguez-Ferran, A.; Pérez-Foguet, A.; Huerta, A. Arbitrary Lagrangian-Eulerian (ALE) formulation for hyperelastoplasticity. Int. J. Numer. Methods Eng. 2001, 53, 1831–1851. [Google Scholar] [CrossRef]
- Susila, E.; Hryciw, R. Large displacement FEM modelling of the cone penetration test (CPT) in normally consolidated sand. Int. J. Numer. Anal. Methods Geomech. 2003, 27, 585–602. [Google Scholar] [CrossRef]
- Nazem, M.; Sheng, D.; Carter, J. Stress integration and mesh refinement for large deformation in geomechanics. Int. J. Numer. Methods Eng. 2006, 65, 1002–1027. [Google Scholar] [CrossRef]
- Nazem, M.; Sheng, D.; Carter, J.; Sloan, S. Arbitrary Lagrangian-Eulerian method for large-strain consolidation problems. Int. J. Numer. Anal. Methods Geomech. 2007, 32, 1023–1050. [Google Scholar] [CrossRef]
- Di, Y.; Yang, J.; Sato, T. An operator-split ALE model for large deformation analysis of geomaterials. Int. J. Numer. Anal. Methods Geomech. 2007, 31, 1375–1399. [Google Scholar] [CrossRef]
- Liyanapathirana, D. Arbitrary Lagrangian Eulerian based finite element analysis of cone penetration in soft clay. Comput. Geotech. 2009, 36, 851–860. [Google Scholar] [CrossRef]
- Sheng, D.; Nazem, M.; Carter, J. Some computational aspects for solving deep penetration problems in geomechanics. Comput. Mech. 2009, 44, 549–561. [Google Scholar] [CrossRef]
- Bardenhagen, S.; Kober, E. The Generalized Interpolation Material Point Method. CMES–Comput. Model. Eng. Sci. 2004, 5, 477–496. [Google Scholar]
- Bardenhagen, S.; Brackbill, J.; Sulsky, D. The material-point method for granular materials. Comput. Methods Appl. Mech. Eng. 2000, 187, 529–541. [Google Scholar] [CrossRef]
- Więckowski, Z. The material point method in large strain engineering problems. Comput. Methods Appl. Mech. Eng. 2004, 193, 4417–4438. [Google Scholar] [CrossRef]
- Monaghan, J. Smoothed Particle Hydrodynamics. Annu. Rev. Astron. Astrophys. 1992, 30, 543–574. [Google Scholar] [CrossRef]
- Monaghan, J. Smoothed particle hydrodynamics. Rep. Prog. Phys. 2005, 68, 1703–1759. [Google Scholar] [CrossRef]
- Liu, G.; Liu, M. Smoothed Particle Hydrodynamics; World Scientific: New Jersey, NJ, USA, 2009. [Google Scholar]
- Oñate, E.; Idelsohn, S.; Del Pin, F.; Aubry, R. The particle finite element method—An overview. Int. J. Comput. Methods 2004, 1, 267–307. [Google Scholar] [CrossRef]
- Oñate, E.; Celigueta, M.; Idelsohn, S.; Salazar, F.; Suárez, B. Possibilities of the particle finite element method for fluid-soil-structure interaction problems. Comput. Mech. 2011, 48, 307–318. [Google Scholar] [CrossRef]
- Sauer, M. Simulation of high velocity impact in fluid-filled containers using finite elements with adaptive coupling to smoothed particle hydrodynamics. Int. J. Impact Eng. 2011, 38, 511–520. [Google Scholar] [CrossRef]
- Attaway, S.; Heinstein, M.; Swegle, J. Coupling of smooth particle hydrodynamics with the finite element method. Nucl. Eng. Des. 1994, 150, 199–205. [Google Scholar] [CrossRef]
- Fernández-Méndez, S.; Bonet, J.; Huerta, A. Continuous blending of SPH with finite elements. Comput. Struct. 2005, 83, 1448–1458. [Google Scholar] [CrossRef]
- Verbrugghe, T.; Domínguez, J.; Crespo, A.; Altomare, C.; Stratigaki, V.; Troch, P.; Kortenhaus, A. Coupling methodology for smoothed particle hydrodynamics modelling of non-linear wave-structure interactions. Coast. Eng. 2018, 138, 184–198. [Google Scholar] [CrossRef]
- Durr, N.; Sauer, M.; Hiermaier, S. A numerical study on mesoscale simulation of quartzite and sandstone under shock loading. Int. J. Impact Eng. 2017, 108, 73–88. [Google Scholar] [CrossRef]
- Johnson, G.; Petersen, E.; Stryk, R. Incorporation of an SPH option into the EPIC code for a wide range of high velocity impact computations. Int. J. Impact Eng. 1993, 14, 385–394. [Google Scholar] [CrossRef]
- Liu, W.; Chen, Y.; Chang, C.; Belytschko, T. Advances in multiple scale kernel particle methods. Comput. Mech. 1996, 18, 73–111. [Google Scholar] [CrossRef]
- Liu, W.; Uras, R.; Chen, Y. Enrichment of the Finite Element Method with the Reproducing Kernel Particle Method. J. Appl. Mech. 1997, 64, 861–870. [Google Scholar] [CrossRef]
- Belytschko, T.; Krongauz, Y.; Dolbow, J.; Gerlach, C. On the completeness of meshfree particle methods. Int. J. Numer. Methods Eng. 1998, 43, 785–819. [Google Scholar] [CrossRef]
- Huerta, A.; Fernández-Méndez, S. Enrichment and coupling of the finite element and meshless methods. Int. J. Numer. Methods Eng. 2000, 48, 1615–1636. [Google Scholar] [CrossRef]
- Huerta, A.; Fernández-Méndez, S.; Liu, W. A comparison of two formulations to blend finite elements and mesh-free methods. Comput. Methods Appl. Mech. Eng. 2004, 193, 1105–1117. [Google Scholar] [CrossRef][Green Version]
- Yosef, T.Y.; Fang, C.; Kim, S.; Faller, R.K. Dynamic response of piles embedded in granular soil to lateral impacts. Soil Dyn. Earthq. Eng. 2024, 180, 108593. [Google Scholar] [CrossRef]
- Yosef, T.Y.; Fang, C.; Faller, R.K.; Kim, S.; Stolle, C.S. Simulating dynamic thin-walled structures-soil interaction under vehicular impacts using coupled FEM-ALE approach. Eng. Struct. 2024, 136, 118588. [Google Scholar] [CrossRef]
- Yosef, T.Y.; Fang, C.; Faller, R.K.; Kim, S. Experimental and numerical investigations on the dynamic response of steel piles embedded in crushed limestone material under impact loading. Geotech. Geol. Eng. 2024, 42, 6253–6277. [Google Scholar] [CrossRef]
- AASHTO. Manual for Assessing Safety Hardware, 2nd ed.; American Association of State Highway and Transportation Officials: Washington, DC, USA, 2016. [Google Scholar]
- Wood, D.M. Soil Behaviour and Critical State Soil Mechanics; Cambridge University Press: Cambridge, UK, 1990. [Google Scholar]
- Shibuya, S.; Tatsuoka, F.; Teachavorasinskun, S.; Kong, X.J.; Abe, F.; Kim, Y.; Park, C. Elastic deformation properties of geomaterials. Soils Found. 1992, 32, 26–46. [Google Scholar] [CrossRef]
- Campbell, C. Rapid granular flows. Annu. Rev. Fluid Mech. 1990, 22, 57–90. [Google Scholar] [CrossRef]
- Campbell, C. Granular shear flows at the elastic limit. J. Fluid Mech. 2002, 465, 261–291. [Google Scholar] [CrossRef]
- Campbell, C. Granular material flows—An overview. Powder Technol. 2006, 162, 208–229. [Google Scholar] [CrossRef]
- Goldhirsch, I. Rapid granular glows. Annu. Rev. Fluid Mech. 2003, 35, 267–293. [Google Scholar] [CrossRef]
- Ross, H.; Sicking, D.; Zimmer, R.; Michie, J. Recommended Procedures for the Safety Performance Evaluation of Highway Features; NCHRP Report 350; Transportation Research Board: Washington, DC, USA, 1993. [Google Scholar]
- Meyer, D.; Ammon, T.; Bielenberg, R.; Stolle, C.; Holloway, C.; Faller, R. Quasi-Static Tensile and Dynamic Impact Testing of Guardrail Components; Draft Report to U.S. Army SDDCTEA, TRP-03-350-17, MwRSF; University of Nebraska–Lincoln: Lincoln, NE, USA, 2017. [Google Scholar]
- Wood, D.M. Geotechnical Modelling; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Hicher, P.-Y.; Shao, J.-F. Constitutive Modeling of Soils and Rocks; Wiley Online Library: Hoboken, NJ, USA, 2008. [Google Scholar]
- Puzrin, A. Constitutive Modelling in Geomechanics: Introduction; Springer: Berlin, Germany, 2012. [Google Scholar]
- Truesdell, C. Hypo-elasticity. J. Ration. Mech. Anal. 1955, 4, 83–1020. [Google Scholar] [CrossRef]
- Truesdell, C. Hypo-elastic shear. J. Appl. Phys. 1956, 27, 441–447. [Google Scholar] [CrossRef]
- Coon, M.D.; Evans, R.J. Recoverable deformation of cohesionless soils. J. Soil Mech. Found. Div. 1971, 97, 375–391. [Google Scholar] [CrossRef]
- Mysore, R.K. Finite Element Analysis of a Sand as a Hypoelastic Material. Master’s Thesis, State University of New York, Buffalo, NY, USA, 1979. [Google Scholar]
- Holubec, I. Elastic behavior of cohesionless soil. J. Soil Mech. Found. Div. 1968, 94, 1215–1231. [Google Scholar] [CrossRef]
- Biot, M.A. Linear Thermodynamics and the Mechanics of Solids; Cornell Aeronautical Lab., Inc.: Buffalo, NY, USA, 1958. [Google Scholar]
- Makris, N.; Zhang, J. Time-domain viscoelastic analysis of earth structures. Earthq. Eng. Struct. Dyn. 2000, 29, 745–768. [Google Scholar] [CrossRef]
- LST. Volume II Material Models; Livermore Software Technology (LST), an ANSYS company: Fishermans Bend, VIC, Australia, 2020. [Google Scholar]
- Mullin, M.J. Finite Element Modeling of Energy-Absorbing Materials in Blast-Loaded Structures; University of Nevada: Las Vegas, NV, USA, 2004. [Google Scholar]
- Wang, J. Simulation of Landmine Explosion Using LS-DYNA3D Software; DSTO Aeronautical and Maritime Research Laboratory: Livermore, CA, USA, 2001. [Google Scholar]
- Fasanella, E.L.; Jackson, K.E.; Kellas, S. Soft soil impact testing and simulation of aerospace structures. In Proceedings of the 10th International LS-DYNA User’s Conference, Dearborn, MI, USA, 8–10 June 2008. [Google Scholar]
- Ren, Y.; Xiang, J.; Meng, S.; Yan, Y.; Zhuang, N. Crashworthiness of civil aircraft subject to soft soil and concrete impact surface. Procedia Eng. 2014, 80, 193–201. [Google Scholar] [CrossRef]
- Wright, A. Tyre/Soil Interaction Modelling within a Virtual Proving Ground Environment; Cranfield University: Bedfordshire, UK, 2012. [Google Scholar]
- Hurley, R.C.; Andrade, J.E. Continuum modeling of rate-dependent granular flows in SPH. Comput. Part. Mech. 2017, 4, 119–130. [Google Scholar] [CrossRef]
- Krieg, R. A Simple Constitutive Description for Cellular Concrete; SC-DR-72-0883; Sandia National Laboratories: Albuquerque, NM, USA, 1972. [Google Scholar]
- Janbu, N. Soil compressibility as determined by oedometer and triaxial tests. In Proceedings European Conference SMFE; Wiesbaden, Germany, 1963; pp. 19–25. [Google Scholar]
- Ko, H.; Scott, R. Deformation of sand in shear. J. Soil Mech. Found. Div. 1967, 93, 283–310. [Google Scholar] [CrossRef]
- Zytynski, M.; Randolph, M.; Nova, R.; Wroth, C. On modelling the unloading-reloading behaviour of soils. Int. J. Numer. Anal. Methods Geomech. 1978, 2, 87–93. [Google Scholar] [CrossRef]
- Hashash, Y.M.; Fu, Q.; Ghaboussi, J.; Lade, P.V.; Saucier, C. Inverse analysis–based interpretation of sand behavior from triaxial compression tests subjected to full end restraint. Can. Geotech. J. 2009, 46, 768–791. [Google Scholar] [CrossRef]
- Vermeer, P. A double hardening model for sand. Géotechnique 1978, 28, 413–435. [Google Scholar] [CrossRef]
- Hill, R. The Mathematical Theory of Plasticity; Oxford University Press: Oxford, UK, 1998. [Google Scholar]
- Smith, I.M.; Griffiths, D.V.; Margetts, L. Programming the Finite Element Method; John Wiley & Sons: Chichester, UK, 2013. [Google Scholar]
- Drucker, D.C.; Prager, W. Soil mechanics and plastic analysis or limit design. Q. Appl. Math. 1952, 10, 157–165. [Google Scholar] [CrossRef]
- Chen, W.F.; Mizuno, E. Nonlinear Analysis in Soil Mechanics; Elsevier: Amsterdam, The Netherlands, 1990. [Google Scholar]
- Bui, H.H.; Fukagawa, R.; Sako, K.; Ohno, S. Lagrangian meshfree particles method (SPH) for large deformation and failure flows of geomaterial using elastic–plastic soil constitutive model. Int. J. Numer. Anal. Methods Geomech. 2008, 32, 1537–1570. [Google Scholar] [CrossRef]
- Chen, W.F. Plasticity in Reinforced Concrete; J. Ross Publishing: Fort Lauderdale, FL, USA, 2007. [Google Scholar]
- Goodman, R.E.; Taylor, R.L.; Brekke, T.L. A model for the mechanics of jointed rock. J. Soil Mech. Found. Div. 1968, 94, 637–659. [Google Scholar] [CrossRef]
- Zienkiewicz, O.; Pande, G. Time-dependent multilaminate model of rocks—A numerical study of deformation and failure of rock masses. Int. J. Numer. Anal. Methods Geomech. 1977, 1, 219–247. [Google Scholar] [CrossRef]
- Liu, J.; Sun, S.; Yue, L.; Wei, J.; Wu, J. Mechanical and failure characteristics of rock-like material with multiple crossed joint sets under uniaxial compression. Adv. Mech. Eng. 2017, 9, 1687814017708710. [Google Scholar] [CrossRef]
- Kulatilake, P.; He, W.; Um, J.; Wang, H. A physical model study of jointed rock mass strength under uniaxial compressive loading. Int. J. Rock Mech. Min. Sci. 1997, 34, 165.e1–165.e15. [Google Scholar] [CrossRef]
- Lewis, B.A. Manual for LS-DYNA Soil Material Model 147; Federal Highway Administration: McLean, VA, USA, 2004. [Google Scholar]
- Abbo, A.; Sloan, S. A smooth hyperbolic approximation to the Mohr-Coulomb yield criterion. Comput. Struct. 1995, 54, 427–441. [Google Scholar] [CrossRef]
- Nayak, G.C.; Zienkiewicz, O.C. Convenient form of stress invariants for plasticity. J. Struct. Div. 1972, 98, 949–954. [Google Scholar] [CrossRef]
- Abbo, A.; Lyamin, A.; Sloan, S.; Hambleton, J. A C2 continuous approximation to the Mohr–Coulomb yield surface. Int. J. Solids Struct. 2011, 48, 3001–3010. [Google Scholar] [CrossRef]
- Zienkiewicz, O. Some useful forms of isotropic yield surface for soil and rock mechanics. In Finite Elements in Geomechanics; Gudehus, G., Ed.; Wiley: Chichester, UK, 1977; pp. 179–190. [Google Scholar]
- Klisinski, M. Degradation and Plastic Deformation of Concrete; Institute of Fundamental Technology Research (IFTR); Polish Academy of Sciences: Warsaw, Poland, 1985. [Google Scholar]
- Simo, J.C.; Hughes, T.J. Computational Inelasticity; Springer Science & Business Media: New York, NY, USA, 2006. [Google Scholar]
- Dey, G.; Faller, R.; Hascall, J.; Bielenberg, R.; Polivka, K.; Molacek, K. Dynamic impact testing of W152×13.4 (W6×9) steel posts on a 2:1 slope. In Final Report TRP-03-165-07 to the Midwest States Regional Pooled Fund Program, MwRSF; University of Nebraska–Lincoln: Lincoln, NE, USA, 2007. [Google Scholar]
- McGhee, M.; Lechtenberg, K.; Bielenberg, R.; Faller, R.; Sicking, D.; Reid, J. Dynamic impact testing of wood posts for the Midwest Guardrail System (MGS) placed adjacent to a 2H:1V fill slope. In Final Report TRP-03-234-10 to the Midwest States Regional Pooled Fund Program, MwRSF; University of Nebraska–Lincoln: Lincoln, NE, USA, 2010. [Google Scholar]
- Schmidt, T.; Mongiardini, M.; Bielenberg, R.; Lechtenberg, K.; Reid, J.; Faller, R. Dynamic testing of MGS W6×8.5 posts at decreased embedment. In Final Report TRP-03-271-12 to the Nebraska Department of Roads, MwRSF; University of Nebraska–Lincoln: Lincoln, NE, USA, 2012. [Google Scholar]
- Ju, J. On energy-based coupled elastoplastic damage theories: Constitutive modeling and computational aspects. Int. J. Solids Struct. 1989, 25, 803–833. [Google Scholar] [CrossRef]
- Simo, J.; Ju, J. Strain-and stress-based continuum damage models—I. Formulation. Int. J. Solids Struct. 1987, 23, 821–840. [Google Scholar] [CrossRef]
- Lubliner, J. Plasticity Theory; Courier Corporation: North Chelmsford, MA, USA, 2008. [Google Scholar]
- Duvaut, G.; Lions, J.-L. Inéquations en thermoélasticité et magnétohydrodynamique. Arch. Ration. Mech. Anal. 1972, 46, 241–279. [Google Scholar] [CrossRef]
- Murray, Y. Modeling rate effects in rock and concrete. In Proceedings 8th International Symposium on the Interaction of the Effects of Munitions with Structures; Defense Special Weapons Agency: McLean, VA, USA, 1997. [Google Scholar]
- Simo, J.; Kennedy, J.; Govindjee, S. Non-smooth multisurface plasticity and viscoplasticity. Loading/unloading conditions and numerical algorithms. Int. J. Numer. Methods Eng. 1988, 26, 2161–2185. [Google Scholar] [CrossRef]
- Sandler, I.S.; Baladi, G.Y.; DiMaggio, F.L. Generalized cap model for geological materials. J. Geotech. Eng. Div. 1976, 102, 683–699. [Google Scholar] [CrossRef]
- Sandler, I.; Rubin, D. An algorithm and a modular subroutine for the cap model. Int. J. Numer. Anal. Methods Geomech. 1979, 3, 173–186. [Google Scholar] [CrossRef]
- Schwer, L.E.; Murray, Y.D. A three-invariant smooth cap model with mixed hardening. Int. J. Numer. Anal. Methods Geomech. 1994, 18, 657–688. [Google Scholar] [CrossRef]
- Schwer, L.E.; Murray, Y.D. Continuous surface cap model for geomaterial modeling: A new LS-DYNA material type. In Proceedings of the 7th International LS-DYNA Users Conference, Dearborn, MI, USA, 19–21 May 2002; pp. 35–50. [Google Scholar]
- Pelessone, D. A modified formulation of the cap model. In Gulf Atomic Report GA-C19579, Prepared for the Defense Nuclear Agency under Contract DNA-001086-C-0277; Gulf Atomic: San Diego, CA, USA, 1989. [Google Scholar]
- Murray, Y.D. Theory and evaluation of concrete material model 159. In Proceedings 8th International LS-DYNA Users Conference; APTEK Inc.: Colorado Springs, CO, USA, 2004; pp. 25–36. [Google Scholar]
- Schwer, L.E. Viscoplastic augmentation of the smooth cap model. Nucl. Eng. Des. 1994, 150, 215–223. [Google Scholar] [CrossRef]
- Chiang, D.; Beck, J. A new class of distributed-element models for cyclic plasticity—I. Theory and application. Int. J. Solids Struct. 1994, 31, 469–484. [Google Scholar] [CrossRef]
- Spears, R.; Veeraraghavan, S.; Coleman, J. Nonlinear modeling of ground motions at Lotung LSST site with nested surface soil constitutive model. Nucl. Technol. 2019, 205, 1205–1218. [Google Scholar] [CrossRef]
- Iwan, W.D. On a class of models for the yielding behavior of continuous and composite systems. J. Appl. Mech. 1967, 34, 612–617. [Google Scholar] [CrossRef]
- Baltaji, O.; Numanoglu, O.A.; Hashash, Y.; Veeraraghavan, S.; Coleman, J.L.; Bolisetti, C. Non-linear time domain site response and soil structure interaction analyses for nuclear facilities using MOOSE. In Proceedings of the 24th Conference on Structural Mechanics in Reactor Technology, Busan, Republic of Korea, 20–25 August 2017. [Google Scholar]
- Lehane, B.M.; Simpson, B. Modelling glacial till under triaxial conditions using a BRICK soil model. Can. Geotech. J. 2000, 37, 1078–1088. [Google Scholar] [CrossRef]
- Clarke, S. Enhancement of the BRICK Constitutive Model to Incorporate Viscous Soil Behavior; University of Sheffield: Sheffield, UK, 2009. [Google Scholar]
- Simpson, B. Retaining structures: Displacement and design. Géotechnique 1992, 42, 541–576. [Google Scholar] [CrossRef]
- Ellison, K.; Soga, K.; Simpson, B. A strain space soil model with evolving stiffness anisotropy. Géotechnique 2012, 62, 627–641. [Google Scholar] [CrossRef]



| Model | Advantages | Limitations |
|---|---|---|
| Elastic | Conceptually and mathematically simple | Does not include coupling between deviatoric and volumetric responses, so it cannot simulate dilation during shear deformation. |
| Requires few material parameters and is easy to calibrate | Behavior is incrementally reversible and does not capture yielding or stress-dependent stiffness and strength. | |
| Supported by a wide range of experimental data | Inadequate for modeling behavior near failure, and cannot simulate strain softening or strain rate effects | |
| Have been used successfully in many practical applications | Cannot simulate strain-softening as well as strain rate effects | |
| Commonly used in practice for preliminary assessments | Does not account for low confinement conditions, which are important in roadside barrier systems involving shallow soil fill | |
| Biot Hysteretic | Capable of simulating hysteretic energy dissipation under cyclic or dynamic loading | Cannot represent strain rate effects or strain softening. |
| Cannot simulate strain rate as well as strain softening effects. | ||
| Does not capture yielding or stress-dependent stiffness | ||
| Neglects low confinement effects, which are essential in the context of roadside barrier systems embedded in granular soil |
| Model | Advantages | Limitations |
|---|---|---|
| Soil and Foam and Soil and Foam Failure | Relatively simple to implement when tabulated pressure versus volumetric strain data is available | Requires confinement to maintain numerical stability; developed primarily for high-pressure condition |
| Material parameters can be calibrated using Mohr–Coulomb cohesion and friction angle | Unable to capture volumetric expansion (dilation) of granular soil during shear under impact loading | |
| Does not account for pore pressure build-up or moisture effects during undrained shear failure | ||
| Inadequate for modeling strain-softening behavior and strain rate effects | ||
| Assumes a circular yield surface in the deviatoric plane, which is inconsistent with experimental observations for granular soils | ||
| Pseudo Tensor | Straightforward to use when yield stress versus pressure data is available in tabulated form | Neglects low-confinement effects, which are significant in roadside safety applications |
| Capable of simulating strain softening and rate-dependent behavior | Cannot represent pore pressure build-up or moisture-related effects in undrained dynamic loading | |
| Fails to capture dilative volumetric behavior of soil during impact-driven shear |
| Model | Advantages | Limitations |
|---|---|---|
| Drucker–Prager | Simple to use | Exhibits excessive plastic dilation during yielding |
| Can be calibrated with Mohr–Coulomb parameters by appropriate selection of constants | Cannot capture hysteretic stress–strain behavior within the yield surface | |
| Satisfies uniqueness conditions due to associated flow rule | Does not model pore pressure build-up or moisture effects during undrained shear under dynamic loading | |
| Smooth, continuous yield surface in stress space | Circular deviatoric section disagrees with experimental data for granular soils | |
| Fails to represent low-confinement effects typical in roadside safety applications | ||
| Does not simulate material damage or strain rate effects | ||
| Mohr–Coulomb | Simple to use | May cause numerical instability due to sharp corners in the yield surface |
| Its validity is well-established for many granular soils | Neglects influence of intermediate principal stress | |
| Hexagonal deviatoric section inconsistent with laboratory results | ||
| Does not capture low-confinement behavior characteristic of surface-embedded systems | ||
| Cannot model moisture effects or pore pressure generation in undrained shear under impact conditions |
| Advantages | Limitations |
|---|---|
| Captures low confinement behavior in granular backfill | Requires intensive parameter calibration |
| Incorporates strain-softening and strain rate effects | Requires detailed experimental data |
| Accurately reflects deviatoric yield shape evolution | |
| Constructed for simulating soil behavior in roadside barrier systems |
| Model | Advantages | Limitations |
|---|---|---|
| Geologic Cap | Can simulate low confinement effects, which is critical in most roadside safety applications | Cannot predict moisture or pore-pressure build-up during undrained failure under dynamic shear loading |
| Satisfies the theoretical requirements of uniqueness, stability, and continuity | Does not account for strain-softening or damage and strain rate effects | |
| Provides proper control of dilatancy | Two-invariant formulation; cannot simulate lower strength in triaxial extension | |
| Non-smooth yield surface behavior at very low shear stresses causes the algorithm to be complex and inefficient | ||
| Schwer Murray Cap | Accounts for strain-softening or damage and strain rate effects | Relatively complicated model with more than 25 input parameters |
| Can simulate low confinement effects, which is critical in roadside safety applications | Relatively complicated model with more than 25 input parameters | |
| Three-invariant formulation; can simulate lower strength in triaxial extension | Cannot predict moisture or pore-pressure build-up during undrained failure under dynamic shear loading | |
| Smooth yield surface behavior at very low shear stresses; suitable for finite element implementations |
| Advantages | Limitations |
|---|---|
| Can reproduce the hysteretic response within the failure surface | Cannot simulate moisture or pore-pressure build-up during undrained dynamic shear loading |
| Accounts for dilatancy and strain rate effects | Does not incorporate strain-softening or continuum damage |
| Cannot accurately simulate low-confinement behavior, which is critical in many roadside safety applications | |
| Requires extensive soil characterization to calibrate more than 20 input parameters |
| Type of Soil Model | Soil Model | Type of Soil | Failure Surface | Flow Rule: Associated or Non-associated | Hardening Criteria | ||
|---|---|---|---|---|---|---|---|
| Granular | Cohesive | Rock | |||||
| Elastic | Elastic | Yes | Yes | Yes | NA | NA | NA |
| Biot Hysteretic | Yes | Yes | Yes | NA | NA | NA | |
| Simple Elastoplastic | Soil and Foam | Yes | Yes | Yes | Extended von Mises | Associated | None |
| Soil and Foam Failure | Yes | Yes | Yes | Extended von Mises | Associated | None | |
| Pseudo Tensor | Yes | Yes | Yes | Extended von Mises | Associated | None | |
| Elastoplastic | Soil Concrete | Yes | Yes | Yes | Extended von Mises | Associated | None |
| Mohr–Coulomb | Yes | Yes | Yes | Mohr–Coulomb | Non-associated | None | |
| Drucker–Prager | Yes | Yes | Yes | Extended von Mises | Non-associated | None | |
| Jointed Rock | No | No | Yes | Mohr–Coulomb | Non-associated | None | |
| Elasto-viscoplastic | FHWA | Yes | Yes | Yes | Modified Mohr–Coulomb | Associated | Isotropic |
| Cap | Geologic Cap | Yes | Yes | Yes | Curved extended von Mises | Associated | Isotropic |
| Schwer Murray Cap | Yes | Yes | Yes | Curved extended von Mises | Non-associated | Kinematic | |
| Nested surface | Hysteretic | Yes | Yes | Yes | Extended von Mises | Non-associated | Nested surfaces |
| Soil Brick | No | Yes | No | Extended von Mises | Associated | Nested surfaces | |
| Soil Model | Does Model Include/Predict | Model Group | |||||
|---|---|---|---|---|---|---|---|
| Three-Dimensional Behavior | Low Confinement Effects | Dilation | Strain Softening | Strain rate Effects | Moisture/Pore pressure | ||
| Elastic | Yes | No | No | No | No | No | Foundational Yield Model |
| Biot Hysteretic | Yes | No | No | No | No | No | Foundational Yield Model |
| Soil and Foam | Yes | No | No | No | No | No | Foundational Yield Model |
| Soil and Foam Failure | Yes | No | No | No | No | No | Foundational Yield Model |
| Pseudo Tensor | Yes | No | No | Yes | Yes | No | Intermediate Capability Model |
| Soil Concrete | Yes | No | No | Yes | No | No | Foundational Yield Model |
| Mohr–Coulomb | Yes | No | Yes | No | No | No | Foundational Yield Model |
| Drucker–Prager | Yes | No | Yes | No | No | No | Foundational Yield Model |
| Jointed Rock | Yes | No | Yes | No | No | No | Foundational Yield Model |
| FHWA | Yes | Yes | Yes | Yes | Yes | Yes | Comprehensive Constitutive Model |
| Geologic Cap | Yes | Yes | Yes | No | No | No | Intermediate Capability Model |
| Schwer Murray Cap | Yes | Yes | Yes | Yes | Yes | No | Intermediate Capability Model |
| Hysteretic Soil | Yes | No | Yes | No | Yes | No | Intermediate Capability Model |
| Soil Brick | Yes | No | No | No | No | No | Foundational Yield Model |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yosef, T.Y.; Fang, C.; Faller, R.K.; Kim, S.; Alomari, Q.A.; Atash Bahar, M.; Kumar, G.S. A Review of Soil Constitutive Models for Simulating Dynamic Soil–Structure Interaction Processes Under Impact Loading. Geotechnics 2025, 5, 40. https://doi.org/10.3390/geotechnics5020040
Yosef TY, Fang C, Faller RK, Kim S, Alomari QA, Atash Bahar M, Kumar GS. A Review of Soil Constitutive Models for Simulating Dynamic Soil–Structure Interaction Processes Under Impact Loading. Geotechnics. 2025; 5(2):40. https://doi.org/10.3390/geotechnics5020040
Chicago/Turabian StyleYosef, Tewodros Y., Chen Fang, Ronald K. Faller, Seunghee Kim, Qusai A. Alomari, Mojtaba Atash Bahar, and Gnyarienn Selva Kumar. 2025. "A Review of Soil Constitutive Models for Simulating Dynamic Soil–Structure Interaction Processes Under Impact Loading" Geotechnics 5, no. 2: 40. https://doi.org/10.3390/geotechnics5020040
APA StyleYosef, T. Y., Fang, C., Faller, R. K., Kim, S., Alomari, Q. A., Atash Bahar, M., & Kumar, G. S. (2025). A Review of Soil Constitutive Models for Simulating Dynamic Soil–Structure Interaction Processes Under Impact Loading. Geotechnics, 5(2), 40. https://doi.org/10.3390/geotechnics5020040







