Site Component—k₀ and Its Correlation to V_S30 and the Site Fundamental Frequencies for Stations Installed in N. Macedonia

Abstract

This study focuses on determining the high-frequency decay parameter kappa (k) and its site component (k₀) for sixteen accelerometric stations installed in suitable locations in North Macedonia. Kappa characterizes the attenuation of ground motion at high frequencies, describing the decrease in the acceleration amplitude spectrum. It is defined using a regression line in log-linear space, starting from the point where the S-wave amplitude spectrum begins to decay rapidly. The site characteristics of the stations are determined through geophysical and borehole investigations, as well as HVSR mean curves derived from earthquake data. The strong-motion data used in this analysis originate from earthquake events with a moment magnitude greater than 3 (M_W > 3), an epicentral distance less than 120 km (R_epi < 120 km), and a focal depth lower than 30 km (h < 30 km). The records undergo visual inspection and filtering, with those having a signal-to-noise ratio (SNR) below 3 excluded from further analysis. The study examines the correlation between kappa values and various parameters, including magnitude, epicentral distance, average shear-wave velocity in the top 30 m depth (V_S30), and fundamental site frequency (f₀). The importance of this study is the application in the future evaluation/update of seismic hazard analysis of the region.

1. Introduction

Seismic wave attenuation refers to the reduction in wave amplitude due to propagation effects, including both path and local site conditions. This reduction occurs primarily due to internal friction, absorption, and scattering [1]. Observed seismic attenuation plays a crucial role in seismic hazard assessment and site response analysis, as it helps to estimate the expected acceleration values at specific locations.

The Republic of North Macedonia is a seismically active region with low to moderate seismicity, though some areas exhibit nearly high levels of seismic activity. In the past, numerous earthquakes have struck the country’s territory, with some devastating almost entire cities. Over the years, various studies have been conducted to assess the seismic hazard in this country. However, no study has yet focused on the local attenuation of seismic waves at high frequencies.

To characterize these effects, Anderson and Hough (1984) [2] introduced the empirical high-frequency decay parameter kappa (k), aiming to explain deviations in the shape of the spectral acceleration curve from the theoretical Brune’s model (1970) [3] at frequencies higher than the source corner frequency. Using earthquake records with magnitudes greater than 5, they calculated the spectral parameter kappa for different stations by analyzing log-linear spectral space within constrained frequency ranges. Currently, there are many available approaches for estimating kappa [4], and this parameter is widely used for site characterization, especially given empirical k₀-V_S30 correlations [4,5,6,7,8,9,10,11,12], among other uses such as site amplification [13], input parameters for creation and calibration of GMPEs, host to target adjustments of GMPEs to different regions [14,15,16], as well as its correlation with engineering parameters like peak ground acceleration (PGA) and Arias intensity [17].

Previous studies have shown that the high-frequency decay parameter, kappa (k), is primarily influenced by site conditions [2,5,8,11]. Although some research has investigated its correlation with source characteristics [18,19], the impact of source effects is generally considered to be less significant than that of local site effects. Other studies have explored the relationship between kappa and the seismic wave propagation path [20,21], while some have examined the role of seismic sensor installation conditions [22].

The aim and scope of this study is to estimate the high-frequency decay parameter kappa (k), and its site component (k₀) for sixteen accelerometric stations installed in North Macedonia. Although numerous studies have investigated k globally, no research has focused on the attenuation characteristics specific to this region. To address this gap, the study provides the first detailed estimation of k₀ derived from local strong-motion data. The IZIIS strong motion network, equipped with accelerometers installed across various locations and soil types in North Macedonia, provides valuable data for investigating the high-frequency decay parameter (k). In this study, strong motion records from earthquakes with moment magnitudes (M_w) greater than 3.0 and epicentral distances (R_epi) less than 120 km were analyzed. The data were collected from sixteen seismic stations across the country.

The study begins with a brief overview of the study area and the locations of the seismic stations. This includes the collection of strong motion records and the necessary data for station characterization. The records are then systematically organized, processed, and selected for analysis. The method used for kappa calculation is described and applied, and the resulting values are analyzed in relation to parameters such as earthquake magnitude, epicentral distance, average shear-wave velocity in the top 30 m depth V_S30, and fundamental site frequency (f₀). Finally, the results are presented, discussed, and compared with previous studies to highlight key observations and implications.

2. Study Area and Strong Motion Data

The study area is in the Balkan Peninsula, specifically in the Republic of North Macedonia, between latitudes 40–43° and longitudes 19–23°. This region is characterized by low to moderate seismicity, although certain areas exhibit nearly high levels of seismic activity.

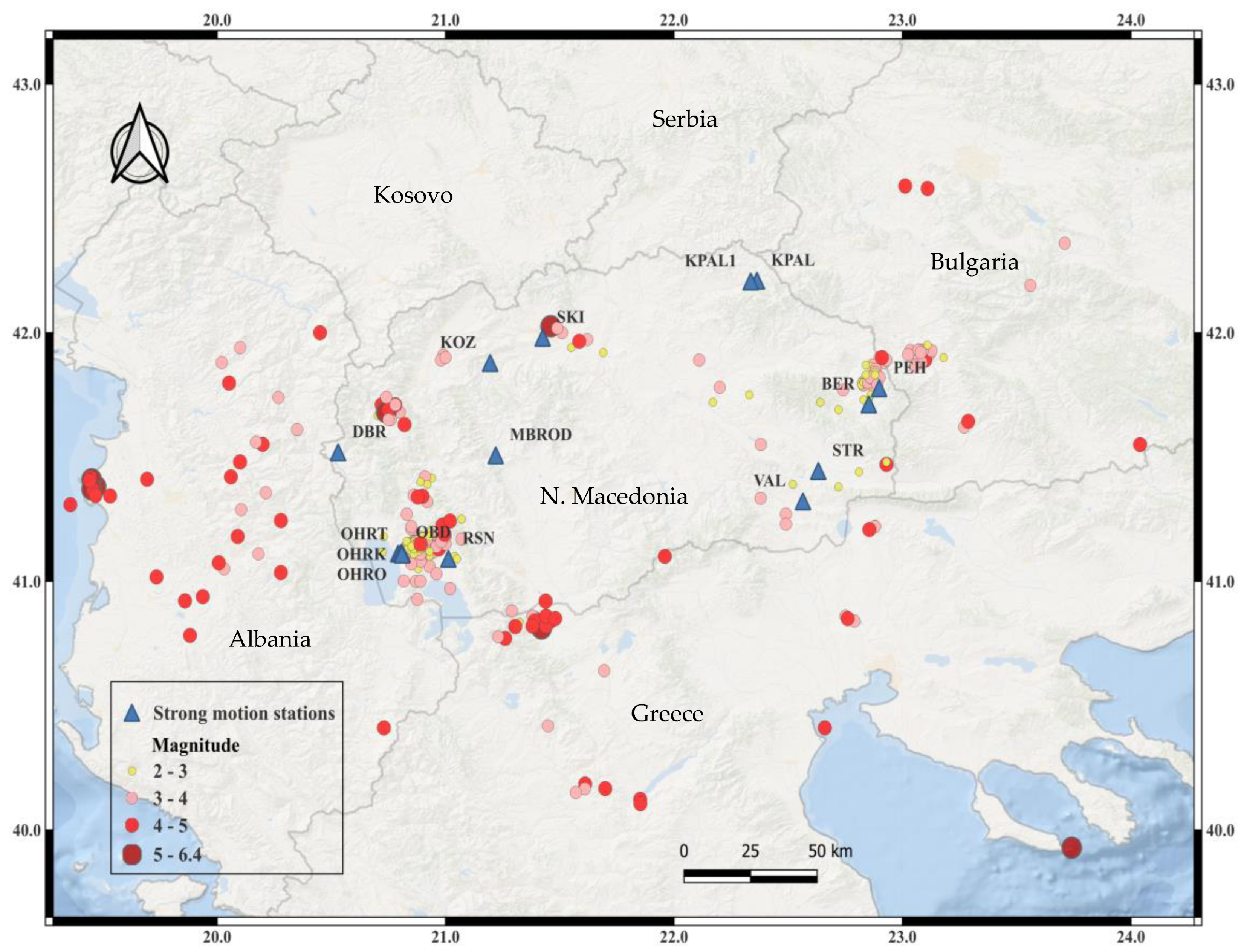
The dataset used in this study is obtained from strong-motion stations that have recorded at least five earthquakes. These stations are part of the UKIM-IZIIS strong-motion network in North Macedonia (Figure 1). In total, sixteen stations are included in the study, installed on three different types of soil, A, B, and C, according to EC8 [23]. The records are collected using 200 Hz sampling three-component accelerometers (Guralp CMG-5TD and ETNA-2), which are placed either in free-field conditions or within small structures, typically in the basement or on the ground floor.

Between 2012 and 2024, these stations recorded 336 earthquake events with moment magnitudes (M_w) ranging from 2.1 to 6.4 and epicentral distances (R_epi) from 1.6 to 810 km. Figure 1 illustrates the spatial distribution of recorded earthquakes and the locations of the strong-motion stations, which are marked with blue triangles.

To characterize local site characteristics of each seismic station, V_S30 values are determined through geophysical measurements [24,25,26,27,28,29] for seven stations (DBR, PEH, SKI, OHR, OHRK, VAL, KPAL), and borehole geotechnical investigations [30] for three stations (OHRK, OHRT, OBD). The other six stations’ characteristics were obtained from the USGS V_S30 model [31], and it was followed with a definition of the horizontal-to-vertical spectral ratio (HVSR) using earthquake records.

The HVSR method was used to estimate the predominant site frequency and potential site amplification for all stations [32]. HVSR (horizontal-to-vertical spectral ratio) was calculated from earthquake records using the smoothed Fourier amplitude spectrum by Konno and Ohmachi (1998) [33] (b-value = 20). Figure 2 shows the HVSR derived from earthquakes for all sixteen stations, with the horizontal black line at H/V = 2 representing the non-amplification amplitude, following the SESAME criteria [34]. According to Figure 2, the observed predominant site frequencies range from 0.6 to 9 Hz. The wide range of observed predominant site frequencies (0.6 to 9 Hz) across the sixteen stations can be attributed to site-specific geological and geotechnical conditions, as well as site geometry (topography). These include variations in sediment thickness (with thicker sediments typically associated with lower fundamental frequencies and thinner sediments with higher ones), differences in the properties of the deeper soil column, the degree of soil consolidation, and variations in impedance contrast between layers (soft surface layers overlying stiffer sediments and bedrock) with differing shear-wave velocities.

Parolai and Bindi (2004) [35] demonstrated that resonant effects do not influence the k parameter when the fundamental resonance frequency is below the frequency range used for its calculation, provided that the range is sufficiently wide to average out local peaks caused by site amplification. However, if not properly accounted for, site effects can still bias the selection process and lead to underestimated k values if measured before the resonance peak, and overestimated values when measured after it. To minimize such effects in the k estimation, the lower boundary frequency (f_1min) is set to 10 Hz, as explained in more detail in Section 3.

Figure 2. Adapted from Poposka et al., 2025 [36]. Horizontal to vertical spectral ratios (HVSR) curves from earthquake records using the Konno and Ohmachi (1998) [33] (b-value = 20) smoothed Fourier amplitude spectrum. Horizontal black line (H/V = 2) represents the “non-amplification” amplitude according to the SESAME criteria [34].

Figure 2. Adapted from Poposka et al., 2025 [36]. Horizontal to vertical spectral ratios (HVSR) curves from earthquake records using the Konno and Ohmachi (1998) [33] (b-value = 20) smoothed Fourier amplitude spectrum. Horizontal black line (H/V = 2) represents the “non-amplification” amplitude according to the SESAME criteria [34].

Table 1. Station information, soil investigation type 1—geophysics, type 2—HVSR with microtremors, type 3—HVSR with earthquakes, type 4—borehole investigation, fundamental frequency obtained from earthquake data. The symbol “/” indicates no available data.

Station	Lat [°]	Lon [°]	VS30 [m/s]	VS30/USGS [m/s]	Investigation Type	f0 [Hz]
BER	41.711	22.852	/	500	2, 3	3.4
DBR	41.518	20.529	400–450	450	1, 3	1.0
KOZ	41.878	21.195	/	800	2, 3	6.0
KPAL	42.209	22.363	>800	850	1, 2, 3	10.0
KPAL1	42.206	22.335	/	350	2, 3	3.5
MBROD	41.506	21.219	/	380–400	2, 3	5.8
OBD	41.114	20.807	350–400	380	2, 3, 4	1.0
OHR	41.111	20.792	>1000	900	1, 2, 3	15.0
OHRK	41.109	20.811	350–400	380	1, 2, 3, 4	1.4
OHRO	41.114	20.803	/	380	2, 3	2.9
OHRT	41.107	20.809	350–400	380	2, 3, 4	1.1
PEH	41.776	22.897	380–450	420	1, 2, 3	0.8
SKI	41.090	21.012	330	400	1, 2, 3	8.8
RSN	41.979	21.425	/	360–400	2, 3	0.6
STR	41.443	22.631	/	350–380	2, 3	3.0
VAL	41.321	22.564	774	650	1, 2, 3	4.0

presents the station names and coordinates, the type of soil investigation conducted, and the estimated V_S30 values obtained from both site-specific investigations and the USGS V_S30 Map Viewer [31]. It also includes the fundamental site frequency determined using the HVSR method with earthquake data. The comparison of V_S30 values from different sources reveals some differences, which remain within acceptable limits. However, it is essential that these values be validated through detailed site investigations, such as geophysical surveys or borehole investigations.

3. Signal Processing and Kappa Calculation

3.1. Signal Processing and Data Systematization

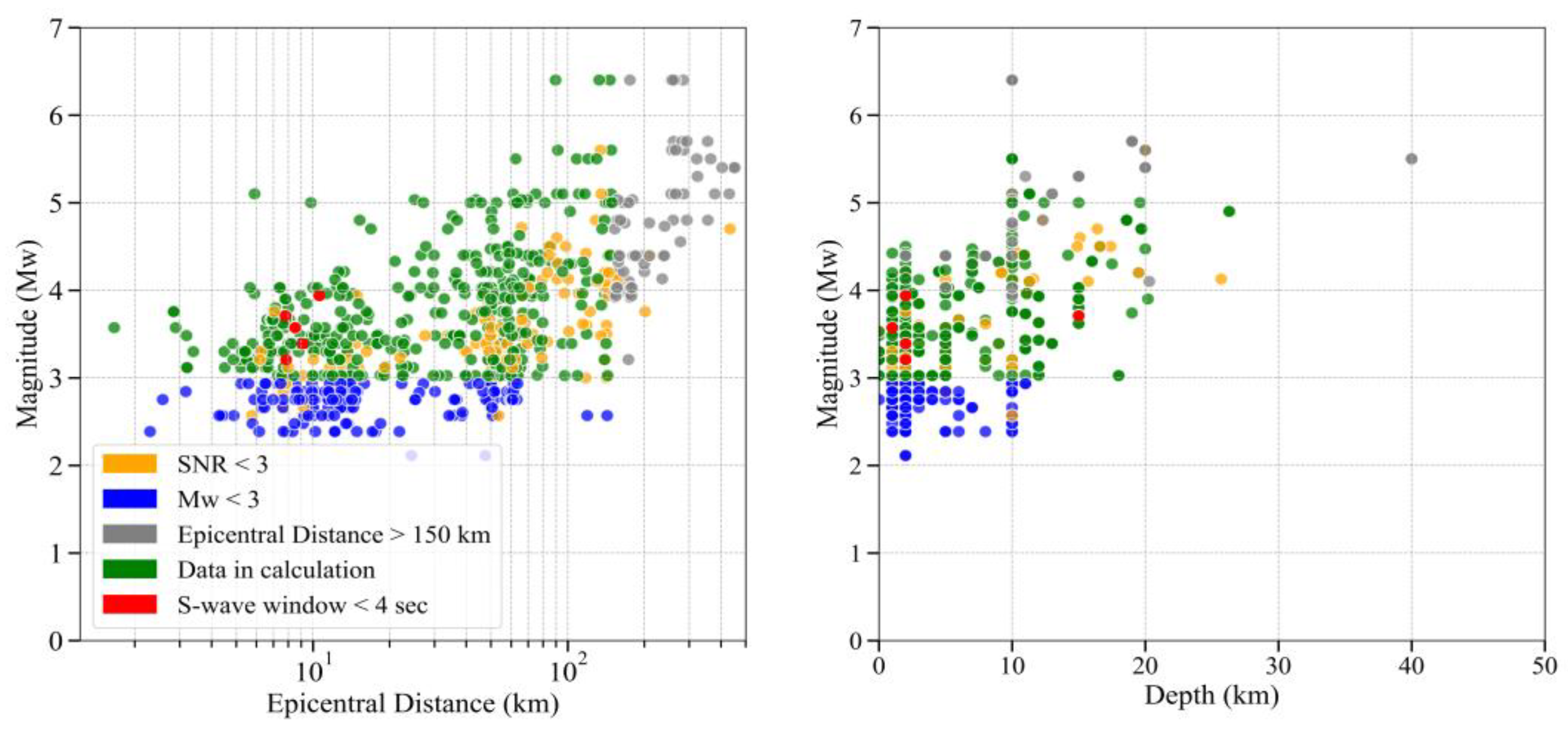
The data selection for this analysis was based on earthquake depth, magnitude, and epicentral distance. The applied selection criteria (depth < 30 km, M_W > 3, R_epi ≤ 120 km) are important for improving the reliability of kappa value calculations. Limiting the depth to less than 30 km ensures that only shallow earthquakes occurring within the Earth’s crust are considered, as kappa is primarily representative of near-surface attenuation. The magnitude threshold (M_W > 3) helps reduce the influence of source effects, as larger magnitude events generally have lower corner frequencies, minimizing potential overlap with the high-frequency range used for kappa estimation. Finally, restricting the epicentral distance to 120 km ensures that the signal is not overly affected by regional attenuation or path effects, allowing for a clearer observation of the site-specific high-frequency decay.

Figure 3 illustrates the classification of strong motion records based on magnitude, epicentral distance, earthquake depth, and S-wave portion duration. Green dots represent the analyzed data, while blue, yellow, grey, and red dots indicate excluded data, corresponding to M_W < 3, R_epi > 120 km, SNR < 3, and S-wave portion < 4 s, respectively.

The data were visually inspected and baseline corrected. The Nyquist frequency for all the recordings is 100 Hz, and a bandpass filter ranging from 0.1 to 100 Hz was applied. Poor-quality data, records with SNR < 3, and those with an S-wave portion shorter than 4 s (to ensure good spectral resolution) were excluded from the analysis.

The N-S and E-W components of accelerograms have been used in the present analysis. A total of 210 earthquakes were available after quality control processing, with 1560 individual horizontal records.

3.2. Kappa Calculation

There are different methods available for kappa (k) calculations, which are listed and explained in Ktenidou et al. (2014) [4], depending on factors such as the underlying approach, the frequency range over which k is calculated, how distance dependence is handled, and other considerations. For this study, the classical and most commonly used acceleration spectral method, defined by Anderson and Hough (1984) [2], was employed.

Using earthquake parameters, the corner frequency f_c and the theoretical spectrum, based on Brune’s model [3], were computed to examine the difference when the attenuation parameter (kappa) is included. The corner frequencies have been estimated using Brune’s method (1970, 1971) [3] as given by Equation (1):

$$f_c=4.9\times {10}^6{\beta }_s({\Delta \sigma /M_0)}^{1/3}$$

(1)

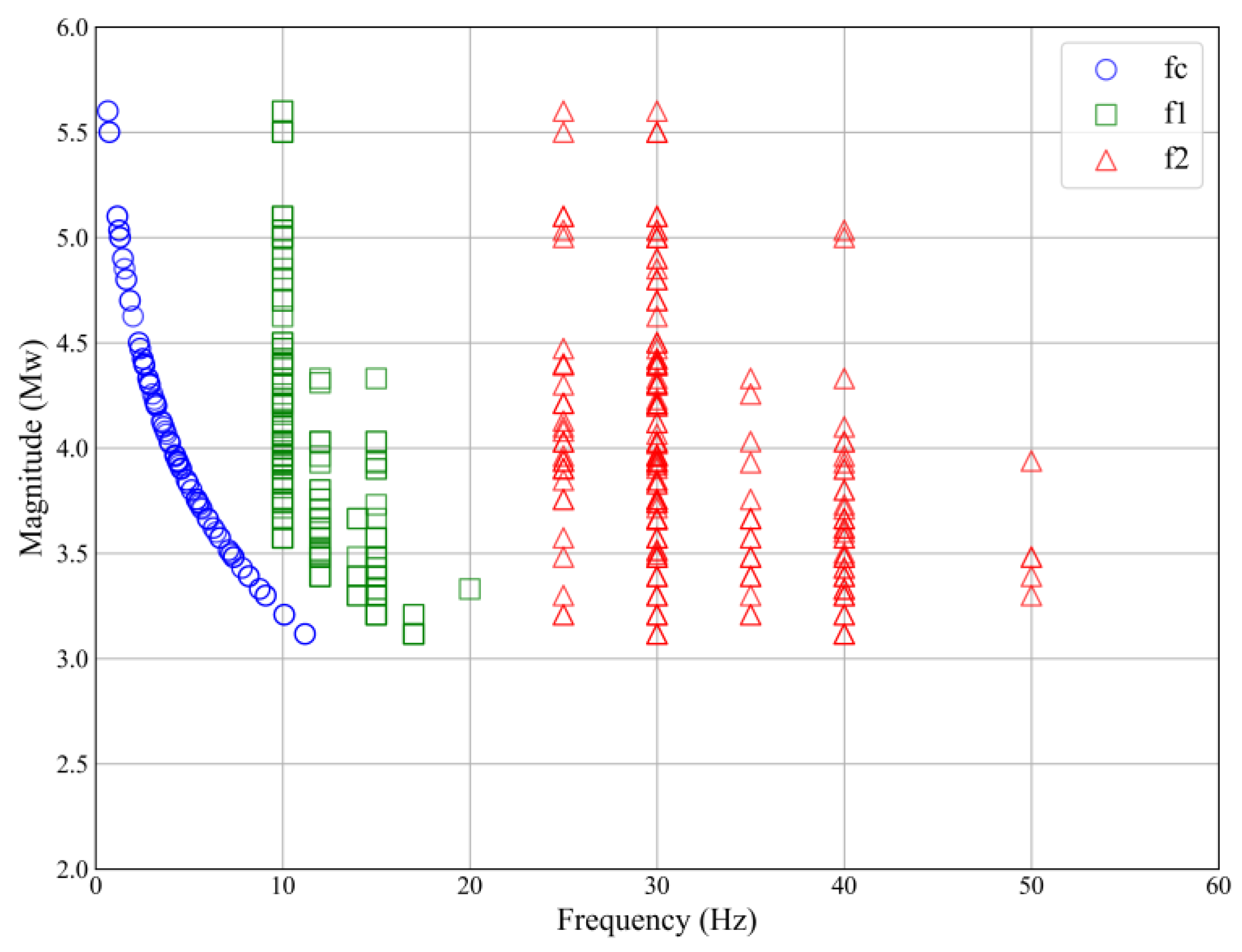
The next step was to define the boundary frequencies, f₁ and f₂, which were manually selected: f₁ was chosen to be greater than 1.5 × f_c to ensure that source effects would not bias the kappa calculation. Additionally, if f₁ < 10 Hz, then f₁ = 10 Hz was used to avoid potential site resonance effects (Figure 2). f₂ was selected at the point where the spectrum flattens, ensuring that the signal-to-noise ratio (SNR) between the S-wave and noise windows was greater than 3, or up to 50 Hz—above which spectra are considered unreliable (half the Nyquist frequency). The frequency band ∆f had a minimum required width of 10 Hz. Spectra with Δf < 10 Hz were discarded to maintain robustness in the slope computation. Depending on the event magnitude and distance, f₁ ranges from 10 to 20 Hz, while f₂ ranges between 25 and 50 Hz (Figure 4 shows the distribution of selected frequencies with respect to moment magnitude M_w).

This classical method uses the S-wave window, and the calculation follows the recommended procedure from Ktenidou et al. (2013) [10]. Initially, good-quality records were manually selected, ensuring a sufficient noise window before the signal and S-wave windows longer than 4 s (Figure 5, top row). A 5% cosine taper was applied to both windows, and the Fourier amplitude spectrum (FAS) was then calculated for each window (Figure 5, middle row). The theoretical spectrum based on Brune’s model [3] is also shown in Figure 5 (black line).

Within the selected frequency range, data were regressed in log-linear space between f₁ and f₂ (Figure 4—blue line) using the following equation [2]:

k = −λ π   where   λ = Δ(ln a)/Δf

(2)

This procedure was applied to both horizontal components (N-S and E-W), and the average value from the two was computed. Figure 4 illustrates the kappa calculation procedure for three stations located on different types of soil: A (left), B (middle), and C (right), based on the EC8 soil classification [23].

Following the procedure for kappa calculation, results from three stations are presented: OHR station, located on soil class A using the horizontal component of an earthquke record with M_w = 3.8 and R_epi = 8.01 km, DBR station, located on soil class B using horizontal component of an earthquake record M_w = 3.66 and R_epi = 23.5 km, and SKI station, located on soil class C using horizontal component of an earthquake record with M_w = 5.03, R_epi = 65.5 km. The obtained kappa values for these records are k = 0.0226 s, k = 0.0407 s, and k = 0.0651 s for the OHR, DBR, and SKI stations, respectively. The slope of the FAS for kappa calculation is steeper for looser soil (stations DBR and SKI), and less steep for rock (OHR station).

4. Results

4.1. York Weighed Regression

The high-frequency decay parameter kappa and its site component (k₀) were calculated for each station using regression with distance. In this study, York weighted regression analysis [37], which accounts for errors in both variables, was applied. The uncertainties were represented as one standard deviation for kappa and a fixed error of 3 km for R_epi.

Two of the stations, installed on different soil classes, A and B, are shown in Figure 6, while the results for all sixteen stations are presented in

Table 2. Adapted from Poposka et al., 2025 [33]. Site component (k₀) values were obtained from regression analysis using error-in-variables and mean values for distances up to 25 km, along with the number of records included in each analysis and V_S30 values for each station. The symbol “/” indicates insufficient data for a reliable regression or mean value analysis.

Station	k0regression	No. Records	k0 mean up to 25 km	No. Records (0–25 km)	Vs,30 [m/s]
BER	0.0257 ± 0.004	7	0.0268	4	500
DBR	0.0408 ± 0.006	49	0.0506	2	400–450
KOZ	0.0261 ± 0.008	7	0.0268	2	800
KPAL	0.0185 ± 0.060	6	/	/	>800
KPAL1	0.0355 ± 0.018	8	/	/	350
MBROD	0.0272 ± 0.006		/	/	380–400
OBD	/	/	0.0657	35	350–400
OHR	0.0181 ± 0.003	28	0.0232	16	>1000
OHRK	/	/	0.0281	5	350–400
OHRO	/	/	0.0322	6	350–400
OHRT	/	/	0.0558	9	350–400
PEH	0.0281 ± 0.010	10	0.0396	10	380–450
SKI	0.0311 ± 0.011	6	/	/	330
RSN	0.0356 ± 0.002	62	0.040	48	360–400
STR	0.0418 ± 0.008	11		2	350–380
VAL	0.0317 ± 0.008	9	0.0320	2	774

. The site component (k₀) was determined both from the regression line extrapolated to zero distance and from the mean value of the records within 25 km, particularly for stations with a majority of nearby data.

Averaged values from the two horizontal components were considered if their difference was less than 25%; otherwise, they were excluded from the regression. Exceptions were made for stations with a limited number of near-distance records, allowing good-quality data with differences greater than 25% to be included.

The regression analysis was performed twice: once using the full dataset (Figure 6, blue line), and once excluding outliers beyond one standard deviation (Figure 6, red dashed line). There was no significant difference between the two results, except in the coefficient of determination (R²). The York regression without outliers yielded higher R² values, indicating a better fit.

In Figure 6, a clear difference is observed between soil classes A and B, particularly in the site component (k₀). Lower local attenuation values were recorded at the station on rock, while higher values were found at the station on looser soil. Regarding regional attenuation analysis, even small variations in the slope of the regression line, on the order of the third or fourth decimal place, can significantly affect the results. These variations in the slopes could be further explored in future investigations, particularly for estimating the quality factor Q. The number of records from the station installed on soil class C is limited, so further studies should be conducted as more data become available.

Table 2 presents the site-specific parameter values obtained for the sixteen stations, including results from both the regression analysis and the mean values within 25 km, along with the number of records used in the analysis. If a station had at least ten records at close distances, the mean value was selected.

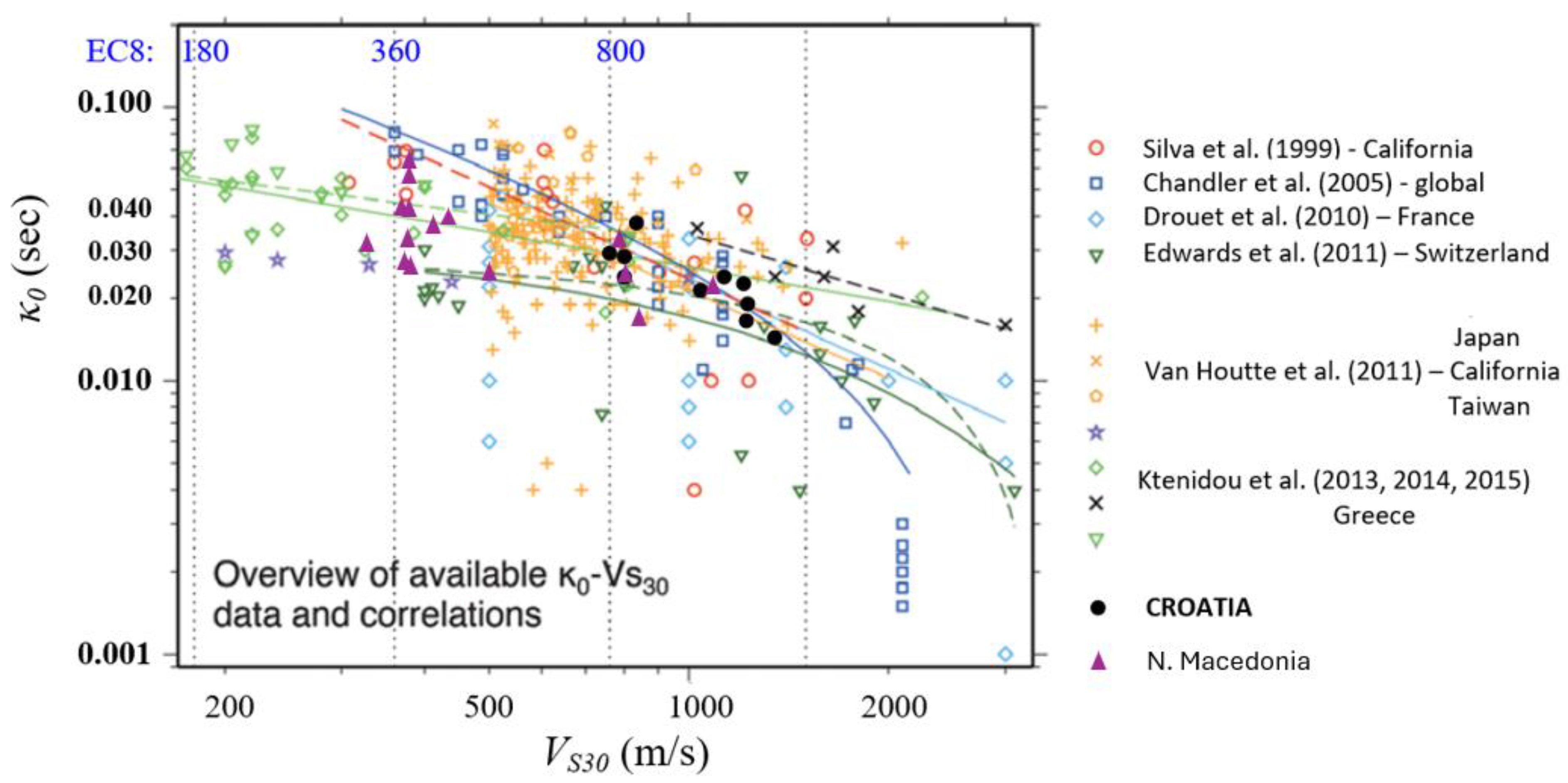
4.2. k₀-V_S30 Correlation

When there are insufficient data to directly measure k₀, empirical correlations are often used to estimate it. These correlations are primarily based on V_S30, as introduced by Silva et al. (1998) [5], and later expanded upon by Chandler et al. (2006) [6], Ktenidou et al. (2014) [4], among others.

The V_S30 values for the sixteen stations in N. Macedonia range from 330 to 1000 m/s, corresponding to three soil types, A, B and C according to the EC8 classification [23]. Figure 7 (an updated version based on Ktenidou et al. (2014) [4] and Stanko et al. (2017) [12]) presents the compiled k₀-V_S30 values for various global regions where k₀ was calculated using the AH84 method, alongside the measured k₀ and V_S30 values for stations in North Macedonia. Given that k₀ is a site-specific parameter, it is reasonable to expect that stiffer (harder) sites will exhibit lower attenuation, and thus k₀ will decrease as shear-wave velocity increases. However, this expected trend can vary, and a degree of scatter in the results obtained is evident, as shown in Figure 7.

Ktenidou et al. (2014) [4] revisited the existing k₀-V_S30 correlations and discussed their scatter and applicability. According to their study, the large scatter is expected due to differences in how V_S30 is calculated (invasive vs. non-invasive methods) and how well it represents the subsurface structure beneath the station. In some cases, a bedrock-based correlation may better approximate the deeper soil structure relevant to k₀. Other contributing factors to the variability include regional differences in the shallow crustal quality factor (Q), as well as the methods and frequency ranges used for calculating kappa and its site component k₀.

In line with this study and previous research, the scatter in κ₀ values remains considerable, making it impractical to assign a single k₀ value to a typical site class. For example, for soil type B (with V_S30 values ranging from 350 to 800 m/s), κ₀ values range from 0.028 s to 0.067 s. Most of the data correspond to site types A and B, and Figure 7 shows that the near-site attenuation (k₀) values observed at North Macedonian stations are closely aligned with global κ₀ values from previous studies.

There are currently no available data for very hard rock sites or very soft soils (EC8 classes C and D), so future measurements will be important for refining and expanding the k₀-V_S30 relationship for North Macedonia.

Figure 8 illustrates the site component values in relation to soil classification. The dotted lines represent the boundaries between different site velocities. The correlation coefficient is 40%, indicating a better or similar correlation than previous studies for surface data—for instance, Japan is below 15% [9], Greece is around 25% [11], and France is around 38% [7]—but still a loose correlation. This relatively low correlation has shown that k₀ is influenced not only by the average shear-wave velocity in the upper 30 m (V_S30), but also by deeper velocity structures, site-specific stratigraphy, and other local geological factors not captured by V_S30 alone. Therefore, while V_S30 provides a useful first-order proxy for site conditions, it may not fully explain the variability in k₀ across stations.

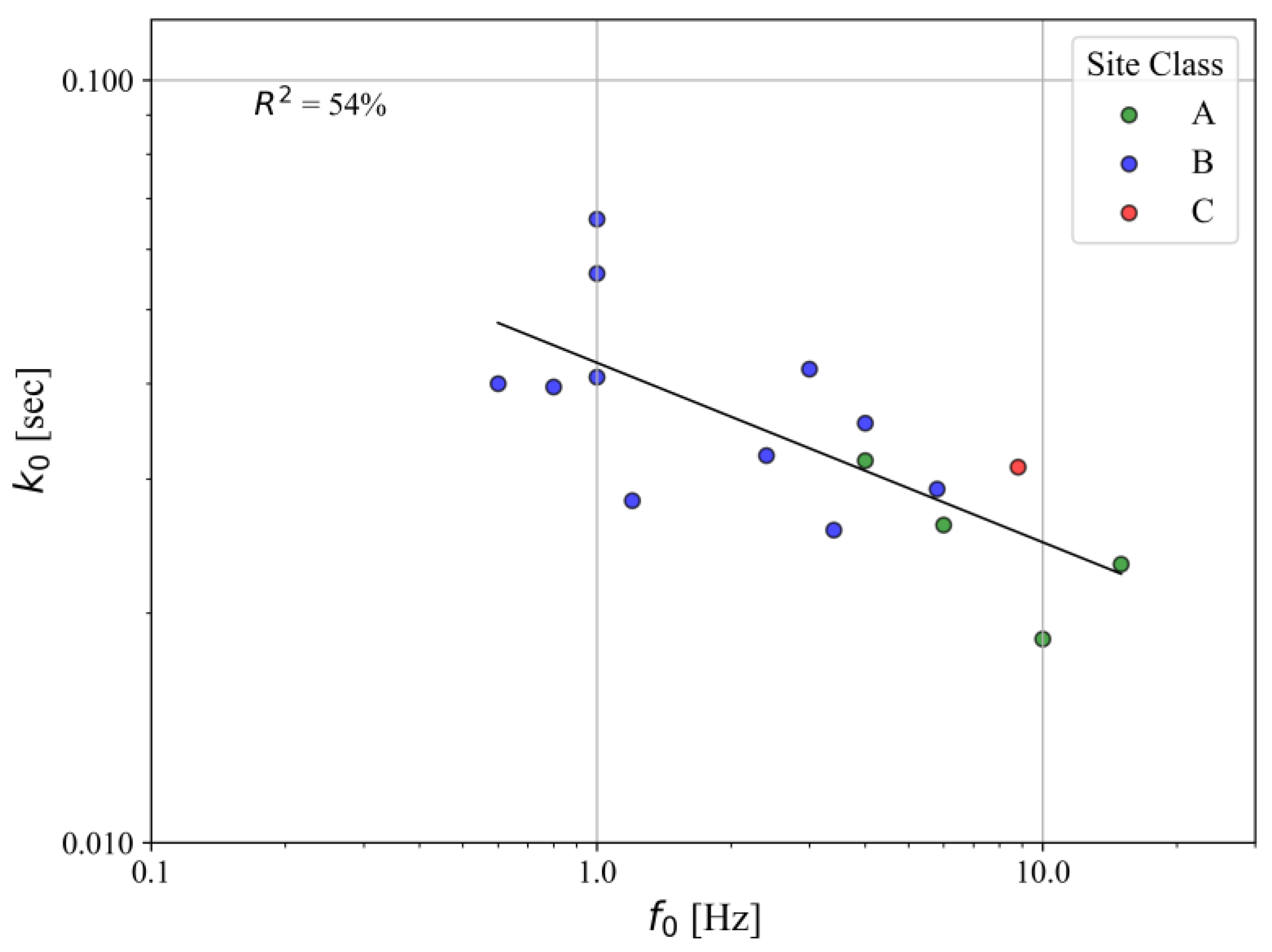
4.3. k₀-V_S30-f₀ Correlation

To improve the correlation between V_S30 and k₀, an additional relationship incorporating the site’s resonance frequency is considered. Since V_S30 values alone may be insufficient for accurate site classification, incorporating the site’s fundamental frequency (f₀) can enhance the classification by accounting for deeper basin structures. Previous studies [9,11,38] have explored the relationship between the site component k₀ and the fundamental site frequency.

Figure 9 shows the correlation between the fundamental site frequency, determined using the HVSR method with earthquake data, and the site component k₀, calculated as described in the previous sections. Different colors indicate soil types—A, B, and C—according to the EC8 classification [23].

The correlation coefficient is R² = 54%, indicating a moderate relationship between the site component κ₀ and the deeper soil basin structure. This correlation is higher than those reported in previous studies conducted in other countries, such as Japan, California, and Taiwan [9,38] which found 12.6%, and Northern Greece [11], which reported 49%.

Overall, the site component k₀ tends to decrease slightly as the site fundamental frequency increases, similar to V_S30 observations (Figure 7).

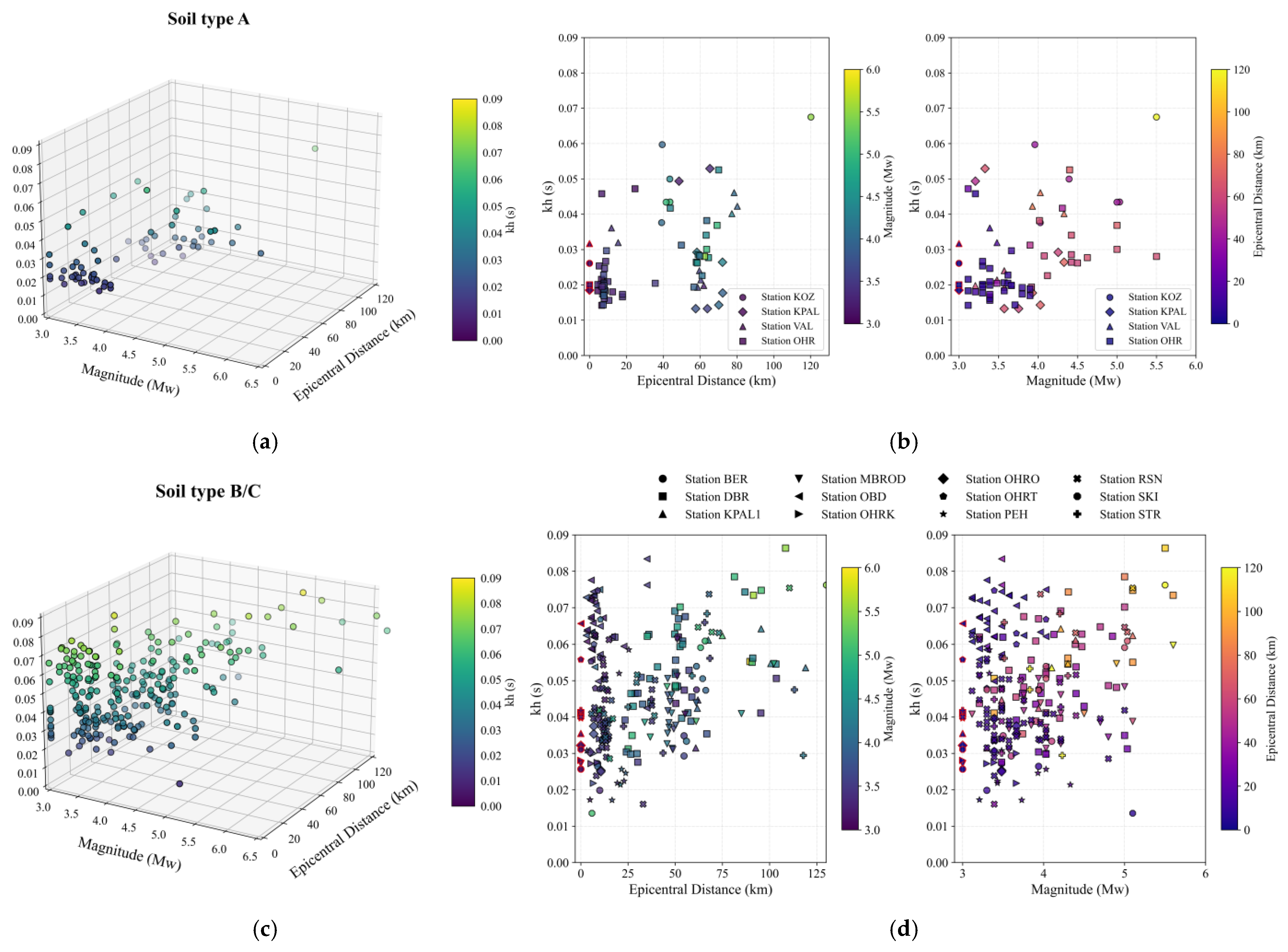
4.4. Kappa Correlation with Epicentral Distance and Magnitude

This chapter investigates the dependence of the high-frequency decay parameter kappa (k) on distance and magnitude. Figure 10 presents both 3D and 2D plots of kappa values as a function of earthquake magnitude and epicentral distance for stations installed on soil type A (plots a and b) and for stations located on soil types B and C (plots c and d). The site-specific component k₀ for each station is marked as a symbol with a red outline. The site component is noticeably lower for soil type A, as most of the data fall at the lower bound of the plot, while a significant increase is observed for soil type B, with higher values evident. Regarding epicentral distance, the empirical parameter shows clear dependence, increasing with greater distance and decreasing with shorter distance. In terms of magnitude, no clear correlation is observed, especially in the range from 3 to 4. Earthquakes with high magnitudes and short epicentral distances are rare, so the influence of magnitude on kappa at close distances cannot be fully evaluated.

In addition to local attenuation, regional attenuation should also be considered and examined. The results obtained from the regression analysis, where sufficient data and slope calculations are available, should be further incorporated and compared with the analysis of the quality factor Q.

5. Conclusions

This study focuses on determining the high-frequency decay parameter kappa (k) and its site-specific component (k₀) for sixteen accelerometric stations in North Macedonia. Only high-quality earthquake records from the IZIIS strong motion network were used for the calculation. The study investigates the parameter’s dependence on epicentral distance, site conditions (including the V_S30 parameter and site resonant frequency f₀), as well as earthquake magnitude.

A reasonable correlation was observed between k₀ and the site parameters (V_S30 and f₀) of the analyzed locations. Due to geological conditions, sites with higher shear-wave velocity tend to exhibit lower k₀ values, while sites with lower share wave velocity show higher values, indicating regions with significant high-frequency attenuation. Regarding site resonance frequency, a slight decrease in the site component is evident with increasing f₀.

The estimated values for the site-specific component k₀ vary from k₀ = 0.0185 s to k₀ = 0.0261 s (or 0.0317 s) for stations installed on soil class A, and from k₀ = 0.0272 s to k₀ = 0.0657 s for stations installed on soil class B/C. The variation in values within the same soil class suggests that it is not feasible to assign a single k₀ value to a specific V_S30. However, the results are consistent with the expected range reported in previous studies conducted in other countries. It should be noted that for stations where V_S30 values were retrieved from the USGS V_S30 Map Viewer, additional site-specific investigations (e.g., geophysical surveys or borehole data) are required to validate and refine these estimates.

As a potential extension of this study, it is proposed to refine the estimation of the site-specific component k₀ by excluding the path effect through the incorporation of the regional component kappa (k_R) and Q-factor correction in the regression analysis.

The findings of this study may contribute to improved ground motion attenuation modeling and the refinement of seismic hazard maps for the region. Specifically, k₀ is one of the seismological parameters that can be used to characterize the host region in the context of Ground Motion Prediction Equations (GMPEs). The same parameter should also be available for the target region so that adjustments can be made.