Uncertainty Analysis and Quantification of Rainfall-Induced Slope Instability in Fine-Grained Clayey Soils
Abstract
1. Introduction
1.1. Probabilistic Analysis Configuration
1.2. Sensitivity Analysis Configuration
2. Fine-Grained Clayey Soil
2.1. Shear Strength
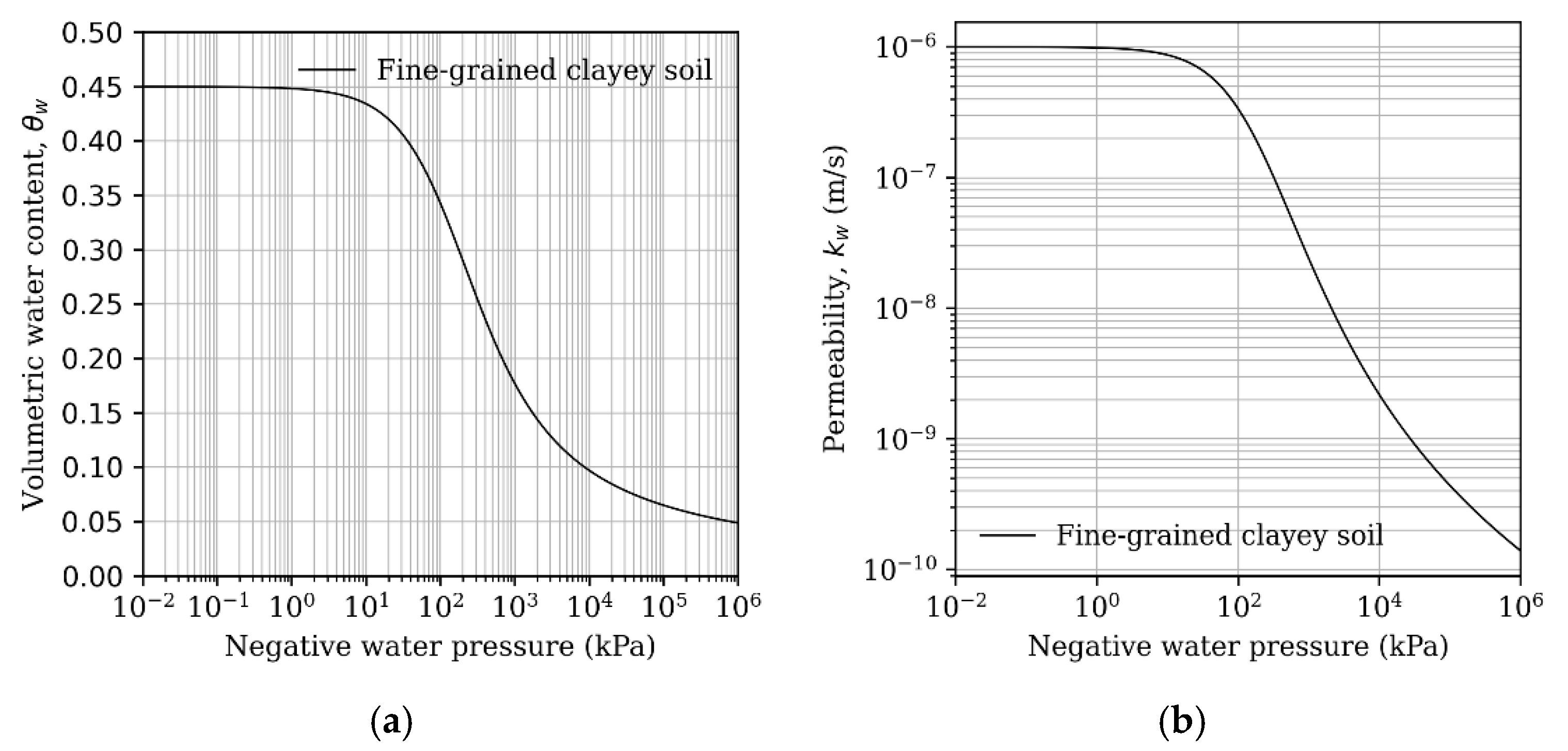
2.2. Soil Water Characteristic Curve
2.3. Hydraulic Conductivity
3. Analysis
Model Validation
4. Results
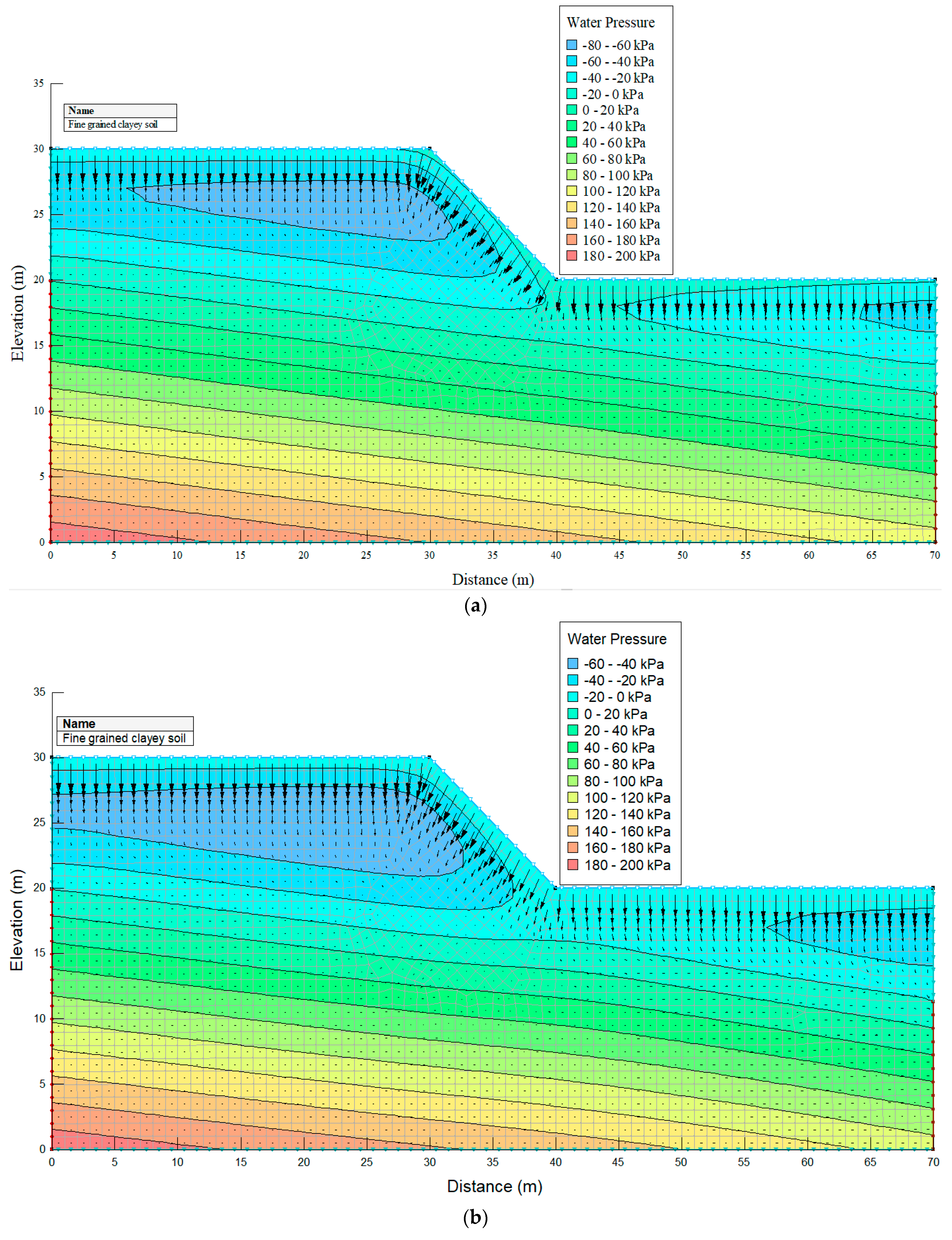
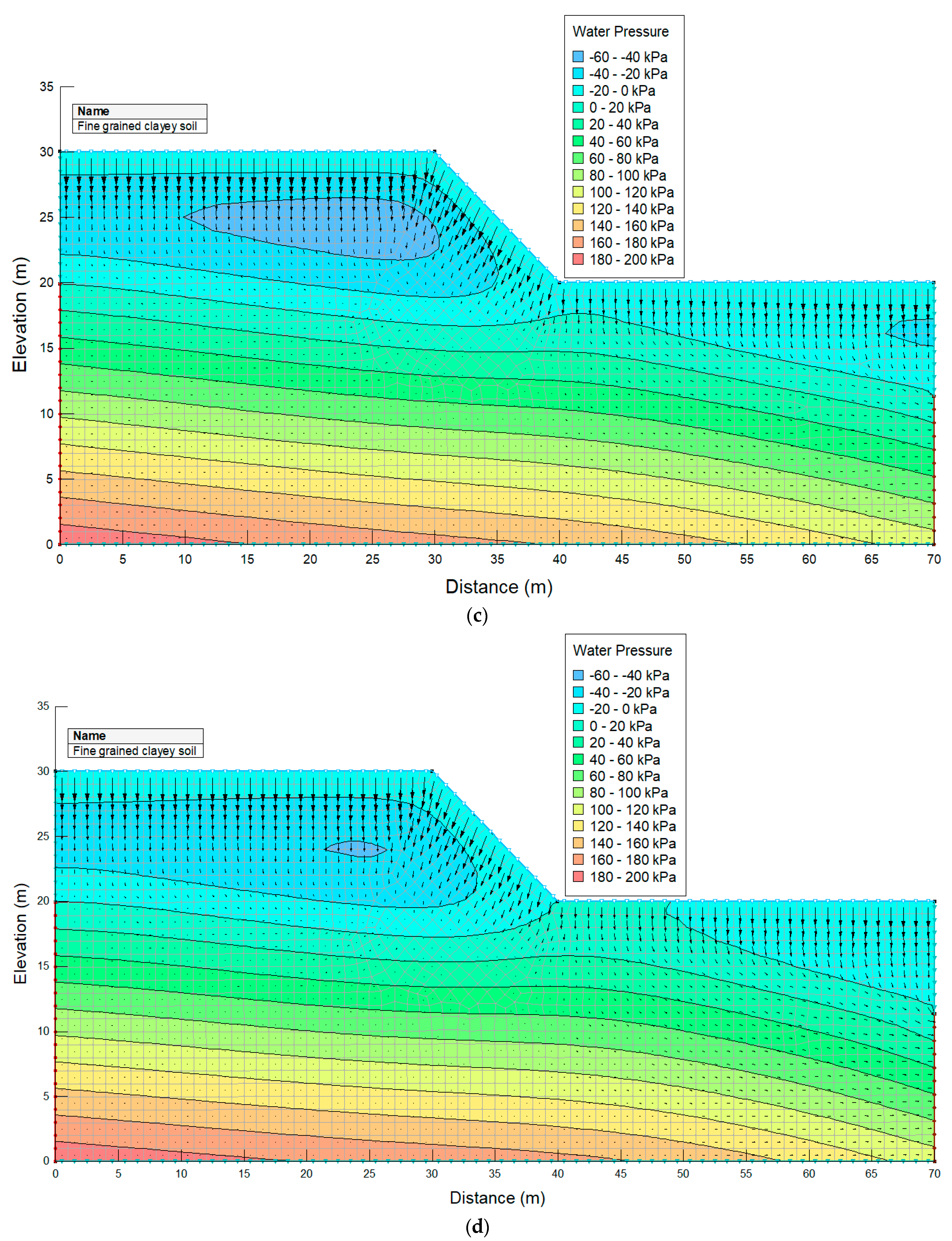
4.1. Infiltration Analysis
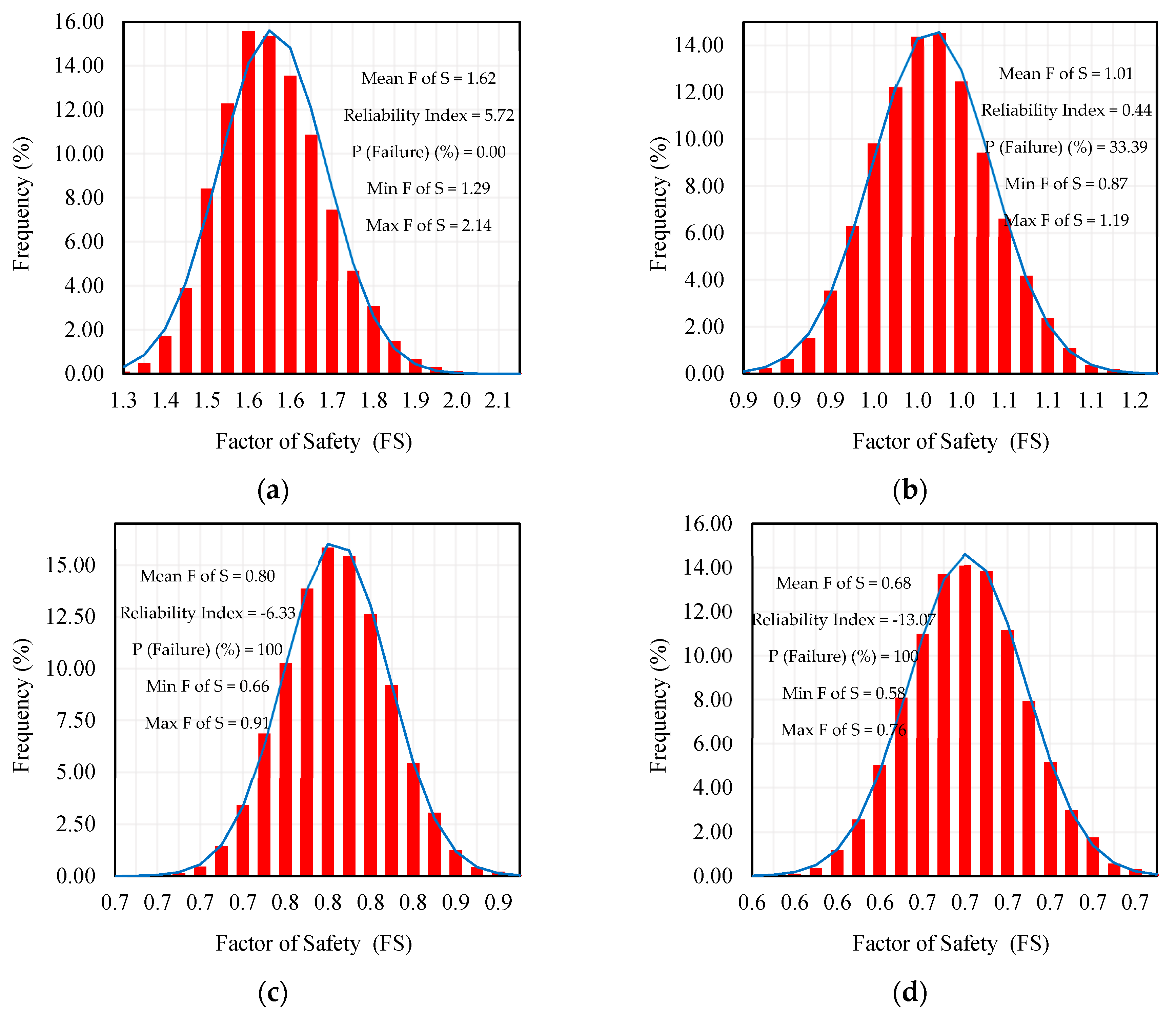
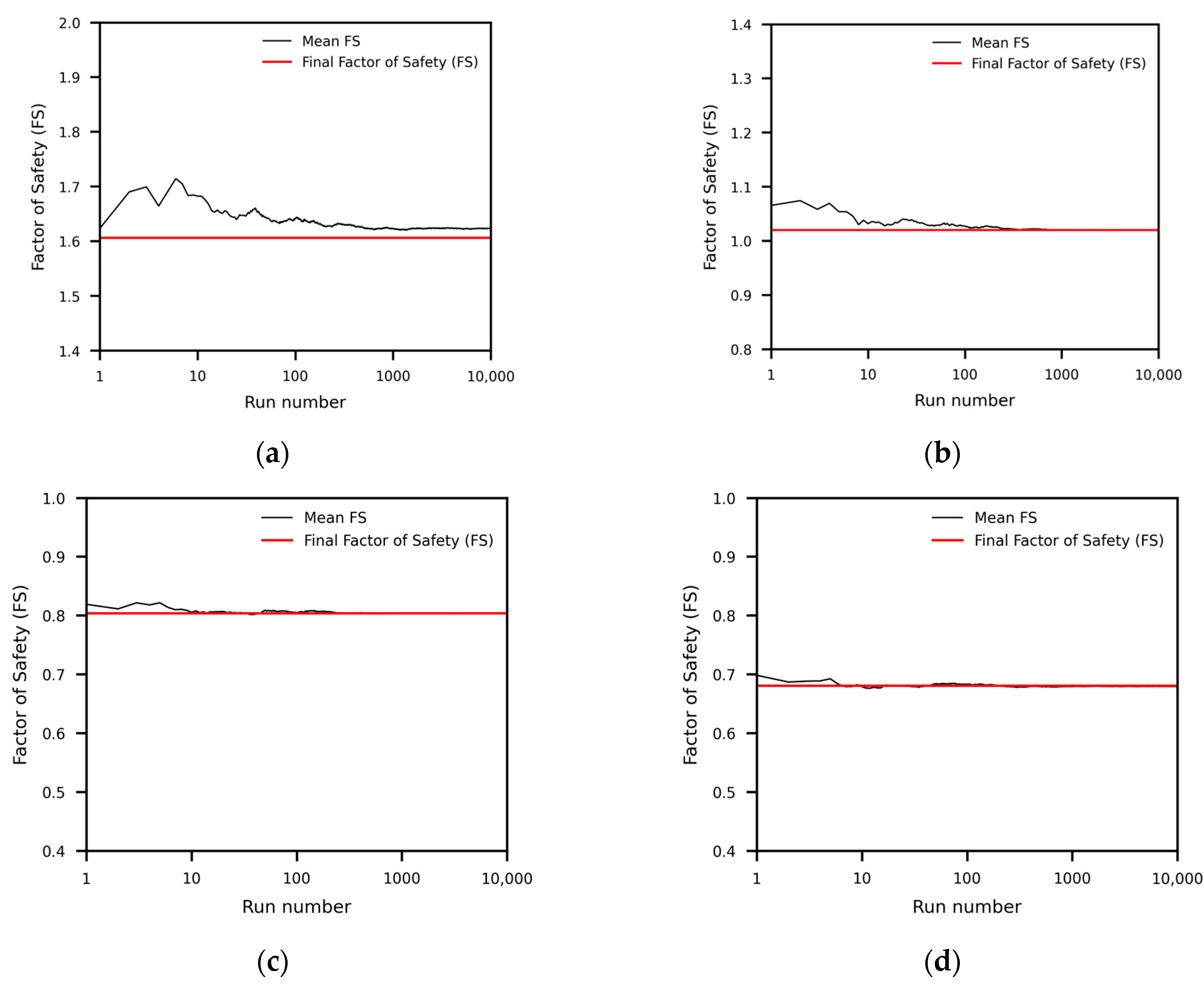
4.2. Probabilistic Analysis Results
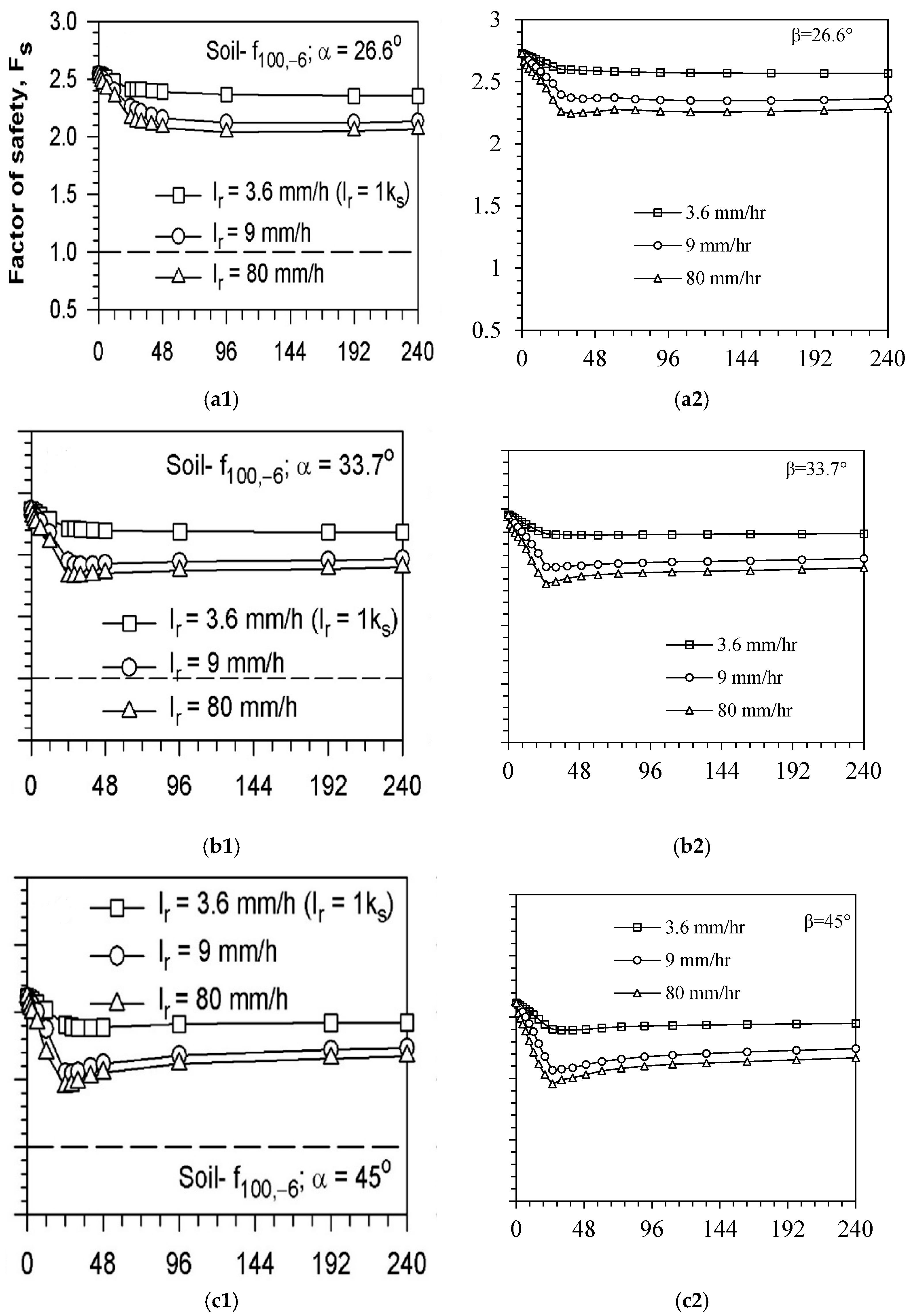
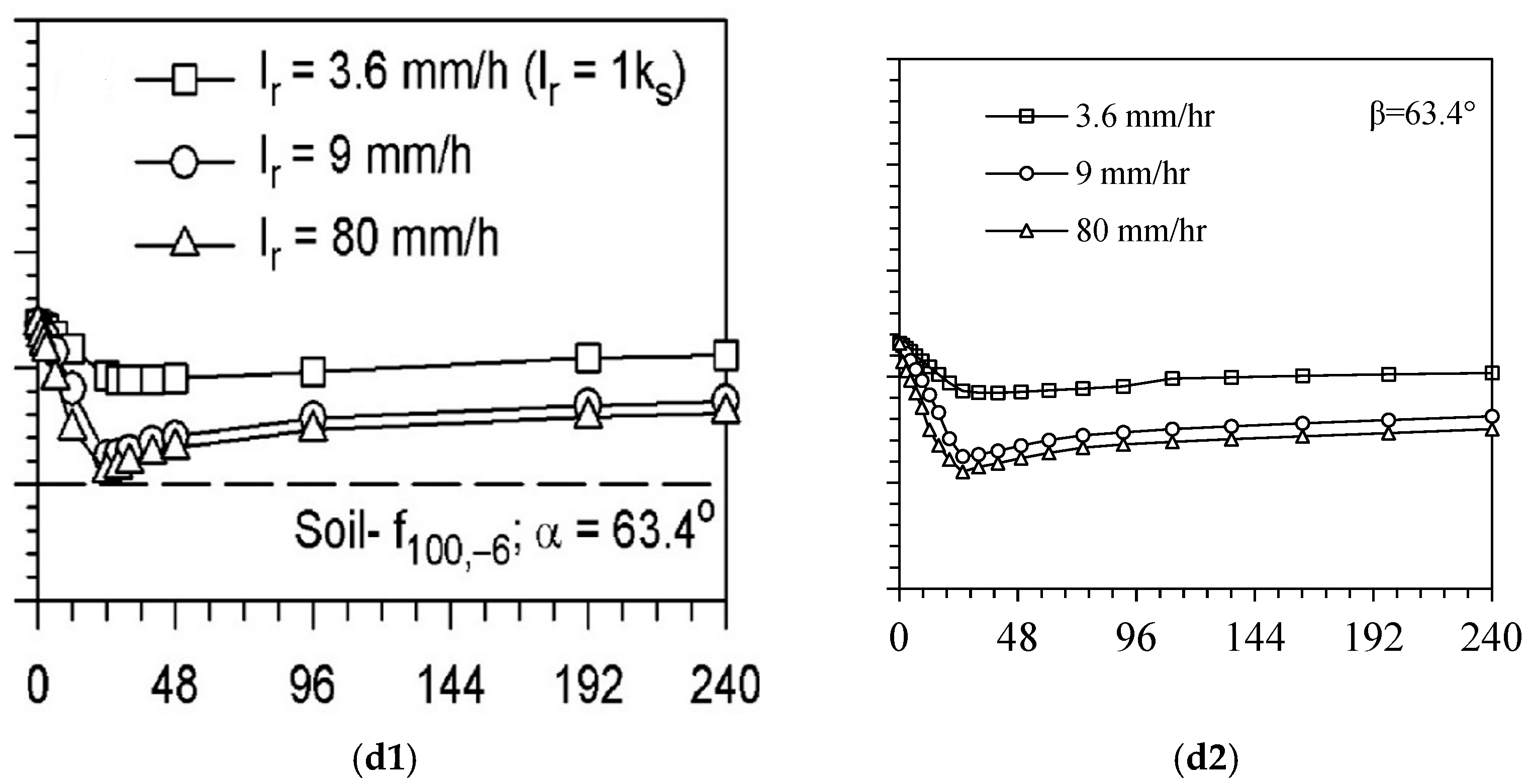
4.3. Sensitivity Analysis
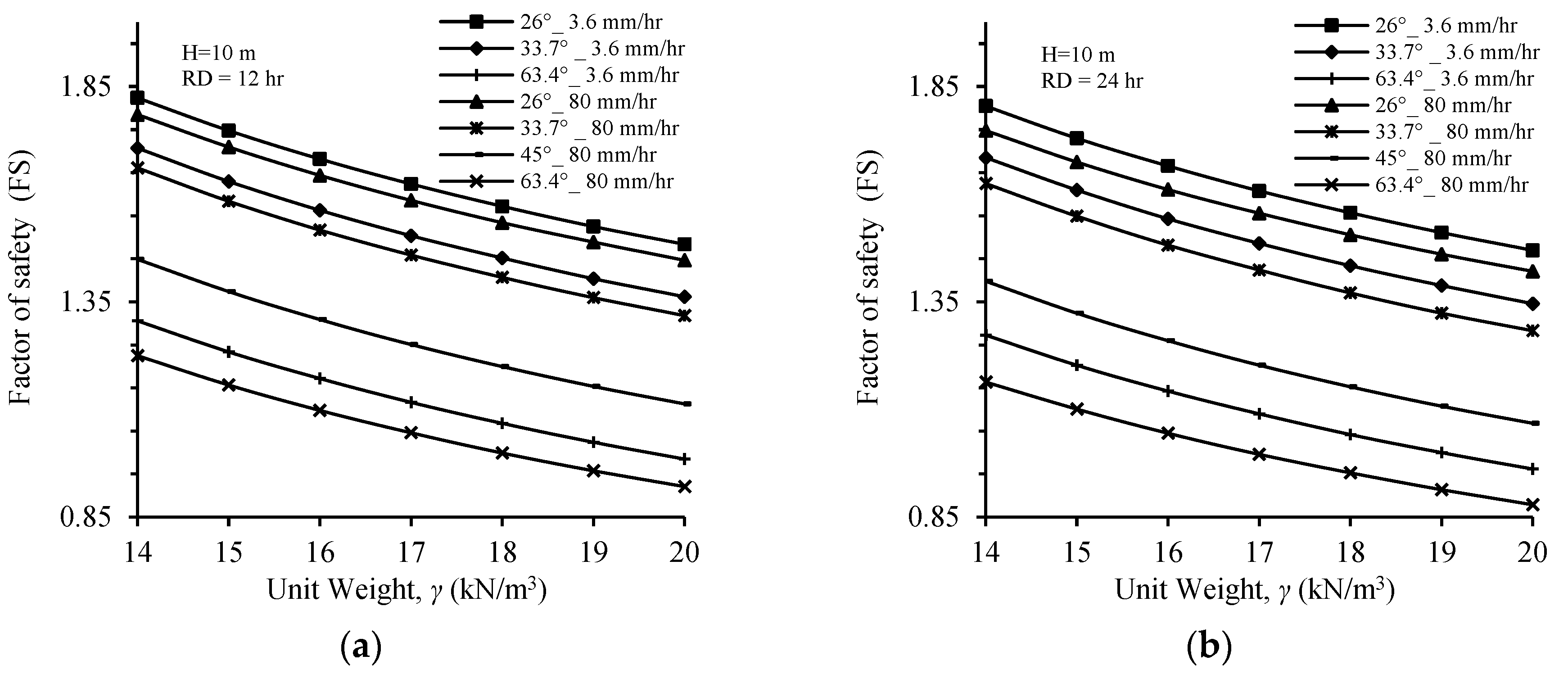
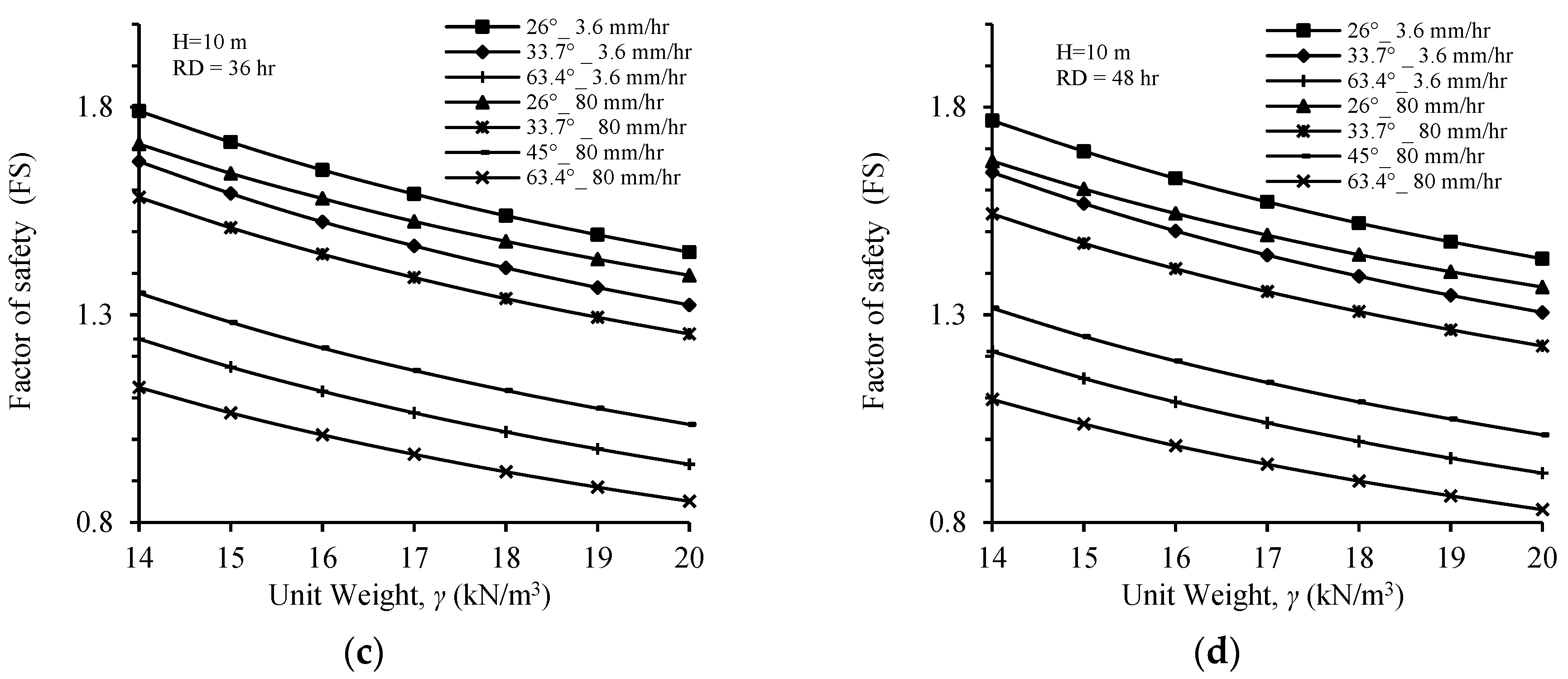
4.3.1. Soil Unit Weight
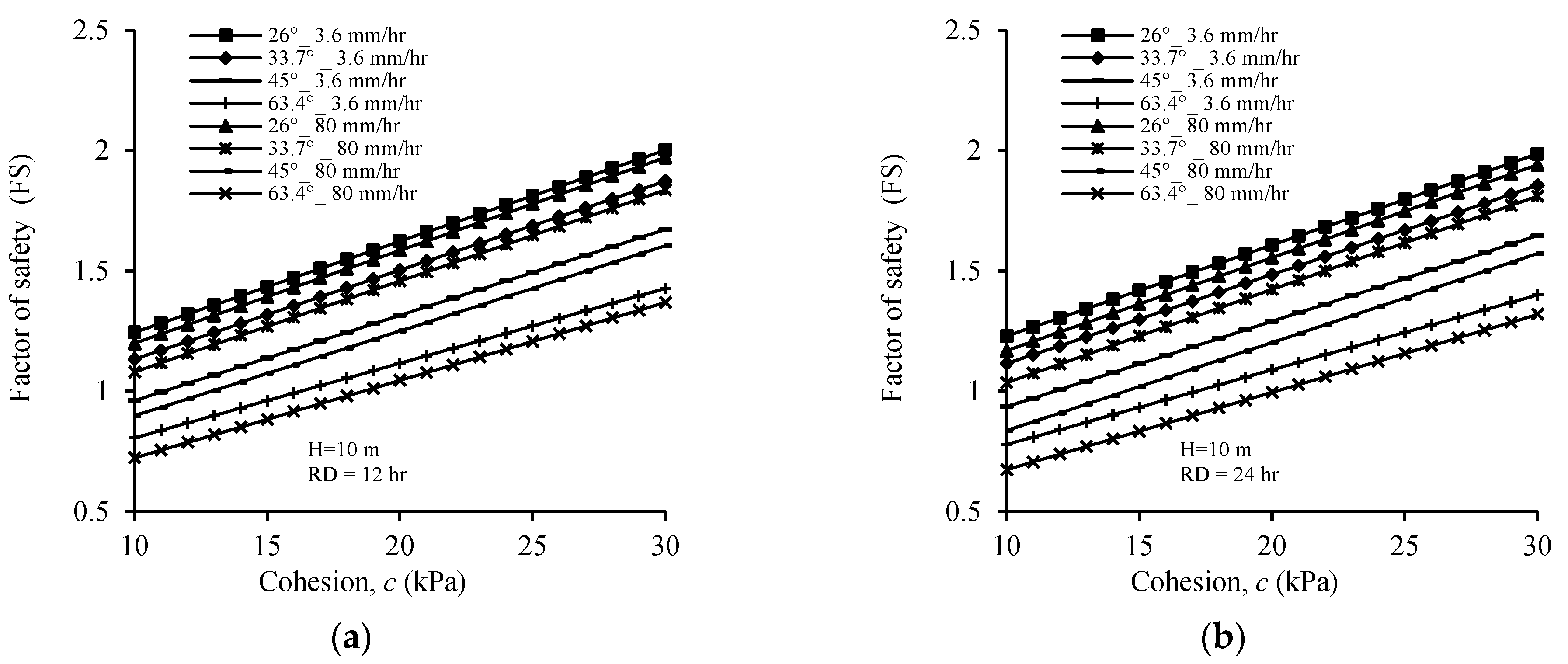
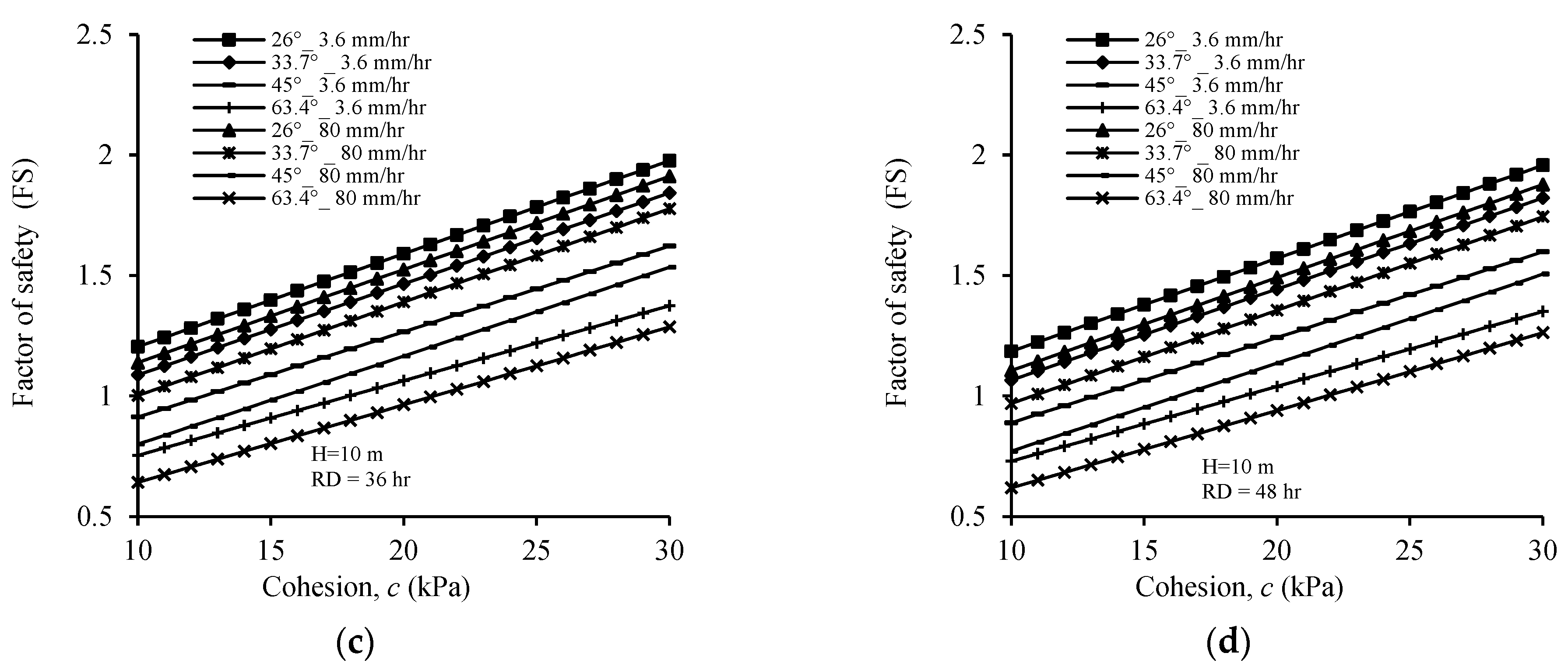
4.3.2. Cohesion
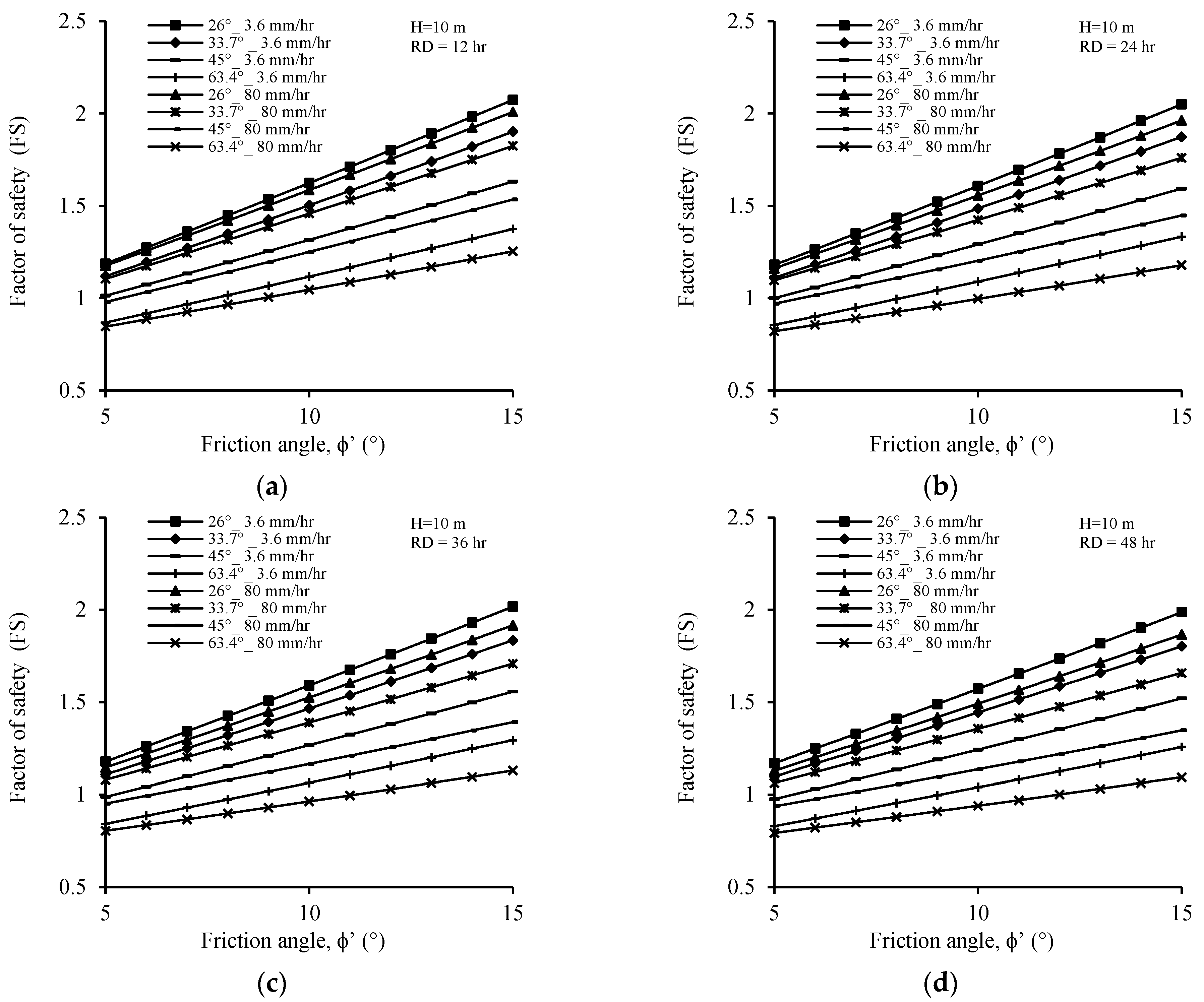
4.3.3. Friction Angle
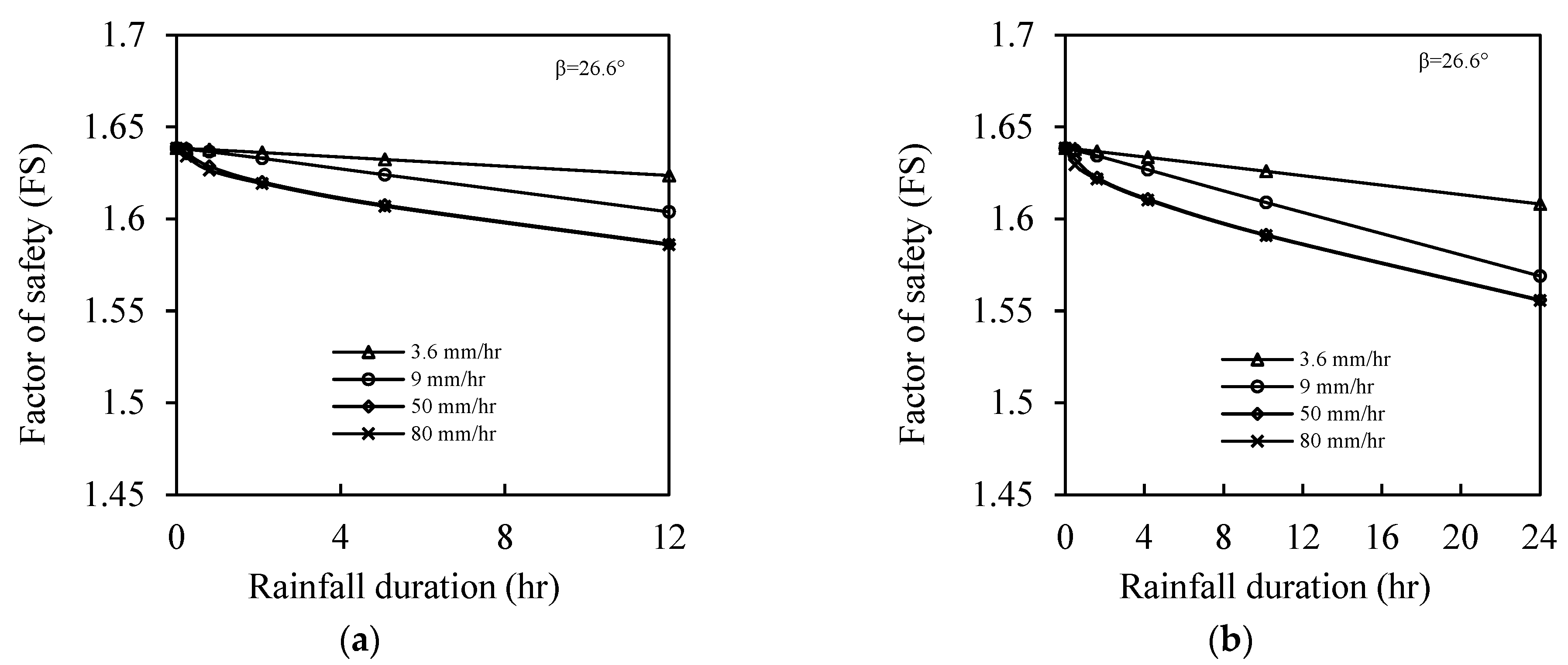
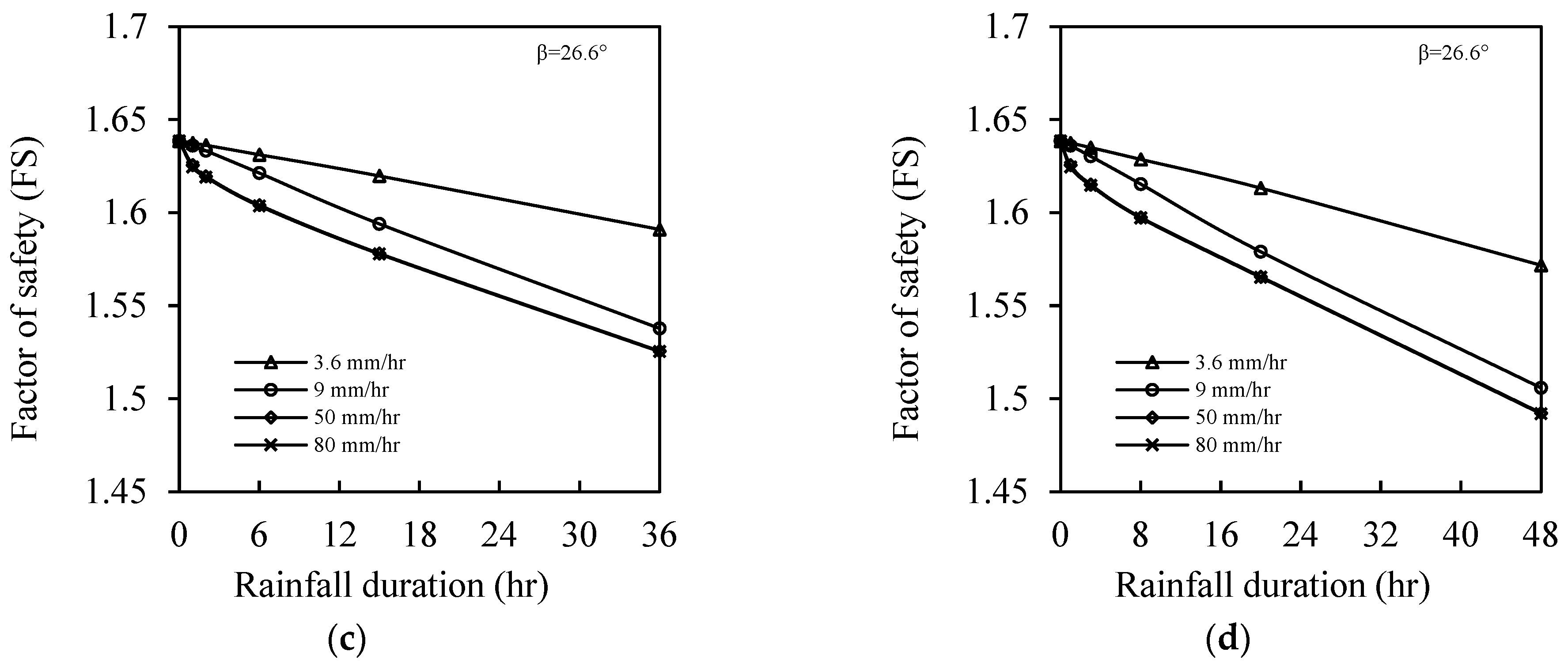
4.3.4. Rainfall Intensity and Duration
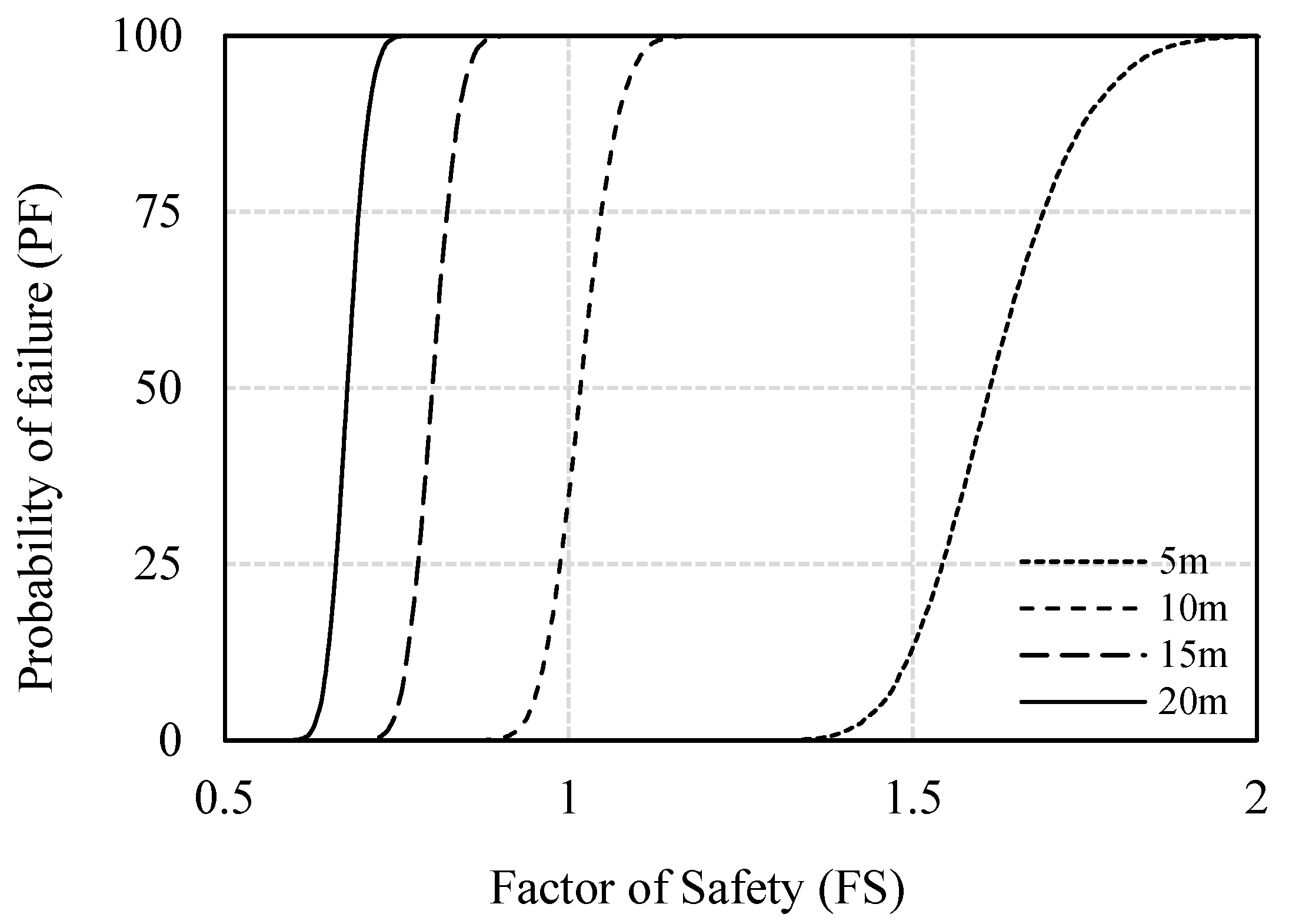
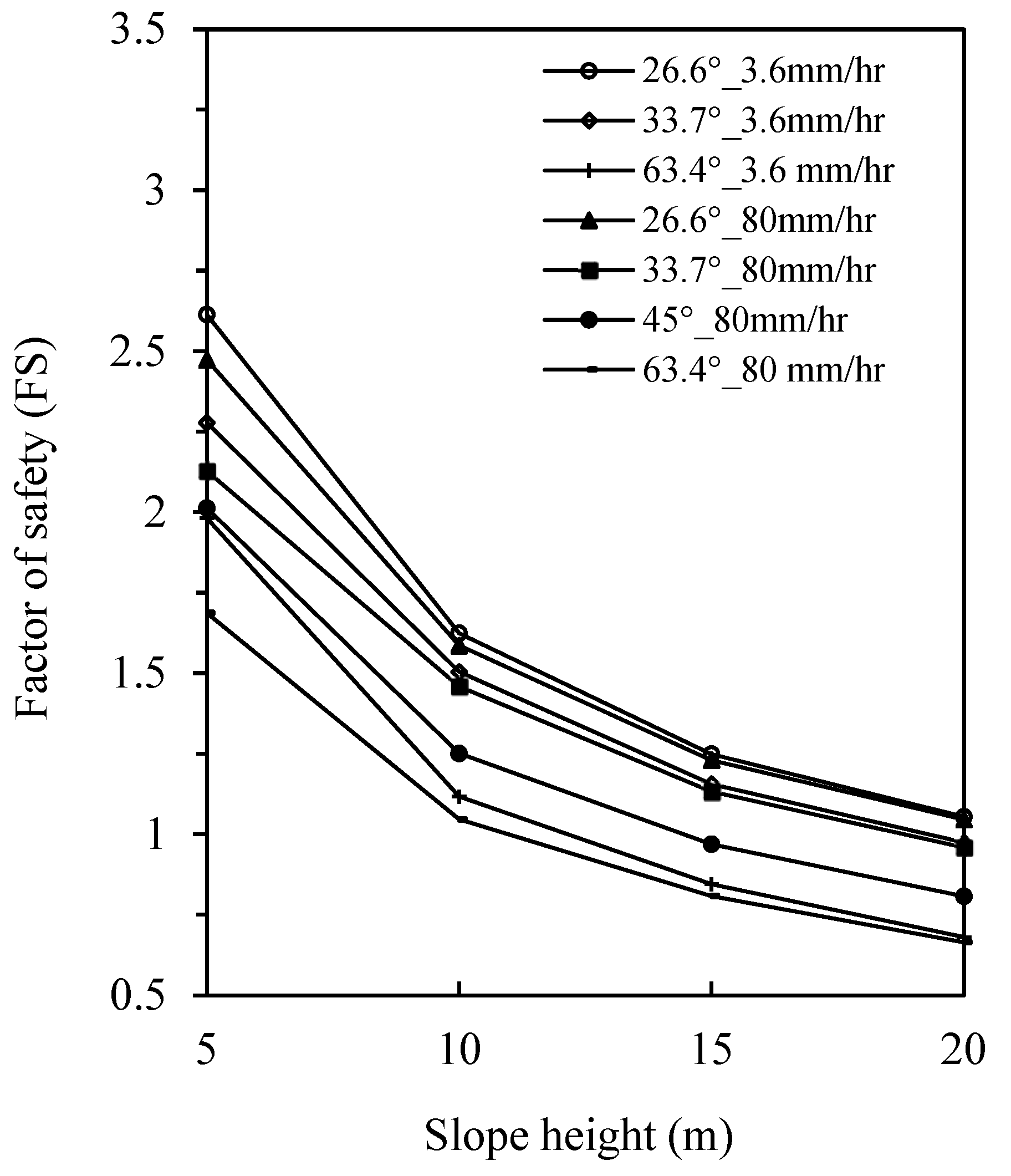
4.3.5. Effect of Slope Height
5. Dataset for Machine Learning
6. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sassa, K.; Canuti, P. Landslides Disaster Risk Reduction; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Leroueil, S. Natural slopes and cuts: Movement and failure mechanisms. Géotechnique 2001, 51, 197–243. [Google Scholar] [CrossRef]
- Tang, Q.; Gratchev, I.; Ravindran, S. Effect of Rainfall Intensity on Landslide Initiation: Flume Tests and Numerical Analysis. Geotechnics 2023, 3, 104–115. [Google Scholar] [CrossRef]
- Froude, M.J.; Petley, D.N. Global fatal landslide occurrence from 2004 to 2016. Nat. Hazards Earth Syst. Sci. 2018, 18, 2161–2181. [Google Scholar] [CrossRef]
- Lin, S.; Zheng, H.; Han, C.; Han, B.; Li, W. Evaluation and prediction of slope stability using machine learning approaches. Front. Struct. Civ. Eng. 2021, 15, 821–833. [Google Scholar] [CrossRef]
- Xu, H.; He, X.; Sheng, D. Rainfall-Induced Landslides from Initialization to Post-Failure Flows: Stochastic Analysis with Machine Learning. Mathematics 2022, 10, 4426. [Google Scholar] [CrossRef]
- Lu, P.; Rosenbaum, M.S. Artificial Neural Networks and Grey Systems for the Prediction of Slope Stability. Nat. Hazards 2003, 30, 383–398. [Google Scholar] [CrossRef]
- Bai, G.; Hou, Y.; Wan, B.; An, N.; Yan, Y.; Tang, Z.; Yan, M.; Zhang, Y.; Sun, D. Performance Evaluation and Engineering Verification of Machine Learning Based Prediction Models for Slope Stability. Appl. Sci. 2022, 12, 7890. [Google Scholar] [CrossRef]
- Qi, C.; Tang, X. Slope stability prediction using integrated metaheuristic and machine learning approaches: A comparative study. Comput. Ind. Eng. 2018, 118, 112–122. [Google Scholar] [CrossRef]
- He, X.; Xu, H.; Sabetamal, H.; Sheng, D. Machine learning aided stochastic reliability analysis of spatially variable slopes. Comput. Geotech. 2020, 126, 103711. [Google Scholar] [CrossRef]
- Wang, Y.; Imai, K.; Miyashita, T.; Ariyoshi, K.; Takahashi, N.; Satake, K. Coastal tsunami prediction in Tohoku region, Japan, based on S-net observations using artificial neural network. Earth Planets Space 2023, 75, 154. [Google Scholar] [CrossRef]
- Chakraborty, R.; Dey, A. Probabilistic slope stability analysis: State-of-the-art review and future prospects. Innov. Infrastruct. Solut. 2022, 7, 177. [Google Scholar] [CrossRef]
- Chuaiwate, P.; Jaritngam, S.; Panedpojaman, P.; Konkong, N. Probabilistic Analysis of Slope against Uncertain Soil Parameters. Sustainability 2022, 14, 14530. [Google Scholar] [CrossRef]
- Sharma, R.K. Reliability Analysis of Slope Stability Using Monte Carlo Simulation and Comparison with Deterministic Analysis; Elsevier: Amsterdam, The Netherlands, 2000. [Google Scholar]
- Mahdiyar, A.; Hasanipanah, M.; Armaghani, D.J.; Gordan, B.; Abdullah, A.; Arab, H.; Majid, M.Z.A. A Monte Carlo technique in safety assessment of slope under seismic condition. Eng. Comput. 2017, 33, 807–817. [Google Scholar] [CrossRef]
- Wang, Y.; Cao, Z.; Au, S.-K. Practical reliability analysis of slope stability by advanced Monte Carlo simulations in a spreadsheet. Can. Geotech. J. 2011, 48, 162–172. [Google Scholar] [CrossRef]
- Alitabar, A.; Noorzad, R.; Qolinia, A. Evaluation of the Instability Risk of the Dam Slopes Simulated with Monte Carlo method (Case Study: Alborz Dam). Geotech. Geol. Eng. 2021, 39, 4237–4251. [Google Scholar] [CrossRef]
- Rahman, N.U.A. Investigation on Slope Stability Using Monte Carlo Simulation: A Case Study of Ulu Jelai Hydroelectric Project Slope Parameters & Design Concept. Mater. Today 2019, 19, 1216–1224. [Google Scholar] [CrossRef]
- Cho, S.E. Probabilistic Assessment of Slope Stability That Considers the Spatial Variability of Soil Properties. J. Geotech. Geoenvironmental Eng. 2010, 136, 975–984. [Google Scholar] [CrossRef]
- Zhang, W.; Gu, X.; Han, L.; Wu, J.; Xiao, Z.; Liu, M.; Wang, L. A short review of probabilistic slope stability analysis considering spatial variability of geomaterial parameters. Innov. Infrastruct. Solutions 2022, 7, 249. [Google Scholar] [CrossRef]
- Srivastava, A.; Babu, G.S.; Haldar, S. Influence of spatial variability of permeability property on steady state seepage flow and slope stability analysis. Eng. Geol. 2010, 110, 93–101. [Google Scholar] [CrossRef]
- Cho, S.E. Effects of spatial variability of soil properties on slope stability. Eng. Geol. 2007, 92, 97–109. [Google Scholar] [CrossRef]
- Montoya-Araque, E.A.; Montoya-Noguera, S. Sensitivity Analysis of a Physically Based Model to Assess Rainfall-Triggered Shallow Landslides. Geotech. Geol. Eng. 2023, 41, 2797–2814. [Google Scholar] [CrossRef]
- Chakraborty, A.; Goswami, D. Prediction of slope stability using multiple linear regression (MLR) and artificial neural network (ANN). Arab. J. Geosci. 2017, 10, 385. [Google Scholar] [CrossRef]
- Fukuhara, M.; Uchimura, T.; Wang, L.; Tao, S.; Tang, J. Study on the Prediction of Slope Failure and Early Warning Thresholds Based on Model Tests. Geotechnics 2023, 4, 1–17. [Google Scholar] [CrossRef]
- Espinosa, F.S.A.; El Naggar, M.H. Parametric Study of Rainfall-Induced Instability in Fine-Grained Sandy Soil. Geotechnics 2024, 4, 1159–1174. [Google Scholar] [CrossRef]
- Kavvadas, M.; Karlaftis, M.; Fortsakis, P.; Stylianidi, E. Probabilistic analysis in slope stability. In Proceedings of the 17th International Conference on Soil Mechanics and Geotechnical Engineering: The Academia and Practice of Geotechnical Engineering, Alexandria, Egypt, 5–9 October 2009; pp. 1650–1653. [Google Scholar] [CrossRef]
- Wu, X.Z. Development of fragility functions for slope instability analysis: Fragility functions for slope instability analysis. Landslides 2015, 12, 165–175. [Google Scholar] [CrossRef]
- Cho, S.E. Failure distribution analysis of shallow landslides under rainfall infiltration based on fragility curves. Landslides 2020, 17, 79–91. [Google Scholar] [CrossRef]
- Rahardjo, H.; Ong, T.H.; Rezaur, R.B.; Leong, E.C. Factors Controlling Instability of Homogeneous Soil Slopes under Rainfall. J. Geotech. Geoenviron. Eng. 2007, 133, 1532–1543. [Google Scholar] [CrossRef]
- Martinović, K.; Reale, C.; Gavin, K. Fragility curves for rainfall-induced shallow landslides on transport networks. Can. Geotech. J. 2018, 55, 852–861. [Google Scholar] [CrossRef]
- Hu, H.; Bao, Y.; Han, X.; Wang, W. Non-parametric fragility curves for probabilistic risk assessment of rainfall-triggered landslides. Comput. Geotech. 2024, 173, 106546. [Google Scholar] [CrossRef]
- He, Z.; Huang, Y.; Li, Y.; Li, X. Probabilistic fragility assessment of slopes considering uncertainty associated with temporal patterns of rainfall intensity. Comput. Geotech. 2024, 173, 106534. [Google Scholar] [CrossRef]
- Dou, H.-Q.; Han, T.-C.; Gong, X.-N.; Zhang, J. Probabilistic slope stability analysis considering the variability of hydraulic conductivity under rainfall infiltration-redistribution conditions. Eng. Geol. 2014, 183, 1–13. [Google Scholar] [CrossRef]
- Rahardjo, H.; Lim, T.; Chang, M.; Fredlund, D. Shear-strength characteristics of a residual soil. Can. Geotech. J. 1995, 32, 60–77. [Google Scholar] [CrossRef]
- Farouk, A.; Lamboj, L.; Kos, J. Influence of Matric Suction on the Shear Strength Behaviour of Unsaturated Sand. Acta Polytechnica 2004, 44. [Google Scholar] [CrossRef] [PubMed]
- Jigheh, H.S.; Rasulifard, A. Assessing the Potential Improvement of Fine-grained Clayey Soils by Plastic Wastes. Soils Rocks 2016, 39, 333–339. [Google Scholar] [CrossRef]
- Yamin, M.; Attom, M.F.; Atabay, S.; Vandanapu, R. The Effect of Compaction Effort on Shear Strength Parameters of Low/High Plasticity Clay Soils. Geotech. Eng. J. SEAGS AGSSEA 2021, 52, 1–8. [Google Scholar]
- KKayabali, K.; Yilmaz, N.P.; Balci, M.C.; Yılmaz, D. An Attempt to Predict the Effective Angle of Internal Friction for Remolded Clayey Soils Using the Vane Shear Test: Some Important Implications. Arab. J. Sci. Eng. 2024, 49, 5639–5651. [Google Scholar] [CrossRef]
- Lukić, D. Friction Angle of Soil and Rock. In Contemporary Achievements in Civil Engineering; Gradevinski Fakultet Subotica/Faculty of Civil Engineering Subotica: Subotica, Serbia, 2018; pp. 349–357. [Google Scholar] [CrossRef]
- Yang, Z.; Xu, Z.; Qin, X.; Cai, G.; Ling, X.; Shi, W. Evaluation of correlation between plasticity indicator and residual friction angle of fine-grained soils based on the flow index. Bull. Eng. Geol. Environ. 2024, 83, 52. [Google Scholar] [CrossRef]
- Vanapalli, S.K.; Fredlund, D.G.; Pufahl, D.E.; Clifton, A.W. Model for the prediction of shear strength with respect to soil suction. Can. Geotech. J. 1996, 33, 379–392. [Google Scholar] [CrossRef]
- Razeghi, H.R.; Ensani, A. Clayey Sand Soil Interactions with Geogrids and Geotextiles Using Large-Scale Direct Shear Tests. Int. J. Geosynth. Ground Eng. 2023, 9, 24. [Google Scholar] [CrossRef]
- Fredlund, D.; Xing, A. Equations for the soil-water characteristic curve. Can. Geotech. J. 1994, 31, 521–532. [Google Scholar] [CrossRef]
- Leong, E.C.; Rahardjo, H. Review of soil-water characteristic curve equations. J. Geotech. Geoenviron. Eng. 1997, 123, 1106–1117. [Google Scholar] [CrossRef]
- Leong, E.C.; Rahardjo, H. Permeability functions for unsaturated soils. J. Geotech. Geoenviron. Eng. 1997, 123, 1118–1126. [Google Scholar] [CrossRef]
- GEO-SLOPE International Ltd., SLOPE/W for Stability Modeling: User’s Guide 2021, Seequent Limited, Calgary, Alberta, Canada: 8. Available online: https://www.geo-slope.com (accessed on 11 November 2024).
- Spencer, E. A method of analysis of the stability of embankments assuming parallel inter-slice forces. Geotechnique 1967, 17, 11–26. [Google Scholar] [CrossRef]
- Paswan, A.P.; Shrivastava, A. Modelling of rainfall-induced landslide: A threshold-based approach. Arab. J. Geosci. 2022, 15, 795. [Google Scholar] [CrossRef]
- Lee, K.; Suk, J.; Kim, H.; Jeong, S. Modeling of rainfall-induced landslides using a full-scale flume test. Landslides 2021, 18, 1153–1162. [Google Scholar] [CrossRef]
- Matziaris, V.; Marshall, A.M.; Heron, C.M.; Yu, H.S. Centrifuge model study of thresholds for rainfall-induced landslides in sandy slopes. In IOP Conference Series: Earth and Environmental Science; Institute of Physics Publishing: Bristol, UK, 2015. [Google Scholar] [CrossRef]
- Kim, J.; Kim, Y.; Jeong, S.; Hong, M. Rainfall-induced landslides by deficit field matric suction in unsaturated soil slopes. Environ. Earth Sci. 2017, 76, 808. [Google Scholar] [CrossRef]
- Liu, Y.; Tian, G.; Wang, S.; Satyanaga, A.; Zhai, Q. Parametric Analysis of Rainfall-Induced Loess Soil Slope Due to the Rainwater Infiltration. Urban. Sci. 2022, 6, 54. [Google Scholar] [CrossRef]
- Oh, S.; Lu, N. Slope stability analysis under unsaturated conditions: Case studies of rainfall-induced failure of cut slopes. Eng. Geol. 2015, 184, 96–103. [Google Scholar] [CrossRef]
- Rahardjo, H.; Lee, T.T.; Leong, E.C.; Rezaur, R.B. Response of a residual soil slope to rainfall. Can. Geotech. J. 2005, 42, 340–351. [Google Scholar] [CrossRef]
- Dhanai, P.; Singh, V.P.; Soni, P. Rainfall Triggered Slope Instability Analysis with Changing Climate. Indian. Geotech. J. 2022, 52, 477–492. [Google Scholar] [CrossRef]
- Yan, G.; Li, Z.; Torres, S.A.G.; Scheuermann, A.; Li, L. Transient Two-Phase Flow in Porous Media: A Literature Review and Engineering Application in Geotechnics. Geotechnics 2022, 2, 32–90. [Google Scholar] [CrossRef]
- Tohari, A.; Nishigaki, M.; Komatsu, M. Laboratory Rainfall-Induced Slope Failure with Moisture Content Measurement. J. Geotech. Geoenviron. Eng. 2007, 133, 575–587. [Google Scholar] [CrossRef]
- Wu, L.Z.; Huang, R.Q.; Xu, Q.; Zhang, L.M.; Li, H.L. Analysis of physical testing of rainfall-induced soil slope failures. Environ. Earth Sci. 2015, 73, 8519–8531. [Google Scholar] [CrossRef]
- Krisnanto, S.; Rahardjo, H. Characteristics of rainfall-induced slope instability in Cisokan Region, Indonesia. J. Eng. Technol. Sci. 2021, 53, 210504. [Google Scholar] [CrossRef]
- Yubonchit, S.; Chinkulkijniwat, A.; Horpibulsuk, S.; Jothityangkoon, C.; Arulrajah, A.; Suddeepong, A. Influence Factors Involving Rainfall-Induced Shallow Slope Failure: Numerical Study. Int. J. Geomech. 2017, 17, 04016158. [Google Scholar] [CrossRef]
- Wang, S.; Idinger, G.; Wu, W. Centrifuge modelling of rainfall-induced slope failure in variably saturated soil. Acta Geotech. 2021, 16, 2899–2916. [Google Scholar] [CrossRef]
- Askarinejad, A.; Akca, D.; Springman, S.M. Precursors of instability in a natural slope due to rainfall: A full-scale experiment. Landslides 2018, 15, 1745–1759. [Google Scholar] [CrossRef]
- Hung, W.-Y.; Tran, M.-C.; Yeh, F.-H.; Lu, C.-W.; Ge, L. Centrifuge modeling of failure behaviors of sandy slope caused by gravity, rainfall, and base shaking. Eng. Geol. 2020, 271, 105609. [Google Scholar] [CrossRef]
- Rahardjo, H.; Leong, E.C.; Deutscher, M.S.; Gasmo, J.M.; Tang, S.K. Rainfall-Induced Slope Failures. 2000. Available online: https://dr.ntu.edu.sg (accessed on 7 April 2025).
- Ling, H.; Ling, H.I.; Asce, M. Centrifuge Model Simulations of Rainfall-Induced Slope Instability. J. Geotech. Geoenviron. Eng. 2012, 138, 1151–1157. [Google Scholar] [CrossRef]
- Sorbino, G.; Nicotera, M.V. Unsaturated soil mechanics in rainfall-induced flow landslides. Eng. Geol. 2013, 165, 105–132. [Google Scholar] [CrossRef]
- Wu, L.; Zhou, Y.; Sun, P.; Shi, J.; Liu, G.; Bai, L. Laboratory characterization of rainfall-induced loess slope failure. Catena 2017, 150, 1–8. [Google Scholar] [CrossRef]
- Sagitaningrum, F.H.; Bahsan, E. Parametric study on the effect of rainfall pattern to slope stability. In MATEC Web of Conferences; EDP Sciences: Les Ulis, France, 2017. [Google Scholar] [CrossRef]
- Özçelik, F.V.; Selçuk, M.E. Parametric Analysis of Factors that Affects the Rainfall Induced Slope Stability. Turk. J. Geosci. 2022, 3, 49–57. [Google Scholar] [CrossRef]
- Mburu, J.W.; Li, A.-J.; Lin, H.-D.; Lu, C.-W. Investigations of Unsaturated Slopes Subjected to Rainfall Infiltration Using Numerical Approaches—A Parametric Study and Comparative Review. Sustainability 2022, 14, 14465. [Google Scholar] [CrossRef]
- World Meteorological Organization (WMO). Guide to Instruments and Methods of Observation Volume I—Measurement of Meteorological Variables, Vol. 1. WMO, 2023. Available online: https://library.wmo.int/idurl/4/68695 (accessed on 18 October 2024).
- Igwe, O.; Mode, W.; Nnebedum, O.; Okonkwo, I.; Oha, I. The analysis of rainfall-induced slope failures at Iva Valley area of Enugu State, Nigeria. Environ. Earth Sci. 2014, 71, 2465–2480. [Google Scholar] [CrossRef]
- Liao, W.; Ji, J. Time-dependent reliability analysis of rainfall-induced shallow landslides considering spatial variability of soil permeability. Comput. Geotech. 2021, 129, 103903. [Google Scholar] [CrossRef]
- Collins, B.D.; Asce, S.M.; Znidarcic, D.; Asce, M. Stability Analyses of Rainfall Induced Landslides. J. Geotech. Geoenviron. Eng. 2004, 130, 362–372. [Google Scholar] [CrossRef]
- Cai, F.; Ugai, K. Numerical Analysis of Rainfall Effects on Slope Stability. Int. J. Géoméch. 2004, 4, 69–78. [Google Scholar] [CrossRef]
- Zhang, L.L.; Zhang, J.; Zhang, L.M.; Tang, W.H. Stability analysis of rainfall induced slope failure: A review. Proc. Inst. Civ. Eng. Geotech. Eng. 2011, 164, 299–316. [Google Scholar] [CrossRef]
- Zhao, X.; Sun, Y.; Feng, Q. Analysis on the influence of heavy rainfall on slope stability. In IOP Conference Series: Earth and Environmental Science; Institute of Physics Publishing: Bristol, UK, 2018. [Google Scholar] [CrossRef]
- Caine, N. The Rainfall Intensity: Duration Control of Shallow Landslides and Debris Flows. Geogr. Ann. Ser. A Phys. Geogr. 1980, 62, 3–27. [Google Scholar]
- Ng, C.W.W.; Shi, Q. Influence of Rainfall Intensity and Duration on Slope Stability in Unsaturated Soils 1998. Available online: https://www.lyellcollection.org (accessed on 7 April 2025).
- Tsutsumi, D.; Fujita, M. Relative importance of slope material properties and timing of rainfall for the occurrence of landslides. Int. J. Eros. Control. Eng. 2008, 1, 79–89. [Google Scholar] [CrossRef][Green Version]

| Variables of Soil Parameters | |||||
|---|---|---|---|---|---|
| Parameter | Mean | Standard Dev. | COV | Distribution | Range |
| Unit weight | 17 kN/m3 | 1.5 kN/m3 | 0.088 | Normal | 14–20 kN/m3 |
| Cohesion (c′) | 20 kPa | 5 kPa | 0.25 | Normal | 10–30 kPa |
| Friction angle (ϕ′) | 10° | 2.5° | 0.25 | Normal | 5–15° |
| Fine-Grained Clayey Soil | SWCC | Hydraulic Conductivity | ||||
| a(kPa) | m | n | θs | ks (m/s) | p | |
| 100 | 1 | 1 | 0.45 | 1 × 10−6 | 4 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Espinosa Fuentes, S.A.; El Naggar, M.H. Uncertainty Analysis and Quantification of Rainfall-Induced Slope Instability in Fine-Grained Clayey Soils. Geotechnics 2025, 5, 31. https://doi.org/10.3390/geotechnics5020031
Espinosa Fuentes SA, El Naggar MH. Uncertainty Analysis and Quantification of Rainfall-Induced Slope Instability in Fine-Grained Clayey Soils. Geotechnics. 2025; 5(2):31. https://doi.org/10.3390/geotechnics5020031
Chicago/Turabian StyleEspinosa Fuentes, Samuel A., and M. Hesham El Naggar. 2025. "Uncertainty Analysis and Quantification of Rainfall-Induced Slope Instability in Fine-Grained Clayey Soils" Geotechnics 5, no. 2: 31. https://doi.org/10.3390/geotechnics5020031
APA StyleEspinosa Fuentes, S. A., & El Naggar, M. H. (2025). Uncertainty Analysis and Quantification of Rainfall-Induced Slope Instability in Fine-Grained Clayey Soils. Geotechnics, 5(2), 31. https://doi.org/10.3390/geotechnics5020031






