Abstract
The fracture network largely determines the efficiency of heat extraction from fractured geothermal reservoirs. Fracture openings are influenced by thermo-poroelastic stresses during cold fluid flow, with the interplay between fracture length and fracture opening regulating heat transfer. The lack of field data concerning fluctuating fracture openings underscores the necessity for computational models. This work emphasizes the impact of such gaps in the literature. Factors such as temperature, pressure, stress, thermal breakthrough time, and cumulative energy are evaluated to analyze the system’s behavior. A sensitivity analysis is employed to ascertain the significance of stress on fracture opening, compared with thermo-hydraulic behavior. The results show that stress field alterations, due to intersections with minor fractures, can cause up to a 15% variation in the largest fracture’s opening. The impact of thermoelastic stress outweighs the impact of poroelastic stress approximately threefold. Such stress-induced variations in fracture openings can lead to an up to 30% increase in cumulative heat extraction, while the drop in production temperature is limited to around 50%.
1. Introduction
The characterization of geothermal reservoirs has emerged as a pivotal endeavor for the comprehensive evaluation of the potential for harnessing the renewable geothermal energy from any specified field. This endeavor is underpinned by the aspiration to unveil the prospective geothermal resources concealed beneath the Earth’s surface. Within the structured framework of the EU-H2020 funded MEET (Multidisciplinary and multi-context Engagement for Enabling geothermal Technology) project, an extensive corpus of data, elucidating varying fracture properties, was collected from a set of geographically diverse locales, encompassing Göttingen, Havelange, Cornwall, the arid terrain of Death Valley, and Soultz-sous-Forets [1,2,3,4,5,6,7]. An observation about this data corpus was the discernible variability in the fracture aperture and its potential correlative relationship with the overarching fracture length. This observation furnishes a nuanced understanding of the fracture dynamics that are intrinsic to geothermal reservoirs. Nonetheless, empirically monitoring this intricate dependency in real-world field settings during the course of geothermal operations presents itself as a significant challenge, warranting attention and innovative solutions. From an empirical vantage point, the daunting task of replicating the in situ conditions of geothermal fields within the controlled confines of a laboratory, and furthermore, conducting precise and comprehensive measurements for a discrete fracture network, emerges as a formidable task, replete with inherent complexities. The objective of emulating the natural geological and fracture dynamics is crucial for the deeper comprehension and accurate characterization of geothermal reservoirs. Historically, the realm of numerical simulations has employed a robust statistical methodology as a navigational tool to traverse this complex issue, thereby furnishing a semblance of understanding pertaining to fracture dynamics and associated geothermal reservoir characteristics [8,9,10,11,12]. However, notwithstanding these historical endeavors, the statistical simulations crafted through the MEET project were adjudged to be insufficient in encapsulating the real-world dynamics with precision. This conclusion germinated from the divergence observed between the operational data harvested from Soultz-sous-Forets, the hydraulic stimulation data accrued from Cornwall, and the theoretical production rates that were gleaned from the rigorous numerical simulations. These simulations were predicated on a stochastically generated fracture network, intricately constructed from the measured field data amassed during the investigative endeavor [13]. This scenario underscores the exigent necessity for further research and innovative methodologies to bridge the apparent chasm between the theoretical simulations and the empirical operational data, thereby bolstering the accuracy and reliability of the geothermal reservoir characterizations, which are imperative for the sustainable exploitation of geothermal resources.
Fractures indisputably constitute the principal conduits for fluid flow within the confines of heat-containing rock formations characterized by their inherently low permeability, which is a fundamental aspect governing the efficacious exploitation of subsurface resources [14,15]. Therefore, in a bid to markedly enhance the veracity and predictive capability of numerical models, and to judiciously inform the design and execution of future field measurement campaigns, it becomes quintessentially imperative to ascertain the multifaceted impact exerted by the synergistic interplay of fully coupled thermo-poroelastic processes on the morphological attributes of fracture aperture within a discretely fractured reservoir. The epoch of contemporary technological advancements has bequeathed upon the scientific community an array of sophisticated field measurement techniques. These encompass stress field measurement methodologies, comprehensive fracture network topology analyses, and the real-time acquisition of temperature and pressure data. Such technological boons are capable of furnishing the requisite input parameters, which are indispensable for the formulation of robust fully coupled thermo-hydro-mechanical (THM) numerical models, which embody the precision required when simulating the complex subsurface processes. In the context of discrete fracture network (DFN) simulations, the recent advancements in this realm have unfurled a treasure trove of invaluable information. This information, being of seminal importance, harbors the potential to significantly impact both the technical and economic dimensions of geothermal operations, thereby acting as a catalyst in optimizing exploitation strategies [16]. In order to precisely predict the dynamic behavior that manifests in a geothermal reservoir, it is of paramount importance that the DFN is seamlessly incorporated within the THM framework. Such an integration is instrumental in enabling the appropriate consideration of the inherent variability exhibited in fracture apertures which is fundamental to understanding fluid flow and heat transfer dynamics within fractured geothermal reservoirs. The outcomes engendered by this study transcend the boundaries of geothermal energy exploitation and hold profound implications for a spectrum of subsurface resource management endeavors. These include the environmentally critical domain of CO2 geosequestration [17], the intricate and highly regulated realm of subsurface nuclear waste disposal [18,19], and the economically significant sector of hydrocarbon reservoir management [20]. Each of these domains, being of paramount importance, necessitates a thorough understanding of fracture dynamics and the associated thermo-hydro-mechanical processes to ensure the sustainable and safe exploitation of subsurface resources.
Despite the potential benefits, lab experiments to investigate single fracture flow coupled with THM modeling are limited, due to the restrictive nature of in situ conditions and measurements. Numerical simulations are typically designed to mimic these experimental results. A similar single fracture concept is broadly utilized between the injection and production wells for field applications. However, recent advancements in computational tools have enabled us to examine the THM process on a DFN. As a result, the need for multiphysics simulators has grown, in order to bridge the gap between complex geological settings and numerical simulations [21].
The scholarly literature methodically categorizes the impact of THM processes on fracture apertures into three distinct echelons: (a) an examination of the stress effect on a singular fracture system, (b) positing a constant aperture for a DFN that remains impervious to the distribution of stress, and (c) architecting a THM model for a system characterized by a uniform fracture aperture across all fractures embodied in a DFN, whilst eschewing the correlation between fracture aperture and length. This triadic categorization elucidates the multifarious dimensions of the THM process’ impact on fracture aperture dynamics. De Dreuzy et al. embarked on an in-depth exploration of a single fracture system in three dimensions (3D), accentuating the heterogeneity inherent in fracture apertures [8]. Their seminal work laid the foundation for unraveling the complex interplay between stress and the fracture aperture. Subsequent scholarly endeavors delved into the efficacy of heat extraction within a tri-dimensional THM framework, meticulously analyzing the variations in fracture apertures and thereby contributing to a nuanced understanding of the THM processes in geothermal systems [22,23]. Salimzadeh et al. [24] conducted a scrupulous examination of the fluctuations in fracture apertures, engendered by thermo-poroelastic stress on heat extraction within a 3D system, forging a linkage between the injection and production wells. Their study illuminated the critical role of thermo-poroelastic stresses in dictating the efficacy of geothermal energy extraction. Vik et al. [25] extended this methodological approach to a dual parallel fracture system to scrutinize the evolution of the stress field transiting from one fracture to another, thereby broadening the scope of understanding of the stress dynamics in DFNs. Furthermore, Li et al. [26] orchestrated the development of a THM model endowed with constant and heterogeneous apertures, devoid of a correlation with fracture length, to simulate heat extraction from geothermal systems by employing a spectrum of working fluids. Their work underscored the potential for optimizing geothermal energy extraction through a nuanced understanding of fracture aperture dynamics. Zhang et al. [27] adopted a stochastic methodology to generate fracture networks for modeling geothermal energy extraction, utilizing the THM process with a fixed fracture aperture for all the fractures. However, a notable lacuna in their model was the lack of accounting for alterations in fracture aperture engendered by the THM process. Aliyu and Archer [28] simulated the THM process for a conceptual DFN, wherein all fractures were parallel and the impact of stress alteration at the fracture intersection point was disregarded, thus providing insights into the behavior of parallel fracture networks under THM processes. Additionally, Zhao et al. proffered an optimization scale for an enhanced geothermal system (EGS) with a consideration of heterogeneity in fracture apertures, thereby contributing to the ongoing discourse on optimizing geothermal energy extraction [29]. Through the array of studies delineated herein, the scientific community is gradually inching towards a more comprehensive and nuanced understanding of the THM processes and their impact on fracture aperture dynamics, which is quintessential for the optimization of geothermal energy extraction and the advancement of geothermal technology.
Preceding endeavors within this domain have predominantly assumed a constant aperture for all fractures encompassed within a discrete fracture network (DFN), principally due to limited field and experimental data. This assumption, albeit convenient for simplifying the analysis, may inadvertently obfuscate the nuanced dynamics intrinsic to fracture interactions and their consequential impact on geothermal energy extraction. Nonetheless, gleanings from observations at outcrop or wellbore locales intriguingly indicate the potential existence of a correlative relationship between a fracture’s length and its corresponding aperture. This insightful revelation beckons a deeper delve to unravel the ramifications of this relationship on the efficacy of heat extraction, a pivotal aspect for the advancement of geothermal technology. To robustly illuminate the effect of this potentially consequential relationship on the efficiency of heat extraction, we embarked on conducting rigorous numerical simulations in a fully coupled THM manner. In this framework, the fracture aperture is governed by the dynamics of thermo-poroelastic stress, thereby embodying a more realistic representation of the fracture dynamics. This analytical paradigm endeavors to bridge the gap between simplistic assumptions and complex real-world geothermal reservoir behavior. Furthermore, complementing our numerical exploration, we conducted experimental measurements to ascertain the thermal expansion coefficient—a paramount factor instrumental in dictating the evolution of thermo-poroelastic stress within the fracture network. The thermal expansion coefficient is a crucial parameter that intricately influences thermo-poroelastic stress, and by extension, the apertures of fractures within the geothermal reservoir. This experimental venture was geared towards acquiring a precise quantification of this coefficient, which is pivotal for enhancing the accuracy and reliability of our numerical simulations. Subsequent to obtaining the thermal expansion coefficient, we assessed the temperature-dependent impact of this coefficient on the overarching process, through numerical simulation. This assessment was crafted to unveil the nuanced temperature-induced variations in the thermal expansion coefficient and their consequential impact on the thermo-poroelastic stress and fracture aperture dynamics. Through this integrative numerical and experimental methodology, we aimed to foster a holistic understanding of the interplay between fracture length, aperture, and thermo-poroelastic stress, and their collective impact on the efficiency of heat extraction from geothermal reservoirs. This endeavor not only augments our comprehension of geothermal reservoir dynamics but also significantly contributes to the ongoing discourse on optimizing geothermal energy extraction methodologies.
2. Methodology
The discrete fracture network consists 100 fractures which is taken from an outcrop in Otsego County in New York, NY, USA [30,31] as black lines in Figure 1. The size of the geometry is 1000 × 600 m in a two-dimensional domain, where the coordinates of the injection well are 200 m × 300 m (blue circle) and those of the production well are 800 m × 300 m (red circle). Injection and production wellbore radii are 0.2 m. Fracture apertures are assigned based on three functions of fracture lengths. For the sake of consistency between different cases, a constant value of for these three cases was used and the results are shown in Figure 2. For rock, the permeability is 10 mD, porosity is 10%, density is 2700 kg/m3, Poisson’s ratio is 0.25, Young’s modulus is 40 GPa, thermal conductivity is 3 W/mK, specific heat capacity is 1000 J/kgK, and the Biot coefficient is 0.7. The thermal expansion coefficient is assumed to be a constant throughout the numerical simulation, as its magnitude is 8 × 10−6 1/K. Outer boundaries include no flow for the fluid and heat transfer. The domain boundaries are restricted for displacement. Fifty MPa is used as the boundary stress for the two horizontal stress components. The assumed depth of this cross-sectional plane is 3 km. The initial pressure of the system is 30 MPa, and we injected the fluid at 50 MPa through the injection wellbore. The initial domain temperature is 150 °C and the water is injected for five years at 50 °C. The production wellbore is constrained based on the constant downhole production pressure of 30 MPa.
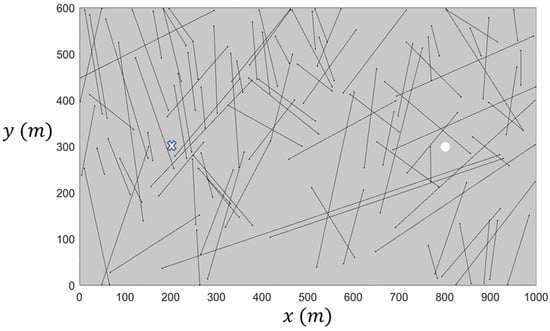
Figure 1.
Geometry of the fracture map used in this study. The cross is the injection well location and the circle is the production well location (well dimensions are not to the scale).
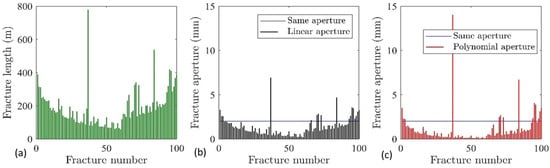
Figure 2.
(a) Fracture length, (b) fracture aperture distribution comparing the linear function and same aperture, and (c) fracture aperture distribution comparing the polynomial function and same aperture. The functions are explained by Equations (2) and (3).
Mass, momentum, and energy conservation equations are fully coupled with thermoelastic and poroelastic stresses through the finite element modeling approach, which showed its potential for similar coupling problems [32,33]. These equations are solved in COMSOL Multiphysics [34]. A local thermal non-equilibrium is adopted to model the heat exchange between the rock matrix and water, as the local thermal equilibrium model underestimates the fluid production rate [35]. Fluid flow along the fracture width is ignored to compensate for the ratio of fracture length to fracture aperture. A linear elastic model and plain strain formulation are used to simulate the geomechanical process. The water properties are dynamic functions of temperature. Based on these functions, water density, viscosity, thermal conductivity, and specific heat capacity are updated throughout the simulation process. The governing equation and the thermophysical properties equation details are presented elsewhere [15,31]. The fracture aperture () relationship with the normal stress () is defined by the following equation, adopted from Barton and Bandis’ model [36,37]:
In the above equation, the reference normal stress is considered as = 150 MPa. Here, is used as a coefficient to control the fracture aperture’s sensitivity to stress; = 0, 1, 2 and 3 are used to perform the sensitivity analysis. stands for the initial aperture of the fracture. Three types of fracture aperture variation results are shown in Figure 2. The first function is the same aperture for all fractures ( is same for all fractures as 2 mm). The second model has a linear function of the deviation of each fracture aperture from that fracture’s length (fracture aperture, , where is the fracture length, see Equation (2)). The third model has a polynomial function in which the fracture’s aperture is correlated with the fracture’s length to the power of two(fracture aperture, ∝ , see Equation (3)). The mesh contains 74,195 domain elements and 4498 boundary elements and the total number of degrees of freedom is 1,051,050. The backward differential formula is used with an absolute tolerance value for convergence as 10−8, and automatic time stepping is adopted. The THM process is validated against Bai [38] in the previous work [39].
As mentioned earlier, and are coefficients, which are selected in a way that is same for all three cases. In Equations (2) and (3), the subscript i shows the order of the fractures.
3. Results and Discussions
Considering a network of 100 fractures in a two-dimensional domain, the effects of fracture aperture changes, governed by the fully coupled thermos-poroelastic stress on the heat extraction, using water as the working fluid, are examined. Three functions are considered for the fracture aperture: a single constant aperture value, a linear function, and a polynomial function. Due to the absence of a connected fracture pathway between the injection and production well, the injected fluid front finds the pathway that has better connectivity to the production well, avoiding the alternate fracture network (see Figure 3a). The pressure development is restricted near the wellbore zones (Figure 3b). The cold front propagates in a wider region compared to the pressure development, as seen in Figure 3a,b. A comparison of the stress field component in the direction () with the temperature and pressure evolution indicate that the temperature has a higher resemblance with the stress across the domain (see Figure 3c). With the progress towards the production well, the water viscosity increases, eventually reducing the mass flux (Figure 3d).
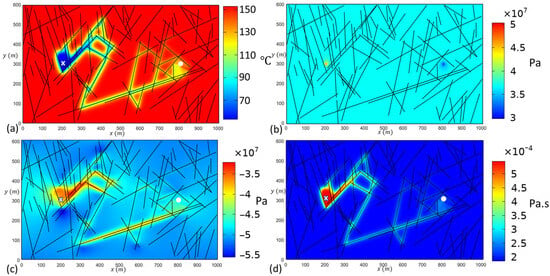
Figure 3.
Distribution of (a) temperature, (b) pressure, (c) stress, and (d) viscosity of water for the case of the same opening fracture with a stress contribution level of three () after 5 years of injection.
To understand the behavior of fracture openings due to temperature, pressure, stress reorientation, and the thermodynamic properties of water, the largest fracture in the system is considered, and the impact of its intersections with small fractures is analyzed too. Figure 4a shows the temperature variation along the longest fracture, where the convective heat transfer is dominant, and the temperature gradient is towards the production well. Considering the cold fluid intersection with this fracture (≈100 m), the zone behind this intersection remains at a high temperature. However, for the pressure, due to the high permeability of the fractured zone, the pressure remains constant along the fracture (see Figure 4b). As time progresses, the viscosity increases, due to the temperature reduction, and it restricts the fluid flow inside the fracture, despite the fact that the fracture aperture increases (see Figure 4d). In the left part of the fracture, where temperature is constant, this is primarily controlled by poroelastic behavior. The cold fluid front, entering into the fracture (≈100 m), is a combination of thermo and poroelastic stress behavior. Comparing the maximum stress with the stress resulting from poroelasticity in this zone indicates that the thermoelasticity has at least three times more impact than poroelasticity, considering the initial 100 m in Figure 4a from the left side where the temperature is not affected with the injection. However, the pressure is changed in comparison to the initial value and the fracture aperture increases from 4 mm to 4.1 mm due to the poroelasticity (aperture change is ). After this point and after entering the cold fluid, the fracture aperture jumped to more than 4.4 mm, resulting from the coupled impacts of the thermoelasticity and poroelasticity. By considering that the pressure gradient inside the fracture is negligible due to the high permeability, the poroelasticity impacts are almost constant along the fracture. Therefore, the thermoelasticity resulted in at least a 0.3 mm increase in the fracture aperture, which is at least three times higher than the poroelasticity impact. Without considering the intersection effects with small scale fractures, the expected outcome is that the stress field remains higher than the initial value, throughout the fracture, due to the lower temperature and higher pressure, in comparison with the initial state (see Figure 4a–c). Obviously, intersections with small scale fractures change the stress affecting the large scale fracture, and this results in oscillation along the fracture length (see Figure 4c). Equation (1) shows the relation between the fracture opening and normal stress acting on the fracture. Figure 4d show that the fracture aperture may change up to 15% in five years due to the small scale fracture intersections with the large scale fracture. As the large scale fracture with a higher opening is the main path for the fluid and heat transfer, the small scale fracture may restrict the greater relevance of previous expectations (namely, that there is a slow contribution in the fluid flow and that heat transfer is the higher conductive zone).
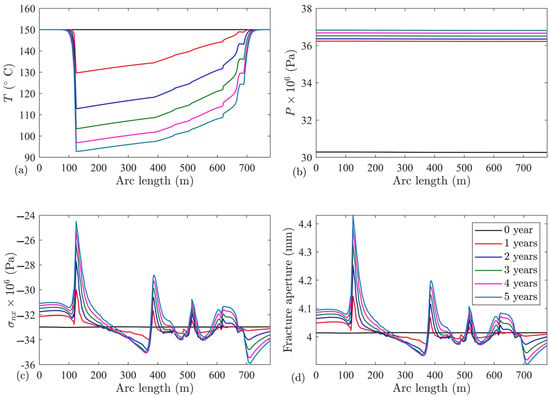
Figure 4.
(a) Temperature along the fracture length from left to right, (b) pressure, (c) normal stress acting on the fracture, and (d) fracture aperture for the longest available fracture for the case of the same opening fracture with stress contribution level of three () at different times.
A sensitivity analysis is performed to estimate the impact of fracture aperture variation on two key economic aspects involved in the energy extraction process: thermal breakthrough time and the cumulative heat extraction. By increasing the stress contribution to the process (resulting in a higher sensitivity of the fracture on the stress), the production fluid temperature would remain high as shown in Figure 5(a1–a3)). For the same aperture case, thermal breakthrough restriction may show more than 50% (instead of the decrease from 150 °C to 106 °C where = 0, temperature decreases from 150 °C to 129 °C where = 3), whereas for linear and polynomial functions it is ≈40% (instead of the decrease from 150 °C to 118 °C where = 0, temperature decreases from 150 °C to 102 °C where = 3) and ≈25% (instead of the decrease from 150 °C to 119 °C where = 0, temperature decreases from 150 °C to 109 °C where = 3), respectively, for five years of operation. In other words, thermal breakthrough receives the smallest stress impact on the polynomial function and obtains the highest effect for the same size aperture. A similar behavior is observed for cumulative energy extraction, where the same size fracture aperture shows a higher dependency on stress, resulting in ≈30% (instead of the cumulative heat extraction of ≈2450 TJ where = 0, it increases up to ≈3200 TJ when = 3) higher cumulative energy extraction (see Figure 5(b1–b3)). On the other hand, polynomial and linear fracture aperture functions show 16% (instead of the cumulative heat extraction of ≈2480 TJ where = 0, it increases up to ≈2850 TJ when = 3) and 31% (instead of the cumulative heat extraction of ≈2250 TJ where = 0, it increases up to ≈2900 TJ when = 3) higher cumulative energy extraction, respectively. Higher energy extraction happens for the same size aperture, and again it confirms the importance of small scale fractures; as for other two functions, the small scale fracture has a lower aperture.
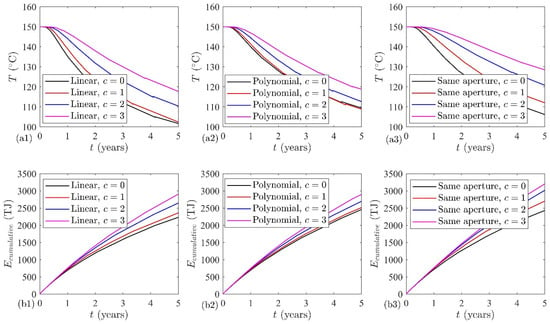
Figure 5.
Sensitivity of production temperature for (a1) linear function, (a2) polynomial function, (a3) same aperture, and cumulative energy extraction for (b1) linear function, (b2) polynomial function, (b3) same aperture regarding the stress field impact on the fracture aperture.
Our analysis so far reveals that thermoelasticity is an important factor for the production fluid temperature, which is primarily controlled by the thermal expansion coefficient (). During this study, a constant thermal expansion coefficient is considered. To examine this assumption, thermal expansion coefficients are measured experimentally using a dilatometer for two different sandstone rock samples, Remlinger and Flechtinger, as shown in Figure 6a. Figure 6a shows that the thermal expansion coefficient is an increasing function of temperature in all three directions. The average value of the measured data is used to define . To understand the temperature dependency of on the final fluid production temperature, two cases of linear fracture opening function and are compared: (a) = 10.47 × 10−6 1/°C, measured at the mean temperature of 50 and 150 °C, and (b) , for temperatures of 50–150 °C. Figure 6b shows that the production temperature changes negligibly for a temperature-dependent thermal expansion coefficient function (less than 1 °C) for the examined rock samples. It seems that one measurement at the average temperature is enough to perform the numerical simulation.
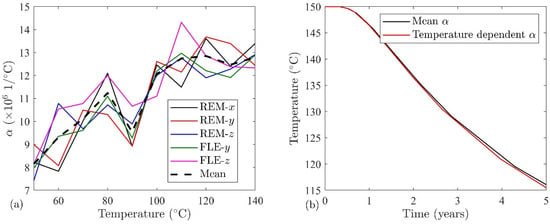
Figure 6.
(a) Thermal expansion coefficient (α) variation with temperature for two different sandstone samples (Remlinger (REM) and Flechtinger (FLE)) in and directions (b) temperature of the production well for two scenarios: average thermal expansion coefficient and temperature-dependent thermal expansion coefficient.
4. Conclusions
This study investigates the importance of the relationship between fracture length and opening as a missing gap from the data obtained from field studies. A fully coupled thermo-poroelastic model, used to identify and estimate the physical processes relating to the heat extraction from a fractured geothermal system, is developed. The relative importance of the thermoelasticity to the poroelasticity for the studied cases indicates almost a 3:1 impact on the normal stress acting on the fracture. The thermal expansion coefficient, as a controlling factor of the thermoelastic stress, is measured experimentally and its temperature dependency does not change the production well temperature. Therefore, a single value of the thermal expansion coefficient at the mean temperature accurately predicts the THM process. Furthermore, a single fracture study is not a good representation of the relationship between the fracture aperture and the stress field, because the stress field significantly changes at the intersection point of fractures. The small-scale fractures are the deciding factor in the energy extraction process and have no less importance than large-scale fractures. Therefore, considering an equivalent permeability field by ignoring small-scale fractures may result in significantly different outcomes, compared to a discretely fractured network model. The fracture aperture functions have ≈10% sensitivity among themselves, and the dependency of the fracture on the stress may result in up to 30% higher cumulative heat extraction. By increasing the impact of stress on the fracture aperture, the production temperature drop is restricted by ≈50%. Simulation results reveal that the fracture aperture’s dependency on fracture length is an important factor for heat extraction efficiency from the fractured geothermal systems; this missing factor in the literature requires future attention. Considering the same aperture results in the later thermal breakthrough would affect the techno-economic analysis, in comparison to the real field data. The possibility of a linear relationship between fracture aperture and fracture length eventuates in the lowest performance between the examined cases.
Author Contributions
Conceptualization, S.M. and M.S.; methodology, S.M. and M.S.; software, S.M. and M.S.; validation, S.M. and M.S. writing—original draft preparation, S.M. and M.S.; writing—review and editing, K.B.; visualization, S.M. and M.S.; supervision, K.B. and I.S.; project administration, K.B.; funding acquisition, K.B. All authors have read and agreed to the published version of the manuscript.
Funding
The work was conducted as part of the MEET project, which received funding from the European Union’s Horizon 2020 research and innovation programme, under grant agreement No. 792037. Authors have received support from the Group of Geothermal Science and Technology, Institute of Applied Geosciences, and Technische Universität Darmstadt.
Data Availability Statement
The data used for the thermal expansion coefficient in the study are available at TU Datalib via (Mahmoodpour et al., 4 November 2021) as open access.
Acknowledgments
The Group of Geothermal Science and Technology, Institute of Applied Geosciences, and Technische Universität Darmstadt provided institutional support to authors.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Dalmais, E.; Genter, A.; Trullenque, G.; Leoutre, E.; Leiss, B.; Wagner, B.; Mintsa, A.C.; Bär, K.; Rajsl, I. MEET Project: Toward the spreading of EGS across Europe. In Proceedings of the European Geothermal Congress, Den Haag, The Netherlands, 11–14 June 2019; pp. 11–14. [Google Scholar]
- Chabani, A.; Trullenque, G.; Ledésert, B.A.; Klee, J. Multiscale Characterization of Fracture Patterns: A Case Study of the Noble Hills Range (Death Valley, CA, USA), Application to Geothermal Reservoirs. Geosciences 2021, 11, 280. [Google Scholar] [CrossRef]
- Chabani, A.; Trullenque, G.; Klee, J.; Ledésert, B.A. Fracture Spacing Variability and the Distribution of Fracture Patterns in Granitic Geothermal Reservoir: A Case Study in the Noble Hills Range (Death Valley, CA, USA). Geosciences 2021, 11, 520. [Google Scholar] [CrossRef]
- Klee, J.; Potel, S.; Ledésert, B.A.; Hébert, R.L.; Chabani, A.; Barrier, P.; Trullenque, G. Fluid-Rock Interactions in a Paleo-Geothermal Reservoir (Noble Hills Granite, California, USA). Part 1: Granite Pervasive Alteration Processes away from Fracture Zones. Geosciences 2021, 11, 325. [Google Scholar] [CrossRef]
- Reinecker, J.; Gutmanis, J.; Foxford, A.; Cotton, L.; Dalby, C.; Law, R. Geothermal exploration and reservoir modelling of the United Downs deep geothermal project, Cornwall (UK). Geothermics 2021, 97, 102226. [Google Scholar] [CrossRef]
- Peacock, D.C.P.; Sanderson, D.J.; Leiss, B. Use of Mohr Diagrams to Predict Fracturing in a Potential Geothermal Reservoir. Geosciences 2021, 11, 501. [Google Scholar] [CrossRef]
- Baujard, C.; Rolin, P.; Dalmais, É.; Hehn, R.; Genter, A. Soultz-sous-Forêts Geothermal Reservoir: Structural Model Update and Thermo-Hydraulic Numerical Simulations Based on Three Years of Operation Data. Geosciences 2021, 11, 502. [Google Scholar] [CrossRef]
- De Dreuzy, J.R.; Méheust, Y.; Pichot, G. Influence of fracture scale heterogeneity on the flow properties of three-dimensional discrete fracture networks (DFN). J. Geophys. Res. Solid Earth 2012, 117, B11. [Google Scholar] [CrossRef]
- Frampton, A.; Hyman, J.D.; Zou, L. Advective transport in discrete fracture networks with connected and disconnected textures representing internal aperture variability. Water Resour. Res. 2019, 55, 5487–5501. [Google Scholar] [CrossRef]
- Makedonska, N.; Hyman, J.D.; Karra, S.; Painter, S.L.; Gable, C.W.; Viswanathan, H.S. Evaluating the effect of internal aperture variability on transport in kilometer scale discrete fracture networks. Adv. Water Resour. 2016, 94, 486–497. [Google Scholar] [CrossRef]
- Karra, S.; O’Malley, D.; Hyman, J.D.; Viswanathan, H.S.; Srinivasan, G. Modeling flow and transport in fracture networks using graphs. Phys. Rev. E 2018, 97, 033304. [Google Scholar] [CrossRef]
- Zou, L.; Cvetkovic, V. Inference of transmissivity in crystalline rock using flow logs under steady-state pumping: Impact of multiscale heterogeneity. Water Resour. Res. 2020, 56, e2020WR027254. [Google Scholar] [CrossRef]
- Mahmoodpour, S.; Singh, M.; Turan, A.; Bär, K.; Sass, I. Hydro-Thermal Modeling for Geothermal Energy Extraction from Soultz-sous-Forêts, France. Geosciences 2021, 11, 464. [Google Scholar] [CrossRef]
- Gao, X.; Li, T.; Zhang, Y.; Kong, X.; Meng, N. A Review of Simulation Models of Heat Extraction for a Geothermal Reservoir in an Enhanced Geothermal System. Energies 2022, 15, 7148. [Google Scholar] [CrossRef]
- Mahmoodpour, S.; Singh, M.; Turan, A.; Bär, K.; Sass, I. Simulations and global sensitivity analysis of the thermo-hydraulic-mechanical processes in a fractured geothermal reservoir. Energy 2022, 247, 123511. [Google Scholar] [CrossRef]
- Viswanathan, H.S.; Ajo-Franklin, J.; Birkholzer, J.; Carey, J.W.; Guglielmi, Y.; Hyman, J.D.; Karra, S.; Pyrak-Nolte, L.J.; Rajaram, H.; Srinivasan, G.; et al. From fluid flow to coupled processes in fractured rock: Recent advances and new frontiers. Rev. Geophys. 2021, 60, e2021RG000744. [Google Scholar] [CrossRef]
- Singh, M.; Tangirala, S.K.; Chaudhuri, A. Potential of CO2 based geothermal energy extraction from hot sedimentary and dry rock reservoirs, and enabling carbon geo-sequestration. Geomech. Geophys. Geo-Energy Geo-Resour. 2020, 6, 16. [Google Scholar] [CrossRef]
- Rutqvist, J.; Barr, D.; Birkholzer, J.T.; Fujisaki, K.; Kolditz, O.; Liu, Q.S.; Fujita, T.; Wang, W.; Zhang, C.Y. A comparative simulation study of coupled THM processes and their effect on fractured rock permeability around nuclear waste repositories. Environ. Geol. 2009, 57, 1347–1360. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, C.; Liu, Q.; Birkholzer, J. Multiple-point statistical prediction on fracture networks at Yucca Mountain. Environ. Geol. 2009, 57, 1361–1370. [Google Scholar] [CrossRef][Green Version]
- Hyman, J.D.; Jiménez-Martínez, J.; Viswanathan, H.S.; Carey, J.W.; Porter, M.L.; Rougier, E.; Karra, S.; Kang, Q.; Frash, L.; Chen, L.; et al. Understanding hydraulic fracturing: A multi-scale problem. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2016, 374, 20150426. [Google Scholar] [CrossRef]
- Hyman, J.D.; Sweeney, M.R.; Frash, L.P.; Carey, J.W.; Viswanathan, H.S. Scale-Bridging in Three-Dimensional Fracture Networks: Characterizing the Effects of Variable Fracture Apertures on Network-Scale Flow Channelization. Geophys. Res. Lett. 2021, 48, e2021GL094400. [Google Scholar] [CrossRef]
- Pandey, S.N.; Chaudhuri, A.; Kelkar, S. A coupled thermo-hydro-mechanical modeling of fracture aperture alteration and reservoir deformation during heat extraction from a geothermal reservoir. Geothermics 2017, 65, 17–31. [Google Scholar] [CrossRef]
- Guo, T.; Gong, F.; Wang, X.; Lin, Q.; Qu, Z.; Zhang, W. Performance of enhanced geothermal system (EGS) in fractured geothermal reservoirs with CO2 as working fluid. Appl. Therm. Eng. 2019, 152, 215–230. [Google Scholar] [CrossRef]
- Salimzadeh, S.; Nick, H.M.; Zimmerman, R.W. Thermoporoelastic effects during heat extraction from low-permeability reservoirs. Energy 2018, 142, 546–558. [Google Scholar] [CrossRef]
- Vik, H.S.; Salimzadeh, S.; Nick, H.M. Heat recovery from multiple-fracture enhanced geothermal systems: The effect of thermoelastic fracture interactions. Renew. Energy 2018, 121, 606–622. [Google Scholar]
- Li, J.; Sun, Z.; Zhang, Y.; Jiang, C.; Cherubini, C.; Scheuermann, A.; Torres, S.A.G.; Li, L. Investigations of heat extraction for water and CO2 flow based on the rough-walled discrete fracture network. Energy 2019, 189, 116184. [Google Scholar] [CrossRef]
- Zhang, W.; Qu, Z.; Guo, T.; Wang, Z. Study of the enhanced geothermal system (EGS) heat mining from variably fractured hot dry rock under thermal stress. Renew. Energy 2019, 143, 855–871. [Google Scholar] [CrossRef]
- Aliyu, M.D.; Archer, R.A. Numerical simulation of multifracture HDR geothermal reservoirs. Renew. Energy 2021, 164, 541–555. [Google Scholar] [CrossRef]
- Zhao, Y.; Shu, L.; Chen, S.; Zhao, J.; Guo, L. Optimization Design of Multi-Factor Combination for Power Generation from an Enhanced Geothermal System by Sensitivity Analysis and Orthogonal Test at Qiabuqia Geothermal Area. Sustainability 2022, 14, 7001. [Google Scholar] [CrossRef]
- Tran, N.H.; Chen, Z.; Rahman, S.S. Object-based global optimization in modeling discrete-fracture network map: A case study. In Proceedings of the SPE Annual Technical Conference and Exhibition, Denver, CO, USA, 5–8 October 2003. [Google Scholar]
- Mahmoodpour, S.; Singh, M.; Bär, K.; Sass, I. Impact of Well Placement in the Fractured Geothermal Reservoirs Based on Available Discrete Fractured System. Geosciences 2022, 12, 19. [Google Scholar] [CrossRef]
- Abbas, I.A.; Kumar, R. 2D deformation in initially stressed thermoelastic half-space with voids. Steel Compos. Struct 2016, 20, 1103–1117. [Google Scholar] [CrossRef]
- Marin, M.; Hobiny, A.; Abbas, I. The Effects of Fractional Time Derivatives in Porothermoelastic Materials Using Finite Element Method. Mathematics 2021, 9, 1606. [Google Scholar] [CrossRef]
- Multiphysics, COMSOL. Comsol Multiphysics®. COMSOL Multiphysics, Burlington, MA, USA. Available online: https://www.comsol.com/ (accessed on 5 February 2020).
- Shaik, A.R.; Rahman, S.S.; Tran, N.H.; Tran, T. Numerical simulation of fluid-rock coupling heat transfer in naturally fractured geothermal system. Appl. Therm. Eng. 2011, 31, 1600–1606. [Google Scholar] [CrossRef]
- Bandis, S.C.; Lumsden, A.C.; Barton, N.R. Fundamentals of rock joint deformation. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1983, 20, 249–268. [Google Scholar] [CrossRef]
- Barton, N.; Bandis, S.; Bakhtar, K. Strength, deformation and conductivity coupling of rock joints. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1985, 22, 121–140. [Google Scholar] [CrossRef]
- Bao, B. One-dimensional thermal consolidation characteristics of geotechnical media under non-isothermal condition. Eng. Mech. 2005, 22, 186–191. [Google Scholar]
- Mahmoodpour, S.; Singh, M.; Bär, K.; Sass, I. Database to “Impact of the Fracture Aperture Changes through the Fully Coupled Thermoporoelastic Stress on the Heat Extraction from a Fractured Reservoir”. Technical University of Darmstadt, 2021. Available online: https://tudatalib.ulb.tu-darmstadt.de/handle/tudatalib/3099 (accessed on 28 May 2022).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).