Evaluation of Shear Wave Velocity Prediction Models from Standard Penetration Test N Values Depending on Geologic Attributes: A Case Study in Busan, South Korea
Abstract
:1. Introduction
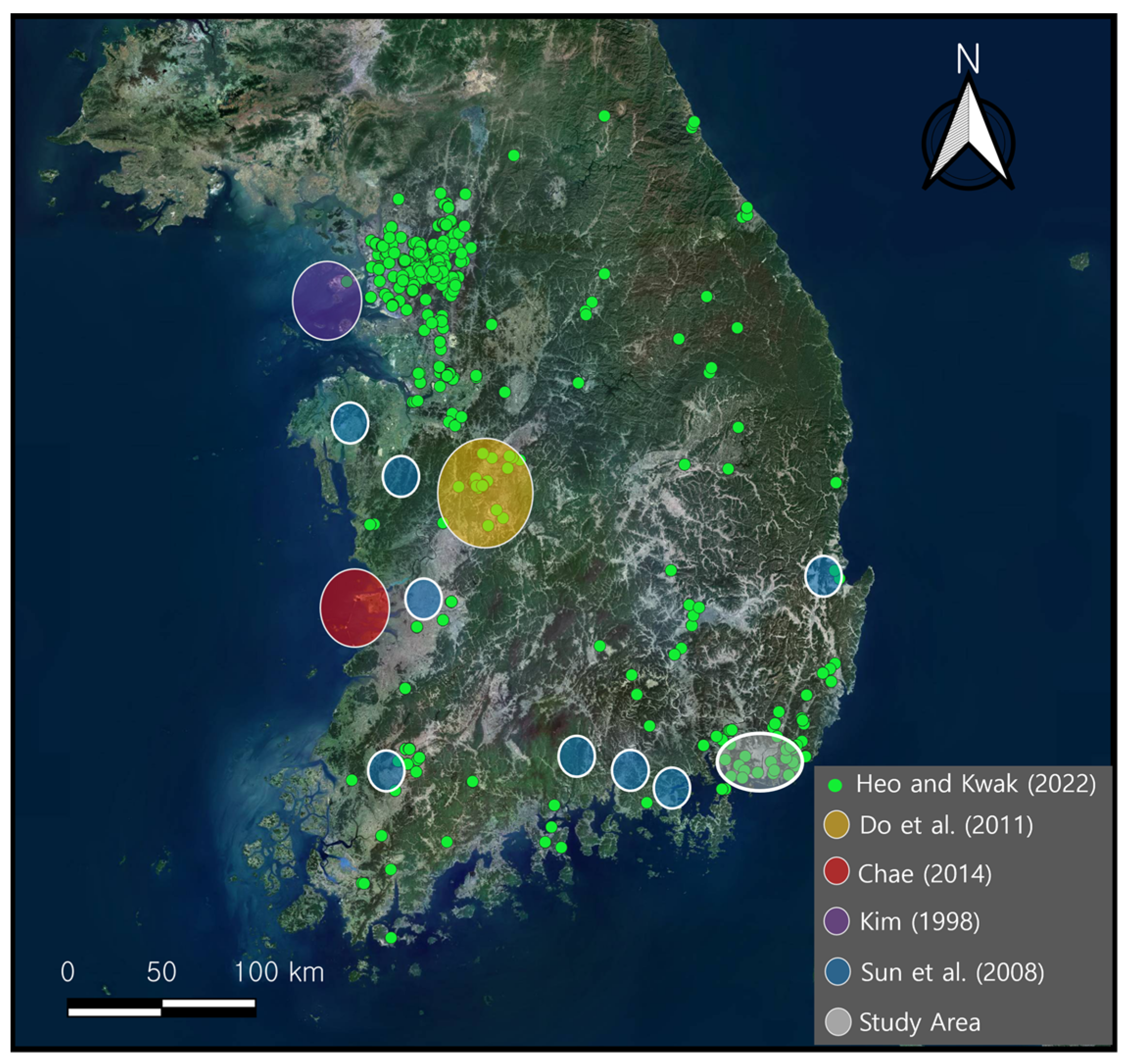
2. Study Area and Dataset
2.1. Study Area
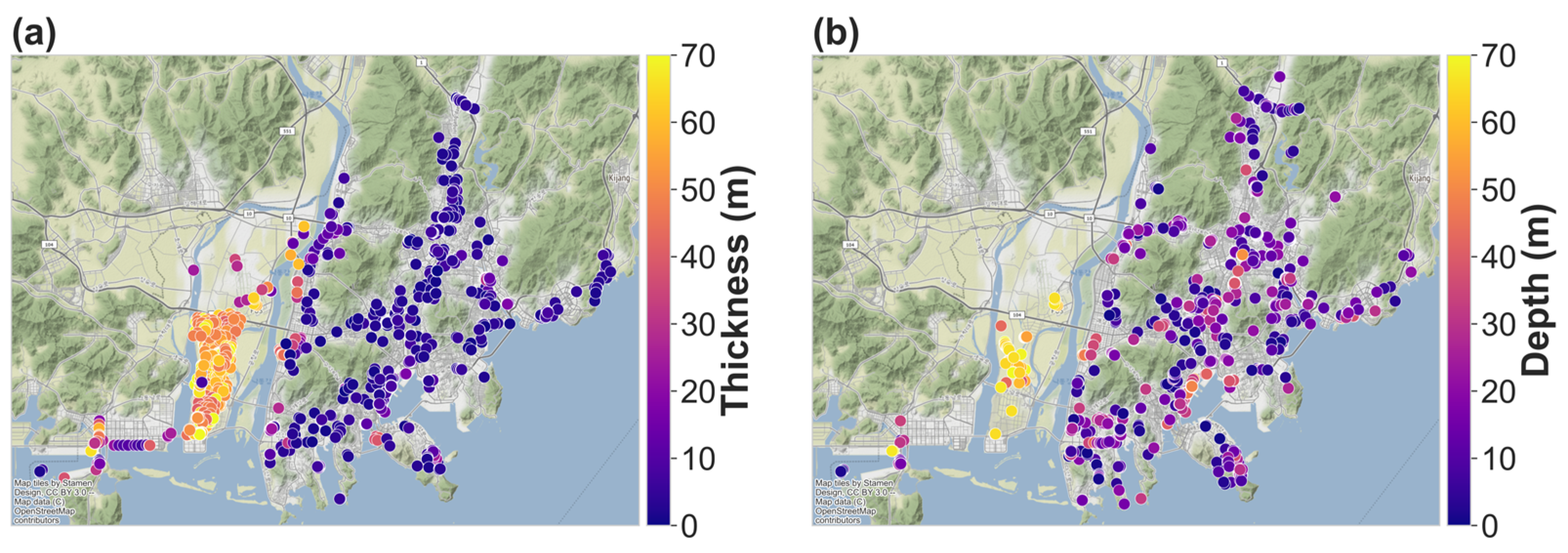
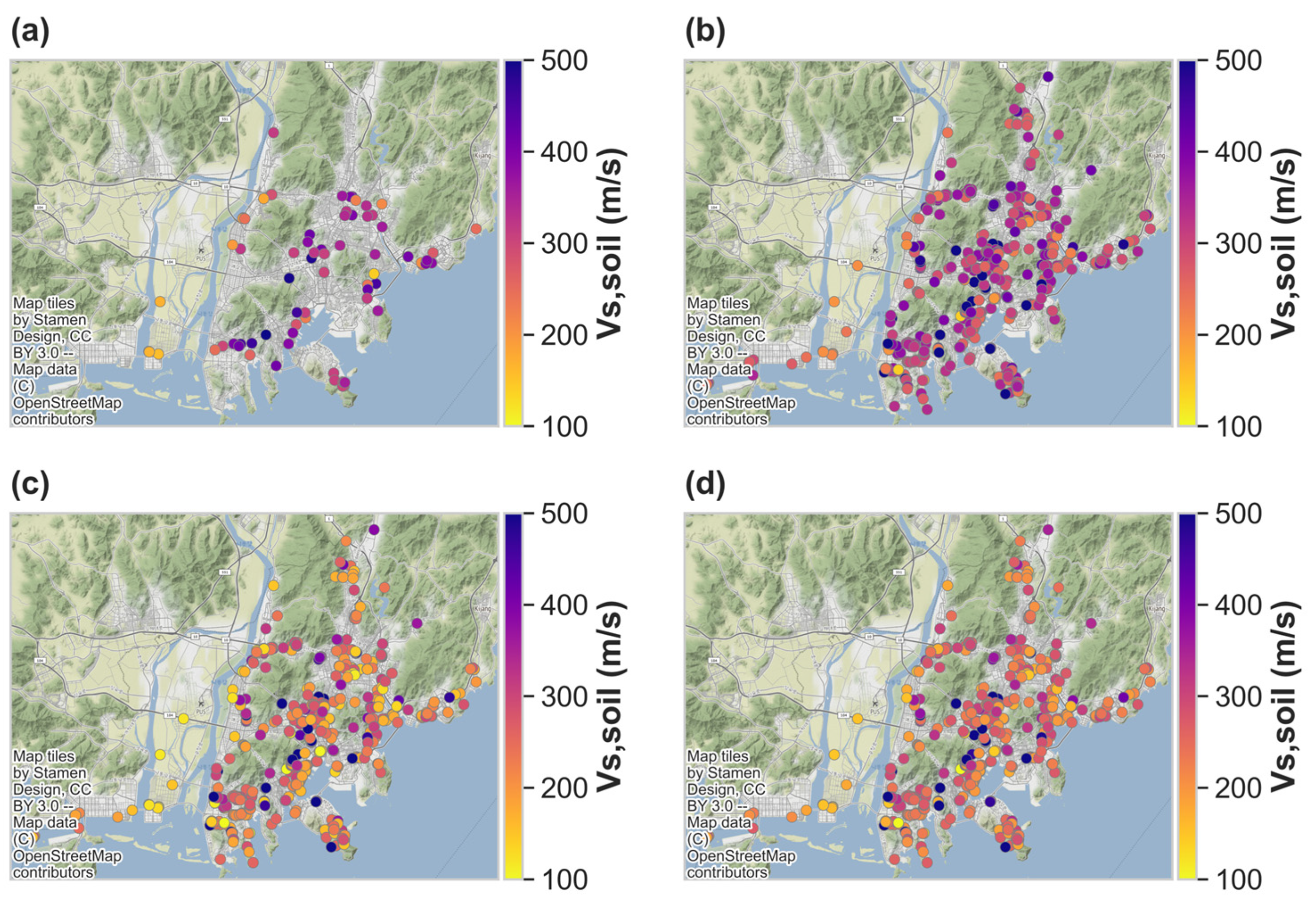
2.2. Dataset
3. Methodology
- The depth of the borehole was shallower than both the bedrock depth and 30 m;
- SPT measurements were conducted with intervals greater than 5 m;
- Neither SPT nor VS measurements were available down to a depth of 30 m.
4. Result and Discussions
5. Conclusions
- International N-VS models tend to exhibit consistent trends when the geological attributes of the dataset used for model developments are similar. This pattern was observed in cases of deep sedimentary basins including Kim [6] and Chae [1] in South Korea, Rao and Choudhury [9] in India, and Imai and Tonouchi [4] and Ohsaki and Iwasaki [7] in Japan;
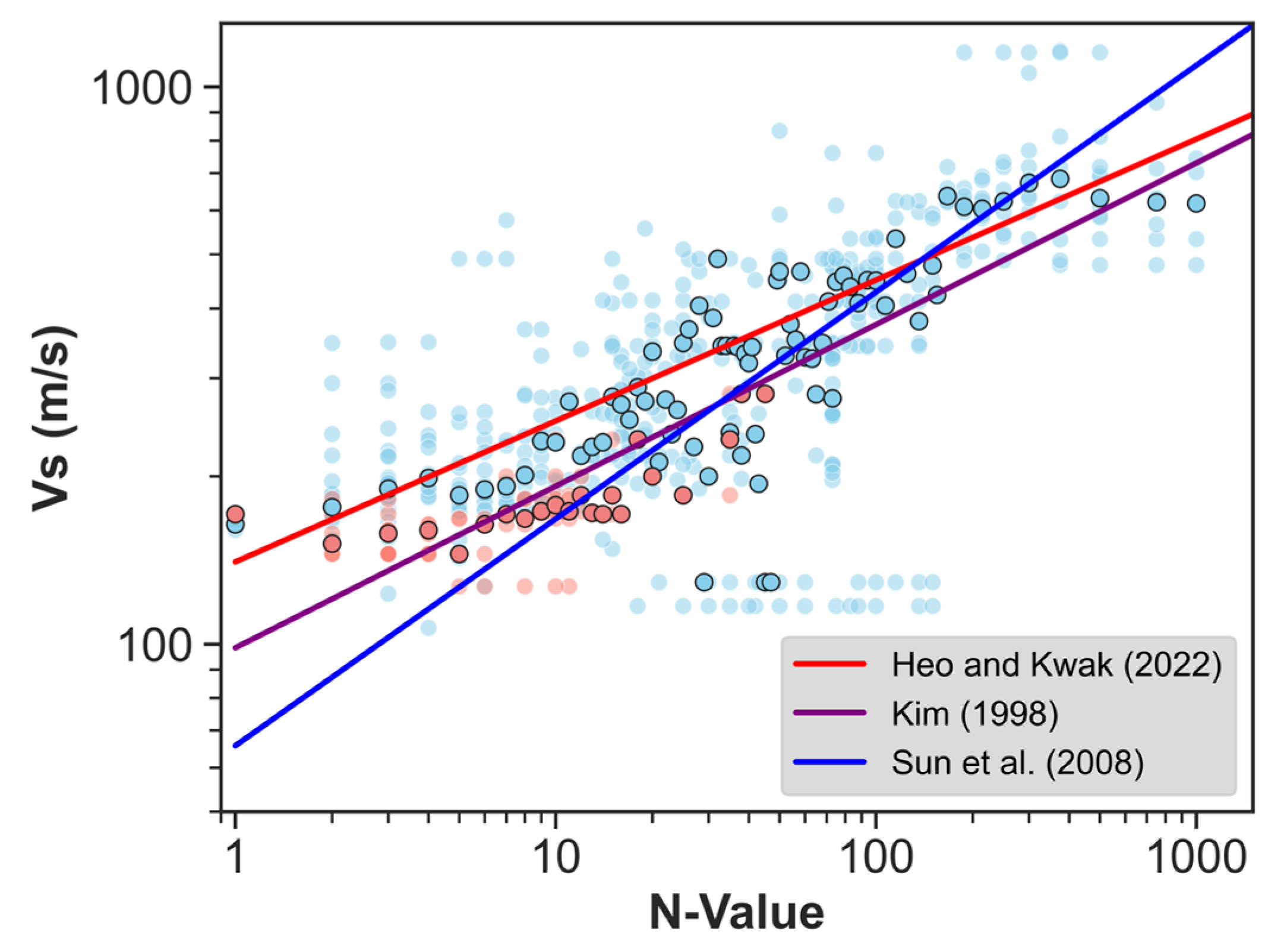
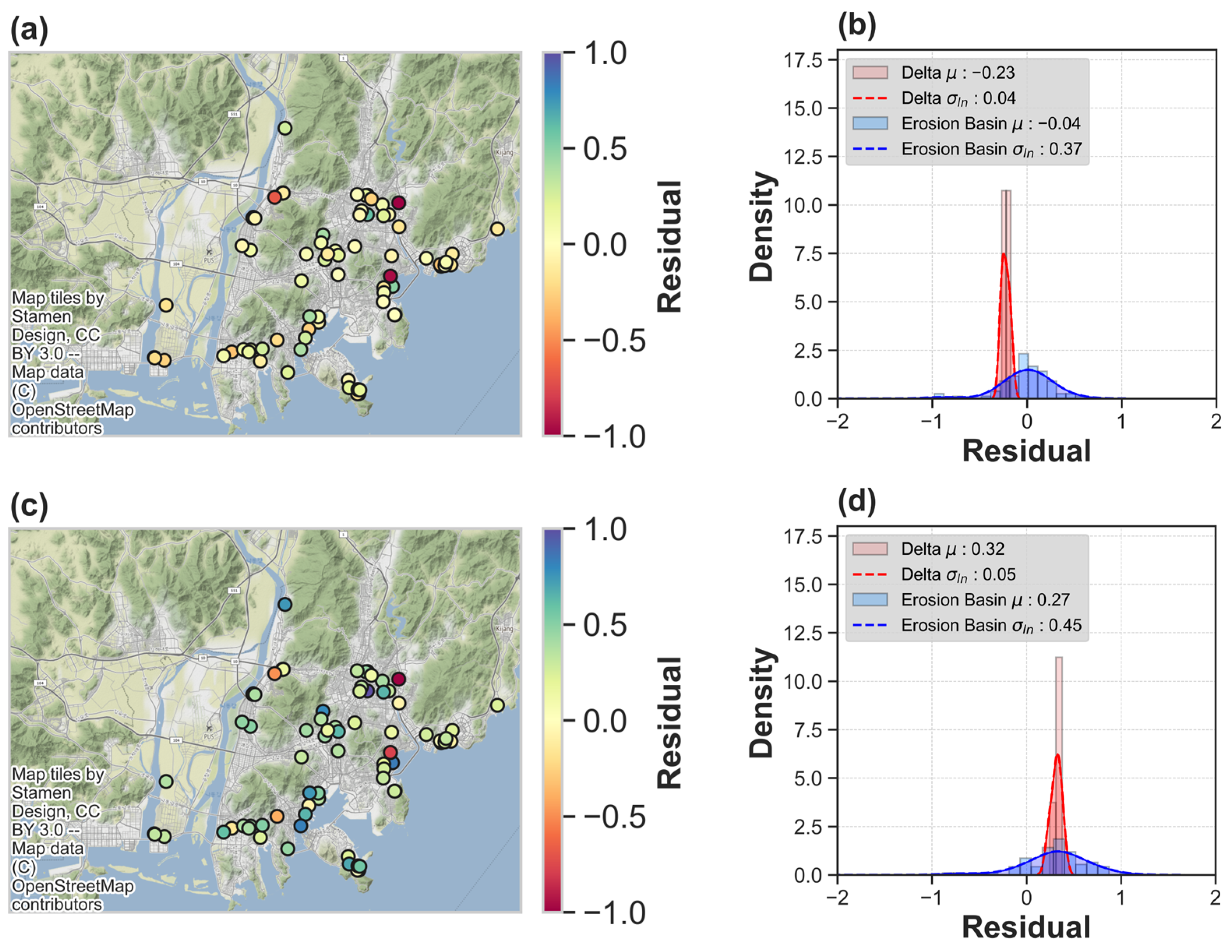
- Through residual analyses, comparisons were made between Vs,soil values derived from field-measured VS and those calculated using N-VS models by Kim [6], Sun et al. [10], and Heo and Kwak [3]. These analyses were conducted separately for the Nakdonggang delta and erosion basin regions. The model developed for reclamation land [6] exhibited satisfactory performance for the delta region. Conversely, the model based on locally sourced data [3] performed well in the erosion basin regions. Residual analyses were conducted, comparing field-measured Vs,soil values with those calculated using N-VS models developed by Kim, Sun et al., and Heo and Kwak. These analyses were performed separately for the Nakdonggang delta and erosion basin regions. The model developed for reclamation land showed satisfactory performance for the delta region, while the model based on data primarily from the urban area demonstrated good performance in the erosion basin regions;
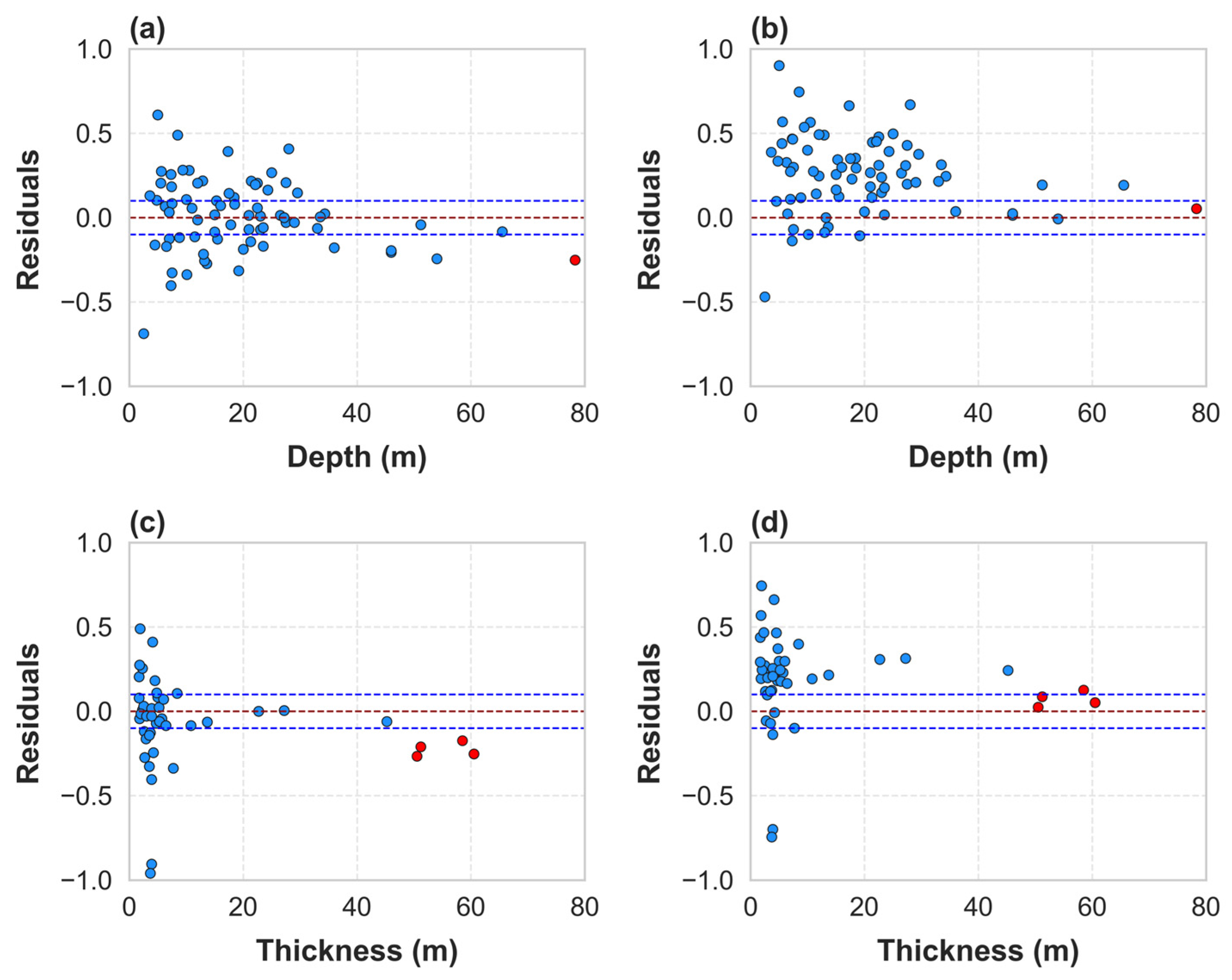
- In the erosion basin region, a more detailed analysis of the residuals predicted by Heo and Kwak [3] and Kim [6] was conducted, focusing on factors like bedrock depth and sedimentary layer thickness. The presence of negative residuals in areas with deep bedrock depths, similar to the delta region, indicates that geological conditions significantly influence the performance of N-VS relationships.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chae, H.Y. Evaluation of Saemangeum Dreged Solil by Shear Wave Velocity in the Geophysical Logging. Ph.D. Thesis, Hanyang University, Seoul, Republic of Koea, 2014. [Google Scholar]
- Do, J.; Hwang, P.; Chung, S.; Chun, B. Analysis on Relation of S-wave Velocity and N Value for Stratums in Chungcheong Buk-do. J. Korean GEO-Environ. Soc. 2011, 12, 13–22. [Google Scholar]
- Heo, G.S.; Kwak, D.Y. Vs Prediction Model Using SPT-N Values and Soil Layers in South Korea. J. Korean Geotech. Soc. 2022, 38, 53–66. [Google Scholar]
- Imai, T.; Tonoughi, K. Correlation of N value with S-wave velocity and shear modulus. In Penetration Testing, Volume 1; Routledge: Oxfordshire, UK, 2021; pp. 67–72. [Google Scholar]
- Imai, T.; Yoshimura, Y. Elastic wave velocity and soil properties in soft soil. Tsuchito-Kiso 1970, 18, 17–22. [Google Scholar]
- Kim, D.S. Development of Quality Evaluation Technique of Ground Improvement on Sands Using SASW Method; Ministry of Land, Infrastructure and Transport: Sejong-Si, Republic of Koea, 1998.
- Ohsaki, Y.; Iwasaki, R. On dynamic shear moduli and Poisson’s ratios of soil deposits. Soils Found. 1973, 13, 61–73. [Google Scholar] [CrossRef]
- Ohta, Y.; Goto, N. Empirical shear wave velocity equations in terms of characteristic soil indexes. Earthq. Eng. Struct. Dyn. 1978, 6, 167–187. [Google Scholar] [CrossRef]
- Rao, V.D.; Choudhury, D. Estimation of shear wave velocity and seismic site characterization for new nuclear power plant region, India. Nat. Hazards Rev. 2020, 21, 06020004. [Google Scholar] [CrossRef]
- Sun, C.-G.; Kim, H.-J.; Chung, C.-K. Deduction of correlations between shear wave velocity and geotechnical in-situ penetration test data. J. Earthq. Eng. Soc. Korea 2008, 12, 1–10. [Google Scholar]
- Akkaya, İ.; Özvan, A.; Özvan, E.E. A new empirical correlation between pressuremeter modules (EM) and shear wave velocity (Vs) for clay soils. J. Appl. Geophys. 2019, 171, 103865. [Google Scholar] [CrossRef]
- Hasancebi, N.; Ulusay, R. Empirical correlations between shear wave velocity and penetration resistance for ground shaking assessments. Bull. Eng. Geol. Environ. 2007, 66, 203–213. [Google Scholar] [CrossRef]
- Pitilakis, K.; Raptakis, D.; Lontzetidis, K.; Tika-Vassilikou, T.; Jongmans, D. Geotechnical and geophysical description of EURO-SEISTEST, using field, laboratory tests and moderate strong motion recordings. J. Earthq. Eng. 1999, 3, 381–409. [Google Scholar] [CrossRef]
- Uma Maheswari, R.; Boominathan, A.; Dodagoudar, G. Use of surface waves in statistical correlations of shear wave velocity and penetration resistance of Chennai soils. Geotech. Geol. Eng. 2010, 28, 119–137. [Google Scholar] [CrossRef]
- Brandenberg, S.J.; Bellana, N.; Shantz, T. Shear wave velocity as function of standard penetration test resistance and vertical effective stress at California bridge sites. Soil Dyn. Earthq. Eng. 2010, 30, 1026–1035. [Google Scholar] [CrossRef]
- Kwak, D.Y.; Brandenberg, S.J.; Mikami, A.; Stewart, J.P. Prediction equations for estimating shear-wave velocity from combined geotechnical and geomorphic indexes based on Japanese data set. Bull. Seismol. Soc. Am. 2015, 105, 1919–1930. [Google Scholar] [CrossRef]
- Rahimi, S.; Wood, C.M.; Wotherspoon, L.M. Influence of soil aging on SPT-Vs correlation and seismic site classification. Eng. Geol. 2020, 272, 105653. [Google Scholar] [CrossRef]
- Piratheepan, P. Estimating Shear-Wave Velocity from SPT and CPT Data. Master’s Thesis, Clemson University, Clemson, SC, USA, 2002. [Google Scholar]
- Dikmen, Ü. Statistical correlations of shear wave velocity and penetration resistance for soils. J. Geophys. Eng. 2009, 6, 61–72. [Google Scholar] [CrossRef]
- Jeong, E. Evolution Study of Sedimentary Environments of Late Pleistocene Caused by Sea-Level Changes in the Nakdong River Estuary, Korea; Kangwon National University: Chuncheon, Republic of Korea, 2017. [Google Scholar]
- Yoon, H.S.; Yoo, C.-I.; Kang, Y.-K.; Ryu, C.-R. Delta development in the Nakdong river estuary: A literature survey. J. Ocean Eng. Technol. 2007, 21, 22–34. [Google Scholar]
- Lee, S.; Yang, M.; Lee, C. Time series analysis of area of deltaic barrier island in Nakdong River using Landsat satellite image. J. Korean Soc. Surv. Geod. Photogramm. Cartogr. 2016, 34, 457–469. [Google Scholar] [CrossRef]
- Chang, C.H. A study on shapes and genetic process of erosion basins. J. Photo Geogr. 1997, 6, 1–16. [Google Scholar]
- Lee, G.R. Formation Ages of Alluvial Fans in Granite Erosional Basins, South Korea. J. Korean Geomorphol. Assoc. 2022, 29, 21–34. [Google Scholar] [CrossRef]
- Lee, G.R.; Park, C.S.; Kim, J.Y.; Lee, H.B.; Jeong, J.-Y. Analysis on Surface Relief of Granitic Erosional Basin in the Middle Part of the Korean Peninsula—A Case Study on the Chuncheon, Wonju, Yeongju and Boeun Basins–. J. Korean Geomorphol. Assoc. 2022, 29, 1–12. [Google Scholar]
- Youn, I.H. The Geomorphic Characteristics of Okcheon Basin & Jincheon Basin. J. Korean Assoc. Reg. Geogr. 2001, 7, 93–104. [Google Scholar]
- Hwang, S.I. The Geomorphic development of alluvial fans in Cheongdo basin, Gyeongsangbuk-do (Province), South Korea. J. Korean Geogr. Soc. 2004, 39, 514–527. [Google Scholar]
- Bull, W.B. The alluvial-fan environment. Prog. Phys. Geogr. 1977, 1, 222–270. [Google Scholar] [CrossRef]
- Yoon, S.O.; Saito, K.; Hwang, S.I.; Oguchi, T.; Tanaka, Y. Morphometric Characteristics of Alluvial Fans in South Korea and Comparisons with those of Japan, Taiwan and the Philippines. J. Korean Geogr. Soc. 2010, 45, 431–443. [Google Scholar]
- Yoon, S.O.; Saito, K.; Hwang, S.I.; Tanaka, Y.; Oguchi, T. The theoretical study and distributional characteristics of alluvial fans in Korean Peninsula. J. Korean Geogr. Soc. 2005, 40, 335–352. [Google Scholar]
- Oguchi, T.; Saito, K.; Kadomura, H.; Grossman, M. Fluvial geomorphology and paleohydrology in Japan. Geomorphology 2001, 39, 3–19. [Google Scholar] [CrossRef]
- Yoshikawa, T. Denudation and tectonic movement in contemporary Japan. Bull. Dep. Geogr. Univ. Tokyo 1974, 6, 1–14. [Google Scholar]
- Choi, I.H.; Kwak, D.Y. Comparison of Methods Predicting Vs30 from Shallow Vs Profiles and Suggestion of Optimized Coefficients. J. Korean Geotech. Soc. 2020, 36, 15–23. [Google Scholar]
- Kim, J.; Heo, G.; Kwak, D.; Jeong, S. The Relationship between Bedrock Depth and Site Fundamental Frequency in the Nakdonggang Delta Region, South Korea. Geotechnics 2023, 3, 550–560. [Google Scholar] [CrossRef]
- Andrus, R.D.; Stokoe II, K.H. Liquefaction resistance of soils from shear-wave velocity. J. Geotech. Geoenviron. Eng. 2000, 126, 1015–1025. [Google Scholar] [CrossRef]
- Andrus, R.D.; Piratheepan, P.; Ellis, B.S.; Zhang, J.; Juang, C.H. Comparing liquefaction evaluation methods using penetration-Vs relationships. Soil Dyn. Earthq. Eng. 2004, 24, 713–721. [Google Scholar] [CrossRef]
- Aytaş, Z.; Alpaslan, N.; Özçep, F. Evaluation of liquefaction potential by standard penetration test and shear wave velocity methods: A case study. Nat. Hazards 2023, 118, 2377–2417. [Google Scholar] [CrossRef]
- Ji, Y.; Kim, B.; Kim, K. Evaluation of liquefaction potentials based on shear wave velocities in Pohang City, South Korea. Int. J. Geo-Eng. 2021, 12, 3. [Google Scholar] [CrossRef]
- Johari, A.; Khodaparast, A.; Javadi, A. An analytical approach to probabilistic modeling of liquefaction based on shear wave velocity. Iran. J. Sci. Technol. Trans. Civ. Eng. 2019, 43, 263–275. [Google Scholar] [CrossRef]
- Kayabali, K. Soil liquefaction evaluation using shear wave velocity. Eng. Geol. 1996, 44, 121–127. [Google Scholar] [CrossRef]
- Oshnavieh, D.; Bagherzadeh Khalkhali, A. Use of shear wave velocity in evaluation of soil layer’s condition after liquefaction. J. Civ. Eng. Mater. Appl. 2019, 3, 119–135. [Google Scholar]
- Ulmer, K.J.; Green, R.A.; Rodriguez-Marek, A. A consistent correlation between Vs, SPT, and CPT metrics for use in liquefaction evaluation procedures. In Proceedings of the Geo-Congress 2020, Minneapolis, MN, USA, 25–28 February 2020; pp. 132–140. [Google Scholar]
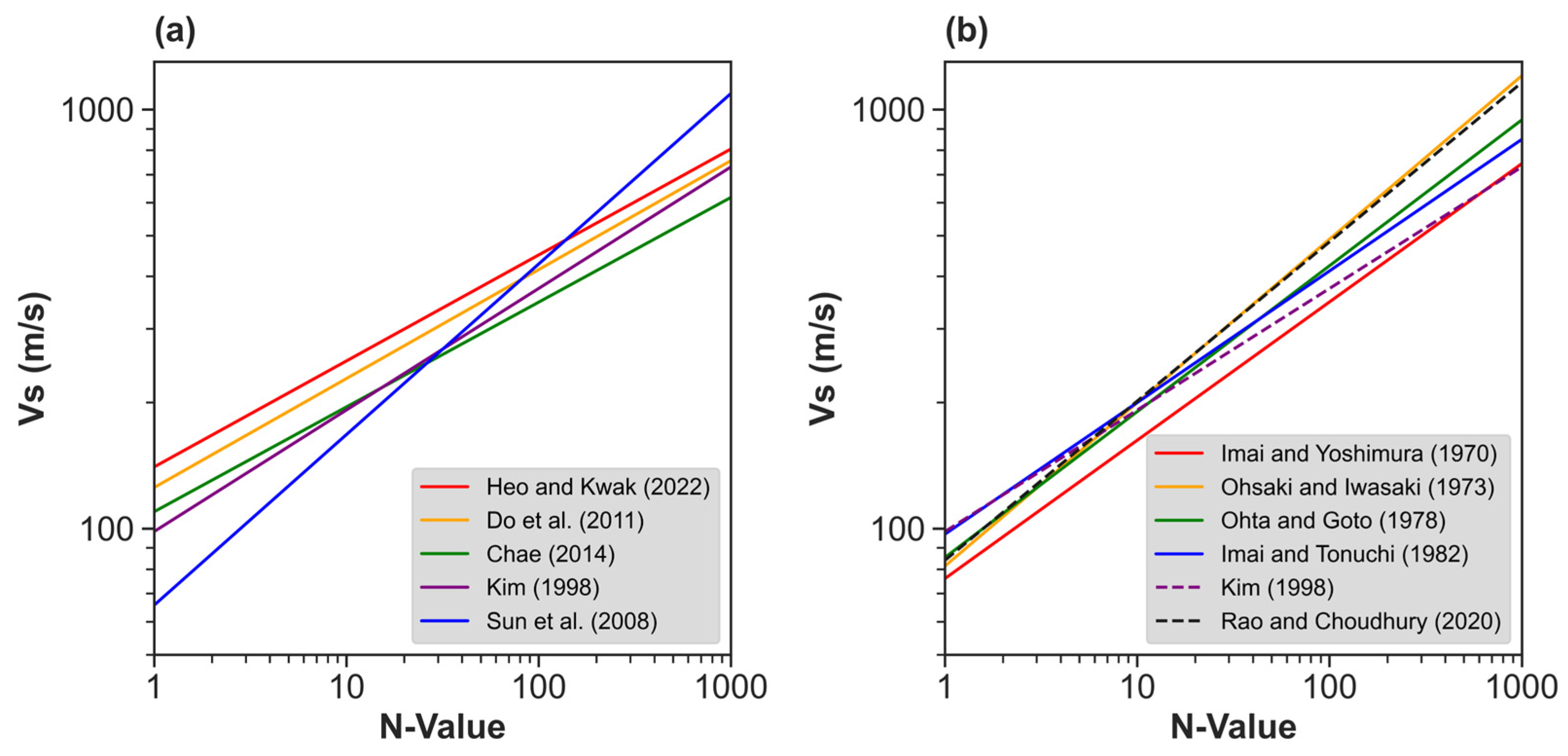


| Country | Study | N-VS (m/s) Model * | Type | |
|---|---|---|---|---|
| Japan | Imai and Yoshimura [5] | All soil | - | |
| Ohsaki and Iwasaki [7] | All soil | 0.89 | ||
| Sand | - | |||
| Ohta and Goto [8] | All soil (Pleistoene) | 0.72 | ||
| All soil (Holocene) | - | |||
| Sand (Pleistoene) | - | |||
| Clay (Pleistoene) | - | |||
| Imai and Tonouchi [4] | All soil | 0.87 | ||
| Sand | 0.69 | |||
| Clay | 0.72 | |||
| Korea | Sun et al. [10] | All soil | 0.56 | |
| Sand and Silt | 0.34 | |||
| Gravel | 0.33 | |||
| Weathered soil | 0.25 | |||
| Weathered rock | 0.22 | |||
| Do et al. [2] | All soil | 0.70 | ||
| Sand | 0.65 | |||
| Clay | 0.49 | |||
| Gravel | 0.59 | |||
| Weathered soil | 0.29 | |||
| Weathered rock | 0.25 | |||
| Heo and Kwak [3] | All soil | 0.72 | ||
| All soil | 0.73 | |||
| Sand | 0.17 | |||
| Clay and Silt | 0.18 | |||
| Gravel | 0.23 | |||
| Weathered soil | 0.32 | |||
| Weathered rock | 0.06 | |||
| Chae [1] | All soil | 0.69 | ||
| All soil | 0.83 | |||
| Sand | 0.77 | |||
| Clay and Silt | 0.41 | |||
| Kim [6] | All soil | - | ||
| India | Rao and Choudhury [9] | All soil | 0.90 |
| Delta | Erosion Basin | |||||||
|---|---|---|---|---|---|---|---|---|
| Top–Bot (m) | Top–Bot (m) | |||||||
| Layer | Count | 25% | 50% | 75% | Count | 25% | 50% | 75% |
| Fill | 435 | 0.0–0.8 | 0.0–1.4 | 0.0–3.5 | 1449 | 0.0–1.5 | 0.0–2.3 | 0.0–4.0 |
| AS | 471 | 0.7–49 | 1.2–59 | 2.8–65 | 726 | 1.5–5.0 | 2.4–7.5 | 4.0–15 |
| WS | 46 | 27–31 | 65–67 | 67–70 | 1154 | 2.0–6.5 | 4.2–11 | 8.0–18 |
| WR | 115 | 59–65 | 67–73 | 73–81 | 1077 | 6.5–10 | 12–18 | 19–28 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Heo, G.; Kim, J.; Jeong, S.; Kwak, D. Evaluation of Shear Wave Velocity Prediction Models from Standard Penetration Test N Values Depending on Geologic Attributes: A Case Study in Busan, South Korea. Geotechnics 2023, 3, 1004-1016. https://doi.org/10.3390/geotechnics3040054
Heo G, Kim J, Jeong S, Kwak D. Evaluation of Shear Wave Velocity Prediction Models from Standard Penetration Test N Values Depending on Geologic Attributes: A Case Study in Busan, South Korea. Geotechnics. 2023; 3(4):1004-1016. https://doi.org/10.3390/geotechnics3040054
Chicago/Turabian StyleHeo, Giseok, Jaehwi Kim, Seokho Jeong, and Dongyoup Kwak. 2023. "Evaluation of Shear Wave Velocity Prediction Models from Standard Penetration Test N Values Depending on Geologic Attributes: A Case Study in Busan, South Korea" Geotechnics 3, no. 4: 1004-1016. https://doi.org/10.3390/geotechnics3040054
APA StyleHeo, G., Kim, J., Jeong, S., & Kwak, D. (2023). Evaluation of Shear Wave Velocity Prediction Models from Standard Penetration Test N Values Depending on Geologic Attributes: A Case Study in Busan, South Korea. Geotechnics, 3(4), 1004-1016. https://doi.org/10.3390/geotechnics3040054