Physical Modelling of High Stiffness Large Diameter Steel Tubular Pile Subjected to One-Way Horizontal Cyclic Loading
Abstract
1. Introduction
2. Centrifuge Model Tests
3. Results and Discussion
3.1. Experimental Results
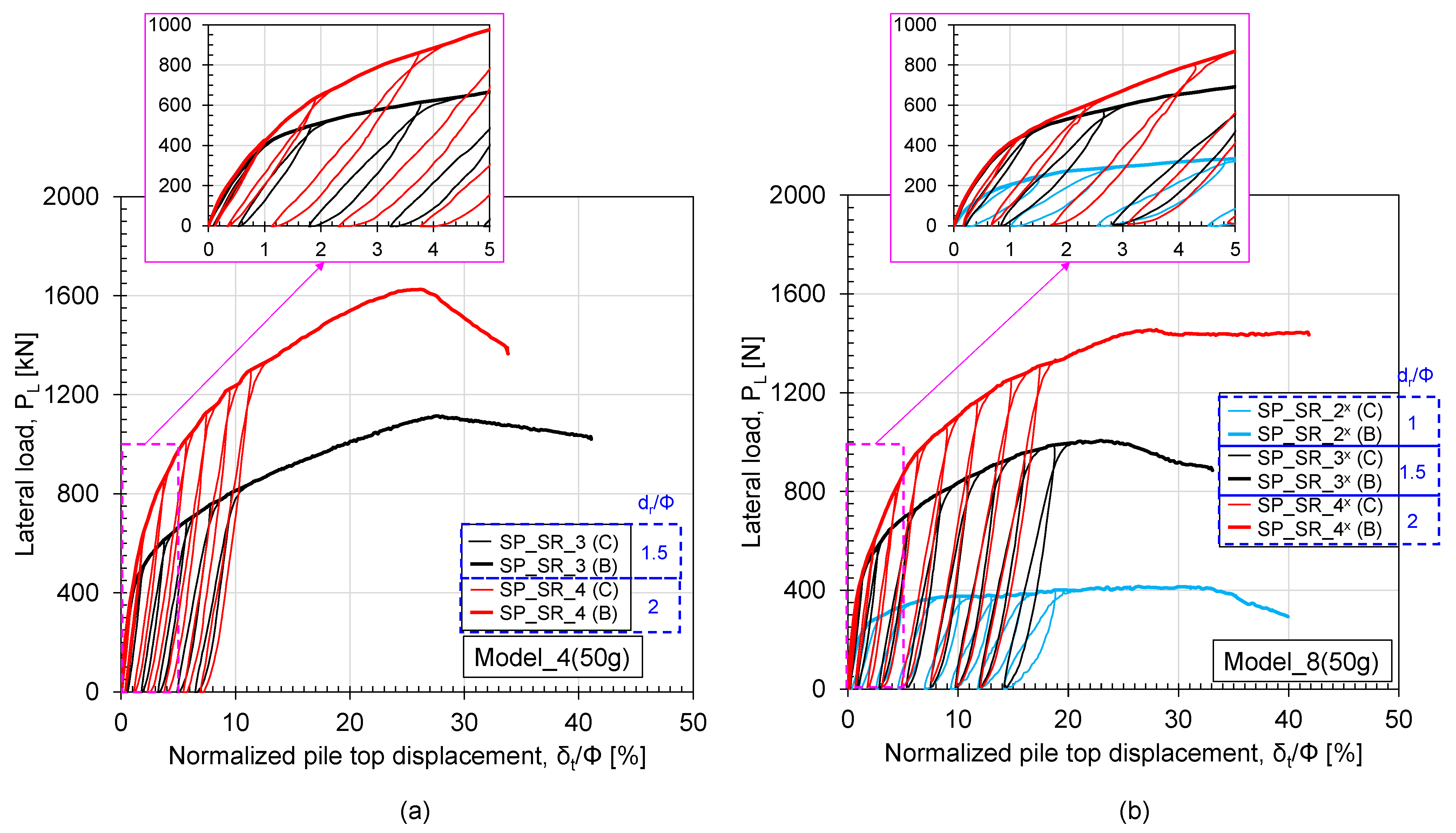
3.1.1. Observed Results from 50 g Centrifuge Model Tests
3.1.2. Observed Results from 1 g Centrifuge Model Tests
3.2. Discussions
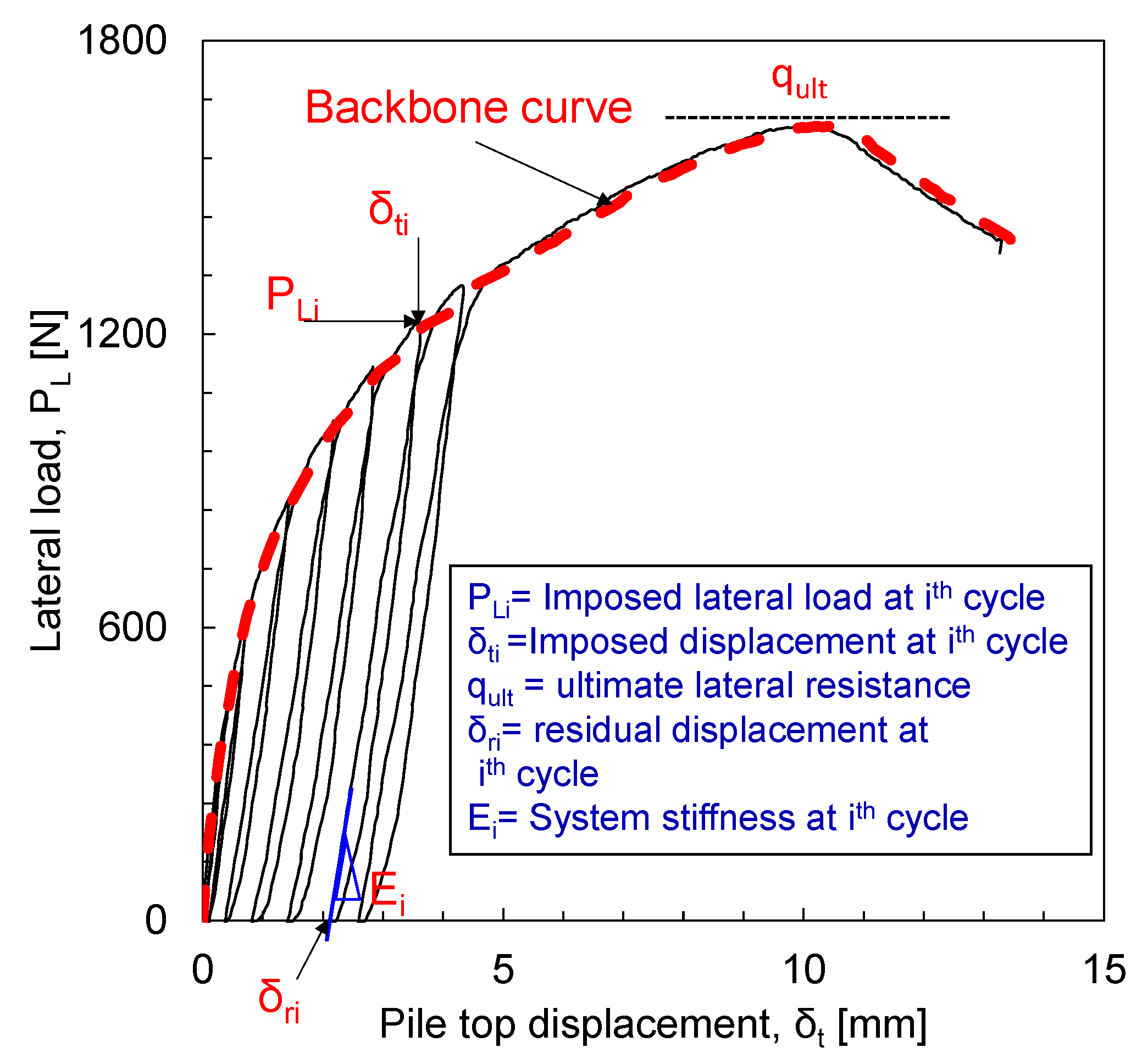
3.2.1. Load Displacement and the Effect of Failure Mechanisms on the Load-Displacement Behaviour of the Pile Loading Test
3.2.2. Rock-Pile Confinement Condition
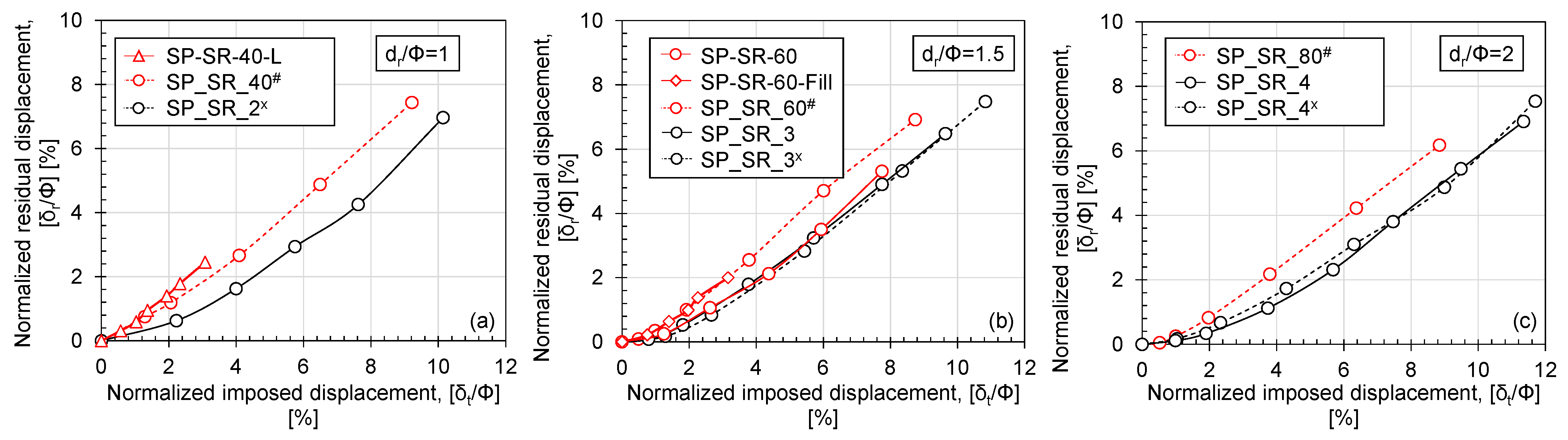
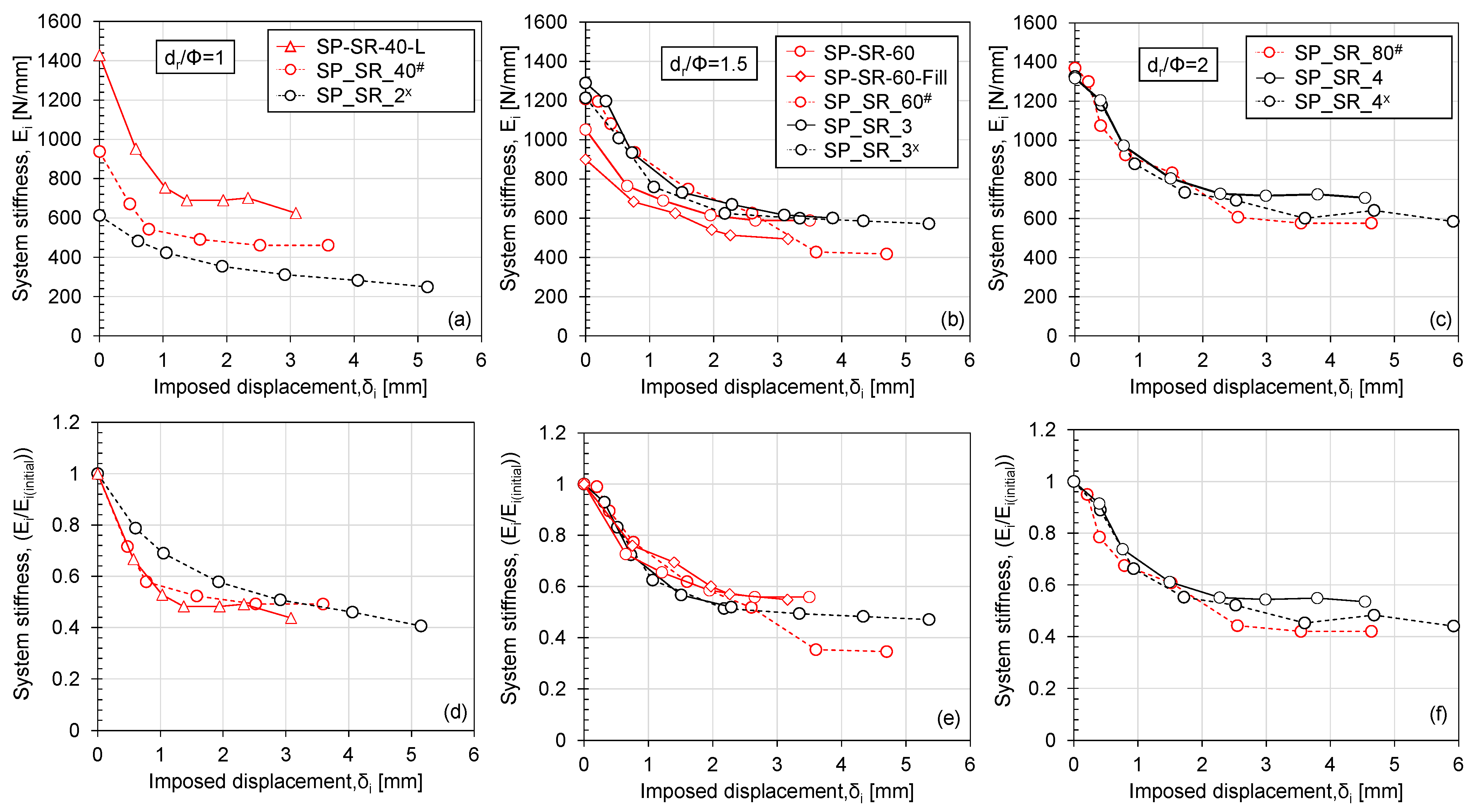
3.2.3. Accumulation of Residual Displacement and Change in System Stiffness
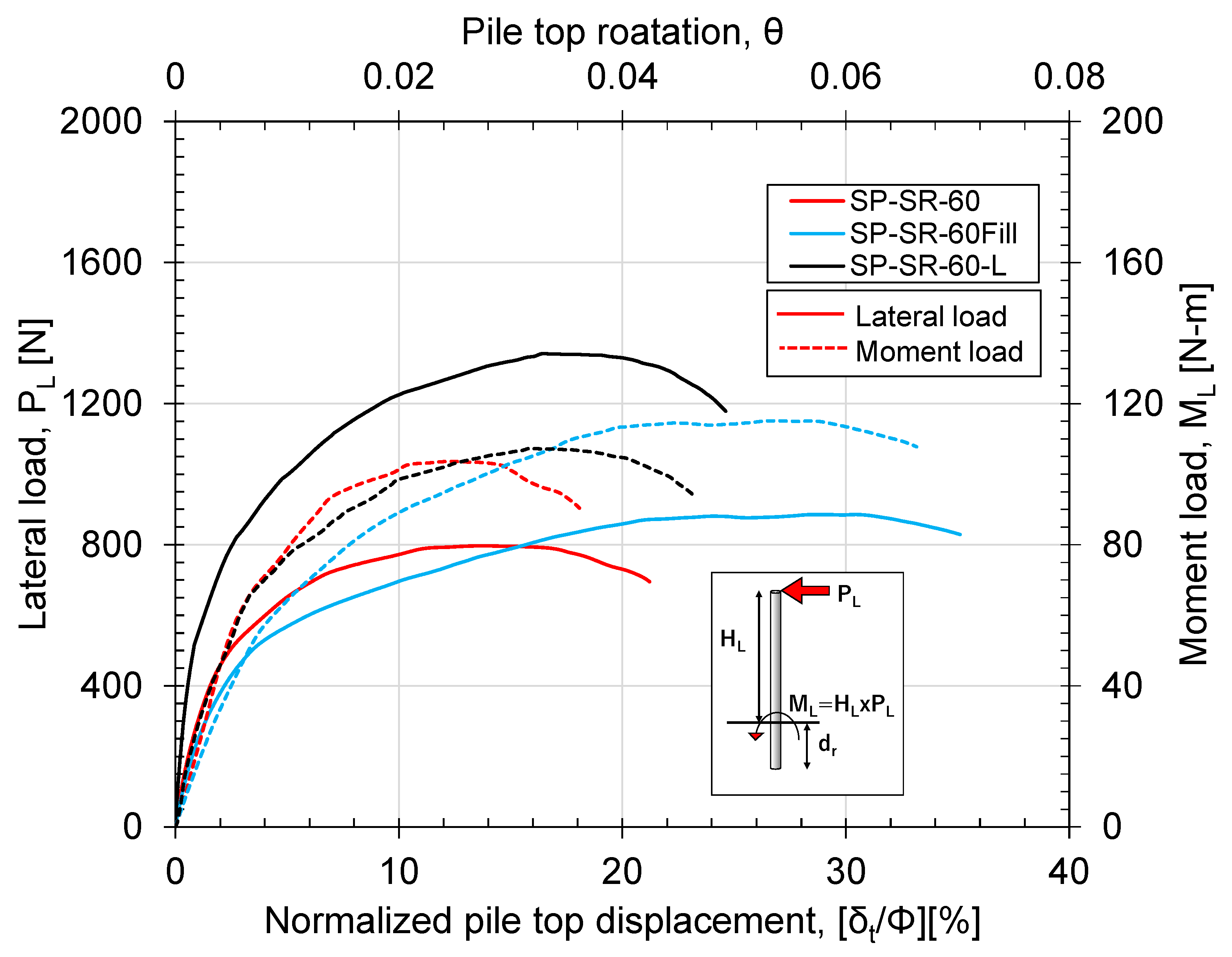
3.2.4. Effect of Loading Height and Filling Conditions
4. Conclusions
- The lateral resistance of the pile increases with the increase in rock socketing depth, which can be effectively captured by both the 50 g and 1 g model tests. Both models show the effect of ∆dr/Φ = 0.5. However, the 1 g model underestimates the lateral resistance of the pile compared to the 50 g model, especially after the formation of tension cracks near the rock surface. This kind of tension crack formation in the 1 g model test can be considered as a limitation;
- The failure mechanism affects the load-displacement behaviour, especially the post-peak behaviour for both the 50 g and 1 g models. Both ground and structural failure were observed in the 50 g model test for dr/Φ = 2, but the 1 g model always showed ground failure;
- No effect of confining pressure or rock socketing depth can be confirmed up to δt = 1%Φ for dr/Φ = 1.5 and 2 in the 50 g model test. However, in the 1 g model test, this behaviour is limited to δt = 0.5%Φ. For dr/Φ = 1, due to the rigid nature of the pile, no effect of material weight or gravity can be expected;
- With an increase in loading cycles, residual displacement also increases with a reduction in system stiffness. This observation is confirmed in both the 1 g and 50 g model tests. The 1 g model overestimates the accumulation of residual displacement and underestimates the system stiffness, particularly for dr/Φ = 1;
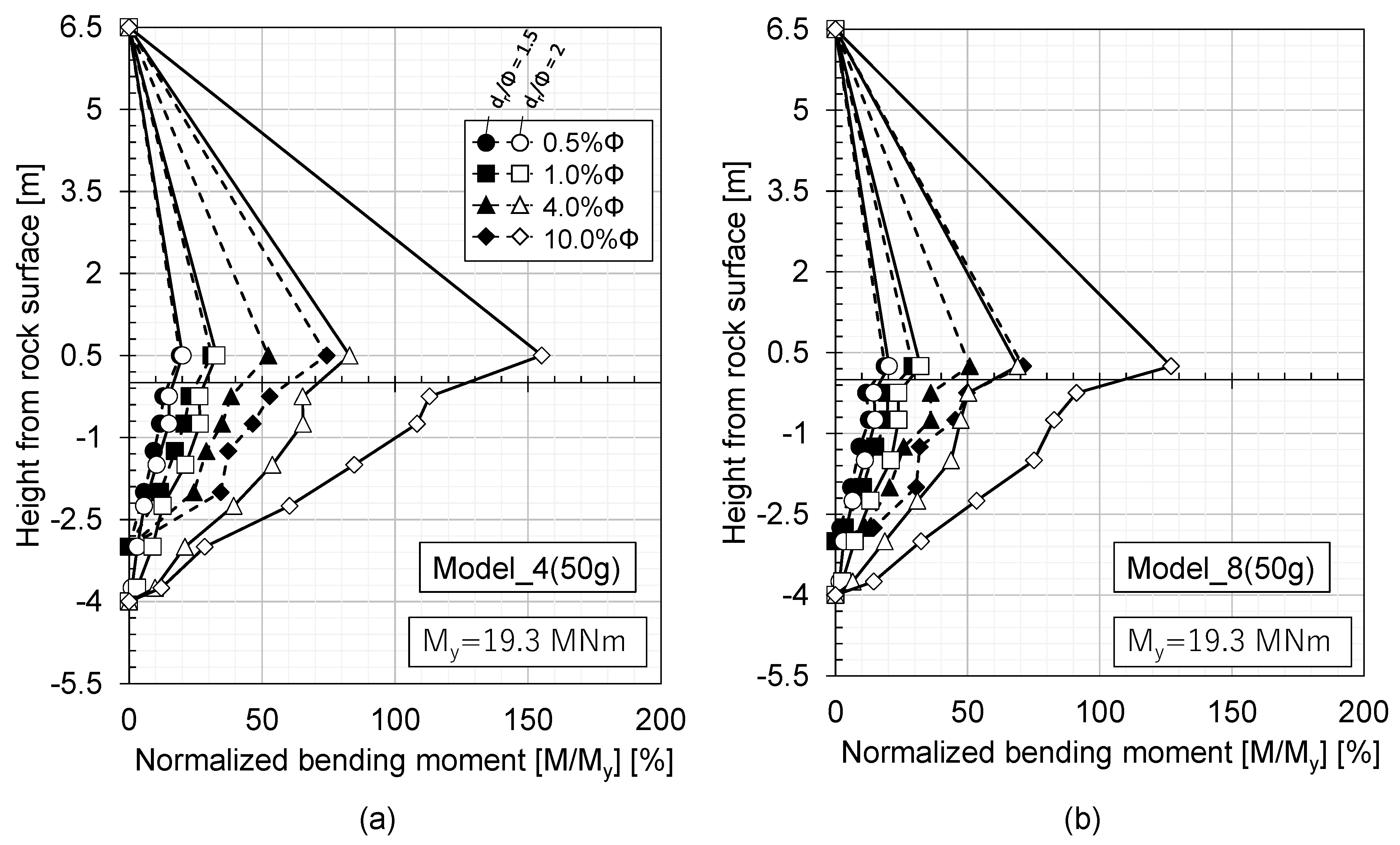
- Based on the 50 g model test, the rock-pile system can be considered as a perfect cantilever. The maximum bending moment will always occur at the rock surface. However, the nonlinearity in the bending moment measurement becomes significant with an increase in dr/Φ. This effect of nonlinearity is more pronounced in flexible piles than in rigid piles;
- Based on the 50 g model test, the contribution of the shallow rock layer can be expected, even at δt = 10%Φ;
- The effect of loading height and moment load on the load-displacement behaviour can be confirmed. The lateral resistance of the pile increases with a decrease in the loading height or the corresponding moment load. However, the rigid nature of the pile can affect the moment load-rotation relationship;
- No significant effect of the filling conditions on the lateral resistance of the pile can be confirmed unless the relative stiffness changes significantly.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kallehave, D.; Byrne, B.W.; LeBlanc Thilsted, C.; Mikkelsen, K.K. Optimization of Monopiles for Offshore Wind Turbines. Phil. Trans. R. Soc. A 2015, 373, 20140100. [Google Scholar] [CrossRef] [PubMed]
- Wu, X.; Hu, Y.; Li, Y.; Yang, J.; Duan, L.; Wang, T.; Adcock, T.; Jiang, Z.; Gao, Z.; Lin, Z.; et al. Foundations of Offshore Wind Turbines: A Review. Renew. Sustain. Energy Rev. 2019, 104, 379–393. [Google Scholar] [CrossRef]
- Kitamura, M.; Kamimura, S. Cantilevered Road Retaining Wall Constructed of 2000 mm Diameter Steel Tubular Piles Installed by the Gyro Press Method with the GRB System. In Proceeding of the First International Conference on Press-in Engineering, Kochi, Japen, 19–20 September 2018; International Press-in Association: Kochi, Japan, 2018. [Google Scholar]
- Miyanohara, T.; Kurosawa, T.; Harata, N.; Kitamura, K.; Suzuki, N.; Kajino, K. Overview of the Self-Standing and High Stiffness Tubular Pile Walls in Japan. In Proceedings of the International Conference on Press-in Engineering First International Conference, Kochi, Japen, 19–20 September 2018. [Google Scholar]
- Ishihama, Y.; Takemura, J.; Kunasegaram, V. Analytical Evaluation of Deformation Behavior of Cantilever Type Retaining Wall Using Large Diameter Steel Tubular Piles into Stiff Ground. In Geotechnics for Sustainable Infrastructure Development; Duc Long, P., Dung, N.T., Eds.; Lecture Notes in Civil Engineering; Springer: Singapore, 2020; Volume 62, pp. 91–98. [Google Scholar] [CrossRef]
- Matsuzawa, K.; Hayashi, T.; Shirasaki, K. Construction of Retaining Wall for River Disaster Restoration by Gyropress Method. In Proceedings of the Second International Conference on Press-in Engineering 2021, Kochi, Japan, 29 May–7 June 2021; CRC Press: London, UK, 2021; pp. 422–429. [Google Scholar] [CrossRef]
- Kanji, M.A. Critical Issues in Soft Rocks. J. Rock Mech. Geotech. Eng. 2014, 6, 186–195. [Google Scholar] [CrossRef]
- Fragio, A.G.; Santiago, J.L.; Sutton, V.J.R. Load Tests on Grouted Piles in Rock. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 6–9 May 1985. [Google Scholar] [CrossRef]
- Guo, F.; Lehane, B.M. Lateral Response of Piles in Weak Calcareous Sandstone. Can. Geotech. J. 2016, 53, 1424–1434. [Google Scholar] [CrossRef]
- Cho, K.H.; Gabr, M.A.; Clark, S.; Borden, R.H. Field P—y Curves in Weathered Rock. Can. Geotech. J. 2007, 44, 753–764. [Google Scholar] [CrossRef]
- Carter, J.P.; Kulhawy, F.H. Analysis of Laterally Loaded Shafts in Rock. J. Geotech. Eng. 1992, 118, 839–855. [Google Scholar] [CrossRef]
- Reese, L.C. Analysis of Laterally Loaded Piles in Weak Rock. J. Geotech. Geoenviron. Eng. 1997, 123, 1010–1017. [Google Scholar] [CrossRef]
- Liang, R.; Yang, K.; Nusairat, J. P-y Criterion for Rock Mass. J. Geotech. Geoenviron. Eng. 2009, 135, 26–36. [Google Scholar] [CrossRef]
- Erbrich, C.T. A New Method for the Design of Laterally Loaded Anchor Piles in Soft Rock. In All Days; OTC: Houston, TX, USA, 2004; p. OTC-16441-MS. [Google Scholar] [CrossRef]
- Brown, D.A.; Shie, C.-F. Three Dimensional Finite Element Model of Laterally Loaded Piles. Comput. Geotech. 1990, 10, 59–79. [Google Scholar] [CrossRef]
- Kunasegaram, V.; Shafi, S.M.; Takemura, J.; Ishihama, Y. Centrifuge Model Study on Cantilever Steel Tubular Pile Wall Embedded in Soft Rock. In Geotechnics for Sustainable Infrastructure Development; Duc Long, P., Dung, N.T., Eds.; Lecture Notes in Civil Engineering; Springer: Singapore, 2020; Volume 62, pp. 1045–1052. [Google Scholar] [CrossRef]
- Kunasegaram, V.; Takemura, J. Mechanical Behaviour of Laterally Loaded Large-Diameter Steel Tubular Piles Embedded in Soft Rock. Geotech. Geol. Eng. 2022, 40, 2967–3005. [Google Scholar] [CrossRef]
- Lehane, B.M.; Guo, F. Lateral Response of Piles in Cemented Sand. Géotechnique 2017, 67, 597–607. [Google Scholar] [CrossRef]
- Randolph, M.F. The Response of Flexible Piles to Lateral Loading. Géotechnique 1981, 31, 247–259. [Google Scholar] [CrossRef]
- Poulos, H.G. Pile Behaviour—Theory and Application. Géotechnique 1989, 39, 365–415. [Google Scholar] [CrossRef]
- Hetényi, M.; Hetbenyi, M.I. Beams on Elastic Foundation: Theory with Applications in the Fields of Civil and Mechanical Engineering; University of Michigan Press: Ann Arbor, MI, USA, 1946; Volume 16. [Google Scholar]
- Arany, L.; Bhattacharya, S.; Macdonald, J.; Hogan, S.J. Design of Monopiles for Offshore Wind Turbines in 10 Steps. Soil Dyn. Earthq. Eng. 2017, 92, 126–152. [Google Scholar] [CrossRef]
- Bhattacharya, S. Challenges in Design of Foundations for Offshore Wind Turbines. Eng. Technol. Ref. 2014, 1, 922. [Google Scholar] [CrossRef]
- Kunasegaram, V.; Takemura, J. Deflection and Failure of High-Stiffness Cantilever Retaining Wall Embedded in Soft Rock. Int. J. Phys. Model. Geotech. 2021, 21, 114–134. [Google Scholar] [CrossRef]
- Takemura, J.; Kondoh, M.; Esaki, T.; Kouda, M.; Kusakabe, O. Centrifuge Model Tests on Double Propped Wall Excavation in Soft Clay. Soils Found. 1999, 39, 75–87. [Google Scholar] [CrossRef] [PubMed]
- Fukushima, S.; Tatsuoka, F. Strength and Deformation Characteristics of Saturated Sand at Extremely Low Pressures. Soils Found. 1984, 24, 30–48. [Google Scholar] [CrossRef] [PubMed]
- Tatsuoka, F.; Goto, S.; Sakamoto, M. Effects of Some Factors on Strength and Deformation Characteristics of Sand at Low Pressures. Soils Found. 1986, 26, 105–114. [Google Scholar] [CrossRef]
- Leblanc, C.; Houlsby, G.T.; Byrne, B.W. Response of Stiff Piles in Sand to Long-Term Cyclic Lateral Loading. Géotechnique 2010, 60, 79–90. [Google Scholar] [CrossRef]
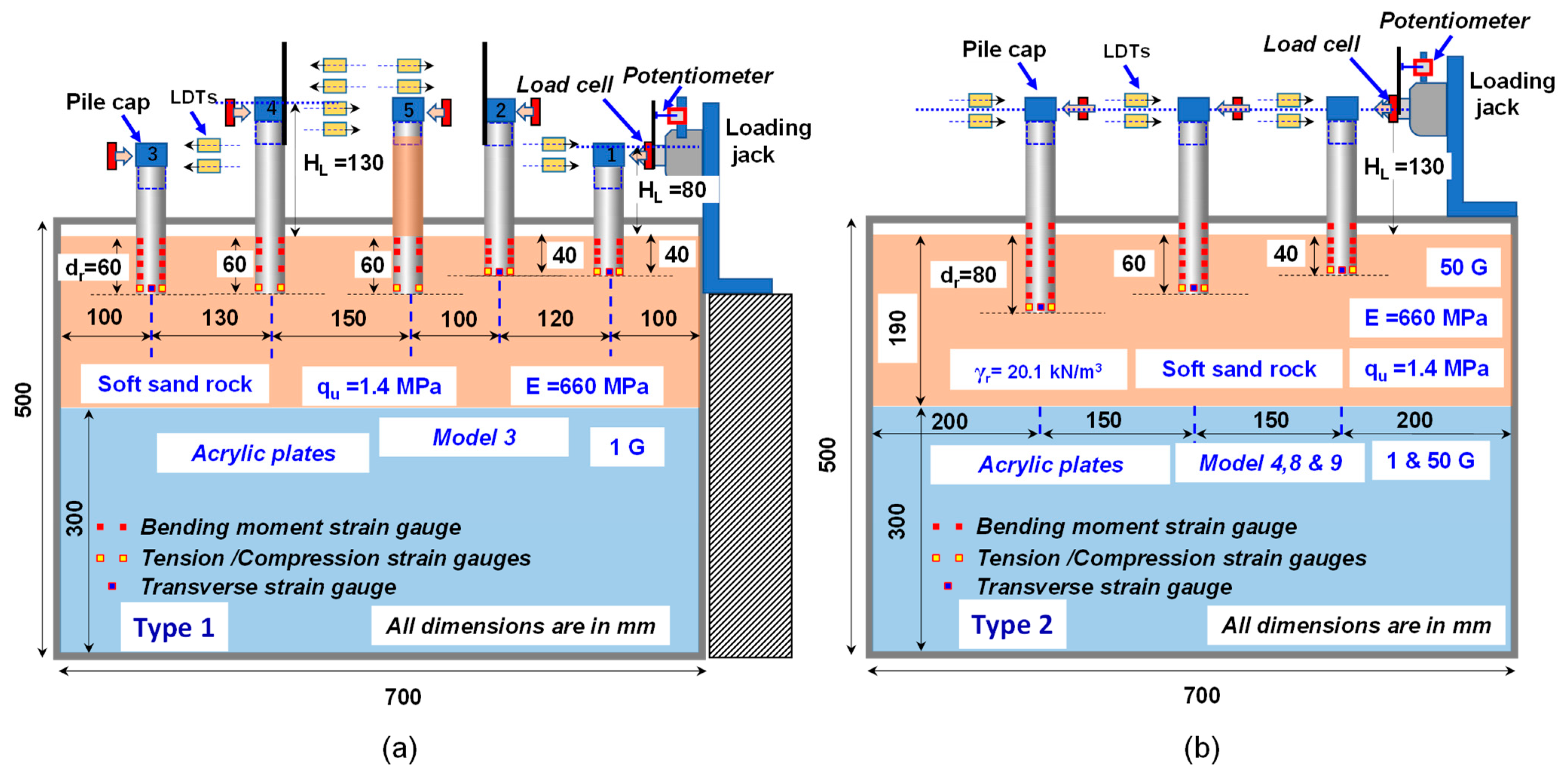


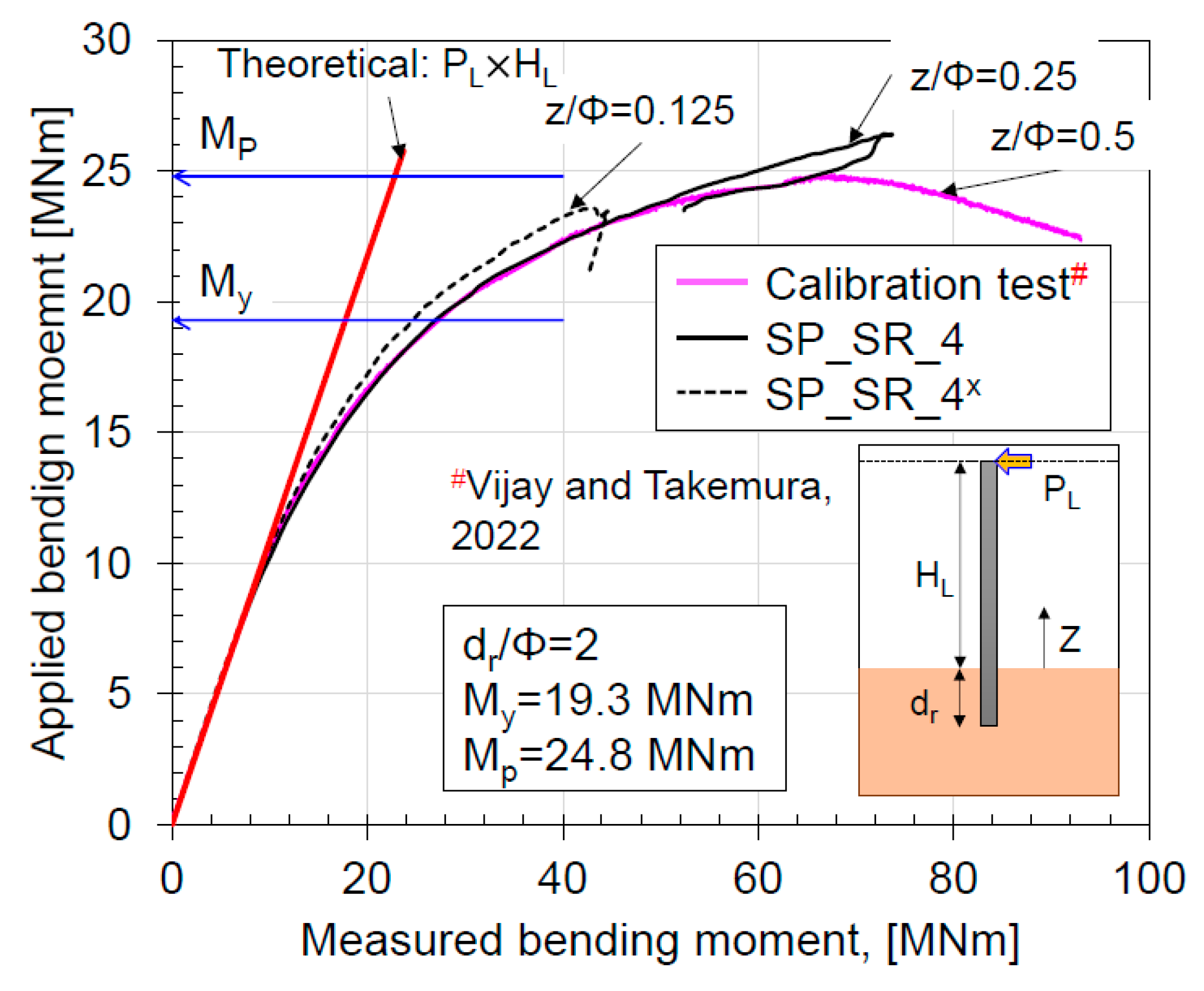
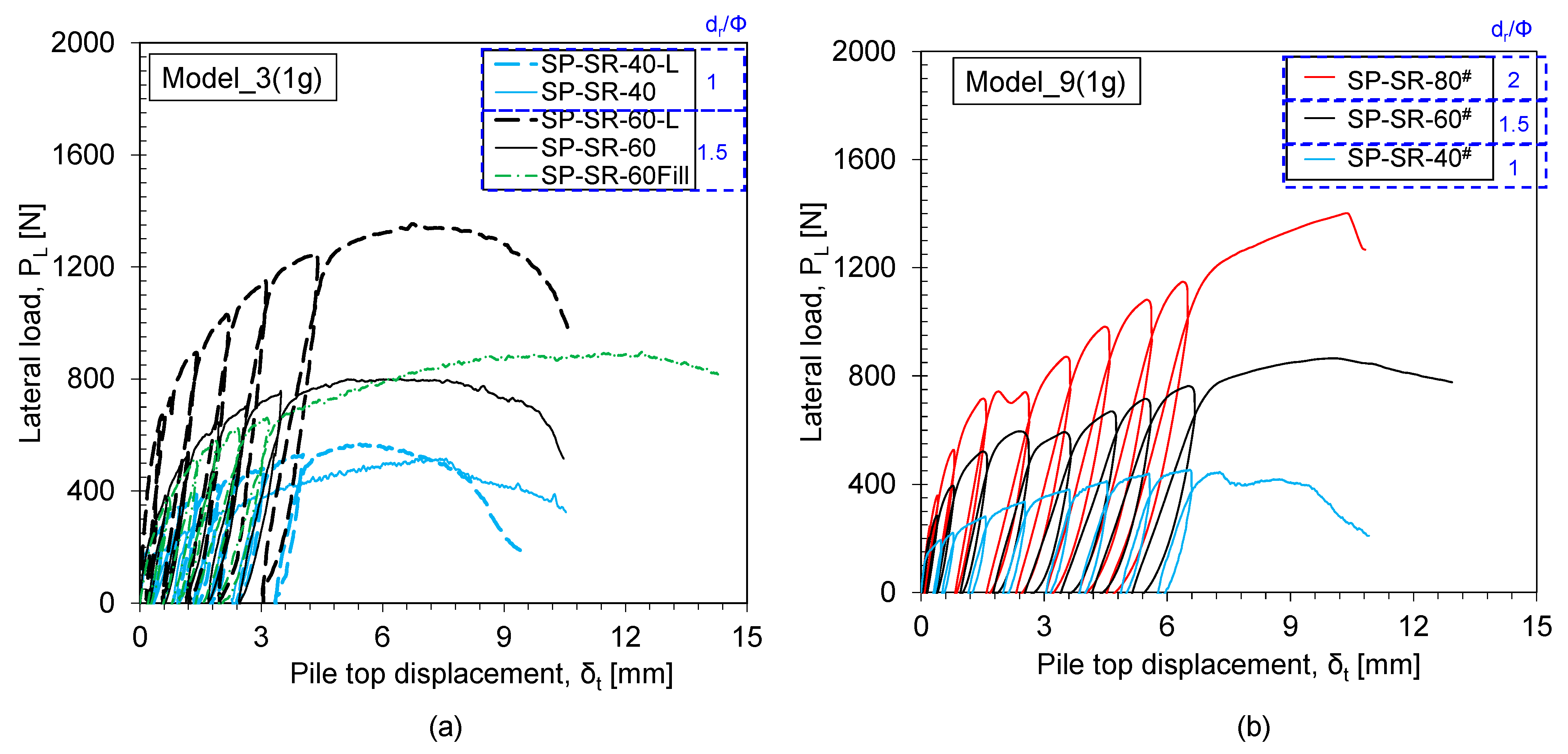

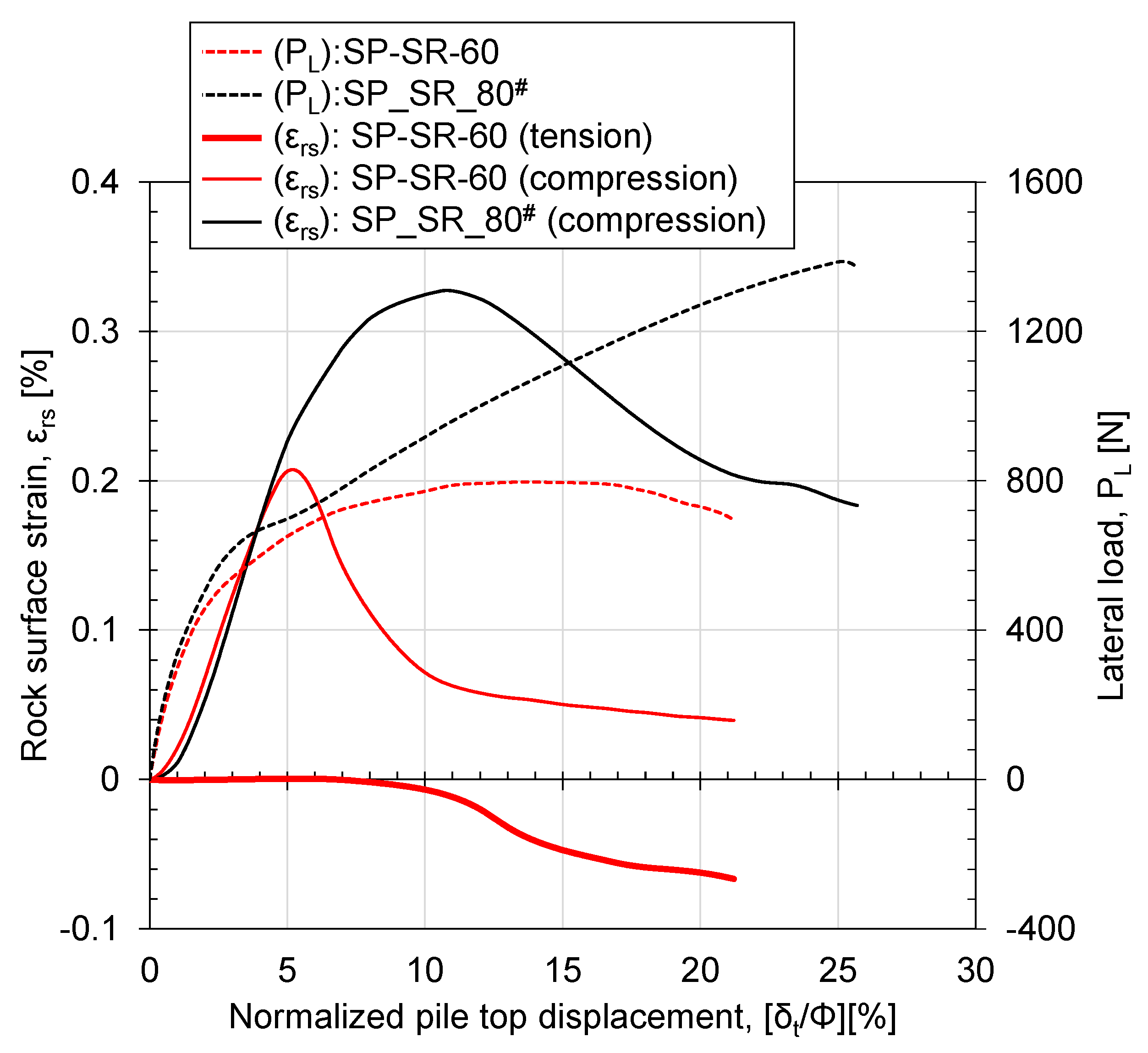
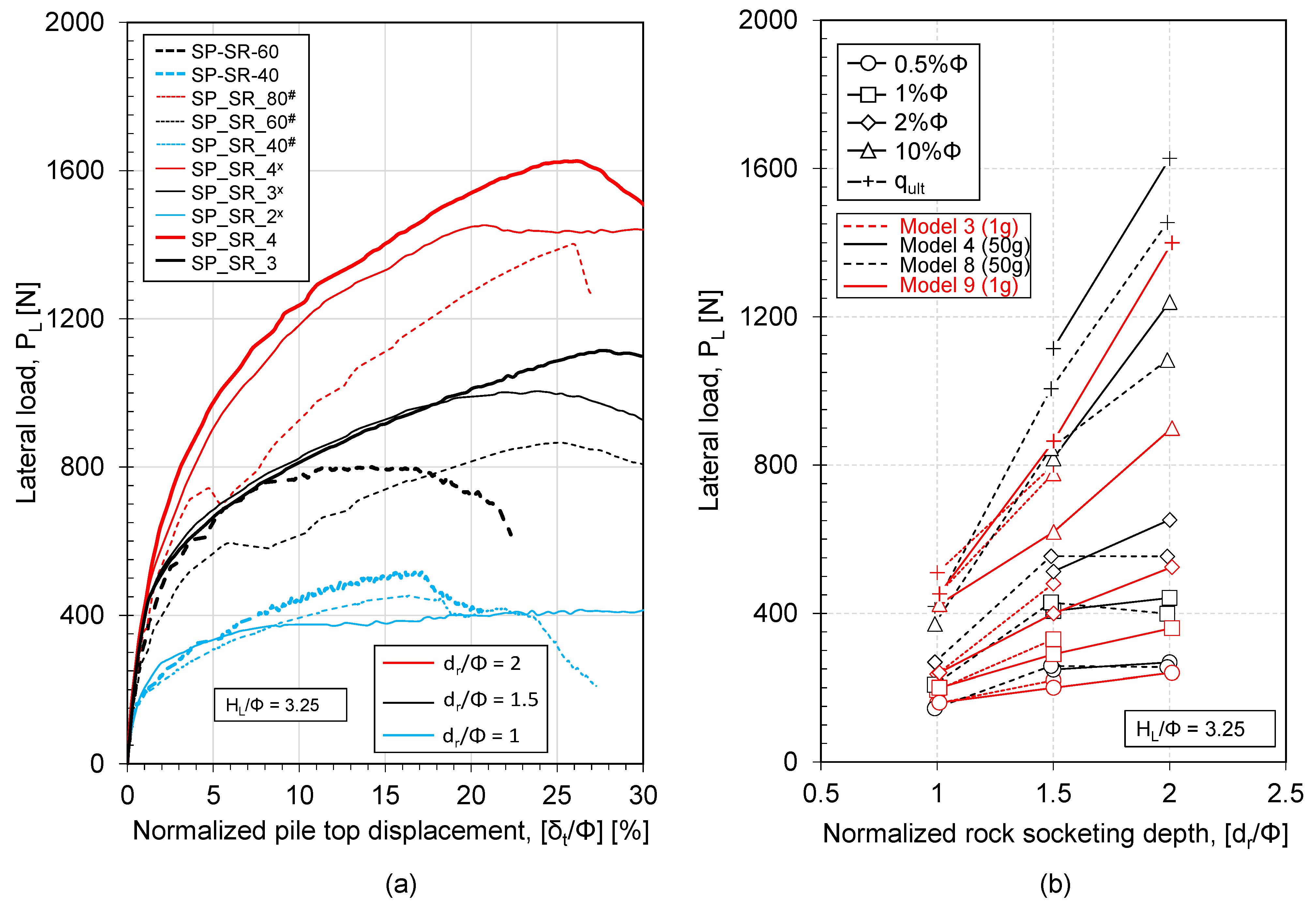
| Model No. | Acceleration | Pile Notation (Pile No.) | Rock Socketing Depth: dr [dr/Φ] | Loading Height: HL [HL/Φ] | Pile Properties |
|---|---|---|---|---|---|
| Model 3 | 1 g | SP-SR-40 SP-SR-60 SP-SR-60-Fill | 40 mm [1.0] 60 mm [1.5] 60 mm [1.5] | 130 mm [3.25] | Φ = 40 mm (2 m) t = 0.5 mm (25 mm) EI = 2.34 × 10−6 GNm2 (14.6 GNm2) My = 1.54 × 10−4 MNm (19.3 MNm) Mp = 1.99 × 10−4 MNm (24.9 MNm) |
| SP-SR-40-l SP-SR-60-L | 40 mm [1.0] 60 mm [1.5] | 80 mm [2.0] | |||
| Model 4 | 50 g | SP_SR_2 * SP_SR_3 SP_SR_4 | 40 mm (2) $ [1.0] 60 mm (3) [1.5] 80 mm (4) [2.0] | 130 mm [3.25] | |
| Model 8 | 50 g | SP_SR_2x SP_SR_3x SP_SR_4x | 40 mm (2) [1.0] 60 mm (3) [1.5] 80 mm (4) [2.0] | 130 mm [3.25] | |
| Model 9 | 1 g | SP_SR_40# SP_SR_60# SP_SR_80# | 40 mm [1.0] 60 mm [1.5] 80 mm [2.0] | 130 mm [3.25] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shafi, S.M.; Takemura, J.; Kunasegaram, V. Physical Modelling of High Stiffness Large Diameter Steel Tubular Pile Subjected to One-Way Horizontal Cyclic Loading. Geotechnics 2023, 3, 515-530. https://doi.org/10.3390/geotechnics3020028
Shafi SM, Takemura J, Kunasegaram V. Physical Modelling of High Stiffness Large Diameter Steel Tubular Pile Subjected to One-Way Horizontal Cyclic Loading. Geotechnics. 2023; 3(2):515-530. https://doi.org/10.3390/geotechnics3020028
Chicago/Turabian StyleShafi, S M, Jiro Takemura, and Vijayakanthan Kunasegaram. 2023. "Physical Modelling of High Stiffness Large Diameter Steel Tubular Pile Subjected to One-Way Horizontal Cyclic Loading" Geotechnics 3, no. 2: 515-530. https://doi.org/10.3390/geotechnics3020028
APA StyleShafi, S. M., Takemura, J., & Kunasegaram, V. (2023). Physical Modelling of High Stiffness Large Diameter Steel Tubular Pile Subjected to One-Way Horizontal Cyclic Loading. Geotechnics, 3(2), 515-530. https://doi.org/10.3390/geotechnics3020028





