The Dynamic Properties of Sand under Torsion: A Literature Review
Abstract
1. Introduction
2. Dynamic Behavior of Soils
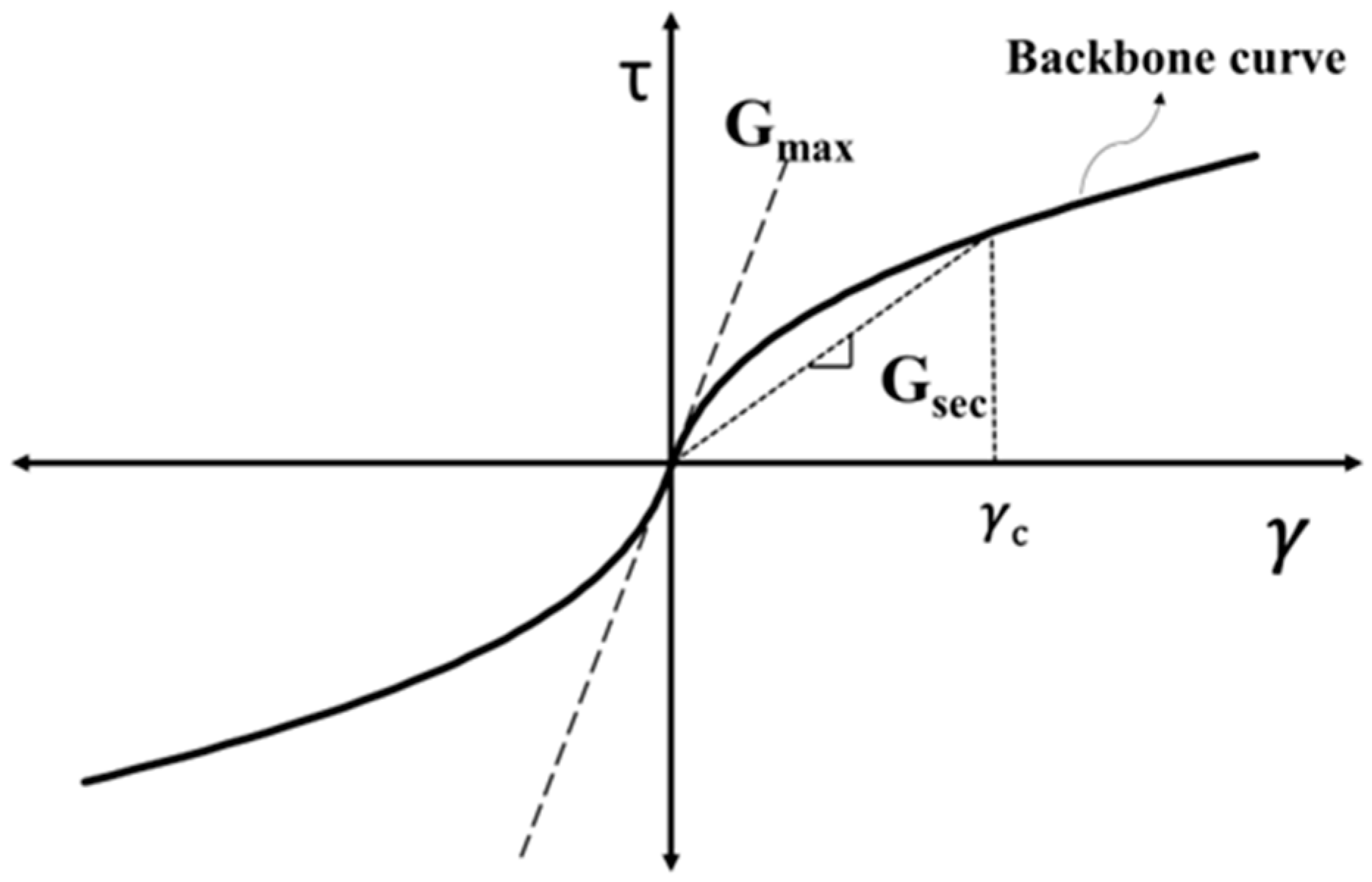
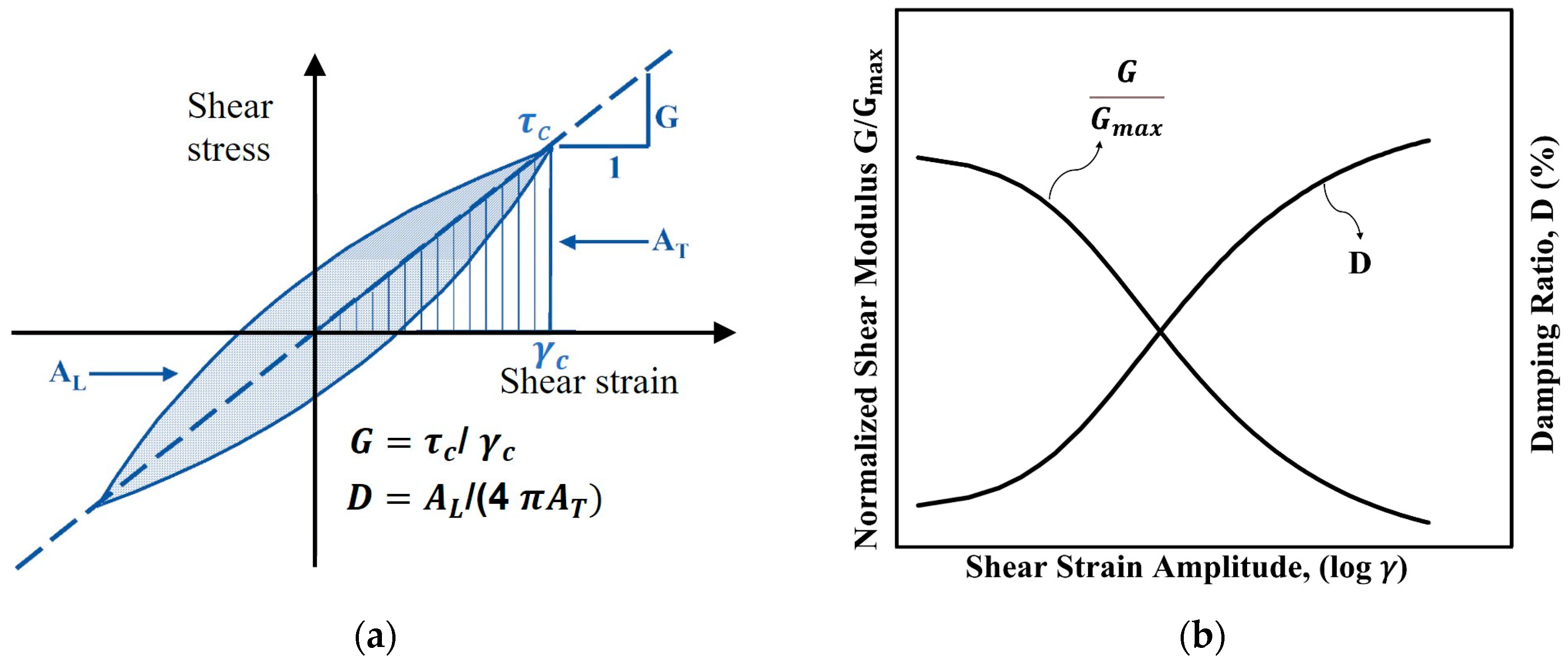
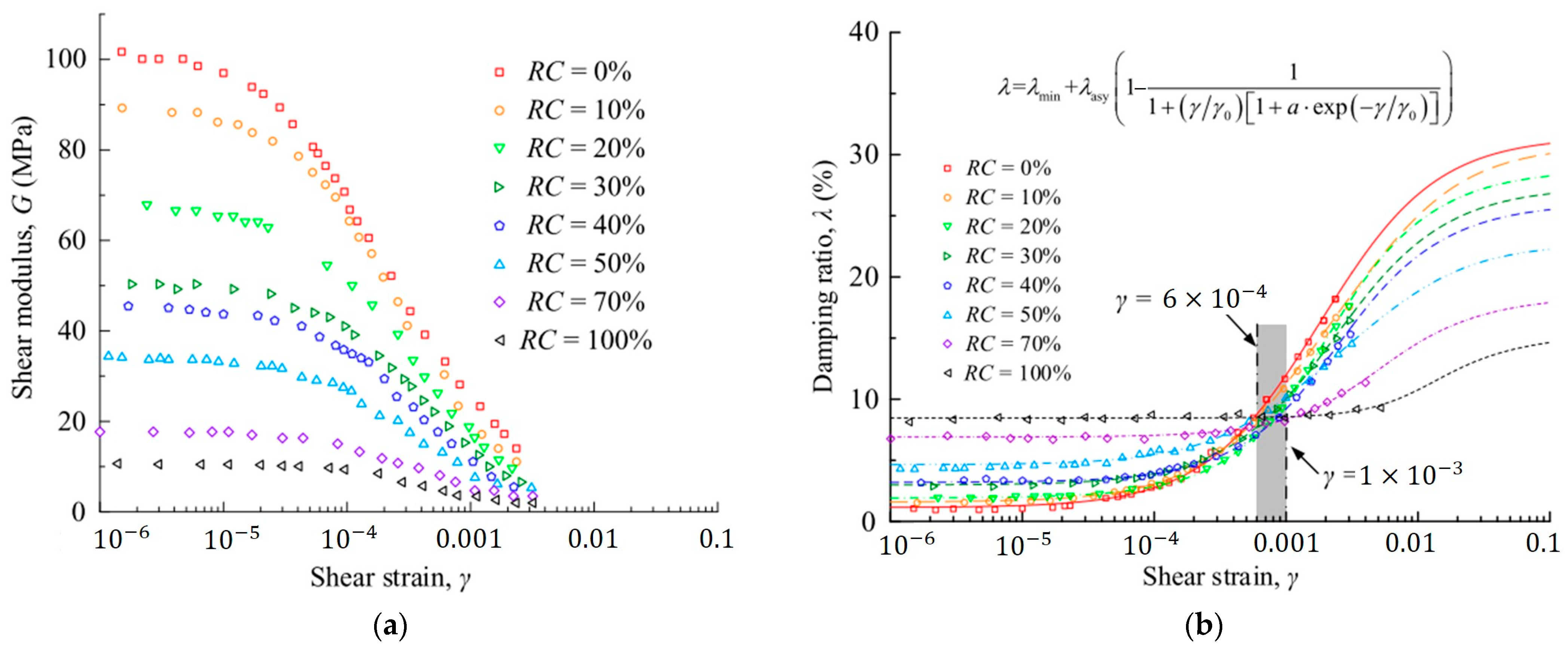
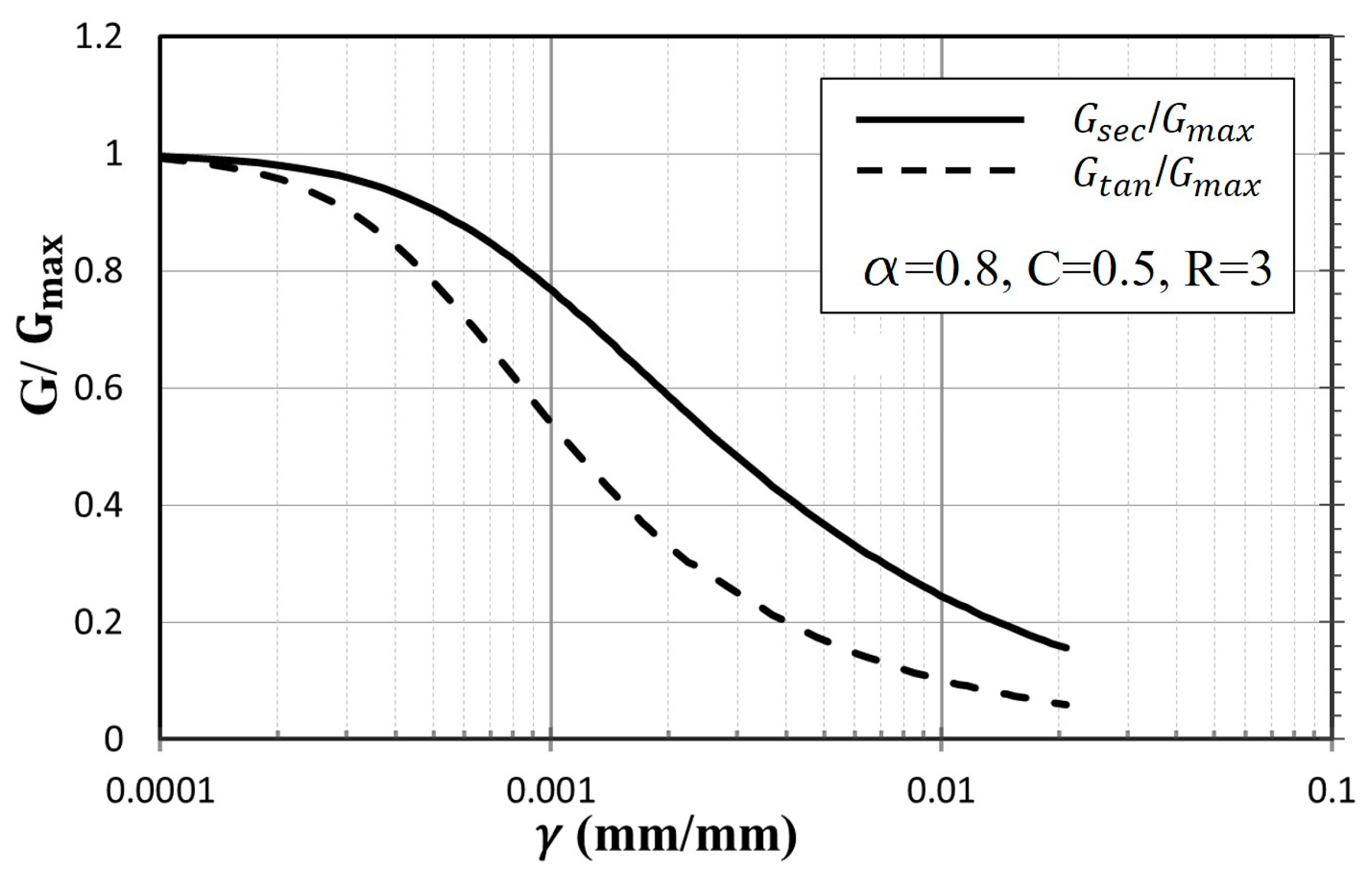
2.1. Dynamic Shear Modulus
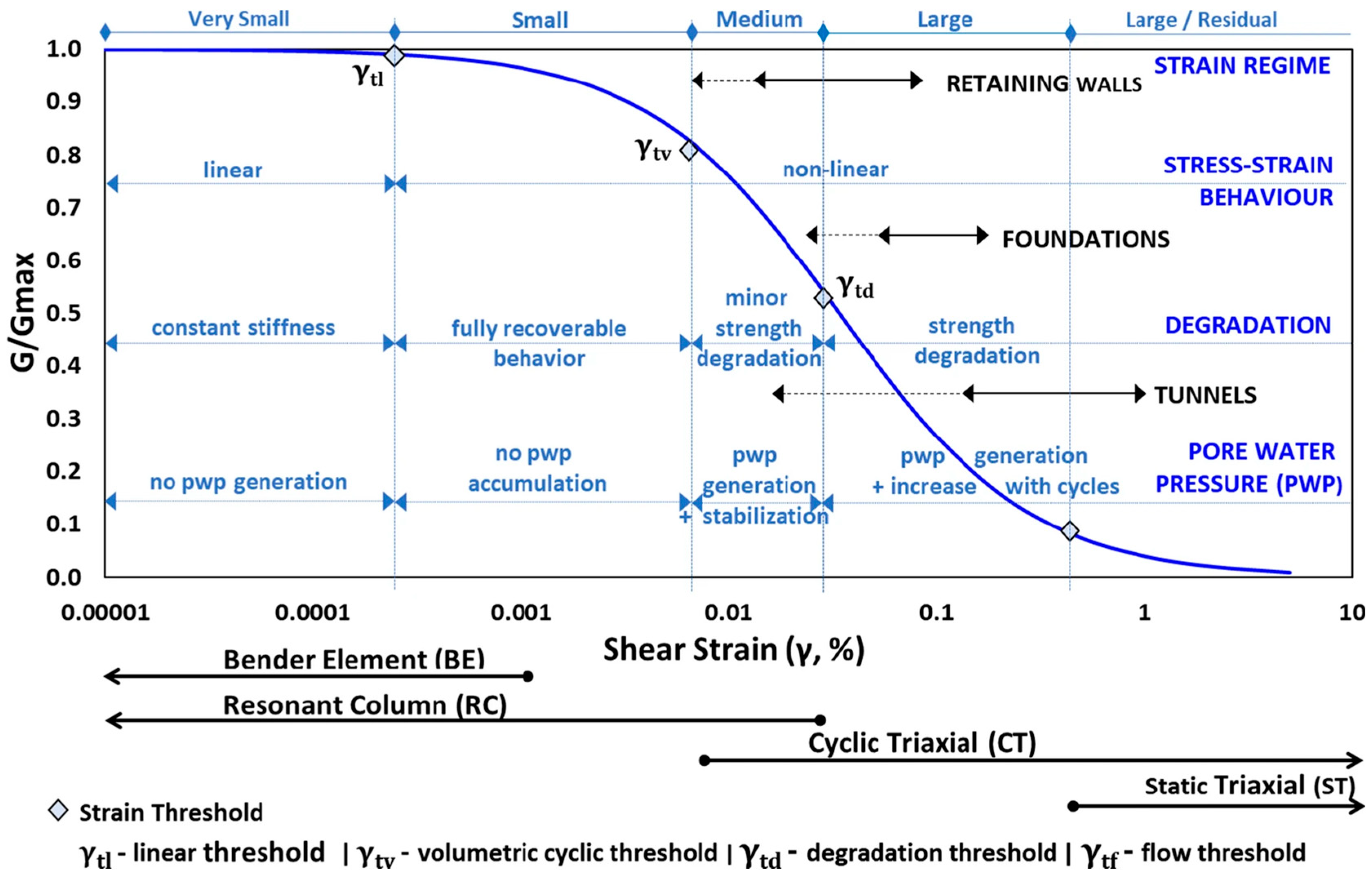
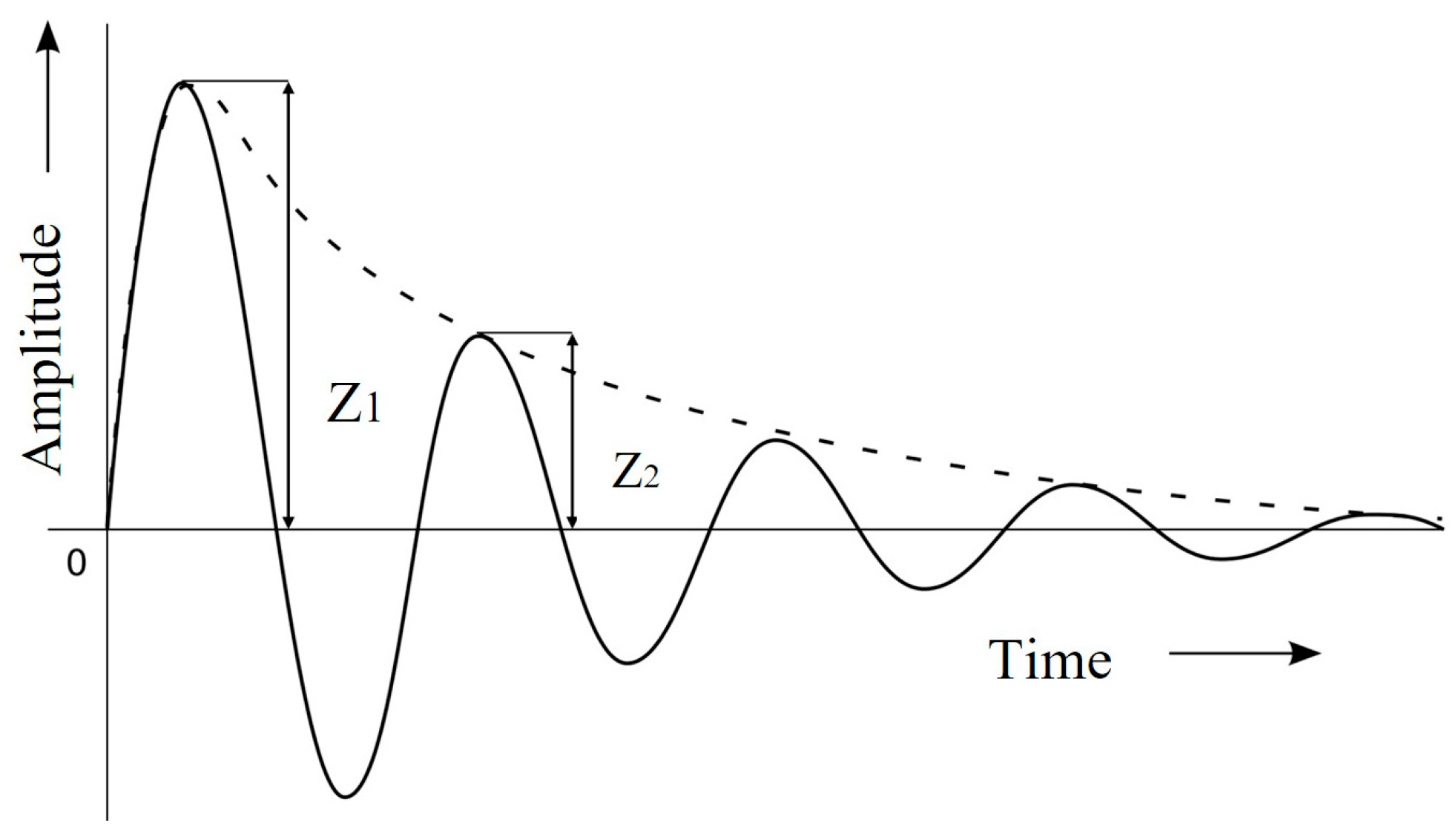
2.2. Damping Ratio
3. Device Performance in RC-TOSS Testing
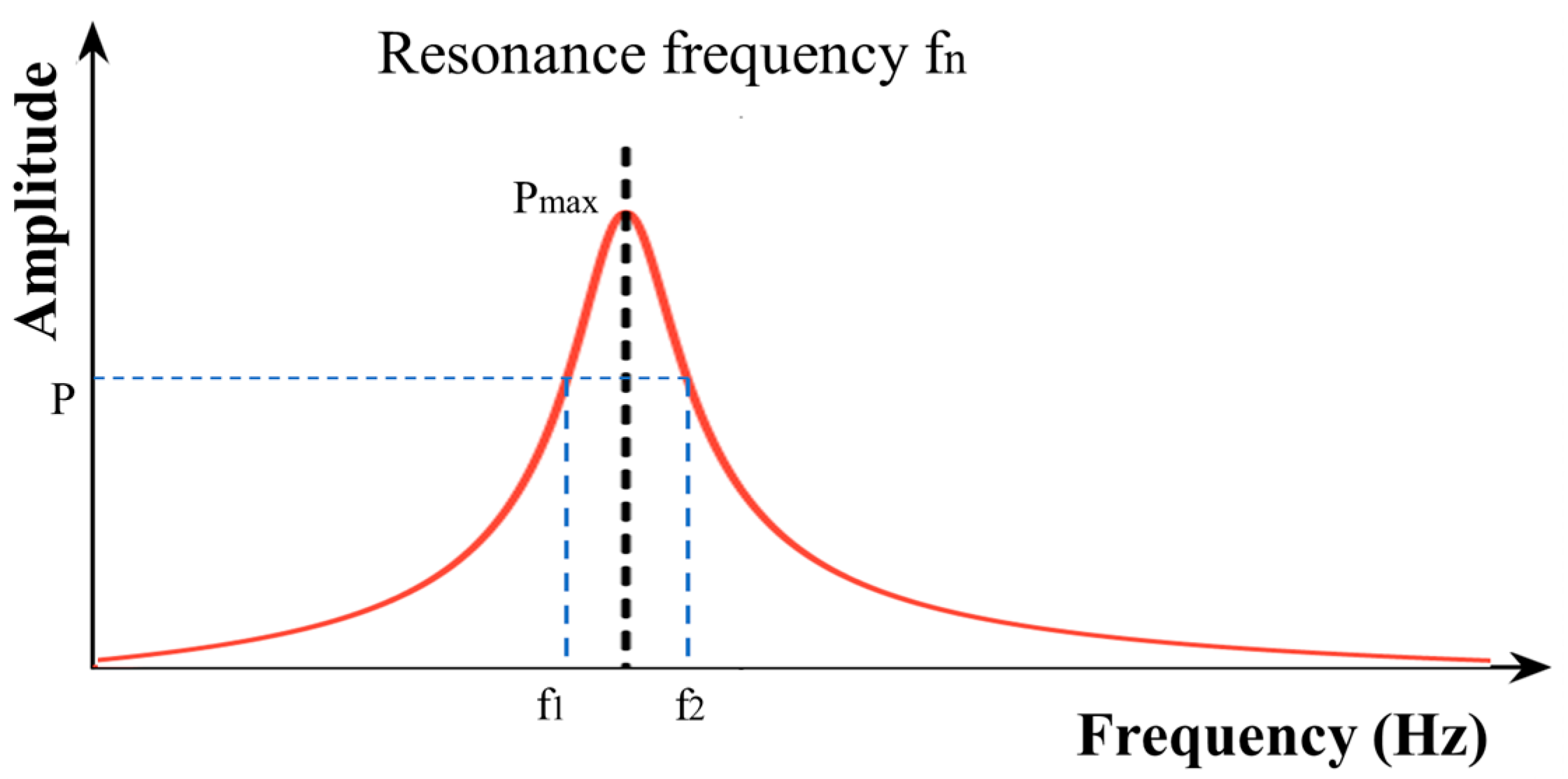
3.1. Fundamental Concepts
3.2. Advantages and Disadvantages
4. Factors Affecting the Dynamic Behavior of Soil
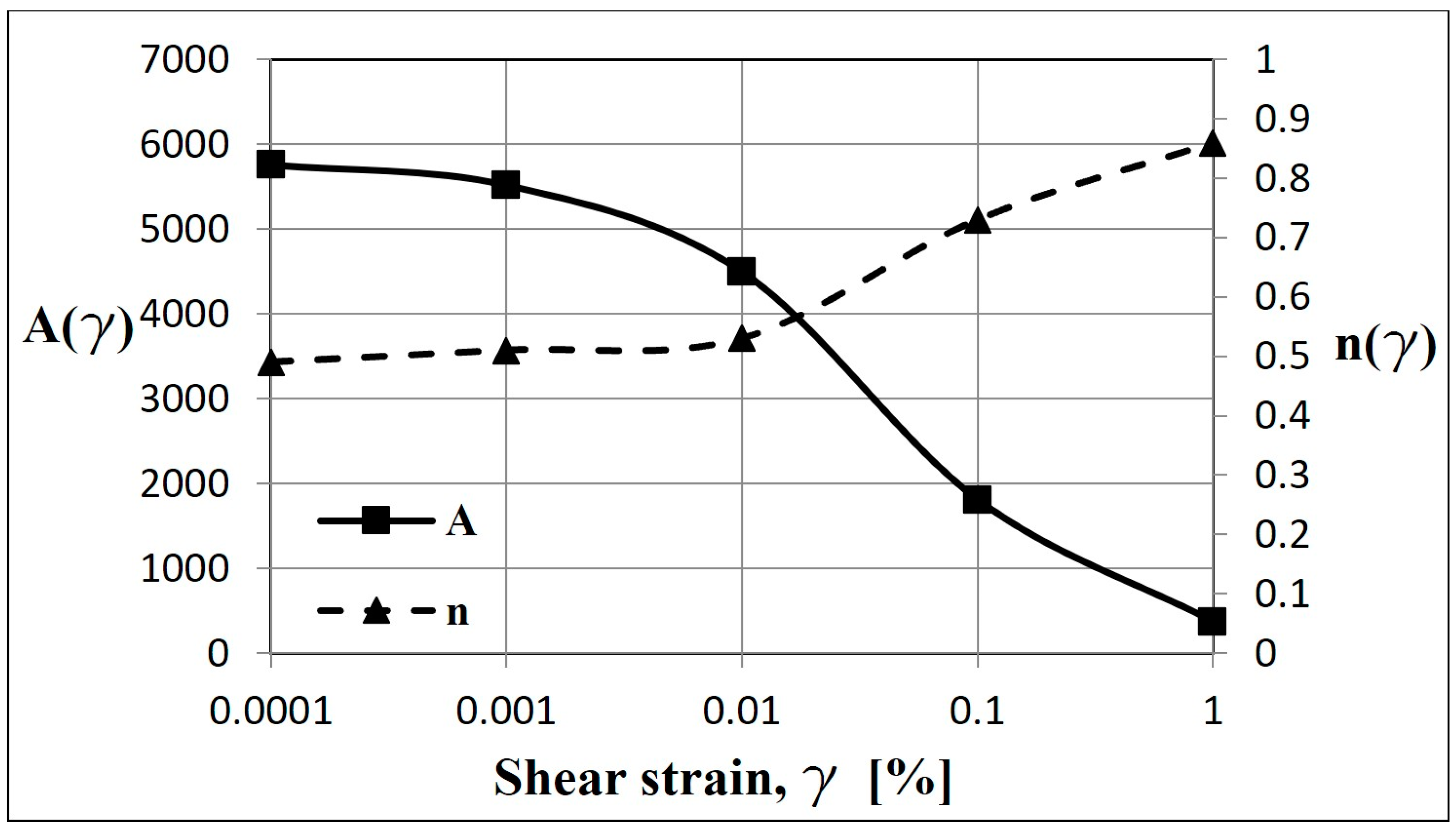
4.1. Strain Amplitude
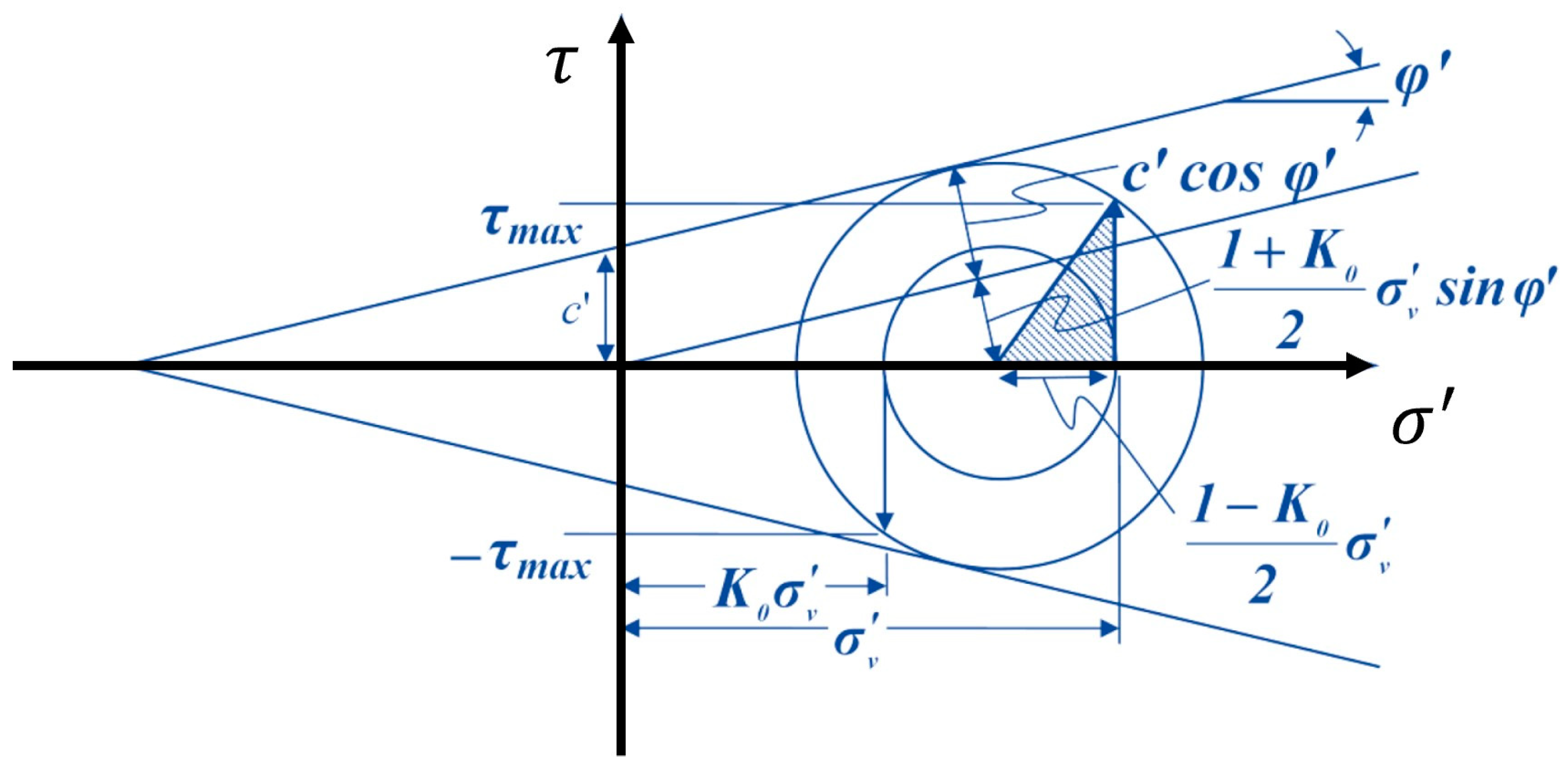
4.2. Magnitude of the Effective Confining Pressure
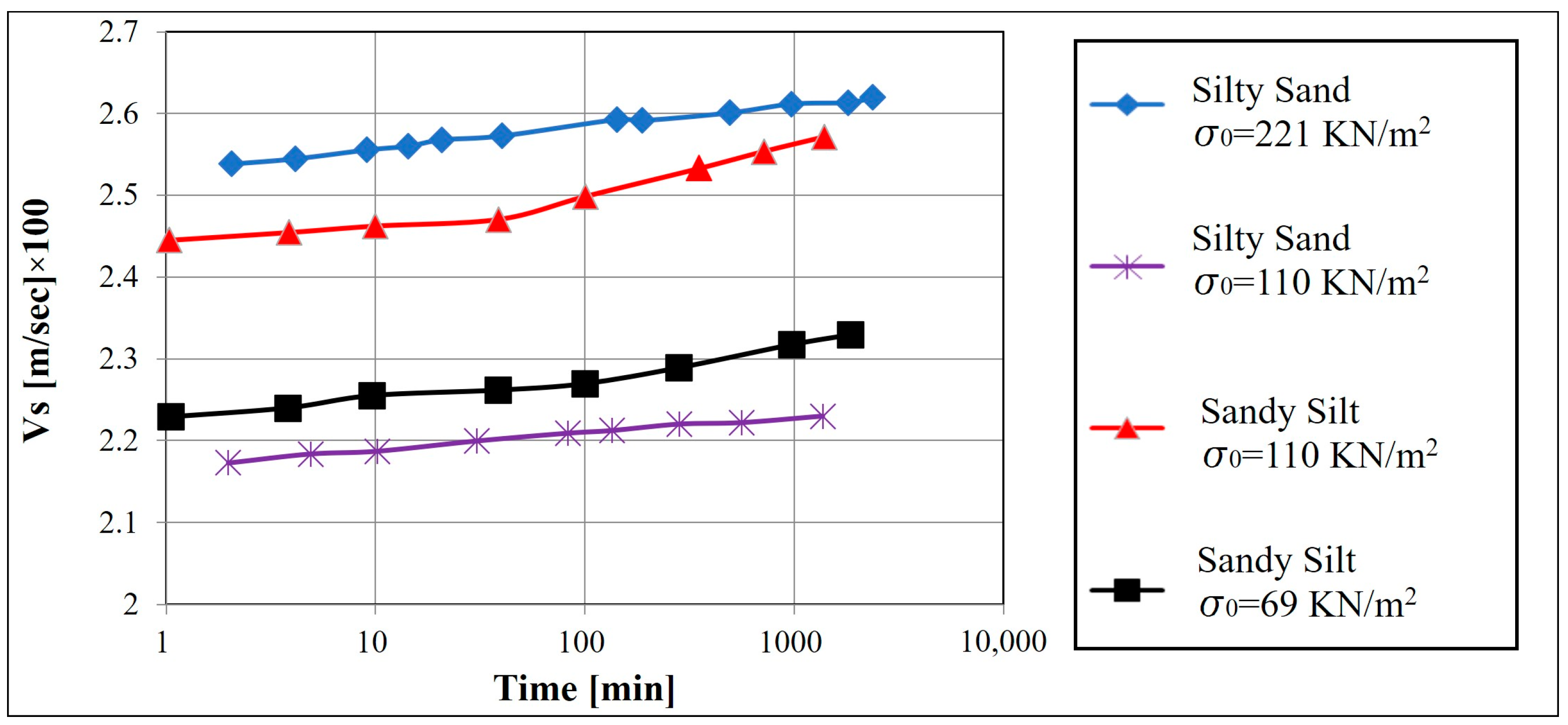
4.3. Duration of the Effective Confinement Pressure
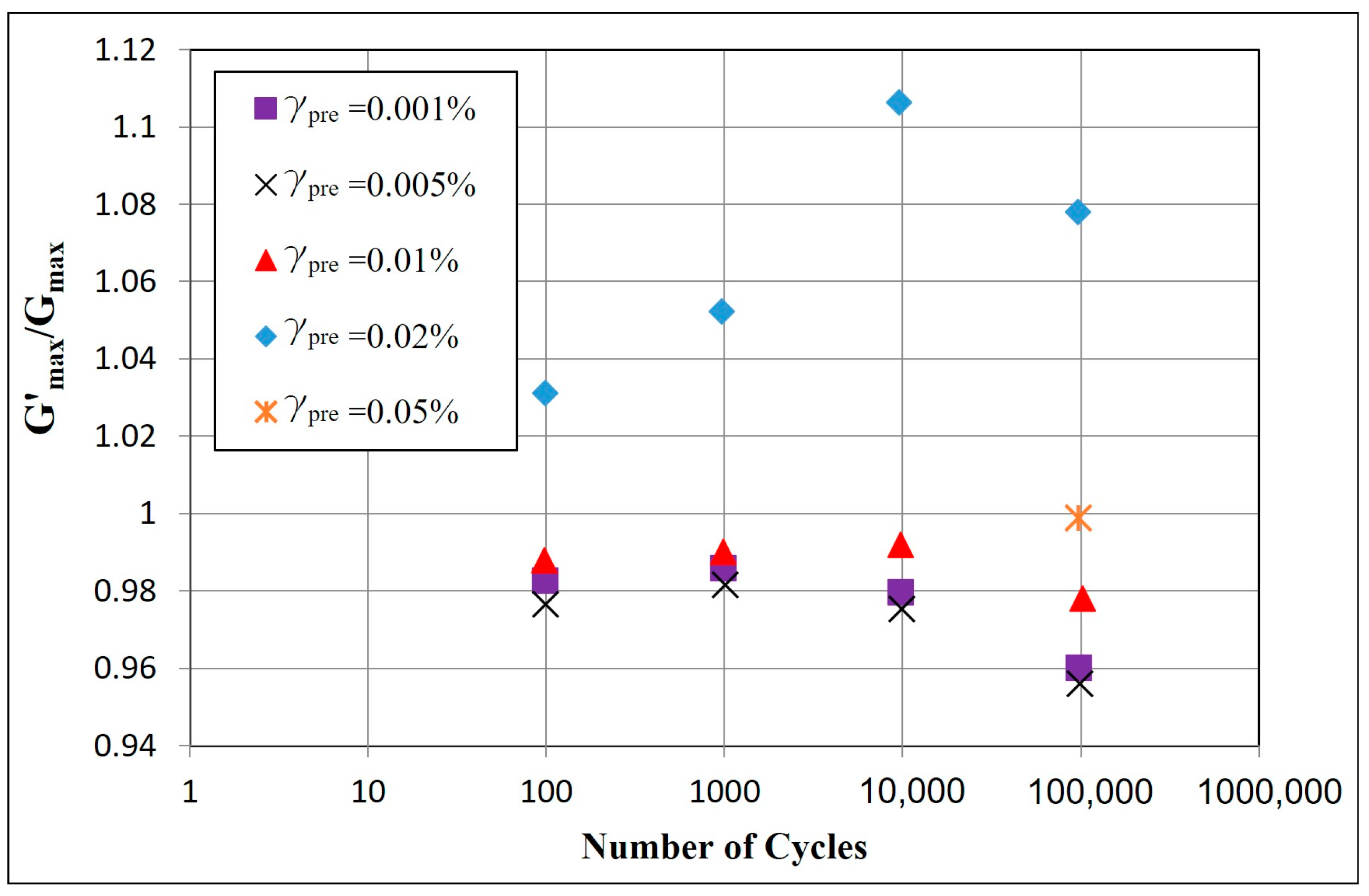
4.4. Number of Loading Cycles
4.5. Loading Frequency
4.6. Void Ratio
| Soil Tested | D50 [mm] | CU [−] | A [−] | F(e) [−] | n [−] | Reference |
|---|---|---|---|---|---|---|
| Ottawa sand No. 20–30 | 0.72 | 1.20 | 69 | 0.5 | (Hardin and Richart, 1963) [10] | |
| Ticino sand (subangular) | 0.54 | 1.50 | 71 | 0.43 | (Lo Presti, et al., 1993) [81] | |
| Toyoura sand (subangular) | 0.22 | 1.35 | 72 | 0.45 | (Lo Presti, et al., 1993) [81] | |
| Quiou carbonate sand | 0.75 | 4.40 | 71 | 0.62 | (Lo Presti, et al., 1993) [81] | |
| Kenya carbonate sand | 0.13 | 1.86 | 101–129 | 0.45–0.52 | (Fioravante, 2000) [48] | |
| Ticino sand (subangular) | 0.55 | 1.66 | 79–90 | 0.43–0.48 | (Fioravante, 2000) [48] | |
| Hostun sand (angular) | 0.31 | 1.94 | 80 | 0.47 | (Hoque and Tatsuoka, 2000) [82] | |
| H.River sand (subangular) | 0.27 | 1.67 | 72–81 | 0.50–0.52 | (Kuwano and Jardine, 2002) [83] | |
| Glass ballotini (spheres) | 0.27 | 1.28 | 64–69 | 0.55–0.56 | (Kuwano and Jardine, 2002) [83] | |
| Silica sand (subangular) | 0.20 | 1.10 | 80 | 0.5 | (Kallioglou, et al., 2003) [84] | |
| Silica sand (subangular) | 0.20 | 1.70 | 62 | 0.5 | (Kallioglou, et al., 2003) [84] | |
| Silica sand (subangular) | 0.20 | 1.10 | 62 | 0.5 | (Kallioglou, et al., 2003) [84] | |
| Silica sand (angular) | 0.32 | 2.80 | 48 | 0.5 | (Kallioglou, et al., 2003) [84] | |
| Toyoura sand (subangular) | 0.16 | 1.46 | 71–87 | 0.41–0.51 | (Hoque and Tatsuoka, 2004) [49] | |
| Toyoura sand (subangular) | 0.19 | 1.56 | 84–104 | 0.50–0.57 | (Chaudhary, et al., 2004) [50] | |
| Ticino sand (subangular) | 0.50 | 1.33 | 61–64 | 0.44–0.53 | (Hoque and Tatsuoka, 2004) [49] | |
| Silica sand | 0.55 | 1.80 | 275 | 0.42 | (Wichtmann and Triantafyllidis, 2004) [51] | |
| SLB sand (subround) | 0.62 | 1.11 | 82–130 | 0.44–0.53 | (Hoque and Tatsuoka, 2004) [49] | |
| Natural quartz sand | 0.27–1.33 | 1.34–2.76 | −5.88 Cu+57.1 | 0.47 | (Senetakis et al., 2012) [85] | |
| Quarry sand | 0.16–2 | 2–2.5 | −9.54 Cu+78.1 | 0.63 | (Senetakis et al., 2012) [85] | |
| Volcanic sand | 0.23–1.6 | 1.53–4.18 | −3.04 Cu+52 | 0.55 | (Senetakis et al., 2012) [85] | |
| Blue sand | 1.01–1.94 | 1.41–8.22 | (Payan et al., 2016) [13] | |||
| Danube Sand | 0.107–0.424 | 2.06–9.85 | 62 | 0.45 | (Szilvágyi, 2017) [52] |
4.7. Effect of Sample Disturbance
4.8. Temperature Effect
4.9. Soil Improvement Effect
5. Soil Models
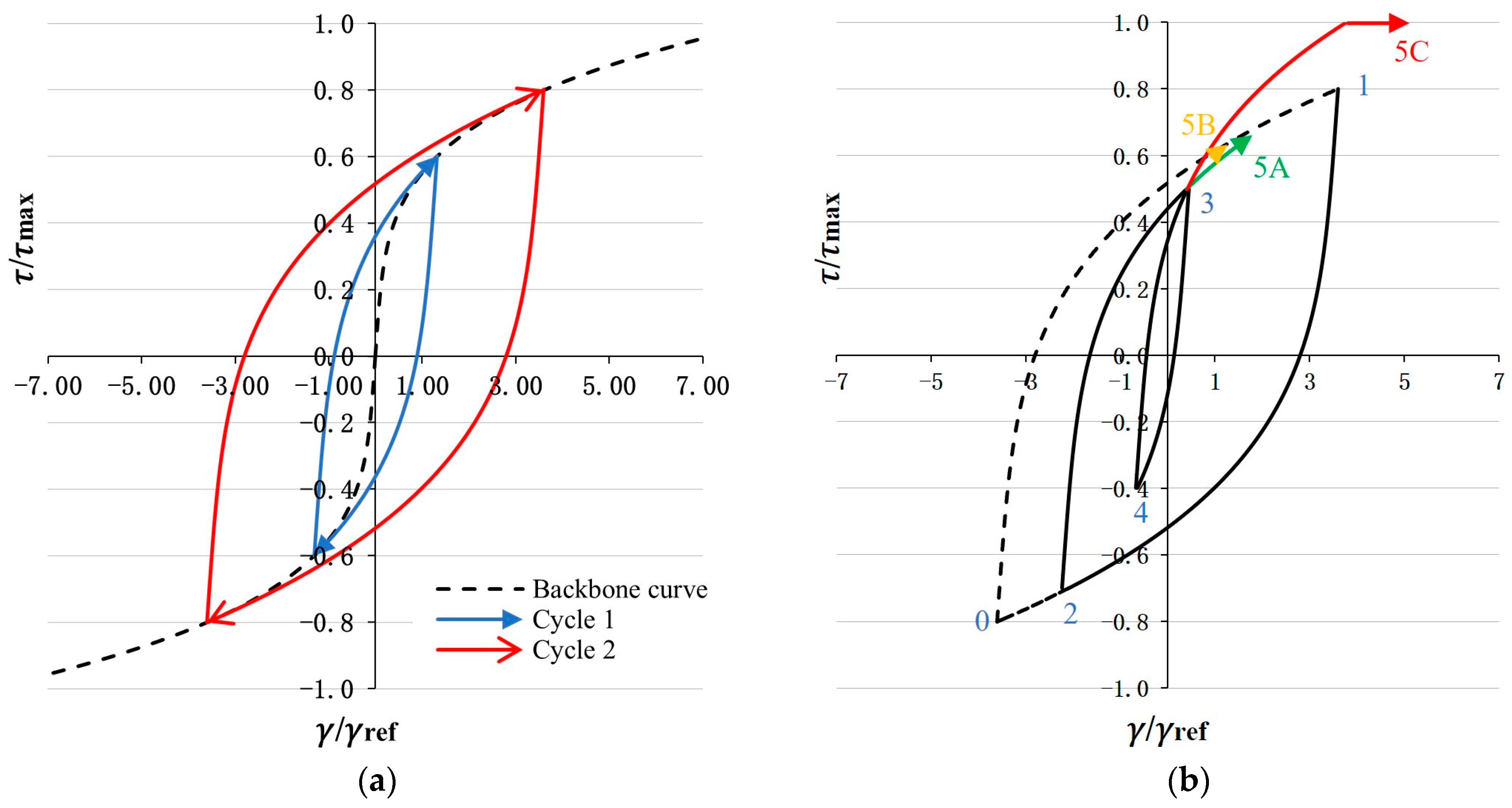
5.1. Irregular Loading and Masing Criteria
- The shear modulus in unloading is equal to the initial tangent modulus for the initial loading curve (Figure 16);
- The unloading and reloading curve duplicate the initial curve, except that its scale increases by a factor of two in both directions. The variables τ and γ in the formulation are replaced by (τ − τi)/2 and (γ − γi)/2 (Figure 16).
- 3.
- Unloading and reloading curves should follow the initial curve if the condition exceeds the previous maximum shear strain;
- 4.
- If the current loading or unloading curve intersects a previous one, it should follow the previous curve.
5.2. Modified Ramberg-Osgood Model
5.3. The Hyperbolic Model
6. Evaluation of Soil Models
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ijaz, Z.; Zhao, C.; Ijaz, N.; Rehman, Z.; Ijaz, A. Development and optimization of geotechnical soil maps using various geostatistical and spatial interpolation techniques: A comprehensive study. Bull. Eng. Geol. Environ. 2023, 82, 1–21. [Google Scholar] [CrossRef]
- Yang, H.-C.; Chou, H.-C.; Hsu, S.-Y.; Chang, W.-K. The influence of boundary conditions on nonlinear time domain site response analysis using LS-DYNA. Comput. Geotech. 2023, 159, 105477. [Google Scholar] [CrossRef]
- Kegyes-Brassai, O.; Wolf, Á.; Szilvágyi, Z.; Ray, R. Effects of local ground conditions on site response analysis results in Hungary. Proceedings of 19th International Conference On Soil Mechanics and Geotechnical Engineering, Seoul, Republic of Korea, 17–21 September 2017; pp. 2003–2006. [Google Scholar]
- Bordoni, P.; Gori, S.; Akinci, A.; Visini, F.; Sgobba, S.; Pacor, F.; Cara, F.; Pampanin, S.; Milana, G.; Doglioni, C. A site-specific earthquake ground response analysis using a fault-based approach and nonlinear modeling: The Case Pente site (Sulmona, Italy). Eng. Geol. 2013, 314, 106970. [Google Scholar] [CrossRef]
- Majidi, N.; Riahi, H.T.; Zandi, S.M. Reducing computational costs in site response analysis and its application for the nonlinear dynamic analysis of structures. Structures 2022, 46, 1345–1368. [Google Scholar] [CrossRef]
- Upreti, K.; Leong, E.C. Effect of mean grain size on shear modulus degradation and damping ratio curves of sands. Géotechnique 2021, 71, 205–215. [Google Scholar]
- Szilvágyi, Z.; Ray, R.P. Verification of the Ramberg-Osgood Material Model in Midas GTS NX with the Modeling of Torsional Simple Shear Tests. Period. Polytech. 2018, 62, 1–7. [Google Scholar] [CrossRef]
- Zhou, H.; Wotherspoon, L.M.; Hayden, C.P.; Stolte, A.C.; McGann, C.R. Applicability of existing CPT-Vs correlations to shallow Holocene Christchurch soils based on direct Push crosshole testing. Eng. Geol. 2023, 313, 106927. [Google Scholar] [CrossRef]
- Rehman, M.A.; Rahman, N.A.; Masli, M.N.; Razali, S.F.M.; Taib, A.M.; Kamal, N.A.; Jusoh, H.; Ahmad, A. Relationship between soil erodibility and shear wave velocity: A feasibility study. Phys. Chem. Earth Parts A/B/C 2022, 128, 103246. [Google Scholar] [CrossRef]
- Hardin, B.; Richart, F. Elastic wave velocities in granular soils. J. Soil Mech. Found. Div. 1963, 89, 33–65. [Google Scholar] [CrossRef]
- Hardin, B.; Black, W. Sand stiffness under various triaxial stresses. J. Soil Mech. Found. Div. 1966, 92, 27–42. [Google Scholar] [CrossRef]
- Wichtmann, T.; Hernández, M.N.; Triantafyllidis, T. On the influence of a non-cohesive fines content on small strain stiffness, modulus degradation and damping of quartz sand. Soil Dyn. Earthq. Eng. 2015, 69, 103–114. [Google Scholar] [CrossRef]
- Payan, M.; Senetakis, K.; Khoshghalb, A.; Khalili, N. Influence of particle shape on small-strain damping ratio of dry sands. Geotechnique 2016, 66, 610–616. [Google Scholar] [CrossRef]
- Szilvágyi; Hudacsek, P.; Ray, R.P. Soil shear modulus from Resonant Column, Torsional Shear and Bender Element Tests. Int. J. Geomate 2016, 10, 1822–1827. [Google Scholar] [CrossRef]
- Shi, J.; Haegeman, W.; Xu, T. Effect of non-plastic fines on the anisotropic small strain stiffness of a calcareous sand. Soil Dyn. Earthq. Eng. 2020, 139, 106381. [Google Scholar] [CrossRef]
- Vucetic, M. Cyclic threshold shear strains in soils. J. Geotech. Eng. 1994, 120, 2208–2228. [Google Scholar] [CrossRef]
- Anderson, B.A. Deformation Characteristics of Soft, High-Plastic Clays under Dynamic Loading Conditions; Chalmers University of Technology: Gothenburg, Sweden, 1979. [Google Scholar]
- Ladd, R.S. Geotechnical Laboratory Testing Program for Study and Evaluation of Liquefaction Ground Failure Using Stress and Strain Approaches: Heber Road site, October 15, 1979 Imperial Valley Earthquake; Woodward- Clyde Consultants, Eastern Region: Wayne, NJ, USA, 1982. [Google Scholar]
- Georgiannou, V.N.; Rampello, S.; Silvestri, F. Static and dynamic measurements of undrained stiffness of natural overconsolidated clays. In Proceedings of the X European Conference on Soil Mechanics and Foundation Engineering, Florence, Italy, 26–30 May 1991. [Google Scholar]
- Wong, J.K.H.; Wong, S.Y.; Wong, K.Y. Extended model of shear modulus reduction for cohesive soils. Acta Geotech. 2022, 17, 2347–2363. [Google Scholar] [CrossRef]
- White, J.E. Underground Sound: Applications of Seismic Waves; Elsevier: Amsterdam, The Netherlands, 1983; Volume 18, pp. 83–137. [Google Scholar]
- Kramer, S.L. Geotechnical Earthquake Engineering; Prentice Hall: Upper Saddle River, NJ, USA, 1996; p. 643. ISBN 978-0133749434. [Google Scholar]
- Kokusho, T. In situ Dynamic Soil Properties and Their Evaluations. In Proceedings of the 8th Asian Regional Conference of SMFE, Kyoto, Japan, 20–24 July 1987. [Google Scholar]
- Hardin, B. The Nature of Damping in Sands. J. Soil Mech. Found. Div. 1965, 91, 63–98. [Google Scholar] [CrossRef]
- Dobry, R. Damping in Soils: Its Hysteretic Nature and the Linear Approximation; Massachusetts Institute of Technology: Cambridge, MA, USA, 1970. [Google Scholar]
- Bae, Y.-S. Modeling Soil Behavior in Large Strain Resonant Column and Torsional Shear Tests. Ph.D. Dissertation, Utah State University, Logan, UT, USA, 2007. [Google Scholar]
- Richart, F.E.; Hall, J.R.; Woods, R.D. Vibrations of Soils and Foundations; Prentice-Hall: Englewood Cliffs, NJ, USA, 1970. [Google Scholar]
- Ishihara, K. Soil Behavior in Earthquake Geotechnics; Oxford University Press: New York, NY, USA, 1996; pp. 33–39. ISBN 0-19-856224-1. [Google Scholar]
- Xu, Z.; Tao, Y.; Hernandez, L. Novel Methods for the Computation of Small-Strain Damping Ratios of Soils from Cyclic Torsional Shear and Free-Vibration Decay Testing. Geotechnics 2021, 1, 330–346. [Google Scholar] [CrossRef]
- Drnevich, V.P.; Hardin, B.O.; Shippy, D.J. Modulus and Damping of Soils by the Resonant Column Method; ASTM STP 654, Dynamic Geotechnical Testing; ASTM: West Conshohocken, PA, USA, 1978; pp. 91–125. [Google Scholar]
- Ray, R.P. Changes in Shear Modulus and Damping in Cohesionless Soils due to Repeated Loading. Ph.D. Dissertation, University of Michigan, Ann Arbor, MI, USA, 1984; p. 417. [Google Scholar]
- ASTM D4015; Standard Test Methods for Modulus and Damping of Soils by Resonant-Column Method. Annual Book of ASTM Standards; ASTM International: West Conshohocken, PA, USA, 1992.
- Gabryś, K.; Soból, E.; Sas, W.; Szymański, A. Material damping ratio from free-vibration method. Ann. Wars. Univ. Life Sci. SGGW Land Reclam. 2018, 50, 83–97. [Google Scholar] [CrossRef]
- Mog, K.; Anbazhagan, P. Evaluation of the damping ratio of soils in a resonant column using different methods. Soils Found. 2022, 62, 101091. [Google Scholar] [CrossRef]
- Chopra, A.K.; Structures, D.O. Theory and Applications to Earthquake Engineering, 3rd ed.; Prentice Hall: Hoboken, NJ, USA, 2007. [Google Scholar]
- Meng, J. The influence of Loading Frequency on Dynamic Soil Properties. Ph.D. Dissertation, Georgia Institute of Technology, Atlanta, GA, USA, 2003. [Google Scholar]
- Senetakis, K.; Anastasiadis, A.; Pitilakis, K. A comparison of material damping measurements in resonant column using the steady-state and free-vibration decay methods. Soil Dyn. Earthq. Eng. 2015, 74, 10–13. [Google Scholar] [CrossRef]
- Facciorusso, J. An archive of data from resonant column and cyclic torsional shear tests performed on Italian clays. Earthq. Spectra 2020, 73, 545–562. [Google Scholar] [CrossRef]
- Ishimoto, M.; Iida, K. Determination of Elastic Constants of Soils by means of Vibration Methods. Part 1, Young’s Modulus. Bull. Earthq. Res. Inst. Univ. Tokyo 1936, 14, 632–657. [Google Scholar]
- Hardin, B.; Drnevich, V. Shear modulus and damping in soils: Design equations and curves. J. Soil Mech. Found. Div. 1972, 98, 667–692. [Google Scholar] [CrossRef]
- Sherif, M.A.; Ishibashi, I. Dynamic shear modulus for dry sands. J. Geotech. Eng. Div. 1976, 102, 1171–1184. [Google Scholar] [CrossRef]
- Iwasaki, T.; Tatsuoka, F. Effects of grain size and grading on dynamic shear moduli of sands. Soils Found. 1977, 17, 19–35. [Google Scholar] [CrossRef]
- Woods, R.D. Measurement of Dynamic Soil Properties; American Society of Civil Engineer: New York, NY, USA, 1978. [Google Scholar]
- Lentini, V.; Castelli, F. Resonant column and torsional shear tests for the evaluation of the shear modulus and damping ratio of soil. In Proceedings of the International Conference of Computational Methods in Sciences and Engineering 2017 (ICCMSE-2017), Thessaloniki, Greece, 21–25 April 2017. [Google Scholar]
- Castelli, F.; Cavallaro, A.; Grasso, S.; Lentini, V. Undrained Cyclic Laboratory Behavior of Sandy Soils. Geosciences 2019, 9, 512. [Google Scholar] [CrossRef]
- Ahmad, M.; Ray, R. Comparison between Ramberg-Osgood and Hardin-Drnevich soil models in Midas GTS NX. Pollack Period. 2021, 16, 52–57. [Google Scholar] [CrossRef]
- Saxena, S.K.; Reddy, K.R. Dynamic Moduli and Damping Ratios for Monterey No. 0 Sand by Resonant Column Tests. Soils Found. 1989, 29, 37–51. [Google Scholar] [CrossRef]
- Fioravante, V. Anisotropy of Small Strain Stiffness of Ticino and Kenya Sands from Seismic Wave Propagation Measured in Triaxial Testing. Soils Found. 2000, 40, 129–142. [Google Scholar] [CrossRef]
- Hoque, E.; Tatsuoka, F. Effects of stress ratio on small-strain stiffness during triaxial shearing. Géotechnique 2004, 54, 429–439. [Google Scholar] [CrossRef]
- Chaudhary, S.; Kuwano, J.; Hayano, Y. Measurement of quasi-elastic stiffness parameters of dense Toyoura sand in hollow cylinder apparatus and triaxial apparatus with bender elements. Geotech. Test. J. 2004, 27, 1–13. [Google Scholar] [CrossRef]
- Wichtmann, T.; Triantafyllidis, T. Influence of a cyclic and dynamic loading history on dynamic properties of dry sand, Part i: Cyclic and dynamic torsional prestraining. Soil Dyn. Earthq. Eng. 2004, 24, 127–147. [Google Scholar] [CrossRef]
- Szilvágyi, Z. Dynamic Soil Properties of Danube Sands. Ph.D. Dissertation, Széchenyi István University, Győr, Hungary, 2017. [Google Scholar]
- Stokoe, K.H.; Richart, F.E. Shear moduli of soils, in-situ and from laboratory tests. In Proceedings of the 5th World Conference in Earthquake Engineering, Rome, Italy, 25–29 June 1973. [Google Scholar]
- Darendeli, B. Development of a New Family of Normalized Modulus Reduction and Material Damping Curves. Ph.D. Dissertation, University of Texas, Austin, TX, USA, 2001; pp. 1–362. [Google Scholar]
- Afifi, S.S.; Woods, R.D. Long -Term Pressure Effects on Shear Modulus of Soils. J. Soil Mech. Found. Div. ASCE 1971, 97, 1445–1460. [Google Scholar] [CrossRef]
- Anderson, D.G.; Richart, F.E.J. Effects of straining on shear modulus of clays. J. Geotech. Eng. Div. 1976, 102, 975–987. [Google Scholar] [CrossRef]
- Alarcon-Guzman, A.; Chameau, J.; Leonards, G.A.; Frost, J.D. Shear Modulus and Cyclic Undrained Behavior of Sands. Soils Found. 1989, 29, 105–119. [Google Scholar] [CrossRef]
- Kim, D.S.; Stokoe, K.H.; Hudson, W.R. Deformational Characteristics of Soils at Small to Intermediate Strains from Cyclic Tests; Center for Transportation Research, Bureau of Engineering Research, University of Texas: Austin, TX, USA, 1991. [Google Scholar]
- Silver, M.L.; Seed, H.B. Volume changes in sands during cyclic loading. J. Soil Mech. Found. Div. 1971, 97, 1171–1182. [Google Scholar] [CrossRef]
- Ray, R.; Woods, R. Modulus and damping due to uniform and variable cyclic loading. J. Geotech. Eng. 1988, 114, 861–876. [Google Scholar] [CrossRef]
- Edil, T.B.; Luh, G.F. Dynamic Modulus and Damping Relationships for Sands; American Society of Civil Engineers: Pasadena, CA, USA, 1978. [Google Scholar]
- Cherian, A.C.; Kumar, J. Effects of Vibration Cycles on Shear Modulus and Damping of Sand Using Resonant Column Tests. J. Geotech. Geoenviron. Eng. 2016, 142, 1–6. [Google Scholar] [CrossRef]
- Yang, Z.; Wen, Y.; Kun, P. Previbration Signature on Dynamic Properties of Dry Sand. J. Test. Eval. 2019, 47, 1–27. [Google Scholar] [CrossRef]
- Dobry, R.; Vucetic, M. Dynamic properties and response of soft clay deposits. State of the art report. In Proceedings of the International Symposium on Geotechnical Engineering of Soft Soils, Mexico City, Mexico, 3–14 August 1987. [Google Scholar]
- Tatsuoka, F.; Shibuya, S. Deformation characteristics of soils and rocks from field and laboratory tests. Rep. Inst. Ind. Sci. Univ. Tokyo 1992, 37, 101–190. [Google Scholar]
- Tatsuoka, F.; Iwasaki, T.; Yoshida, S.; Fukushima, S.; Sudo, H. Shear modulus and damping by drained tests on clean sand specimen reconstituted by various methods. Soils Found. 1979, 19, 39–54. [Google Scholar] [CrossRef]
- Presti, D.C.F.L.; Jamiolkowski, M.; Pallara, O.; Cavallaro, A.; Pedroni, S. Shear modulus and damping of soils. Geotechnique 1997, 47, 603–617. [Google Scholar] [CrossRef]
- Carraro, J.; Prezzi, M.; Salgado, R. Shear strength and stiffness of sands containing plastic or nonplastic fines. J. Geotech. Geoenviron. Eng. 2009, 135, 1167–1178. [Google Scholar] [CrossRef]
- Qian, X.; Gray, D.H.; Woods, R.D. Resonant column tests on partially saturated sands. Geotech. Test. J. 1991, 14, 266–275. [Google Scholar]
- Kagawa, T. Moduli and damping factors of soft marine clays. J. Geotech. Eng. 1992, 118, 1360–1375. [Google Scholar] [CrossRef]
- Qian, X.; Gray, D.H.; Woods, R.D. Voids and Granulometry: Effects on Shear Modulus of Unsaturated Sands. J. Geotech. Eng. 1993, 119, 295–314. [Google Scholar] [CrossRef]
- Guha, S. Dynamic Characteristics of Old Bay Clay Deposits in the East San Francisco Bay Area. Ph.D. Dissertation, Graduate School, Purdue University, Fort Wayne, IN, USA, 1995. [Google Scholar]
- Baig, S.; Picornell, M.; Nazarian, S. Low strain shear moduli of cemented sands. J. Geotech. Geoenviron. Eng. ASCE 1997, 123, 540–545. [Google Scholar] [CrossRef]
- Simonini, P.; Cola, S. Use of piezocone to predict maximum stiffness of Venetian soils. J. Geotech. Geoenviron. Eng. ASCE 2000, 126, 378–382. [Google Scholar] [CrossRef]
- Fam, M.A.; Cascante, G.; Dusseault, M.B. Large and Small Strain Properties of Sands Subjected to Local Void Increase. J. Geotech. Geoenviron. Eng. 2002, 12, 1018–1025. [Google Scholar] [CrossRef]
- Kallioglou, P.; Tika, T.; Pitilakis, K. Shear Modulus and Damping Ratio of Cohesive Soils. J. Earthq. Eng. 2008, 12, 879–913. [Google Scholar] [CrossRef]
- Wichtmann, T.; Triantafyllidis, T. On the correlation of ”static” and ”dynamic” stiffness moduli of non-cohesive soils. Bautechnik 2009, 86(S1), 28–39. [Google Scholar] [CrossRef]
- Iwasaki, T.; Tatsuoka, F.; Takagi, Y. Shear moduli of sands under cyclic torsional shear loading. Soils Found. 1978, 18, 39–50. [Google Scholar] [CrossRef]
- Oztoprak, S.; Bolton, M. Stiffness of sands through a laboratory test database. Géotechnique 2013, 63, 54–70. [Google Scholar] [CrossRef]
- Krumbein, W.C.; Sloss, L.L. Stratigraphy and Sedimentation; W.H. Freeman and Co.: San Francisco, CA, USA, 1963; 660p. [Google Scholar]
- Presti, D.L.; Pallara, O.; Lancellotta, R.; Armandi, M.; Maniscalco, R. Monotonic and cyclic loading behaviour of two sands at small strains. Geotech. Test. J. 1993, 16, 409–424. [Google Scholar] [CrossRef]
- Hoque, E.; Tatsuoka, F. Kinematic elasticity of a granular material. In Proceedings of the ISRM International Symposium, Melbourne, Australia, 19–24 November 2000; Available online: https://www.onepetro.org/conference-paper/ISRM-IS-2000-231 (accessed on 5 June 2023).
- Kuwano, R.; Jardine, R. On the application of cross-anisotropic elasticity to granular materials at very small strains. Géotechnique 2002, 52, 727–749. [Google Scholar] [CrossRef]
- Kallioglou, T.; Papadopoulou, A.; Pitilakis, K. Shear modulus and damping of natural sands. In Deformation Characteristics of Geomaterials, In Proceedings of the 3rd International Symposium on Deformation Characteristics of Geomaterials, Lyon, France, 22–24 September 2003; Swets & Zeitlinger: Lisse, The Netherlands; pp. 401–407.
- Senetakis, K.; Anastasiadis, A.; Pitilakis, K. Small strain shear modulus and damping ratio of quartz and volcanic sands. Geotech. Test. J. 2012, 36, 1–17. [Google Scholar] [CrossRef]
- Biarez, J.; Hicher, P. Elementary Mechanics of Soil Behavior; Balkema: Boca Raton, FL, USA, 1994; ISBN 9054101571. [Google Scholar]
- Wichtmann, T.; Triantafyllidis, T. Influence of the grain-size distribution curve of quartz sand on the small strain shear modulus Gmax. J. Geotech. Geoenviron. Eng. 2009, 135, 1404–1418. [Google Scholar] [CrossRef]
- Szilvágyi, Z.; Panuska, J.; Kegyes-Brassai, O.; Wolf, Á.; Tildy, P.; Ray, R. Ground Response Analyses in Budapest Based on Site Investigations and Laboratory Measurements. Int. J. Environ. Chem. Ecol. Geol. Geophys. Eng. 2017, 11, 307–317. [Google Scholar]
- Rocha, B.P.; Fernandes, J.; Giacheti, H.L. Dynamic shear modulus and stiffness decay curves of a tropical sandy soil via laboratory and in situ tests. In Proceedings of the 6th International Conference on Geotechnical and Geophysical Site, Budapest, Hungary, 6–11 September 2021. [Google Scholar]
- Fernandes, J.B.; Rocha, B.P.; Giacheti, H.L. Maximum shear modulus and modulus degradation curves of an unsaturated tropical soil. Soils Rocks 2023, 46, e2023013122. [Google Scholar] [CrossRef]
- Lashin, I.; Abdellaziz, M.; Karray, M. Experimental Assessment of Shear Modulus Reduction Curve for Granular Soils. In Proceedings of the 74th Canadian Geotechnical Conference, Niagra Falls, ON, Canada, 26–29 September 2021. [Google Scholar]
- Yu, X.; Yuan, X.; Chen, Z.; Zhang, J. Resonant Column Test on the Frozen Silt Soil Modulus and Damping at Different Temperatures. Period. Polytech. Civ. Eng. 2017, 61, 762–769. [Google Scholar]
- Das, S.; Bhowmik, D. Small Strain Dynamic Behavior of Sand and Sand-Crumb Rubber Mixture In Dry Condition. In Proceedings of the Indian Geotechnical Conference 2017 GeoNEst, Guwahati, India, 14–16 December 2017. [Google Scholar]
- Im, J.; Tran, T.P.A.; Chang, I.; Cho, G.-C. Dynamic properties of gel-type biopolymer-treated sands evaluated by Resonant Column (RC) Tests. Geomech. Eng. 2017, 12, 815–830. [Google Scholar] [CrossRef]
- Li, W.; Lang, L.; Wang, D.; Wu, Y.; Li, F. Investigation on the dynamic shear modulus and damping ratio of steel slag sand mixtures. Constr. Build. Mater. 2018, 162, 170–180. [Google Scholar] [CrossRef]
- Basas, V.; Pantazopoulos, I.; Atmatzidis, D. Torsional and flexural resonant column testing of grouted sands. Soil Dyn. Earthq. Eng. 2020, 139, 106360. [Google Scholar] [CrossRef]
- Wu, Q.; Ma, W.J.; Liu, Q.; Zhao, K.; Chen, G. Dynamic shear modulus and damping ratio of rubber-sand mixtures with a wide range of rubber. Mater. Today Commun. 2021, 27, 102341. [Google Scholar] [CrossRef]
- Masing, G. Eigenspannungen und Verfestigung beim Messing. In Proceedings of the 2nd International Congress Applied Mechanics, Zurich, Switzerland, 12–17 September 1926. [Google Scholar]
- Pyke, R. Nonlinear soil models for irregular cyclic loadings. J. Geotech. Eng. Div. 1979, 105, 715–726. [Google Scholar] [CrossRef]
- Jennings, P. Earthquake Response of a Yielding Structures. J. Geotech. Eng. Div. 1965, 91, 41–68. [Google Scholar] [CrossRef]
- Constantopoulos, I.V.; Roesset, J.M.; Christian, J.T. A Comparison of Linear and Exact Nonlinear Analyses of Soil Amplification. In Proceedings of the Fifth World Conference on Earthquake Engineering, Rome, Italy, 25–29 June 1973. [Google Scholar]
- Finn, W.D.L.; Lee, K.W.; Martin, G. An Effective Stress Model for Liquefaction. J. Geotech. Eng. Div. ASCE 1977, 103, 517–533. [Google Scholar] [CrossRef]
- Valera, J.E.; Berger, E.; Kim, H.-S.; Reaugh, J.E.; Golden, R.D.; Hofmann, R. Study of Nonlinear Effects on One-Dimensional Earthquake Response; Report No. NP-865; Electric Power Research Institute: Palo Alto, CA, USA, 1978. [Google Scholar]
- Rosenblueth, E.; Herrera, I. On a kind of hysteretic damping. J. Eng. Mech. Div. 1964, 91, 37–48. [Google Scholar] [CrossRef]
- Ramberg, W.; Osgood, W.R. Description of Stress Strain Curves by Three Parameters; Technical Note No. 902; National Advisory Committee for Aeronautics: Washington, DC, USA, 1943. [Google Scholar]
- Faccioli, E.; Santayo, V.; Leone, J. Microzonation Criteria and Seismic Response Studies for the City of Managua. In Proceedings of the Earthquake Engineering Research Institution Conference, San Francisco, CA, USA, 29–30 November 1973. [Google Scholar]
- Streeter, V.L.; Wylie, E.B.; Richart, F.E.J. Soil Motion Computation by Characteristics Method. J. Geotech. Geoenviron. Eng. 1974, 100, 247–263. [Google Scholar]
- Benz, T. Small Strain Stiffness of Soils and Its Numerical Consequences. Ph.D. Dissertation, Universität Stuttgart, Institut für Geotechnik, Stuttgart, Germany, 2006; p. 209. [Google Scholar]
- Midas, L.; Information Technology Co. Midas GTS NX 2014 v2.1 Analysis Reference, Chapter 4. Materials. pp. 105–211. 2014. Available online: https://globalsupport.midasuser.com/ (accessed on 5 June 2023).
- Matasovic, N.; Vucetic, M. Cyclic Characterization of Liquefiable Sands. J. Geotech. Eng. 1993, 119, 1805–1822. [Google Scholar] [CrossRef]
- Ahmad, M.; Ray, R. Numerical study of random material properties within a soil specimen. In Proceedings of the IOP Conference Series: Materials Science and Engineering, Iasi, Romania, 27–29 May 2021. [Google Scholar]
- Ahmad, M.; Ray, R. Modelling of the Torsional Simple Shear Test with Randomized Tresca Model Properties in Midas GTS NX. Geotech. Geol. Eng. 2023, 41, 1937–1946. [Google Scholar] [CrossRef]

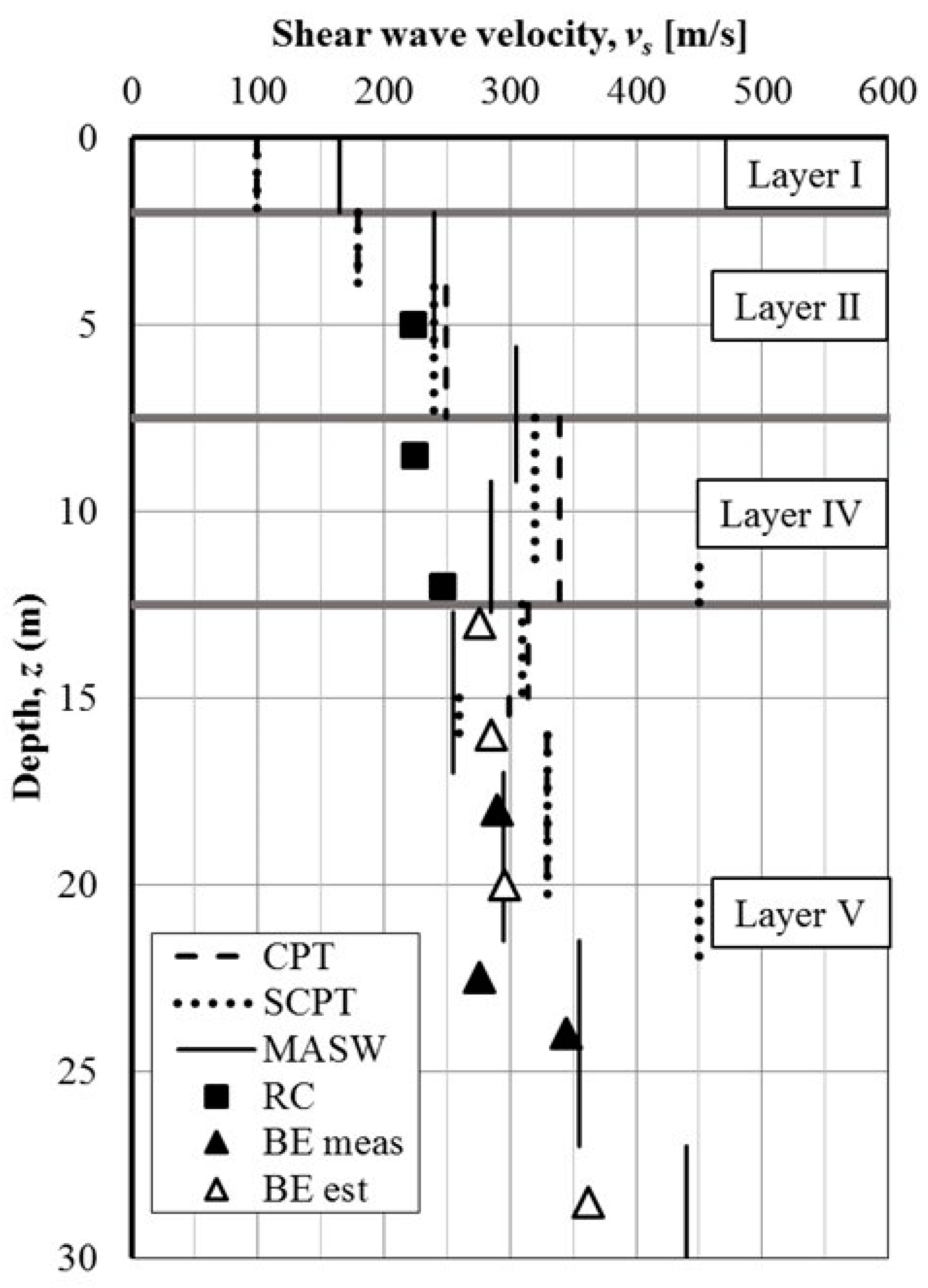
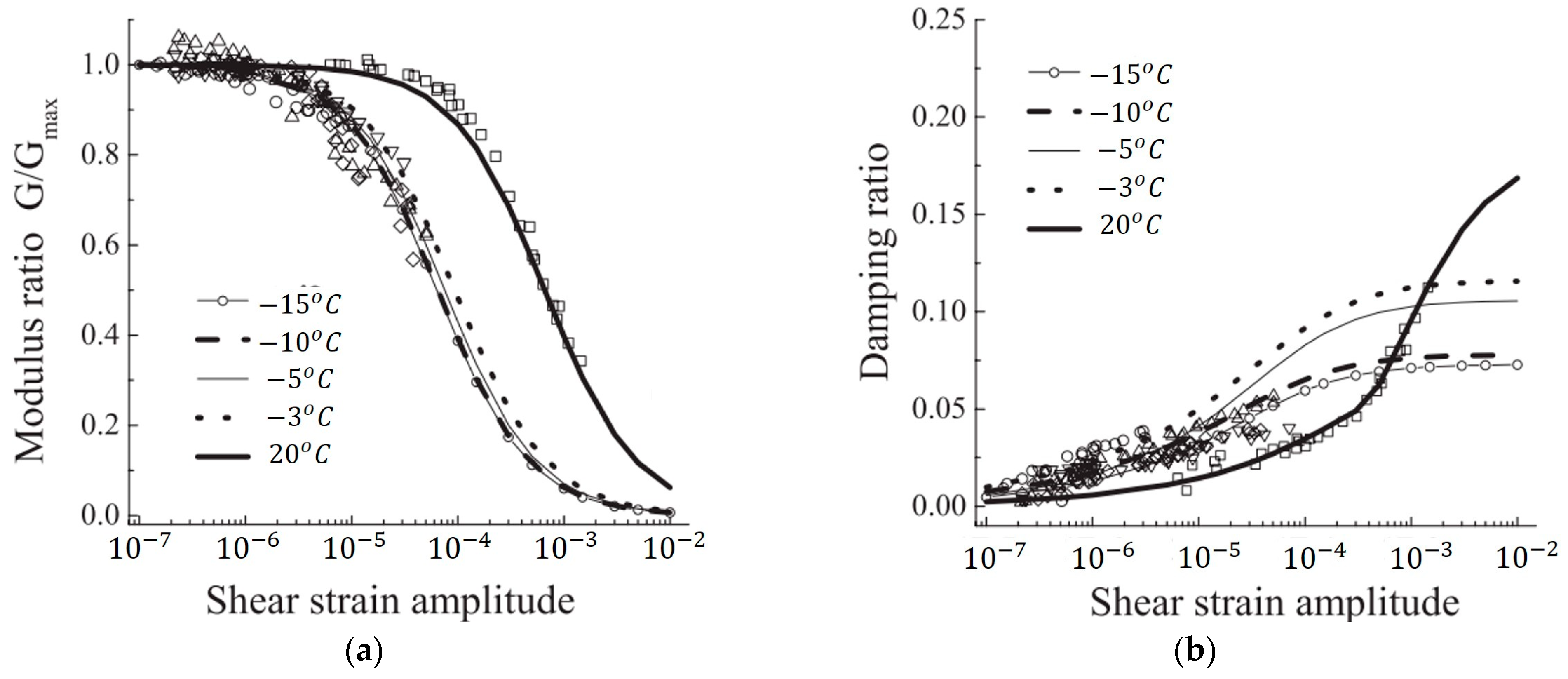

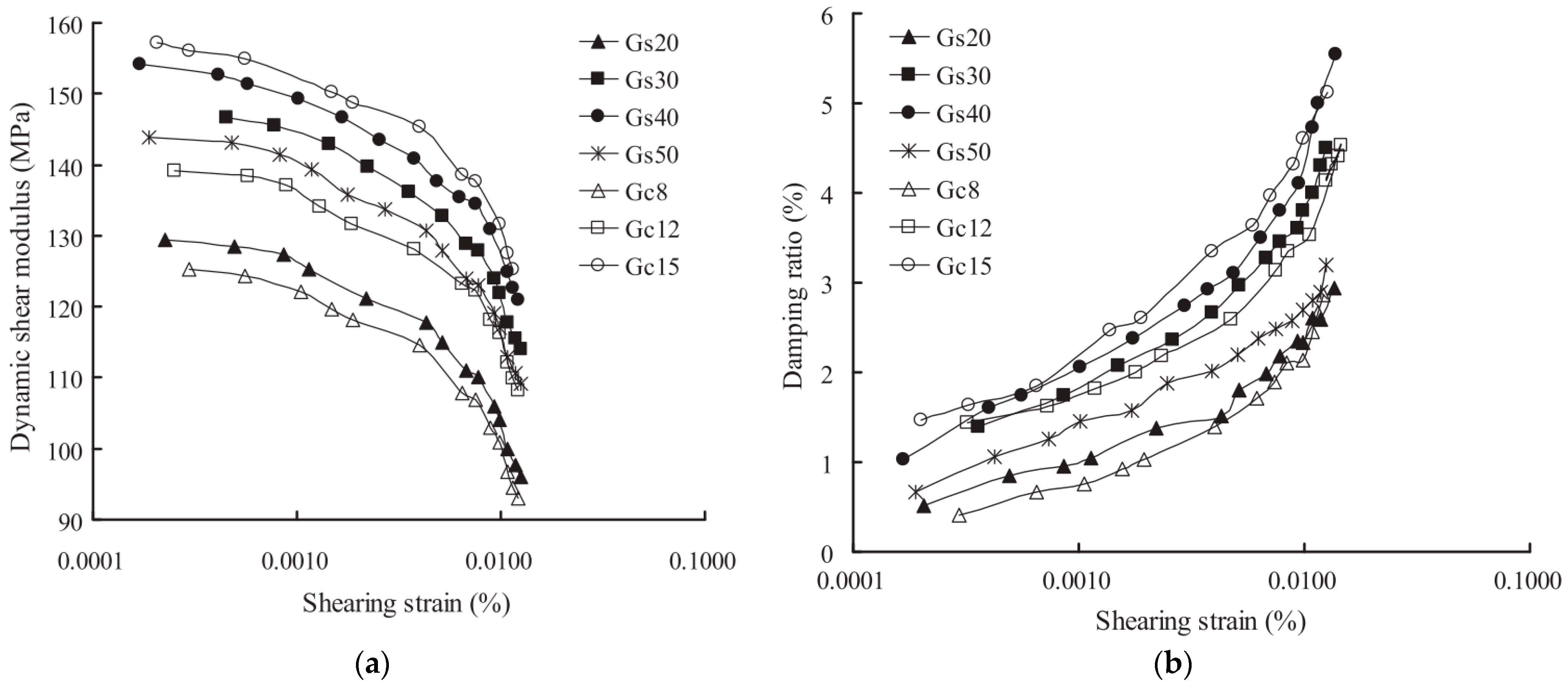
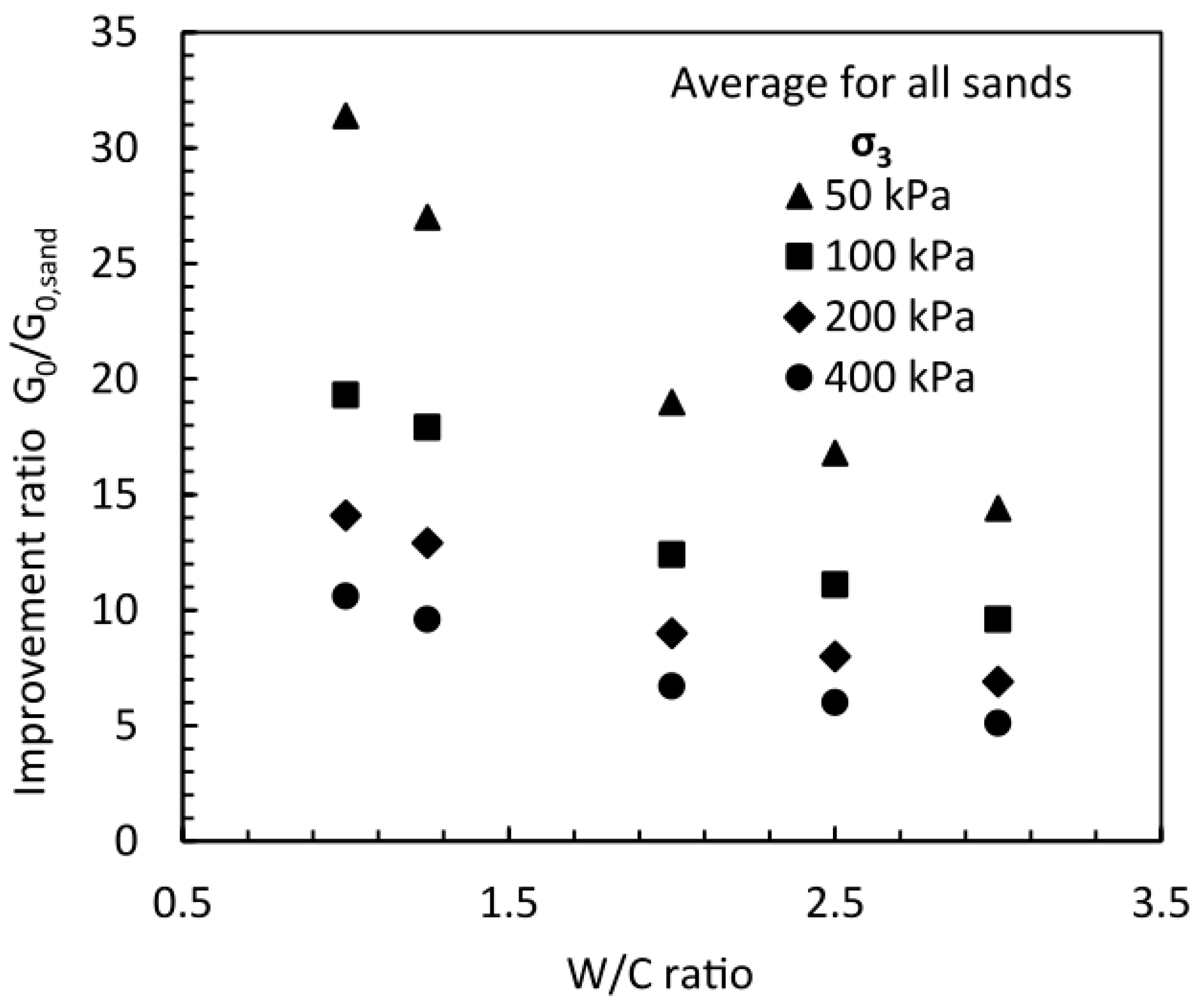


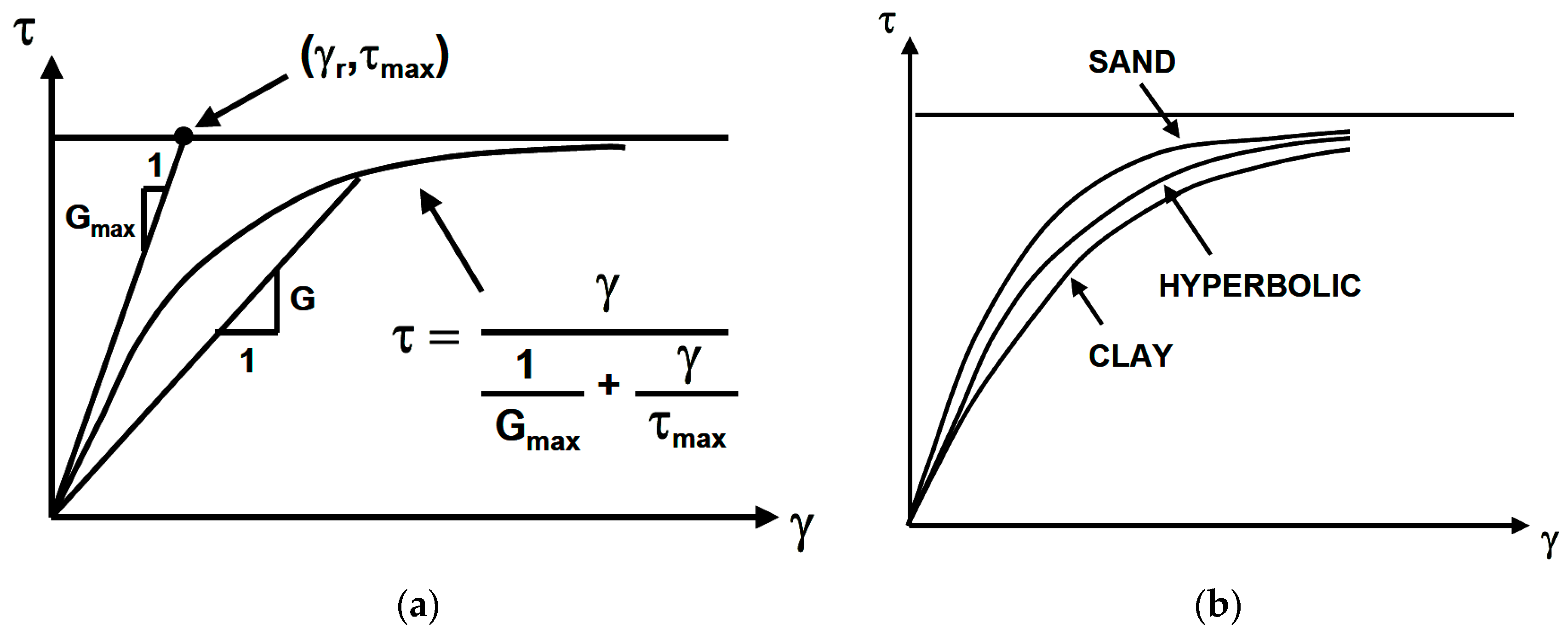
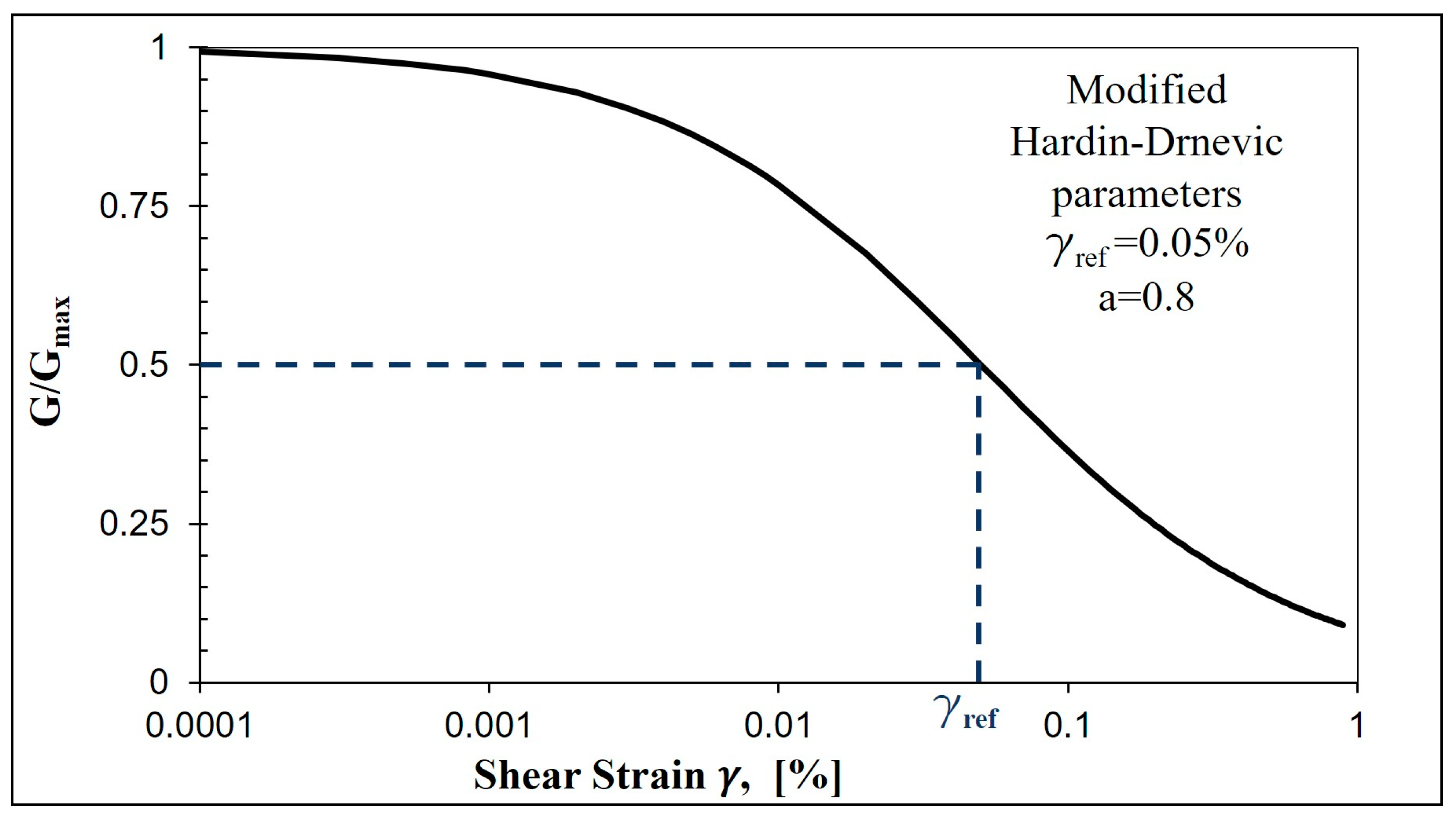
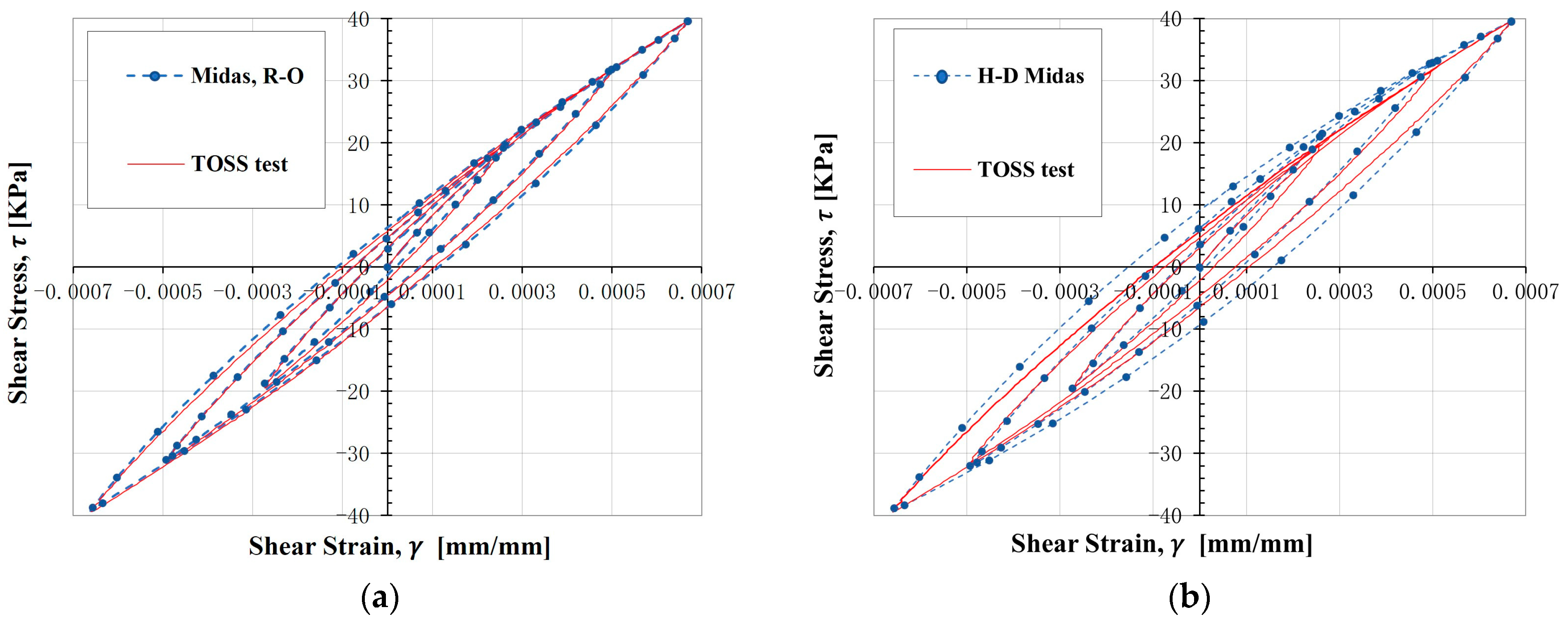
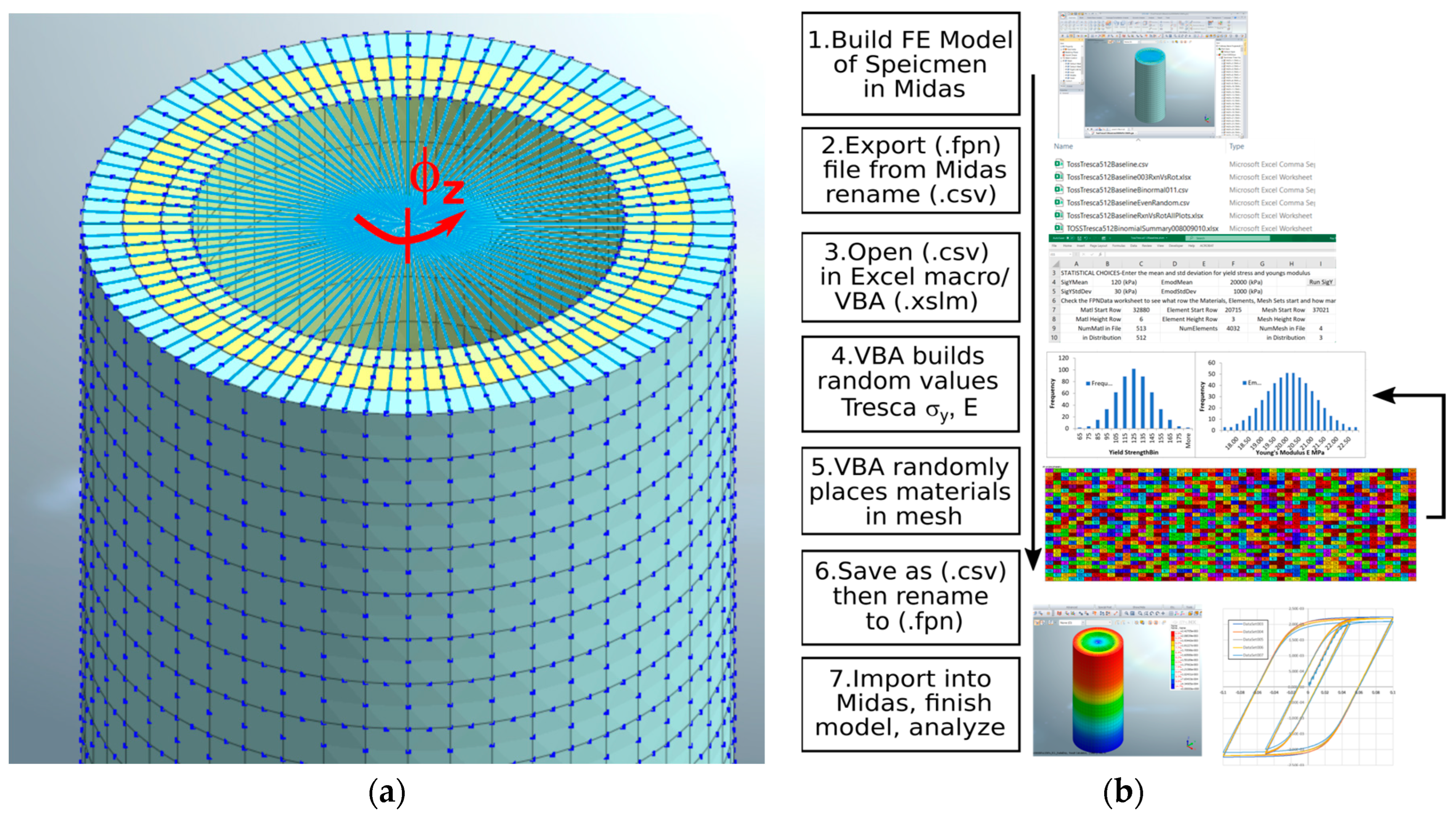
| Feature | Advantage | Disadvantage |
|---|---|---|
| RC (accelerometer) | Very accurate and repeatable readings over a broad strain range. | Test must be dynamically excited |
| TOSS (proximitors) | Accurate over a slightly smaller strain range. Cyclic, cyclic with static offset, irregular loading programmed in the control software | Proximitor response is nonlinear and requires careful calibration, set-up, and computation during the test. |
| RC-TOSS (hollow cylinder specimen | More uniform strains in the specimen. Highly tolerant of voids/inclusions (gravel, organics). | Two membranes (inner, outer) and a more complex system to construct specimens. Dry pluviation, vibrating, or hand trimming (cohesive) in special mold requires ~2–3 h prep time. |
| RC-TOSS (coil-magnet loading) | RC and TOSS tests are performed on the same specimen in multiple stages. | Limit to a maximum torque of about 55 N-m |
| Temperature [°C] | Gmax [MPa] | Dmax [−] | N [−] | |
|---|---|---|---|---|
| −15 | 1539.2 | 6.312 × 10−5 | 0.073 | 0.42 |
| −10 | 1467.4 | 6.670 × 10−5 | 0.078 | 0.36 |
| −5 | 1341.8 | 7.520 × 10−5 | 0.106 | 0.44 |
| −3 | 1238.4 | 9.354 × 10−5 | 0.116 | 0.36 |
| Room temperature (15 °C to 25 °C) | 64.2 | 6.602 × 10−4 | 0.183 | 0.60 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahmad, M.; Ray, R. The Dynamic Properties of Sand under Torsion: A Literature Review. Geotechnics 2023, 3, 480-514. https://doi.org/10.3390/geotechnics3020027
Ahmad M, Ray R. The Dynamic Properties of Sand under Torsion: A Literature Review. Geotechnics. 2023; 3(2):480-514. https://doi.org/10.3390/geotechnics3020027
Chicago/Turabian StyleAhmad, Majd, and Richard Ray. 2023. "The Dynamic Properties of Sand under Torsion: A Literature Review" Geotechnics 3, no. 2: 480-514. https://doi.org/10.3390/geotechnics3020027
APA StyleAhmad, M., & Ray, R. (2023). The Dynamic Properties of Sand under Torsion: A Literature Review. Geotechnics, 3(2), 480-514. https://doi.org/10.3390/geotechnics3020027








