Dynamic Properties of a Compacted Residual Soil from the West Indies
Abstract
1. Introduction
2. Materials and Methods
2.1. Sampling
2.2. Specimen Preparation
2.3. Resonant Column Tests
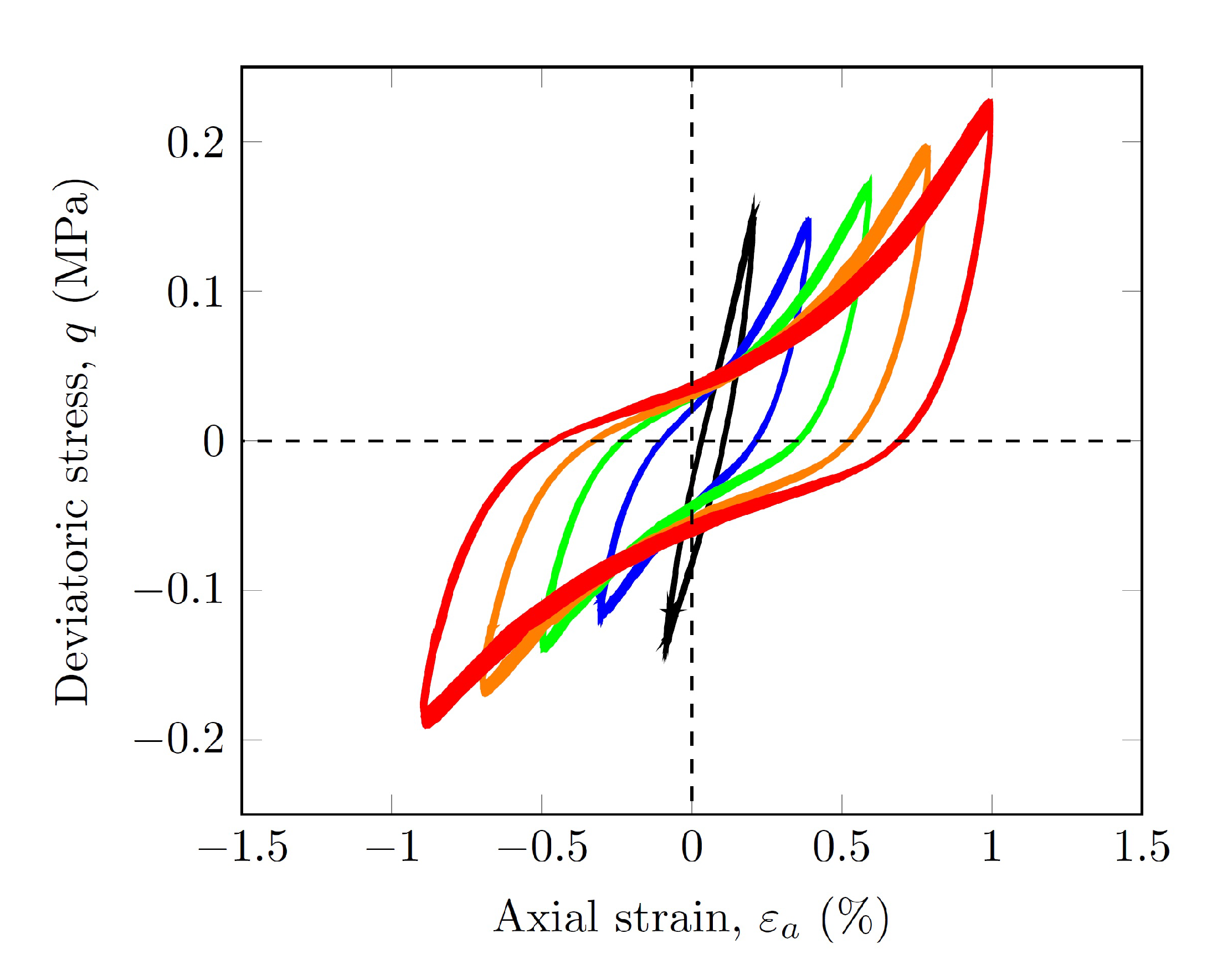
2.4. Cyclic Triaxial Tests
3. Results and Discussion
3.1. Identification
3.2. Scanning Electron Microscopy
3.3. Energy Dispersive Spectrometry
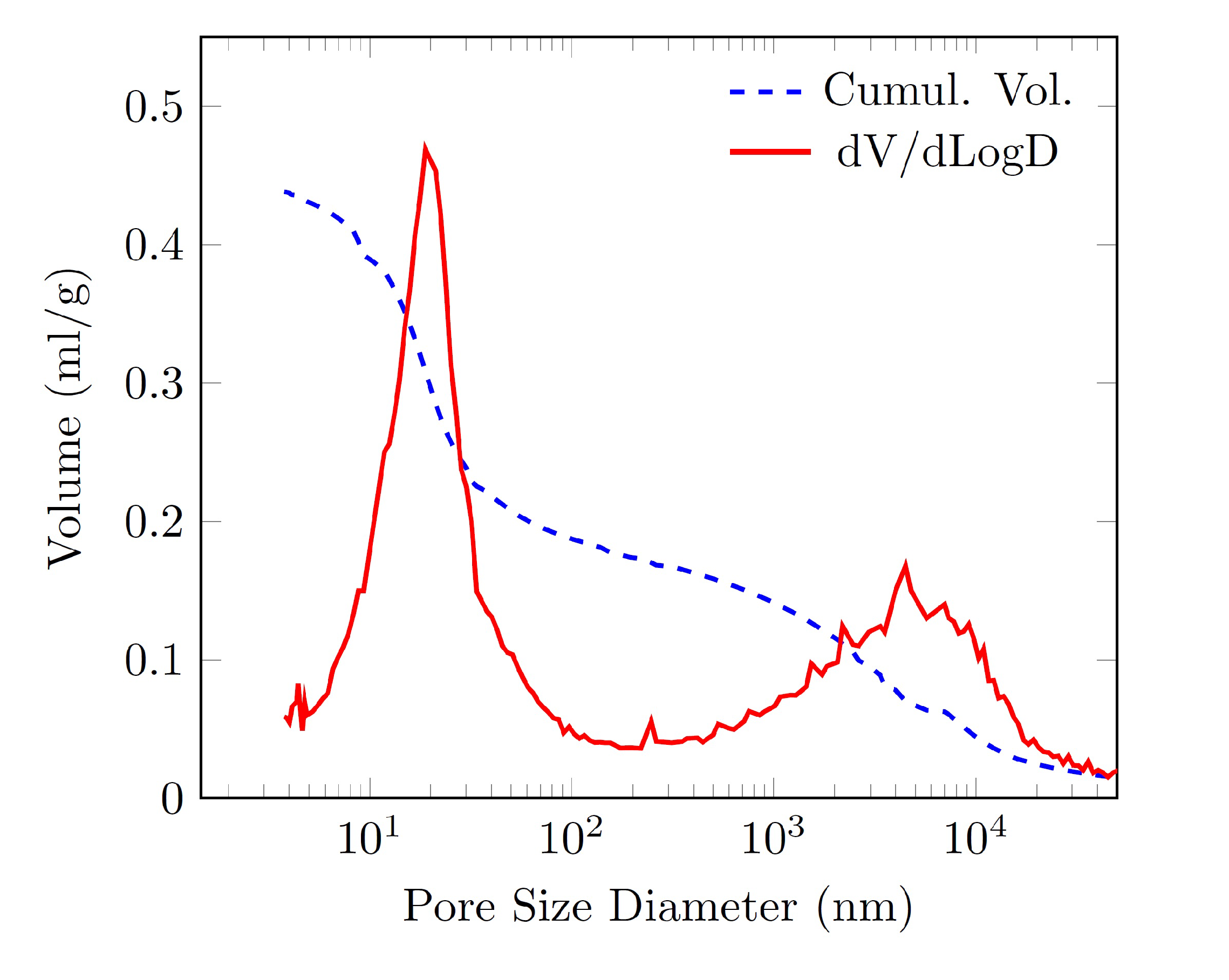
3.4. Mercury Porosimetry
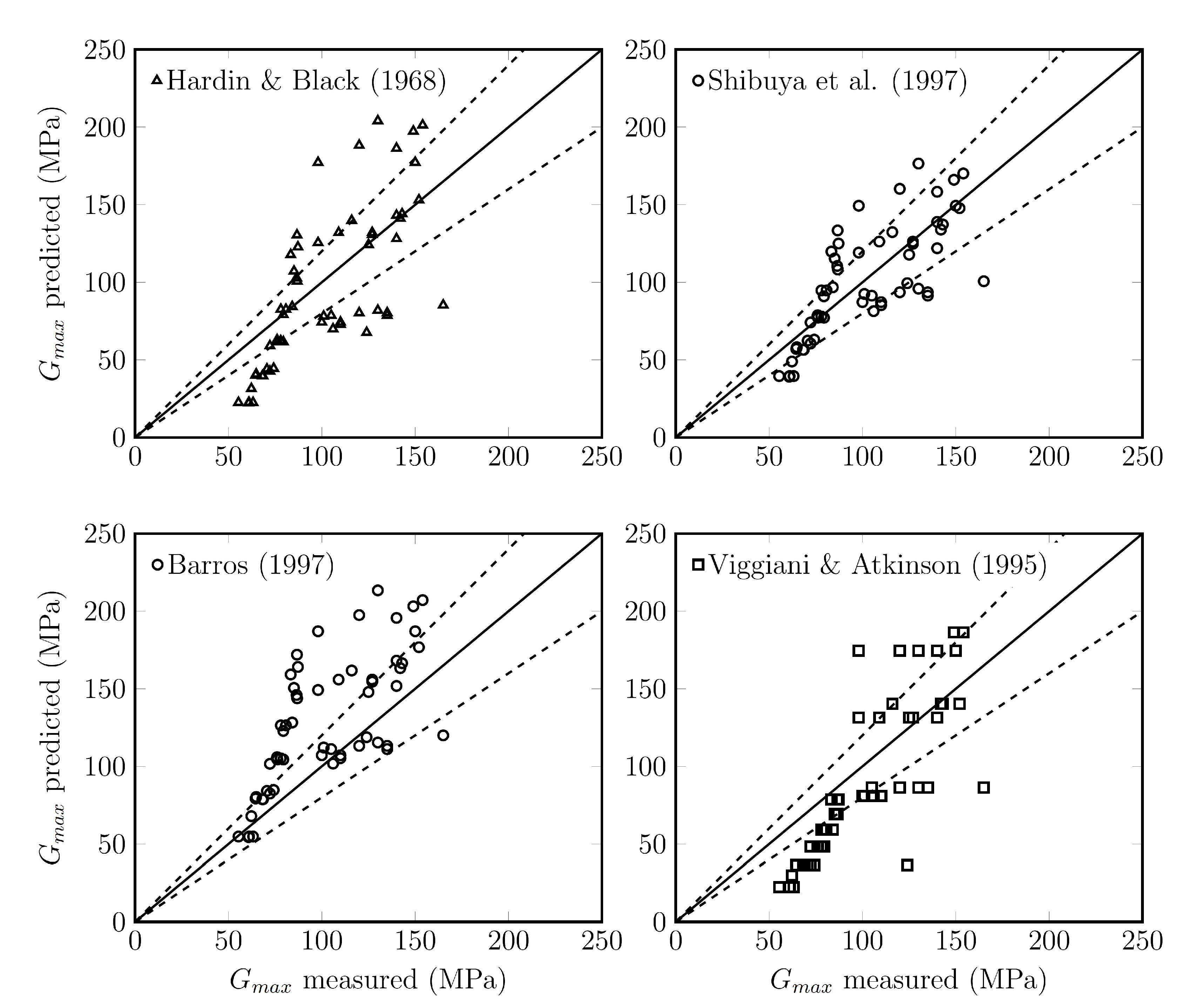
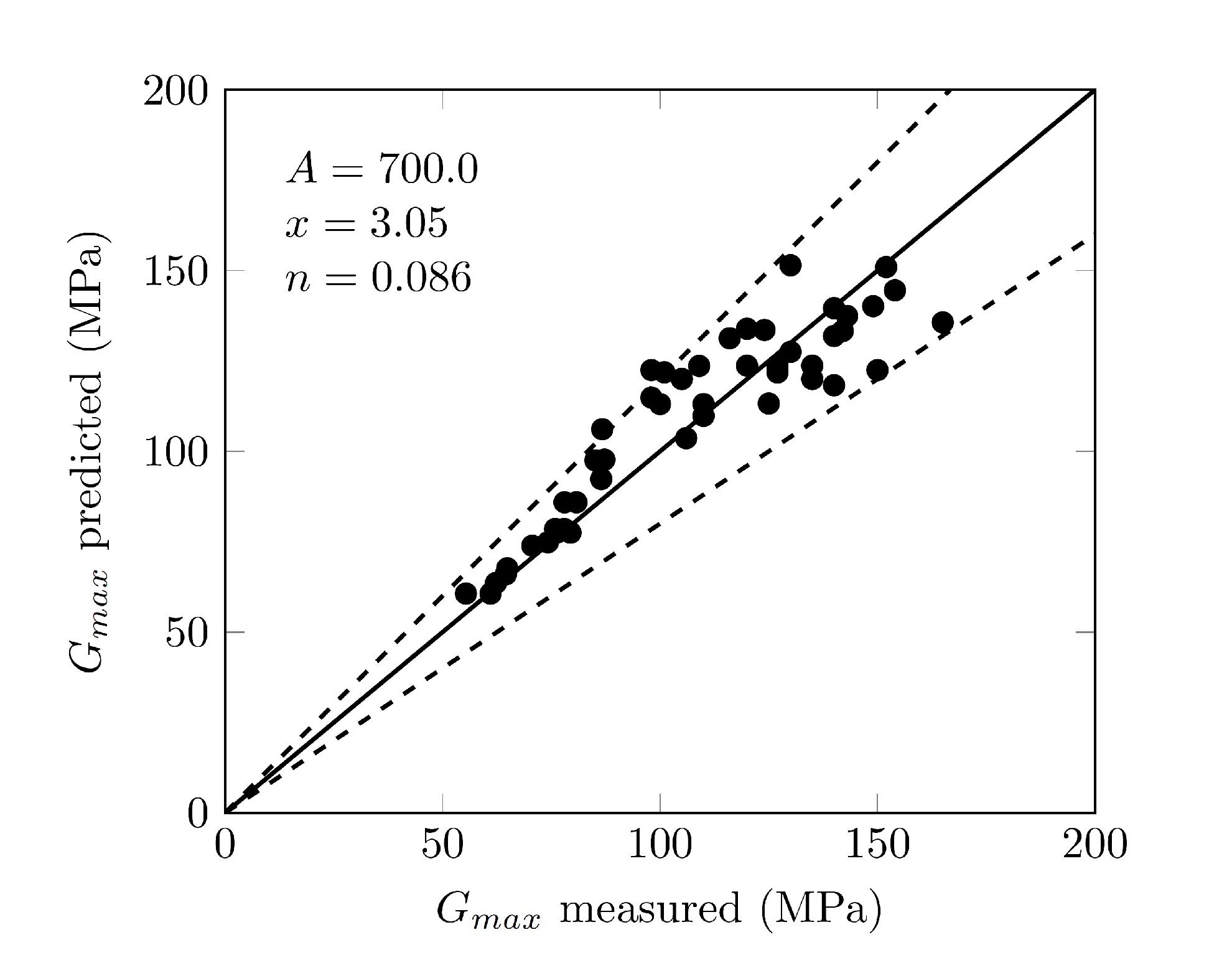
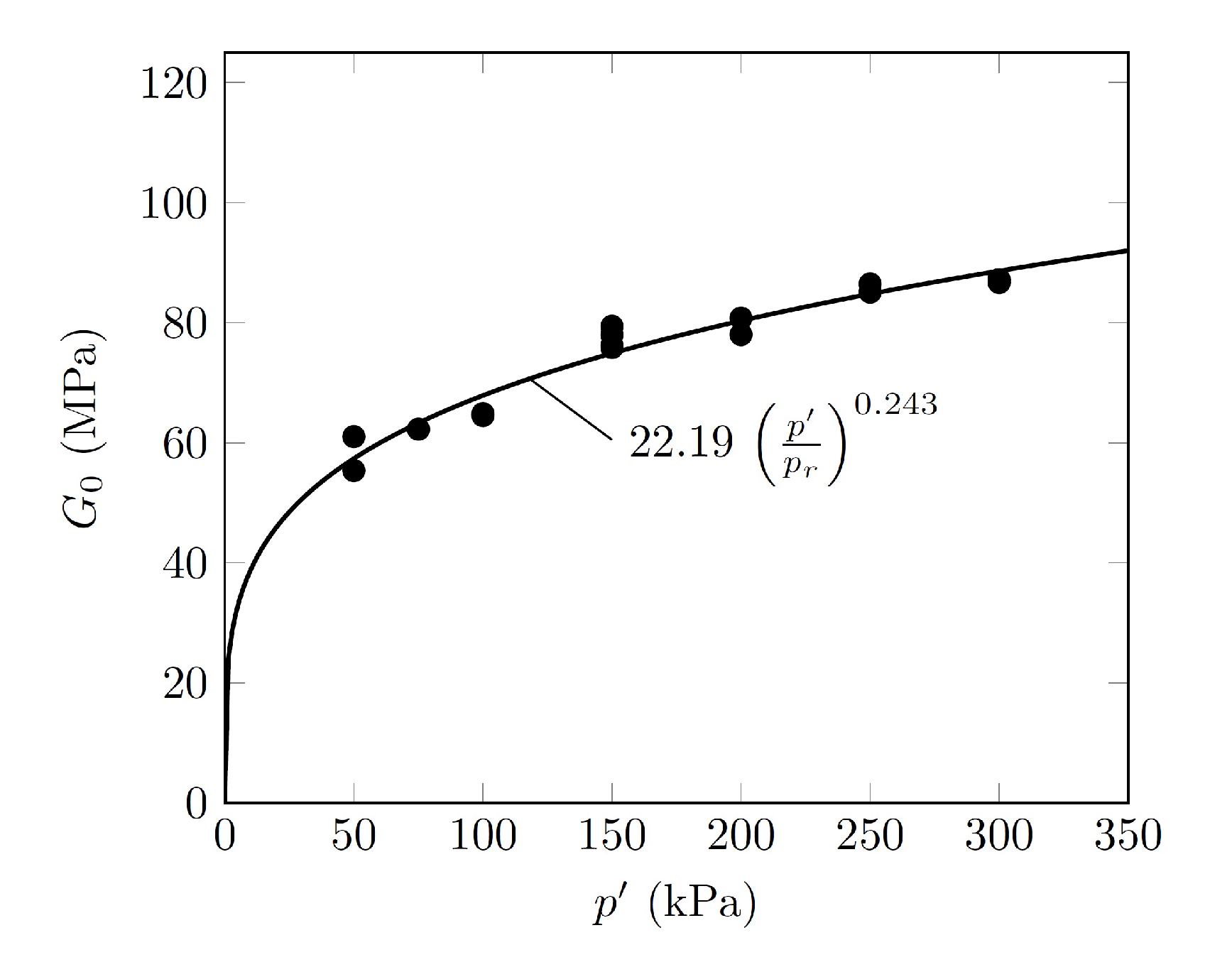
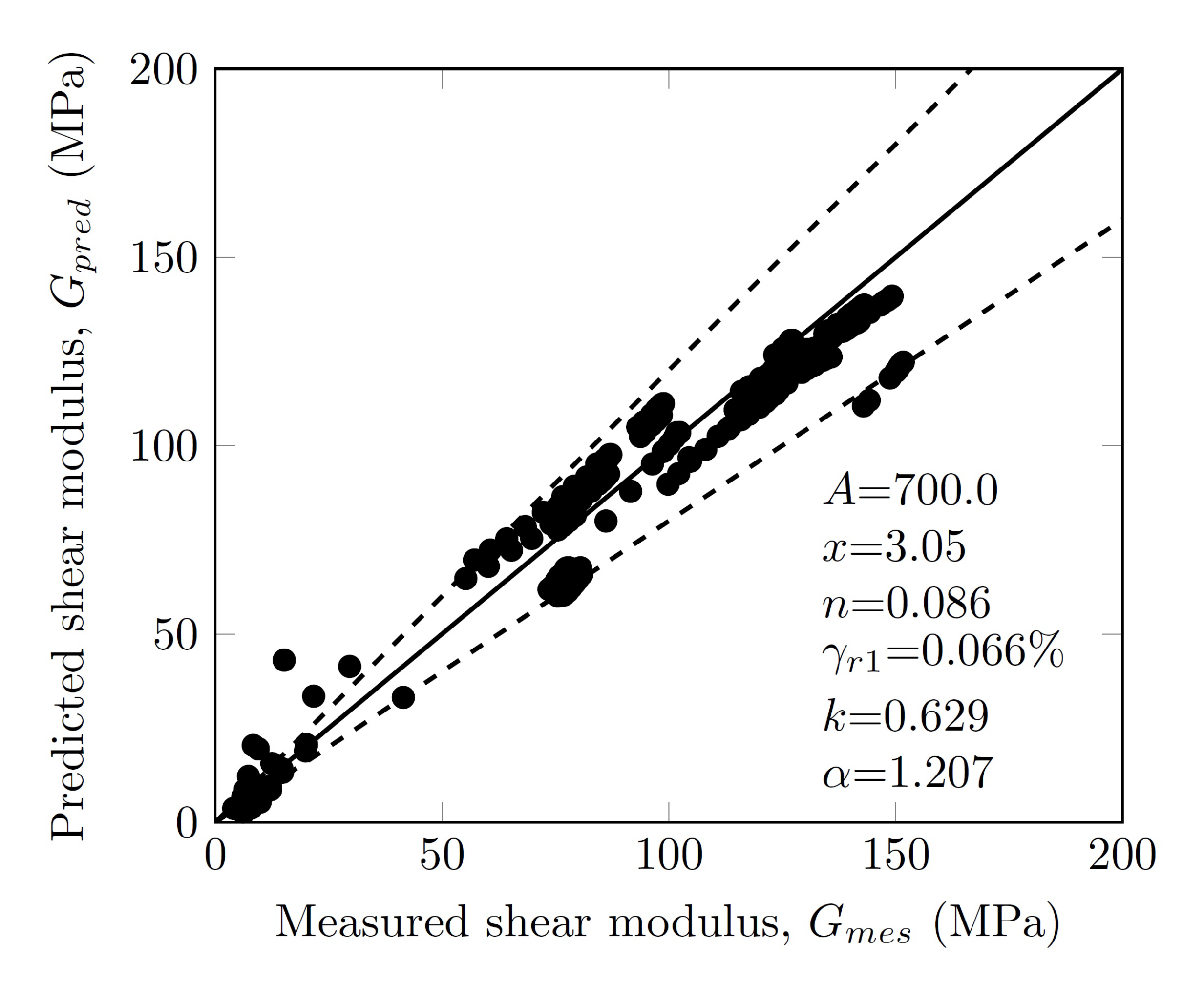
3.5. Small Strain Shear Modulus
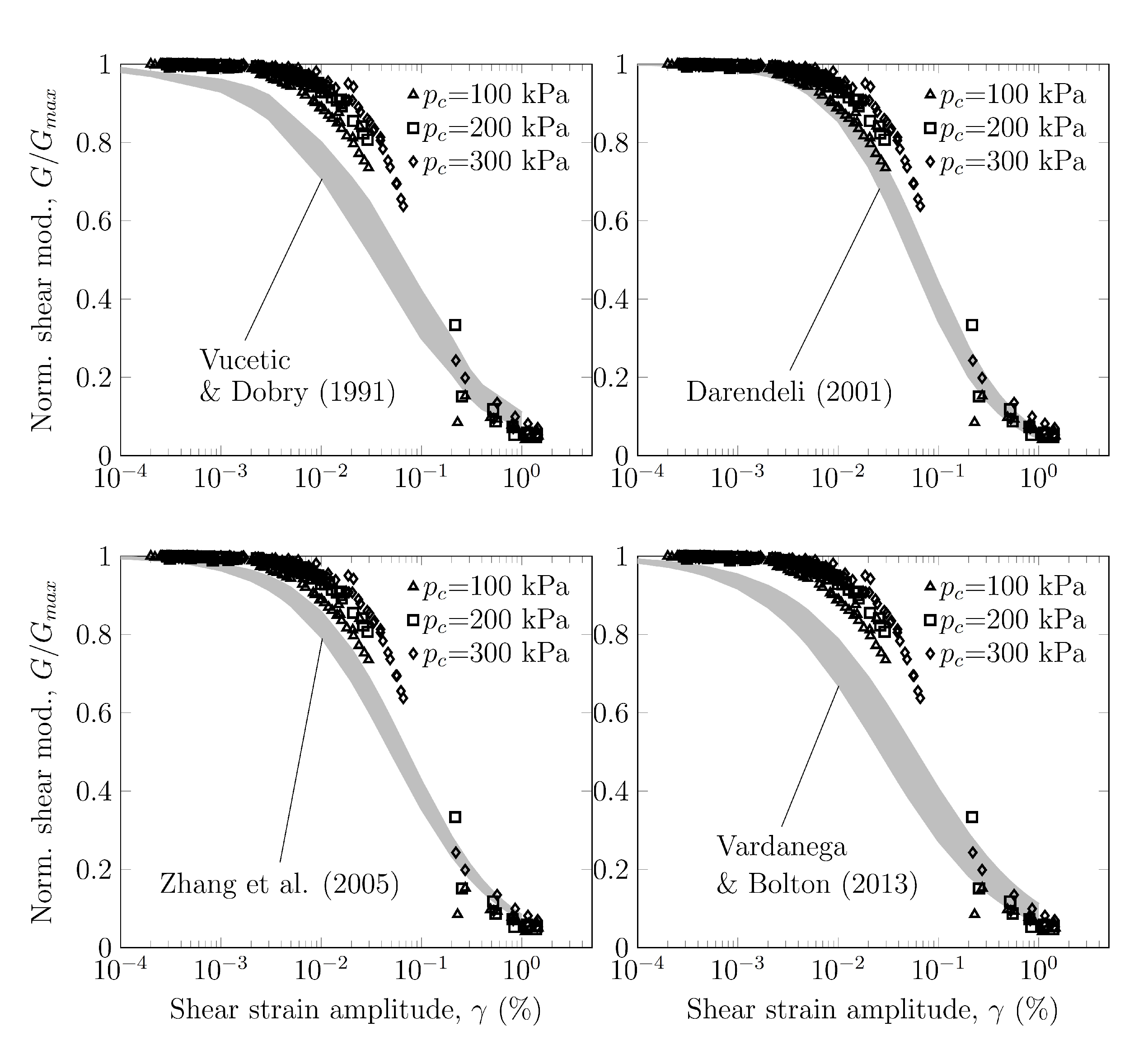
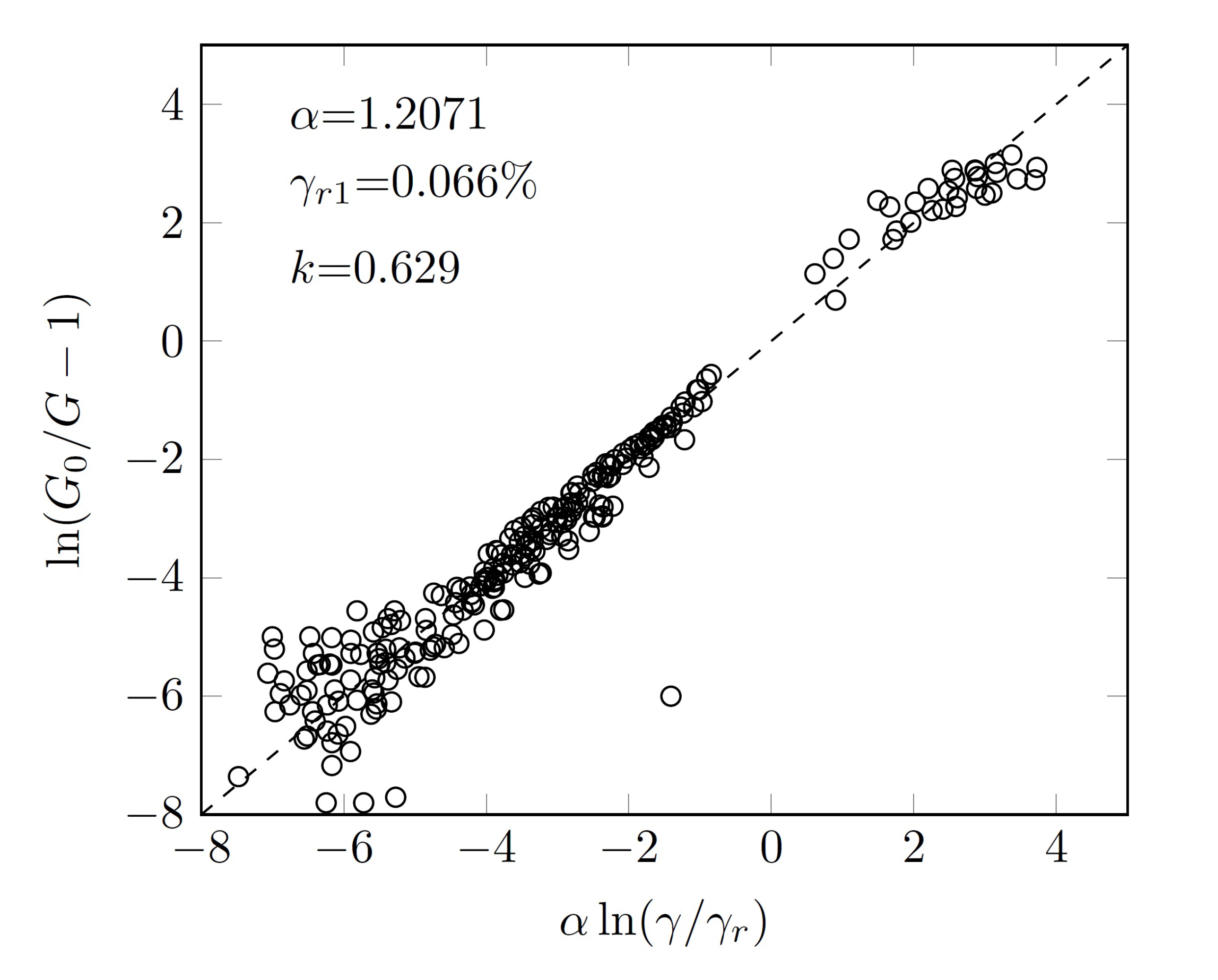
3.6. Normalized Shear Modulus
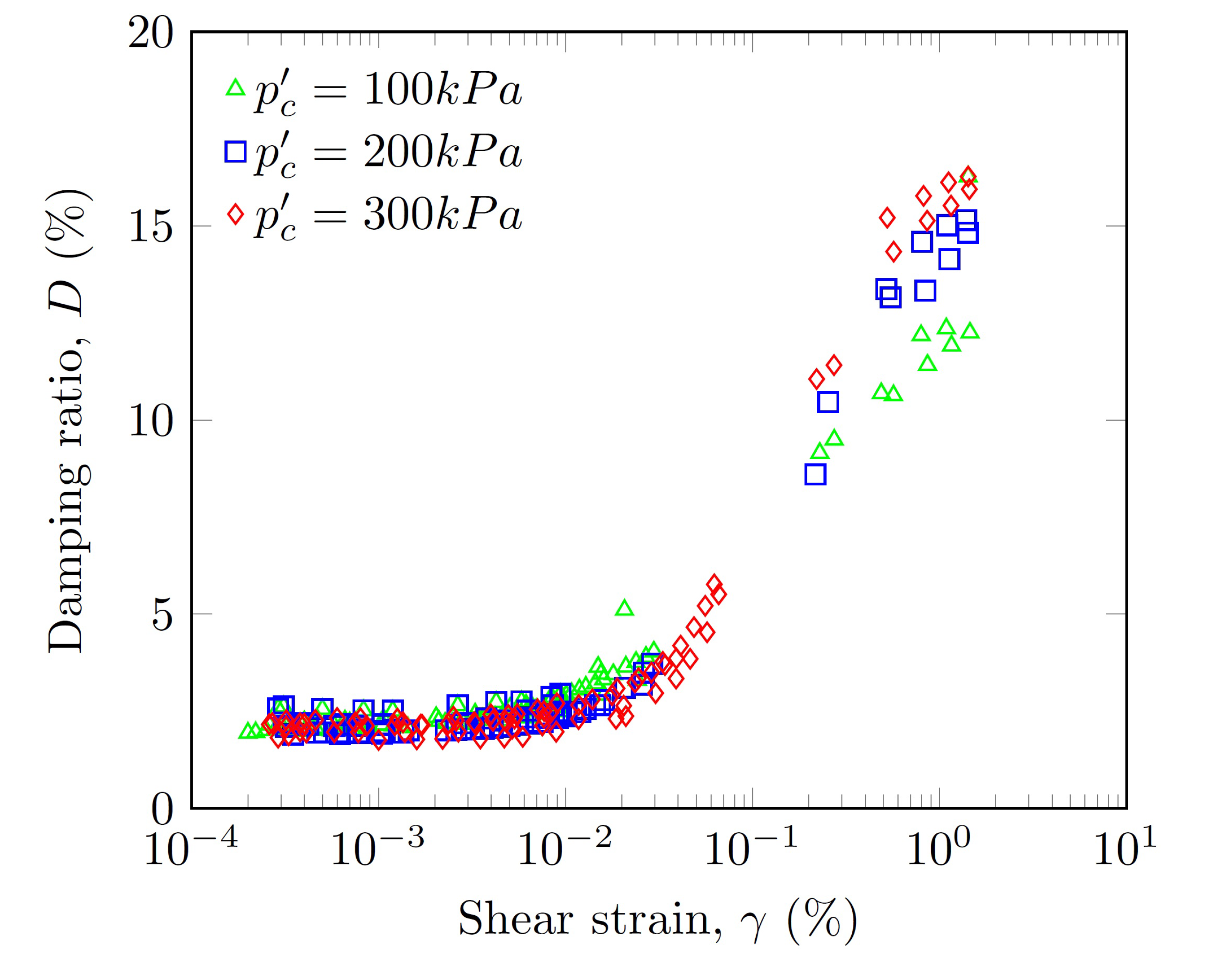
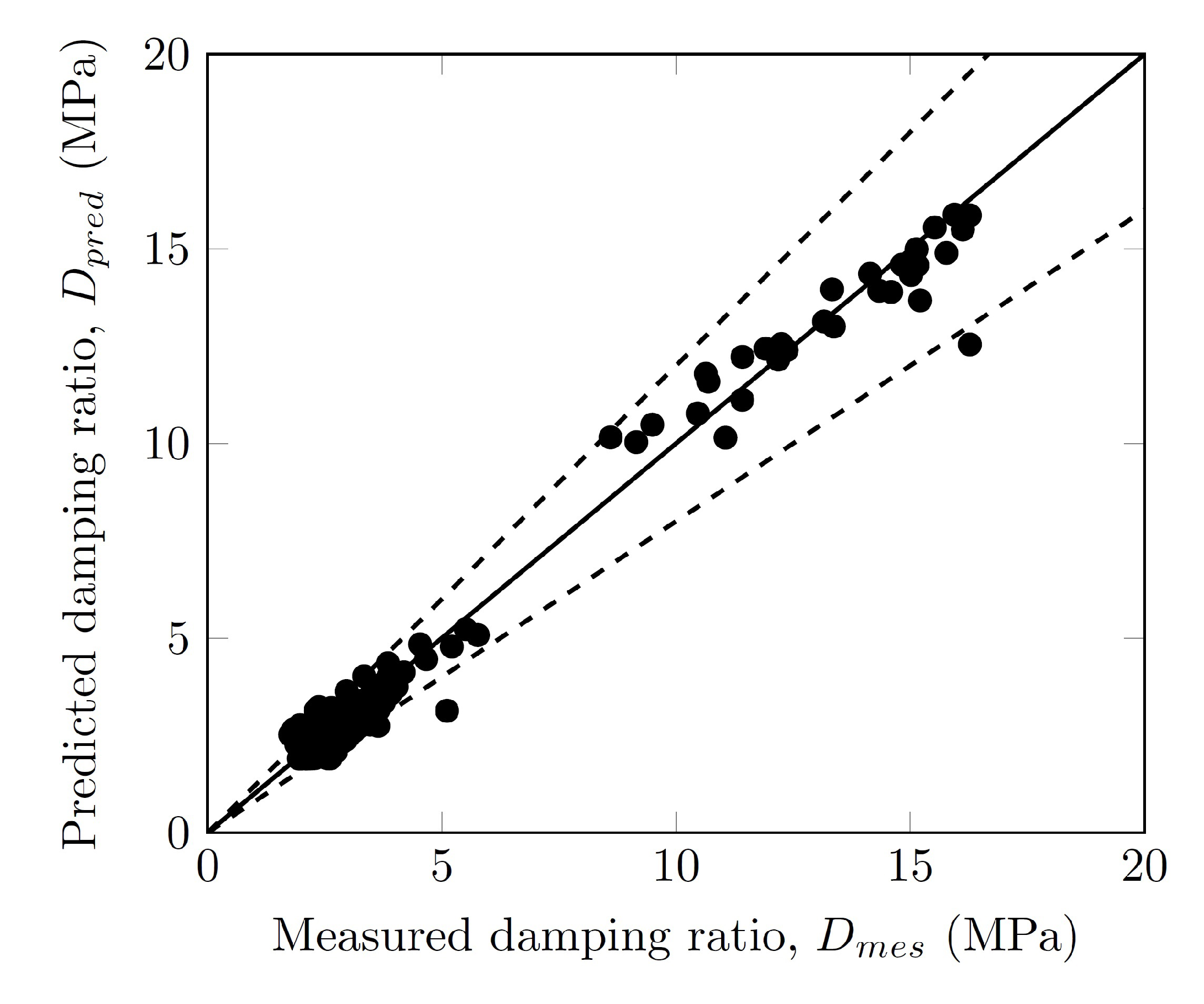
3.7. Damping Ratio
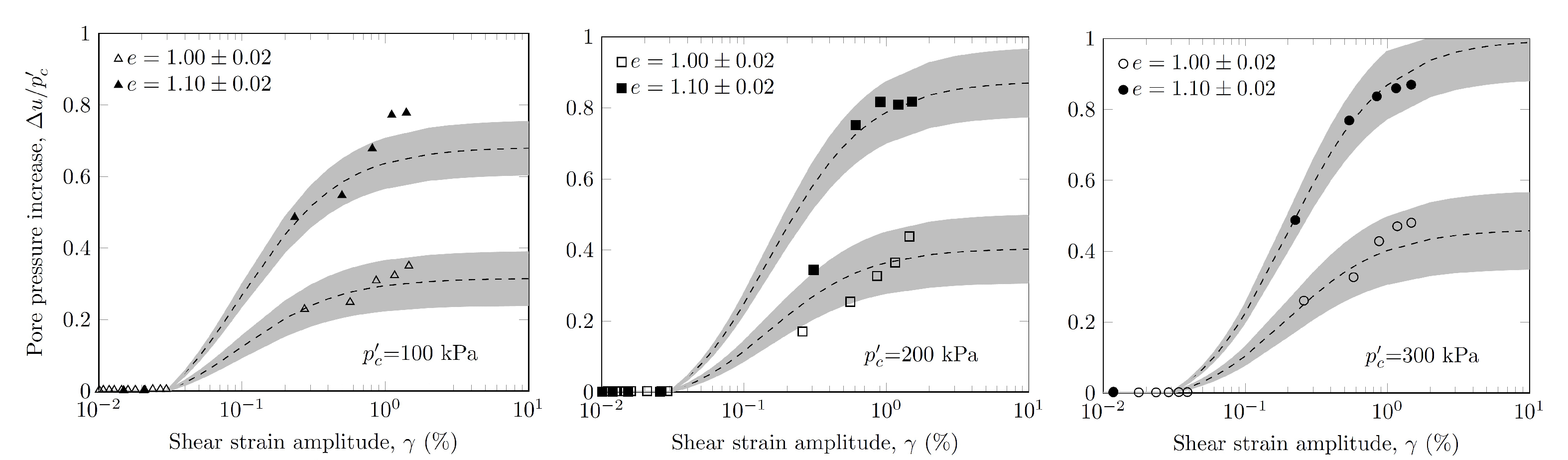
3.8. Pore Water Pressure Ratio
4. Conclusions
- The small-strain shear modulus mainly depended on the void ratio and to a lesser extent on the confinement pressure.
- The curvature of the curve vs. and the reference shear strain , corresponding to , increased with the confinement pressure. When , the normalized shear modulus increased significantly with confinement pressure while the influence of confinement pressure became negligible for .
- Unlike the normalized shear modulus, the damping ratio was influenced only by the confinement pressure when . The maximum damping ratio depended on the confinement pressure and varied between 12% and 16%.
- The pore water pressure developed when the shear strain amplitude reached a threshold shear strain evaluated at 0.03%. It increased linearly with the damping ratio and the void ratio.
- The specificity of the mechanical behavior of this compacted, saturated residual soil could be attributed to the crushing of the cemented aggregates constituting the material when the threshold shear strain was exceeded.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zarfl, C.; Lumsdon, A.; Berlekamp, J.; Tydecks, L.; Tockner, K. A global boom in hydropower dam construction. Aquat. Sci. 2015, 77, 161–170. [Google Scholar] [CrossRef]
- Marulanda, A.; Radchenko, V.E.A. Bulletin 151—Tropical Residual Soils as Dam Foundation and Fill Material; Technical Report; ICOLD: Paris, France, 2017. [Google Scholar]
- Fookes, P. Tropical Residual Soils; A Geological Society Engineering Group Working Party Revised Report; Geological Society: London, UK, 1997. [Google Scholar]
- Wesley, L. Geotechnical Engineering in Residual Soils; John Wiley & Sons: Hoboken, NJ, USA, 2010. [Google Scholar]
- Jacquet, D. Sensitivity to remoulding of some volcanic ash soils in New Zealand. Eng. Geol. 1990, 28, 1–25. [Google Scholar] [CrossRef]
- Wang, C.E.; Borden, R.H. Deformation Characteristics of Piedmont Residual Soils. J. Geotech. Eng. 1996, 122, 822–830. [Google Scholar] [CrossRef]
- Samingan, A.S.; Leong, E.C.; Rahardjo, H. A flexible wall permeameter for measurements of water and air coefficients of permeability of residual soils. Can. Geotech. J. 2003, 40, 559–574. [Google Scholar] [CrossRef]
- Futai, M.M.; Almeida, M.S.S.; Lacerda, W.A. Yield, Strength, and Critical State Behavior of a Tropical Saturated Soil. J. Geotech. Geoenviron. Eng. 2004, 130, 1169–1179. [Google Scholar] [CrossRef]
- Futai, M.M.; Almeida, M.S.S. An experimental investigation of the mechanical behaviour of an unsaturated gneiss residual soil. Géotechnique 2005, 55, 201–213. [Google Scholar] [CrossRef]
- Hernandez, O.; Cordão Neto, M.P.; Caicedo, B. Structural features and hydro-mechanical behaviour of a compacted andesitic volcanic soil. Géotechnique Lett. 2018, 8, 195–200. [Google Scholar] [CrossRef]
- Seed, H.B.; Idriss, I.M.; Lee, K.L.; Makdisi, F.I. Dynamic Analysis of the Slide in the Lower San Fernando Dam during the Earthquake of February 9, 1971. J. Geotech. Eng. Div. 1975, 101, 889–911. [Google Scholar] [CrossRef]
- Ohmachi, T.; Tahara, T. Nonlinear Earthquake Response Characteristics of a Central Clay Core Rockfill Dam. Soils Found. 2011, 51, 227–238. [Google Scholar] [CrossRef]
- Cascone, E.; Rampello, S. Decoupled seismic analysis of an earth dam. Soil Dyn. Earthq. Eng. 2003, 23, 349–365. [Google Scholar] [CrossRef]
- Veylon, G.; Luu, L.H.; Mercklé, S.; Bard, P.Y.; Delvallée, A.; Carvajal, C.; Frigo, B. A simplified method for estimating Newmark displacements of mountain reservoirs. Soil Dyn. Earthq. Eng. 2017, 100, 518–528. [Google Scholar] [CrossRef]
- Sica, S.; Pagano, L. Performance-Based Analysis of Earth Dams: Procedures and Application to a Sample Case. Soils Found. 2009, 49, 921–939. [Google Scholar] [CrossRef]
- Rampello, S.; Cascone, E.; Grosso, N. Evaluation of the seismic response of a homogeneous earth dam. Soil Dyn. Earthq. Eng. 2009, 29, 782–798. [Google Scholar] [CrossRef]
- Pelecanos, L.; Kontoe, S.; Zdravković, L. A case study on the seismic performance of earth dams. Géotechnique 2015, 65, 923–935. [Google Scholar] [CrossRef]
- Amir-Faryar, B.; Aggour, M.S.; McCuen, R.H. Universal model forms for predicting the shear modulus and material damping of soils. Geomech. Geoengin. 2017, 12, 60–71. [Google Scholar] [CrossRef]
- Stokoe, H.; Darendeli, M.; Andrus, R.; Brown, L. Dynamic soil properties: Laboratory, field and correlation studies. Conf. Earthq. Geotech. Eng. 1999, 3, 811–845. [Google Scholar]
- Hardin, B.; Black, W. Closure to: Vibration Modulus of Normally Consolidated Clays. J. Soil Mech. Found. Div. 1969, 95, 1531–1537. [Google Scholar] [CrossRef]
- Kagawa, T. Moduli and Damping Factors of Soft Marine Clays. J. Geotech. Eng. 1992, 118, 1360–1375. [Google Scholar] [CrossRef]
- Ishibashi, I.; Zhang, X. Unified Dynamic Shear Moduli and Damping Ratios of Sand and Clay. Soils Found. 1993, 33, 182–191. [Google Scholar] [CrossRef]
- Hardin, B.; Drnevich, V. Shear Modulus and Damping in Soils: Design Equations and Curves. J. Soil Mech. Found. Div. 1972, 98, 667–692. [Google Scholar] [CrossRef]
- Sun, J.; Golesorkhi, R.; Seed, H. Dynamic Moduli and Damping Ratios for Cohesive Soils; Technical Report UCB/EERC-88/15; University of California: Berkeley, CA, USA, 1988. [Google Scholar]
- Kokusho, T.; Yoshida, Y.; Esashi, Y. Dynamic properties of soft clay for wide strain range. Soils Found. 1982, 22, 1–18. [Google Scholar] [CrossRef] [PubMed]
- Lo Presti, D.C.F.; Jamiolkowski, M.; Pallara, O.; Cavallaro, A.; Pedroni, S. Shear modulus and damping of soils. Géotechnique 1997, 47, 603–617. [Google Scholar] [CrossRef]
- Rampello, S.; Viggiani, G.M.B.; Amorosi, A. Small-strain stiffness of reconstituted clay compressed along constant triaxial effective stress ratio paths. Géotechnique 1997, 47, 475–489. [Google Scholar] [CrossRef]
- Darendeli, M.B. Developement pf a New Family of Normalized Modulus Reduction and Material Damping Curves. Ph.D. Thesis, University of Texas at Austin, Austin, TX, USA, 2001. [Google Scholar]
- Stokoe, K.; Darendeli, M.; Gilbert, R.; Menq, F.Y.; Choi, W.K. Development of a New Family of Normalized Modulus Reduction and Material Damping Curves; Technical Report; University of California: Berkeley, CA, USA, 2004. [Google Scholar]
- Okur, D.; Ansal, A. Stiffness degradation of natural fine grained soils during cyclic loading. Soil Dyn. Earthq. Eng. 2007, 27, 843–854. [Google Scholar] [CrossRef]
- Kawaguchi, T.; Tanaka, H. Formulation of Gmax from Reconstituted Clayey Soils and its Application to Gmax Measured in the Field. Soils Found. 2008, 48, 821–831. [Google Scholar] [CrossRef]
- Vardanega, P.; Bolton, M. Stiffness of Clays and Silts: Normalizing Shear Modulus and Shear Strain. J. Geotech. Geoenviron. Eng. 2013, 139, 1575–1589. [Google Scholar] [CrossRef]
- Seed, H.B.I.I. Soil moduli and damping factors for dynamic response analysis. Earthq. Eng. Res. Cent. 1970, 70, 1–15. [Google Scholar]
- Shibuya, S.; Tanaka, H. Estimate of Elastic Shear Modulus In Holocene Soil Deposits. Soils Found. 1996, 36, 45–55. [Google Scholar] [CrossRef]
- Vucetic, M.; Dobry, R. Effect of soil plasticity o cyclic response. J. Geotech. Eng. 1991, 117, 89–107. [Google Scholar] [CrossRef]
- Iwasaki, T.; Tatsuoka, F.; Takagi, Y. Shear modulus of sands under cyclic torsional shear loading. Soils Found. 1978, 18, 39–56. [Google Scholar] [CrossRef]
- Keshavarz, A.; Mehramiri, M. New Gene Expression Programming models for normalized shear modulus and damping ratio of sands. Eng. Appl. Artif. Intell. 2015, 45, 464–472. [Google Scholar] [CrossRef]
- Senetakis, K.; Anastasiadis, A.; Pitilakis, K. Normalized shear modulus reduction and damping ratio curves of quartz sand and rhyolitic crushed rock. Soils Found. 2013, 53, 879–893. [Google Scholar] [CrossRef]
- Menq, F. Dynamic Properties of Sandy and Gravelly Soils. Ph.D. Thesis, University of Texas at Austin, Austin, TX, USA, 2003. [Google Scholar]
- Rollins, K.M.; Evans, M.D.; Diehl, N.B.; Daily, W.D., III. Shear Modulus and Damping Relationships for Gravels. J. Geotech. Geoenviron. Eng. 1998, 124, 396–405. [Google Scholar] [CrossRef]
- Borden, R.H.; Shao, L.; Gupta, A. Dynamic Properties of Piedmont Residual Soils. J. Geotech. Eng. 1996, 122, 813–821. [Google Scholar] [CrossRef]
- Pineda, J.; Colmenares, J.; Hoyos, L. Effect of Fabric and Weathering Intensity on Dynamic Properties of Residual and Saprolitic Soils via Resonant Column Testing. Geotech. Test. J. 2014, 37, 800–816. [Google Scholar] [CrossRef]
- Barros, J. Dynamic Shear Modulus of Tropical Soils. Ph.D. Thesis, Universidade de Sao Paulo, Sao Polo, Brazil, 1997. [Google Scholar]
- Zhang, J.; Andrus, R.D.; Juang, C.H. Normalized Shear Modulus and Material Damping Ratio Relationships. J. Geotech. Geoenviron. Eng. 2005, 131, 453–464. [Google Scholar] [CrossRef]
- Melinda, F.; Rahardjo, H.; Han, K.K.; Leong, E.C. Shear Strength of Compacted Soil under Infiltration Condition. J. Geotech. Geoenviron. Eng. 2004, 130, 807–817. [Google Scholar] [CrossRef]
- Rahardjo, H.; Heng, O.B.; Choon, L.E. Shear strength of a compacted residual soil from consolidated drained and constant water content triaxial tests. Can. Geotech. J. 2004, 41, 421–436. [Google Scholar] [CrossRef]
- Rahardjo, H.; Melinda, F.; Leong, E.; Rezaur, R. Stiffness of a compacted residual soil. Eng. Geol. 2011, 120, 60–67. [Google Scholar] [CrossRef]
- Macari, E.J.; Hoyos, L. Effect of Degree of Weathering on Dynamic Properties of Residual Soils. J. Geotech. Eng. 1996, 122, 988–997. [Google Scholar] [CrossRef]
- Leong, E.C.; Cahyadi, J.; Rahardjo, H. Stiffness of a Compacted Residual Soil. In Proceedings of the Fourth International Conference on Unsaturated Soils, Carefree, AZ, USA, 2–6 April 2006; pp. 1169–1180. [Google Scholar] [CrossRef]
- Pineda, J.A.; Hoyos, L.R.; Colmenares, J.E. Stiffness Response of Residual and Saprolitic Soils Using Resonant Column and Bender Element Testing Techniques. In GeoFlorida 2010; American Society of Civil Engineers: Reston, VA, USA, 2010; pp. 783–792. [Google Scholar] [CrossRef]
- Torres, C.E.; Colmenares, J.E. Influence of Confining Stress on the Small Strain Stiffness of a Residual Soil under K0 Conditions. In PanAm Unsaturated Soils 2017; American Society of Civil Engineers: Reston, VA, USA, 2018; pp. 408–419. [Google Scholar] [CrossRef]
- Francisca, F.; Bogado, G. Weathering effect on the small strains elastic properties of a residual soil. Geotech. Geol. Eng. 2019, 37, 4031–4041. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, X.; Kong, L.; Li, X.; Wang, G. Effect of cementation on the small-strain stiffness of granite residual soil. Soils Found. 2021, 61, 520–532. [Google Scholar] [CrossRef]
- Stokoe, K.; Isenhower, W.M.; Hsu, J. Dynamic Properties of Offshore Silty Samples. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 5–8 May 1980. [Google Scholar]
- ASTM. D4015-07; Standard Test Methods for Modulus and Damping of Soils by Resonant-Column Method. ASTM International: West Conshohocken, PA, USA, 2013.
- Richart, F. Some effects of dynamic soil properties on soil structure interaction. J. Geotech. Eng. Div. 1975, 101, 21–24. [Google Scholar] [CrossRef]
- Ni, S. Dynamic Properties of Sand under True Triaxial Stress States from Resonant Column-Torsional Shear Tests. Ph.D. Thesis, University of Texas, Austin, TX, USA, 1987. [Google Scholar]
- Fedrizzi, F.; Raviolo, P.; Vigano, A. Resonant column and cyclic torsional shear experiments on soils of the Trentino valleys (NE Italy). In Proceedings of the 16th ECSMGE Geotechnical Engineering for Infrastructure and Development, Edinburgh, UK, 13–17 September 2015; pp. 3437–3442. [Google Scholar]
- ASTM. D5311; Standard Test Method for Load Controlled Cyclic Triaxial Strength of Soil. Technical Report. ASTM International: West Conshohocken, PA, USA, 2013.
- Matasović, N.; Vucetic, M. Cyclic Characterization of Liquefiable Sands. J. Geotech. Eng. 1993, 119, 1805–1822. [Google Scholar] [CrossRef]
- Cabidoche, Y.; Maurizot, P.; Théveniaut, H. Sols tropicaux des Outre-mer français tropicaux: Une diversité ordonnée par la géochimie de l’altération des roches. Géosciences 2011, 14, 22–31. [Google Scholar]
- AFNOR. XP P94-041-Sols; Reconnaissance et Essais. Identification granulométrique. Méthode de tamisage par voie humide. Groupe AFNOR: La Plaine Saint-Denis, France, 1995.
- AFNOR. NF P94-057-Sols; Reconnaissance et Essais—Analyse Granulométrique des Sols—Méthode par sédimentation. Groupe AFNOR: La Plaine Saint-Denis, France, 1992.
- Casagrande, A. Research on the Atterberg limits of soils. Public Roads 1932, 13. [Google Scholar]
- Wesley, L.D. Classification and characterisation of tropical residual soils. In Proceedings of the XIV Congreso Colombiano de Geotecnia, Bogotá, Colombia, 15–18 October 2014; pp. 1–15. [Google Scholar]
- Giacheti, H. Experimental study of dynamical properties of some tropical soils in Sao Polo state. Ph.D. Thesis, Universidade de Sao Paulo, Sao Paulo, Brazil, 1991. [Google Scholar]
- Otálvaro, I.F.; Neto, M.P.C.; Caicedo, B. Compressibility and microstructure of compacted laterites. Transp. Geotech. 2015, 5, 20–34. [Google Scholar] [CrossRef]
- Hardin, B.; Black, W. Vibration Modulus of Normally Consolidated Clays. J. Soil Mech. Found. Div. 1968, 94, 353–369. [Google Scholar] [CrossRef]
- Viggiani, G.; Atkinson, J. Stiffness of fine grained soil at very small strains. Géotechnique 1995, 45, 249–265. [Google Scholar] [CrossRef]
- Shibuya, S.; Hwang, S.; Mitachi, T. Elastic shear modulus of soft clays from shear wave velocity measurement. Géotechnique 1997, 47, 593–601. [Google Scholar] [CrossRef]
- Richart, F.; Hall, J.; Woods, R. Vibration of Soils and Foundations; Technical Report; Prentice Hall: London, UK, 1970. [Google Scholar]
- Shibata, T.; Soelarno, D. Stress-strain characteristics of clays under cyclic loading. J. JSCE 1978, 276, 101–110. [Google Scholar] [CrossRef] [PubMed]
- Jamiolkowski, M.; Lancellotta, R.; Lo Presti, D.C.F. Remarks on the stiffness at small strains of six Italian clays. In Prefailure Behavior of Geomaterials; S. Shibuya, T.M., Miura, S., Eds.; Balkema: Rotterdam, The Netherlands, 1994; Volume 2, pp. 817–854. [Google Scholar]
- Santagata, M.; Germaine, J.T.; Ladd, C.C. Factors Affecting the Initial Stiffness of Cohesive Soils. J. Geotech. Geoenviron. Eng. 2005, 131, 430–441. [Google Scholar] [CrossRef]
- Hoyos, L.; Macari, E. Influence of In Situ Factors on Dynamic Response of Piedmont Residual Soils. J. Geotech. Geoenviron. Eng. 1999, 125, 271–279. [Google Scholar] [CrossRef]
- Houlsby, G.; Wroth, C. The Variation of Shear Modulus of a Clay with Pressure and Overconsolidation Ratio. Soils Found. 1991, 31, 138–143. [Google Scholar] [CrossRef]
- Santos, J.; Correia, A. Shear Modulus of Soils under Cyclic Loading at Small and Medium Strain Level. In Proceedings of the 12th World Conference on Earthquake Engineering, Auckland, New Zealand, 30 January–4 February 2000; Volume 530. [Google Scholar]
- Cha, M.; Santamarina, J.C.; Kim, H.S.; Cho, G.C. Small-Strain Stiffness, Shear-Wave Velocity, and Soil Compressibility. J. Geotech. Geoenviron. Eng. 2014, 140, 06014011. [Google Scholar] [CrossRef]
- Goddard, J.D. Nonlinear elasticity and pressure-dependent wave speeds in granular media. Proc. R. Soc. A 1990, 37, 430105–430131. [Google Scholar] [CrossRef]
- ASTM D3999; Standard Test Methods for the Determination of the Modulus and Damping Properties of Soils Using the Cyclic Triaxial Apparatus. ASTM International: West Conshohocken, PA, USA, 2012.
- Hardin, B. The nature of damping in sands. J. Soil Mech. Found. Div. 1965, 91, 63–97. [Google Scholar] [CrossRef]
- Sheriff, M.; Gaddah, A.; Ishibashi, I. Damping ratio for dry sands. J. Soil Mech. Found. Div. 1977, 103, 743–756. [Google Scholar] [CrossRef]
- Uchida, K.; Sawada, T.; Hasegawa, T. Dynamic Properties of Sand Subjected to Initial Shear Stress. In Proceedings of the International Symposium on Soils under Cyclic and Transient Loading, Swansea, UK, 7–11 January 2013; pp. 121–133. [Google Scholar]
- Zhang, X. Effect of coupled motions on the dynamic properties of sands. PhD Thesis, University of Texas, College Park, TX, USA, 1994. [Google Scholar]
- Cetin, K.O.; Bilge, H.T. Cyclic Large Strain and Induced Pore Pressure Models for Saturated Clean Sands. J. Geotech. Geoenviron. Eng. 2012, 138, 309–323. [Google Scholar] [CrossRef]
- Hsu, C.C.; Vucetic, M. Threshold Shear Strain for Cyclic Pore-Water Pressure in Cohesive Soils. J. Geotech. Geoenviron. Eng. 2006, 132, 1325–1335. [Google Scholar] [CrossRef]
- Ichii, K.; Mikami, T. Cyclic threshold shear strain in pore water pressure generation in clay in situ samples. Soils Found. 2018, 58, 756–765. [Google Scholar] [CrossRef]









| Specimen ID | Type of Test | Tested | |
|---|---|---|---|
| (−) | (kPa) | ||
| RC-1 | RC | 1.01 | 100, 200, 300 |
| RC-2 | RC | 1.09 | 100, 200, 300 |
| RC-3 | RC | 1.00 | 100, 200 |
| RC-4 | RC | 1.10 | 100, 200, 300 |
| RC-5 | RC | 1.08 | 100, 200 |
| RC-6 | RC | 1.13 | 100 |
| RC-7 | RC | 1.45 | 100, 200, 300 |
| RC-8 | RC | 1.47 | 100, 200, 300 |
| RC-9 | RC | 1.48 | 100, 200 |
| TX-1 | CyTX | 1.01 | 100 |
| TX-2 | CyTX | 1.00 | 200 |
| TX-3 | CyTX | 0.99 | 300 |
| TX-4 | CyTX | 1.08 | 100 |
| TX-5 | CyTX | 1.10 | 200 |
| TX-6 | CyTX | 1.08 | 300 |
| Mineral Species from X-ray Diffraction Analyses | Weight (%) |
|---|---|
| Kaolinite | 44.1–44.2 |
| Goethite | 21.8–22.5 |
| Gibbsite | 9.1–10.9 |
| Quartz | 5.0–5.4 |
| Halloysite | 3.1–11.6 |
| Anatase | 2.6–3.3 |
| Nacrite | 0.0–12.1 |
| Chemical elements from ICP analyses | |
| 30.5–30.6 | |
| 30.6–30.8 | |
| 16.3–16.3 | |
| 0.04 | |
| 0.2 | |
| 0.2 | |
| 0.2 | |
| 1.4 | |
| 19.8 |
| Reference | Type of Clay | x | m | n | |
|---|---|---|---|---|---|
| Hardin et al. [68] | Edgar plastic kaolin (R) | - | - | 0.5 | |
| Shibata et al. [72] | 3 Japanese clays (U) | - | - | 0.5 | |
| Kagawa et al. [21] | Soft marine clays (R) | - | - | 1.0 | |
| Viggiani and Atkinson [69] | Speswhite kaolin (R) | - | - | 0.653 | 0.195 |
| London clay (R) | - | - | 0.51 | 0.25 | |
| Shibuya et al. [34] | 5 types of clays (R) | 1.5 | - | 0.5 | |
| Shibuya et al. [70] | 8 Japanese clays (U) | 2.4 | 0.64–0.94 | 0.40–0.68 | |
| Jamiolkowski et al. [73] | 8 Italian clays (U) | 1.11–1.52 | - | 0.40–0.58 | |
| Barros [43] | 8 Brazilian residual soils (R) | 0.95 | 0.485 | 0.515 | |
| Borden et al. [41] | 4 Piedmont residual soils (U) | - | - | - | 0.34–0.41 |
| Hoyos and Macari [75] | 6 Piedmont residual soils (U) | - | - | - | 0.80–1.15 |
| Pineda et al. [42] | 4 Colombian residual soils (U) | - | - | - | 0.37–0.48 |
| Santagata et al. [74] | Boston Blue clay (R) | - | - | 0.15 | 0.80 |
| Boston Blue clay (R) | 2.44 | - | 0.44 | ||
| Vardanega and Bolton [32] | 10 types of clays (R) | 2.4 | - | 0.50 | |
| Francisca and Bogado [52] | Basaltic residual soils (R) | - | - | - | 0.12–0.24 |
| Liu et al. [53] | Granitic residual soils (R) | 1.3 | - | 0.48 | |
| Torres and Colmenares [51] | Lateritic residual soils (R) | - | - | - | 0.28 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mouali, L.; Veylon, G.; Dias, D.; Peyras, L.; Carvajal, C.; Duriez, J.; Antoinet, E. Dynamic Properties of a Compacted Residual Soil from the West Indies. Geotechnics 2023, 3, 254-277. https://doi.org/10.3390/geotechnics3020015
Mouali L, Veylon G, Dias D, Peyras L, Carvajal C, Duriez J, Antoinet E. Dynamic Properties of a Compacted Residual Soil from the West Indies. Geotechnics. 2023; 3(2):254-277. https://doi.org/10.3390/geotechnics3020015
Chicago/Turabian StyleMouali, Lila, Guillaume Veylon, Daniel Dias, Laurent Peyras, Claudio Carvajal, Jérôme Duriez, and Eric Antoinet. 2023. "Dynamic Properties of a Compacted Residual Soil from the West Indies" Geotechnics 3, no. 2: 254-277. https://doi.org/10.3390/geotechnics3020015
APA StyleMouali, L., Veylon, G., Dias, D., Peyras, L., Carvajal, C., Duriez, J., & Antoinet, E. (2023). Dynamic Properties of a Compacted Residual Soil from the West Indies. Geotechnics, 3(2), 254-277. https://doi.org/10.3390/geotechnics3020015










