Numerical Modelling Techniques for Stability Analysis of Slopes Reinforced with Shallow Roots
Abstract
1. Background
2. Methodology
2.1. Finite Element Method
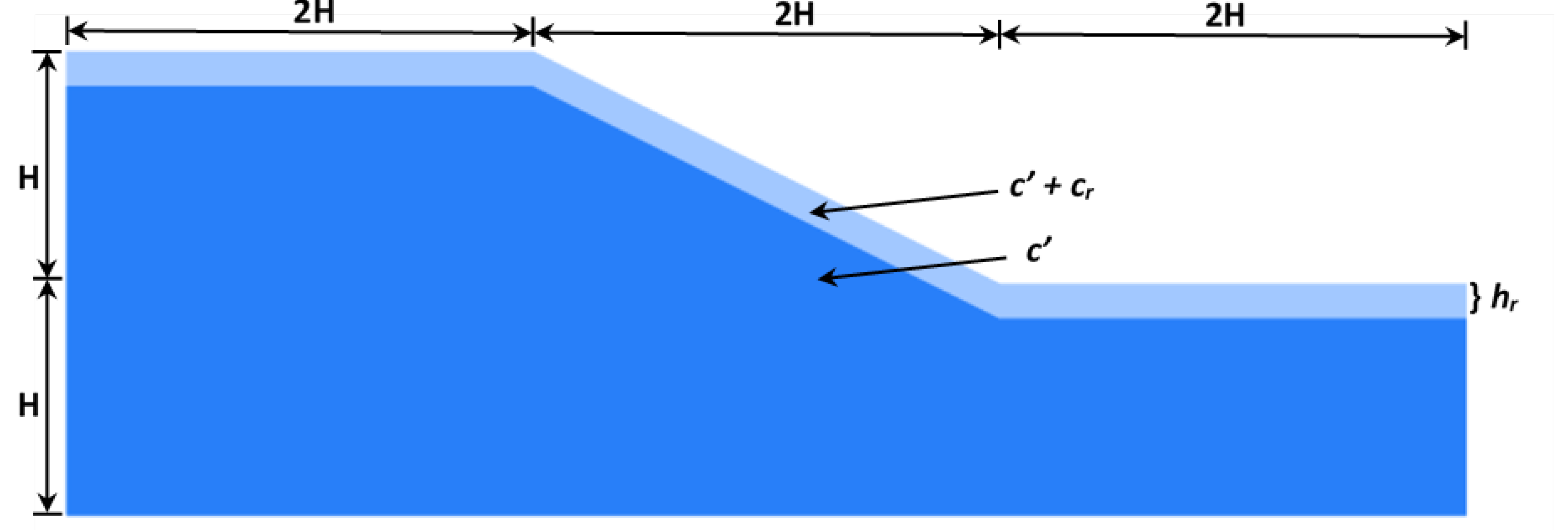
2.2. Simulation of Apparent Root Cohesion
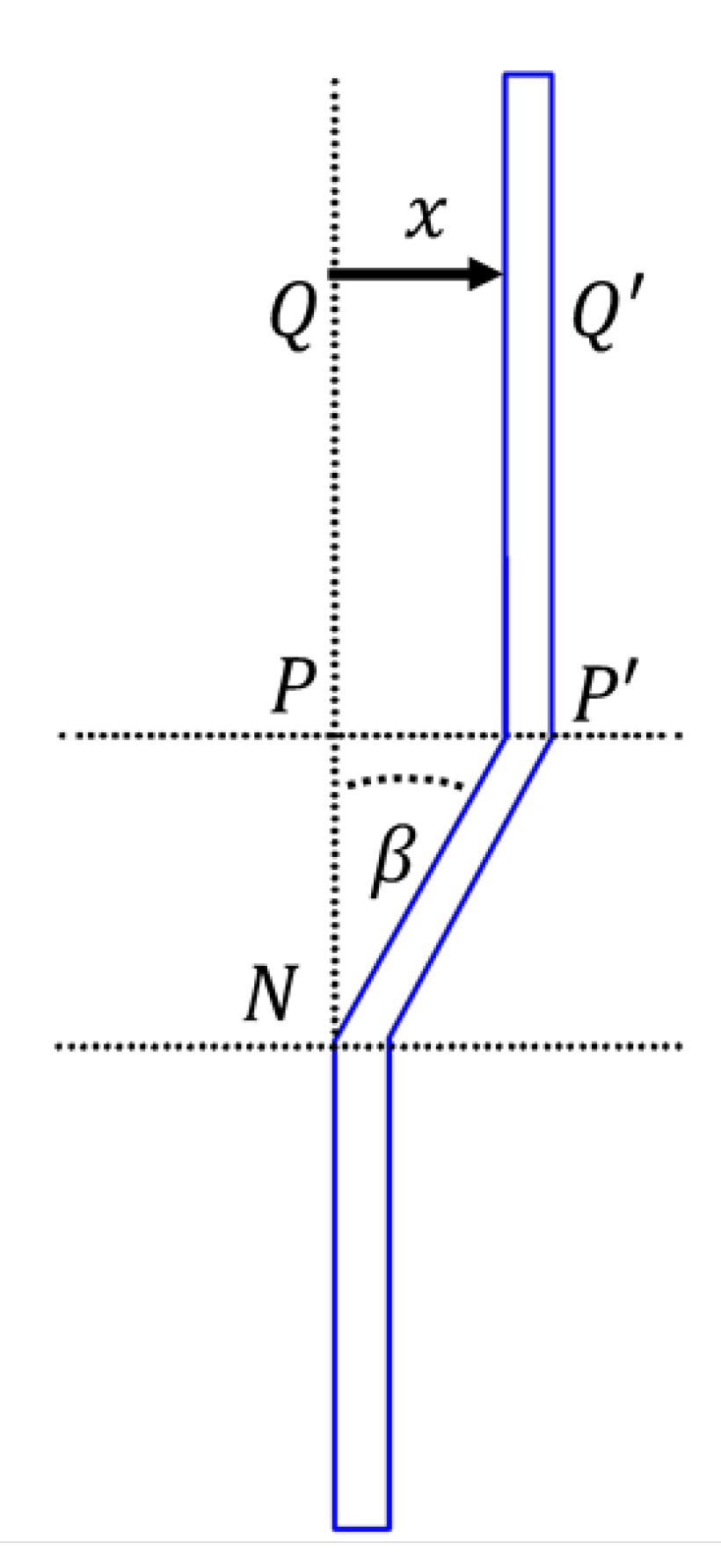
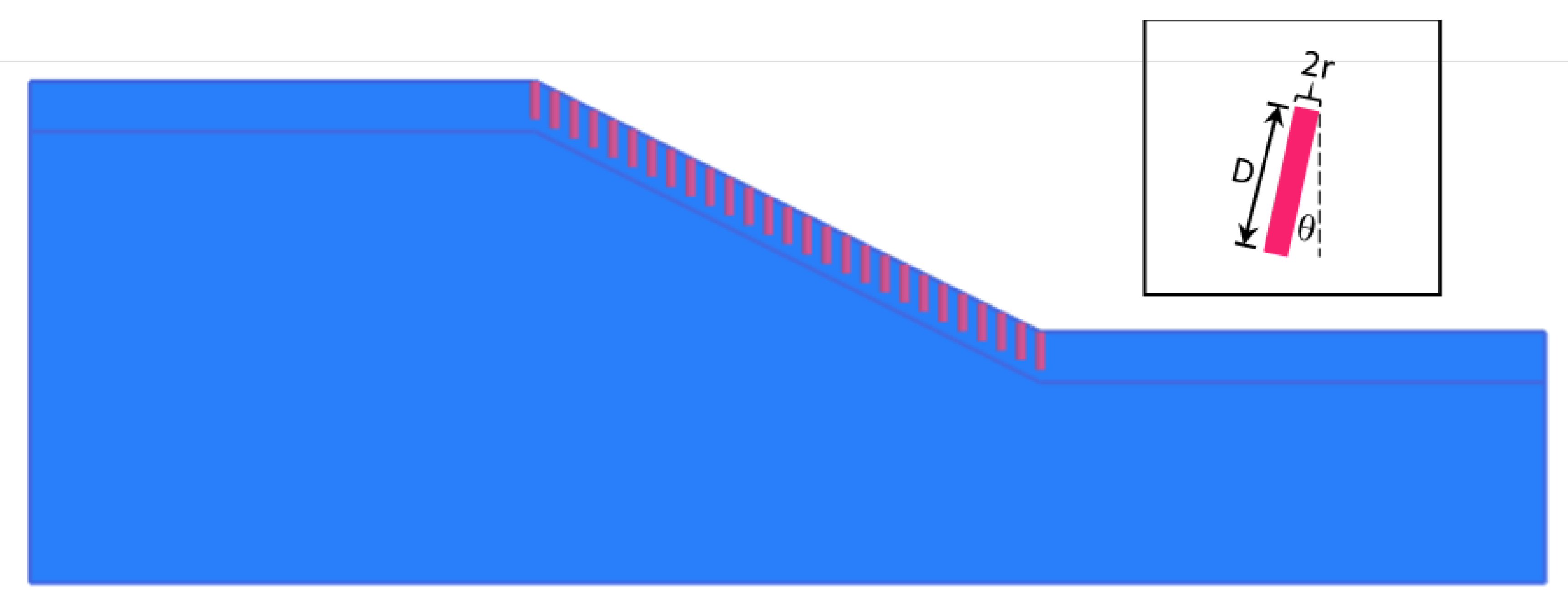
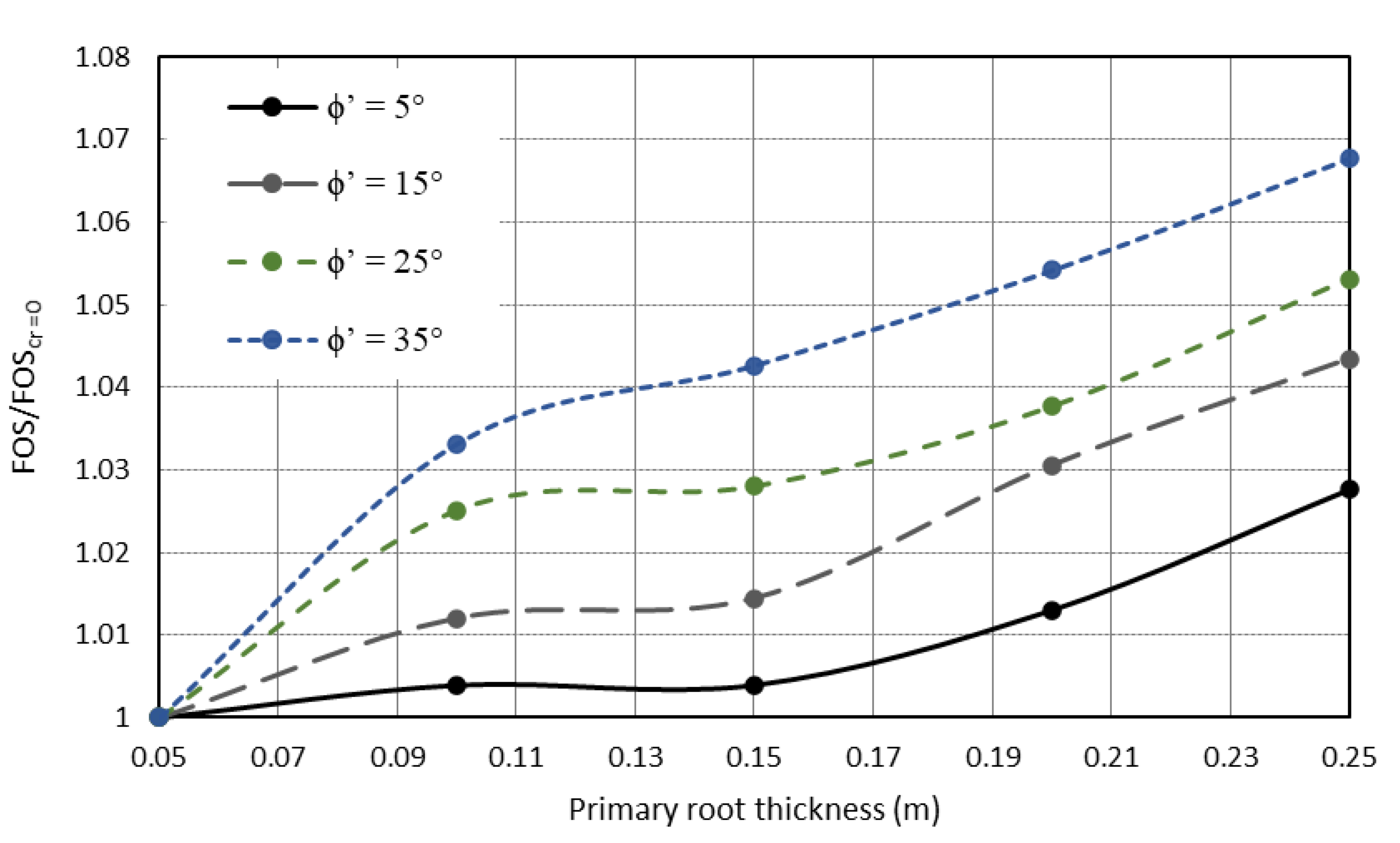
2.3. Primary Taproot Modelling
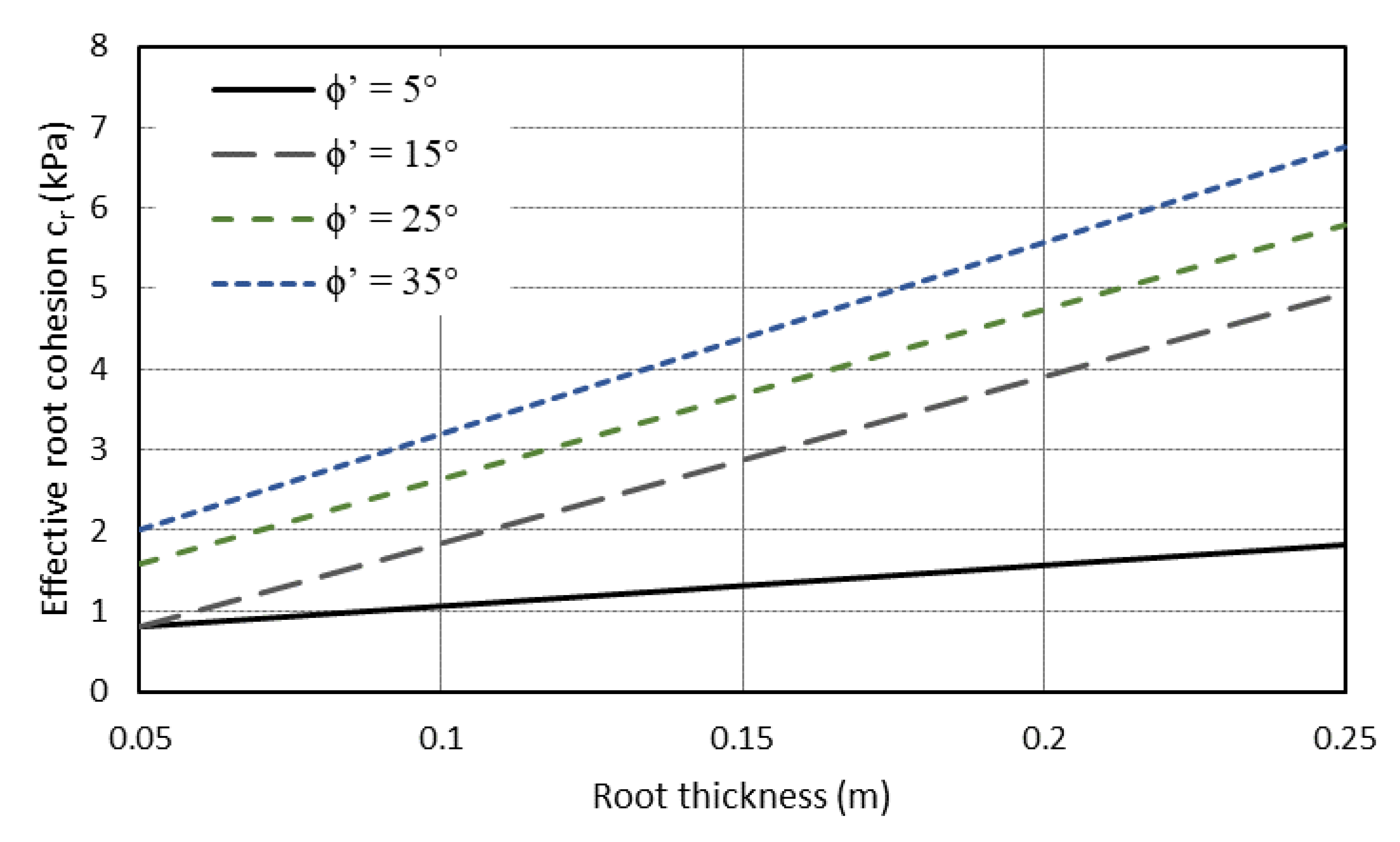
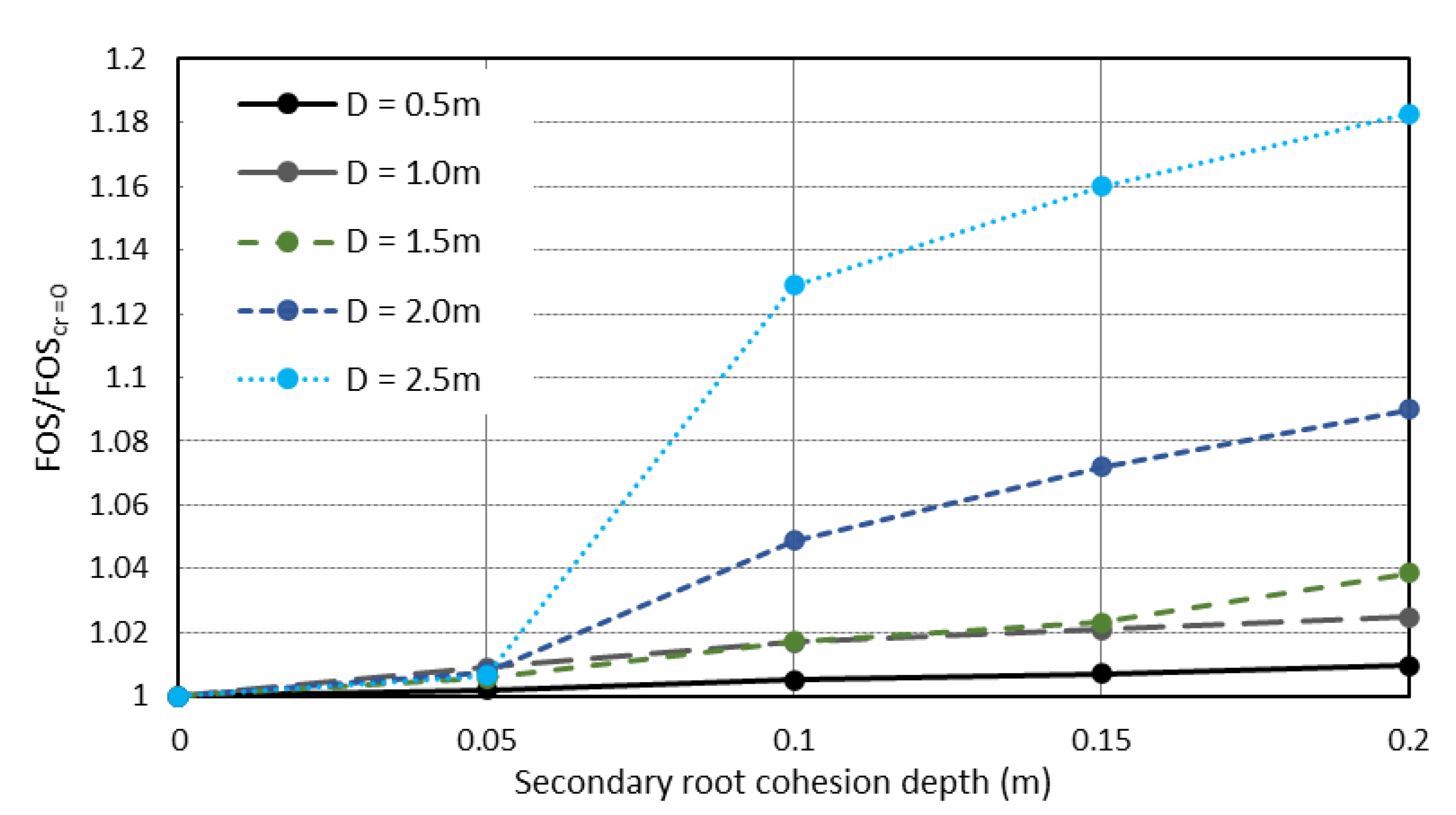
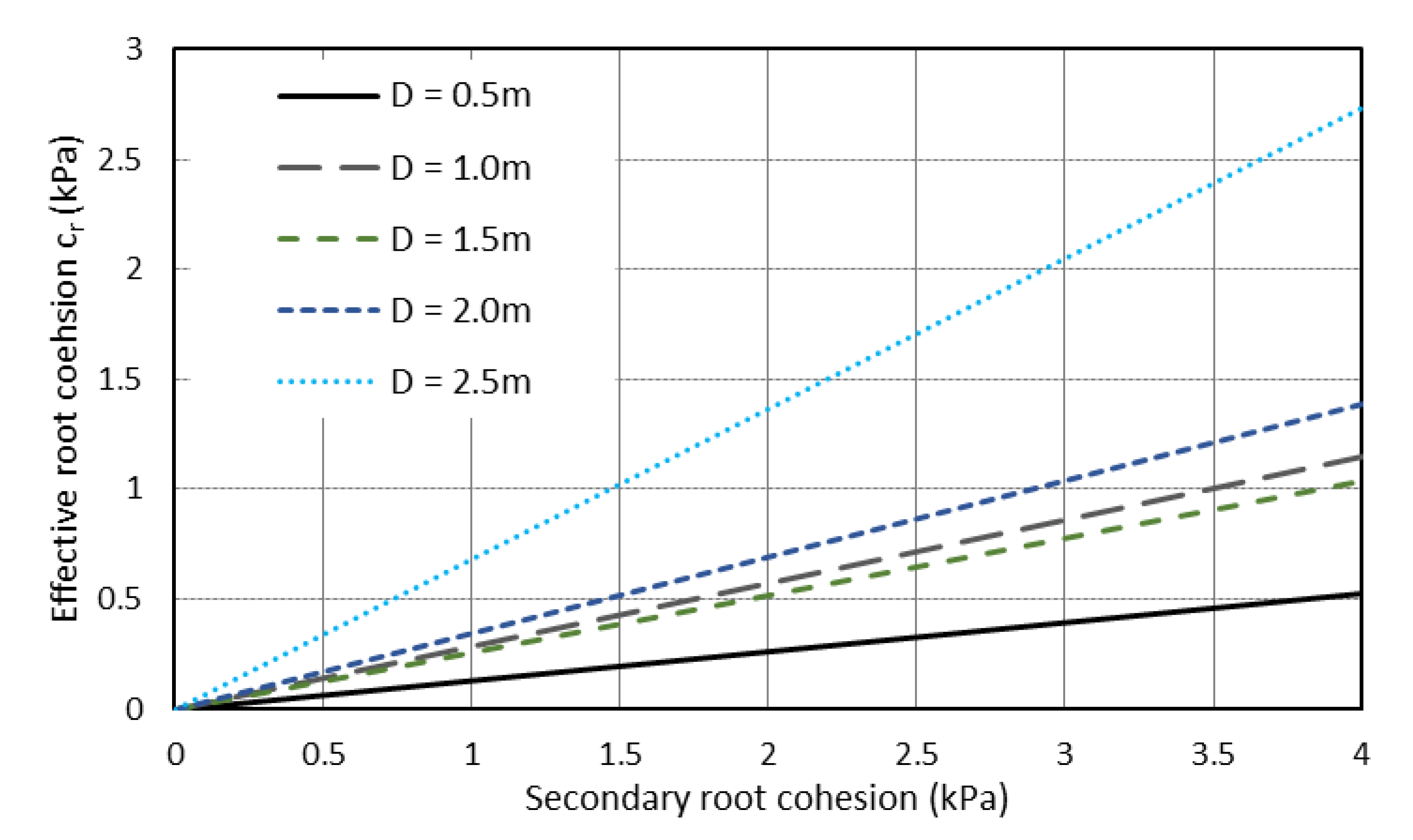
2.4. Secondary Cohesion Modelling
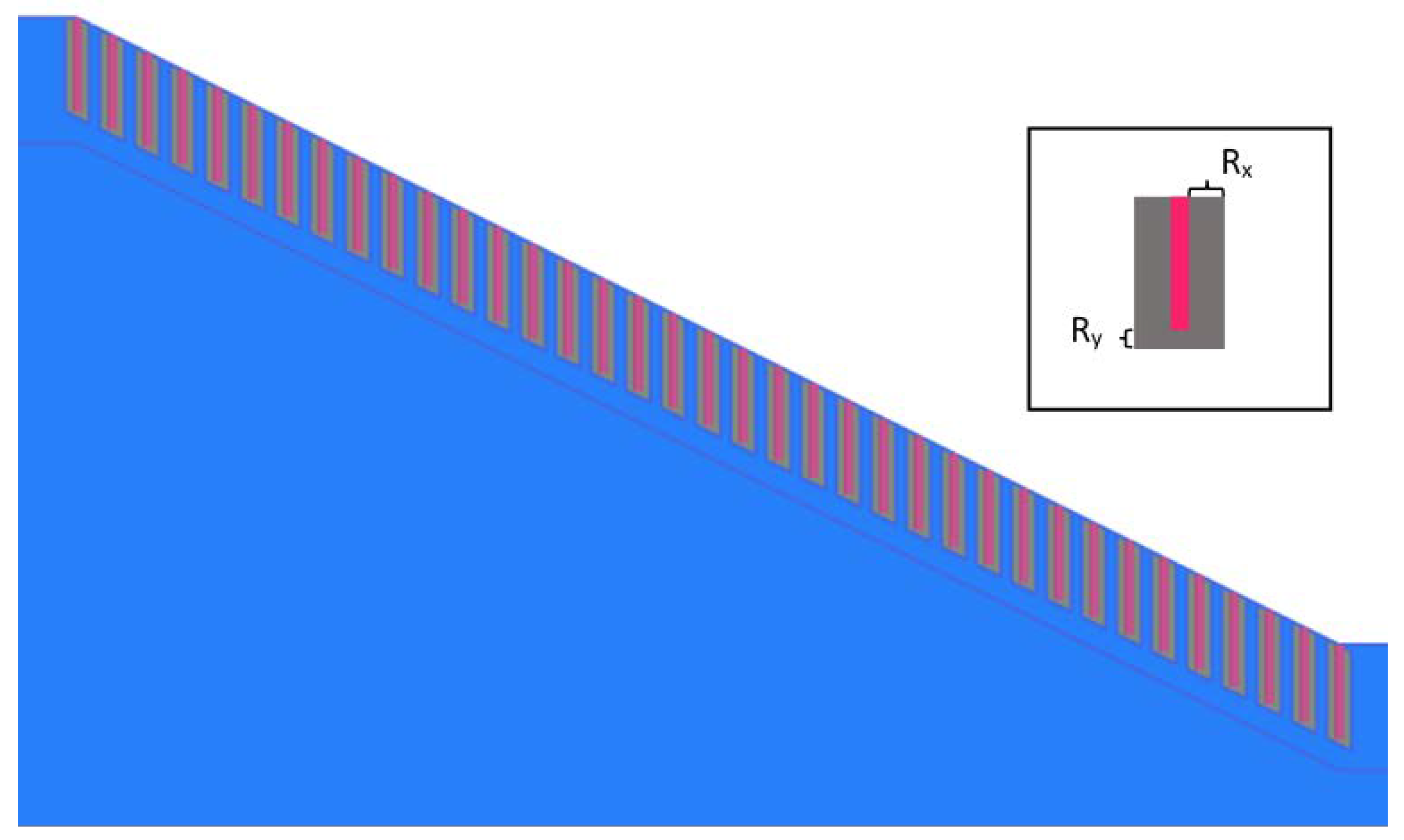
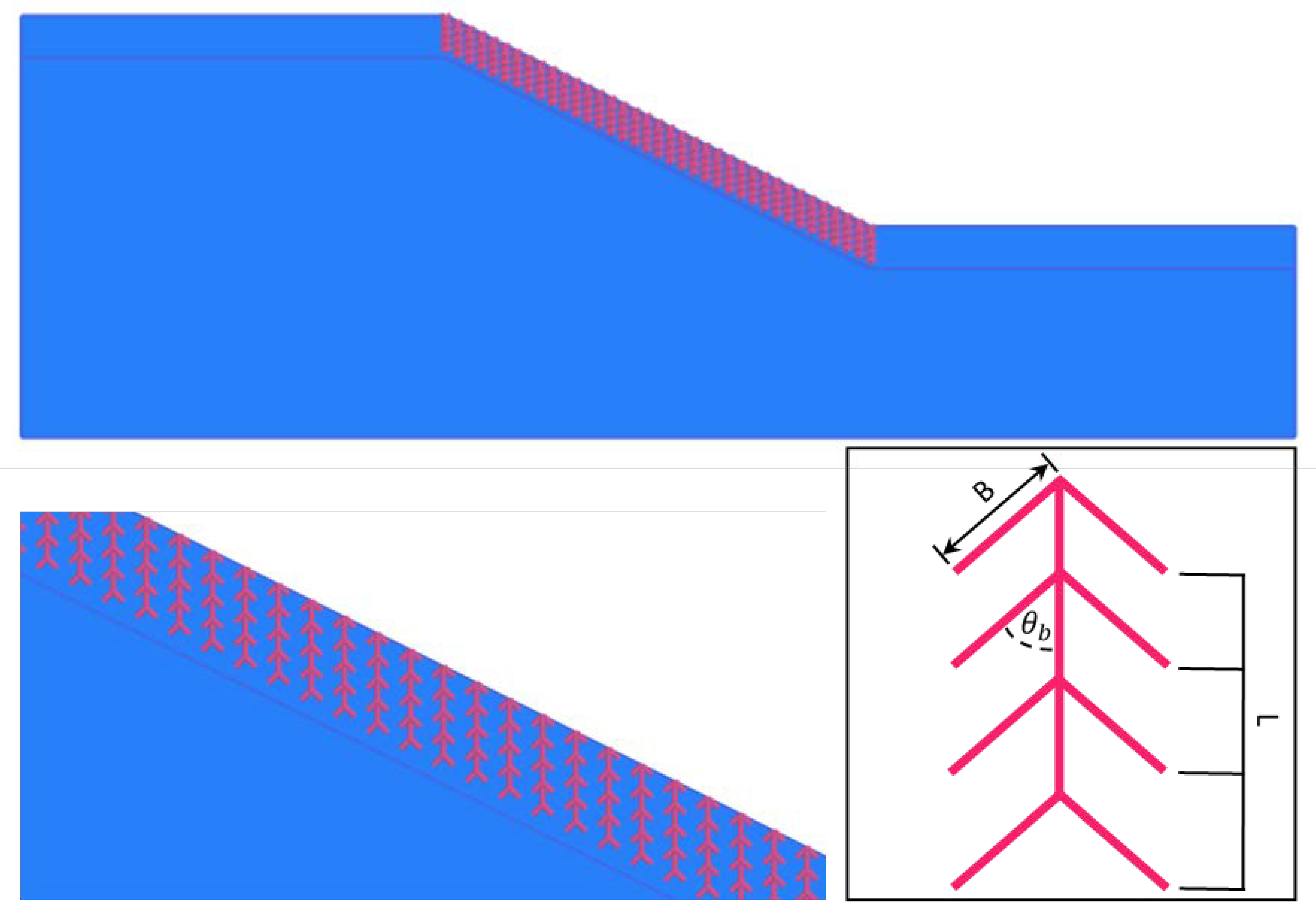
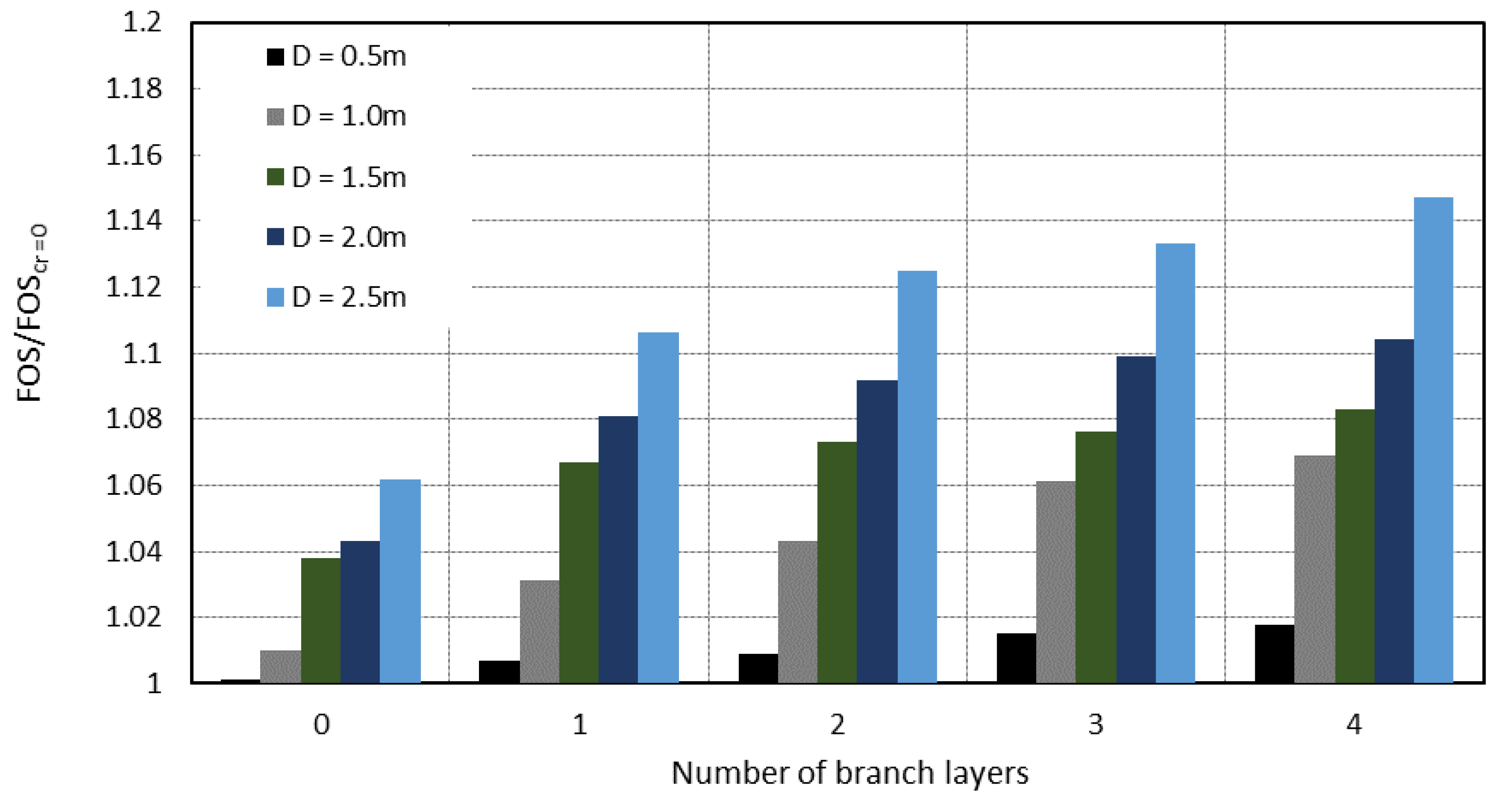
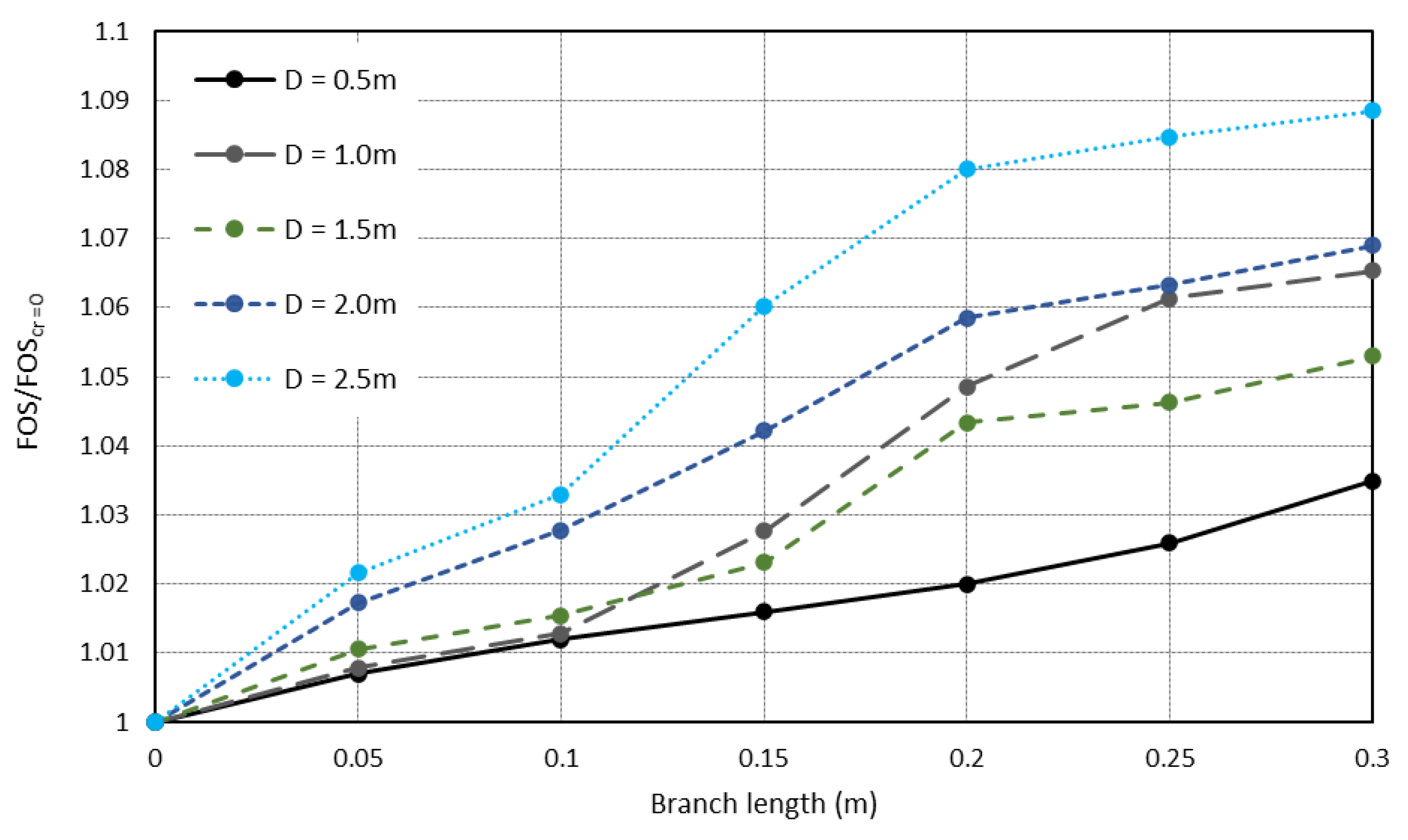
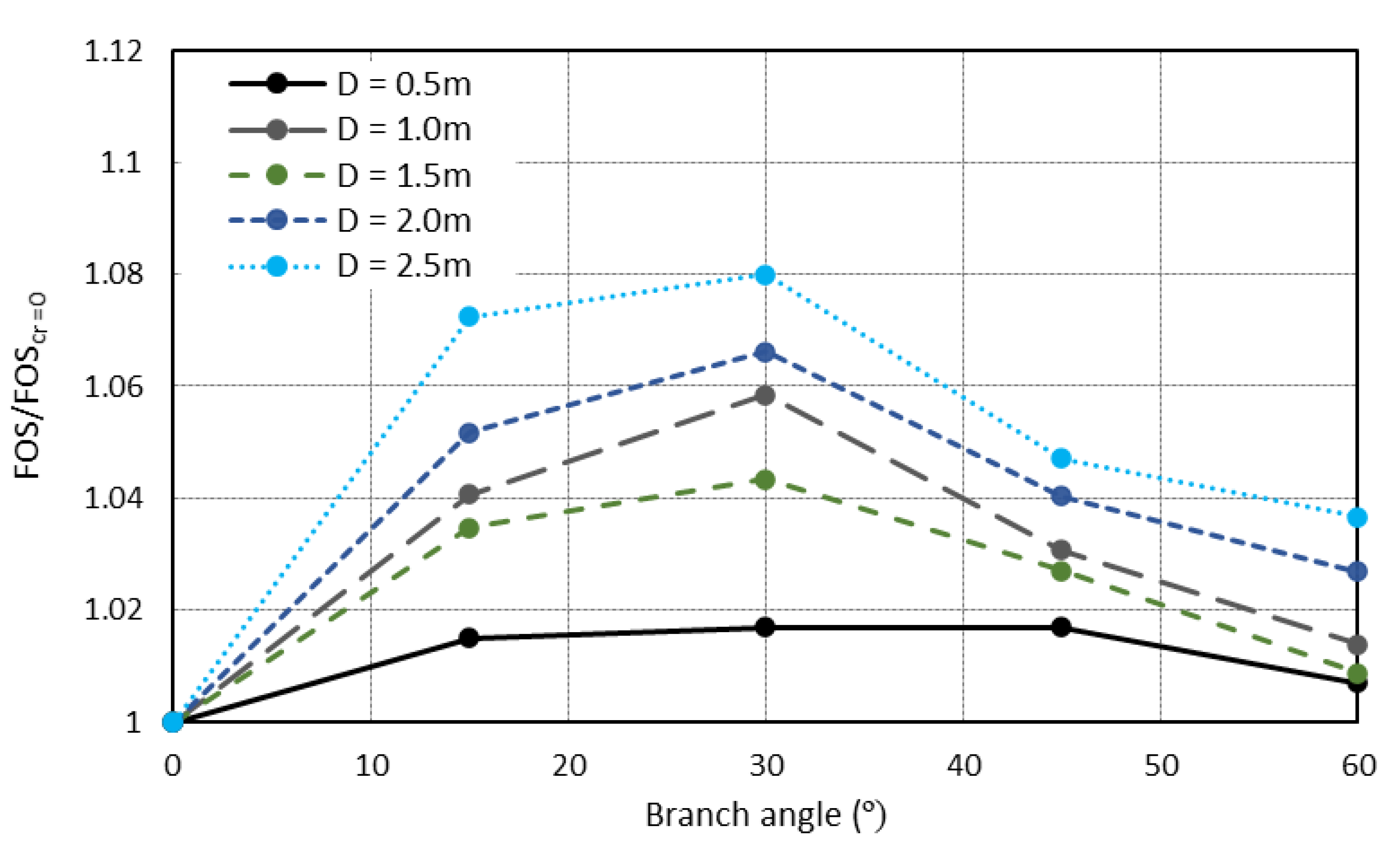
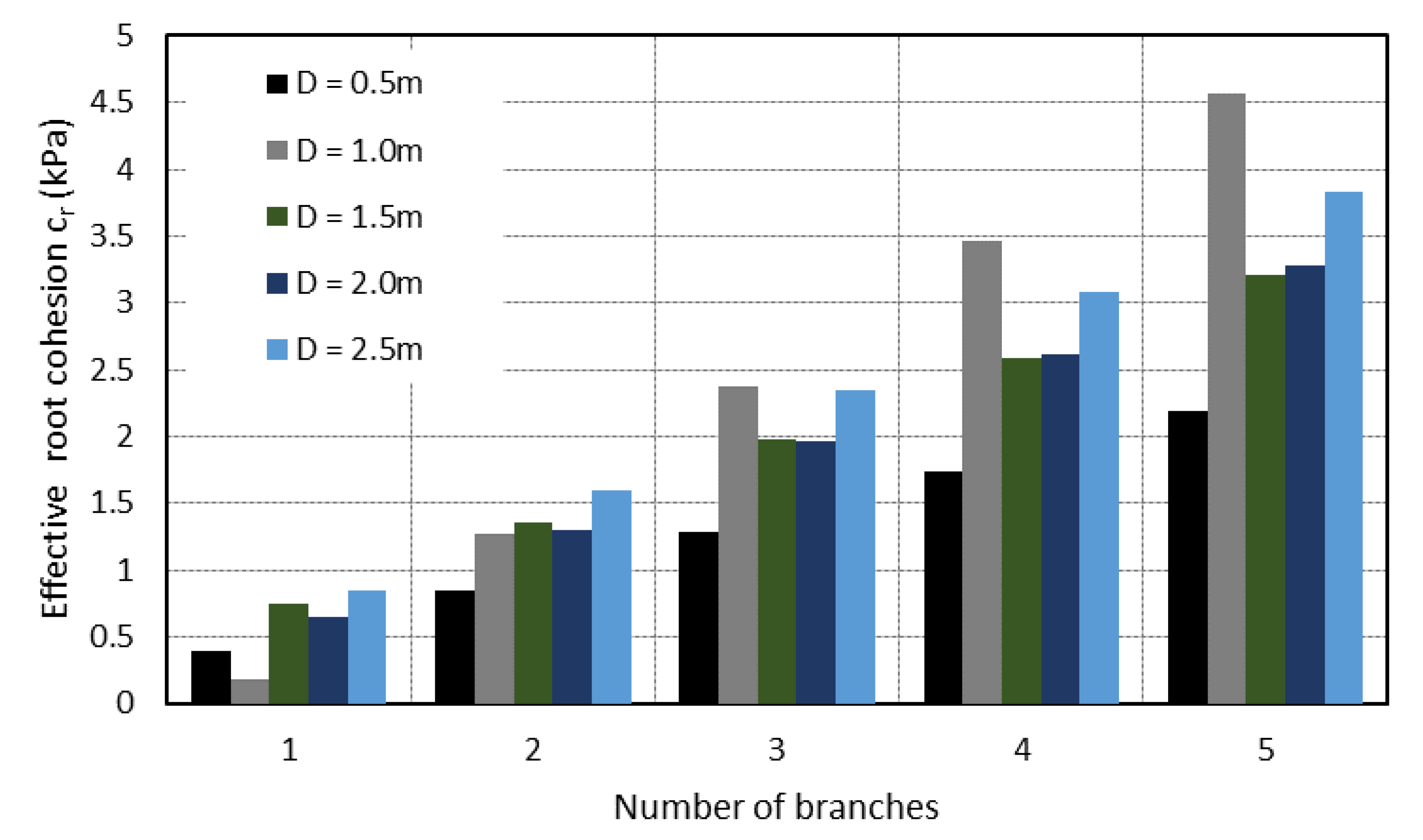
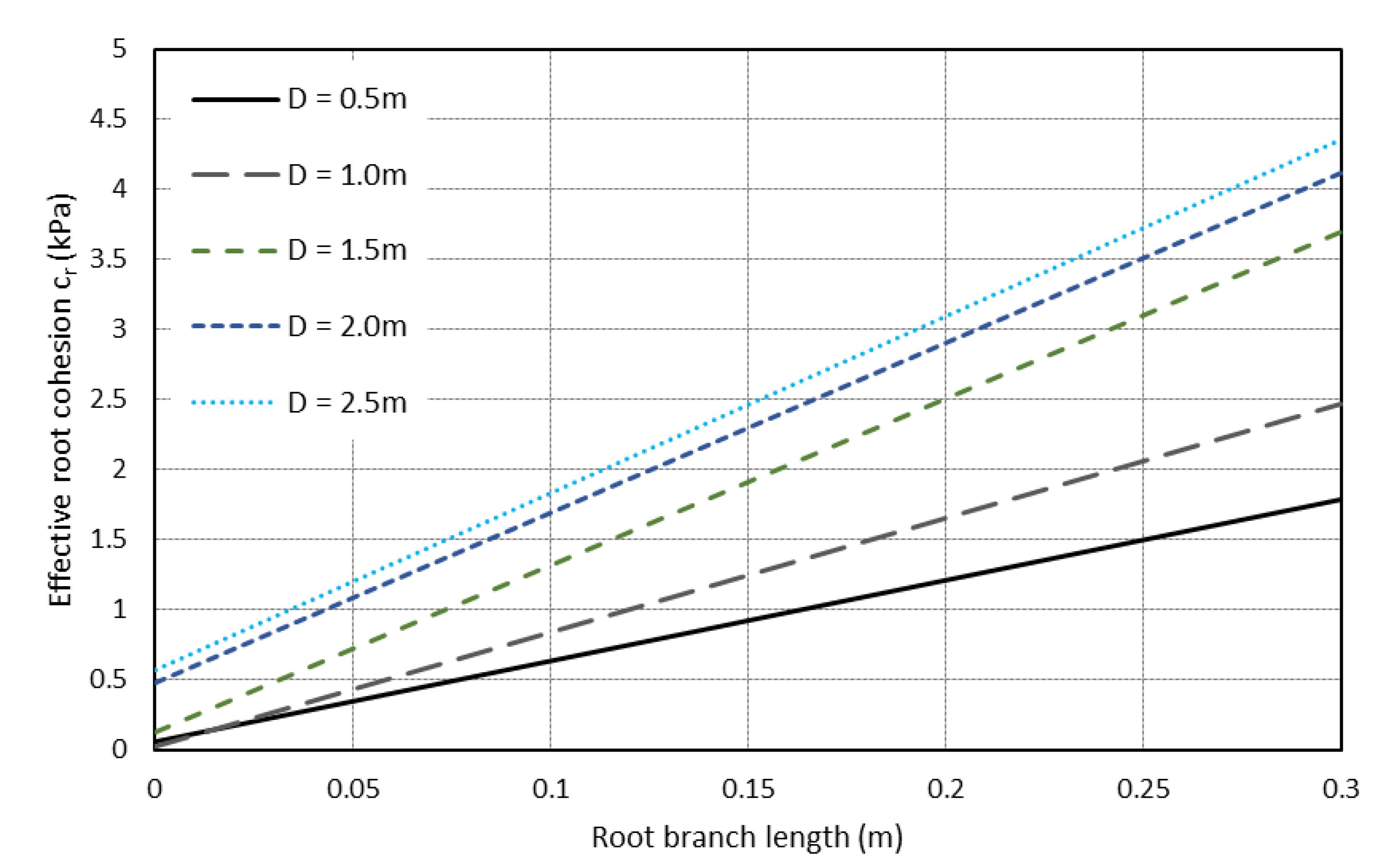
2.5. Branched Root Model
3. Concluding Remarks
- (1)
- The proposed method provides a mechanism of comparative assessment whereby complex root structures can be associated with a suitable effective root cohesion, exhibiting comparable deformation characteristics and slope safety factors. As a result of the method, the direct simulation of root architectures can be replaced with somewhat simplified effective root cohesion parameters, whose relationships have been provided.
- (2)
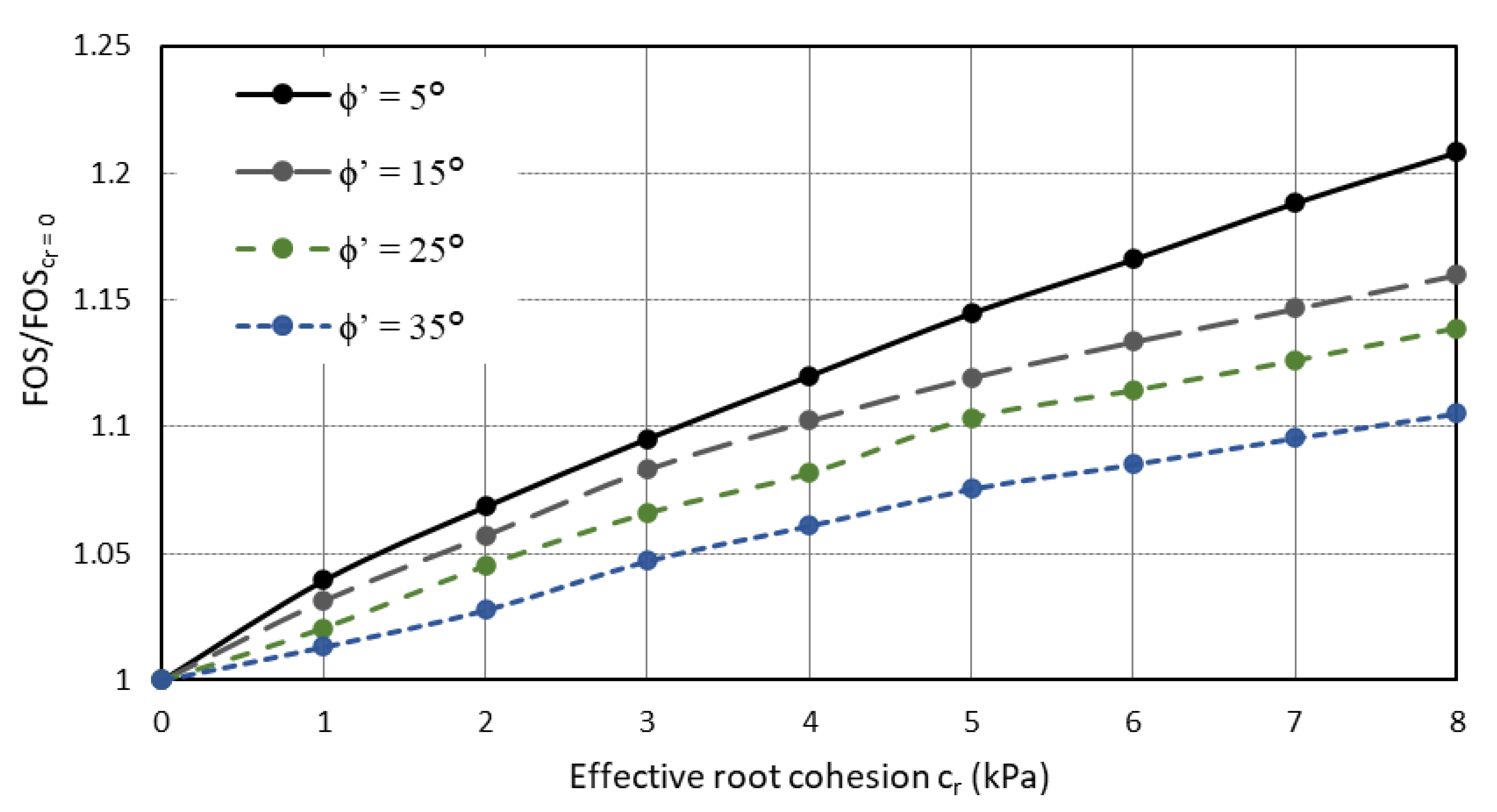
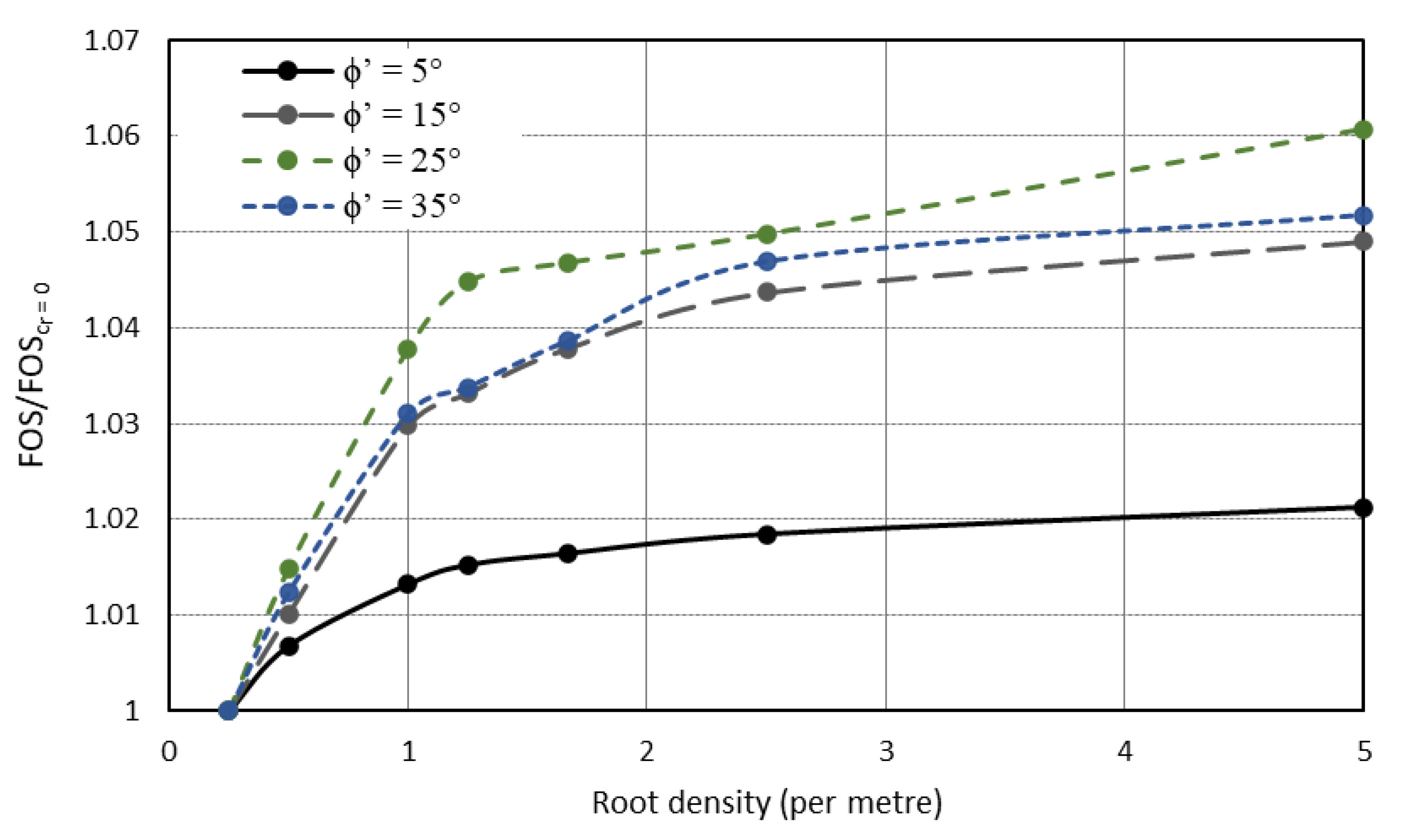
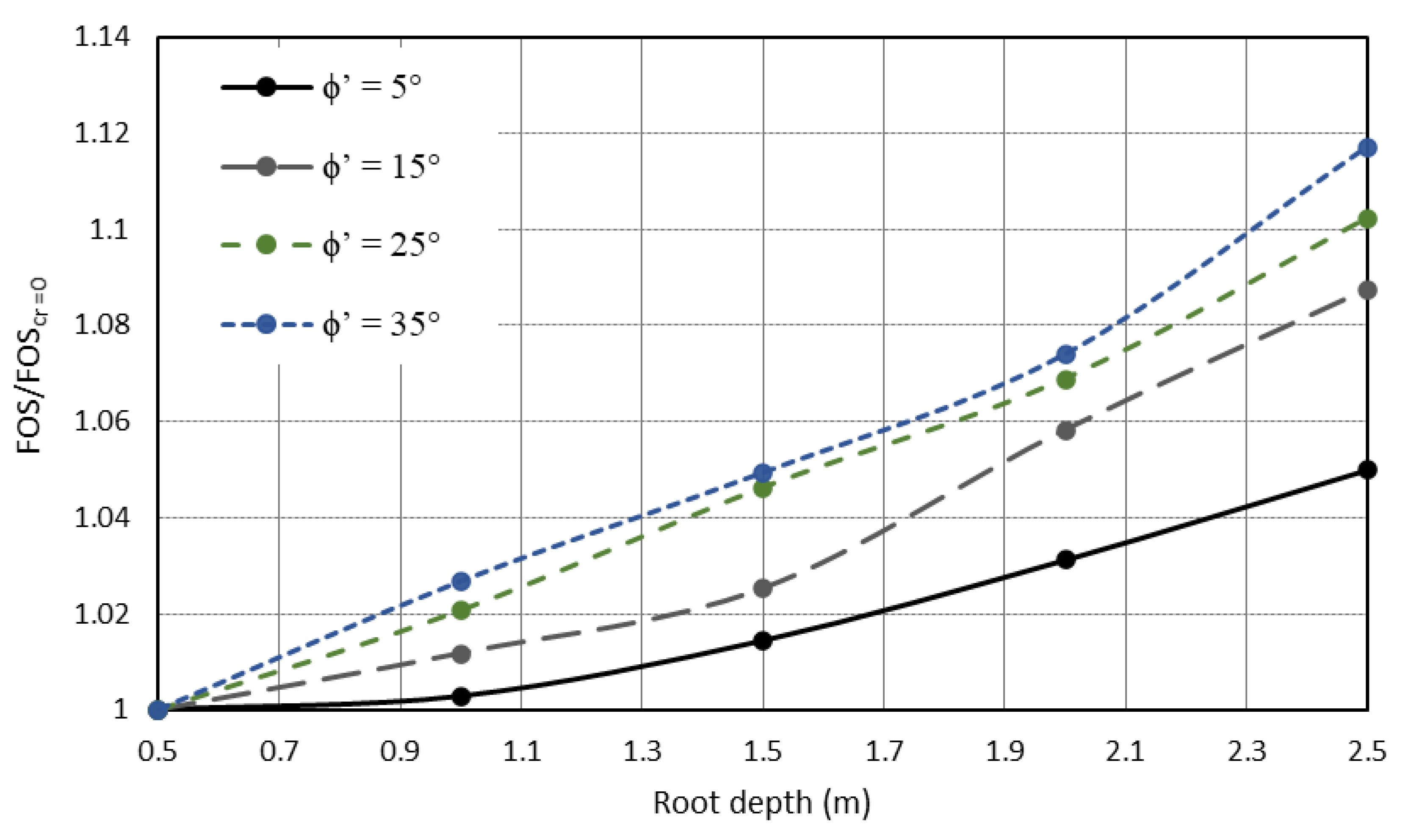
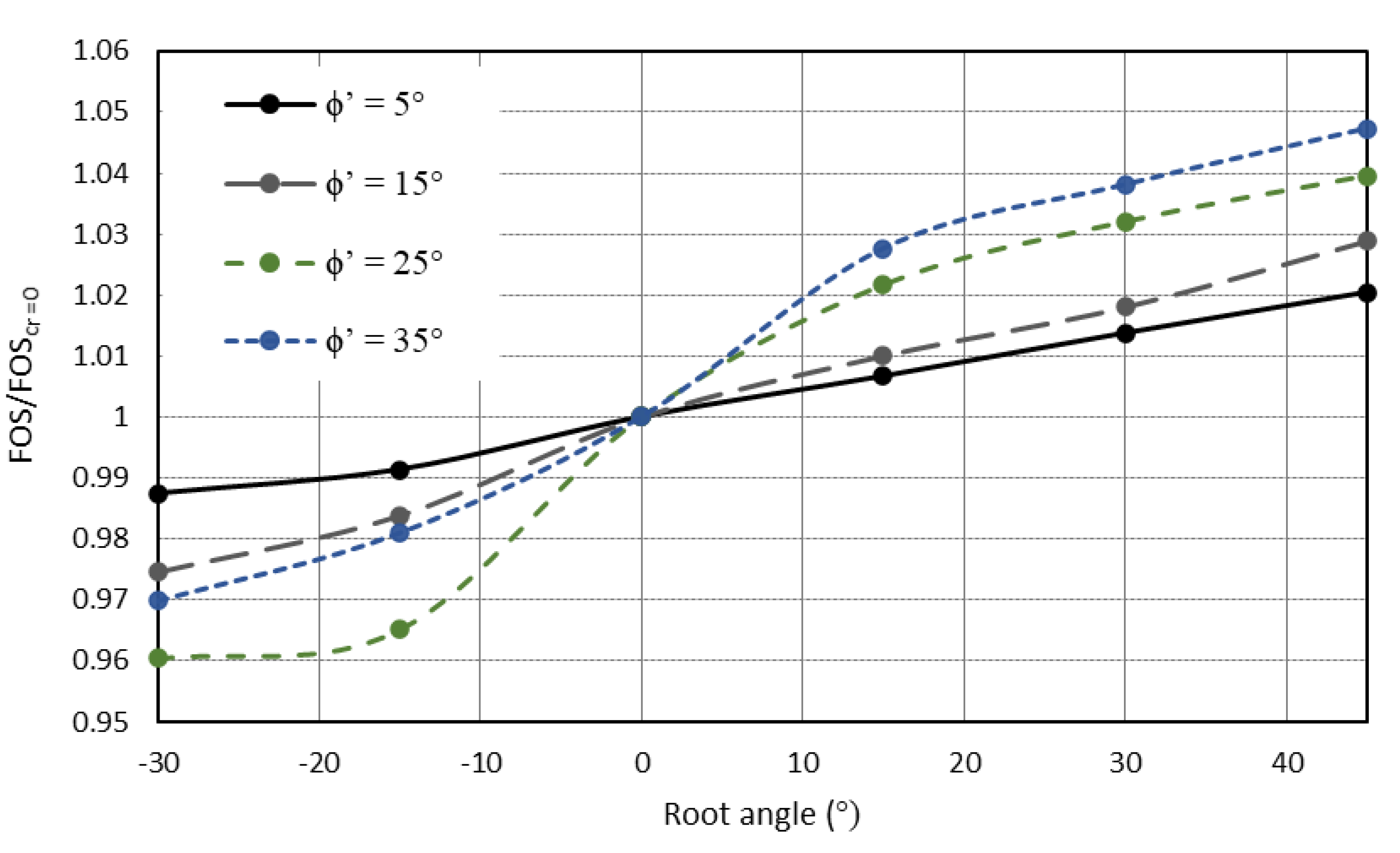
- In all cases presented, the relationships were found to be either linear or logarithmic in nature, except when comparing the angles of branched root structures and apparent root cohesion values.
- (3)
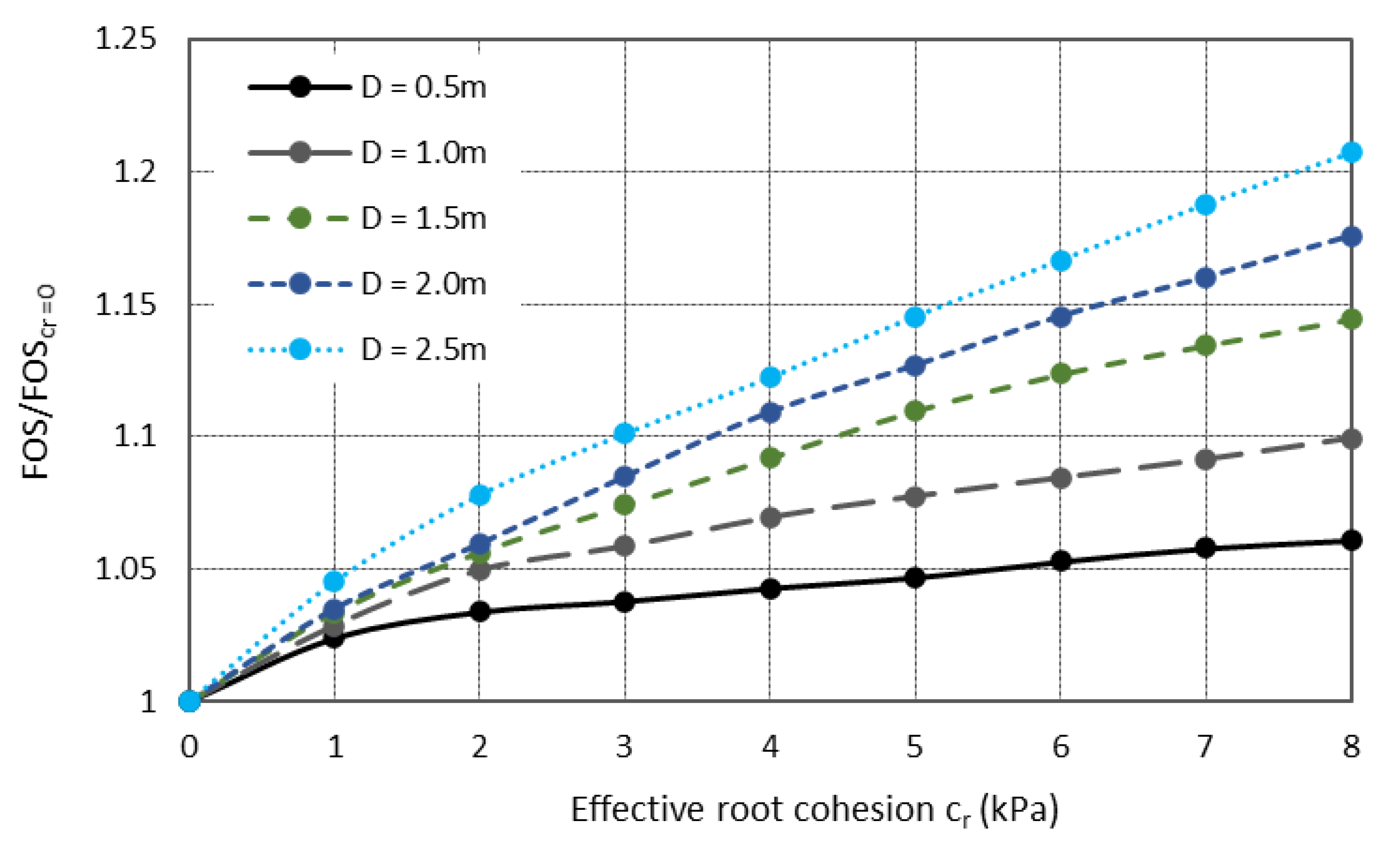
- For extremely shallow root structures of the order of half a metre in depth, minimal root cohesion is provided regardless of the structural root characteristics, suggesting little benefit in modelling the roots through structural elements.
- (4)
- The changes in the observed FOS values for the chosen examples are often quite modest, with most FOS values of the order of 1.0 to 1.3; however, the method provides a framework that can be further extended to coupled mechanical and hydrological models.
- (1)
- The current study provides a point of comparison between effective root cohesion and direct root simulation without the presence of groundwater. In addition to the mechanical benefits in strengthening soil slopes, roots provide significant hydromechanical benefits through the uptake of groundwater, which has not been considered within the current research.
- (2)
- Direct simulation consists of idealised root architectures that have not taken into account the heterogeneity of root geometries. The simulation methods presented within this study can be considered as amenable to Monte-Carlo-style simulation to determine how complex, spatially variable root patterns can impact the stability of soil slopes and the associated effective root cohesion that is considered comparable to simulations involving root geometries.
- (3)
- While root architecture is a central focus of this research, above-ground tree and shrub structures and their toppling loads were not considered as within the scope of investigation.
- (4)
- An initial single-layered slope was presented for a variety of root parameters, indicating the process whereby more complex multilayered soil layers and slope geometries may be assessed.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Galvão, T.C.d.B.; Pereira, A.R.; Parizzi, M.G.; Alves da Silva, H. Bioengineering techniques associated with soil nailing applied to slope stabilization and erosion control. Nat. Hazards Rev. 2010, 11, 43–48. [Google Scholar] [CrossRef]
- Greenwood, J.R.; Norris, J.; Wint, J. Assessing the contribution of vegetation to slope stability. Proc. Inst. Civ. Eng. Geotech. Eng. 2004, 157, 199–207. [Google Scholar] [CrossRef]
- Tsige, D.; Senadheera, S.; Talema, A. Stability analysis of plant-root-reinforced shallow slopes along mountainous road corridors based on numerical modeling. Geosciences 2020, 10, 19. [Google Scholar] [CrossRef]
- Gonzalez-Ollauri, A.; Mickovski, S.B. Hydrological effect of vegetation against rainfall-induced landslides. J. Hydrol. 2017, 549, 374–387. [Google Scholar] [CrossRef]
- Schwarz, M.; Giadrossich, F.; Cohen, D. Modeling root reinforcement using a root-failure Weibull survival function. Hydrol. Earth Syst. Sci. 2013, 17, 4367–4377. [Google Scholar] [CrossRef]
- Bethlahmy, N. Soil-moisture sampling variation as affected by vegetation and depth of sampling. Soil Sci. 1963, 95, 211–213. [Google Scholar] [CrossRef]
- Bishop, D.M.; Stevens, M.E. Landslides on Logged Areas in Southeast Alaska; US Forest Service research paper NOR;-1; United States Department of Agriculture: Washington, DC, USA, 1964.
- Endo, T. Effect of the Tree’s Roots upon the Shear Strength of Soil; United States Department of Agriculture: Washington, DC, USA, 1969.
- Gray, D.H.; Sotir, R.B. Biotechnical and Soil Bioengineering Slope Stabilization: A Practical Guide For Erosion Control; John Wiley & Sons: Hoboken, NJ, USA, 1996. [Google Scholar]
- Fan, C.-C.; Su, C.-F. Effect of soil moisture content on the deformation behaviour of root-reinforced soils subjected to shear. Plant Soil 2009, 324, 57–69. [Google Scholar] [CrossRef]
- Nakamura, H.; Nghiem, Q.; Iwasa, N. Reinforcement of tree roots in slope stability: A case study from the Ozawa slope in Iwate Prefecture, Japan. In Eco-and Ground Bio-Engineering: The Use of Vegetation to Improve Slope Stability; Springer: Dordrecht, The Netherlands, 2007; pp. 81–90. [Google Scholar]
- Wu, T.H.; McKinnell III, W.P.; Swanston, D.N. Strength of tree roots and landslides on Prince of Wales Island, Alaska. Can. Geotech. J. 1979, 16, 19–33. [Google Scholar] [CrossRef]
- Huang, B.; Nobel, P.S. Root hydraulic conductivity and its components, with emphasis on desert succulents. Agron. J. 1994, 86, 767–774. [Google Scholar] [CrossRef]
- Osman, N.; Barakbah, S. Parameters to predict slope stability—Soil water and root profiles. Ecol. Eng. 2006, 28, 90–95. [Google Scholar] [CrossRef]
- Temgoua, A.G.T.; Kokutse, N.K.; Kavazović, Z. Influence of forest stands and root morphologies on hillslope stability. Ecol. Eng. 2016, 95, 622–634. [Google Scholar] [CrossRef]
- Chiaradia, E.A.; Vergani, C.; Bischetti, G.B. Evaluation of the effects of three European forest types on slope stability by field and probabilistic analyses and their implications for forest management. For. Ecol. Manag. 2016, 370, 114–129. [Google Scholar] [CrossRef]
- Cislaghi, A.; Bordoni, M.; Meisina, C.; Bischetti, G. Soil reinforcement provided by the root system of grapevines: Quantification and spatial variability. Ecol. Eng. 2017, 109, 169–185. [Google Scholar] [CrossRef]
- Chok, Y.; Jaksa, M.; Kaggwa, W.; Griffiths, D. Assessing the influence of root reinforcement on slope stability by finite elements. Int. J. Geo-Eng. 2015, 6, 12. [Google Scholar] [CrossRef]
- Gentile, F.; Elia, G.; Elia, R. Analysis of the stability of slopes reinforced by roots. Des. Nat. V Comp. Des. Nat. Sci. Eng. WIT Trans. Ecol. Environ. 2010, 138, 189–200. [Google Scholar]
- Kamchoom, V.; Leung, A.K.; Ng, C.W.W. Effects of root geometry and transpiration on pull-out resistance. Géotech. Lett. 2014, 4, 330–336. [Google Scholar] [CrossRef]
- Norris, J.; Greenwood, J. In situ shear and pull out testing to demonstrate the enhanced shear strength of root reinforced soil. In Proceedings of the 8th International Symposium on Landslides, Cardiff, UK, 26–30 June 2000. [Google Scholar]
- Zhu, H.; Zhang, L.M.; Xiao, T.; Li, X. Enhancement of slope stability by vegetation considering uncertainties in root distribution. Comput. Geotech. 2017, 85, 84–89. [Google Scholar] [CrossRef]
- Dupuy, L.; Fourcaud, T.; Stokes, A. A numerical investigation into factors affecting the anchorage of roots in tension. Eur. J. Soil Sci. 2005, 56, 319–327. [Google Scholar] [CrossRef]
- Mickovski, S.B.; Stokes, A.; Van Beek, R.; Ghestem, M.; Fourcaud, T. Simulation of direct shear tests on rooted and non-rooted soil using finite element analysis. Ecol. Eng. 2011, 37, 1523–1532. [Google Scholar] [CrossRef]
- Li, Y.; Wang, Y.; Ma, C.; Zhang, H.; Wang, Y.; Song, S.; Zhu, J. Influence of the spatial layout of plant roots on slope stability. Ecol. Eng. 2016, 91, 477–486. [Google Scholar] [CrossRef]
- Ng, C.W.; Zhang, Q.; Ni, J.; Li, Z. A new three-dimensional theoretical model for analysing the stability of vegetated slopes with different root architectures and planting patterns. Comput. Geotech. 2021, 130, 103912. [Google Scholar] [CrossRef]
- Bischetti, G.B.; Chiaradia, E.A.; Simonato, T.; Speziali, B.; Vitali, B.; Vullo, P.; Zocco, A. Root strength and root area ratio of forest species in Lombardy (Northern Italy). In Eco-and Ground Bio-Engineering: The Use of Vegetation to Improve Slope Stability, Proceedings of the First International Conference on Eco-Engineering, Thessaloniki, Greece, 13–17 September 2004; Springer: Dordrecht, The Netherlands, 2007; pp. 31–41. [Google Scholar]
- Pisano, M.; Cardile, G. Probabilistic Analyses of Root-Reinforced Slopes Using Monte Carlo Simulation. Geosciences 2023, 13, 75. [Google Scholar] [CrossRef]
- Nguyen, T.S.; Likitlersuang, S.; Jotisankasa, A. Influence of the spatial variability of the root cohesion on a slope-scale stability model: A case study of residual soil slope in Thailand. Bull. Eng. Geol. Environ. 2019, 78, 3337–3351. [Google Scholar] [CrossRef]
- Abernethy, B.; Rutherfurd, I.D. The distribution and strength of riparian tree roots in relation to riverbank reinforcement. Hydrol. Process. 2001, 15, 63–79. [Google Scholar] [CrossRef]
- Wu, W.; Sidle, R.C. A distributed slope stability model for steep forested basins. Water Resour. Res. 1995, 31, 2097–2110. [Google Scholar] [CrossRef]
- Waldron, L. The shear resistance of root-permeated homogeneous and stratified soil. Soil Sci. Soc. Am. J. 1977, 41, 843–849. [Google Scholar] [CrossRef]
- Waldron, L.; Dakessian, S. Soil reinforcement by roots: Calculation of increased soil shear resistance from root properties. Soil Sci. 1981, 132, 427–435. [Google Scholar] [CrossRef]
- Brinkgreve, R.; Kumarswamy, S.; Swolfs, W.; Waterman, D.; Chesaru, A.; Bonnier, P. PLAXIS 2016; PLAXIS Company (Plaxis bv): Delft, The Netherlands, 2016. [Google Scholar]
- Griffiths, D.; Lane, P. Slope stability analysis by finite elements. Geotechnique 1999, 49, 387–403. [Google Scholar] [CrossRef]
- Dyson, A.P.; Tolooiyan, A. Optimisation of strength reduction finite element method codes for slope stability analysis. Innov. Infrastruct. Solutions 2018, 3, 38. [Google Scholar] [CrossRef]
- Coppin, N.J.; Richards, I.G. Use of Vegetation in Civil Engineering; Butterworths: Ciria, Spain, 1990. [Google Scholar]
- Gray, D.H.; Leiser, A.T. Biotechnical Slope Protection and Erosion Control; Van Nostrand Reinhold Company Inc.: New York, NY, USA, 1982. [Google Scholar]
- Schenk, H.J.; Jackson, R.B. Rooting depths, lateral root spreads and below-ground/above-ground allometries of plants in water-limited ecosystems. J. Ecol. 2002, 90, 480–494. [Google Scholar] [CrossRef]
- Operstein, V.; Frydman, S. The influence of vegetation on soil strength. Proc. Inst. Civ. Eng. Ground Improv. 2000, 4, 81–89. [Google Scholar] [CrossRef]
- Ali, F. Use of vegetation for slope protection: Root mechanical properties of some tropical plants. Int. J. Phys. Sci. 2010, 5, 496–506. [Google Scholar]









| Input Variable | Value(s) |
|---|---|
| Elastic modulus (E, kN/m2) | |
| Poisson’s ratio (ν) | 0.2 |
| Unit weight (γ, kN/m3) | 20 |
| Input Variable | Value(s) |
|---|---|
| Effective root cohesion (, kN/m2) | 0, 1, 2, 3, 4, 5, 6, 7, 8 |
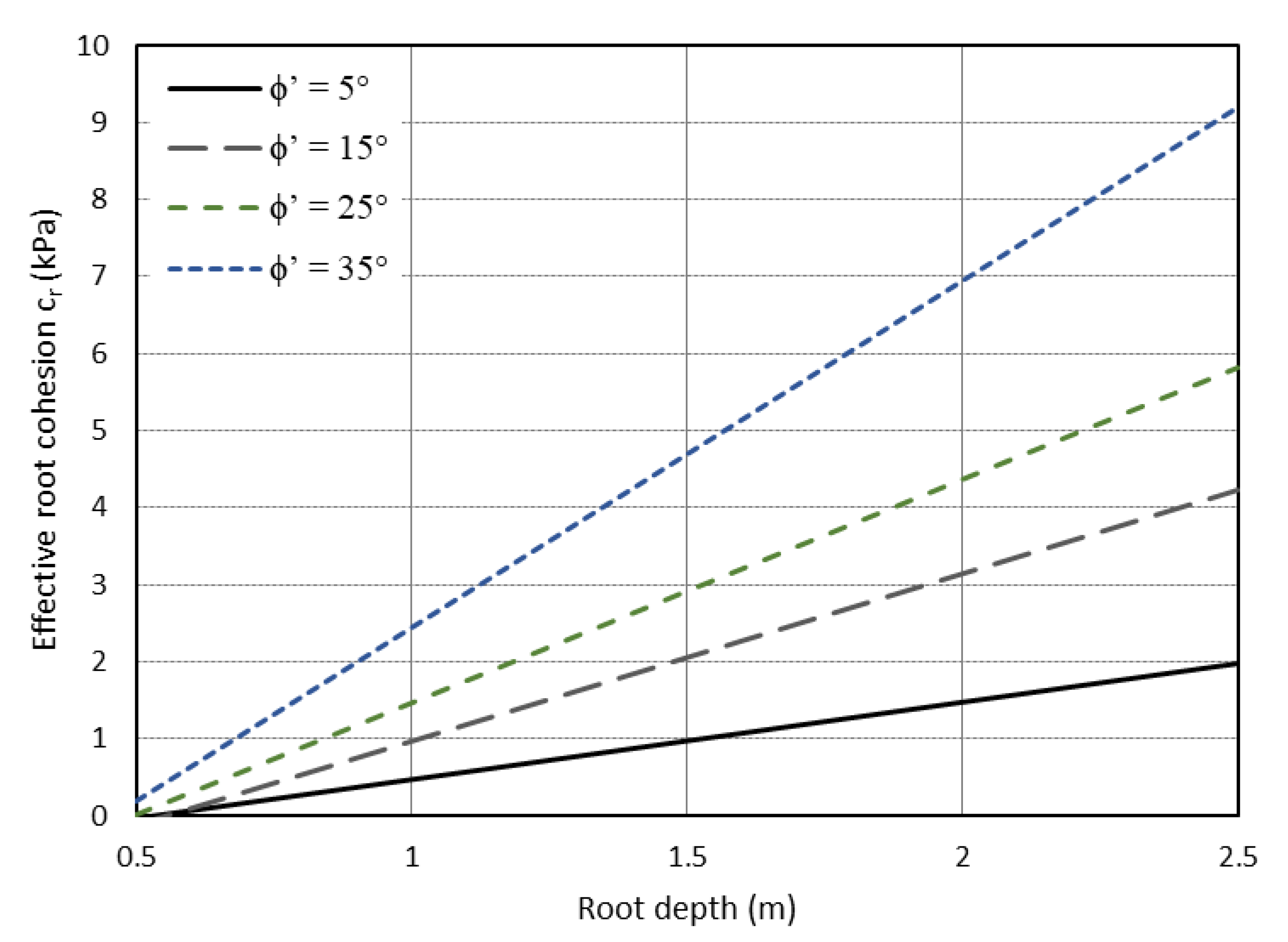
| Root cohesion zone depth (m) | 0.5, 1, 1.5, 2, 2.5 |
| Effective friction angle (, °) | 5, 15, 25, 35 |
| Parameter | Symbol | Value |
|---|---|---|
| Root pull-out resistance | P (kN/m) | 2.5 |
| Root tensile capacity | T (kN) | 12.5 |
| Root shear capacity | Q (kN) | 6.25 |
| Input Variable | Value(s) |
|---|---|
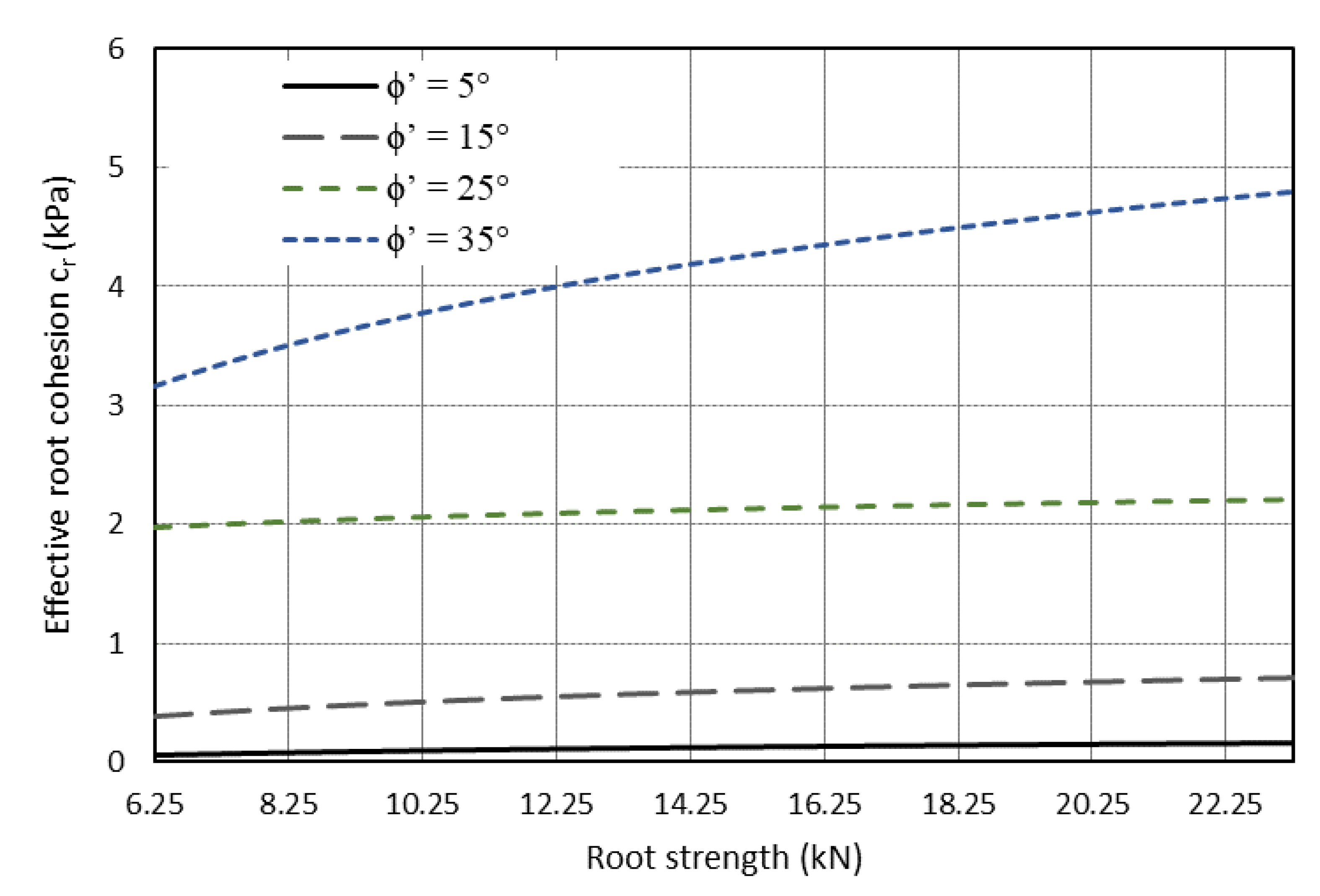
| Root strength (kN) | 6.5, 9.5, 12.5, 15.5, 23.5 |
| Root thickness (m) | 0.05, 0.1, 0.15, 0.2, 0.25 |
| Root spacing (m) | 0.25, 0.5, 1, 1.25, 1.67, 2.5, 5 |
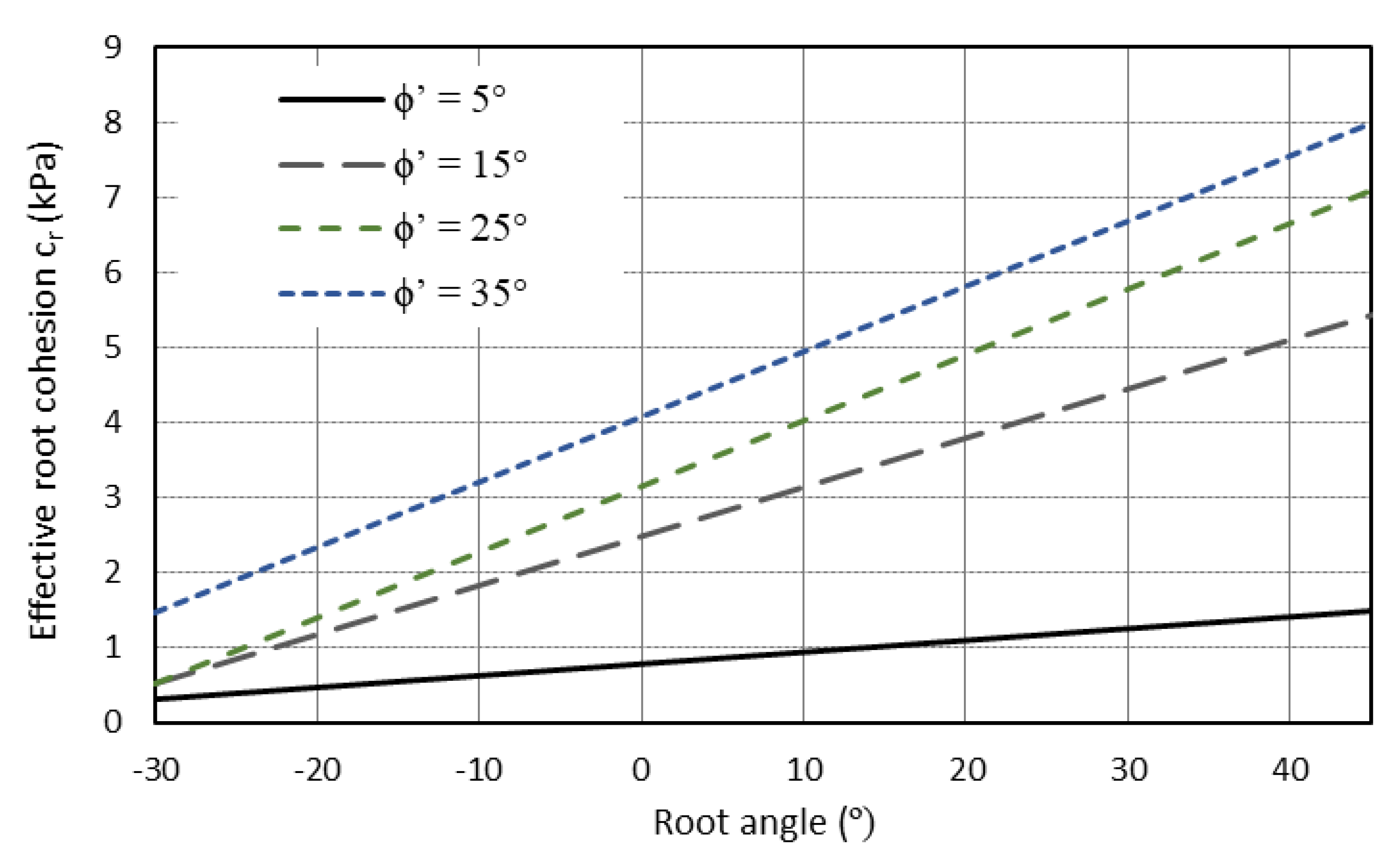
| Friction angle (ϕ′, °) | 5, 15, 25, 35 |
| Root depth (m) | 0.5, 1, 1.5, 2, 2.5 |
| Input Variable | Value(s) |
|---|---|
| Secondary root cohesion (kPa) | 1, 2, 3, 4 |
| Secondary root cohesion radius (m) | 0.05, 0.1, 0.15, 0.2 |
| Secondary root cohesion depth (m) | 0.05, 0.1, 0.15, 0.2 |
| Input Variable | Value(s) |
|---|---|
| Branch length (m) | 0.05, 0.1, 0.15, 0.2, 0.25, 0.3 |
| Branch angle (°) | 15, 30, 45, 60 |
| Number of branch layers | 1, 2, 3, 4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dyson, A.P.; Tolooiyan, A.; Griffiths, D.V. Numerical Modelling Techniques for Stability Analysis of Slopes Reinforced with Shallow Roots. Geotechnics 2023, 3, 278-300. https://doi.org/10.3390/geotechnics3020016
Dyson AP, Tolooiyan A, Griffiths DV. Numerical Modelling Techniques for Stability Analysis of Slopes Reinforced with Shallow Roots. Geotechnics. 2023; 3(2):278-300. https://doi.org/10.3390/geotechnics3020016
Chicago/Turabian StyleDyson, Ashley P., Ali Tolooiyan, and D. V. Griffiths. 2023. "Numerical Modelling Techniques for Stability Analysis of Slopes Reinforced with Shallow Roots" Geotechnics 3, no. 2: 278-300. https://doi.org/10.3390/geotechnics3020016
APA StyleDyson, A. P., Tolooiyan, A., & Griffiths, D. V. (2023). Numerical Modelling Techniques for Stability Analysis of Slopes Reinforced with Shallow Roots. Geotechnics, 3(2), 278-300. https://doi.org/10.3390/geotechnics3020016








