Density-Driven Convection for CO₂ Solubility Trapping in Saline Aquifers: Modeling and Influencing Factors

Abstract

Industrial development has significantly increased the concentration of CO₂ in the atmosphere, resulting in the greenhouse effect that harms the global climate and human health. CO₂ sequestration in saline aquifers is considered to be one of the efficient ways to eliminate atmospheric CO₂ levels. As an important mechanism, the solubility trapping greatly determines the efficiency of CO₂ sequestration in saline aquifers, and this depends, in turn, on the density-driven convection that occurs during the sequestration. Density-driven convection is influenced by multiple factors. However, existing discussions on some of these influential factors are still ambiguous or even reach contradictory conclusions. This review summarizes the common modeling approaches and the influence of factors on density-driven convection. We suggest that saline aquifers with high values of depth, permeability, pH, and SO₂ impurity concentration are the ideal CO₂ sequestration sites. A certain degree of porosity, fractures, stratification, slope, hydrodynamic dispersion, background flow, and formation pressure are also considered advantageous. Meanwhile, the geological formation of the Permian White Rim Sandstone or carbonate is important, but it should not contain brine with excessive viscosity and salinity. Finally, we discuss the contents in need of further research.

1. Introduction

As the negative impacts of global warming are becoming more and more significant, the general policy on climate-change prevention is universally being recognized around the world. Based on the extent of global warming, the mid- to long-term (2041–2100) impact was predicted to be several times higher than currently observed for some of the major risks that have been identified [1,2]. Geological storage of CO₂ is a promising resolution to the growing global climate and environmental issues, as it would reduce the atmospheric CO₂ concentration [3,4,5]. Among the various options for CO₂ sequestration, subsurface saline aquifers are considered the most feasible due to the presence of large, porous, and permeable formation in sedimentary basins worldwide, as these have the greatest potential for CO₂ sequestration compared to others. Additionally, large pores with high permeability require fewer injection wells and facilitate pressure dissipation for these formations [5,6].

There are four trapping mechanisms in saline aquifers, i.e., structural trapping, capillary trapping, solubility trapping, and mineral trapping [7]. The CO₂ injected into saline aquifers assumes a supercritical state under high temperature and pressure stratigraphic conditions [8]. Despite the dramatic increase in density due to the reduction in volume, supercritical CO₂ is still lighter than the brine of the formation. It therefore rises under buoyancy and accumulates at the top of the saline aquifer by the barrier of the caprock, which is called structural trapping. CO₂ in an irreducible gas saturation state is trapped in the pores and cannot move because of the interfacial tension between CO₂ and formation, known as capillary trapping. The accumulated CO₂ below the caprock gradually dissolves with time into the brine and is thus isolated from the atmosphere, known as the solubility trapping in saline aquifers. The dissolved CO₂ reacts chemically with the minerals in the formation and eventually transforms into solid carbonate minerals, which are precipitated in the pore space, known as mineral trapping. Among them, solubility trapping is regarded as a more effective and secure mechanism in the medium to long term, as well as providing the necessary requirements for permanent mineral trapping [9].

In the early stages of solubility trapping, CO₂ transfers to brine in the form of diffusion. The density of the brine in contact with CO₂ thus increases, creating a density difference with the surrounding CO₂-free brine. This determines that the CO₂–brine interface is unstable. The sharp vertical concentration gradient of CO₂ results in molecular diffusion being the main mass transfer mechanism, and the development of the instability is arrested. As an increase in the thickness of the diffusion boundary layer occurs, the diffusive flux decreases, instability develops, and eventually the CO₂-rich brine with a large density settles downward by gravity and the surrounding lighter brine thus migrates upward, creating convection called density-driven convection. Once it occurs, it replaces molecular diffusion as the dominant form for the mass transfer of CO₂ into the brine. This will greatly facilitate the flow of aquifer fluids and greatly improve the efficiency of CO₂ dissolution and migration. It accelerates the transfer of CO₂ into the brine and therefore facilitates the practical benefits of the long-term security of CO₂ injection and storage. Studying the occurrence and form of density-driven convection is necessary to understand the role and mechanisms of solubility trapping.

Understanding subsurface flow dynamics is necessary to evaluate the effectiveness of geological storage, which in turn necessitates the comprehension of a wide range of geologic characteristics in a candidate reservoir. Several significant potential CO₂ reserves showed sedimentary architecture that reflected river deposition, such as the Morrow Sandstone [10] and the lower Paaratte Formation [11], which were mainly made of conglomerate or sandstone. The spatial structure of textural facies, which were, in fact, of fundamental relevance, could be explained by depositional architecture, and those finer- and coarser-grained sedimentary textures might be a major factor influencing the variation of a petrophysical property such as permeability [12]. The sedimentary architecture could be found in both contemporary fluvial environments and historical fluvial reservoirs, and its mean particle sizes range from sand (e.g., the Mt. Simon Sandstone [13]) to gravel (e.g., the Ivishak Formation conglomerate [14]). Moreover, the sharp, abrupt boundaries between cross-sets of coarse and fine grains could lead to aquifer connectedness and possibly tortuous flow channels, which limited the movement of CO₂ [15,16]. Consequently, when constructing a fundamental scientific understanding of CO₂ injection and transport, it is necessary to take into account the complexity of the sedimentary structure found within such reservoirs.

Many investigations have been conducted on the density-driven convection for CO₂ solubility trapping in saline aquifers [17,18]. However, the coupling of flow and mass transfer makes the convection process highly nonlinear, resulting in complex hydrodynamic behavior and CO₂ distribution. The modeling in these investigations will therefore vary depending on the studying problem. Numerous simplified models have been used to analyze convective mixing processes under the assumption of a single-phase system [18,19,20], two-phase system [21,22], and multiphase system [23,24]. Moreover, although many studies have been conducted in the past to address the factors influencing the convective mixing process, such as the slope of caprock [25,26], permeability [27,28], fractures [29,30], impurities [31,32], etc., these influencing factors have not been systemically summarized and generalized. To accurately perceive how CO₂ behaves in the subsurface after it has been injected into the saline aquifer, the influence of various factors on convection must be taken into account. By reviewing the relevant literature, this review discusses the influence mechanism of factors on density-driven convection, aims to guide CO₂ saline aquifer sequestration projects, and highlights the areas that require intensive study of geological storage.

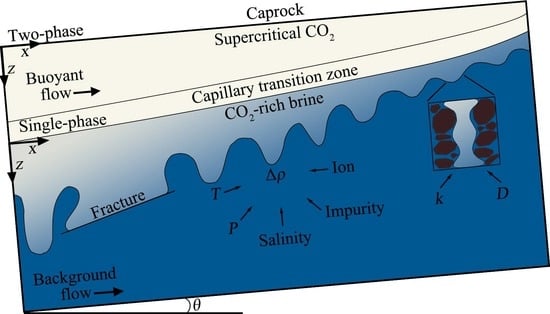
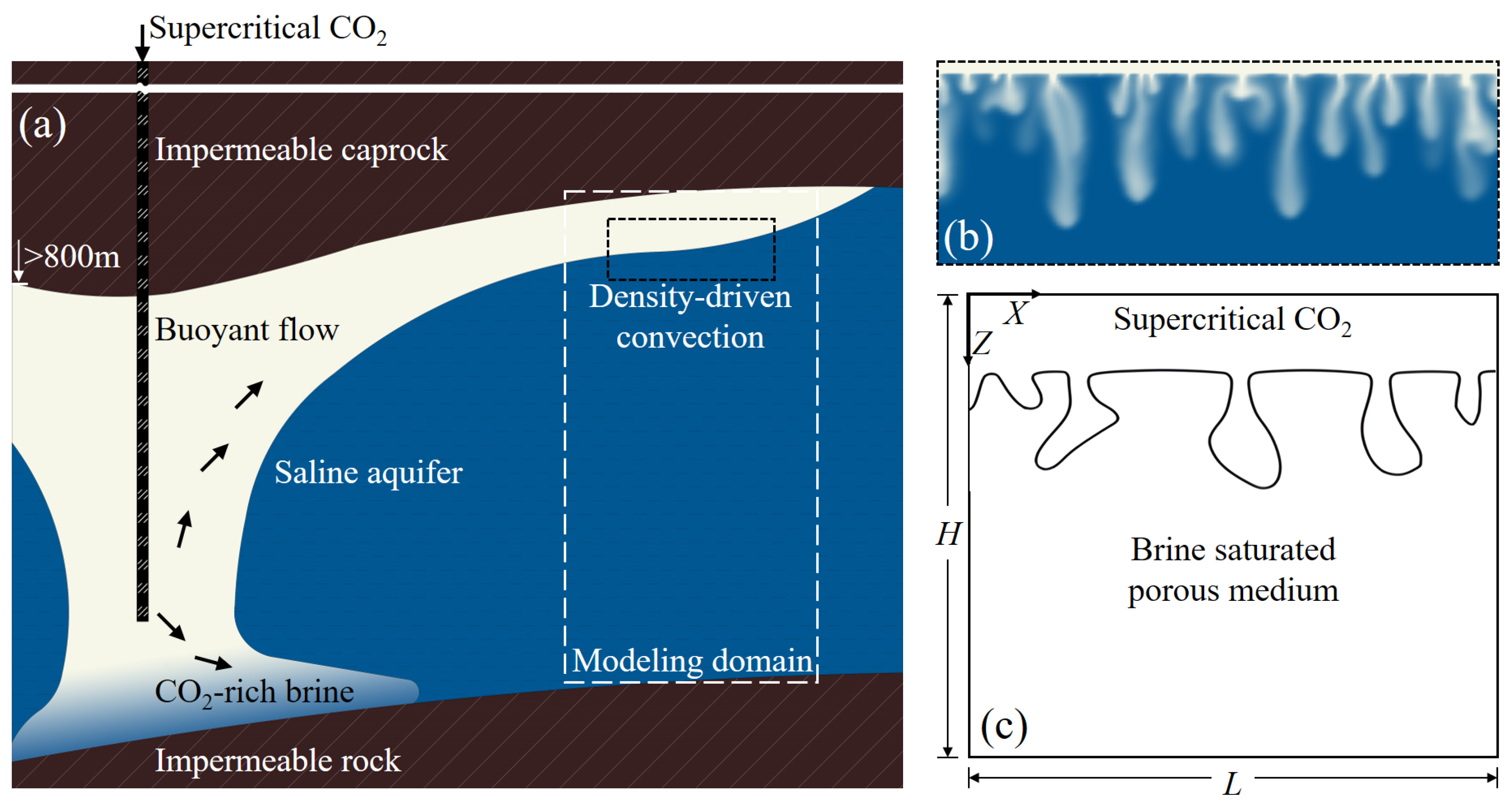
2. Modeling

2.1. Modeling Methodology

Figure 1 illustrates the typical modeling setup for CO₂ solubility trapping in a saline aquifer. The spatial characteristic of the saline aquifer is that the horizontal length is much greater than the vertical depth, so the influence of the lateral boundary on the convection is insignificant. The convection that is of interest occurs in the space between the lower part of the caprock and the impermeable rock at the base of the saline aquifer, as shown in Figure 1a. Within the limited space of the saline aquifer, more attention was paid to the vertical development and horizontal migration behavior of CO₂-rich brine in convection, as shown in Figure 1b. The rock pore space is initially completely filled with brine. An ideal rectangular porous medium is commonly considered to describe the density-driven convection for CO₂ solubility trapping in the saline aquifer, as shown in Figure 1c. The medium is permeable and heterogeneous. Incompressible Newtonian fluids are considered a two-dimensional laminar flow with non-slip boundaries. Moreover, the fluid thermophysical properties (other than density) are considered to be constant.

Single-phase flow system was commonly applied to CO₂ density-driven convection [33,34,35]. In this system, the dissolved CO₂ no longer exists as a separate phase but as a solute. In most studies employing a single-phase flow system, the fluid flow within the pore space is described by Darcy’s law, and the degree of dissolved CO₂ is represented by the concentration for which the mass transport equation is solved. Based on the above perceptions, the continuity equation can be written as follows [36]:

$$\frac{\partial \left(\varphi \rho \right)}{\partial t}=-\nabla ·\left(\rho \mathit{v}\right)$$

(1)

where ϕ is the porosity of the saline aquifer, ρ is the fluid density (kg/m³), t is the time (s), and v is the Darcy velocity vector. The Darcy velocity vector can then be calculated as follows [37]:

$$\mathit{v}=-\frac{k}{\mu }·\left(\nabla p-\rho g\nabla z\right)$$

(2)

where k is the absolute permeability (m²), μ is the fluid dynamic viscosity (kg/(m·s)), p is the fluid pressure (Pa), g is the gravitational acceleration (m/s²), and z means vertical downward is the positive direction.

The mass transfer equation for the dissolution of CO₂ into the brine is then given by the following [36]:

$$\frac{\partial \left(\varphi c\right)}{\partial t}=\nabla ·\left(\varphi D\nabla c-c\mathit{v}\right)$$

(3)

where c is the concentration of CO₂ (mol/m³), and D is the effective diffusion coefficient (m²/s).

The change of fluid density is very important here, as it causes the convection of the static fluid. Fluid density is normally determined linearly by the CO₂ concentration,

$$\rho ={\rho }_0\left[1+{\beta }_c\left(c-c_0\right)\right]$$

(4)

where β_c is the solute volume expansion coefficient (m³/mol).

It should be noted that the density instability caused by the geothermal gradient prevalent in saline aquifers with large longitudinal scales would trigger extra convection, which, jointly with the convection generated by CO₂ solubility trapping, was known as double-diffusive convection and has been extensively studied [38,39,40,41,42,43]. By introducing an energy balance equation to account for this temperature-induced extra convection, we obtain the following [44]:

$${\left(\rho c_{\mathrm{h}}\right)}_{\mathrm{m}}\frac{\partial T}{\partial t}=\nabla ·\left(k_{\mathrm{m}}\nabla T\right)-{\left(\rho c_{\mathrm{h}}\right)}_{\mathrm{f}}\mathit{v}·\nabla T$$

(5)

where c_h is the specific heat capacity (J/(kg·K)), T is the fluid temperature (K), and k_m is the effective thermal conductivity of porous medium (W/(m·K)). (ρc_h)_m = ϕ(ρc_h)_f + (1−ϕ) (ρc_h)_s represents the effective heat capacity, and the subscripts m, f, and s refer to the matrix, fluid, and solid phase, respectively. Thus, Equation (4) becomes as follows [45]:

$$\rho ={\rho }_0\left[1+{\beta }_{\mathrm{c}}\left(c-c_0\right)-{\beta }_{\mathrm{T}}\left(T-T_0\right)\right]$$

(6)

where β_T is the volumetric thermal expansion coefficient (1/K). However, Javaheri et al. [39] pointed out that the effect of the geothermal gradient on density-driven convection was negligible compared to the solute effect caused by the dissolution and diffusion of CO₂ in saline aquifers. Thus, modeling for CO₂ solubility trapping in saline aquifers could be postulated as isothermal in terms of density-driven convection.

The fluid viscosity also increased slightly with the CO₂ concentration, which affected density-driven convection, as shown in Equation (2), and could be quantified as a monotonic logarithmic relationship for concentration [46]:

$$\mu ={\mu }_0{e}^{\Gamma \left(c-c_0\right)}$$

(7)

where μ₀ is the dynamic viscosity for c = c₀, and Γ is the viscosity variation parameter. However, the viscosity difference caused by this change was rather insignificant [47,48,49]. Although it has been suggested that this difference in viscosity would trigger similar transversal convection (called viscous fingering) at the base of the saline aquifer caprock during the initial stages of CO₂ injection [50,51,52,53,54], the change in density was apparently more significant compared with the change in viscosity during the stage when CO₂ stabilized and began to dissolve [55,56,57]. Therefore, the change of viscosity is generally ignored in the modeling of the convective flow.

However, the geological storage of CO₂ involves multicomponent and multiphase processes, and, similarly, the convective mixing process is also a multiphase-involved process. The results based on multiphase flow were shown to be different from those of single-phase flow [58,59,60]. The simplification of single-phase systems would pose problems and lead to biased conclusions for density-driven convection. It is suggested that the accuracy of the results of convective mixing process studies could be effectively improved by considering multiphase flow, as well as permeability field variations [61,62]. The modeling using simplifying assumptions might cause the results to be underestimated, while unnecessary assumptions might increase the computational cost. Emami-Meybodi et al. [63] pointed out that the single-phase system ignored the transversal flow of CO₂-rich brine at the interface and the volume expansion of brine caused by CO₂ dissolution. This would lead to an overestimation of the convection onset with an underestimation of the CO₂ dissolution flux. A series of investigations [62,64,65,66,67] further showed that a two-phase flow system would correct the misestimation of convective onset time and dissolution flux. This implied a more-than-three-times increase in the CO₂ convective dissolution flux, along with a three-to-six-times reduction in the onset time of convection.

The two-phase system of saline aquifers is formed by the non-wetting phase CO₂ and the wetting phase brine. To introduce the concept of saturation, the continuity equation can be written as follows [68]:

$$\frac{\partial }{\partial t}\left(\varphi S_i{\rho }_i\right)+\nabla ·\left({\rho }_i{\mathit{v}}_i\right)=I_i^{\mathrm{c}}$$

(8)

where the subscript i is the phase involving the non-wetting phase (nw) and the wetting phase (w), S_i refers to the phase saturation, ρ_i is the phase density (kg/m³), and I_i^c refers to the rate of CO₂ mass transfer by the interface of two-phase (kg/(m³·s)). Moreover, v_i is the Darcy velocity vector of the phase, which can be calculated as follows:

$${\mathit{v}}_i=-\frac{k{k}_{\mathrm{r}i}}{{\mu }_i}\left(\nabla p_i-{\rho }_{i}g\right)$$

(9)

where k_ri is the relative permeability of the phase, μ_i is the dynamic viscosity of the phase (kg/(m·s)), and p_i is the pressure of the phase (Pa).

The distribution for CO₂ in brine is then given by the following [69]:

$$\frac{\partial }{\partial t}\left(\varphi S_{\mathrm{w}}{\rho }_{\mathrm{w}}{m}_{\mathrm{w}}^{\mathrm{c}}\right)+\nabla ·\left({\rho }_{\mathrm{w}}{\mathit{v}}_{\mathrm{w}}{m}_{\mathrm{w}}^{\mathrm{c}}\right)+\nabla ·\left(-{\mathit{D}}_{\mathrm{w}}^{\mathrm{c}}\varphi S_{\mathrm{w}}{\rho }_{\mathrm{w}}\nabla m_{\mathrm{w}}^{\mathrm{c}}\right)=I_{\mathrm{w}}^{\mathrm{c}}$$

(10)

where m_w^c is the CO₂ mass fraction in the wetting phase, D_w^c is the CO₂ diffusion coefficient in the wetting phase (m²/s), and I_w^c refers to the rate of CO₂ mass transfer by the interface of two-phase to the wetting phase (kg/(m³·s)).

The above equation is closed by the Brooks–Corey model [70]:

$$\left\{\begin{array}{c}{S}_{\mathrm{nw}}+S_{\mathrm{w}}=1\\ S_{\mathrm{e}}=\frac{S_{\mathrm{w}}-S_{\mathrm{wr}}}{1-S_{\mathrm{wr}}-S_{\mathrm{nwr}}}\\ k_{\mathrm{rw}}=S_e^{\frac{2+3\lambda }{\lambda }}\\ k_{\mathrm{rnw}}={\left(1-S_e\right)}^2\left(1-S_e^{\frac{2+\lambda }{\lambda }}\right)\\ p_{\mathrm{c}}=p_{\mathrm{nw}}-p_{\mathrm{w}}=p_{\mathrm{d}}{S}_{\mathrm{e}}^{-\frac{1}{\lambda }} \left(p_{\mathrm{c}}\ge p_{\mathrm{d}}\right)\end{array}\right.$$

(11)

where S_e is the effective saturation; S_nwr and S_wr are the residual saturation of the non-wetting and the wetting phase, respectively; λ is the Brooks–Corey coefficient; and p_c and p_d are the capillary and pore-injection pressure, respectively (Pa).

Zhang et al. [71] further adopted the three-phase model, meaning that the rock as the matrix of porous media was also considered as an independent phase. Although the influence of geochemical reaction on density-driven convection was accommodated based on this consideration, the discussion of it even exceeded the dissolution effect and should be investigated in the relevant content of CO₂ mineral trapping in a saline aquifer.

2.2. Coordinate Selection and Boundary Conditions

For a more realistic simulation of CO₂ density-driven convection development in a saline aquifer, the two coordinate settings proposed based on the 2D physical layout represent different degrees of consideration, as shown in Figure 2, which will induce the discussion of top-boundary conditions.

When the injected CO₂ contacts the brine in a saline aquifer, a zone forms at the interface of these two miscible phases. It is governed by a combination of capillary forces with gravity and is called the capillary transition zone. In this zone, CO₂ coexists in equilibrium with brine and freely flows, and the CO₂ effective saturation decreases nonlinearly in the gravitational direction [67,72]. Thereafter, the free-phase CO₂ becomes a solute of brine by dissolution, contributing to the diffusion boundary layer in the lower part of the capillary transition zone. The consideration for the presence of the capillary transition zone therefore determines whether the model is a multiphase system.

The coordinate system built on the lower part of the capillary transition zone almost corresponds to the single-phase system. By ignoring the capillary transition zone between the gas and liquid phase, the CO₂–brine interface could be sharp and fixed. Therefore, only the liquid phase is modeled, and the CO₂ that accumulates at the top of the aquifer saline is represented as a top boundary condition with a fixed value. A constant concentration top boundary condition is employed in most studies accordingly, with the CO₂-pure and -rich region in the upper part of the saline aquifer being replaced by an impermeable concentration boundary with the value of the maximum dissolved concentration under initial conditions. This simplification might lead to the neglect of multiphase processes affecting CO₂ density-driven convection, such as capillary effects, upward transport and volume expansion of brine, and decreases in CO₂ phase partial pressure [62,63,73,74,75]. On the other hand, Amooie et al. [35] mentioned the constant flux boundary condition. They pointed out that density-driven convection based on both top boundary conditions developed a quasi-steady state to balance the formation and merging of the CO₂ plume. For the constant concentration boundary condition, the quasi-steady state is typically represented by a plateau in dissolution flux, but this would not apply to the constant flux boundary condition. Furthermore, in the case of the constant flux boundary condition, the changes in maximum density and concentration were time dependent.

On the other hand, the coordinate system established at the top considers the presence of CO₂ as a separate phase, implying a two-phase system, and thus additionally considers the capillary transition zone. CO₂ is in contact with brine through microscopic pores in the zone, and the two fluids are in equilibrium, with the average fluid density increasing from the density of CO₂ to the CO₂–brine solution density in maximum equilibrium. The phase interface in the two-phase system was commonly defined as the interface separating the brine-saturated zone from the capillary transition zone [62,66]. The capillary pressure increases from 0 at the interface, and the CO₂ dissolution flux is controlled by the mass transfer via the interface. A separate CO₂ single-phase region with a constant permeability different from the brine-saturated porous media is considered a capillary transition zone [64,66,76,77].

The capillary transition zone permitted CO₂–brine flow to cross the phase interface longitudinally, which increased the instability of the system [66,78]. This accelerates the onset of density-driven convection even up to several times [62,64,65,66,67]. Zhang et al. [78] similarly noted that the capillary transition zone destabilizes the diffusion boundary layer by allowing transversal flow through the phase interface. However, further investigations on the influence of the capillary transition zone on the CO₂ density-driven convection development are awaited.

In the actual aquifer, natural background flow is always present [79,80], which will probably have an impact on CO₂ sequestration. The background flow is taken into account in the modeling of CO₂ density-driven convection by the laterally fixed velocity boundary condition [81,82,83,84]. The intensity of the background flow is characterized by the value of the fixed velocity, v₀, or Peclet number,

$$\mathit{Pe}=\frac{v_{0}H}{\varphi D}$$

(12)

where v₀ is the transversal velocity of background flow (m/s), and H is the height of the porous medium (m). The larger transversal flow due to background flow would allow mixed convection to play an important role in CO₂ solubility trapping. In mixed convection, the background flow in saline aquifers prevents the construction of the longitudinal velocity field of the CO₂–brine solution and may delay or even inhibit density-driven convection from occurring [82].

3. Influencing Factors

To accurately perceive how CO₂ behaves in the subsurface after it has been injected into the saline aquifer, the influence of various factors on convection must be taken into account, and these factors can be divided into two categories. One category of factors directly affects the hydrodynamics of convection, often those of reservoir characteristics. Another category of factors relates to the dissolution dynamics of CO₂ in the saline aquifer. These factors generally include fluid properties, which affect the pattern of changes in fluid density by influencing the CO₂ dissolution process, thus determining the convection process. This section describes the impact of these factors on the convection process based on the CO₂–brine system.

3.1. Fluid Dynamics

3.1.1. Permeability

Fluids within porous media flow and transfer mass through the interstices of particles. Permeability indicates the degree of difficulty in passing fluids through porous media. Its value depends on the porous structure of the media and is an important characterization parameter for the properties of porous media. A porous medium composed of geological rocks with a certain degree of permeability is a prerequisite to ensure that density-driven convection of brine occurs. In general, density-driven convection for CO₂ solubility trapping in saline aquifers can be determined by the Rayleigh number. When the Rayleigh number exceeds 4π² [85,86], convection will occur:

$$Ra=\frac{k∆\rho gH}{\varphi \mu D}$$

(13)

where Δρ is the maximum density difference between CO₂-rich brine and CO₂-free brine (kg/m³). Ra is an important parameter for quantifying convection in porous media and is expressed by the ratio of buoyancy to diffusion forces. It determines the intensity of fluid flow and mass transfer in convection, and convection with different Ra presents differences in fluid flow and development characteristics. It is easy to see from Equation (13) that Ra is determined by the properties of the porous medium and fluid, which vary with the location of the CO₂ sequestration. For these parameters, only the variation in permeability across different trapping sites is of orders of magnitude, meaning that Ra, or the state of density-driven convection for CO₂ solubility trapping in the saline aquifer, is highly dependent on the permeability value of the local saline aquifer. This is further illustrated by the research of Pau et al. [33] on the influence of parameter fluctuation on the initial stability of CO₂ density-driven convection, where the initial stability of the CO₂–brine system showed high sensitivity to slight fluctuation in permeability. Furthermore, they found that the dissolution flux of CO₂ at the top boundary would reach a steady state after a certain time. This flux was proportional to permeability, unrelated to effective diffusion coefficient and porosity, indicating that the flow was predominantly convective.

The analysis of CO₂ dissolution flux allows the description of the important dynamic behavior of CO₂ convection processes caused by changes in aquifer conditions. Slim [77] described the hydrodynamics of CO₂ density-driven convection from the diffusion to the shutdown in a two-dimensional porous medium with Ra between 100 and 5 × 10⁴. From the time-dependent profile of the dissolved CO₂ flux at the top boundary, this convective process was described in six stages, and it is found that Ra controlled the transition of convective stages and the mass transfer characteristic of convection within the different stages. Moreover, as the permeability of the porous medium increased, convection delayed the time to end the constant flux stage, as shown in Figure 3a. Erfani et al. [87] further gave dissolution flux for different permeabilities corresponding to Ra from 350 to 95,000, as shown in Figure 3b. As the permeability increased, there was a significant advance in the onset of convection with a corresponding increase for the maximum CO₂ dissolution flux during the flux growth stage. In general, as the permeability of porous media increased, density-driven convection would become more intense, not only in terms of an earlier onset of convection, but also in terms of a longer flux growth stage, which meant that the maximum dissolution flux of CO₂ would also increase significantly. In addition, the convection would experience a longer period of merging. CO₂ convection would also undergo a constant flux stage in porous media with high permeability, and this would be more pronounced at higher permeability, implying a later shutdown of convection and a higher level of CO₂ dissolution and mixing.

The morphological characteristics of convective fingering movements can also be used to determine the state of convection. Teng et al. [88,89] investigated density-driven flow transport processes by magnetic resonance images. It was found that, as the permeability increased, the rate of convection development and the amount of convective fingering increased, with an earlier onset of convection. Numerical simulations by Ching et al. [90] showed a significant increase in the wavelength of convective fingering in high-permeability porous media, while experimental results by Amarasinghe et al. [91] showed that the mixing rate of CO₂ convection in porous media increased with increased permeability. It was also observed that the morphology of the convective fingering of CO₂ depends on the permeability, with the observed fingering in highly permeable porous media being consistent with previous studies, in contrast to the piston displacement of brine with dissolved CO₂ in low permeability porous media (e.g., 500 mD).

However, actual saline aquifers are heterogeneous, and this heterogeneity in reservoir conditions, particularly in permeability, will significantly affect the mixing process of density-driven convection. The flow characteristics of the mixing due to convective processes depend on the aquifer permeability heterogeneity. Thus, when considering convection in heterogeneous porous media, spatial variation in permeability is often used to introduce heterogeneity, which means that the absolute permeability, k, in Equation (2) will become k(x, z) or a tensor.

The degree of heterogeneity of reservoir permeability can be expressed by the value of fluctuation in the random field attached to the permeability. In the CO₂- brine model of Pau et al. [33], the onset time of convection exhibited sensitivity to the magnitude of fluctuation in the permeability field, with the convective onset time decreasing as the magnitude of fluctuation increased. However, this decreasing trend is gradually diminishing; when the fluctuation reaches 15% or higher, the onset time of convection shows a certain degree of certainty. Lengler et al. [92] used a similar stochastic approach to create a spatially varying permeability field for a real CO₂ sequestration site. In their random field, the permeability values varied from 0.02 to 5000 mD, resulting in reservoirs with permeability heterogeneity having higher CO₂ dissolution storage capacity compared to homogeneous reservoirs. On the other hand, Mahyapour et al. [18] used sequential Gaussian simulation methods to generate stochastic permeability fields to elucidate the influence of permeability heterogeneity for CO₂ convection in saline aquifers. Convective results in the stochastic permeability field showed that an increase in permeability fluctuation enhanced the CO₂ dissolution flux and the tendency for convective fingering.

The Dykstra–Parsons coefficient and correlation length were also considered as the measure of the degree of permeability heterogeneity. The permeability variation was first introduced by Dykstra and Parsons [93] to quantify the degree of reservoir heterogeneity:

$$V_k=\frac{S_k}{A_k}$$

(14)

where S_k and A_k are the standard deviation and the average value of k, respectively. V_k is the so-called Dykstra–Parsons coefficient, a dimensionless measure for the variability of porous media that characterizes the heterogeneity of k [94]. Values for V_k range between 0 for a completely homogeneous aquifer and 1.0 for a completely heterogeneous aquifer. In between, it is generally suggested that when V_k was less than 0.25, the heterogeneity of the aquifer was slight and could be approximated by the homogeneous model in numerical simulation. As 0.25 < V_k < 0.75, the influence of the aquifer heterogeneity was gradually significant. Once V_k exceeded 0.75, the aquifer was extremely heterogeneous and required special treatment methods for numerical simulation. Note that S_k and A_k usually tend to vary in tandem; thus, V_k is relatively constant in a saline aquifer. Bestehorn et al. [95] examined permeability heterogeneity over a wide range, using V_k and correlation lengths. The results pointed to the convective onset time being significantly correlated with perturbation strength and correlation length. Using different degrees of permeability heterogeneity achieved by spectral methods, Farajzadeh et al. [96] identified different flow states characterized by V_k for density-driven convection. For a smaller V_k (0.1), convective fingering close to the same occurrence in homogeneous porous media was observed. However, even though the phenomena are similar, CO₂ dissolution in the heterogeneous porous medium generally occurs in larger quantities as compared to the homogeneous ones. Convection in heterogeneous porous media with a larger V_k (0.3, 0.5, and 0.8) exhibits more direct mass transfer than convective fingering. The different patterns exhibited by density-driven convection at different heterogeneities are thus classified into three groups: fingering, dispersive, and channeling. Chen et al. [97] noted that, in dispersion, the square of the dissolved mass of CO₂ was approximately proportional to time, while the dissolved mass of CO₂ is approximately proportional to time in both fingering and channeling. However, fingering was largely controlled by gravitational instability, while channeling depended on the permeability structure.

Similarly, these three patterns of density-driven convection were observed in the heterogeneous saline aquifers of Ranganathan [98] and Kong et al. [99], with the latter referring to these three flow patterns of density-driven convection as dispersive, preferential, and unbiased fingering. It was noted that the unbiased fingering converted to preferential and dispersive fingering was largely dependent on V_k, while the preferential fingering converted to dispersive fingering was determined by the length of the permeability dependence.

The dissolution flux and convective onset time of CO₂ certainly increase with increasing permeability heterogeneity regardless of how heterogeneity is introduced and evaluated in the CO₂–brine system. This indicates that the introduction of heterogeneity introduces more instability, dissolution rates, and flow opportunities to density-driven convection, which will further contribute to the efficiency of CO₂ solubility trapping in saline aquifers.

The work by Green et al. [100] also considered two models of permeability heterogeneity. Even though the initial flow state of density-driven convection was sensitive to changes in local permeability, the flow in the constant flux stage of each case was well approximated by the anisotropic homogeneous porous media model. This suggested that the average permeability properties of the porous media actually affected the flow of density-driven convection, meaning that heterogeneity could be expressed equivalently by the permeability anisotropy of a homogeneous porous medium. The consistency between the anisotropic model and heterogeneous porous media in estimating the dissolved mass flux of CO₂ by Elenius and Gasda [101] also illustrates this point well. Anisotropy can be described by the anisotropy ratio,

$$\gamma =\frac{k_{\mathrm{v}}}{k_{\mathrm{h}}}$$

(15)

where k_v and k_h are the vertical and horizontal permeability of the reservoir, respectively. In practical reservoirs, thin structures are often found in saline aquifers, which means that the horizontal permeability is usually much greater than the vertical permeability. Therefore, it is generally reasonable to believe that γ is less than 1.0.

Previous studies [102,103,104] have investigated the effect of anisotropy ratios on density-driven convection by holding k_h constant while lowering k_v to reduce γ. The results of their stability analysis showed that gravitational instability was mitigated to some extent with decreasing γ, as evidenced by a delay in the convection onset, a decrease in the critical wave number for convective fingering, an increase in the critical wavelength, and a decrease in the CO₂ dissolution rate. It is important to note that, although it is geologically more reasonable to keep k_h constant, Xu et al. [105] further considered the reduction in γ caused by increasing k_h while keeping k_v constant. In this case, the reduced γ would instead cause the opposite of the previous conclusion. This is because an increase in permeability, either k_h or k_v, would destroy the solute interface during CO₂ solubility trapping in saline aquifers, resulting in an earlier onset of instability causing higher CO₂ dissolution rates. This view was also supported by the results of several numerical simulation studies [87,97,106]. Notably, the results further indicated that the effect of γ on dissolution flux was more significant at a lower value of Ra and permeability of porous medium [107]. It can therefore be established that, regardless of how γ is varied, for k_h and k_v, while keeping one constant, the higher the value of the other, the more unstable the convection system, the earlier the onset time, and the higher the CO₂ dissolution flux. In this process, k_v has a more significant effect on density-driven convection than k_h.

New representations of permeability anisotropy have recently been proposed. For example, Li et al. [108] represented anisotropic permeability fields in terms of vertical and horizontal correlation lengths, i.e., l_v and l_h. The results showed that for a relatively small l_v and l_h, competing phenomena of scale coupling and anisotropy were found, with resonance effects accelerating the downward brine as l_h increased to a scale close to the convective fingering, leading to the earlier onset time and correspondingly lower dissolution, while once l_h increased to a scale much larger than the convective fingering, anisotropy became the dominant effect so that the onset of convection was delayed. On the other hand, for changes in l_v, consistent results of change were observed for relatively large l_h, i.e., later onset of convection with higher CO₂ dissolution.

3.1.2. Porosity

The rock particles that contribute to the matrix of saline aquifers are normally incompletely integrated due to the highly irregular shape. The resulting void space that can be occupied by CO₂ or brine is called pore and quantified as porosity:

$$\varphi =\frac{V_{\mathrm{p}}}{V_{\mathrm{b}}}$$

(16)

where V_p is the pore volume (m³), and V_b is the bulk volume of the matrix (m³), including the solid and void components. Two distinct categories of porosity are defined in saline aquifers, i.e., absolute porosity and effective porosity. Saline aquifers may have considerable absolute porosity with low fluid conductivity due to the lack of interconnected pores. This is negative for CO₂ sequestration. Therefore, the porosity in studies of CO₂ sequestration in saline aquifers generally refers to the effective porosity.

The porosity significantly influences the density-driven convection by controlling the pattern of CO₂-rich brine front in saline aquifers. Sun et al. [109] showed that for a low ϕ (less than 0.05), CO₂-rich brine maintained the form of a stable boundary layer that slowly diffused downward. In contrast, the instability is further developed in saline aquifers with high ϕ (greater than 0.10), and convective fingering is clearly observed, as shown in Figure 4. The diffuse boundary layer thickness was also influenced by ϕ. A higher ϕ was characterized by a thinner diffusive boundary layer, implying earlier convective onset. The same conclusion was reached by Gasow et al. [110,111].

This increased diffusion instability and decreased convective strength may be explained by the change in the effective diffusion coefficient due to the ϕ. As indicated by the results of Aggelopoulos and Tsakiroglou [112], errors were caused by unconsidered variations in the effective diffusion coefficient due to the ϕ. The effective diffusion coefficient, D, in Equation (3) is thus defined as follows:

$$D=\frac{D_0\varphi }{\tau }$$

(17)

where D₀ is the molecular diffusion coefficient (m²/s), and τ is the tortuosity. Ozgur and Gumrah [113,114] pointed out that the dissolution of CO₂ in diffusion processes increased due to the increase in the effective diffusion coefficient by an increased ϕ. This produced greater instability in the diffusive boundary layer. However, once this increased instability prematurely triggered convection, a reduction in convective strength ensued. This was because the fluid velocity was reduced in aquifers with a high ϕ. More effects of dispersion on density-driven convection are discussed in Section 3.1.5. In addition, Beni et al. [115] pointed out that a change in ϕ would cause a change in k. However, Islam [116] indicated that this change was negligible and therefore would not significantly affect the CO₂ density-driven convection.

In terms of heterogeneity, Jensen and Lake [117] pointed out that the spatial variation of ϕ in aquifers was much more insignificant compared to permeability. However, considering that the common geochemical reactions in aquifers would significantly change the local ϕ [118,119,120,121,122,123], a few relevant studies on ϕ heterogeneity were still developed. The ϕ heterogeneity was generally introduced into numerical models as a perturbation (or fluctuation), leading to instability and correlating with convection onset time [124]. Pau et al. [33] pointed out that the onset time decreased by increased ϕ fluctuation, and this decrease was more significant compared to the same degree of permeability fluctuation. The results by Tilton [125] showed that there was an optimal ϕ perturbation that could minimize the onset time. This suggested that even though a small ϕ perturbation was usually neglected, it was sufficient to trigger nonlinear convection. Future studies should take this factor fully into account.

3.1.3. Fractures and Stratification

When there was a certain structure in the heterogeneous permeability field, such as a low permeability or permeability jump zone, the heterogeneous structure of the aquifer would have a greater impact on the total amount of CO₂ sequestration compared to the equivalent effective permeability of the aquifers [126]. Typical heterogeneous stratigraphic structures include fractures and stratification. Fractures can be found in several sequestration sites, such as the Salah site in Algeria [127], the Kevin Dome site in Montana [128], and the Janggi site in South Kore [129]. Some sequestration sites will increase injectivity by hydraulic fracturing to increase the permeability of the aquifer or oilfield near the wellbore [130,131]. Fractures imply an intense media anisotropy and preferential flow. The consequent uncertainty in fluid flow and solute transport increased the risk of leakage and contamination [132]. Furthermore, a few numerical simulation studies have been developed for the effect of the fracture-skin on solute transport [133,134]. Except for the naturally existing fractures, the injection of CO₂ will lead to artificial fractures in saline aquifers. This occurs due to the increased pore pressure, and the reduced effective stress will result in geo-mechanical deformation. This deformation may also reactivate faults and change permeability to affect the integrity of the reservoir [135]. During the injection process, related studies have revealed that the presence of fractures, whether artificial or natural, can provide the escape pathways for undissolved CO₂ in a saline aquifer, negatively affecting the long-term secure storage of CO₂ [21,22,136]. On the other hand, the presence of the fractures creates a large contact area between CO₂ and brine, thereby facilitating the dissolution of CO₂.

In the studies of solute transport by density-driven convection in fractured formations, the models of single fracture and the fracture network were considered. Compared with the complex fracture network, the single fracture is often treated as a simple system to study the transport between the fracture and the matrix [137]. Graf and Therrien [138] found that a continuous 45° inclined single fracture in a low-permeability matrix system allowed solutes to penetrate through the fractures and migrate downward. Iding and Blunt [139] found that the dissolution rate of gas-phase CO₂ in the system could be increased by 5% by inletting a horizontal single fracture in a 2D model, indicating that fractured aquifers were able to increase the solubility trapping of CO₂. Rezk and Foroozesh [19] used numerical simulations to find that high permeability and big inclination angle of fractures favored the CO₂ solubility trapping process in the single fracture system. Similar findings were found by Kim et al. [140] that a small inclination single fracture structure in the aquifer enhanced the mass transfer between the fracture and matrix, while the large inclination fractures promoted brine movement toward the top boundary, facilitating circulation in the region and enhancing CO₂ dissolution.

The permeability of matrix and fracture also has an impact on CO₂ solubility trapping. Kim et al. [140] investigated the effects of fracture–matrix permeability ratio on convection. When the permeability values of the matrix and the fracture are similar, the influence of fracture on density-driven convection was negligible. In addition, the intersection of two fractures was found to promote the merging of fingering, which enhanced the mass transfer between fractures. Wang et al. [17] showed that the higher permeability of fractures was favorable to solubility trapping, and the greater inclination angle was favorable for mixing between the two-phase fluids. In addition, when the permeability of the fractures was smaller than the matrix, the fractures acted as flow barriers in the system, hindering the fingering development. When the permeability was larger than the matrix, the fractures enhanced the liquid-phase circulation, allowing more brine at the bottom boundary to enter the top region of the fractures.

In a fracture network consisting of multiple fractures, the transport of the plume tends to be much more complicated. The results by Shikaze et al. [141] showed that convection patterns depended on fracture spacing. In porous media with random fracture spacing, irregularly shaped convective cells were formed. The intricate convection patterns were also found in porous media with orthogonal fractures, regardless of the uniform spacing and pore size of the fractures. In addition, it is suggested that solute migration and mass transfer rates properly not be predicted in complex fractured formations. The above findings suggest that the geometry of fractures is highly related to the stability of density-driven convection within the fractured system. Graf and Therrien [142] investigated the dense plume transport in the orthogonal and irregular fracture networks. The geometry of the porosity network had a significant impact on the dense plume transport. In the orthogonal network, the variable density flow was mainly controlled by the convective patterns found in the large fracture network. In an irregular fracture grid, density-driven transport was favored if there were few uniformly distributed fractures close to the source. On the other hand, a large number of fractures near the solute source had a stabilizing effect. Vujevic et al. [143] investigated the density-driven flow and transport patterns in uninterrupted, interrupted, perpendicular, and inclined fracture networks in low-permeability matrices. The results revealed that the influence of irregular networks on stability was more difficult to predict than that of regular networks, but it was possible to determine that the average length of fractures had a greater influence on density-driven convection than the distribution density of fractures.

In fractured formations, a 2D fracture is essentially represented by a line, so convection within the fractures is disregarded due to this restriction on the spatial dimension. Although the fractures models used in the previous studies have small apertures, making their permeability vastly different from that of the reservoir matrix. There was evidence that an increase in fracture aperture increased the velocity of the upward flow of brine within the fractures, leading to an increase in early convective instability [144], which favored CO₂ solubility trapping [19]. The results also implied that the heterogeneity of permeability between the fracture and matrix might have a dramatic influence on the flow pattern in the convective mixing process. Moreover, it has been suggested that both the flow between fractures and the storability of the fractures play a significant part in the stability behavior of the system, and the convection within the fractures may have an impact on CO₂ solubility trapping. However, currently, the relevant studies are still lacking. One of the reasons may be attributed to the fact that it is challenging to study in different dimensions in fractured systems considering the heterogeneity, especially in more complex 3D systems, and that the consistency between 2D and 3D results needs to be further demonstrated. Vujevic and Graf [145] tried to study the convective behavior within fractures by using a 3D model and found that the mass transport between fractures was greater than within fractures. However, in the more complex 3D fracture networks, it was difficult to use the Rayleigh criterion to predict the convective behavior. Only under specific conditions were the 2D results useful for predicting the convective onset time and intensity in a 3D fracture network. In addition, the impact of the physical properties of the fracture (e.g., roughness, tortuosity, etc.) on the convection in the fracture system has not been fully understood. Note that the current study of CO₂ solubility trapping in fractured systems is mainly focused on single-phase flows, and further study of two-phase flows, especially from the beginning of injection to the post-injection, involving the drainage process, capillary action, and reinfiltrating phenomena, is more helpful to understand the convection behavior in the fracture network.

Stratification is another common heterogeneous structure, and the influence of such aquifers with a certain number of different permeability layers on convection has also gained much attention in recent years. It is suggested that low permeability zones in saline aquifers play an important role in avoiding CO₂ leakage [146,147]. At the same time, the heterogeneity of the layering permeability affects the migration of injected CO₂ and the subsequent process of mass transfer [121,148].

Wang et al. [149] used the non-destructive technique of X-ray micro-tomography to capture the fingering development process in the 3D layered formation and found that the wavelength of fingering increased when fingering passed through the stratified interface in the decreasing-permeability aquifers. By using a numerical modeling method in multilayered porous media, Farajzadeh et al. [150] discovered that when the higher permeability layer was posed at the top layer, the mass transfer increased and fingering moved more quickly as Ra increased. However, the convection weakened as fingering moved into the low permeability layer.

Taheri et al. [151] defined the concept of strong and weak heterogeneity by the magnitude of the ratio of the permeability in the upper and lower layers. It was found by numerical simulation methods that when the low permeability layer was in the upper layer, either strong or weak heterogeneity, the upper layer controlled the convection behavior of the whole system. When the upper layer was a high permeability layer, the upper layer also acted as a control layer in the weak heterogeneous system. However, in strong heterogeneous systems, the lower permeability of the lower layer facilitated the dissolution of more CO₂. This work was later extended by upgrading the Hele-Shaw to study convection in a two-layer heterogeneous system [152]. It is found that when the high permeability layer was posed above the low permeability layer, the dissolution rate would be more than twice as large as that in a low-permeability homogeneous system. This implied that the higher permeability upper layer facilitates the rapid dissolution of CO₂ in brine. Agartan and Trevisan [153] used a laboratory tank with analog fluids to study density-driven convection. It was found that the process of diffusive mixing would be more pronounced than density-driven convection in the stratified formations and that a longer retention time in the lower permeable layer might favor long-term secure storage of CO₂. Similar findings were also found in the laboratory experiments by Wang et al. [154], who used magnetic resonance imaging techniques to visualize the evolution of convection in multilayered porous media. It was found that the permeability heterogeneity had a significant impact on the dissolution rate of CO₂, and the presence of low permeability layers hindered the fingering flow and decreased the dissolution rate of CO₂ but promoted the transversal diffusion of the permeable transition region.

In addition to the slope caprock, as mentioned earlier, there is a certain inclination at the stratified interface in the actual aquifers, which may also affect the convection. Tsai et al. [155] found that, compared with the horizontal case, the presence of the inclined stratified interface increased the propagation velocity of fingering by about 20%. Both Agartan et al. [153] and Wang et al. [156] used tank experiments to investigate the convection in the inclined stratification aquifers, and they found that the presence of an inclined interface altered the behavior of fingering. For example, in the coarse/fine layers system, fingering migrated along the lower part of the stratified interface, enhancing the fingering spreading in the vertical direction. Unfortunately, there are no available studies focusing on the specific behavior of fingering and the mass transport during convection within the inclined layered system. Moreover, the transformation involving convective dissolution processes at multiple spatial and temporal scales associated with CO₂ sequestration in saline aquifers poses a challenge to the widespread application of it. Macroscopic spatial scales up to thousands of meters and has a timescale of up to hundreds or thousands of years. Related results suggested that the heterogeneity of pore size and wettability altered the inherent flow permeability of the stratified structure [157]. The transport of dissolved CO₂ was intimately related to pore geometry, and the difference in solute distribution between large and small pores dramatically influenced the upscaling process, making the study of pore scale vital [158]. Therefore, this challenge is faced in both laboratory experiments and numerical simulations. To consider the effects of the multiphase and multicomponent flows occurring at the actual CO₂ sequestration field, as well as the possible geochemical reactions, and geo-mechanical effects, the appropriately fine-scale discretization may need to be used in the numerical model to obtain an accurate result to assess the effectiveness of CO₂ sequestration in the stratification formations, which is a topic worth discussing in the future.

Different lithologies are associated with the stratification of aquifers, which affects structural geometry and aquifer properties (e.g., permeability and porosity) [159]. Take the White Rim Sandstone reservoir as an example; Wheatley et al. [160] explained the relevant reservoir characteristics (e.g., sedimentary structure, facies, and diagenesis). Seven independent litho-facies were used to describe the White Rim Sandstone: grain-flow facies, wind-ripple facies, ripple-laminated facies, soft-sediment deformation facies, symmetrically ripped facies, bioturbated facies, and massive facies. They discovered that the quantity and relative spacing of internal laminae or boundary surfaces that were horizontally or obliquely oriented, which impeded fluid flow, accounting for a major portion of permeability variances in facies. White et al. [159] compared the potential reservoirs, including Jurassic Navajo Sandstone, Jurassic Wingate Sandstone, Permian White Rim Sandstone, and Mississippian Redwall Limestone, and found that the Permian White Rim Sandstone was the best reservoir for CO₂ injection, with great permeability and porosity. In fact, it was not rigorous to judge the applicability of geological storage based on permeability and porosity. The composition of the rocks, sedimentary diagnostic eolian features, thickness and depth of the layers, etc., should all be considered [161].

In addition, transmissibility plays an important role in the stratification and subsequent fault of aquifers. It implies a measure of how much brine can be transmitted horizontally and is commonly present in studies of aquifers with pumping behavior [162]. The transmissibility of an aquifer can be defined as follows:

$$T_t=\sum T_i=\sum K_i{d}_i$$

(18)

where T_t is the total transmissibility of the aquifer (m²/day), T_i is the transmissibility of a horizontal flow for the ith aquifer layer, K_i is the horizontal hydraulic conductivity, and d_i is the layer thickness.

The transmissibility multiplier was commonly used in studies [163]. A transmissibility multiplier of 0 implied that the fault was sealed, and therefore the flow across the fault zone is considered to be restricted. A transmissibility multiplier of 1 implied that the fault zone was free-flowing, similar to the rock matrix. Alexander et al. [164] noted that a transmissibility multiplier significantly affected the amount of CO₂ that could be injected into an aquifer and ultimately stored. For a transmissibility multiplier of less than 0.01, the injectable CO₂ was completely stored. This was because the injected CO₂ was not reaching the production well and therefore remained in an aquifer. For a transmissibility multiplier greater than 0.01, the amount of injectable and stored CO₂ increased linearly. For a transmissibility multiplier greater than 0.1, the amount of stored CO₂ was almost constant, although the amount of injectable CO₂ still increased dramatically. Therefore, a transmissibility multiplier between 0.01 to 0.1 seemed to be the optimal range for CO₂ sequestration in saline aquifers.

However, Hsieh et al. [165] suggested that a saline aquifer with an optimal transmissibility multiplier might not be the best option for CO₂ sequestration safety. Other risks still need to be assessed in order to find the best solution. Based on this perception, Ghanbari et al. [166] pointed out that the key to the distribution of CO₂ plume and solute was not the transmissibility multiplier; instead, it was the location of the injection well.

3.1.4. Slope of Caprock

The fact that saline aquifers are generally tilted and discontinuous may have an impact on the convective process in CO₂ solubility trapping. Given the differences in scale, the influence of saline aquifer structure on density-driven convection occurs more often at the upper and lower boundaries, i.e., at the caprock or the bottom impermeable rock layer (Figure 1a). Here, the caprock is a prerequisite for the successful retention of injected supercritical CO₂, providing the potential for the occurrence of dissolved sequestration and later density-driven convection. For a long period of time, the injected CO₂ will remain and migrate as a plume at the bottom of the caprock under buoyancy, and the state of the caprock will still have an impact on the flow and mass transfer of density-driven convection even after the stage of solubility trapping. On the other hand, Vilarrasa et al. [167] pointed out that the effect of the inclined impermeable rock layer at the bottom of the saline aquifer acted only after the convective fingering front in density-driven convection contacted the rock. Therefore, the caprock is considered to be the primary target for considering the effect of saline aquifer slope and integrity on CO₂ solubility trapping.

In the study by Tsai et al. [155], the tilt of the saline aquifer was considered an inclined modeling domain, and numerical simulations showed that a sloped boundary would enhance density-driven convection, as reflected in the large transversal movement, merging, and coarsening of the convective fingering, which enhanced convection and implied that a sloped saline aquifer would be the ideal site for CO₂ solubility trapping. However, Macminn et al. [168] found that a small slope of the caprock was indeed beneficial for CO₂ solubility trapping, resulting in a sharp reduction in the time that the CO₂ plume was present, with the maximum transport distance only slightly increased. However, a continued increase in slope would still pose some risks, such as greater increases in transport distance and very little reduction in the time the CO₂ plume was present. Even though residual trapping provided a strong complement to density-driven convection in solubility trapping, the increase in slope was expected to still expose the CO₂ plume to fresh water and cause pollution.

Sung et al. [121] evaluated the potential for an ideal CO₂ geological sequestration site, and their study noted that the prevalence of tilted saline aquifers in sequestration sites would significantly affect the fate of injected CO₂, resulting in a marginal asymmetry of CO₂ plume in the direction of upslope, as shown in Figure 5. Meng and Jiang [25] considered the inclined saline aquifer as the slope of the top boundary of the modeling domain. For both 2D and 3D numerical simulations, as the slope of the caprock increased, the diffusion of the boundary layer became smoother, and the number of convective fingerings decreased, and this was accompanied by a significantly different fingering merging behavior than in the horizontal caprock case. While the interaction between fingering weakened and the flow showed more reliance on the direction of the caprock slope. This implies a more stable density-driven convection, as the component of gravity in the slope direction increases with the increasing caprock slope, thus making it more difficult for the top boundary layer to satisfy the thickness for sufficient instability. Note that the slope of the caprock in the 3D numerical simulations would result in a later onset of convection than the horizontal caprock case for the same reservoir, and this effect was more pronounced than in the 2D numerical simulations.

In general, the influence of a tilted saline aquifer on the fate of injected CO₂ is mainly reflected in the effect of the caprock slope on CO₂ plume flow and density-driven convection. The presence of a caprock slope will cause the CO₂ plume to migrate upslope under buoyancy, meaning that, even if there are benefits, the slope of the caprock should not be overly steep. Because the overly steep slope often implies an unexpectedly large migration of the CO₂ plume and the consequent risk of CO₂ exposure to fresh water, it is contrary to the original intention of CO₂ solubility trapping in saline aquifers to isolate it from the atmosphere and to limit its migration. However, a slightly sloping caprock may have an advantage in that once solubility trapping is dominant, density-driven convection will be intensified, as evidenced by the transversal migration of convective fingering downslope by both gravity and slope, as well as the consequent consolidation and coarsening of fingering. This will greatly facilitate the process of density-driven convection and ensure efficient CO₂ solubility trapping to further secure CO₂ sequestration in the saline aquifer.

3.1.5. Hydrodynamic Dispersion

The mass transfer of mechanical dispersion, jointly with molecular diffusion, is widely present in aquifers [169] and is called hydrodynamic dispersion [170,171,172]. Note that hydrodynamic dispersion is generated by the local variations in fluid velocity due to the micro- and/or macroscopic heterogeneity and structure of the porous media, such as friction on the pore walls, heterogeneous pore sizes, and different trajectories, and presents an enhancement of dissolution [173] with the heterogeneity of velocity. This velocity heterogeneity will enhance molecular diffusion, which has a substantial impact on solute migration, also known as mechanical dispersion. Therefore, when the effect of mechanical dispersion is considered, the effective diffusion coefficient, D, in Equation (3) should be given by the hydrodynamic dispersion tensor as follows [174]:

$${\mathit{D}}_{xy}={\mathit{D}}_0{\delta }_{xy}+\left({\alpha }_l-{\alpha }_t\right)\frac{{\mathit{v}}_x{\mathit{v}}_y}{\varphi \left|\mathit{v}\right|}+{\alpha }_t\frac{\left|\mathit{v}\right|}{\varphi }{\delta }_{xy}$$

(19)

where δ is the Kronecker delta; α_l and α_t indicate longitudinal and transversal dispersity lengths, respectively (m); and subscripts x and y refer to the axes of the Cartesian coordinate system. The first part on the right of the equation is a representation of the effect of molecular diffusion, where D₀ is a constant that takes into account the volume diffusion coefficient with the tortuous effect of the porous medium and is proportional to the local gap velocity. The second and third parts are the effects due to mechanical dispersion. In most analyses of hydrodynamic dispersion, Equation (19) is usually given in the dimensionless form, which leads to different dimensionless parameters being derived to characterize the effects of dispersion, commonly the dispersion ratio, α, and the longitudinal dispersion strength, S. The dispersion ratio characterizes the degree of mechanical dispersion anisotropy of porous media and is usually expressed as follows:

$$\alpha =\frac{{\alpha }_t}{{\alpha }_l}$$

(20)

The numerical results by Emami-Meybodi [84] showed that both longitudinal and transversal dispersity had a considerable influence on the fingering patterns and dissolution mass flux. As for α, it represents the ratio of the strength of longitudinal dispersion to molecular diffusion and is given in different forms depending on the purpose of the analysis. In the study by Hidalgo and Carrera [175], the longitudinal dispersion strength was expressed in the following form:

$$S=\frac{{\alpha }_l{u}_b}{\varphi D_0+{\alpha }_l{u}_b}$$

(21)

where u_b = kΔρg/μ is the velocity scalar (m/s), also known as the reference velocity. Although they refer to the same α as in Equation (20), it is kept constant at 0.1, which is commonly presented in most subsurface aquifers. The results showed a significant linear reduction in the convective onset time of even two orders of magnitude with increasing mechanical dispersion strength. Ghesmat et al. [176] used the same representation of dispersion, and their results revealed that the presence of dispersion affected the fingering development pattern, with higher dispersion implying faster dissolution of CO₂ in brine, enhancing mixing and significantly reducing the convection onset. In addition, the effect of α on density-driven convection was investigated, and the results were similar to the prediction of the numerical study by Xie et al. [177], where aquifers with different dispersion ratios was saturated with dissolved CO₂ almost simultaneously, and its overall effect on density-driven convective efficiency was negligible.

However, it is important to note that a dimensionless way of generating this form of S will lead to a non-independence of the dimensionless number, meaning that an increase in S will lead to the same change in Ra. It is consistently agreed upon that an increase in Ra will significantly reduce the convective onset time and increase the intensity of convection, which antagonizes and may easily override the influence of an increasing S on density-driven convection, and this probably explains the significantly reduced convective onset time as S increases. Recent work by Dhar et al. [178] indicated that the convective onset time should increase with S for α = 0.1, which was also consistent with previous experimental results [179,180]. In their simulations, S was independent of Ra according to the following form:

$$S=\frac{{\alpha }_l{u}_b}{\varphi D_0}$$

(22)

This dimensionless approach may also lead to a more significant role in the dispersion ratio. Their results further suggest that transversal dispersion accelerates this process, implying that an increase in the dispersion ratio promotes the onset of density-driven convection, which seems to be explained by an increase in the dispersion ratio that would destabilize the diffusion boundary layer. Moreover, the increase in transversal dispersion has facilitated the development of transversal growth of the fingering, thus contributing to reducing the density of fingering and possibly tending to homogenize the CO₂ concentration field, which is similar to the results of Wang et al. [181,182] and Nakanishi et al. [183]. This phenomenon is attributed to the strength of transversal dispersion between downward and upward flow significantly influencing the interaction, merging, and coarsening of fingering.

Hidalgo and Carrera [175] showed that the onset time of the density-driven convection might be shortened by up to two orders of magnitude when hydrodynamic dispersion was taken into consideration in the no-background flow model. The similar results by Ghesmat et al. [176] demonstrated that the existence of dispersion impacted the fingering development patterns, with larger dispersion meaning faster dissolution of CO₂ in brine, this promoting mixing and greatly slowing the onset time of convection.

Particularly, the results of Chevalier et al. [61] revealed that, in the Hele-Shaw cell, an experimental device commonly used to visualize density-driven convection, mechanical dispersion was diminished to a Taylor dispersion due to changes in Poiseuille-type velocity over the cell pore. However, even though the Taylor dispersion increased the hydrodynamic dispersion coefficient by two to five times, it only seemed to retard convection slightly, as expected, because the presence of dispersion tended to reduce the concentration gradient of CO₂ at the top region of the model and was still a non-significant parameter of mass transfer in the Hele-Shaw. The results of Bharath et al. [184] also indicated that the shape boundary of the convective fingering would be blurred by the presence of dispersion. When studying the convective fingering in solubility trapping by numerical simulations, attention should be paid to the inability of the two-phase interface model to catch the boundary. This reflects the superiority of the mass transfer model in this problem.

Furthermore, the existence of natural background flow in the actual aquifers associated with the dispersion should be taken into account, which was usually distinguished by hierarchical nested background flow systems [185]. These systems included background flow systems at the local, intermediate, and regional levels and occurred in a variety of hydrogeological environments. The local flow systems moved water from water table crests to nearby troughs in shallow and small-scale circulations. The flow lines of the intermediate flow systems often extended over numerous water table crests and troughs, and the circulations were typically deeper. A regional flow system covered the entire aquifer’s surface. Local flow systems were characterized by precocious background flow and low solute concentrations because solute concentrations and mean background flow ages rise down the gradient [186]. The hydraulic gradient was treated as a general driving force for background flow [187,188]. It was suggested that the penetration depth of local background flow systems became shallower as the local hydraulic gradient was reduced [189]. Although the above studies reflect the complexity of the subsurface geographic system, background flow is mostly considered to be a simple horizontal single-directional flow during convective mixing, which may change the vertical diffusion layer before convection onset and increase the CO₂ dissolution by transporting it to greater distances. The convective mixing processes when considering background flow and dispersion effects have also been studied by related scholars. The ratio of Pe/Ra was usually used to quantify the magnitude of the horizontal flow. Hassanzadeh et al. [81] found that the horizontal flow was discovered to have the potential to retard the convection onset. Furthermore, it was observed that the convection onset was proportional to Pe. Emami-Meybodi et al. [82] created a 2D semi-analytical model to investigate the influence of the background flow on convection. The intensity of the density-driven convection was strongly affected by the background flow, and the velocities of background flow could extend the convection onset and change the subsequent convection process. The horizontal element of the background flow velocity inhibits the forming of vertical elements, and this impact was more apparent in the formations with a strong background flow. A similar conclusion was conducted by Cserepes and Lenkey [187], who found that the cells of convection were fully eliminated by the strong hydraulic flow and were newly organized in a “unicell” shape.

The situation is much more complicated when considering the hydrodynamic dispersion on the formations with background flow. Emami-Meybodi [84] demonstrated that decreasing either the velocity of the background flow or the dispersity while holding the other fixed accelerated the onset of convection and reduced the total dissolution mass flux. Michel-Meyer et al. [190] discovered that background flow inhibited the fingering forming in laboratory experiments using analog-fluid pairs, resulting in a two-fold reduction in the fingering descending rate and a five-fold reduction in the wavenumber of fingers. However, the presence of hydrodynamic dispersion effects enhanced the dispersion flux. Thus, the dissolution rate may be governed by a combined effect of convection and dispersive processes, which must be carefully considered. Tsinober et al. [191] verified the results by Michel-Meyer and found that, in the range of Pe/Ra < 0.77, the predominant process was density-driven convection, and the dissolution rate was roughly constant. When 0.77 < Pe/Ra < 2, both the forced and density-driven convections were crucial. When Pe/Ra > 2, the pure forced convection governed the dissolution process and increased with the value of Pe/Ra.

In general, when considering the background flow and neglecting the hydrodynamic dispersion, the results are coincident: the presence of the background flow hinders the convective mixing process; however, the results obtained from these simplified models may be inaccurate. When considering hydrodynamic dispersion effects, the current work will become a more complicated problem, consisting of the interaction of background flow, density-driven convection, and diffusion, and the current studies are far from adequate. Meanwhile, the dissolved CO₂ sequestration should be a long-term process, the flow rate of the background flow should not be a constant value, and the corresponding geochemical reactions may occur. When all of these factors are taken into account, it may make the results of the next study more meaningful for long-term and safe CO₂ sequestration.

3.2. Dissolution Dynamics

3.2.1. Temperature, Pressure, and Salinity

The dissolution of CO₂ in brine is necessary for the solubility trapping mechanism, and can be represented by Equations (23)–(26). The injected CO₂ is initially dissolved in brine to form the aqueous solution. A chemical equilibrium between the aqueous solution and the carbonic acid was then minimally established [192]. As a product of the reaction, the carbonic acid subsequently partially dissociates into H+, HCO₃⁻, and further CO₃²⁻. The effect of condition parameters of the saline aquifer on the dissolution of CO₂ in brine has been extensively studied and discussed [63,193,194,195,196,197,198,199,200,201,202,203,204,205,206,207,208,209], and it has been consistently concluded that the solubility of CO₂ in brine increases with increasing pressure and decreasing temperature and salinity. This change can be explained by the fact that an increase in pressure drives a further increase in the density of CO₂, and the dissolution equilibrium shifts to the right, thus reflecting an increase in the solubility of CO₂ in brine. While a decrease in temperature should cause the same change in the dissolution equilibrium. A decrease in salinity leads to the presence of fewer cations, and this increases the solubility of CO₂ in brine given that the cations will form further hydrates and act as barriers to CO₂ dissolution.

$${\mathrm{CO}}_2\left(\mathrm{g}\right)\to {\mathrm{CO}}_2\left(\mathrm{aq}\right)$$

(23)

$${\mathrm{CO}}_2\left(\mathrm{g}\right)+{\mathrm{H}}_2\mathrm{O}\left(\mathrm{l}\right)\leftrightarrow {\mathrm{H}}_2{\mathrm{CO}}_3\left(\mathrm{aq}\right)$$

(24)

$${\mathrm{H}}_2{\mathrm{CO}}_3\left(\mathrm{aq}\right)\leftrightarrow {\mathrm{H}}^{+}\left(\mathrm{aq}\right)+{\mathrm{HCO}}_3^{-}\left(\mathrm{aq}\right)$$

(25)

$${\mathrm{HCO}}_3^{-}\left(\mathrm{aq}\right)\leftrightarrow {\mathrm{H}}^{+}\left(\mathrm{aq}\right)+{\mathrm{CO}}_3^{2-}\left(\mathrm{aq}\right)$$

(26)

The solubility of CO₂ in brine affects the maximum value of the density change (i.e., Δρ) of the brine in an aquifer, which affects Ra and the formation of the diffusion boundary layer, implying a change in the development of instability and subsequent density-driven convection. A low maximum value of Δρ will retard or even inhibit the development of instability and convection.

Seyyedi et al. [203,206] pointed out that an increase in temperature or salinity of brine in an aquifer negatively affected the convection, as expected, with increased convective onset time and smaller length and development rate of fingering in higher salinity brine. This is because the suppression of the maximum value of Δρ at higher brine salinities or higher temperatures leads to smaller values of Ra and thus the Sherwood number. The Sherwood number is a characterization of the dissolution rate of CO₂ in brine and is defined as follows:

$$Sh=\frac{FH}{\varphi D∆c}$$

(27)

where F = ϕvΔc is the CO₂ dissolution flux (mol/(m²·s)), and Δc is the solute concentration difference (mol/m³). This dimensionless number could be used to approximate and evaluate the dissolution and mixing of CO₂ in brine [203,210]. A reduction in Ra and Sh would make convection and CO₂ dissolution flux retarded and moderated, and this will negatively affect the CO₂ solubility trapping in a saline aquifer, and the same conclusion was reached by Teng et al. [211]. Jiang et al. [212] further showed that high pressure and low salinity represented an early convective onset time, a lower fingering number, and a large fingering wavelength and mobility, which implied more efficient convection and had a positive consequence for CO₂ solubility trapping in saline aquifers. Nomeli et al. [204] similarly suggested that the aquifer with high pressure and low temperature might be most suitable for CO₂ solubility trapping. However, it is noteworthy that their conclusions regarding the effect of salinity on density-driven convection are contrary those of other authors, and the reason for this deviation may stem from the definition of the density of the solution in the saline aquifer by their model, which is the density of a saturated H₂O-CO₂-NaCl solution and thus accounting for the effects of CO₂ molar fraction and volume, which need to be further investigated and discussed.

It is also important to note that, even though the increase in saline aquifer pressure has a positive effect on CO₂ solubility trapping, it is still frequent and not entirely desirable. A high CO₂ injection volume and rate, as well as a high aquifer depth, will lead to additional increases in aquifer pressure, which will overburden the caprock of the saline aquifer, especially in naturally fractured areas, and make it susceptible to the risk of CO₂ leakage. Szulczewksi et al. [213] pointed out that the ability of saline aquifers to store CO₂ was limited by the increase in pressure due to CO₂ injection, particularly in aquifers with high CO₂ injection rate requirements. The risks and limitations caused by increased pressure may perhaps be mitigated by optimizing other condition parameters. Abbaszadeh et al. [214] increased the solubility of CO₂ in the injection well by cooling it so that the risk of pressure fluctuation during injection was eliminated.

3.2.2. Ions and Impurities

The value of pH characterizes the concentration of H⁺ in solution, and it is easily seen from Equations (25) and (26) that a decrease in the pH of the aquifer will tend to shift the chemical equilibrium of the CO₂ dissolution reaction in brine to the left, and this inhibits the dissolution of CO₂. A study by Wan et al. [215] also confirmed this point of view. Some types of rock that form the aquifer induce the opposite effect in a similar way. Geochemical reactions caused by carbonate rocks will reduce the H⁺ concentration of brine. This change drives the dissolution reaction of CO₂ in brine to the right. The CO₂ in an aquifer is thus fixed in the aqueous or mineral phase, with the latter belonging to the CO₂ mineral trapping in a saline aquifer, while the former will lead to an increase in CO₂ solubility. The results of Rosenbauer et al. [216] also supported this conclusion. Note that the solubility of CO₂ in brine was also influenced by the type of salt, with monovalent solutions (such as potassium chloride and sodium chloride) tending to dissolve more CO₂ than divalent solutions (such as calcium chloride and magnesium chloride) [193,215,217,218,219,220,221]. Since saline aquifers often contain multiple ions, such as Mg²⁺, Ca²⁺, K⁺, and SO₄²⁻, the possibility that the solubility of CO₂ in NaCl solution is overestimated compared to that in actual aquifer solution needs to be considered, as the former is often used in experiments to represent aquifer fluids instead of the latter.

The sequestered CO₂ captured from large point sources (typically industrial factories) frequently contained impurities due to process constraints or requirements [222,223,224]. For reasons of separation costs and hazardous substance sequestration, CO₂ injected into saline aquifers was often accompanied by these impurities, which could affect CO₂ dissolution and transport [225,226,227,228]. It has been shown that the SO₂ impurity would enhance the density increase which was caused by CO₂ dissolution, thus enhancing density-driven convection, while N₂ and H₂S showed a negative effect [229,230,231,232,233,234]. This difference stemmed from the different degrees of change in fluid density after dissolution due to the molecular mass of the impurities [235,236]. However, it should be noted that the confrontation between CO₂ and impurity diffusion might lead to a non-monotonic effect of the latter on density-driven convection [237,238,239,240]. Experimental results by Mahmoodpour et al. [241,242] found that a 10 mol% N₂ impurity reduced the convective onset time and increased flux, with a greater pressure drop in CO₂ solubility trapping. The opposite effect was observed in the case of 20 mol% N₂ impurity, suggesting that the concentration level of N₂ is non-monotonic, concerning its effect on density-driven convection. This non-monotonicity is considered to be a macroscopic manifestation of the difference in diffusion coefficients and is more pronounced in the case of the lighter impurity, H₂S. Raad et al. [243] found a slight barrier to CO₂ dissolution in brine for a H₂S impurity concentration below 30 mol%, as evidenced by an insignificant delay in convective onset time. However, a significant reduction in onset time occurred at 52 mol% H₂S. More extensive studies have shown that H₂S impurity might cause different CO₂ convective mixing dynamics depending on its concentration [233,242,244,245,246].

Even if the effect on CO₂ dissolution is not significant at some concentration, the volume of impurities will reduce CO₂ sequestration efficiency. Yu et al. [228] showed that 10 mol% N₂ reduced CO₂ sequestration efficiency by at least 32%, with a consequent reduction in the economics of the CO₂ sequestration project. Wei et al. [247] similarly showed that CO₂ injection accompanied by N₂ would reduce its sequestration effectiveness in saline aquifers.

It is also noted that the preferential dissolution of CO₂ compared to N₂ in brine would result in chromatographic partitioning at the fluid flow front [248,249,250], which was a consequence of the difference in solubility and would result in gas mixtures with different compositions exhibiting different characteristics in a saline aquifer. Numerical simulations by Wei et al. [247] showed that the presence of N₂ would enhance the migration rate and saturation of the CO₂-N₂ gas mixture. Li et al. [251] further showed that, as the concentration of N₂ impurity increased, the mixture migrated laterally over longer distances and tended to accumulate below the caprock. These phenomena were caused by an enhanced buoyancy effect and resulted in an increase in CO₂ solubility as the contact area between CO₂ and brine increased. This would obviously enhance density-driven convection. However, the effect was not significant in the case of co-injection with H₂S impurity.

In addition, Darvish et al. [252] and Li and Jiang [253] showed that the preferential solubility of H₂S over CO₂ would result in its breakthrough being delayed. This might also lead to different sequestration results. For example, CO₂ in saline aquifers would be predominantly sequestered in saline aquifers as CaCO₃ [254], while H₂S is in the form of FeS₂. Similarly, Choi et al. [255] noted that the SO₂ impurity was also fixed in the form of FeS₂, and their results for the change in permeability of porous media due to SO₂-induced geochemical reactions might explain the enhancement of CO₂ density-driven convection by SO₂ impurity. Yu et al. [228] found that H₂S and N₂ impurity would increase and decrease CO₂ dissolution efficiency, respectively, due to the presence of chromatographic partitioning phenomena, which would have an impact on density-driven convection, especially in low-temperature aquifers. They also noted that the increase in the CO₂ migration rate due to 10 mol% N₂ impurity caused an increase of up to 25%, which could be reduced by increasing the aquifer temperature, thereby reducing the risk of CO₂ leakage.

4. Conclusions and Future Prospects

This paper reviewed the influencing factors and the current state of research on density-driven convection in saline aquifers. It is clarified that the density-driven convection dominating CO₂ solubility trapping is influenced by several factors. Considering the safety of CO₂ sequestration in saline aquifers, the mechanisms of these factors need to be further investigated for a more comprehensive understanding. Based on this review, the following conclusions and future perspectives are presented:

(1)

The simplification of the single-phase system in a two-dimensional ideal rectangular porous medium will lead to an incorrect estimate of the CO₂ convective onset time and flux. The two-phase system additionally considers the capillary transition zone to correct this misestimate. Density change is the main key to density-driven convection and is controlled linearly by CO₂ concentration. The geothermal gradient prevalent in the saline aquifer will also trigger a density change, which is described by introducing an energy equation into modeling. However, the effect of this additional convection will not be significant. The viscosity difference of fluids can trigger similar transversal convection early in CO₂ injection and should be discussed in the context of studies related to structural trapping, as its role is insignificant compared to density difference after CO₂ dissolution has generally occurred. The background flow can be introduced by a fixed velocity boundary condition that would significantly delay the onset of density-driven convection. To fully approximate the real CO₂ saline aquifer sequestration situation, future studies should consider and model the modeling simplifications comprehensively and appropriately.

(2)

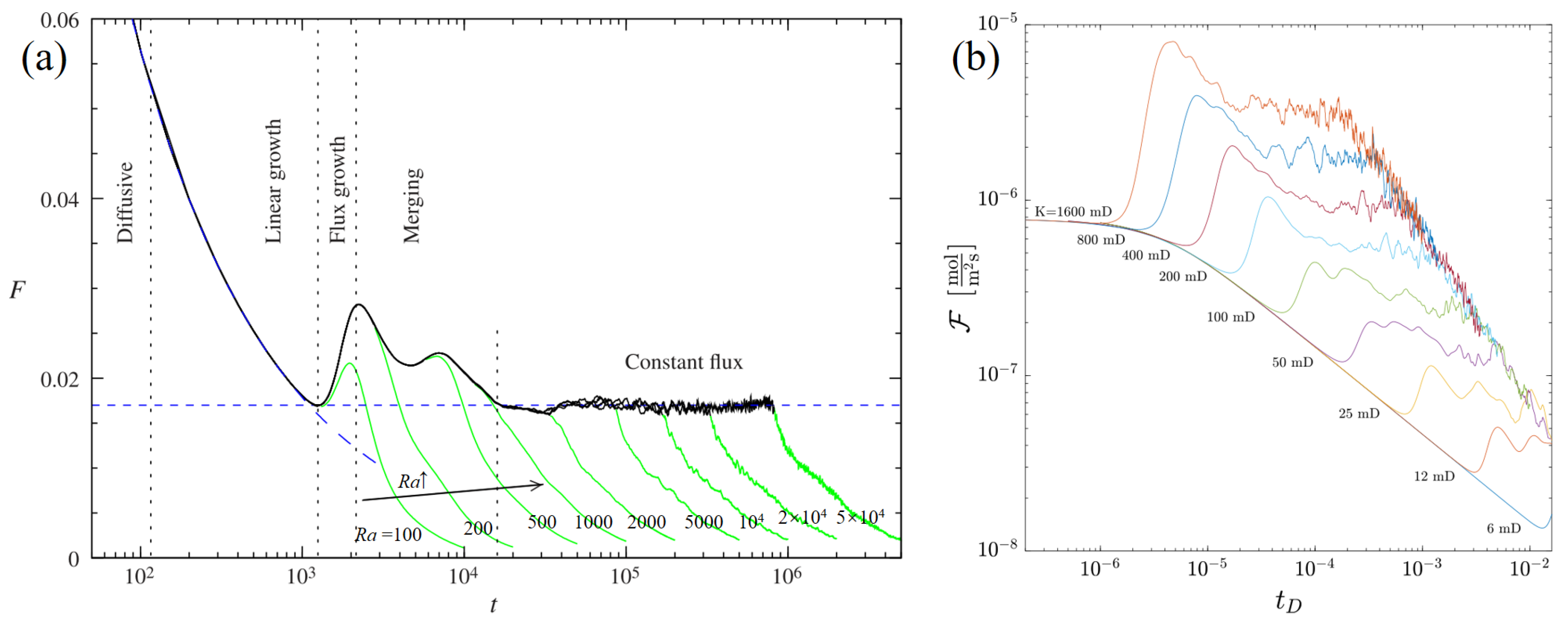
Permeability is an important property of aquifers and determines the magnitude of Ra that controls convection. An increase in permeability advances the onset of convection, which often implies a larger CO₂ dissolution flux with a larger number and wavelength of convective fingers. This leads to more CO₂ dissolution and is positive for CO₂ solubility trapping in saline aquifers. The heterogeneity of the saline aquifer is taken into account through several permeability representations, and similar to the findings in homogeneous porous media, fluctuating and enhancing permeability in either direction in heterogeneous saline aquifers promotes CO₂ density-driven convection. It is important to note that incomplete consideration of the sensitivity analysis may produce a biased perception of the permeability anisotropy impact on CO₂ density-driven convection. This requires further research to gain insight into the heterogeneity of saline aquifers since it is frequently observed in CO₂ sequestration projects.

(3)

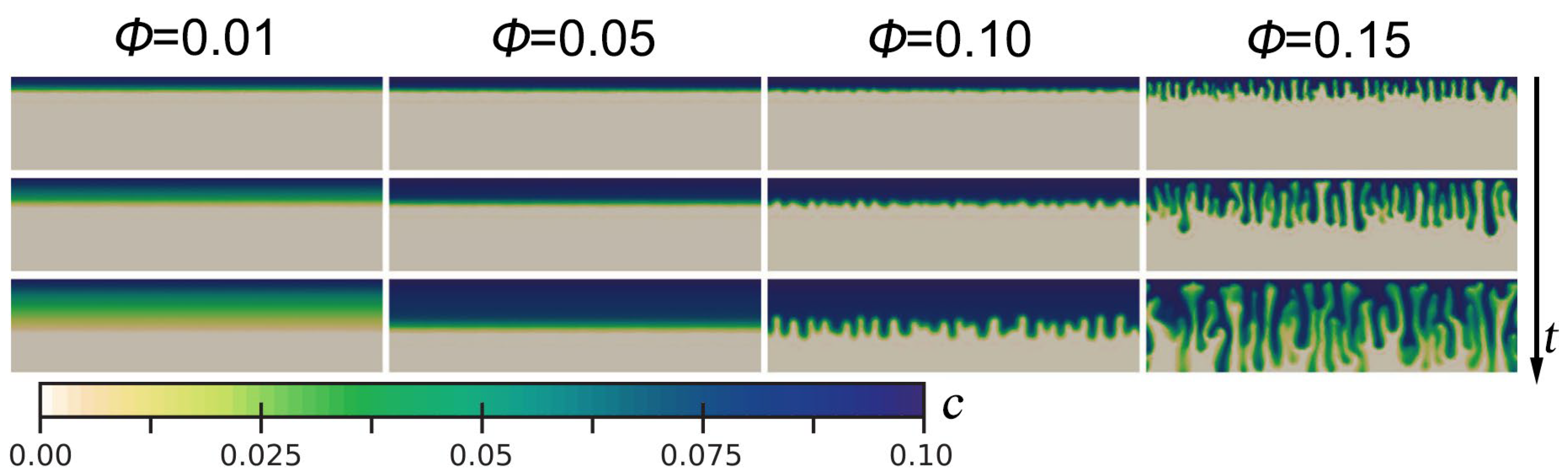
The porosity significantly influences the density-driven convection by controlling the pattern of CO₂-rich brine front in saline aquifers. For low porosity, CO₂-rich brine maintained the form of a stable boundary layer that slowly diffused downward. Furthermore, the convective fingering is clearly observed in the saline aquifer with high porosity. Implying a thinner diffusion boundary layer, an earlier onset of convection, and a smaller Sh. This is explained as an effect caused by the change in the effective diffusion coefficient. Meanwhile, the effect caused by varying the permeability is insignificant. The porosity heterogeneity is introduced into the numerical model as fluctuation, leading to instability and correlating with convection onset time. As the porosity fluctuation increases, the convection onset time decreases and is more significant than the permeability fluctuation. An optimal porosity fluctuation that minimizes the convection onset time exists. This suggests that even small porosity fluctuations are sufficient to trigger nonlinear convection. Future research and CO₂ sequestration projects should take this factor fully into account.

(4)

In a single fracture system, the greater inclination angle of the fracture is equivalent to providing a preferential channel for solute transport, which facilitates the solubility trapping process. In the more complex multi-fracture systems, the situation can be more complicated. In general, regarding the concerned results, the impact of fractures on convection should be further emphasized, which will be more relevant to the practical applications of CO₂ solubility trapping. In stratified heterogeneous formations, the arrangement of layers with different permeability for convection has been extensively studied, and although there are relevant findings at each scale, from pore to the field, the corresponding up/downscale studies are still relatively rare, but they are overwhelmingly important for the practical application of CO₂ sequestration. Different lithologies are associated with the stratification of aquifers, and this affects the structural geometry and aquifer properties. The quantity and relative spacing of internal laminae or boundary surfaces that are horizontally or obliquely oriented, which impede fluid flow, account for a major portion of permeability variances in facies. The Permian White Rim Sandstone is the best reservoir for CO₂ injection, with great permeability and porosity. The composition of the rocks, sedimentary diagnostic eolian features, thickness and depth of the layers, etc., should all be considered to judge the applicability of geological storage. Transmissibility plays an important role in the stratification and subsequent fault of aquifers. A saline aquifer with optimal transmissibility may not be the best option for CO₂ sequestration safety. Other risks in CO₂ sequestration projects still need to be assessed to find the best solution.

(5)

The slope of caprock is prevalent in saline aquifers and is usually considered to be the top boundary tilt in the model. The slope of caprock will induce massive transversal movement, merging, and coarsening of convective fingering, which implies an enhancement of density-driven convection. However, the increasing slope will lead to an excessive migration of CO₂, which increases the risk of contamination from CO₂ exposure to freshwater. More reservoir parameters and chemical reactions associated with the caprock should be considered in further studies to achieve a more realistic calculation of optimal slope that can guide the site selection for CO₂ sequestration projects.

(6)

Some contradictory conclusions are reached on the effect of hydraulic dispersion, and the deviations may stem from the non-independence of the dimensionless number and can be resolved by specific dimensionless methods. It shows that an increase in the dispersion ratio accelerates the onset of density-driven convection. Nevertheless, it is important to further explore the practical effects of hydraulic dispersion anisotropy in conjunction with experiments to gain insight and a consistent conclusion. Density-driven convection becomes more complex when both background flow and diffusion are considered, and further research is needed to provide as much guidance as possible for CO₂ sequestration projects.

(7)

The increase in pressure and decrease in temperature or salinity in the aquifer will promote the dissolution of CO₂ in brine, which accelerates the development of density-driven convection. It is important to note that the positive impact of increased pressure on CO₂ solubility trapping comes with a burden on caprock, particularly in a naturally fractured one. The ability of saline aquifers to sequester CO₂ is limited by this risk, and future studies should consider the interaction between these parameters to maximize CO₂ sequestration with acceptable risk. The brine properties also significantly influence the dissolution of CO₂. A low pH and high concentration of divalent ions in brine will inhibit the dissolution of CO₂, and, conversely, an aquifer composed of carbonate rocks will accelerate this process. Moreover, for reasons of economic efficiency and environmental protection, CO₂ injection into the saline aquifer is frequently accompanied by impurities. It is generally accepted that SO₂ has a greater solubility density, and this will enhance density-driven convection, while N₂ and H₂S show the opposite impact. However, the actual effect of impurities on density-driven convection may be non-monotonic, depending on the molar percentage of impurities in brine. Chromatographic partitioning should also be noted, as it accelerates density-driven convection in some cases. For reasons of economy and safety, a more specific study of these effects is awaited, as there is an optimum impurity ratio to enhance density-driven convection. These saline aquifer parameters also significantly affect CO₂ structural and mineral trapping, thus revealing that the actual saline aquifer sequestration of CO₂ is complex and involves multiple trapping mechanisms. For an accurate assessment of the ability of saline aquifers to sequester CO₂, other trapping mechanisms and their coupling with solubility trapping should be taken into account.

Overall, for CO₂ saline aquifer sequestration projects, permeability is the first concern, as it almost determines the CO₂ sequestration capacity of the saline aquifer. A deep saline aquifer is also an ideal site, which directly represents a high sequestration capacity, due to the high volume, low temperature, and high temperature gradient. However, a highly heterogeneous saline aquifer is not the best choice, it triggers CO₂ migration without causing additional sequestration capacity. Fractures, stratification, slope, and background flow also lead to additional CO₂ migration, and formation pressure may even result in sequestration failure, but these factors contribute to sequestration efficiency to a certain degree. Similarly, both the porosity, hydrodynamic dispersion, and viscosity cause positive and negative effects simultaneously. Depending on the type and content, impurities and lithology also lead to non-monotonic effects.

Further research on the methods of coupling, monitoring, and regulating of various factors will allow for a better estimation of the saline aquifer’s sequestration capacity. Moreover, it is possible to better understand and control the state of CO₂ in saline aquifers. This is beneficial in providing the optimal option for siting and operation of CO₂ sequestration projects.