Comparison of Different Dielectric Models to Estimate Penetration Depth of L- and S-Band SAR Signals into the Ground Surface
Abstract
1. Introduction
2. Theoretical Background and Methodology
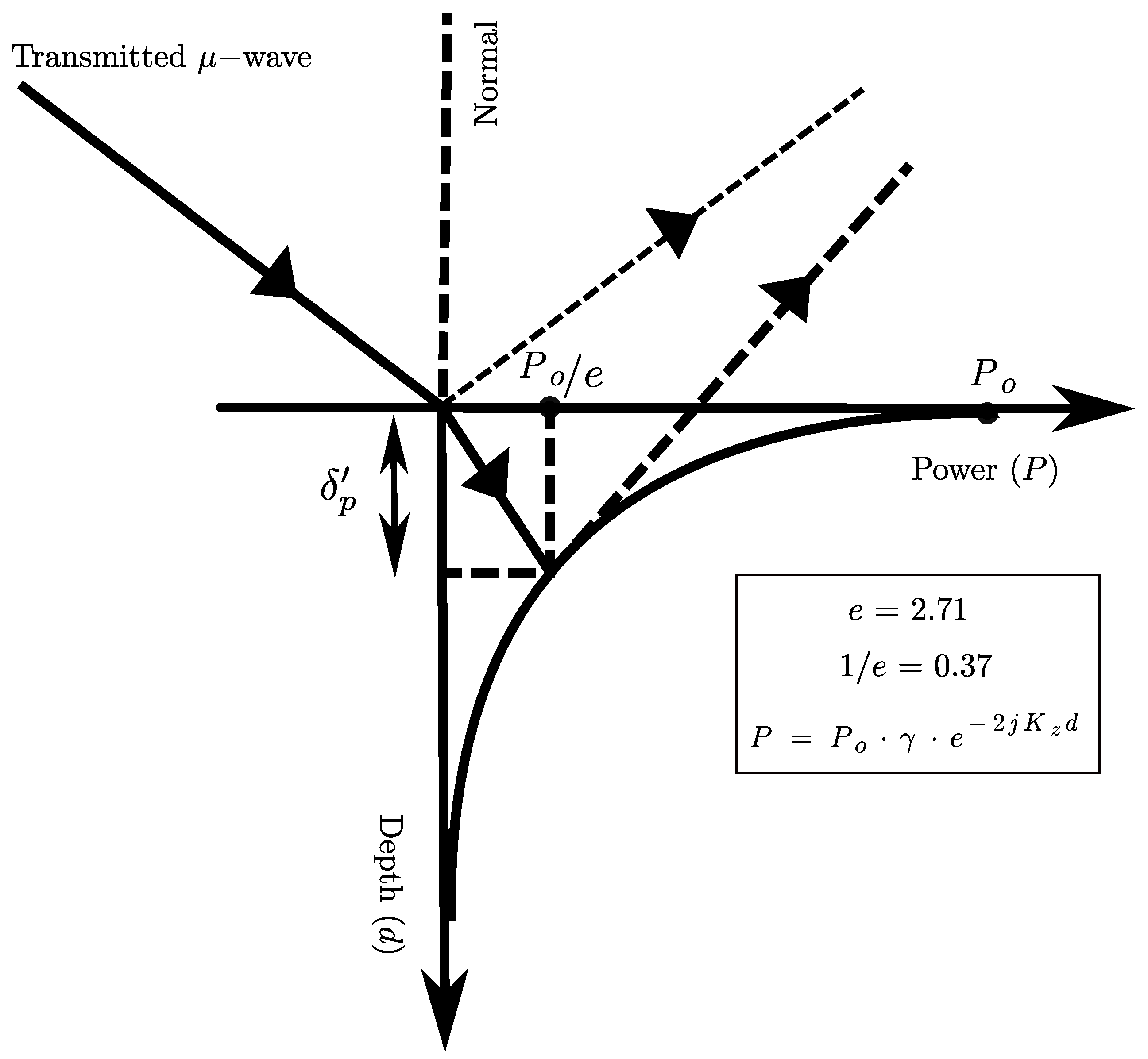
2.1. Penetration Depth and Its Dependency
2.2. Dobson Empirical Model
2.3. Hallikainen Empirical Model
2.4. Dobson Semi-Empirical Model
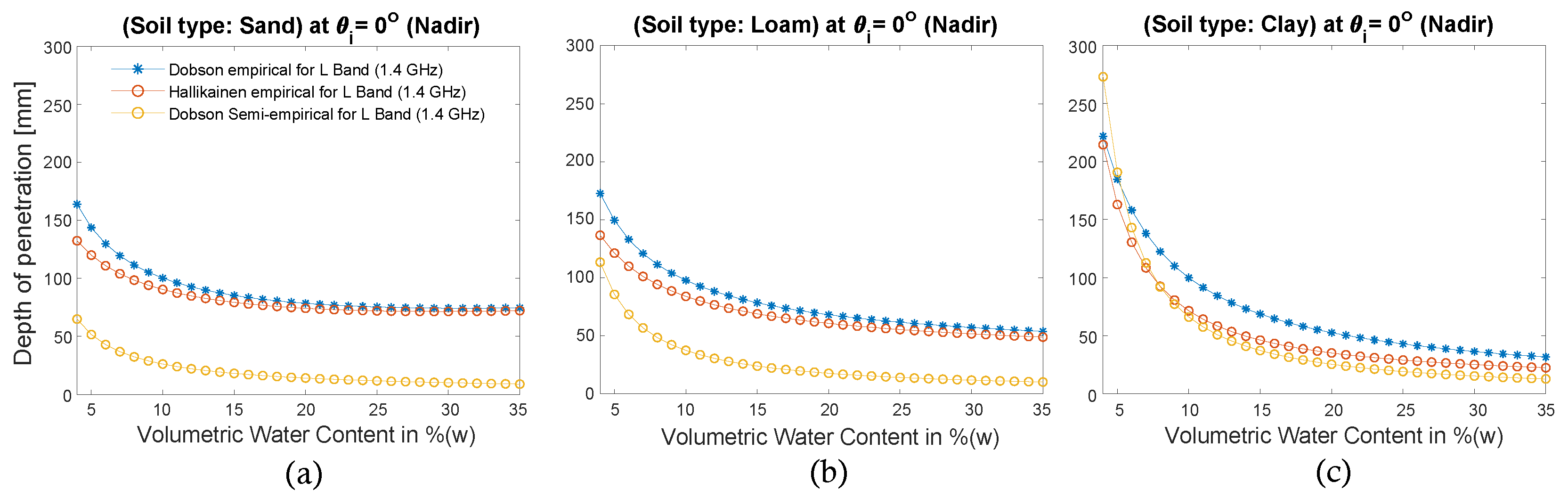
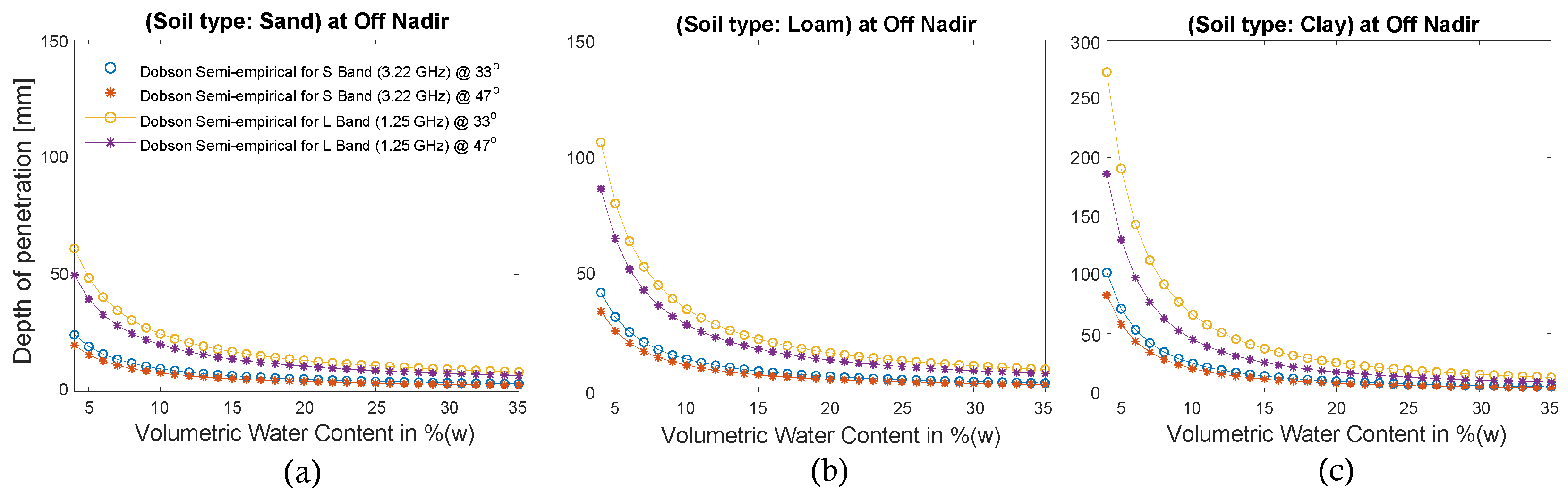
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- El Hajj, M.; Baghdadi, N.; Bazzi, H.; Zribi, M. Penetration analysis of SAR signals in the C and L bands for wheat, maize, and grasslands. Remote Sens. 2018, 11, 31. [Google Scholar] [CrossRef]
- Fluhrer, A.; Jagdhuber, T.; Tabatabaeenejad, A.; Alemohammad, H.; Montzka, C.; Friedl, P.; Forootan, E.; Kunstmann, H. Remote Sensing of Complex Permittivity and Penetration Depth of Soils Using P-Band SAR Polarimetry. Remote Sens. 2022, 14, 2755. [Google Scholar] [CrossRef]
- Fluhrer, A.; Jagdhuher, T.; Tabatabaeenejad, A.; Alemohammad, H.; Montzka, C.; Schumacher, M.; Kunstmann, H. Complex Permittivity and Penetration Depth Estimation from Airborne P-Band SAR Data Applying a Hybrid Decomposition Method. In Proceedings of the 2021 IEEE International Geoscience and Remote Sensing Symposium IGARSS, Brussels, Belgium, 11–16 July 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 5884–5887. [Google Scholar]
- Dobson, M.C.; Kouyate, F.; Ulaby, F.T. A reexamination of soil textural effects on microwave emission and backscattering. IEEE Trans. Geosci. Remote Sens. 1984, GE-22, 530–536. [Google Scholar] [CrossRef]
- Hallikainen, M.T.; Ulaby, F.T.; Dobson, M.C.; El-Rayes, M.A.; Wu, L.K. Microwave dielectric behavior of wet soil-part 1: Empirical models and experimental observations. IEEE Trans. Geosci. Remote Sens. 1985, GE-23, 25–34. [Google Scholar] [CrossRef]
- Singh, A.; Meena, G.K.; Kumar, S.; Gaurav, K. Analysis of the effect of incidence angle and moisture content on the penetration depth of L- and S-band SAR signals into the ground surface. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2018, IV-5, 197–202. [Google Scholar] [CrossRef]
- Singh, A.; Meena, G.K.; Kumar, S.; Gaurav, K. Evaluation of the penetration depth of L-and S-band (NISAR mission) microwave SAR signals into ground. In Proceedings of the 2019 URSI Asia-Pacific Radio Science Conference (AP-RASC), New Delhi, India, 9–15 March 2019; IEEE: Piscataway, NJ, USA, 2019; p. 1. [Google Scholar]
- Baghdadi, N.; Zribi, M. Evaluation of radar backscatter models IEM, OH and Dubois using experimental observations. Int. J. Remote Sens. 2006, 27, 3831–3852. [Google Scholar] [CrossRef]
- Thoma, D.P.; Moran, M.S.; Bryant, R.; Rahman, M.; Holifield-Collins, C.D.; Skirvin, S.; Sano, E.E.; Slocum, K. Comparison of four models to determine surface soil moisture from C-band radar imagery in a sparsely vegetated semiarid landscape. Water Resour. Res. 2006, 42, W01418. [Google Scholar] [CrossRef]
- Baghdadi, N.; King, C.; Chanzy, A.; Wigneron, J.P. An empirical calibration of the integral equation model based on SAR data, soil moisture and surface roughness measurement over bare soils. Int. J. Remote Sens. 2002, 23, 4325–4340. [Google Scholar] [CrossRef]
- Dobson, M.C.; Ulaby, F.T.; Hallikainen, M.T.; El-rayes, M.A. Microwave Dielectric Behavior of Wet Soil-Part II: Dielectric Mixing Models. IEEE Trans. Geosci. Remote Sens. 1985, GE-23, 35–46. [Google Scholar] [CrossRef]
- Peplinski, N.R.; Ulaby, F.T.; Dobson, M.C. Dielectric properties of soils in the 0.3–1.3-GHz range. IEEE Trans. Geosci. Remote Sens. 1995, 33, 803–807. [Google Scholar] [CrossRef]
- Rosen, P.A.; Kumar, R. NASA-ISRO SAR (NISAR) Mission Status. In Proceedings of the 2021 IEEE Radar Conference (RadarConf21), Atlanta, GA, USA, 7–14 May 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1–6. [Google Scholar]
- Falk, A.; Gerald, B.; Falk, A.; Gerald, B.; Adrian, B.; Sean, B.; Susan, C.; Manab, C.; Bruce, C.; Anup, D.; et al. NASA-ISRO SAR ( NISAR ) Mission Science Users’ Handbook; Jet Propulsion Laboratory, California Institute of Technology: California, CA, USA, 2018; pp. 1–350. [Google Scholar]
- Narvekar, P.S.; Entekhabi, D.; Kim, S.; Njoku, E.G. Soil Moisture Retrieval Using L-Band Radar Observations. IEEE Trans. Geosci. Remote Sens. 2015, 53, 3492–3506. [Google Scholar] [CrossRef]
- Njoku, E.G.; Entekhabi, D. Passive microwave remote sensing of soil moisture. J. Hydrol. 1996, 184, 101–129. [Google Scholar] [CrossRef]
- Engman, E.T. Applications of microwave remote sensing of soil moisture for water resources and agriculture. Remote Sens. Environ. 1991, 35, 213–226. [Google Scholar] [CrossRef]
- Singh, A.; Gaurav, K.; Meena, G.K.; Kumar, S. Estimation of soil moisture applying modified dubois model to Sentinel-1; a regional study from central India. Remote Sens. 2020, 12, 2266. [Google Scholar] [CrossRef]
- Li, B.; Good, S.P. Information-based uncertainty decomposition in dual-channel microwave remote sensing of soil moisture. Hydrol. Earth Syst. Sci. 2021, 25, 5029–5045. [Google Scholar] [CrossRef]
- Park, J.; Bindlish, R.; Bringer, A.; Horton, D.; Johnson, J.T. Soil Moisture Retrieval using a Time-Series Ratio Algorithm for the Nisar Mission. In Proceedings of the 2021 IEEE International Geoscience and Remote Sensing Symposium IGARSS, Brussels, Belgium, 11–16 July 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 5873–5876. [Google Scholar]
- Rao, K.S.; Chandra, G.; Narasimha Rao, P.V. Study on penetration depth and its dependence on frequency, soil moisture, texture and temperature in the context of microwave remote sensing. J. Indian Soc. Remote Sens. 1988, 16, 7–19. [Google Scholar] [CrossRef]
- Ulaby, F.T.; Moore, R.K.; Fung, A.K. Microwave Remote Sensing-Active and Passive-Volume I-Microwave Remote Sensing Fundamentals and Radiometry (v. 1). In Radar Remote Sensing and Surface Scattering and Emission Theory; NASA Technical Report; Kansas University: Lawrence, KS, USA, 1981; pp. 848–902. [Google Scholar]
- Singh, A.; Gaurav, K.; Rai, A.K.; Beg, Z. Machine learning to estimate surface roughness from satellite images. Remote Sens. 2021, 13, 3794. [Google Scholar] [CrossRef]
- Nolan, M.; Fatland, D.R. Penetration depth as a DInSAR observable and proxy for soil moisture. IEEE Trans. Geosci. Remote Sens. 2003, 41, 532–537. [Google Scholar] [CrossRef]
- Kamal, H. Amera, Amal Elsharkawib, A.S.H. Revising wetted soil volume under trickle source for irrigation scheduling. Misr J. Agric. Eng. 2010, 27, 1162–1183. [Google Scholar]
- Lacava, T.; Matgen, P.; Brocca, L.; Bittelli, M.; Pergola, N.; Moramarco, T.; Tramutoli, V. A First Assessment of the SMOS Soil Moisture Product With In Situ and Modeled Data in Italy and Luxembourg. IEEE Trans. Geosci. Remote Sens. 2012, 50, 1612–1622. [Google Scholar] [CrossRef]
- Owe, M.; Van de Griend, A.A. Comparison of soil moisture penetration depths for several bare soils at two microwave frequencies and implications for remote sensing. Water Resour. Res. 1998, 34, 2319–2327. [Google Scholar] [CrossRef]
- Quan, C.; Jiuli, L.; Zhihua, T.; Jiangyuan, Z.; Yan, L. Study on the relationship between soil moisture and its dielectric constant obtained by space-borne microwave radiometers and scatterometers. IOP Conf. Ser. Earth Environ. Sci. 2014, 17, 012143. [Google Scholar] [CrossRef]
| Soil | Soil Proportion | Bulk Density | ||
|---|---|---|---|---|
| Type | Sand | Silt | Clay | (g/cm) |
| Sand | 86.7 | 7.8 | 5.5 | 1.57 |
| Loam | 61.3 | 23.1 | 15.6 | 1.42 |
| Clay | 17.79 | 31.14 | 51.07 | 1.28 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Singh, A.; Niranjannaik, M.; Kumar, S.; Gaurav, K. Comparison of Different Dielectric Models to Estimate Penetration Depth of L- and S-Band SAR Signals into the Ground Surface. Geographies 2022, 2, 734-742. https://doi.org/10.3390/geographies2040045
Singh A, Niranjannaik M, Kumar S, Gaurav K. Comparison of Different Dielectric Models to Estimate Penetration Depth of L- and S-Band SAR Signals into the Ground Surface. Geographies. 2022; 2(4):734-742. https://doi.org/10.3390/geographies2040045
Chicago/Turabian StyleSingh, Abhilash, M. Niranjannaik, Shashi Kumar, and Kumar Gaurav. 2022. "Comparison of Different Dielectric Models to Estimate Penetration Depth of L- and S-Band SAR Signals into the Ground Surface" Geographies 2, no. 4: 734-742. https://doi.org/10.3390/geographies2040045
APA StyleSingh, A., Niranjannaik, M., Kumar, S., & Gaurav, K. (2022). Comparison of Different Dielectric Models to Estimate Penetration Depth of L- and S-Band SAR Signals into the Ground Surface. Geographies, 2(4), 734-742. https://doi.org/10.3390/geographies2040045









