1. Introduction
Many studies have shown that extreme precipitation events are increasing in frequency and intensity at both global and continental scales [
1,
2,
3,
4,
5,
6,
7]. The increase in the temperature of the planet’s surface and the consequent increase in the rate of evaporation and addition of water vapor in the atmosphere is one of the main causes of the observed increase in extreme precipitation events. The increase in precipitation in a given location impacts both the climate in that region and the ability to provide adequate climate services. The increase in precipitation thresholds that trigger disasters related to this hazard are crucial to polices related to disaster risk reduction and disaster risk management.
Particularly in urban regions, the increase in surface temperature is due to both local and global factors. Urbanization changes the land cover and increases pollution emissions, which in turn changes the water cycle. Climate change leads to variations in the frequency, intensity, spatial extent, duration, and timing of weather and climate extremes [
8]. Observations and modeling [
9,
10,
11] indicate that urban convectional rainfall can be triggered by the surface roughness of tall buildings, which enhances low-level moisture convergence [
12].
There is no doubt that understanding the drivers of extreme urban precipitation is crucial to building more resilient cities. However, from the point of view of its impacts, it does not matter what the cause of extreme events is. Seneviratne et al. [
13] emphasized that many weather and climate extremes result from natural climate variability, and even if there were no anthropogenic changes in climate, a wide variety of natural weather and climate extremes would nonetheless occur. In other words, for decision makers the forecast of extreme events is more important than the explanation of their cause.
Projection of extreme precipitation events using climate models is challenging due to notoriously noisy data with large scatter that are lacking in apparent patterns or trends. On the other hand, it is first necessary to answer the question of what is meant by an extreme event. Generally speaking, it is a time and place in which weather, climate, or environmental conditions rank above a threshold value. Although the threshold is subjective, a consensus about the precise definition of extreme weather events is lacking.
As a consequence, an alternative framework to support decision-makers in mitigating the risks of future urban disasters must rely on the analysis of trend detection of extreme events in time series. For instance, according to Westra et al. [
14], annual maximum daily precipitation data are frequently used as input for assessments of flood risk.
Many of the world’s largest cities live with structural problems and vulnerable economic assets. The same is true of millions of residents of these cities, most of them poor and living in areas susceptible to flooding and landslides. One of these cities is the capital of São Paulo state in Brazil and its surrounding area.
The last decades of the 19th century marked the beginning of the real estate boom in São Paulo, which led to an expansion in its urban area, superior to the demographic growth. The MRSP expanded from 170 km
2 to more than 8000 km² from 1930 to 2020 [
15]. Nowadays the city has approximately the same dimensions as Lebanon or Jamaica, while its density has fallen from supposed colonial levels of around 150 inhab/ha to the range of 80 inhab/ha. It is the largest metropolitan region in Brazil, with approximately 21.5 million inhabitants, and one of the ten most populous metropolitan regions in the world. Every summer it suffers the effects of flooding caused by extreme precipitation. In the last twenty years, more than 1500 floods events have been recorded in the MRSP due to extreme rainfall events [
16].
Changes in rainfall extremes in the MRSP have been have been studied by several authors [
17,
18,
19,
20,
21]. Nobre et al. [
22], documented an annual rainfall increase of 395 mm from 1936 to 2005 in the MRSP, while Silva Dias et al. [
15] reported this to be 425 mm from 1933 to 2010. These authors noted an increase in daily rainfall thresholds, and posited that total precipitation from more intense rainfall events may have contributed to this, with the possibility of long dry periods between days with intense rain. Based on the same dataset used in these studies, Marengo et al. [
8] reported an increase in total and heavy precipitation and a decrease in light precipitation.
This study aims use a simple methodology to identify the increase in daily precipitation in an urban area, specifically, the increase in the daily precipitation for different thresholds in the Metropolitan Region of São Paulo (MRSP). The study is not limited to verifying that extreme precipitation events have been occurring in the last nine decades in São Paulo; rather, it shows the rate of increase in daily precipitation for different thresholds, starting from 50 mm and continuing up to 90 mm. Precipitation thresholds above 100 mm, although they are observed (mainly from the 1980s), are not enough for a statistical analysis. Based on the correlation between rainfall and hydrometeorological disaster in the MRSP as presented by Marengo et al. [
23], we selected a daily precipitation of 50 mm as the lowest threshold for this study.
This paper is organized as follows. Section two contains a description of the dataset used in this study. The methodology is described in section three, followed by the results in section four. Discussions and conclusions are provided in section five.
4. Results
In order to analyze daily total precipitations trends in São Paulo for the last nine decades, we counted the number of days with daily precipitation for five thresholds.
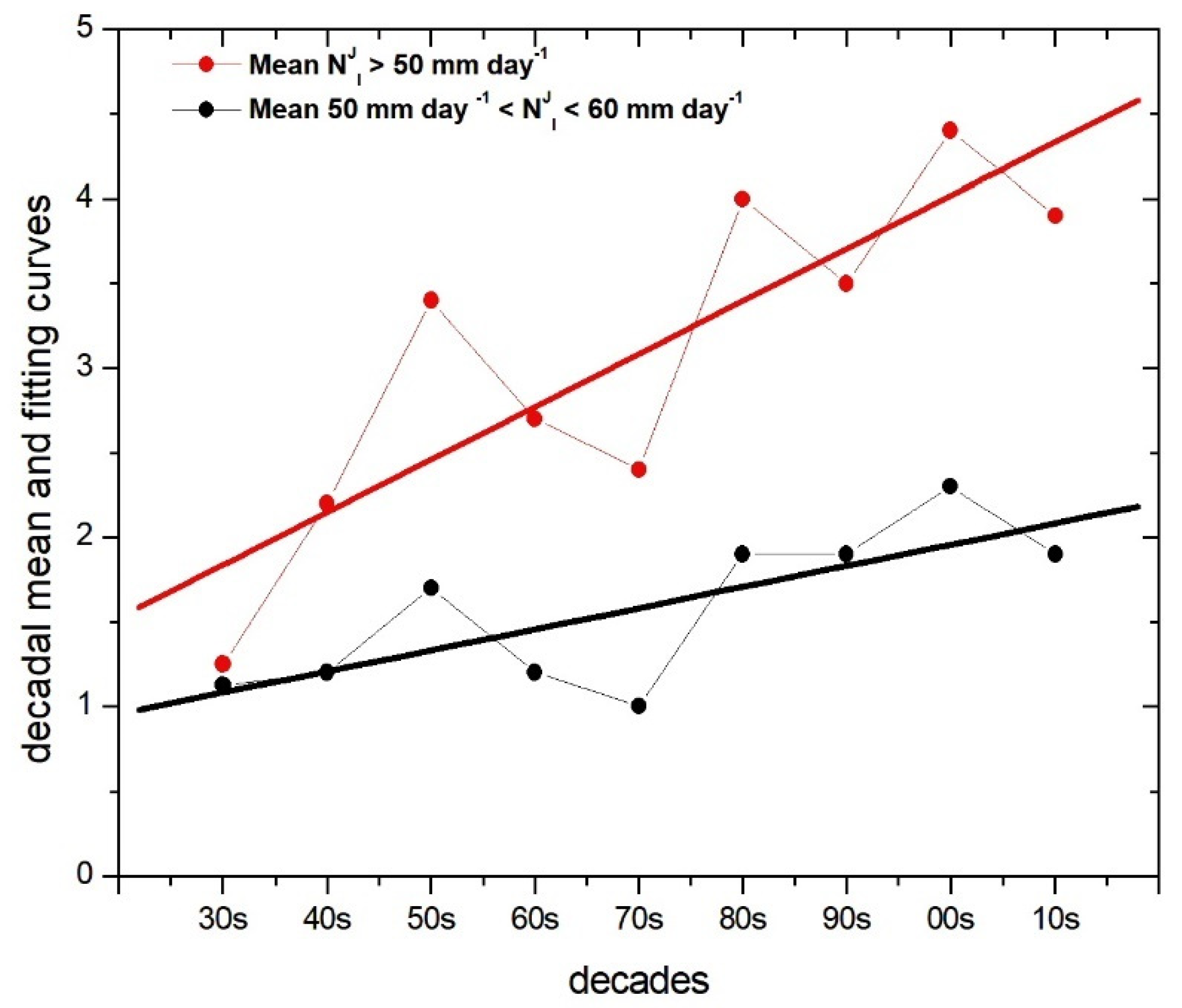
Figure 1A shows the decadal average of days with daily precipitation higher than 50, 60, 70, 80, and 90 mm. Each threshold is represented by a different color.
Figure 1B has, as a reference, the fitting curves for each threshold shown in
Figure 1A. Notably, the bias in these averages is positive for all curves but decreases with increasing threshold, i.e., the bias in
, where the bars indicate decadal average values.
The angular coefficient for the fitting curves is 0.31, 0.18, 0.14, 0.09, and 0.08 for
and
, respectively. The physical interpretation of these coefficients can be elucidated considering the ratio of the difference between the mean values from 2010 to 1930 divided by the number of decades. For the threshold of 50 mm, this ratio is approximately 0.3, very similar to the angular coefficient of the fitting curve. In other words, in the nine decades between the 1930s and 2010s, the increase in the number of days with precipitation greater than 50 mm was approximately 200%. This threshold includes the other four thresholds and, as a consequence, the angular coefficient for the other ranges decreases. A reasonable justification for the adoption of the above methodology is that it allows for analyzing changes in the number of days of precipitation over any desired range. For example, the previous result shows an increase of 200% in the number of days with rain above 50 mm in the last nine decades. However, we may want to know the contribution to this threshold of days with rain in the range of 50 and 60 mm as well.
Figure 2 shows
and
as well as their fitting curves. The angular coefficient of
is 0.12. This means that for approximately one third of the 200% increase in the number of days with precipitation higher than 50 mm, the precipitation was between 50 and 60 mm.
The previous results show that the decadal average of daily precipitation increased over the last ninety years in the MRSP. In other words, these results show a positive linear trend in the number of days with precipitation above multiple thresholds when considering decadal periods. We then carried out a detailed examination to analyze the increase in daily precipitation on an annual basis.
From the definition of
, a new time series can be constructed by the following equation:
Here,
is the total number of days and
j is a threshold from 1933 until year
i.
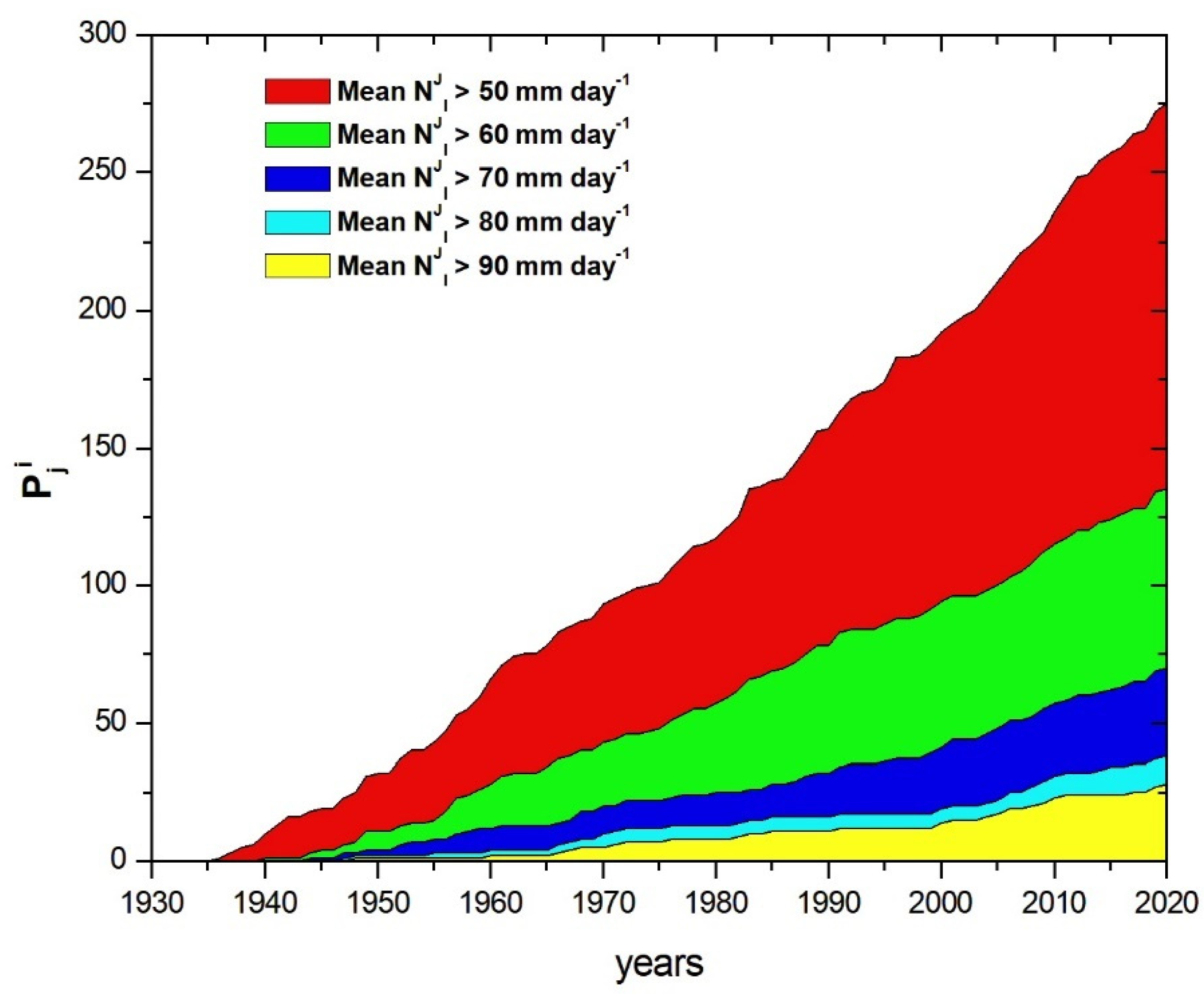
Figure 3 below displays five time series for each threshold used above. For each threshold adopted, the same color is used as shown in
Figure 1.
The picture above, representing the annual cumulative days, can be used for visual identification of the trend of for any j in any period. In the case of RMSP, the figure above illustrates this trend between 1933 and 2020 for five thresholds. It can be seen in this figure that the area between the two curves increases over the period, being greater for lower thresholds. This figure shows in a clear way the appearance of areas that correspond to the higher thresholds in the last decades (cyan and yellow). However, due to the criteria used to construct the time series, the increase in the area between the two curves does not represent a positive bias in the annual number of days with precipitation above the corresponding threshold.
If the values in the annual
time series are strictly equal, then the increment in the series
is constant, which means that the graphic representation of this time series is a straight line and, as a consequence, the area below the time series increases with the increase of the year. The positive bias exists only if the rate of increase in the area is positive. In other words, the derivative of the
function is the rate of increase or decrease of the annual number of days with daily precipitation above
millimeters. To estimate the rate of increase of days with precipitation for the six thresholds, we can search for the best fitting curve for the
time series.
Figure 4 displays, as an example, the
and linear and second-order polynomial fitting curves. The statistical parameters
R2 (R square) and
σ (standard deviation) indicate that the better representation for the corresponding data series is the second-order polynomial.
We search for the best curve fitting for the five thresholds used previously, utilizing the same procedure.
Figure 5 below displays the best fitting function for the data series
, which is
, a second-order polynomial function.
Table 1 below shows the coefficient of the second-order term as well as the statistical parameter (
R2), the measure that determines the proportion of variance in the dependent variable that can be explained by the independent variable.
The statistical result shows how well the regression model fits the data set; it can be seen that the derivative of all
is higher than zero for all thresholds. A positive bias exists in the number of days for the five thresholds analysed. Notably, as the fitting curve is a second-order polynomial, its derivative is of the first order, and as a consequence the trend is linear. The decadal average shows the same behavior. The derivative indicates how many years on average needed to pass in order to increase one day with precipitation above a threshold, and may be used to predict future scenarios. For instance, the derivative of
is proportional to 0.02676. This means that the number of rainy days above 50 mm doubles approximately every 50 years. This is in agreement with the previous result when the analysis was decadal (
Figure 1). In the 1940s, each year had approximately two days with precipitation higher than 50 mm. No precipitation higher than 50 mm day
−1 was reported until 1936. Recently, this average is more than four days each year.
We consider the derivative of the as another example, which is proportional to 0.0122. This means that the number of rainy days above 70 mm doubles approximately every 100 years. In the 1940s, approximately one day with precipitation above this threshold was reported every two and a half years. No precipitation higher than 70 mm day−1 was reported until 1944. On the other hand, in only two years of the last ten years were precipitations above this threshold not reported.
Table 2 below illustrates these two examples, showing the days per year with rainfall above 50 and 70 mm for the first ten and last ten years in the IAG/USP time series. In three years of the first decade was no precipitation higher than 50 mm day
−1 noted, and only one year had four days with precipitation above 50 mm. Importantly, of the 16 days with precipitation higher than 50 mm, only one had precipitation above 60 mm (64.2 mm in 1940). In the last ten years of this time series, half had more than five days with precipitation above 50 mm, and of these 39 days with precipitation above 50 mm more than 50% had precipitation above 60 mm. More crucial is the 70 mm threshold. Between 1933 and 1942, no day, and consequently no year, recorded such precipitation. In the period 2011–2020, however, this threshold was reached in eight separate years. In 2016, this threshold was exceeded five times.
The
time series and the associated best fitting can be used, at the annual timescale, to identify the increase in the number of days with thresholds of 80 or 90 mm day
−1, as well as even higher values. In general, it is observed that
where
is the “speed” of the increase of
, or
Notably, the speed of this increase for
and
is of a smaller magnitude to the previous examples shown in
Table 1 and
Table 2. There was no record of daily precipitation higher than 80 mm between 1933 and 1942. Between 2011 and 2020, daily precipitation higher than 80 mm and 90 mm was recorded on 7 and 5 days, respectively.
According Myher et al. [
5], it is well established that the intensity of extreme precipitation increases more strongly with the average global surface temperature than with the average precipitation, as the latter, on a global scale, is limited by energy constraints. In addition, it is well known [
29,
30] that an overall increasing trend in annual and daily extreme precipitation is occurring, especially in densely populated urban areas. However, the precise relationship between the increase in daily extreme precipitation events and annual precipitation in the MRSP is not fully known. This question is partially answered in Marengo et al. [
23], who showed that the total annual rainfall and the number of days with 20 mm rainfall exhibited a significant increase in the period 1930–2020. Additional details are shown in
Figure 6. The left panel presents the annual precipitation for the same time series used in the previous results. The red line is the linear trend, for which the slope is approximately 5.6. The black line is the average for the entire period (1416 mm), although this value has minor remarkableness. Adopting periods of 30 years, which are standards for climatology, the average rainfall in the RMSP for the periods 1931–1960, 1961–1990, and 1991–2020 was 1238 mm, 1442 mm, and 1555 mm respectively. In other words, the annual climatological precipitation is consistently increasing in the MRSP. The right-hand panel of
Figure 6 is even more illustrative. All annual rainfalls were ordered from highest (2236 in 1983) to lowest (849 in 1933) and the highest and lowest tenth percentiles are displayed in that panel; the red dots are the annual precipitation, while the labels attached to each red dot represent the year of occurrence as well as the number of daily events with precipitation above 50 mm. It is clear that the number of daily extreme events above 50 mm was higher in exactly the year in which precipitation was the highest. The opposite is true as well. In the years of lower total precipitation, the number of days of extreme events were minimal or null. This allows us to conclude, in the same way that Myher et al. [
5] demonstrate, that the total change in extreme amounts of precipitation depends on changes in both intensity and frequency.
5. Discussions and Conclusions
We used high-quality daily precipitation records to investigate changes in the frequency and magnitude of extreme precipitation from 1933–2020 in the Metropolitan Region of São Paulo, Brazil. The dataset was used to construct two databases of time series describing the number of extremes per year (frequency) and for five different thresholds (intensity). The adopted methodology allows analysis for any desired threshold. Changes in the frequency and magnitude for the five extreme daily precipitation thresholds were found by quantifying their average rate of change and the significance based on the slope of fitted trends to the constructed time series. Slopes are expressed as the number of extreme events per decade and extreme events per year. Both analyses indicate substantial positive trends. For instance, on average, the increase in the number of days with daily rainfall above 50, 60, 70, 80, and 90 mm between the 1930s and 2020s was approximately 200%, 80%, 40%, 9%, and 8% respectively. The above averages were estimated from the decadal series constructed from the annual series. A refinement of these results for annual basis was carried out based on fitting procedures. The best fit equation was of the second order, which means that the growth in the number of rainy days with the selected thresholds was at a constant rate.
Extreme daily rainfall totals, i.e., over 50 mm/day, in the MRSP increased noticeably between 1933 and 2020. Extreme daily rainfall totals increased between 1933 and 2020 for all analysed thresholds, being noticeable for daily rainfall exceeding 50, 60, and 70 mm per day. In the 1940s, each year more or less had two days with precipitation higher than 50 mm. Nowadays, this average is more than four days each year. No precipitation higher than 70 mm day−1 was reported until 1944. Contrastingly, between 2011 and 2020, only 2012 and 2016 have not reported such daily precipitation.
We highlight that our analysis and results feature the 1933–2020 period, and we do not claim that the observed trends will continue into the future. These changes may be linked to changes involving urbanization effects, natural climatic variability, or global warming; however, most climate models predict increasing future trends.
Previous studies have shown an increase in total rainfall in São Paulo and that this precipitation was due to an increase in intense precipitation concentrated over a few days [
23]. The same study indicated that heavy rain events occur on fewer days, and are interrupted by more extended periods of dry weather. In addition to confirming part of that previous study, the present study extends further by quantifying the rate of the increase of extreme events; thus, in the future this result can be used as an indicator of the possibility of extreme precipitation events for different thresholds.