A Cellular-Automaton Model for Population-Density and Urban-Extent Dynamics at the Regional Level: The Case of Ukrainian Provinces

Abstract

The efficient modeling of population-density and urban-extent dynamics is a precondition for monitoring urban sprawl and managing the accompanying conflicts. Currently, one of the most promising approaches in this field is cellular automata—spatial models allowing one to anticipate the behavior of unit areas (e.g., evolution or degradation) in response to the influence of their neighborhood. In the present study, the possibility of modeling the population-density and urban-extent dynamics via a cellular automaton with density-specific parameters is tested. Using an adaptive genetic algorithm, three key model parameters (the evolution and degradation thresholds of a cell and its impact upon the neighbors) are optimized to ensure minimal deviation of the model predictions from actual population dynamics data for 24 Ukrainian provinces during three subsequent time windows from 2010–2019. The performance of the obtained optimized models is assessed in terms of the ability to (1) predict population-density classes and (2) discriminate between urban and rural areas. Generally, the obtained optimized models show high performance for both population-density and urban-extent dynamics (with the average Cohen’s Kappa reaching ~0.81 and ~0.91, respectively). Rare cases with poor prediction accuracy usually represent politically and economically unstable Eastern Ukrainian provinces involved in the military conflict since 2014. Statistical analysis of the obtained model parameters reveals significant differences (p < 0.001) in all of them among population-density classes, arguing for the plausibility of the selected density-specific model architecture. Upon exclusion of the above-mentioned Eastern Ukrainian provinces, all model coefficients appear rather stable (p > 0.135) through the three analyzed time windows, indicating the robustness of the model. The ability of the model to discriminate between urban and rural areas depends on the population density threshold. The best correspondence between actual and predicted urban areas emerges upon the 3000 persons/km² population-density threshold. Further improvement of the model seems possible via extending its input beyond the population density data alone, e.g., by accounting for the existing infrastructure and/or natural boundaries—known factors stimulating or inhibiting urban sprawl.

1. Introduction

Recent studies predict that the global urban extent would have increased by 40–67% by 2050, depending on different socioeconomic scenarios [1], and developing economies are likely the main contributors to this trend [2]. Urbanization is often manifested as urban sprawl—a spatial expansion of cities towards neighboring territories, typically non-systematic and poorly controlled (see meta-analysis of the definitions in [3]). Such expansion is driven by population growth and facilitated by an increase in incomes and a decrease in commuting costs [4]. The consequences of urban sprawl are ambiguous. On the one hand, it creates opportunities for higher levels of housing, and on the other hand, urban sprawl sharpens many problems, such as food security, air quality, access to public goods and services, etc. [5]. It may also lead to confrontations between the developmental goals of urban and rural sectors [6]. Concerning the above-mentioned controversies, informed policies are required to manage urban sprawl aiming to prevent fatal market failures [4] and achieve sustainable multisectoral development of regions.

A key task in urban sprawl management is the modeling and anticipation of the population-density and urban-extent dynamics, given that density is a key criterion in urban sprawl definitions [7,8,9]. Today, one of the most promising approaches implies the usage of cellular automata—discrete dynamic models of which the behavior is based on local interactions (reviewed in [10,11,12]). Such a focus on local interactions makes cellular automata a powerful tool for solving spatial-related problems, including that of urban growth. Compared to alternative approaches (e.g., artificial neural networks, reviewed in [13]), cellular-automata models might emerge as more universal, providing flexible configurations with and without the preceding training stage and representing changes in discrete steps, helping researchers not only to make predictions but also to reveal the reasons behind the observed growth patterns [14]. Advanced modifications of cellular automata additionally benefit from extended input information (e.g., geographical, economical, transportation data) and/or complementary techniques (Markov chain stochastic models and artificial neural network reinforcement). The most potent cellular-automata models include SLEUTH [15,16], PURGOM [17], UGBM [18], and FUTURES [19], which prove their high performance for decades.

Yet, despite the undoubted achievements of the previous studies, the usage of cellular automata for modeling the population-density dynamics in developing economies is still limited. Additionally, applying the established well-performing models to other regions may not remain effective, given numerous region-specific factors. In this case, extra resources would be required to rebuild the model architecture. Therefore, it is important to examine the impact of input arguments on the model, minimizing the number of parameters to vary. The aim of the present study is to explore the potential of a relatively simple cellular-automaton model exploiting the population-density data alone. The hypothesis is that the areas with different population densities may differ both in their impact on neighbors and in the response to external impacts, therefore the corresponding model parameters might be considered density-specific. Calibration of the key model parameters (the degradation and evolution thresholds of a cell as well as its impact on neighbors) is performed via an adaptive genetic algorithm using population-density data of 24 Ukrainian provinces during three subsequent time windows spanning 2010–2019. The parameters of the obtained optimized models were tested for their sensitivity to the population density and stability in time. Additionally, the optimized models’ performance was tested with respect to urban areas. For this sake, the levels of population densities were aggregated into two categories—rural and urban—based on alternative population-density thresholds.

2. Materials and Methods

2.1. Study Area and Input Data

The study area represented Ukraine—a developing country in Eastern Europe [20], with a total area of about 600,000 km² and a population of about 41.2 mln as of 1 December 2021 [21]. The country includes 27 administrative units: 24 provinces (also called oblasts), 1 autonomous republic (Crimea), and 2 special-status cities (Kyiv, the capital, and Sevastopol). The analysis was conducted over 24 Ukrainian provinces, with areas varying from ~8000 to ~33,300 km² and populations from ~892,000 to ~4,069,000 persons [22].

For the present study, global population data from the Oak Ridge National Laboratory website [23] were used. These data are a global-coverage raster with each pixel representing the average ambient population in an area of 1 km². In the present analysis, the datasets of 2010, 2013, 2016, and 2019 were used. The data were clipped to the borders of the 24 examined Ukrainian provinces; the shapefile with the regions’ borders was downloaded from the GeoData website [24]. Figure 1 reports the population-density levels of the study area for the year 2019.

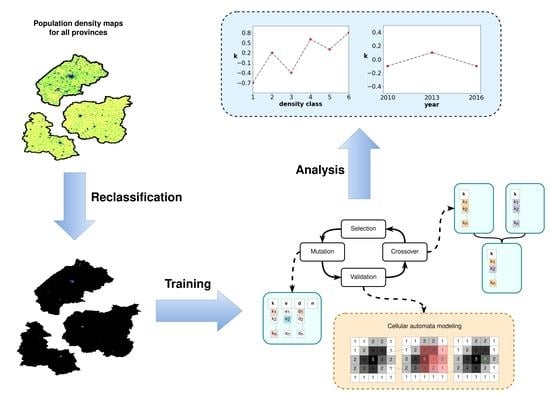
2.2. The Cellular-Automaton Model

In this study, a basic cellular-automaton model was used to simulate the population-density dynamics within each of the 24 Ukrainian provinces for each of the three subsequent time windows (2010–2013, 2013–2016, and 2016–2019). Given the discrete nature of cellular automata, the LandScan-provided population-density values were grouped into six population-density classes: (1) <1000; (2) 1000–2000; (3) 2000–3000; (4) 3000–4000; (5) 4000–5000; and (6) >5000 persons/km². Each pixel of the obtained map was considered a cell of the automaton. The model used reclassified maps of a certain province at a certain period and simulation duration as inputs and generated predicted population-density classes.

At each moment $t$, the state of the cell in position $\left(i,j\right)$ was characterized by its population-density class $c_{i,j}^t$. The state of the cell in the next moment $c_{i,j}^{t+1}$ depended on both the overall impact from neighboring cells $I_{i,j}^t$ and internal peculiarities of the affected (target) cell $e_{i,j}^t$ and $d_{i,j}^t$. Specifically, there exist three possible scenarios: The target cell can either evolve (transform to the higher density class), degrade (transform to the lower density class), or stay intact:

$$c_{i,j}^{t+1}=\{\begin{array}{ccc}{c}_{i,j}^t+1& if& I_{i,j}^t>e_{i,j}^t\\ c_{i,j}^t& if& d_{i,j}^t<I_{i,j}^t\le e_{i,j}^t\\ c_{i,j}^t-1& if& I_{i,j}^t\le d_{i,j}^t\end{array}$$

(1)

Thus, parameters $e_{i,j}^t$ and $d_{i,j}^t$ can be viewed as thresholds for the cell’s class evolution and degradation, respectively. The overall impact of the neighboring cells $I_{i,j}^t$ was calculated as the weighted average of impacts $k$ of all cells from the 3 × 3 neighborhood (larger neighborhoods were previously reported to cause a decrease in accuracy [25]) of the target cell:

$$I_{i,j}^t=\frac{{{\displaystyle \sum }}_{x=-1}^1{{\displaystyle \sum }}_{y=-1}^1{W}_{i+x,j+y}\cdot k_{i+x,j+y}^t}{{{\displaystyle \sum }}_{x=-1}^1{{\displaystyle \sum }}_{y=-1}^1{W}_{i+x,j+y}}$$

(2)

where weights $W_{i,j}$ were defined in the following way:

$$W_{ij}=\left[\begin{array}{ccc}\sqrt{2}/2& 1& \sqrt{2}/2\\ 1& 1& 1\\ \sqrt{2}/2& 1& \sqrt{2}/2\end{array}\right]$$

(3)

Overall, the automaton underwent n transitions, with all cells changing simultaneously according to the above-described transition rules (see Equation (1)).

Importantly, parameters $k_{i,j}^t$, $d_{i,j}^t$, and $e_{i,j}^t$ were considered functions of the cell’s density class $c_{i,j}^t$. Thus, they were formalized as six-element vectors $k=\left(k_1,\dots ,k_6\right)$, $d=\left(d_1,\dots ,d_6\right)$, and $e=\left(e_1,\dots ,e_6\right)$, with the coordinates corresponding to the six population-density classes. For the sake of certainty, the cell’s impact on its neighbors $k_{i,j}^t$ was allowed to vary from −1 (strong suppression effect) to 1 (strong induction effect). The two thresholds—d and e—varied in the same range to ensure the parameters’ comparability (see Equation (1)).

2.3. Estimation of the Optimal Model Parameters

Thus, the model’s architecture was defined by 19 parameters: Three functions, k, d, and e, with a domain size of six, and a scalar variable $n$. Among them, the degradation threshold of the lowest population-density class $d_1$ and the evolution threshold of the highest population-density class $e_6$ were artificially fixed at the levels of −1 and 1, respectively, to keep the density classes within the predefined range (see Equation (1)). The remaining 17 parameters were subjected to optimization with root mean squared relative error (RMSRE) as the objective function:

$$\mathrm{RMSRE}=\sqrt{\frac{{{\displaystyle \sum }}_i{{\displaystyle \sum }}_j{\left(\frac{c_{i,j}^P-c_{i,j}^A}{c_{i,j}^A}\right)}^2}{N}}$$

(4)

where $c_{i,j}^A$ and $c_{i,j}^P$ are the actual and predicted population-density classes, and $N$ is the number of automaton cells, i.e., the number of pixels within the study area. Such an optimization criterion was chosen since mismatches in low-density classes are believed to be more undesirable.

The optimal values of the model parameters were sought using an adaptive genetic algorithm [26]. The core idea of the algorithm is viewing alternative combinations of the parameter values as individuals in a population. The population undergoes a series of specific transformations mimicking biological evolution, such as mutation, selection, reproduction, and crossover. As a result, the population is enriched by fitter individuals, i.e., solutions closer to the sought optimum. Each individual was represented by a combination of the model parameters $\left(k,d,e,n\right)$. The individuals’ fitness was measured in terms of RMSRE (see Equation (4) above). The initial population consisted of 100 identical individuals. In each individual, the elements of vectors k, d, and e were uniformly distributed from −1 to 1, while the value of parameter n was made equal to 20 based on trial simulations.

The population underwent 100 generations, each including mutation, selection, and reproduction with crossover. The mutations occurred in all individuals, in up to three randomly chosen elements of vector k, in up to two randomly chosen elements of vectors d and e (given that one element of these two was artificially fixed), and in parameter n. The range $\mathsf{\Delta }$ of mutation decreased with the individual’s relative fitness: ${\mathsf{\Delta }}_{max}=e^{\frac{1}{\alpha -1.01}}$, where $\alpha$ is the percentile of the individual in the fitness distribution. Such an adaptive mutation function aimed to prevent either random jumping between solutions or sticking to a local optimum. The mutated individuals were subject to selection, resulting in the elimination of the 50 least fit ones. The remaining 50 individuals were randomly divided into pairs; each pair produced two offspring, thereby restoring the initial population size of 100 individuals. The two offspring emerged via crossover, which occurred at three points—in the middle of vectors k, d, and e (i.e., between parameters k₃ and k₄, d₃ and d₄, and e₃ and e₄). The fittest individual in the final population was chosen as the best approximation of the sought optimal solution.

The code used for the optimization of the model parameters is available in Supplementary File S1.

2.4. The Model’s Performance and Statistical Analysis

The performance of the obtained optimized models was estimated based on confusion matrices, showing class-wise mismatches. Proceeding from the confusion matrices, the overall accuracy—as the fraction of correctly predicted cells—was calculated. However, this measure might be biased due to the considerable prevailing of the first (the lowest-density) class. This issue was addressed in two ways. As a rough solution, the accuracy upon exclusion of the first class was calculated. As an alternative, finer solution, the performance was measured in terms of Cohen’s Kappa coefficient—the metric that relates the actual accuracy to that of the statistically independent matrix with the same class frequencies [27].

Since the current study focused on the urban extent, it seemed especially important to also assess the model performance in terms of discrimination between urban and rural areas. For this sake, the six population-density classes were aggregated into two categories—rural and urban—based on five alternative population-density thresholds. Specifically, urban areas were defined as those with a population density exceeding 1000 (population-density classes 2–6), 2000 (classes 3–6), 3000 (classes 4–6), 4000 (classes 5–6), and 5000 (class 6) persons/km². For each type of aggregation, the obtained two-by-two confusion matrix was analyzed in terms of Cohen’s Kappa and Jaccard indices. The latter characterizes the ratio of the intersect of actual and predicted urban areas over their union [28].

The 72 optimized models obtained were tested for the potential effect of population density and time on parameters k, d, and e. For this sake, the repeated-measures ANOVA, with either time windows or population-density classes as the within-subject factors, was used. The method’s assumptions were controlled with Mauchly’s sphericity test. Upon its violation, the repeated-measurement ANOVA was replaced by its non-parametric analog, Friedman’s test. For the sake of integrity, the two artificially fixed parameters (the degradation threshold of the lowest-density class and the evolution threshold of the highest-density class) were excluded from the analysis as a source of bias. The analysis was conducted in JASP v.0.14.x software [29].

3. Results

3.1. The Model’s Performance: Predicting Population Densities

The parameters and the accuracy of the 72 optimized models obtained (twenty-four provinces by three consequent time windows) are reported in

Table A1. The parameters of the optimized models.

Province	Year	n	k1/d1/e1	k2/d2/e2	k3/d3/e3	k4/d4/e4	k5/d5/e5	k6/d6/e6
Dnipro	2013	15	−0.86/−10/0.93	0.36/−0.37/0.56	0.46/−1/0.65	0.18/−1/0.9	0.18/0.03/1	0.6/−1/10
	2016	22	−0.22/−10/0.41	0.02/−1/0.52	0.05/−0.5/0.74	0.06/−0.37/0.43	0.06/−0.91/0.95	0.29/−0.33/10
	2019	15	−0.43/−10/0.88	0.03/−0.78/0.38	−0.32/−0.78/0.63	0.31/−0.26/0.86	0.31/−0.68/1	0.16/−0.6/10
Donetsk	2013	17	−0.71/−10/0.26	0.34/−0.23/0.7	0.27/−0.36/0.7	0.02/−0.1/1	0.02/0.11/0.91	0.43/−0.76/10
	2016	24	−0.98/−10/0.58	0.62/−0.07/−0.33	0.09/−0.16/0.09	0.56/0.1/0.28	0.56/0.27/0.87	0.33/−0.78/10
	2019	21	−0.27/−10/0.22	0.13/−0.84/0.42	0/−0.63/0.31	0.3/−0.53/0.26	0.3/−0.76/0.77	0.53/−0.56/10
Kharkiv	2013	14	−0.8/−10/0.68	0.28/−0.38/0.45	0.19/−0.97/0.82	0.36/−0.37/0.88	0.36/−1/1	0.57/−1/10
	2016	11	−0.84/−10/0.63	0.22/−0.35/0.26	0.22/−0.52/0.32	0.24/0.07/0.2	0.24/0.03/0.71	0.15/−0.21/10
	2019	14	−1/−10/0.67	0.23/0.2/−0.69	0.39/0.69/0.56	0.3/−0.55/0.89	0.3/−0.35/0.61	−0.03/−0.24/10
Kyiv	2013	30	−0.72/−10/0.36	0.3/−0.32/0.47	−0.28/−0.92/0.51	0.08/−1/0.41	0.08/−0.99/0.25	0.06/−0.16/10
	2016	17	−0.64/−10/0.38	0.06/−0.34/1	−0.22/−0.77/0.75	0.74/−0.22/0.97	0.74/−1/0.29	0.5/−0.48/10
	2019	22	−1/−10/0.49	0.31/−0.69/0.37	0.32/−0.55/0.45	0.3/−0.55/0.6	0.3/−0.9/1	0.18/−1/10
Luhansk	2013	7	−0.95/−10/0.29	0.17/−0.49/0.66	0.11/−0.56/0.71	0.62/−0.02/1	0.62/−0.08/0.9	0.57/0.66/10
	2016	24	−1/−10/0.21	0.37/−0.32/0.04	0.05/−0.05/−0.03	0.62/0.38/1	0.62/−0.2/0.89	0.88/0.88/10
	2019	16	−0.76/−10/0.6	0.12/−0.68/0.54	0.29/−1/0.56	0.39/−1/0.64	0.39/−0.26/0.57	0.39/−0.72/10
Lviv	2013	22	−0.9/−10/0.21	0.06/−0.51/0.25	−0.22/−0.11/0.54	0.08/−0.86/0.29	0.08/−0.16/0.92	0.31/−0.61/10
	2016	18	−0.84/−10/0.63	0.25/−0.43/1	0.27/−0.67/0.75	0.37/0.06/0.79	0.37/−0.12/−0.89	0.46/0.57/10
	2019	15	−1/−10/0.32	0.04/−0.86/0.42	0.29/−1/0.77	0.38/−0.66/0.97	0.38/−0.74/0.91	0.42/−0.76/10
Cherskasy	2013	20	−0.82/−10/−0.17	−0.6/−0.75/0.16	−0.72/−0.9/0.22	0.23/−0.69/1	0.23/−0.65/0.77	0.29/−0.35/10
	2016	20	−0.9/−10/0.48	−0.6/−0.85/0.16	−0.46/−1/0.65	0.91/−1/0.17	0.91/−0.86/0.83	0.3/−0.87/10
	2019	8	−0.9/−10/0.53	0.08/−0.86/0.15	−1/−1/0.09	0.01/−0.09/0.05	0.01/−0.92/0.46	−0.18/0.96/10
Chernivtsi	2013	10	−0.9/−10/0.69	−0.23/−0.8/0.59	0.2/−1/0.39	0.13/−0.74/0.2	0.13/−0.05/0.45	0.95/−0.48/10
	2016	24	−0.9/−10/0.31	−0.73/−0.85/−0.28	−0.23/−0.92/0.48	0.26/−0.03/−0.85	0.26/−0.38/0.38	0.44/0.48/10
	2019	20	−0.9/−10/0.33	−0.38/−0.87/0.18	−0.16/−0.77/−0.41	0.01/0.24/0.28	0.01/−0.64/0.95	0.43/−0.55/10
Chernihiv	2013	17	−0.67/−10/0.13	−0.34/−1/0.63	−0.01/−0.84/−0.11	0.13/−1/0.28	0.13/−0.76/−0.08	0.36/−0.68/10
	2016	15	−0.9/−10/1	−0.53/−0.8/0.28	−0.34/−1/0.19	0.17/−0.71/0.59	0.17/−0.48/0.93	0.44/−0.58/10
	2019	20	−1/−10/0.49	0.30/−0.69/0.37	0.32/−0.55/0.45	0.2/−0.55/0.6	0.3/−0.91/1	0.18/−1/10
Kherson	2013	12	−0.85/−10/0.27	−0.57/−0.82/0.25	−0.05/−0.76/0.5	0.3/−0.69/0.65	0.3/−0.07/−0.32	−0.03/1/10
	2016	11	−0.9/−10/0.83	−0.34/−0.82/0.15	0.26/−1/1	0/−0.33/1	0/−0.97/0.93	0.01/−0.83/10
	2019	10	−1/−10/1	−0.6/−0.88/0.08	−0.05/−0.67/0.03	−0.28/−0.65/0.43	−0.28/0.96/0.75	0.57/−0.65/10
Ivano-Frankivsk	2013	9	−0.64/−10/0.11	−0.39/−0.98/−0.14	−0.3/−0.9/0.01	0.09/−0.62/0.4	0.09/−0.88/0.31	0.13/−0.56/10
	2016	13	−0.9/−10/0.11	−0.6/−0.79/0.25	0.06/−1/0.51	0.3/−1/0.23	0.3/−0.68/0.7	0.6/−0.04/10
	2019	13	−0.93/−10/−0.01	−0.6/−0.82/0.41	−0.02/−0.61/0.36	−0.17/−0.76/0.29	−0.17/−0.76/0.03	0.76/−0.7/10
Khmelnitsky	2013	19	−1/−10/−0.11	−0.53/−0.85/0.13	0.27/−1/0.15	0.29/−0.75/0.21	0.29/−0.64/0.77	0.6/−0.73/10
	2016	17	−1/−10/0.3	−0.38/−0.79/0.25	−0.58/−0.51/1	0.85/−0.97/0.56	0.85/−0.56/0.91	0.59/−0.73/10
	2019	20	−1/−10/0.4	−0.32/−0.81/−0.07	−0.11/−1/0.14	−0.15/−0.83/0.52	−0.15/−0.86/0.53	0.25/−0.56/10
Kirovohrad	2013	27	−0.95/−10/0.67	−0.59/−0.85/0.05	0.13/−1/0.44	−0.08/−1/1	−0.08/−0.62/0.97	0.45/−0.55/10
	2016	30	−0.9/−10/1	−0.6/−0.86/0.38	−0.38/−0.73/−0.6	0.2/0.74/0.36	0.2/−1/0.67	0.51/0.13/10
	2019	20	−0.95/−10/0.16	−0.46/−1/−0.16	−0.2/−0.59/0.31	0.15/−0.52/0.86	0.15/−0.88/0.59	0.39/−0.76/10
Mykolaiv	2013	18	−0.82/−10/−0.07	−0.69/−1/0.14	−0.77/−1/0.23	−0.03/−0.86/0.43	−0.03/−0.57/0.41	0.36/−0.71/10
	2016	28	−0.9/−10/0.65	−0.57/−0.82/0.29	−0.22/0.04/0.01	−0.14/−0.27/0.45	−0.14/−0.94/0.69	0.25/−0.78/10
	2019	18	−0.76/−10/0.63	−0.52/−1/0.55	−0.17/−0.39/0.36	0.35/−0.19/−0.52	0.35/0.02/0.88	0.71/−0.48/10
Odessa	2013	13	−0.81/−10/0.9	−0.21/−0.73/0.39	0.4/−1/0.36	0.24/−0.7/0.27	0.24/−0.55/0.58	0.14/−0.97/10
	2016	16	−0.93/−10/0.37	−0.6/−0.77/−0.04	−0.72/−0.11/0.16	0.76/0.47/0.64	0.76/0.51/0.48	0.68/0.94/10
	2019	8	−0.97/−10/0.3	−0.32/−0.75/0.56	0.13/−0.1/0.46	0.85/−1/0.37	0.85/−0.6/0.69	−0.25/−1/10
Poltava	2013	9	−0.94/−10/0.77	−0.44/−0.92/0.41	−0.27/−0.79/0.46	0.28/−0.46/0.38	0.28/−0.6/1	0.29/−1/10
	2016	12	−0.9/−10/0.03	−0.69/−0.87/−0.49	−0.22/0.15/0.35	−0.08/−1/0.16	−0.08/−1/0.8	0.49/0.28/10
	2019	14	−1/−10/0.7	−0.49/−0.8/0.32	−0.01/−1/0.21	0.27/−0.88/0.71	0.27/−0.71/−0.41	0.39/0.89/10
Rivne	2013	17	−0.9/−10/0.59	−0.42/−0.86/0.23	−0.3/−0.78/0.34	0.13/−0.86/0.49	0.13/−0.51/0.64	0.51/−0.72/10
	2016	22	−1/−10/−0.2	−0.28/−0.73/0.03	−0.46/−1/0	0.18/−1/0.23	0.18/0.11/−1	0.07/0.55/10
	2019	25	−0.9/−10/−0.15	−0.41/−0.75/0.56	−0.4/−1/0.42	0.21/−0.79/−0.04	0.21/−0.83/0.33	0.46/−0.81/10
Sumy	2013	21	−0.62/−10/0.24	−0.6/−0.92/0.58	−0.21/−0.6/0.69	0.6/−0.7/0.11	0.6/−0.69/0.85	0.46/−0.55/10
	2016	17	−0.91/−10/0.24	−0.21/−0.88/−0.13	0.09/−0.63/0.73	0.3/−0.48/−0.04	0.3/−0.94/0.69	−0.07/−0.73/10
	2019	20	−0.9/−10/0.76	−0.31/−0.74/−0.02	−0.41/−0.67/0.88	0.35/−0.89/0.65	0.35/0.57/0.98	0.41/−0.97/10
Ternopil	2013	20	−0.48/−10/0.95	−0.27/−0.92/0.53	0.19/−0.82/0.77	0.62/−0.3/0.51	0.62/−0.62/0.61	0.39/−0.7/10
	2016	24	−1/−10/−0.37	−0.6/−0.87/0.1	0.1/−0.44/−0.04	0.13/−0.79/0.54	0.13/0.02/−0.96	0.55/0.23/10
	2019	18	−0.88/−10/0.2	−0.43/−0.79/−0.01	−0.59/−1/0.46	0.03/−0.75/0.53	0.03/−0.39/0.71	0.21/−0.7/10
Vinnitsa	2013	23	−0.9/−10/0.27	−0.59/−0.85/0.18	−0.46/−1/0.31	0.29/−1/−0.15	0.29/−0.52/0.12	0.15/−1/10
	2016	10	−1/−10/−0.01	−0.65/−0.88/0.19	−0.78/−0.69/0.24	0.4/−0.68/0.65	0.4/−0.9/0.97	0.08/−1/10
	2019	12	−1/−10/0.88	−0.5/−0.83/0.27	−0.66/−0.79/0.06	0.55/−0.81/0.81	0.55/−0.88/0.89	0.5/0.91/10
Volyn	2013	28	−1/−10/0.45	−0.44/−0.93/−0.02	−0.37/−0.66/0.02	0.14/−1/0.84	0.14/−0.68/0.86	0.27/−0.79/10
	2016	18	−0.9/−10/0.44	−0.24/−0.89/0.35	0.02/−0.89/0.2	0.4/−1/0.71	0.4/−0.55/0.87	0.8/−0.57/10
	2019	13	−0.91/−10/0.57	−0.6/−0.8/0.23	−0.51/−0.91/0.28	0.38/−0.64/0.4	0.38/−0.86/0.64	0.6/−0.61/10
Zakarpattia	2013	13	−0.66/−10/−0.11	−0.6/−0.65/−0.02	−0.27/−0.87/0.18	0.3/−0.91/0.89	0.3/−0.8/0.35	0.49/−0.45/10
	2016	7	−0.91/−10/0.1	−0.47/−0.75/−0.16	−0.05/−0.52/0.57	0.02/−1/0.21	0.02/−0.89/0.86	0.11/−0.73/10
	2019	23	−0.65/−10/0.31	0.03/−0.99/0.37	−0.18/−0.59/0.71	0.3/−1/0.47	0.3/−0.39/1	0.42/−0.4/10
Zaporizhzhia	2013	10	−1/−10/0.91	−0.46/−0.92/0.92	−0.13/−0.97/−0.73	0.46/0.96/0.68	0.46/−0.69/−0.39	0.79/0.99/10
	2016	24	−0.71/−10/0.7	−0.39/−1/0.77	0.02/−0.6/0.36	0.17/−0.32/0.53	0.17/−0.36/0.47	0.39/−0.33/10
	2019	25	−0.41/−10/−0.06	−0.22/−1/0.14	−0.12/−0.9/0.11	0.05/−0.43/0.39	0.05/−0.41/0.64	0.05/−0.91/10
Zhytomyr	2013	12	−0.9/−10/0.82	−0.53/−0.85/0.45	−0.04/−0.82/1	−0.08/−0.76/0.4	−0.08/−0.58/0.21	0.44/−0.63/10
	2016	17	−1/−10/0.85	−0.55/−0.86/−0.18	−0.29/−1/0.16	0.18/−0.73/0.83	0.18/−0.38/0.74	0.12/−0.63/10
	2019	20	−0.52/−10/−0.15	−0.54/−1/1	0.18/−1/0.45	−0.05/−0.84/0.24	−0.05/−0.43/0.94	0.35/−0.3/10

and

Table A2. The performance of the optimized models.

Province	Year	Adj. Acc.	Kappa Coef.	Kappa Coef. by Urban Threshold (Persons/km2)					Jaccard Index by Urban Threshold (Persons/km2)
				>1000	>2000	>3000	>4000	>5000	>1000	>2000	>3000	>4000	>5000
Dnipro	2013	0.821	0.8	0.879	0.930	0.911	0.874	0.898	0.785	0.870	0.838	0.776	0.816
	2016	0.946	0.957	0.983	0.985	0.983	0.966	0.961	0.967	0.971	0.966	0.934	0.924
	2019	0.972	0.981	0.995	0.996	0.975	0.996	0.975	0.990	0.993	0.952	0.993	0.951
Donetsk	2013	0.705	0.554	0.650	0.823	0.611	0.770	0.897	0.484	0.701	0.441	0.626	0.813
	2016	0.514	0.215	0.284	0.411	0.477	0.569	0.691	0.167	0.260	0.314	0.398	0.528
	2019	0.994	0.99	0.993	0.995	0.998	1.000	0.996	0.987	0.989	0.997	1.000	0.991
Kharkiv	2013	0.923	0.822	0.855	0.931	0.956	0.988	0.982	0.748	0.871	0.916	0.976	0.964
	2016	0.826	0.799	0.875	0.944	0.902	0.927	0.957	0.780	0.894	0.822	0.865	0.917
	2019	0.987	0.96	0.966	0.989	0.995	0.995	0.966	0.934	0.978	0.989	0.990	0.934
Kyiv	2013	0.663	0.725	0.873	0.939	0.948	0.929	0.803	0.776	0.885	0.901	0.868	0.671
	2016	0.779	0.81	0.911	0.962	0.944	0.932	0.962	0.838	0.927	0.894	0.873	0.928
	2019	0.96	0.954	0.973	0.983	0.991	0.990	0.986	0.948	0.966	0.982	0.980	0.973
Luhansk	2013	0.676	0.568	0.677	0.851	0.758	0.857	0.000	0.514	0.741	0.611	0.750	0.000
	2016	0.346	0.251	0.373	0.508	0.622	0.598	0.000	0.230	0.341	0.452	0.427	0.000
	2019	0.975	0.967	0.980	0.986	0.989	0.980	0.957	0.960	0.972	0.978	0.960	0.917
Lviv	2013	0.616	0.537	0.665	0.857	0.883	0.877	0.841	0.499	0.750	0.790	0.780	0.726
	2016	0.892	0.741	0.782	0.981	0.965	0.974	0.945	0.644	0.963	0.932	0.950	0.897
	2019	0.998	0.912	0.913	0.998	1.000	1.000	1.000	0.841	0.996	1.000	1.000	1.000
Cherskasy	2013	0.745	0.694	0.816	0.891	0.905	0.907	0.906	0.690	0.803	0.827	0.830	0.828
	2016	0.972	0.823	0.839	0.991	0.980	1.000	1.000	0.723	0.981	0.962	1.000	1.000
	2019	0.477	0.794	0.983	1.000	0.784	1.000	0.000	0.967	1.000	0.645	1.000	0.000
Chernivtsi	2013	0.744	0.767	0.835	0.917	0.943	0.944	0.615	0.719	0.848	0.893	0.895	0.444
	2016	0.809	0.798	0.874	0.940	0.981	0.872	0.842	0.777	0.887	0.963	0.773	0.727
	2019	0.92	0.952	0.976	0.990	0.981	0.952	0.952	0.954	0.980	0.963	0.909	0.909
Chernihiv	2013	0.847	0.801	0.883	0.878	0.972	0.867	0.979	0.791	0.783	0.945	0.765	0.958
	2016	0.945	0.866	0.887	0.995	0.956	0.986	1.000	0.797	0.989	0.915	0.971	1.000
	2019	0.96	0.912	1.000	0.994	1.000	1.000	1.000	1.000	0.989	1.000	1.000	1.000
Kherson	2013	1	1	0.958	0.996	0.962	0.989	0.932	0.920	0.993	0.927	0.978	0.873
	2016	0.86	0.901	0.821	0.701	0.675	0.634	0.513	0.698	0.541	0.510	0.464	0.345
	2019	0.644	0	0.983	0.992	1.000	1.000	0.962	0.968	0.985	1.000	1.000	0.926
Ivano-Frankivsk	2013	0.969	0.621	0.787	0.914	0.878	0.947	0.000	0.652	0.843	0.783	0.900	0.000
	2016	0.681	0.698	0.773	0.837	0.962	0.964	0.889	0.633	0.720	0.927	0.931	0.800
	2019	0.881	0.727	0.833	0.987	1.000	1.000	1.000	0.715	0.975	1.000	1.000	1.000
Khmelnitsky	2013	1	0.829	0.905	0.924	0.938	0.862	0.919	0.827	0.858	0.883	0.758	0.850
	2016	0.813	0.831	0.913	0.800	0.959	0.895	0.900	0.841	0.667	0.921	0.811	0.818
	2019	0.816	0.802	0.961	0.975	0.992	0.986	0.977	0.926	0.952	0.984	0.973	0.955
Kirovohrad	2013	0.97	0.939	0.980	0.957	0.937	0.980	0.923	0.960	0.918	0.882	0.962	0.857
	2016	0.899	0.93	0.562	0.816	0.886	0.731	0.526	0.391	0.690	0.796	0.576	0.357
	2019	0.683	0.473	0.997	1.000	0.977	0.980	0.000	0.994	1.000	0.955	0.960	0.000
Mykolaiv	2013	0.814	0.947	0.660	0.692	0.764	0.805	0.833	0.494	0.530	0.619	0.674	0.714
	2016	0.718	0.559	0.968	0.828	0.739	0.800	0.833	0.939	0.707	0.587	0.667	0.714
	2019	0.77	0.843	0.966	1.000	0.995	0.993	0.991	0.935	1.000	0.989	0.986	0.982
Odessa	2013	0.975	0.959	0.268	0.090	0.000	0.000	0.000	0.157	0.049	0.000	0.000	0.000
	2016	0.996	0.192	0.912	0.826	0.962	0.831	0.454	0.840	0.704	0.927	0.711	0.294
	2019	0.669	0.755	0.980	0.989	0.984	0.988	0.990	0.961	0.978	0.969	0.977	0.981
Poltava	2013	0.963	0.957	0.965	0.744	0.731	0.765	0.694	0.933	0.593	0.576	0.620	0.531
	2016	0.679	0.754	0.924	0.972	0.940	0.782	1.000	0.859	0.945	0.888	0.642	1.000
	2019	0.81	0.863	0.987	0.979	0.988	1.000	1.000	0.975	0.958	0.977	1.000	1.000
Rivne	2013	0.985	0.973	0.865	0.940	0.938	0.918	0.905	0.762	0.886	0.884	0.848	0.826
	2016	0.814	0.799	0.878	0.979	0.988	0.955	0.943	0.783	0.958	0.976	0.914	0.893
	2019	0.899	0.844	0.984	0.993	0.975	1.000	1.000	0.968	0.985	0.951	1.000	1.000
Sumy	2013	0.97	0.974	0.911	0.883	0.923	0.988	0.954	0.837	0.791	0.857	0.977	0.912
	2016	0.873	0.83	0.937	0.971	0.968	0.907	0.985	0.883	0.944	0.937	0.829	0.971
	2019	0.898	0.898	0.998	1.000	0.983	1.000	0.969	0.996	1.000	0.967	1.000	0.939
Ternopil	2013	0.967	0.989	0.798	0.846	0.956	0.945	0.851	0.664	0.733	0.917	0.897	0.741
	2016	0.758	0.721	0.861	1.000	0.955	0.982	0.963	0.756	1.000	0.914	0.966	0.929
	2019	0.867	0.833	0.810	0.842	0.955	1.000	0.980	0.682	0.727	0.914	1.000	0.962
Vinnitsa	2013	0.969	0.767	0.896	0.818	0.967	0.886	0.960	0.812	0.692	0.937	0.795	0.923
	2016	0.794	0.817	0.920	0.906	0.887	0.914	0.879	0.852	0.828	0.797	0.841	0.784
	2019	0.695	0.82	0.960	0.959	1.000	0.988	1.000	0.924	0.921	1.000	0.977	1.000
Volyn	2013	0.988	0.94	0.970	0.946	0.982	0.938	0.970	0.942	0.897	0.966	0.884	0.941
	2016	0.9	0.92	0.956	0.951	0.983	0.935	0.919	0.915	0.906	0.967	0.877	0.850
	2019	0.844	0.886	0.974	0.976	1.000	0.925	1.000	0.949	0.953	1.000	0.860	1.000
Zakarpattia	2013	0.914	0.936	0.810	0.939	0.783	0.333	0.308	0.683	0.885	0.644	0.200	0.182
	2016	0.787	0.773	0.873	0.772	0.914	0.875	1.000	0.776	0.629	0.842	0.778	1.000
	2019	0.989	0.975	0.985	0.979	0.989	1.000	1.000	0.972	0.958	0.979	1.000	1.000
Zaporizhzhia	2013	0.746	0.847	0.964	0.922	0.911	0.880	0.968	0.931	0.856	0.837	0.786	0.938
	2016	0.906	0.955	0.996	0.981	0.951	0.978	0.981	0.991	0.964	0.906	0.957	0.963
	2019	0.995	0.997	0.999	1.000	1.000	0.995	1.000	0.997	1.000	1.000	0.991	1.000
Zhytomyr	2013	0.896	0.851	0.899	0.950	0.983	0.939	0.889	0.817	0.906	0.967	0.886	0.800
	2016	0.833	0.823	0.878	0.981	0.885	0.970	1.000	0.782	0.962	0.795	0.941	1.000
	2019	0.99	0.995	0.997	1.000	1.000	1.000	0.973	0.995	1.000	1.000	1.000	0.947

, respectively. The overall accuracy (OA) appeared rather high, with an average of ~0.99. However, as mentioned in Section 2.4, to address the potential bias caused by the inflated low-density class, adjusted accuracy and Cohen’s Kappa coefficient were calculated (see Table A2). Both of them emerged slightly lower (with an average rate of ~0.84 for the adjusted accuracy and of ~0.81 for Cohen’s Kappa coefficient—see Figure 2), still indicating sufficiently strong agreement between model predictions and actual data.

The confusion matrices for all optimized models are given in Supplementary Materials S2. Here, only three matrices are reported, for the models with the best, worst, and average-adjusted accuracies (see

Table 1. (a). Population classes, actual and model-predicted: An example of the best-performing model built for 2016–2019 for the Ivano-Frankivsk province. (b). Population classes, actual and model-predicted: An example of the worst-performing model built for 2013–2016 for the Luhansk province. (c). Population classes, actual and model-predicted: An example of the average-performing model built for 2013–2016 for the Lviv province. The blue cells in the table stand for correct predictions.

(a)
		Actual Population Classes						Positive Predictive Values
		<1000	1000–2000	2000–3000	3000–4000	4000–5000	>5000
Model-predicted population classes	<1000	7628	17	0	0	0	0	0.997
	1000–2000	1	25	0	0	0	0	0.962
	2000–3000	0	1	9	0	0	0	0.9
	3000–4000	0	0	0	4	0	0	1
	4000–5000	0	0	0	0	2	0	1
	>5000	0	0	0	0	0	5	1
True positive rates		0.999	0.581	1	1	1	1	Adjusted acc. = ~99%
(b)
		Actual Population Classes						Positive Predictive Values
		<1000	1000–2000	2000–3000	3000–4000	4000–5000	>5000
Model-predicted population classes	<1000	24,505	62	15	5	4	2	0.996
	1000–2000	1	5	3	1	0	0	0.5
	2000–3000	0	2	1	0	0	0	0.333
	3000–4000	0	0	2	0	0	0	0
	4000–5000	0	0	2	4	4	0	0.267
	>5000	0	0	0	0	0	0	-
True positive rates		0.999	0.072	0.043	0	0.571	0	Adjusted acc. = ~27%
(c)
		Actual Population Classes						Positive Predictive Values
		<1000	1000–2000	2000–3000	3000–4000	4000–5000	>5000
Model-predicted population classes	<1000	30,578	44	0	0	0	0	0.999
	1000–2000	1	25	1	0	0	0	0.926
	2000–3000	0	1	17	3	1	0	0.772
	3000–4000	0	0	0	4	1	0	0.8
	4000–5000	0	0	2	1	7	2	0.7
	>5000	0	0	0	0	0	20	1
True positive rates		0.999	0.357	0.944	0.5	0.778	0.901	Adjusted acc. = ~87%

a–c).

3.2. The Model’s Performance: Discriminating between Urban and Rural Areas

The performance of the obtained optimized models was also tested with respect to urban areas. For this sake, the six population-density classes were aggregated into two categories—rural and urban—via alternative population-density thresholds (see Section 2.4). Figure 3 reports the models’ performance in terms of Cohen’s Kappa and Jaccard indices for urban delineations based on population-density thresholds of 1000 (population-density classes 2–6), 2000 (classes 3–6), 3000 (classes 4–6), 4000 (classes 5–6), and 5000 (class 6) persons/km². As one can see from the figure, both in terms of Cohen’s Kappa and Jaccard indices, the models perform better for urban-area delineations based on 3000 persons/km² threshold (with average Cohen’s Kappa levels of 0.911 vs. <0.906 for other delineations and the average Jaccard index level of 0.860 vs. <0.852 for other delineations). The difference between the models’ performance levels, both in terms of Cohen’s Kappa and Jaccard indices, for alternative delineations is significant (Friedman’s χ² > 23.923, p < 0.001).

3.3. The Effects of Population Density and Time on the Models’ Parameters

The parameters k, d, and e of the obtained optimized models were analyzed for their sensitivity to the population density and stability over time (see

Table 2. The effects of population density and time on the model parameters.

Effect of	Parameter	Mauchly’s Sphericity Test		Repeated Measures ANOVA Test		Friedman’s Test
		W	p	F	p	χ2	p
Population-density class	k	0.626	0.003	-	-	204.38	<0.001
	d	0.466	<0.001	-	-	12.032	<0.001
	e	0.783	0.049	-	-	8.328	<0.001
Time window	k	0.982	0.383	0.051	0.950	0.025	0.988
	d	0.976	0.245	3.400	0.015	6.03	0.049
	e	0.964	0.114	0.070	0.933	0.766	0.682

).

As one can see from the table, the population-density class significantly affects all three model parameters ($p<0.001$), suggesting that none of them is a surplus in the chosen cellular-automaton model architecture. The consistent pattern is an increase in each of them with a higher population density (Figure 4, top row). In the meantime, the effect of the time window was not significant for parameters k and $e$($p>0.933$), but was significant for parameter $d$($p=0.015$), thus raising the question of the models’ robustness (see also Figure 4, bottom row). However, in-depth analysis shows that the revealed effect of time on parameter d disappears ($p=0.135$) upon the exclusion of territories involved in the war conflict since 2014: Luhansk and Donetsk provinces.

4. Discussion and Conclusions

The current study aimed to explore the prognostic potential of a cellular-automaton model with density-specific parameters. The model was fitted to 72 datasets describing population-density dynamics in 24 Ukrainian provinces during three subsequent periods: 2010–2013, 2013–2016, and 2016–2019. The original LandScan-provided data on population densities were initially grouped into six classes: <1000 (class 1), 1000–2000 (class 2), 2000–3000 (class 3), 3000–4000 (class 4), 4000–5000 (class 5), and >5000 (class 6) persons/km². The logic behind such a grouping was the following: The first class covered poorly inhabited rural areas. Among the rest of the classes, the country’s average density (of ~3200 persons/km²) fell into the middle class. The high-density areas (with >5000 persons/km²) were infrequent (<5% of the area of population density exceeding 1000 persons/km²). The range between 1000 and 5000 was evenly ranked into four classes with a step of 1000 persons/km².

The obtained results indicate that cellular-automaton models of the proposed architecture can effectively predict population-density dynamics at the regional level. Thus, the average prediction accuracy exceeded 0.81 in terms of Cohen’s Kappa—a performance indicator accounting for the non-uniformity of classes. Visual inspection suggests that the highest accuracy was achieved when the villages either disappear from the simulation due to a decrease in their significance or develop into small towns by decreasing areas populated with lower classes on the edges and increasing population density in the centers (see an example represented in Figure 5). In the meantime, the poor performance of the models might be caused by unexpected expanded branches from regional centers, which have the highest growth potential. In an attempt to account for them, the models adjust their parameters, leading to rising mismatches in other sites. Figure 6 reports such an example for Mykolaiv province for the 2010–2013 time window. As it can be seen from the figure, some expansion upwards the river was observed in 2010 (Figure 6a). The model, however, removed the expanding branch (Figure 6b). Besides, poor performance was observed for Donetsk and Luhansk provinces for 2013–2016, which were involved in armed conflict since 2014, suggesting that uncontrolled changes, represented in global tendency violations [30], appeared less detectable by the models.

It turned out that the proposed cellular-automaton models succeeded in predicting not only population density but also urban-extent dynamics. Depending on the density threshold for discrimination between urban and rural areas, the models’ performance varied from 0.83 to 0.91 in terms of the Cohen’s Kappa and from 0.78 to 0.86 in terms of the Jaccard index for urban areas. Such a performance is compatible with the results of similar studies exploiting genetic-algorithm optimization, and sometimes even exceeds them. Thus, the cellular-automaton model used to assess urban growth at the core of the Pearl River Delta in the central part of Guangdong (China) demonstrated overall accuracy up to 0.82 and Cohen’s Kappa up to 0.62 [31]. In another study, covering 11 towns of Shanghai’s Jiading District (China), the corresponding numbers emerged remarkably similar: 0.83 and 0.61 [32]. Recently, a cellular-automaton model anticipated urban growth in Azadshahr, Gonbadekavoos, and Gorgan cities (Iran) with a performance of up to 0.82 in terms of Cohen’s Kappa. The slightly higher performance demonstrated by the herein presented model can likely be explained by the larger number of classes: The discrimination between urban and rural areas was performed by artificial aggregation of class-wise results. At that, the quality of such discrimination depended on the population-density threshold. Remarkably, both performance indicators reached their maxima when urban areas were defined as those with population densities exceeding 3000 persons/km² (see Figure 3). It is worth mentioning that currently accepted European regularities define urban cores through a twice lower population-density threshold of 1500 persons/km² [33]. The results obtained in this study prompt further exploration of alternative population-density thresholds as urban delineation criteria.

Overall, the obtained results confirm the study hypothesis that areas with different population densities display different behavioral patterns in terms of both the impact on the neighboring territories and the response to the external impact from neighbors. All three model parameters significantly depended on population density (p < 0.001—see Table 2). At the same time, at least for two parameters (k and d), the type of this dependence appeared rather close to linear (see Figure 4). Presumably, these two parameters might be modeled through just two coefficients describing the line rather than six-element vectors. However, the performance costs of such simplification require additional analysis. Additionally, grouping the territories into discrete density classes is not a trivial task itself and requires further investigation. Thus, the herein used scheme with six classes might be reconsidered in terms of both the number and evenness of classes. It also seems promising to enrich the model with additional input information, such as data on existing infrastructure and natural barriers that may also inhibit or stimulate urban growth. Finally, it is worth exploring the limits of the model’s generality in other geographical areas, including countries with different socio-economic situations.