Understanding Gameplay Acceleration Ability, Using Static Start Assessments: Have We Got It Right?

Abstract

Background/Objectives: Despite athletes initiating sprints from dynamic starts during gameplay, sprint performance is traditionally measured from a static position. This article aimed to determine whether static start or “pickup” acceleration are related or relatively independent motor qualities by assessing their relationship and examining how athletes’ rank order changes between static and pickup conditions. Methods: Thirty-one male athletes (20.3 ± 5.3 years) completed two 30 m sprints from a static start and two 30 m pickup accelerations following 20 m paced entries at 1.5 and 3.0 m/s⁻¹, regulated by an LED system. Peak acceleration (a_max) was measured via a horizontal linear position encoder (LPE; 1080 Sprint). Results: The shared variance between a_max from the static and pickup starts was R² = 11.6–39.6%, indicating, for the most part, a great amount of unexplained variance. The shared variance between pickup acceleration entry velocities was R² = 16.8%. A visual analysis of an individualized rank-order table confirmed that, for the most part, the fastest static-start athletes differed from the fastest pickup athletes. Conclusions: In summary, static and pickup acceleration appear to be distinct motor abilities, most likely requiring a paradigm shift in strength and conditioning practices for acceleration assessment and development.

1. Introduction

Defined as the change in velocity per unit time (a = Δv⁄Δt), acceleration is central to decisive plays in team sports, such as contesting loose balls and creating scoring chances, and differentiates higher-performing athletes [1,2,3]. In team sports, acceleration is often performed from a rolling start, or in coaching terms, a ‘pickup’ [4,5]. These accelerations are initiated from a submaximal entry velocity existing on a continuum spanning low to high velocities (e.g., walk-to-run) in relatively short bursts of effort [6,7]. While the frequency of non-stationary accelerations varies across sports [8], they consistently occur more often than sprints initiated from a static start [3,7]. In elite rugby, for instance, over half of all accelerations (53.4 ± 5.5%) begin from a walking-to-standing speed (0–1.9 m/s⁻¹), with an additional 31.8 ± 5% initiated from a jogging start (>1.9 m/s⁻¹) [4]. Given the common nature of pickup acceleration in gameplay, assessing acceleration capability from a rolling start would be logically valid. Practitioners, however, commonly assess sprint acceleration from a static start [9,10,11], likely due to tradition, the challenge of standardizing entry velocity, and a general lack of understanding of pickup acceleration. Additionally, it may be based on the contention that both static and pickup acceleration are similar motor qualities and therefore do not need to be assessed independently. Whether this is actually the case is unknown and provides the focus of this investigation.

Outside of a select few studies specific to sport [2,12,13,14], most existing research on pickup acceleration stems from gait-transition studies in rehabilitation and biomechanics [15,16,17], leaving the broader understanding of its determinants and relationship to static acceleration unclear. For example, researchers who examine gait transitions have used gradual rather than instantaneous acceleration [15,18]. The select few who have examined a “spontaneous overground acceleration” or “burst transition” have limitations, including a lack of standardized entry velocity, failure to ask performers to achieve maximal acceleration, often terminating trials at a jogging pace, and, importantly, a lack of comparison with general sprint ability [16,17]. Authors who have investigated pickup acceleration in sporting contexts have determined that maximal acceleration (a_max) decreases with the increase in entry velocity [2,13], with Sonderegger [13] finding a strong association between entry velocity and maximal acceleration (r = −0.98), but no researchers have investigated whether static start and pickup acceleration a_max are related or independent motor skills.

Given the paucity of research in the area, the assumption is that most practitioners believe that those athletes who have good static start acceleration will have good pickup acceleration; however, this may not be the case. Drawing parallels from strength research, where static and dynamic strength measures reflect related but distinct qualities [19], it is plausible that these acceleration modes differ in terms of their neuromechanical determinants. A simple statistical approach to test this contention is to assess the strength of association between the a_max values obtained from both types of testing. The purpose of this investigation, therefore, is to examine whether sprinting initiated from static and pickup starts share similar motor qualities. We hypothesize that pickup acceleration and static start acceleration are relatively independent motor qualities; if so, a paradigm shift in how acceleration is assessed may be needed.

2. Materials and Methods

2.1. Experimental Approach to the Problem

Thirty-one team sport athletes performed two 30 m maximum-effort sprint accelerations from a static start and four 30 m maximal pickup accelerations with paced entries (2 × 1.5 m/s⁻¹ and 2 × 3.0 m/s⁻¹). Distance and velocity-time measures were extracted for each trial using an LPE (1080 Sprint, 1080 Motion AB, Lidingö, Sweden) to capture spatiotemporal data at 333 Hz. Correlation coefficients and coefficients of determination (R²) were used to describe the strength of the association and shared variance between conditions. Finally, a rank-order analysis was performed on individualized data to compare static and pickup acceleration capabilities.

2.2. Subjects

An a priori sample size estimate was conducted to determine the number of participants required for the correlational analysis. Using G*Power (version 3.1.9.6), a conservative estimate was derived using the correlation-based model with an anticipated correlation of 0.70, an alpha level of 0.05, and a power of 0.80. This approach yielded a minimum requirement of 14 participants to detect a statistically significant correlation. The criteria for inclusion were: (1) male athletes aged between 16 and 35 years of age; (2) engaged in competitive sporting activities; (3) at least one year of structured sports performance training; and (4) injury-free for at least 12 months prior to the study. Thirty-one injury-free male team sport athletes (age 20.3 ± 5.3 years; height 1.82 ± 0.09 m; body mass 80.1 ± 17.1 kg) from American football, n = 10; baseball, n = 8; basketball, n = 4; track and field (200 and 400 m), n = 4; soccer, n = 3; professional ultimate frisbee (AUDL) n = 1; Gaelic football, n = 1 participated in this study. Before testing, athletes were instructed to refrain from intense exercise for 24 h prior. Written informed consent was obtained from each participant, and ethical approval for the study was granted by the AUT Ethics Committee (AUTEC Approval Number 21/437).

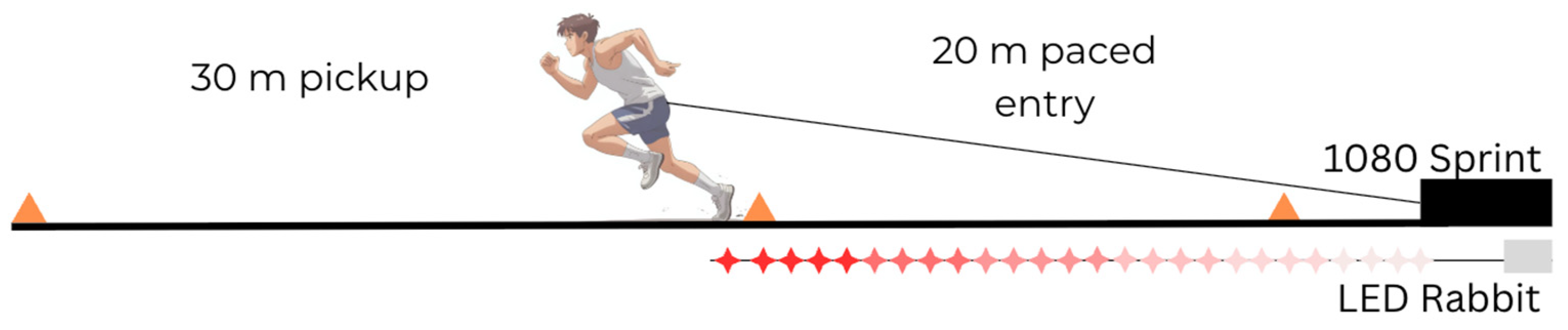
2.3. Procedures

Prior to data collection, athletes participated in a standardized warmup consisting of sprint-specific mobility drills, dynamic stretches, and familiarization with all equipment, including the LED pacing system and LPE setup. During data collection athletes performed two 30 m static sprints and six randomized 30 m pickup accelerations (2 × 1.5, 2 × 3.0, and 2 × 4.5 m/s⁻¹ entry velocities), but only 1.5 and 3.0 m/s⁻¹ entries were analyzed due to the fastest entry velocity inducing greater line sway in the tether, obscuring analysis of the breakpoint by increasing the incidence of false steps on the signal. These entry speeds were selected as they aligned with values observed in sport [4] and with similar values reported in related pickup acceleration research [13,20,21], allowing for the comparison of our findings with those in other studies. Subjects were attached to an LPE via a tether and waist harness, and entries were paced by an LED system (LED Rabbit, BV Systems, LLC, Shawnee, KS, USA). During pilot testing, LED entry velocity accuracy was validated using high framerate (240 fps) distance–time video at velocities up to 8 m/s⁻¹. The authors found that LED pacing accuracy differed by only 0.06 to 0.13 m/s⁻¹ compared with video-established velocities. For each pickup, athletes started at the beginning of the runway and were asked to maintain a paced entry until approaching the 20 m cones, then maximally accelerate through to the end of the 30 m pickup zone. During pilot testing, a minimum distance of 13 m was established to ensure a consistent entry velocity. The LPE provided displacement/time-series data at a 1 kg load (isotonic mode) to minimize impedance to the athlete and provide tension on the tether [22]. Haugen et al. [23] suggested rest times ranging from 2 min (for 20 m accelerations) to 7 min (for elite-level athletes running 40 m sprints), so a rest interval of at least 5 min was chosen to allow for recovery between trials. The 50 m sprint setup (see Figure 1) consisted of a 0–20 m paced zone, used for establishing the pickup entry velocity, and a 30 m pickup zone. For static start trials, athletes using the same track-and-tether setup also performed a 30 m sprint from the same starting point as in the pickup trials. The LED system was configured to “Multiple” mode, stabilizing the entry velocity over the 25 m strip. The trial entry velocity order was randomized using an Excel spreadsheet (Microsoft Excel, Microsoft, Redmond, WA, USA). The instructions to the subjects were, “After the LED Rabbit starts, accelerate to match the speed of the light and maintain this pace until approaching the end of the first cones.” To ensure the athlete matched the LED pacing system, participants were familiarized with it by running at least two submaximal practice accelerations at each paced pickup entry. Furthermore, after each trial during testing, the researcher inspected the entry velocity on the LPE tablet to ensure it was within 10% of the prescribed entry velocity. Seven trials were discarded and repeated, given this criterion. The average of each sprint condition was used for subsequent analysis.

2.4. Data Analysis

For each athlete, all static and pickup trials (collected as raw distance and velocity-time data) were extracted and used to compute the average a_max for static and pickup entry velocities. Each trial was extracted and processed similarly, except for the manual determination of the pickup point on pickup files (static start trials had no breakpoint, rendering the selection process unnecessary). After visual screening, each trial was analyzed in MATLAB (MATLAB R2022, MathWorks, Natick, MA, USA) using a 4th-order 0.5 Hz Butterworth lowpass filter. The decision to use a 0.5 Hz filter was based on the specific objective of extracting the underlying center-of-mass velocity profile rather than the step-to-step velocity fluctuations observed in the raw velocity data during sprint running. The selection of the filter frequency was based on pilot testing with filters ranging from 1 to 5 Hz, which showed that higher frequencies were quite responsive to the individual step’s impact on overall velocity (see Supplemental Figures S1 and S2). Two, 5, 10, and 20 m splits were extracted, v_max, and a_max, with only a_max used in this analysis. For all trials, a_max was the highest acceleration value seen on the ascending limb of the filtered velocity-time waveform. The pickup point was selected after a sudden increase in velocity between 13 and 20 m during pickup trials. Previously, the test-retest reliability over three testing occasions separated by at least seven days was established [24]. Change in the mean was used to indicate systematic bias, coefficient of variation (CV%) to establish absolute consistency, and intraclass correlation coefficients (ICC) to reflect relative consistency. Breakpoint distances and breakpoint sample ICCs were >0.99, and CV% all under 10%, with some under 5%. Finally, the 5 m mean entry velocity before the pickup was collected and analyzed, compared to the prescribed entry to verify the fidelity of the trial entry velocity.

2.5. Statistical Analysis

Data were analyzed for normality, and outliers were removed. Means and standard deviations were used to quantify the centrality and spread of data. To determine the strength of the association between static and pickup acceleration, a correlational analysis using Pearson’s r at an alpha level of p < 0.05 was conducted in JASP (Version 0.18.1, University of Amsterdam, Amsterdam, The Netherlands). Thresholds for correlations were reported as: 0.0 to 0.3 (or 0.0 to −0.3), negligible; 0.3 to 0.5 (−0.3 to −0.5), low; 0.5 to 0.7 (−0.5 to −0.7), moderate; 0.7 to 0.9 (−0.7 to −0.9), high; 0.9 to 1.0 (−0.9 to −1.0), very high [25]. Coefficients of determination (R²) indicated the shared variance between variables. For the rank-order analysis, athletes were manually sorted and ranked from highest to lowest by their a_max values, determined from their static start, and then matched across different entry velocities in an Excel spreadsheet.

3. Results

The mean a_max values were: static start = 4.52 ± 0.58 m/s⁻²; 1.5 m/s: a_max 3.21 ± 0.28 m/s⁻²; 3.0 m/s⁻²: a_max 2.36 ± 0.24 m/s⁻². The correlations between static and pickup acceleration for a_max are detailed in

Table 1. Pearson’s correlation matrix for static-start and pickup acceleration a_max.

	Static Start amax	1.5 m/s−1 amax	3.0 m/s−1 amax
Static start amax		0.63 (p < 0.001)	0.34 (p = 0.06)
1.5 m/s−1 amax	0.63 (p < 0.001)		0.41 (p = 0.02)
3.0 m/s−1 amax	0.34 (p = 0.06)	0.41 (p = 0.02)

Note: p = p-value; bold denotes significant values.

. For a_max, correlations between static start and pickup acceleration ranged from 0.34 to 0.63, corresponding to a shared variance of 11.6–39.6%. The shared variance between the different a_max entry velocities was 16.8%.

The variability in the rank order of subjects from fastest to slowest for static start a_max is shown in

Table 2. Rank order of athletes across static and pickup starts.

	Static Start Entry	1.5 m/s−1 Entry	3.0 m/s−1 Entry
Mean Entry Velocity (m/s)	-	1.62 ± 0.10	3.20 ± 0.18
Athlete	Rank (amax; m/s−2)	Rank (amax; m/s−2)	Rank (amax; m/s−2)
B05	1 (6.05)	1 (3.93)	6 (2.58)
B02	2 (5.66)	13 (3.24)	4 (2.66)
B43	3 (5.28)	10 (1.93)	30 (1.93)
B14	4 (5.19)	16 (3.18)	18 (2.33)
B07	5 (5.10)	19 (3.14)	7 (2.52)
B11	6 (5.05)	14 (3.23)	12 (2.44)
B46	7 (5.04)	2 (3.67)	1 (2.82)
B16	8 (4.99)	26 (2.24)	21 (2.24)
B08	9 (4.89)	4 (3.51)	9 (2.51)
B03	10 (4.77)	6 (3.44)	5 (2.64)
B13	11 (4.76)	5 (3.49)	17 (2.35)
B10	12 (4.69)	12 (3.26)	10 (2.50)
B18	13 (4.53)	24 (3.09)	28 (2.09)
B17	14 (4.50)	3 (3.63)	24 (2.19)
B19	15 (4.47)	7 (3.40)	31 (1.92)
B42	16 (4.35)	22 (3.11)	3 (2.76)
B01	17 (4.34)	9 (3.34)	2 (2.80)
B34	18 (4.339)	11 (3.28)	13 (2.44)
B59	19 (4.32)	17 (3.16)	23 (2.21)
B12	20 (4.29)	15 (3.22)	14 (2.41)
B15	21 (4.25)	8 (3.36)	19 (2.32)
B36	22 (4.21)	18 (3.142)	11(2.46)
B39	23 (4.15)	21(3.13)	16 (2.36)
B40	24 (4.03)	28 (3.00)	20 (2.24)
B44	25 (4.02)	20 (3.139)	8 (2.52)
B37	26 (3.95)	25 (3.04)	26 (2.12)
B45	27 (3.93)	30 (2.75)	27 (2.11)
B60	28 (3.92)	27 (3.01)	22 (2.21)
B38	29 (3.91)	31 (2.46)	25 (2.15)
B57	30 (3.69)	23 (2.40)	15 (2.40)
B58	31 (3.52)	29 (2.06)	19 (2.06)
Mean amax (m/s−2)	4.52 ± 0.58	3.21 ± 0.28	2.36 ± 0.24

Note: m/s⁻¹, meters per second; m/s⁻², meters per second squared; a_max, maximal acceleration.

. The static start rankings appear to have little influence on an individual’s pickup acceleration rankings, as no clear visual trends are observable in this table. For example, the a_max ranking for athlete B43 was 3rd for the static start, 10th for the 1.5 m/s⁻¹ entry condition, and 30th for the 3.0 m/s⁻¹ entry velocity.

4. Discussion

Only two research groups [2,13] have investigated pickup acceleration, using a methodology similar to that employed in this study. Sonderegger et al. [13] reported values of 6.01 ± 0.55, 4.33 ± 0.40, 3.20 ± 0.49, and 2.29 ± 0.34 m/s⁻² for entry velocities of 0 m/s⁻¹ (static start), 1.6, 3.0, and 4.1 m/s⁻¹. The entry velocities were similar across studies; however, the a_max values in this study were lower (~26%) than those reported by Sonderegger et al. [13]. Breddy [2] et al. used a wider range of entry velocities (3–7 m/s⁻¹, excluding the 1.5 m/s⁻¹ condition used here); however, their athletes did not maintain target entry velocities, the authors reporting a mean entry of 4.29 ± 0.52 m/s⁻¹ for the 3 m/s⁻¹ trial, whereas the mean entry velocity in this study was 3.20 ± 0.18 m/s⁻¹, making direct comparison problematic given the effect of entry velocity in flow on metrics. Despite the increased entry velocity, they reported a mean a_max comparable to that in this study (2.34 ± 0.35 m/s⁻² vs. 2.36 ± 0.24 m/s⁻²). The differences between studies in terms of the variables of interest, can be likely explained by (a) subjects’ training status, Sonderegger’s subjects were highly trained junior male soccer players, whereas Breddy used elite developmental Premier League soccer players; and/or (b) the different technologies used for data collection (linear position encoder vs. local position measurement system and GPS).

This study aimed to ascertain if static and pickup acceleration were relatively similar motor qualities; the findings suggested this was not the case, given the low shared variance, 11.6–39.6% for a_max. This is the first study to explore the relationships between static and pickup acceleration across different velocities, which limits the ability to compare findings with other research. Furthermore, it was thought that those with good pickup acceleration ability would rank highly across all entry velocities. Once more, such a contention was unfounded; the shared variance was low (16.8%) between the 1.5 m/s and 3.0 m/s entries for a_max. Moreover, given that the static start’s relationship to the 1.5 m/s⁻¹ pickup was moderate (r = 0.63, p < 0.001), and its relationship to the 3.0 m/s⁻¹ pickup was low (r = 0.34, p = 0.06), it seems that the faster the initial entry speed, the more distinct the motor ability becomes. Again, no other researchers have investigated the relationship between pickup acceleration entry velocities, making comparisons problematic. It is quite likely that pickup acceleration imposes physical and technical demands that differ from those of static start acceleration, which have yet to be identified and could provide direction for future research.

When viewed as a group, a_max values were significantly different and decreased with faster entries. However, at the individual level, a_max values varied substantially across entry velocities, with some athletes performing better than their counterparts from a static start and worse at a walking or jogging start. A visual analysis of Table 2 confirms the relative independence of static and pickup acceleration across the different entry velocities; the static start ranking had little influence on the pickup acceleration ranking. For example, the a_max ranking for athlete B43 was 3rd for the static start, 10th for the 1.5 m/s⁻¹ entry condition, and 30th for the 3.0 m/s⁻¹ entry velocity. The low shared variance and variability in ranking indicate that performance in static starts should not be used to predict pickup acceleration ability.

Several limitations to this study must be noted. First, the athletes tested were from a variety of sports at different points in their competitive seasons at the time of data collection, potentially influencing the results. However, it is worth noting that a random selection of sports/participants enables greater generalizability of results. Second, the LPE’s signal recording at the 4.5 m/s⁻¹ entry was compromised, given that as athletes moved faster, the increased entry velocity led to greater vertical sway along the line. As a result, the signal presented with what Mangine et al. [26] called “false peaks” on the signal, which made distinguishing the start or end point of some steps challenging. To abate this, we used the same strategy Mangine used by integrating the aberrations into the previous step. When approached, the manufacturer suggested setting the tether resistance to 3 kg to mitigate this oscillation; however, the added resistance was less likely to simulate ‘free running’ and was likely to affect outcome variables.

Practical Applications and Future Research

In summary, static start and pickup acceleration performance are relatively distinct motor abilities, given the minimum shared variance. Practitioners must be cognizant that excelling at static start acceleration does not guarantee proficiency across non-static starts and vice versa. Consequently, the assessment and training methods need to differ to understand and develop the two motor qualities optimally. For example, an assessment for deriving pickup acceleration metrics has been outlined in this paper; however, the information remains rudimentary, and a deeper understanding of step kinematics and kinetics, particularly during the approach, transition, and pickup steps, is needed. Technology, such as that used in this study, combined with videography, can provide a deeper understanding of the step-by-step mechanical determinants of pickup acceleration, if such assessments are found to be reliable. In that case, understanding what distinguishes athletes with good pickup acceleration from those with less skill is the natural next step for researchers and coaches seeking to understand and develop this motor quality. Armed with this information, the coach will have a greater appreciation of the technical and physical factors important to optimizing pickup acceleration performance. This deeper level of mechanical understanding of pickup acceleration is currently in its infancy, and there appears to be a plethora of research opportunities to expand the knowledge base. In the future, researchers should determine the mechanical differences associated with each entry velocity, the technical skills that determine proficiency, and the physical factors that influence performance differences across activities/sports.