Biomechanical Evaluation of a Spinal Surgical Instrument: A Numerical–Experimental Approach
Abstract
1. Introduction
2. Materials and Methods
2.1. Development of an ad hoc Measurement System (MS)
2.2. Calibration of the MS: Experimental Tests
2.3. Experimental Test to Verify the MS’s Suitability
3. Results
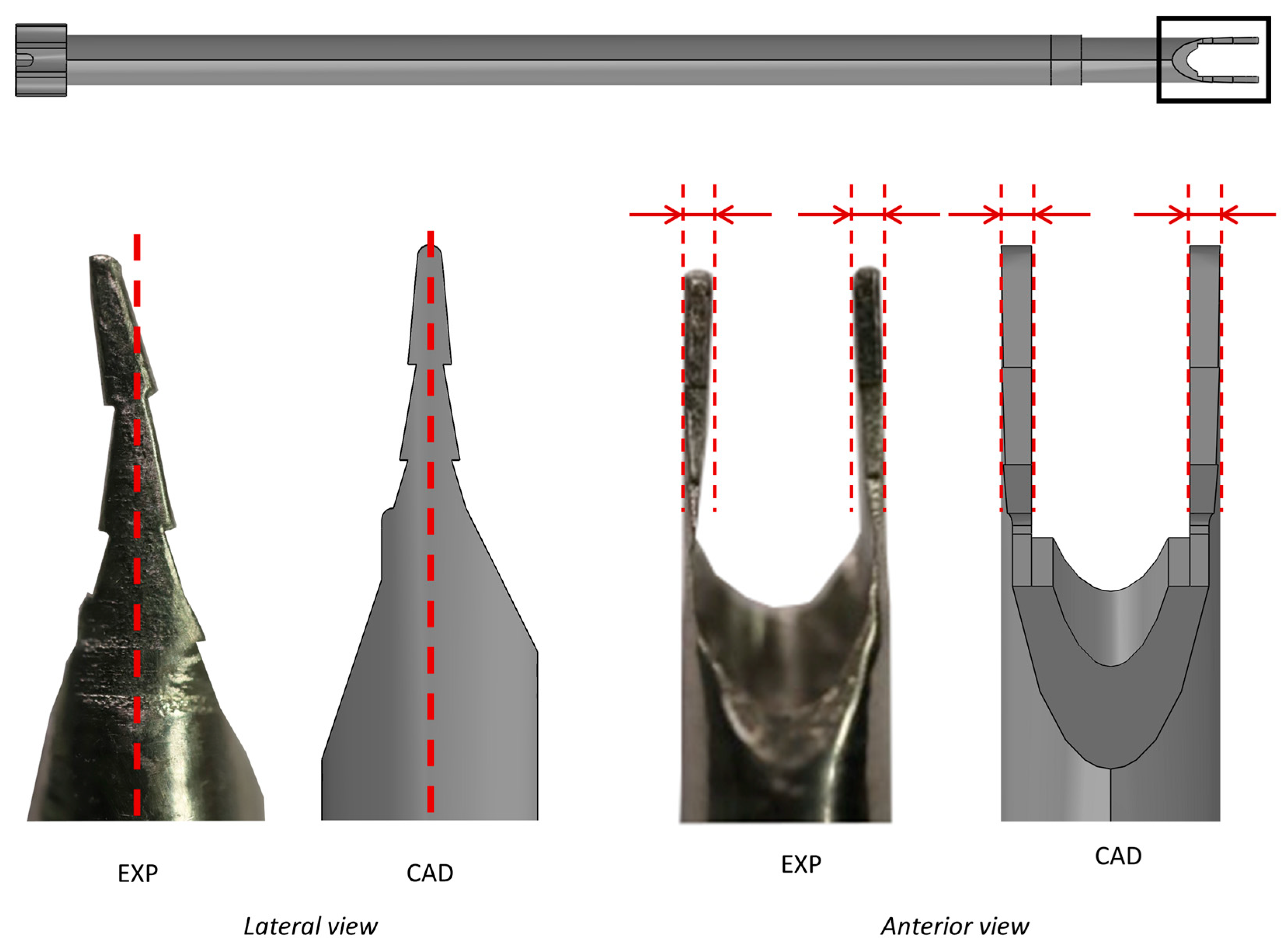
3.1. Development of an ad hoc Measurement System (MS)
3.2. Calibration of the MS: Experimental Tests
3.3. Experimental Test to Verify the MS’s Suitability
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| SI | Surgical instrument |
| MS | Measurement system |
| SGs | Strain gauges |
| FEM | Finite element model |
References
- Mollica, F.; Ambrosio, L. The finite element method for the design of biomedical devices. Biomater. Hand Surg. 2009, 31–45. [Google Scholar] [CrossRef]
- McGain, F.; Moore, G.; Black, J. Hospital steam sterilizer usage: Could we switch off to save electricity and water? J. Heal. Serv. Res. Policy 2016, 21, 166–171. [Google Scholar] [CrossRef] [PubMed]
- Vozzola, E.; Overcash, M.; Griffing, E. An Environmental Analysis of Reusable and Disposable Surgical Gowns. AORN J. 2020, 111, 315–325. [Google Scholar] [CrossRef] [PubMed]
- Dharmshaktu, G.S. Intraoperative instrument breakage during the orthopedic elective procedures: A retrospective single-center experience. J. Orthop. SPINE 2021, 8, 8–13. [Google Scholar] [CrossRef]
- Leiden, A.; Cerdas, F.; Noriega, D.; Beyerlein, J.; Herrmann, C. Life cycle assessment of a disposable and a reusable surgery instrument set for spinal fusion surgeries. Resour. Conserv. Recycl. 2020, 156, 104704. [Google Scholar] [CrossRef]
- de Melo Costa, D.; de Oliveira Lopes, L.K.; Tipple AF, V.; Johani, K.; Hu, H.; Deva, A.K.; Watanabe, E.; Vickery, K. Evaluation of stainless steel surgical instruments subjected to multiple use/processing. Infect. Dis. Heal. 2018, 23, 3–9. [Google Scholar] [CrossRef] [PubMed]
- Rizan, C.; Bhutta, M.F. Environmental impact and life cycle financial cost of hybrid (reusable/single-use) instruments versus single-use equivalents in laparoscopic cholecystectomy. Surg. Endosc. 2022, 36, 4067–4078. [Google Scholar] [CrossRef] [PubMed]
- Young, C.C.; Chiarelli, P.A.; Hofstetter, C.P. Injuries to the Cervical Spine, 4th ed.; Elsevier Inc.: Amsterdam, The Netherlands, 2018. [Google Scholar] [CrossRef]
- Cichos, K.H.; Hyde, Z.B.; Mabry, S.E.; Ghanem, E.S.; Brabston, E.W.; Hayes, L.W.; McGwin, G.; Ponce, B.A. Optimization of Orthopedic Surgical Instrument Trays: Lean Principles to Reduce Fixed Operating Room Expenses. J. Arthroplasty 2019, 34, 2834–2840. [Google Scholar] [CrossRef] [PubMed]
- Mouritsen, J.M.; Ehlers, L.; Kovaleva, J.; Ahmad, I.; El-Boghdadly, K. A systematic review and cost effectiveness analysis of reusable vs. single-use flexible bronchoscopes. Anaesthesia 2020, 75, 529–540. [Google Scholar] [CrossRef] [PubMed]
- Goldberg, T.D.; Maltry, J.A.; Ahuja, M.; Inzana, J.A. Logistical and Economic Advantages of Sterile-Packed, Single-Use Instruments for Total Knee Arthroplasty. J. Arthroplasty 2019, 34, 1876–1883.e2. [Google Scholar] [CrossRef] [PubMed]
- Thiel, C.L.; Schehlein, E.; Ravilla, T.; Ravindran, R.D.; Robin, A.L.; Saeedi, O.J.; Schuman, J.S.; Venkatesh, R. Cataract surgery and environmental sustainability: Waste and lifecycle assessment of phacoemulsification at a private healthcare facility. J. Cataract. Refract. Surg. 2017, 43, 1391–1398. [Google Scholar] [CrossRef] [PubMed]
- Thiel, C.L.; Fiorin Carvalho, R.; Hess, L.; Tighe, J.; Laurence, V.; Bilec, M.M.; Baratz, M. Minimal Custom Pack Design and Wide-Awake Hand Surgery: Reducing Waste and Spending in the Orthopedic Operating Room. Hand 2019, 14, 271–276. [Google Scholar] [CrossRef] [PubMed]
- Nast, K.; Swords, K.A. Decreasing operating room costs via reduction of surgical instruments. J. Pediatr. Urol. 2019, 15, e1–e153. [Google Scholar] [CrossRef] [PubMed]
- Ottardi, C.; Damonti, A.; Porazzi, E.; Foglia, E.; Ferrario, L.; Villa, T.; Aimar, E.; Brayda-Bruno, M.; Galbusera, F. A comparative analysis of a disposable and a reusable pedicle screw instrument kit for lumbar arthrodesis: Integrating HTA and MCDA. Health Econ. Rev. 2017, 7, 17. [Google Scholar] [CrossRef] [PubMed]
- Zhu, X.; Yuan, L.; Li, T.; Cheng, P. Errors in packaging surgical instruments based on a surgical instrument tracking system: An observational study. BMC Health Serv. Res. 2019, 19, 1–6. [Google Scholar] [CrossRef] [PubMed]
- Lee, A.W.L.; Neo, E.R.K.; Khoo, Z.Y.; Yeo, Z.; Tan, Y.S.; Chng, S.; Yan, W.; Lok, B.K.; Low, J.S.C. Life cycle assessment of single-use surgical and embedded filtration layer (EFL) reusable face mask. Resour. Conserv. Recycl. 2021, 170, 105580. [Google Scholar] [CrossRef] [PubMed]
- Salmingo, R.A.; Tadano, S.; Fujisaki, K.; Abe, Y.; Ito, M. A simple method for in vivo measurement of implant rod three-dimensional geometry during scoliosis surgery. J. Biomech. Eng. 2012, 134, 054502. [Google Scholar] [CrossRef] [PubMed]
- Rohlmann, A.; Graichen, F.; Weber, U.; Bergmann, G. Monitoring in vivo implant loads with a telemeterized internal spinal fixation device. Spine 2000, 25, 2981–2986. [Google Scholar] [CrossRef] [PubMed]
- Brown, M.D.; Holmes, D.C.; Heiner, A.D. Measurement of cadaver lumbar spine motion segment stiffness. Spine 2002, 27, 918–922. [Google Scholar] [CrossRef] [PubMed]
- Rohlmann, A.; Bergmann, G.; Graichen, F. A spinal fixation device for in vivo load measurement. J. Biomechanics 1994, 27, 961–967. [Google Scholar] [CrossRef] [PubMed]

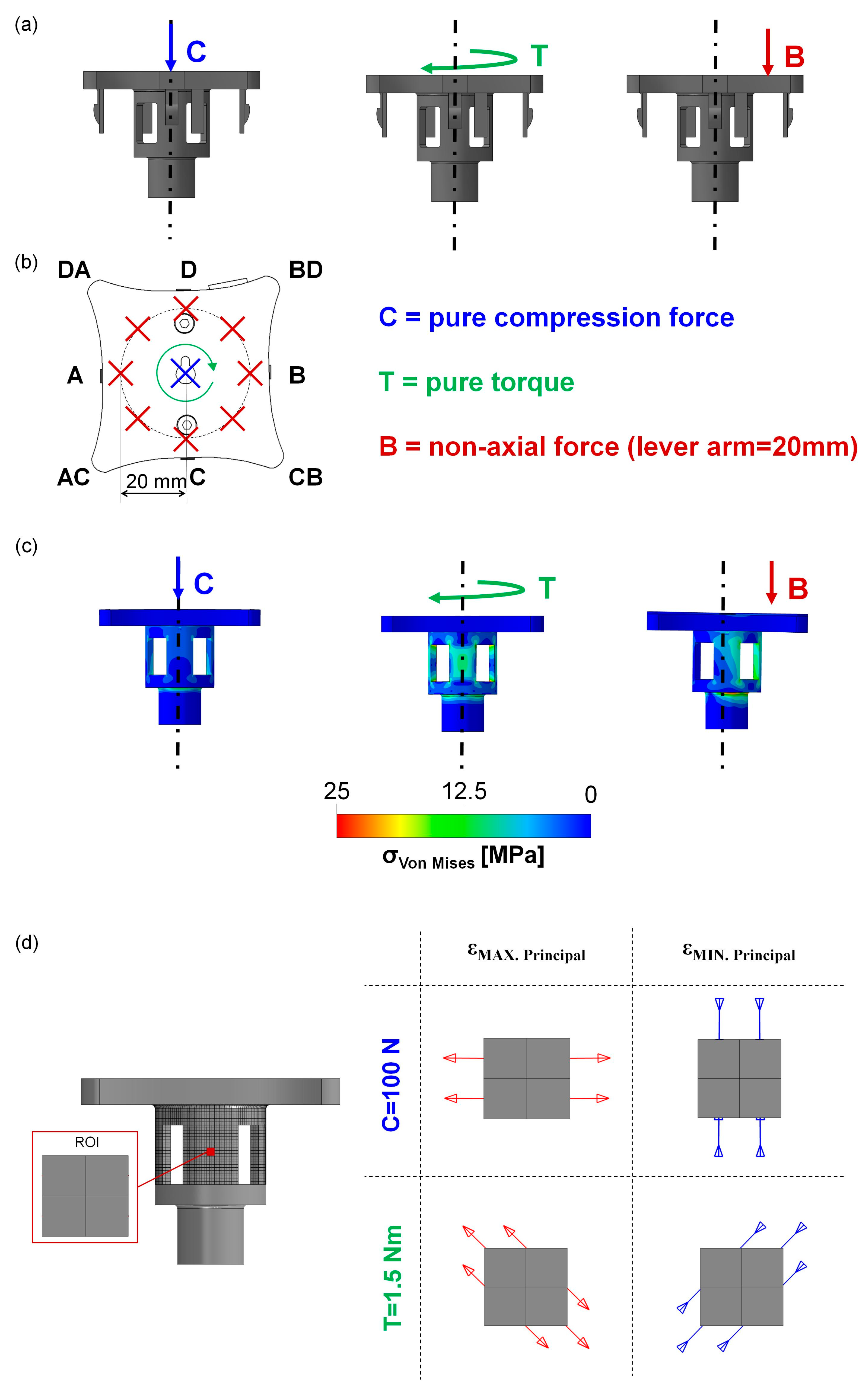



| Rate | Sampling Frequency | Protocols | ||
|---|---|---|---|---|
| Case C | Pure compression force | 1 mm/min | 10 Hz | 5 loading–unloading cycles (10–100 N) |
| Case T | Pure torque | 1°/min | 10 Hz | 2 loading–unloading cycles (−1.5–+1.5 Nm) |
| Case B | Non-axial force (bending) | 1 mm/min | 10 Hz | 5 loading–unloading cycles (10–100 N) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ciriello, L.; Villa, T. Biomechanical Evaluation of a Spinal Surgical Instrument: A Numerical–Experimental Approach. Biomechanics 2025, 5, 26. https://doi.org/10.3390/biomechanics5020026
Ciriello L, Villa T. Biomechanical Evaluation of a Spinal Surgical Instrument: A Numerical–Experimental Approach. Biomechanics. 2025; 5(2):26. https://doi.org/10.3390/biomechanics5020026
Chicago/Turabian StyleCiriello, Luca, and Tomaso Villa. 2025. "Biomechanical Evaluation of a Spinal Surgical Instrument: A Numerical–Experimental Approach" Biomechanics 5, no. 2: 26. https://doi.org/10.3390/biomechanics5020026
APA StyleCiriello, L., & Villa, T. (2025). Biomechanical Evaluation of a Spinal Surgical Instrument: A Numerical–Experimental Approach. Biomechanics, 5(2), 26. https://doi.org/10.3390/biomechanics5020026






