Abstract
This study aimed to evaluate the effects of different target distances on various leg joints in the fencing lunge (lunge). Fifteen fencers performed the lunges from three different target distances (normal, short, and long). Joint angle data in the sagittal plane of the hip, knee, and ankle of the front and rear legs were measured using a 3D motion analysis system (Miqus M3). Joint angle variables were compared between each distance using a one-way repeated-measures analysis of variance and Friedman tests (p < 0.05). The results showed significant differences in various extensions, ranges of motion, and flexion angles in the measured joints for all distances. As the distances increased, there was greater flexion of the rear knee joint early during the lunge, followed by greater extension of the rear hip and knee joints, greater plantar flexion of the rear ankle joint, and higher peak velocity of the body center of mass. Furthermore, target distance extension was suggested to significantly affect front hip and knee joint flexion during the braking phase of the lunge. This study provides insight and information valuable to coaches and fencers operating in actual competition settings.
1. Introduction
The most basic attacking movement in fencing is the fencing lunge (hereafter referred to as “lunge”) [1] because the lunge performance often results directly in points and is one of the main factors affecting victory or defeat [2,3]. In the lunge, the arms are extended first, the rear leg is extended while pushing off the ground, and the front leg is stepped forward as if kicking forward and landing on the heel [4]. The movements of the hip, knee, and ankle joints of the front and rear legs are combined with upper body movements to achieve a “touch” according to the target distance from the opponent. Previous evaluations of the lunge have assessed traveling time [5], traveling distance [5], sword tip velocity [6], body center of mass (CoM) velocity [7,8,9], EMG of the lower extremity [10], lower extremity joint velocity [6,9,11,12], and lower extremity joint angle [6,7,9,13] that have been the focus of various aspects [14]. Of these, the lower extremity joint angle during the lunge has recently received more attention as a factor influencing peak velocity [6,7,9]. Bottoms et al. [6] reported that the range of motion (ROM) of the rear knee joint, rear hip peak flexion angle, and front hip peak flexion angle during lunge are important predictors of the contribution to sword velocity. Guan et al. [9] also concluded that greater ROM of the rear leg knee joint is a factor that increases the horizontal peak velocity of the CoM during the lunge. They also reported that a low posture with a bent knee joint was important for a more effective performance [6,7,9]. From these research reports, we suggest that evaluating lower extremity joint angles during the lunge movements may be useful for gaining insight into improving the technique of the lunge movements.
However, many of these studies were designed using a fixed distance from the opponent, which does not reflect the characteristics of a real game where the target distance from the opponent varies for the attacker. In actual game situations, the target distance is not always constant as opponents repeatedly step backward to avoid a touch or move forward to launch a counterattack [4]. This shows that as the target distance changes, the kinematic factors of the lunge are also expected to change. Therefore, the kinematics of the lunge at different target distances have not been discussed.
In Taekwondo, a combat sport similar to fencing, kinematic performance analyses at different target distances have been conducted [15]. In particular, three target distances were set for the roundhouse kicking motion: normal, short, and long. Moreover, it was demonstrated that the linear displacement of the pelvis and lower extremity joint angles was significantly affected by the differences in target distances [15]. These results suggest that differences in target distance are likely to affect the kinematics of the motion.
In fencing, the CoM moves horizontally toward the target by executing the lunge motion. After these movements, the paths of motion of the front and rear legs change depending on whether the target distance is short or long, which may affect lower extremity joint (hip, knee, and ankle joints) angles. Examining ROM and peak angles of lower extremity joints during the lunge at different target distances and presenting data on the differences may contribute to the development of effective coaching during the attacking technique triggered by the lunge. Therefore, this study aimed to examine the effects of different target distances on lower extremity joint angles (hip, knee, and ankle joints) during the lunge. As a research question, we focused on how ROM and peak angles (extension/flexion) of lower extremity joints (hip, knee, and ankle joints) could change during the lunge performed at three different target distances (normal, short, and long). We hypothesized that the fencer would achieve the adjusted target distance by controlling the peak flexion angle, peak extension angle, and joint ROM of the lower extremity joints (hip, knee, and ankle) of the front and rear legs.
2. Materials and Methods
2.1. Participants
The sample size was calculated a priori with G-power, with alpha set at 0.05, statistical power set at the recommended 0.8 [16], and effect size set at large (0.40); it was determined that a minimum of 12 participants would be required. The fencers were 15 male fencing athletes (age [mean ± standard deviation (SD)]: 19.5 ± 0.9 years, height: 171.3 cm ± 5.1 cm, weight: 63.5 kg ± 5.1 kg, fencing history: 9.9 ± 3.1 years) specializing in fleuret fencing who were members of a university fencing team that had competed in the National Cup. Of these, 14 were right-handed and one was left-handed. Prior to the experiment, the purpose and methods of the study were explained to the participants both in writing and orally and they signed an informed consent form after fully understanding the content. All participants confirmed that they had not suffered any musculoskeletal injuries within 6 months prior to the study. This study was complied with the Declaration of Helsinki and was approved by the Ethics Review Committee of the Graduate School of System Design and Management, Keio University (approval number: SDM-2022-E001).
2.2. Trial Conditions
In this study, three conditions (normal, short, and long) were set for the target distance at which fencers attacked in the lunge. The target distance was defined as the horizontal distance from the rear leg toe to the target during the “En garde” (basic starting posture) of each fencer [17,18]. Since the normal condition has often been defined as 1.5 times the height of each fencer in many previous studies, this study was defined in the same way [7,13,17,18]. Other aspects to consider when determining the target distance were the selection patterns of the defender. Two basic defensive patterns included (1) backstepping backward to avoid an attacker’s lunge and (2) lunge forward when counterattacking against an attacker, which are explained in fencing instruction manuals [4] and are recognized as basic tactics common worldwide. Based on the above, we set the distances assuming these two patterns. The short condition was assumed to be a counterattack by the opponent (closer distance from normal) and the long condition was assumed to be a retreat action by the opponent (farther distance from normal). However, since there was no previous knowledge on how to set these distances, a pilot study was conducted prior to this experiment and, after multiple trials, the counterattack (short condition) was set at −50 cm and the backward movement (long condition) at +30 cm. The distance between the fencer and target was 257.2 ± 7.4 cm for normal, 207.2 ± 7.3 cm for short, and 287.2 ± 7.3 cm for long. The target was attached to a 30 cm × 30 cm square of a lamé jacket cloth, adjusted so that the fencer’s sword tip and the target surface were level at the touch of the lunge.
2.3. Procedure
Before the experiment, the fencers warmed up by stretching, running, and performing fencing footwork for approximately 15 min. A familiarization session was then conducted in which they practiced the lunge several times at three different lunge distances (normal, short, and long) to familiarize themselves with the experimental conditions. The fencer placed their foot in the starting position, ready to start the lunge at any time from a stationary position after preparing with “En garde”. Each fencer was instructed to lunge as fast as possible from the start of the movement to the touch point without stopping. They performed each of the short, normal, and long trials three times (nine trials per athlete). Rest periods between trials were set at 30 s to avoid the effects of fatigue. If the fencer missed the tip of the sword from the 30 cm × 30 cm target area, stopped moving during the lunge, or had a significant loss of balance, it was considered a failed trial. Finally, referring to a previous study [15], fencers performed nine trials (three trials for each target distance) until they succeeded. All fencers achieved the conditions for each target distance. However, including the failed attempts, the average number of attempts was 3.1 for normal, 3.1 for short, and 3.5 for long.
2.4. Data Collection
Data were collected using 3D motion analysis. During each trial, tracking markers (14.0 mm diameter) affixed on the skin of each fencer were photographed and the 3D coordinate values were measured using analysis software. Eight motion cameras (Qualisys Standard Motion Cameras Miqus M3, Goteborg, Sweden) were placed around the fencer and the sampling frequency was set to 500 Hz. The captured data were stored in Qualisys Track Manager (QTM) through a dedicated cable. In this study, a stationary coordinate system was used in which the Y-axis is the direction in which the lunge is moving, the X-axis is orthogonal to the Y-axis, and the Z-axis is vertical. The fencer wore a fencing mask on their head and held a foil in their dominant hand. In this study, based on the Visual 3D Marker Set Guidelines, a total of 51 tracking markers were affixed, including 44 points surrounding the joints of the upper and lower limbs and 7 points on the foil (top of the blade, near the top, center of the blade, near guard, and guard [guard center, guard right, guard left]) (Figure 1). Foils (No. 5, BF Allstar, Reutlingen, Germany, 90 cm blade length) and masks (Allstar, Reutlingen, Germany) were standardized according to international standards and the shoes were those normally used by each individual. Figure 2 shows the experimental setup.
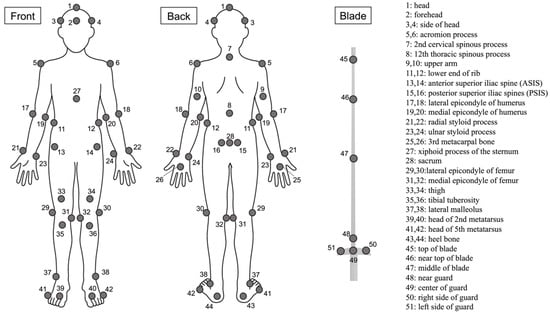
Figure 1.
Positions of reflective markers attached to the landmarks of the body.
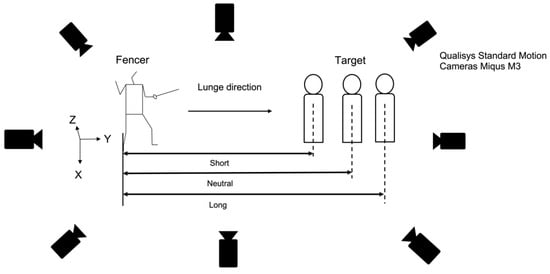
Figure 2.
Experimental setup.
2.5. Data Analysis
The saved data were labeled with each tracking marker using (QTM) and exported as C3D files. Marker coordinates configured in 3-D space were quantified using Visual 3-D and filtered at a frequency of 8 Hz using a Butterworth fourth-order zero-lag filter.
Referring to the Visual 3D skeletal model [19], the CoM was calculated as a weighted average of the CoM positions of 15 segments to obtain the horizontal displacement and peak velocity during a lunge. The En garde position was used as the static starting position and the horizontal displacement of the CoM was calculated by subtracting the value at the start of the movement from the value at the end of the movement. The peak horizontal velocity was calculated using the central finite differences method. The hip center was calculated from a regression equation [20] that defines the pelvis as “Coda_Pelvis” and provides an estimate of the distance from the pelvic origin. The knee joint center was assumed to be on a plane defined by the hip joint center, femoral and knee markers, and midway between the femoral condyles. The ankle joint center was assumed to be on the plane defined by the knee joint center, shank markers, and ankle markers and to be one-half the distance between the ankles.
The lunge interval for data analysis was defined based on previous studies [7,10]. The fencers started movement from the “En garde” position with both legs landed; toe-off of the front leg was defined as the beginning of the propulsive phase and after the participant’s front leg swung forward in coordination with the rear leg, the heel contact of the front leg was defined as the end of the propulsive phase (Figure 3) [7,10]. The braking phase started with heel contact of the front leg and ended with maximum flexion of the front knee (Figure 3) [21]. The trial with the highest peak velocity of the CoM was representative of the three trials that were successful under each target distance condition for each fencer’s trial. The time from the start to the end of the lunge motion was normalized as 100% and the mean and standard deviation were calculated for each 1% interval.
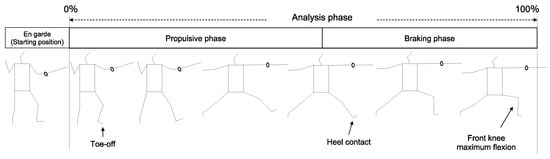
Figure 3.
Analysis phase of the lunge motion.
For joint angle variables, flexion (+)/extension (−) of the hip and knee joints and dorsiflexion (+)/plantar flexion (−) of the ankle joint in the sagittal plane were calculated as the relative angle between two adjacent segments (pelvis and femur for hip, femur and tibia for knee, and tibia and foot for ankle), respectively. Regarding the kinematic variables to be examined, previous studies have shown that the rear leg is involved in the propulsive phase and the front leg in the braking phase [10,11]. Therefore, peak flexion (dorsiflexion) angle, peak extension (plantar flexion) angle, and ROM during the propulsive phase for the rear leg and the braking phase for the front leg were analyzed, respectively.
2.6. Statistical Analyses
Preliminary analysis (Shapiro–Wilk) was used to test the normality for all the variables. With target distance as a within-subjects factor, we used one-way repeated analysis of variance (ANOVA) [15] for parametric data and Friedman tests for nonparametric data to compare dependent variables among distance conditions (short, normal, and long). In one-way repeated ANOVA, Mauchly’s sphericity test was performed to verify equal variances and Greenhouse Geisser’s epsilon correction was performed if the hypothesis was rejected. Multiple comparison tests were adjusted using the Bonferroni correction method and all significance levels were less than 5%. The effect size was defined as Partial Eta squared and the Kendall’s W test value. Statistical analysis software was IBM SPSS Statistics 28 (IBM Corporation, Armonk, NY, USA).
3. Results
Table 1 shows the CoM from the sagittal plane during a lunge in different target distance conditions. Both horizontal displacements of the CoM and peak velocity of the CoM were significantly different between target distance conditions (p < 0.05).

Table 1.
Summary of data on the body center of mass compared under target distance conditions (N = 15).
Figure 4 shows the ensemble-averaged motion patterns of each joint (hip, knee, and ankle) of the rear leg (N = 15) for each target distance condition. Figure 5 provides a summary of the data from the lower extremity joint (hip, knee, and ankle) angles of the rear leg from the sagittal plane during the propulsive phase of the lunge. The joint angle variables for which significant differences (p < 0.05) were confirmed for all target distance conditions were the peak hip extension angle, hip ROM, peak knee flexion angle, peak knee extension angle, knee ROM, peak ankle plantar flexion angle, and ankle ROM. Furthermore, significant differences (p < 0.05) were found between the target distance conditions in the peak hip flexion angle (normal < long) and peak ankle dorsiflexion angle (short and normal < long).
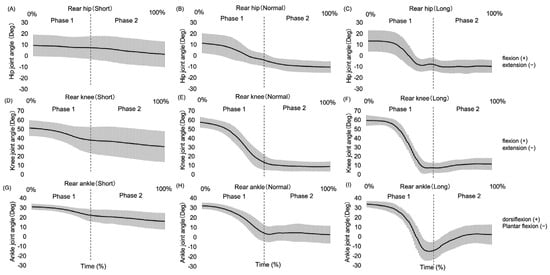
Figure 4.
Generalized pattern of rear leg joint angles in the lunge motion from the sagittal plane (N = 15). Note: (A) Rear leg hip motion pattern in short conditions. (B) Rear leg hip motion pattern in normal conditions. (C) Rear leg hip motion pattern in long conditions. (D) Rear leg knee motion pattern in short conditions. (E) Rear leg knee motion pattern in normal conditions. (F) Rear leg knee motion pattern in long conditions. (G) Rear leg ankle motion pattern in short conditions. (H) Rear leg ankle motion pattern in normal conditions. (I) Rear leg ankle motion pattern in long conditions.
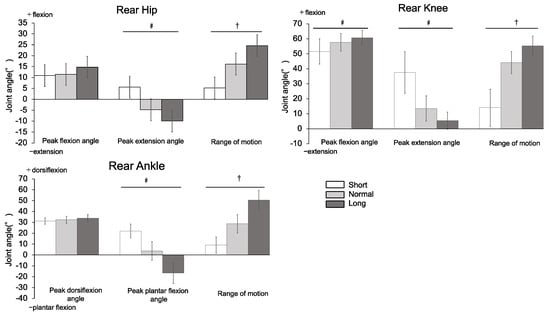
Figure 5.
Summary of motion data at the lower extremity joint (hip, knee, and ankle) angles of the rear leg viewed from the sagittal plane (N = 15; in degrees). Note: Data are presented as Mean ± SD. Error bars indicate ± standard deviation. Hip, Knee, + = flexion/− = extension; Ankle, + = dorsiflexion/− = plantar flexion. ♯, analysis of variance; †, Friedman’s test was applied because normal distribution was not given.
Similarly, Figure 6 shows the ensemble-averaged motion patterns of each joint (hip, knee, and ankle) of the front leg in each target distance condition (N = 15). Figure 7 shows a summary of data at the lower extremity joint (hip, knee, and ankle) angles of the front leg from the sagittal plane during the braking phase of the lunge. The joint angle variables for which significant differences (p < 0.05) were confirmed for all target distance conditions were the peak hip flexion angle, peak hip extension angle, peak knee flexion angle, knee ROM, peak ankle plantar flexion angle, and ankle ROM. Furthermore, significant differences (p < 0.05) were found between the target distance conditions in hip ROM (short < normal and long) and peak ankle dorsiflexion angle (short and normal < long).
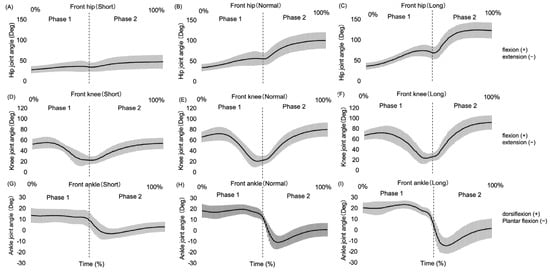
Figure 6.
Generalized pattern of front leg joint angles in the lunge motion from the sagittal plane (N = 15). Note: (A) Front leg hip motion pattern in short conditions. (B) Front leg hip motion pattern in normal conditions. (C) Front leg hip motion pattern in long conditions. (D) Front leg knee motion pattern in short conditions. (E) Front leg knee motion pattern in normal conditions. (F) Front leg knee motion pattern in long conditions. (G) Front leg ankle motion pattern in short conditions. (H) Front leg ankle motion pattern in normal conditions. (I) Front leg ankle motion pattern in long conditions.
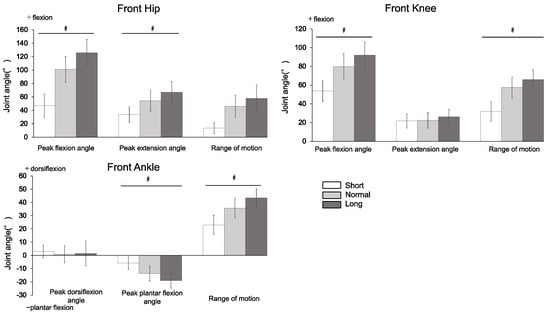
Figure 7.
Summary of motion data at the lower extremity joint (hip, knee, and ankle) angles of the front leg viewed from the sagittal plane (N = 15; in degrees). Note: Data are presented as Mean ± SD. Error bars indicate ± standard deviation. Hip, Knee, + = flexion/− = extension; Ankle, + = dorsiflexion/− = plantar flexion. ♯, analysis of variance.
All statistical comparison results are provided in the Supplementary Materials.
4. Discussion
This is the first study to quantify the effects of different target distances on lower extremity joint (hip, knee, and ankle joints) angles of the front and rear legs in the lunge movement. Although previous studies have clarified kinematics under constant target distance conditions [6,9], we set and evaluated three different target distances, which were assumed to be the distance to the opponent. Our results confirmed significant differences in peak flexion angle, peak extension angle, and joint ROM of several lower extremity joints (hip, knee, and ankle) as the target distance increased, partially supporting our hypothesis.
The peak velocity of the CoM during the lunge has been used as a performance indicator in the case of shortening the opponent’s defensive time [6,7,9]. The results of this study showed that the peak velocity of the CoM during the lunge was significantly higher as the target distance increased. Therefore, it would seem that a farther distance is more effective than a closer distance. However, the results of this study should be considered as “technical actions” in each target distance condition. The long-distance condition set up in this study assumed opponent to retreat, moving away from the normal distance condition, while the short-distance condition assumed a counterattack, moving closer than in the normal distance condition. Therefore, since the focus in the long-distance condition was on touching the target more quickly, the peak velocity of the CoM may have been higher due to the greater flexion of the rear knee joint early in the propulsion phase during the lunge and the greater extension of the rear hip, knee, and leg ankle joints in the latter half [6,7,9]. However, as the short distance condition was the counterattack distance condition, it can be inferred that the focus was on not allowing the opponent to create a counterattack by minimizing lower extremity joint flexion/extension. The distinct characteristics of the rear leg during these attack phases can be understood from the differences in the peak velocity of the CoM observed during the lunge.
During the braking phase of the lunge, the largest increase in the front leg was observed in the peak hip flexion angle (78.7° from short to long), followed by the peak knee flexion angle (38.2° from short to long). This was observed in the middle to final phase of the lunge movement (Figure 6), suggesting that the adjustment of the target distance was compensated for by flexion of the front hip and knee joints. However, the peak dorsiflexion angle of the ankle joint did not significantly differ between target distance conditions. This may be due to the fact that the ankle joint reached its dorsiflexion limit as the target distance increased, resulting in a smaller amplitude of variation in the ankle joint dorsiflexion with distance. In other words, the results indicated that the hip and knee joints of the front leg flexed more as the target distance increased but ankle joint dorsiflexion was not affected by increased target distance.
This study has several limitations. The first is that the study placed 44 markers on participants’ landmarks to collect data using a 3-D motion analysis system and these many markers could have altered the participants’ daily movement patterns. Second, since there are many cases in which attacking movements were not performed in a stationary state in actual matches, rather, preliminary movements were performed before the attacking movement was executed; more realistic data may be obtained by having the participants execute attacking movements including preliminary movements in the future. In future research, we believe that it is necessary to specifically analyze the kinematic characteristics of the upper limbs and other parts of the body in order to thoroughly study fencing execution techniques from a functional perspective. Furthermore, as the fencers who participated in this study were men with an average of 10 years of competition experience, we would like to obtain more comprehensive and detailed results targeting a variety of examinee characteristics (age, sex, competition level, etc.) in the future.
The results of this study would provide several important insights for coaches and trainers. First, regarding coaches, understanding the extent to which changes in target distance could affect kinematic variables during the lunge can aid in forming instruction as a new specific indicator of technique. During a match, the fencer needs to execute the lunge movements adapted to various distances during the attack and defense against the opponent. If the fencer is able to control the necessary lower extremity joint angles according to the target distance, this is expected to reduce counterattacks and defensive opportunities by the opponent. Second, it can also provide useful information for trainers. Fencers have been reported to have a high incidence of hip and knee joint injuries in the front leg [22]. A trainer’s understanding of the peak lower extremity angle and ROM required for each target distance during the lunge will provide useful insights for developing more specific lower extremity training and injury prevention programs.
5. Conclusions
This study aimed to evaluate the effects of different target distances on the front leg and rear leg lower extremity joint (hip, knee, and ankle joints) movements in the lunge. Therefore, detailed kinematic data were obtained for the front leg and rear leg lower limb joints at three different target distances. With increasing target distance, there was greater flexion of the rear knee joint early during the lunge followed by greater extension of the rear hip and knee joints, plantar flexion of the rear ankle joint, and a higher peak velocity of the CoM. It was also suggested that the target distance extension could significantly influence the hip and knee joint flexion of the front leg during the final control phase of the lunge. We suggest that the findings of this study would provide useful information to coaches and trainers in terms of improving athletes’ technical skills and managing conditioning in actual competition settings.
Supplementary Materials
The following supporting information can be downloaded at https://www.mdpi.com/article/10.3390/biomechanics4020020/s1. Table S1. Summary of motion data at the lower extremity joint (hip, knee, and ankle) angles of the rear leg viewed from the sagittal plane (N = 15; in degrees), Table S2. Summary of motion data on the lower extremity joint (hip, knee, and ankle) angles of the front leg viewed from the sagittal plane (N = 15; in degrees).
Author Contributions
Conceptualization, K.C., T.I., S.Y., and N.K.; Methodology, K.C., T.I., S.Y., Y.Y., and N.K.; Investigation, K.C., T.I., S.Y., and Y.Y.; Data Curation, K.C.; Formal Analysis, K.C.; Project Administration, K.C.; Supervision, K.C., T.I., S.Y., and N.K.; Writing—original draft, K.C.; Writing—review and editing: K.C., T.I., S.Y., and N.K. All authors have read and agreed to the published version of the manuscript.
Funding
This study was supported by JST SPRING, Grant Number JPMJSP2123.
Institutional Review Board Statement
The study was conducted according to the guidelines of the Declaration of Helsinki and was approved by the Ethics Committee of the Graduate School of System Design and Management, Keio University, Yokohma, Kanagawa, Japan (approval number: SDM-2022-E001).
Informed Consent Statement
Informed consent was obtained from all participants involved in the study.
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to privacy concerns.
Acknowledgments
We thank the fencers for giving their best performance in the protocol of this study.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Barth, B.; Beck, E. Performance structure, performance capacity and performance development (Chapter 2). In The Complete Guide to Fencing; Barth, B., Beck, E., Eds.; Meyer & Meyer Verlag: Aachen, Germany, 2007. [Google Scholar]
- Aquili, A.; Tancredi, V.; Triossi, T.; De Sanctis, D.; Padua, E.; D’Arcangelo, G.; Melchiorri, G. Performance analysis in sabre. J. Strength Cond. Res. 2013, 27, 624–630. [Google Scholar] [CrossRef]
- Turner, A.; Bishop, C.; Chavda, S.; Edwards, M.; Brazier, J.; Kilduff, L.P. Physical Characteristics Underpinning Lunging and Change of Direction Speed in Fencing. J. Strength Cond. Res. 2016, 30, 2235–2241. [Google Scholar] [CrossRef] [PubMed]
- Wojciechowski, Z. Principles of coaching (Chapter 2). In This is Fencing! Advanced Training and Performance Principles for Foil; Wojciechowski, Z., Ed.; Crowood: Marlborough, UK, 2019. [Google Scholar]
- Gholipour, M.; Tabrizi, A.; Farahmand, F. Kinematics analysis of lunge fencing using stereophotogrametry. World J. Sport Sci. 2008, 1, 32–37. [Google Scholar]
- Bottoms, L.; Greenhalgh, A.; Sinclair, J. Kinematic determinants of weapon velocity during the fencing lunge in experienced épée fencers. Acta Bioeng. Biomech. 2013, 15, 109–113. [Google Scholar] [PubMed]
- Chida, K.; Inami, T.; Yamaguchi, S.; Yoshida, Y.; Kohtake, N. Relationship between Body Center of Mass Velocity and Lower Limb Joint Angles during Advance Lunge in Skilled Male University Fencers. Biomechanics 2023, 3, 377–388. [Google Scholar] [CrossRef]
- Gresham-Fiegel, C.N.; House, P.D.; Zupan, M.F. The effect of nonleading foot placement on power and velocity in the fencing lunge. J. Strength Cond. Res. 2013, 27, 57–63. [Google Scholar] [CrossRef] [PubMed]
- Guan, Y.; Guo, L.; Wu, N.; Zhang, L.; Warburton, D.E.R. Biomechanical insights into the determinants of speed in the fencing lunge. Eur. J. Sport Sci. 2018, 18, 201–208. [Google Scholar] [CrossRef]
- Guilhem, G.; Giroux, C.C.; Couturier, A.; Chollet, D.; Rabita, G. Mechanical and muscular coordination patterns during a high-level fencing assault. Med. Sci. Sports Exerc. 2014, 46, 341–350. [Google Scholar] [CrossRef] [PubMed]
- Morris, N.; Farnsworth, M.; Robertson, D.G. Kinetic analyses of two fencing attacks—Lunge and fleche. Port. J. Sport Sci. 2011, 11, 343–346. [Google Scholar]
- Mulloy, F.; Mullineaux, D.R.; Irwin, G. Use of the kinematic chain in the fencing attacking lunge. In Proceedings of the International Conference on Biomechanics in Sports, Poitiers, France, 28 June–2 July 2016; pp. 1114–1117. [Google Scholar]
- Chida, K.; Inami, T.; Yamaguchi, S.; Nishioka, T.; Yoshida, Y.; Kohtake, N. Assessing the validity of two-dimensional video analysis for measuring lower limb joint angles during fencing lunge. Front. Sports Act. Living 2024, 6, 1335272. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Chen, T.L.; Wong, D.W.; Wang, Y.; Ren, S.; Yan, F.; Zhang, M. Biomechanics of fencing sport: A scoping review. PLoS ONE 2017, 12, e0171578. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.W.; Kwon, M.S.; Yenuga, S.S.; Kwon, Y.H. The effects of target distance on pivot hip, trunk, pelvis, and kicking leg kinematics in Taekwondo roundhouse kicks. Sports Biomech. 2010, 9, 98–114. [Google Scholar] [CrossRef] [PubMed]
- Cohen, J. Statistical Power Analysis for the Behavioral Sciences, 2nd ed.; Lawrence Erlbaum: Hillsdale, NJ, USA, 1988. [Google Scholar]
- Gutiérrez-Dávila, M.; Rojas, F.J.; Antonio, R.; Navarro, E. Response timing in the lunge and target change in elite versus medium-level fencers. Eur. J. Sport Sci. 2013, 13, 364–371. [Google Scholar] [CrossRef] [PubMed]
- Williams, L.R.; Walmsley, A. Response amendment in fencing: Differences between elite and novice subjects. Percept. Mot. Ski. 2000, 91, 131–142. [Google Scholar] [CrossRef] [PubMed]
- Dempster, W.T. Space requirements of the seated operator. Geometrical kinematic and mechanical aspects of the body with special reference to the limbs. Tech. Rep. 1955, 55/159, 1–254. [Google Scholar]
- Bell, A.L.; Brand, R.A.; Pedersen, D.R. Prediction of hip joint centre location from external landmarks. Hum. Mov. Sci. 1989, 8, 3–16. [Google Scholar] [CrossRef]
- Błażkiewicz, M.; Borysiuk, Z.; Gzik, M. Determination of loading in the lower limb joints during step-forward lunge in fencing. Acta Bioeng. Biomech. 2018, 20, 3–8. [Google Scholar] [PubMed]
- Thompson, K.; Chang, G.; Alaia, M.; Jazrawi, L.; Gonzalez-Lomas, G. Lower extremity injuries in U.S. national fencing team members and U.S. fencing Olympians. Phys. Sportsmed. 2022, 50, 212–217. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).