Next Article in Journal
Split-Belt Treadmill Training Improves Mechanical Energetics and Metabolic Cost in Women with Unilateral Hip Osteoarthritis: A Proof-of-Concept Study
Previous Article in Journal
Relationship between Swimming Velocity and Trunk Twist Motion in Short-Distance Crawl Swimming
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Biomechanics
Volume 3
Issue 2
10.3390/biomechanics3020018
biomechanics-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Reliability of a Pendulum Apparatus for the Execution of Plyometric Rebound Exercises and the Comparison of Their Biomechanical Parameters with Load-Matching Vertical Drop Jumps

by
Vassilios Panoutsakopoulos
* and
Iraklis A. Kollias
Biomechanics Laboratory, School of Physical Education and Sport Science at Thessaloniki, Aristotle University of Thessaloniki, 54124 Thessaloniki, Greece
*
Author to whom correspondence should be addressed.
Biomechanics 2023, 3(2), 204-219; https://doi.org/10.3390/biomechanics3020018
Submission received: 6 February 2023 / Revised: 13 April 2023 / Accepted: 18 April 2023 / Published: 22 April 2023
(This article belongs to the Section Sports Biomechanics)
Browse Figures
Versions Notes

Abstract

:
The inability to control the body center of mass (BCM) initial conditions, when executing plyometric exercises, comprises a restrictive factor to accurately compare jumps executed vertically and horizontally. The purpose of the study was to present a methodological approach for the examination of BCM initial conditions during vertical drop jumps (VDJ) and plyometric rebound jumps performed with a pendulum swing (HPRJ). A system consisting of two force plates was used for the evaluation of VDJ. A bifilar pendulum, equipped with a goniometer and accelerometer, was constructed for the evaluation of the HPRJ. Kinematic parameters from both jump modalities were obtained by means of videography (100 Hz). Thirty-eight physically active young males executed VDJ and HPRJ with identical BCM kinetic energy at the instant of impact (KEI). Results revealed that participants produced higher power and lower force outputs at HPRJ (p < 0.01). The rate of force development was larger in VDJ, while hip movement was less in HPRJ. The use of the presented methodology provided the means to reliably determine the exact BCM release height during the execution of the examined jumps. This provided an accurate determination of the amount of KEI, being the main parameter of calculating load during plyometric exercise.

1. Introduction

Drop jumps (DJ) are the most recognized and commonly used method of plyometric training [1,2,3,4,5]. When executing a DJ, athletes drop from a raised surface and perform a maximal vertical jump after landing on the ground in the shortest possible ground contact time. Storage and utilization of muscle elastic energy are characteristic in DJ. During the eccentric (downward) phase, gravity forces the body to move downwards and energy is stored in the elastic components of the stretched muscles. This stored energy is utilized and summed to the energy produced during the concentric (upward) phase, e.g., when the body moves upwards [6].
Vertical ground reaction force (vGRF) and power output are suggested to distinguish the level of ability in terms of DJ performance [7]. Power production is a very important factor that affects drop jumping, which is essential for performance in individual and team sports [8,9]. During DJ, the stretch-shortening cycle of muscle function (SSC) is evident [10], since the impact to the ground forces the activated lower limb muscles to lengthen by acting eccentrically during the braking phase, followed by a concentric (shortening) action during the propulsion. The above mechanism results in enhanced jumping ability.
DJ performance is suggested to be characterized by high reliability and low variability [7,9,11,12,13]. Nevertheless, the kinetic energy at the instant of impact (KEI) is one of the most relevant parameters for the load definition in SSC [14]. However, the inaccurate determination of the initial conditions of the drop, namely the actual dropping height and the vertical body center of mass (BCM) velocity at touchdown, could result in erroneous calculations of DJ performance and its kinetic determinants. Under this perspective, Baca [15] detected the causes of invalid computation of actual dropping height, highlighting the spatiotemporal (flight time and the position of the BCM at the take-off in comparison to landing) and kinematic parameters (limited degrees of freedom of motion analysis methods) that have an effect and should be monitored. Furthermore, the comparison of different methods for the determination of variables concerning DJ performance led to the conclusion that the method using two force plates (one located under the drop platform) should be used as a reference method [16]. In addition, video-based methods were evaluated as the best alternatives as reported by the same researcher [16].
The quest for load specificity during plyometric jumps [17] and the requirement of avoiding injuries during their execution [18], has led to the introduction of alternative devices such as the sledge ergometer [19,20,21] and the pendulum swing [22]. The latter was developed by Kusnetsov [23] and was widely used in Eastern Europe, in order to simulate DJ training [24]. It is suggested that the benefit of the usage of those devices was the lack of the necessity for postural control during execution, since the latter elaborates the athlete to utilize all the energy produced in order to perform the jump [25].
Past research examined the application of the pendulum swing as a research tool to study its effectiveness as a plyometric training device [26,27,28,29,30]. Furthermore, it has been used for the evaluation of parameters determining lower extremity plyometric function and force generation capability [24,31,32,33]. In previous research, the similarity between DJ (DJs from 28 cm) and pendulum jumps (10 consecutive pendulum swings) was examined [28]. Greater ground reaction forces were observed for the DJ, while ankle joint range of motion was larger and hip joint angle was smaller at the instant of first contact and takeoff at the pendulum exercises. Furthermore, during the eccentric phase, smaller ankle and knee joint values were observed in the pendulum swings. However, a similar coordination strategy between the two exercises was observed [28]. In agreement, it was suggested that the neuromuscular system has the ability to provide consistent movement coordination as a response to the plyometric exercise of pendulum rebound jumps, even when the chair of the pendulum is set at different settings [34,35].
Although loading in DJ can be defined by the height of the drop and thus its biomechanics can be examined in relation to the load imposed by the task, this was not established in the past research concerning pendulum jumps. The comparisons of the pendulum jump biomechanics against DJ biomechanics were performed by analyzing a trial that was selected based on the largest amplitude of the pendulum [28] or the flight time between two consecutive pendulum rebound jumps [34]. The lack of monitoring of the BCM initial conditions (height during take-off from the raised platform and kinetic energy at the instant of impact) during the execution of vertical drop jumps (VDJ) and the plyometric jumps performed with a pendulum swing (HPRJ), comprises a restrictive factor to accurately compare those jumping modalities. Another issue is the variability observed for the above-mentioned criterion, as it was found that the amplitude of the pendulum swing in a series of HRPJ is more stable after the first five rebounds [36]. Thus, it is necessary to improve the experimental setup of HPRJ research, so that BCM initial conditions could be accurately defined, in order to accomplish a more valid and reliable execution of the single repetition HPRJ exercise.
The aim of the present study was to present a methodological approach for comparing VDJ and HPRJ when the same initial loading conditions are applied, as this could provide detailed insights into the comparison of HPRJ and VDJ biomechanics. It was hypothesized that, due to the added mass and the equality of kinetic energy at impact, the reaction forces and the power output would be larger in the HPRJ than in the VDJ. In addition, it was also hypothesized that the requirement to overcome the increased loading will result in a larger joint angle range of motion (ROM) in the HPRJ compared to the VDJ.

2. Materials and Methods

2.1. Design of the Study

At first, the validity of the methods to evaluate HPRJ performance was tested. Then, the VDJs were performed to define the target KEI to be set for the execution of the respective HPRJ. Finally, the HPRJs were performed with the same KEI and their parameters were compared to those of the VDJs.

2.2. Participants

Thirty-eight physically active young males (n = 38, age: 22.4 ± 4.0 years, height: 1.85 ± 0.05 m, body mass: 81.8 ± 8.2 kg) volunteered to participate in the study. Participants were informed about the purposes of the study and gave their signed consent. All participants were in good physical condition, and were physically active for at least 6 h/week, with no apparent or reported injury or disability. All participants provided a signed informed consent. The study was conducted following the guidelines of the Declaration of Helsinki and of the Institution’s Research Committee Ethics Code.

2.3. Instruments

2.3.1. Vertical Drop Jumps

For the evaluation of the VDJ, a system consisting of two force plates was used. A one-dimensional force-plate (1-Dynami, ©: Biomechanics Lab AUTh, Thessaloniki, Greece) was used to record the vGRF during the step-off [37] from the raised platform. It was used to calculate the exact BCM dropping height, using the vGRF data and the duration of the impulse. An AMTI Mod. OR6-5-1 (AMTI, Newton, MA, USA) force-plate was used to record the vGRF during contact with the ground. This setup is depicted in Figure 1a and was used to determine VDJ performance variables as described elsewhere [7].

2.3.2. Horizontal Pendulum Rebound Jumps

For the evaluation of the HPRJs, a bifilar pendulum was constructed, which allowed participants to swing toward a dynamometer attached to the wall (Figure 1b). The benefit of using the bifilar pendulum, in comparison to the simple pendulum apparatus used in the previous related literature, is that, when the pendulum is rotated from its two solid axes of rotation, the level that is determined by the lower ends of its arms is constant and parallel to the horizontal. Thus, the motion of the pendulum’s seat is always parallel to the ground and the execution of the HPRJs can be conducted perpendicularly to the dynamometer mounted to the wall. Another advantage is that its arms can be constructed in any desired length, without any effects from its mass [38]. The bifilar pendulum was comprised of a seat suspended by four parallel 250 × 6 × 3 cm aluminum arms. The back of the seat had a 145° inclination. The total mass of the seat and the bifilar pendulum was 42.5 kg. Additional details of the mechanical properties of the pendulum are presented in Appendix A.
The pendulum arms were rotated round two parallel bars attached to a fixation plate on the ceiling. The fixation plate was adjustable in order to allow subjects with different body heights to have contact with the wall dynamometer with fully extended legs, while the seat was at the lowest position of its trajectory. A custom-made dynamometer (2-Dynami, ©: Biomechanics Lab AUTh, Thessaloniki, Greece) was mounted on the wall and was used to record the horizontal wall reaction forces (hWRF). The procedure to calibrate the wall dynamometer and its validity are presented in Appendix B.
For the purpose of monitoring the kinetics of the pendulum and the seated subject, the following instruments were attached to the pendulum:
  • A pendulous foothold with a shock absorbing system connected to a Kistler 932-1B force-transducer (FTD; Kistler Instrumente AG, Winterthur, Switzerland). It was used to guide subjects’ lower extremities to the wall dynamometer; it was also used to calculate any contribution of the lower extremity in the vertical component.
  • A Lucas R60D (Lucas Control Systems Products, Hampton, VA, USA) electronic goniometer, which was used to monitor the temporal angular position of the bifilar pendulum. It was attached at the front-up parallel bar.
  • A Kyowa AS-20GB (Kyowa Electronic Instruments Co., Japan) accelerometer, which was used to monitor the instant velocity of the bifilar pendulum.
Signals from the wall dynamometer and the accelerometer were amplified using Kyowa DPM-601B (Kyowa Electronic Instruments Co., Chofu, Tokyo, Japan) amplifiers. Signals from the force-transducer were amplified using a Kistler 5037A-1211 (Kistler Instrumente AG, Winterthur, Switzerland) amplifier. All signals were simultaneously recorded and stored in a Pentium ΙΙ PC, using a 12-bit analog-to-digital converter (PC-LabCard PCL-812, Advantech Co., Ltd., Taipei, Taiwan) A/D card. Sampling frequency was set to 500 Hz. Signals were digitally smoothed using a 4th-order low-pass Butterworth filter, with cut-off frequency set at 15 Hz.

2.3.3. Video Recording

Both VDJs and HPRJs were filmed using a JVC GR-DVL 9600 EG (Victor Company of Japan Ltd., Yokohama, Japan) digital video camera, operating with a sampling frequency of 100 fps. The camera was placed 5 m perpendicular to the plane of motion and was based on a fixed tripod at a height of 1.2 m. A 2.5 m × 1.25 m calibration frame with 12 markers was also recorded to conduct a 2D-DLT analysis for the calculation of the lower limb joints’ kinematics.

2.4. Experimental Procedure

The warm-up and familiarization procedure has been described in detail previously [7]. At first, the VDJs were performed and the participants were informed about the execution of the step-off from the drop platform and to keep the arms akimbo during the execution. The instruction was to “jump as high as you can with the minimum ground contact time”. Each participant performed, bare-footed, three VDJs from 40 cm. A minimum 60 s interval, in order to avoid fatigue, was allowed between trials. The raised platform dynamometer was adjusted to permit subjects to land at the center of the ground force plate. Such an arrangement contributed to a safe execution and an accurate evaluation of the jumps.
Fifteen minutes after the completion of the last VDJ, the participants were adjusted on the pendulum seat with a five-point fixing belt. The pendulum was fixed in a position so that participants could touch the wall force dynamometer with the joints of their lower extremities fully extended when the pendulum was at its lowest position of its trajectory. Identical KEI to the wall dynamometer was accomplished by elevating the bifilar pendulum to the proper release height (HR) using a Kabit SHZ-500 (Kabit Deutschland GmbH, Ismaning, Germany) electrical hoist. Participants were instructed to execute the HPRJs utilizing a “jump as far as you can with the minimum wall contact time” pattern. All three HPRJ trials were executed bare-footed, while upper extremities were held crossed on the torso. A minimum 60 s interval between trials was also provided.

2.5. Data Analysis

2.5.1. Kinematic and Kinetic Parameters Derived from the Force Recordings

The analysis of the recorded time curves provided the following parameters [7,36,39,40] using the modules of the K-Dynami (©: Iraklis A. Kollias) software:
  • Spatial parameters: jump height (HJUMP); actual drop take-off height (hDROP); height of release (HR) of the pendulum; BCM vertical displacement during the braking (SBR) and propulsion (SPR) phases.
  • Temporal parameters: total ground contact time (tC); braking phase duration (tBR); time to achieve maximum vGRF/hWRF (tFMAX); time to achieve peak power during the propulsion phase (tPMAX).
  • Kinematic parameters: BCM velocity at the instants of touchdown (VTD) and take-off (VTO).
  • Kinetic parameters: peak force output (F); peak rate of force development (RFD); power in the propulsion phase (P); vertical stiffness (KVERT); leg stiffness (KLEG).

2.5.2. Definition of the KEI for the Horizontal Pendulum Rebound Jumps

HPRJ performance was calculated based on initial BCM conditions after push-off phase, which was verified by the signals from the electronic goniometer, the accelerometer, and from the video analysis [40]. During the rest period between the jumping modalities, the analysis of the best VDJ (criterion: HJUMP) provided the exact KEI that was used as input to set the HR for the HPRJ. The bifilar pendulum was set to be released from a HR that would allow identical KEI compared to VDJ as shown in Equation (1):
H R = m S ⋅ h D R O P m S + m P
where HR is the BCM release height for HPRJ condition, mS is the participant’s body mass, mP is the mass of the bifilar pendulum, and hDROP is the BCM drop height for the VDJ condition. The best HPRJ attempt, defined by the criterion of maximal HJUMP calculated from VTO, was selected for further analysis, namely the comparison with the VDJ.

2.5.3. Kinematic Parameters Derived from the Video Analysis

The anatomical points that were manually digitized at each field using the K-Motion (K-Invent, Montpellier, France) software and that were used for the kinematic analysis were the following: head of the 5th metacarpal, ulna-styloid process, lateral epicondyle of the humerus, acromion, top of the head, 7th cervical vertebra, greater trochanter, lateral epicondyle of the femur, posterior surface of the calcaneus, lateral malleolus, tuberosity of the 5th metatarsal, and proximal medial phalanx. In the case of the HPRJs, pairs of markers on each of the pendulum’s arms were also digitized. The coordinates of the center of mass were calculated for every field using the method of segments [41], as follows (Equation (2)):
C B C M = ∑ i = 1 n [ P i − ( P i − D i ) ⋅ q i ] ⋅ m i
where CBCM is the coordinates of BCM, Pi is the coordinates of the proximal point of the ith segment, Di is the coordinates of the distal point of the ith segment, Qi is the distance of the center of mass of the ith segment from its distal point, mi is the relative mass of the ith segment compared to whole body mass, and n is the number of body segments (n = 14).
Temporal position of the center of mass of the system pendulum + participant was calculated using Equation (3):
C Σ = C B C M ⋅ m S + C P C M ⋅ m P m S + m P
where CΣ is the coordinates of the center of mass of the system, CBCM is the coordinates of subject’s BCM, CPCM is the coordinates of the bifilar pendulum’s center of mass, mS is participant’s body mass, and mP is the mass of the bifilar pendulum (=42.5 kg).
A 2nd order low-pass Butterworth filter, with a cut-off frequency ranging from 4 to 6.5 Hz, depending on the noise calculated with residual analysis [42], was used for smoothing the data. The examined angular kinematic parameters were the ankle (ANK), knee (KNEE), and hip (HIP) angle (θ) at the instance of touchdown (td), maximum BCM displacement during contact with the force-plates (low), and take-off (to). In addition, the peak angular velocity (ω) and range of motion (ROM) of the lower limb joints during the braking and propulsion phases were calculated. Furthermore, for the calculation of KLEG, the leg length was extracted as the perpendicular displacement of the greater trochanter relative to the lateral malleolus.

2.5.4. Signal Synchronization

The synchronization of the kinematic and kinetic data was accomplished with Lagrange interpolation, using the K-Motion (K-Invent, Montpellier, France) software. The time instants of take-off, achievement of maximal BCM velocity, and achievement of peak BCM acceleration from both signals, as extracted from both the force and video recordings, were used for reference.

2.6. Statistical Analysis

The collected data were checked for normality in their distribution using the Kolmogorov–Smirnov test (p > 0.05). Intra-test reliability was tested using the two-way random with absolute agreement intraclass correlation coefficient (ICC) for both VDJ and HPRJ on the values using the three trials for each jumping task. Inter-instrument reliability of the HPRJ assessment was also tested using the same ICC test correlating the mean values for each participant among the three instruments (wall dynamometer, accelerometer, and goniometer). For all cases, the single measure ICC values were used, with confidence intervals set at 95%. ICCs of <0.40, 0.40–0.75, and >0.75 were interpreted as poor, fair to good, and excellent reliability, respectively [43].
For the comparison of the kinetic and kinematic characteristics of VDJ and HPRJ, paired samples t-test was used. Cohen’s d was calculated for every comparison to investigate the effect size, with values of ≤0.49, 0.50–0.79, and, ≥0.80 being interpreted as small, medium, and large effect sizes, respectively [44].
The level of significance for all analyses was set at a = 0.05. All statistical procedures were performed using the IBM SPSS Statistics v.27.0.1.0 software (International Business Machines Corp., Armonk, NY, USA).

3. Results

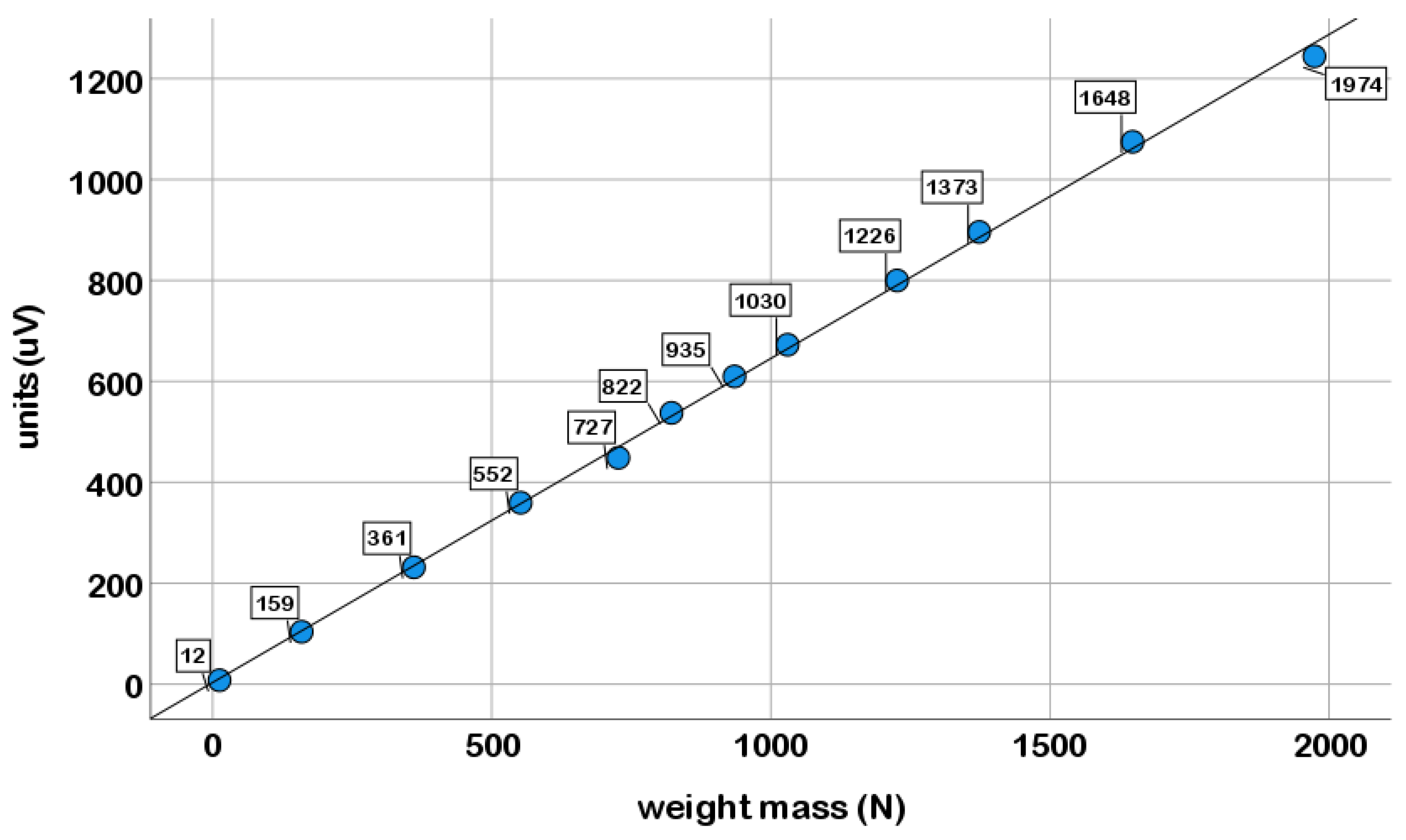
3.1. Reliability Measures

Excellent inter-instrument reliability of the calculation of HPRJ performance was revealed based on the extracted ICC (=0.835, 95% confidence interval = 0.773–0.884). Fair/good to excellent intra-test reliability scores were revealed for the performance of VDJ and HPRJ (ICC = 0.823, 95% confidence interval = 0.640–0.921, and ICC = 0.870, 95% confidence interval = 0.743–0.939, respectively).

3.2. Comparison between VDJ and HPRJ

3.2.1. Spatiotemporal, Kinetic, and Kinematic Parameters

For the VDJ, hDROP was 30.1 ± 4.5 cm instead of the nominal hDROP of 40.0 cm. On the other hand, the monitored bifilar pendulum allowed the initiation of the HPRJ at a HR of 20.0 ± 0.1 cm. Thus, KEI was almost identical between the two jumping modalities (Table 1). Table 1 presents the comparison of the spatiotemporal and kinematic parameters of the VDJ and the HPRJ.
Performance (HJUMP) was not different (p > 0.05) between the two jumping tests. Data analysis revealed significant (p < 0.05) differences between VDJ and HPRJ for SBR, tFMAX, VTO, and VTD.
Table 2 depicts the comparison of the kinetic parameters between VDJ and HPRJ. F was significantly (p < 0.05) larger at VDJ compared to HPRJ. However, F relative to body mass was significantly (p < 0.05) larger in HPRJ. In addition, P was significantly (p < 0.05) larger in HPRJ. However, when P was expressed relative to body mass, no differences (p > 0.05) were observed between the two jumping tests. Concerning the examined stiffness parameters, only KVERT differed significantly (p < 0.05) between VDJ and HPRJ.
The above-mentioned differences are also observed in the mean (n = 38) time curves of the examined parameters (Figure 2). Although similarly progressed during the contact phase, the lower F and SBR resulted in lower KVERT in HPRJ compared to VDJ.

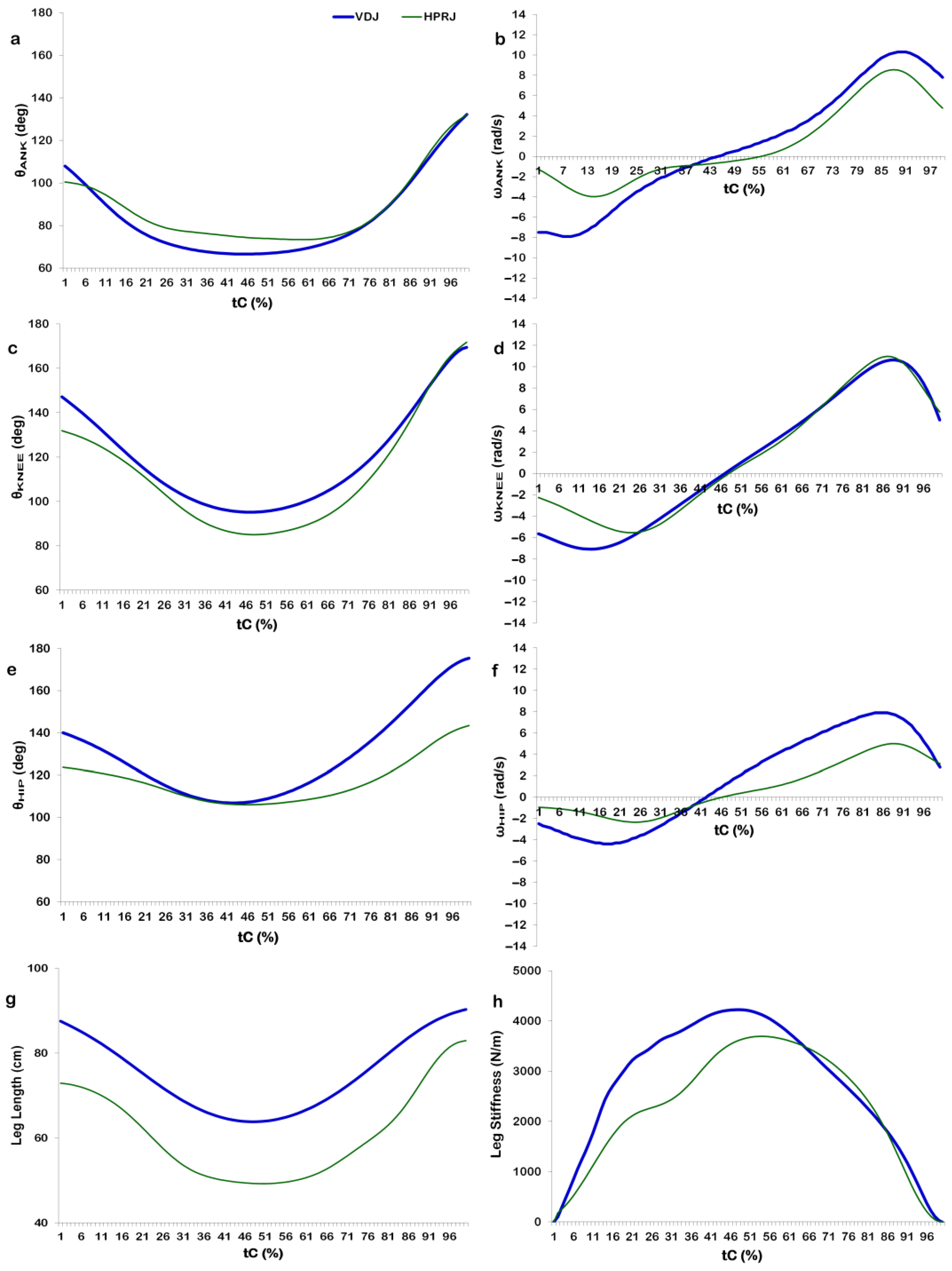
3.2.2. Joint Angular Kinematic Parameters

Table 3 presents the comparison of the joint angular kinematic parameters of the VDJ and the HPRJ. With the exception of the θKNEE and θHIP at the maximum BCM displacement during the braking phase, all other examined angles were significantly (p < 0.05) different. At the same instant, θANK was significantly (p < 0.05) more extended in the HPRJ than the VDJ. All examined lower extremity joints were significantly (p < 0.05) more extended in the VDJ compared to the HPRJ at the instances of touchdown and take-off. In addition, significantly (p < 0.05) larger ROM was observed in the VDJ for both the braking and propulsion phases. With the exception of ωHIP, no differences (p > 0.05) were observed between the jumping tests for the peak joint angular velocity.
The mean (n = 38) time curves of the examined joint angular kinematic parameters are presented in Figure 3. It was observed that at the HPRJ, the ankle and hip joints remain at their maximum flexion point for a relatively longer period compared to the VDJ. In addition, it seems that the knee joint was rapidly extended during the last third of the support phase of the HPRJ.
The time history of lower extremity joints’ angular velocity revealed the existence of a similar progression pattern throughout the contact phase in both jumping tests (Figure 3b,d,f). Although larger leg length values were recorded during the VDJ, a similar progression pattern was also present (Figure 3g).

4. Discussion

The purpose of the present study was to examine the reliability of a novel pendulum swing apparatus for the execution of HPRJ that could subject participants to an identical KEI as in the VDJ in order to allow the comparison of HPRJ and VDJ biomechanics when performed with the same initial loading conditions. The present findings suggest that the execution of HPRJ using a bifilar pendulum was highly reliable. Given the fact that the same initial conditions were applied, jumping height and relative power output were not different, while the relative force output and the lower limb joints’ ROM were larger in the VDJ compared to the HPRJ.
The results of the present study concerning the VDJ biomechanical parameters are in logical agreement with those reported in previous studies [7,16,45,46,47,48]. Differences between the nominal drop height and hDROP have been also found in the past [7,46,49,50]. However, the hDROP values reported for VDJ from 40 cm in previous research [16,48,51] ranged from 35 to 45 cm are not in agreement with the hDROP measured in the present study (30.1 ± 4.5 cm), which is closer to the findings of Geraldo et al. [52].
Comparing the present results with previous studies examining HPRJ, it is concluded that tC is almost identical with what was reported in the past [28]. Reduced relative F and RFD in HPRJ compared to VDJ was also reported [27,28]. The present findings are in agreement with these findings. In addition, larger P values in the propulsive phase of the HPRJ than the VDJ have been reported as well [26,32]. Nevertheless, it is not evident that KEI was controlled in previous studies. The ankle and knee joint angles at the maximum BCM displacement during the contact phase are similar to those reported by Fowler and Lees [28]. With respect to the findings of the same study, although ωANK was similar, different trends concerning the differences in ωKNEE and ωHIP patterns between VDJ and HPRJ were observed in the present research. This finding seems to be connected with the higher mass of the participant + pendulum system during the execution of the HPRJ while keeping the same kinetic energy at initial contact as in the VDJ.
The lower relative F, SBR, and SPR values during HPRJ can be attributed to the immobilization of the torso because of the fixing on the chair and the consequent lack of contribution of the hip extensors to optimally respond to the required prerequisites for the execution of the SSC. This could also explain the decreased lower extremity joints’ ROM during the HPRJ. The changes observed concerning the lower extremity joints’ angular displacement between VDJ and HPRJ may have caused alterations to the force–length relationships of lower extremity muscles, leading to differences in the force and power production capabilities, as it has been suggested that the muscle-tendon length of the biarticular muscles spanning the knee and hip joints were altered during different pendulum seat arrangements [34,35].
Force and power outputs are considered to define VDJ performance [7,9]. The increased loading imposed in the SSC during the braking phase of the VDJ leads to larger power output compared to the squat and countermovement vertical jumps [46,53,54]. In the case of the HPRJ, the larger power output with lesser force output can be interpreted as an absence of the necessity to prevail over the body mass. The fact that applied force is efficiently utilized to enhance jumping ability because of the lack of postural control during contact has been also used to interpret jumping performance when using a sledge ergometer [25]. The latter is also evident during the VDJ propulsion phase, when someone has to produce additional force in the vertical axis in order to overcome the gravitational forces applied to his/her body mass. Contrarily, during the HPRJ, the absence of the influence of the gravitational forces does not require an additional force output, since the movement is entirely executed horizontally. This results in the fact that body mass times acceleration of gravity equals zero and, consequently, the applied force is efficiently utilized to enhance the jumping ability because of the lack of postural control during the contact phase [36]. However, in the case of the HPRJ, the participants had to conduct the plyometric task and to negotiate, besides their body mass, the mass of the pendulum as well. When the stretch load is increased, force output is increased and tFMAX is decreased in the VDJs [46,55,56]. This was also observed during collisions using a human pendulum device [57]. In the present study, relative F was lower and tFMAX was higher in the HPRJ than in the VDJs. Further research should be conducted examining HPRJs with different loading conditions.
A larger knee flexion and a larger shortening velocity induced by the higher stretch loads are factors that enhance the effectiveness of the SSC [10]. It has been suggested that the knee joint angular kinematics is the regulating factor of HPRJ performance [35,36]. Alterations in the knee joint angular kinematics due to the increment of the stretch load were observed in previous impact [57] and SSC studies [25,49,58]. However, in the present study, the maximum knee flexion joint angle and velocity were not different between the two jumping modalities. In addition, the execution of a plyometric exercise in the horizontal plane was found to alter the muscle activation characteristics [49]. Thus, future research in HPRJ should examine its electromyographic characteristics.
Stiffness, although its optimal regulation enhances performance and power output [59,60,61], was not found to be a determining feature for VDJ performance [7,62]. Nevertheless, KVERT was significantly higher in the VDJ than in the HPRJ. This can be related to the increased BCM velocity at the instant of impact in the VDJ. This possibly resulted in higher stimulation of the neuromuscular system during the breaking phase to optimally regulate the power output and stiffness in the VDJ [45,63,64] compared to the HPRJ.
The findings of the present study should be interpreted taking into account its limitations. At first, the comparison of VDJ and HPRJ was conducted by taking as reference only one dropping height. However, this selection was based on the fact that most of the DJ research has been conducted using VDJs with drop heights up to 40 cm [65] and on previous recommendations [46]. Furthermore, SSC effectiveness during a DJ is affected by both the direction of the movement, referred to the gravitational acceleration, and the duration of preactivation [66]. Thus, as mentioned above, recording the electromyographic parameters in the HPRJ test could provide additional information about the neuromuscular function and the mechanisms involved when executing a controlled SSC at the horizontal level.
In the present study, the usage of two dynamometers for the execution of VDJ provided the opportunity to define hDROP and, thus, HR accurately. This assisted in the calculation of the exact amount of KEI for the HPRJ, which has been reported to be the main parameter of evaluating loading during plyometric exercise [67]. It has been reported that the HR deviation compared to the nominal release height for the plyometric jumps performed with a sledge ergometer is ±3 cm [49]. The lower HR deviation (±0.1 cm), compared to the nominal HR set for the HPRJ condition, allows the constructed bifilar pendulum to be classified as a valid and reliable device for executing controlled pendulum rebound exercises. In addition, the excellent intra-test reliability scores for HPRJ performance verified past findings [68]. This can be attributed to the fact that the trunk was constrained by the bifilar pendulum’s seat. This results in a reduced number of degrees of freedom that leads to a higher consistency of the execution of the pendulum plyometric rebound exercise [34]. Furthermore, the utilization of four different methods (dynamometry, goniometry, accelerometry, and video kinematic analysis) for monitoring and accurately measuring HPRJ performance parameters, provides a strong methodological tool for further insight regarding the examination of different modalities of plyometric exercise.
In conclusion, further research should examine the responses of the neuromuscular system and the coordination patterns of the HPRJ in different KEI conditions. Insights into the optimization of the lower limbs’ mechanical efficiency in the HPRJ could provide further information concerning the possible improvement in the training process to provoke adaptations in mechanical power production.

5. Conclusions

The use of two force plates is suggested as a requisite for examining VDJ or landing experiments, as proposed in earlier literature [16]. Furthermore, HPRJs are favorable to be executed with a bifilar pendulum, since their mechanical properties allow the execution of plyometric movement on the horizontal plane. The instrumented bifilar pendulum used in the present study had excellent inter-instrument reliability for the calculation of HPRJ performance. Furthermore, based on the findings of the present study, HPRJs performed with the examined bifilar pendulum apparatus were characterized by excellent intra-test reliability scores. The latter enhances the comparison of plyometric exercise in the vertical and horizontal directions since the initial BCM conditions can be accurately defined. Such an arrangement allows an athlete’s KEI to be defined when executing a VDJ or a HPRJ. This results in the fact that a practitioner can define the desired level of loading when executing a plyometric jump, whatever the jumping modality (vertical or horizontal). Furthermore, the lower extremity joints’ function and range of motion can be selected, so that the execution of the jump can fulfill the principle of specificity and, thus, meet the sport-specific plyometric training requirements. Finally, it is concluded that future research should take into consideration the initial BCM conditions for the accurate determination of the parameters of a plyometric jump.

Author Contributions

Conceptualization, V.P. and I.A.K.; methodology, V.P. and I.A.K.; software: I.A.K.; validation, V.P.; formal analysis, V.P. and I.A.K.; investigation, V.P.; resources, I.A.K.; data curation, I.A.K.; writing—original draft preparation, V.P.; writing—review and editing, V.P. and I.A.K.; visualization, I.A.K.; supervision, I.A.K.; project administration, I.A.K. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

The study was conducted in accordance with the Declaration of Helsinki, and approved by the Institutional Review Board of the Aristotle University of Thessaloniki (16/10.01.2000).

Informed Consent Statement

Informed consent was obtained from all subjects involved in the study.

Data Availability Statement

The data that were used in the present study can be provided by the corresponding author upon reasonable request.

Conflicts of Interest

The authors declare no conflict of interest.

Appendix A

Table A1 depicts the mechanical properties of the pendulum used for the HPRJs.
Table
Table A1. The mechanical properties of the pendulum.
Table A1. The mechanical properties of the pendulum.
Mass
(kg)		Amplitude Period
(s)		Center of Mass
(m)		Moment of Inertia (kg·m2)Radius of Inertia
(m)		Center of Percussion (m)
42.53.01.541461.852.24

Appendix B

The 2-Dynami dynamometer (©: Biomechanics Lab AUTh, Thessaloniki, Greece) was constructed using ST42 steel, on which pairs of Kyowa KL-10-A4 (Kyowa Electronic Instruments Co., Chofu, Tokyo, Japan) strain- gauges were attached. Signals were amplified using Kyowa DPM-601B (Kyowa Electronic Instruments Co., Chofu, Tokyo, Japan) amplifiers and were simultaneously stored in a Pentium ΙΙ PC, after being converted to digital using a PC-LabCard PCL-812PG (Advantech Co. Ltd., Taipei, Taiwan) 12-bit analog-to-digital converter. were calibrated statically and dynamically, using an AMTI Mod. OR6-5-1 (AMTI, Newton, MA, USA) force plate. To check the dynamometer’s concurrent validity, free weights of known mass (commercial plates used in weightlifting) were used. The weight plates were weighed with a Delmac PS400L scale (Delmac Scales PC, Athens, Greece) prior to their use for the calibration procedure. The dynamometer was fixed on the ground and a series of combinations among the known weights, ranging from 1.25 to 194.5 kg, was placed on the middle of the dynamometer plates. In total, 170 different combinations of weights were placed. For each weight, the equivalent measure from the dynamometer was stored (Figure A1). The calibration procedure and the subsequent linear regression analysis (enter method) revealed that the constructed dynamometer was linear (Y = 3.586 + 0.642 × X; F = 9261,467, p < 0.001, R2 = 0.999) and valid (average error = 0.084 ± 0.330 N).
Biomechanics 03 00018 g0a1 550
Figure A1. Data dispersion of 170 measures from known weights for the 2-Dynami dynamometer.
Figure A1. Data dispersion of 170 measures from known weights for the 2-Dynami dynamometer.
Biomechanics 03 00018 g0a1

References

  1. Bobbert, M.F. Drop Jumping as a Training Method for Jumping Ability. Sports Med. 1990, 9, 7–22. [Google Scholar] [CrossRef] [PubMed]
  2. Moran, J.; Ramirez-Campillo, R.; Liew, B.; Chaabene, H.; Behm, D.G.; García-Hermoso, A.; Izquierdo, M.; Granacher, U. Effects of Vertically and Horizontally Orientated Plyometric Training on Physical Performance: A Meta-analytical Comparison. Sports Med. 2020, 51, 65–79. [Google Scholar] [CrossRef] [PubMed]
  3. Ramirez-Campillo, R.; Álvarez, C.; García-Hermoso, A.; Ramírez-Vélez, R.; Gentil, P.; Asadi, A.; Chaabene, H.; Moran, J.; Meylan, C.; García-De-Alcaraz, A.; et al. Methodological Characteristics and Future Directions for Plyometric Jump Training Research: A Scoping Review. Sports Med. 2018, 48, 1059–1081. [Google Scholar] [CrossRef]
  4. De Villarreal, E.S.-S.; Kellis, E.; Kraemer, W.J.; Izquierdo, M. Determining Variables of Plyometric Training for Improving Vertical Jump Height Performance: A Meta-Analysis. J. Strength Cond. Res. 2009, 23, 495–506. [Google Scholar] [CrossRef]
  5. Wilson, J.M.; Flanagan, E.P. The Role of Elastic Energy in Activities with High Force and Power Requirements: A Brief Review. J. Strength Cond. Res. 2008, 22, 1705–1715. [Google Scholar] [CrossRef] [PubMed]
  6. Bosco, C.; Tihanyi, J.; Komi, P.V.; Fekete, G.; Apor, P. Store and recoil of elastic energy in slow and fast types of human skeletal muscles. Acta Physiol. Scand. 1982, 116, 343–349. [Google Scholar] [CrossRef]
  7. Panoutsakopoulos, V.; Chalitsios, C.; Nikodelis, T.; Kollias, I.A. Kinetic time-curves can classify individuals in distinct levels of drop jump performance. J. Sports Sci. 2022, 40, 2143–2152. [Google Scholar] [CrossRef]
  8. Ferreira, L.C.; Weiss, L.W.; Hammond, K.G.; Schilling, B.K. Structural and functional predictors of drop vertical jump. J. Strength Cond. Res. 2010, 24, 2456–2467. [Google Scholar] [CrossRef] [PubMed]
  9. Kollias, I.; Panoutsakopoulos, V.; Papaiakovou, G. Comparing jumping ability among athletes of various sports: Vertical drop jumping from 60 centimeters. J. Strength Cond. Res. 2004, 18, 546–550. [Google Scholar] [PubMed]
  10. Komi, P.V.; Nicol, C. Stretch-Shortening Cycle of muscle function. In Neuromuscular Aspects of Sport Performance; Komi, P.V., Ed.; Blackwell Publishing Ltd.: Oxford, UK, 2011; pp. 15–31. [Google Scholar]
  11. Ball, N.B.; Zanetti, S. Relationship Between Reactive Strength Variables in Horizontal and Vertical Drop Jumps. J. Strength Cond. Res. 2012, 26, 1407–1412. [Google Scholar] [CrossRef]
  12. Feldmann, C.R.; Weiss, L.W.; Schilling, B.K.; Whitehead, P.N. Association of Drop Vertical Jump Displacement with Select Performance Variables. J. Strength Cond. Res. 2012, 26, 1215–1225. [Google Scholar] [CrossRef] [PubMed]
  13. Nedeljkovic, A.; Mirkov, D.M.; Markovic, S.; Jaric, S. Tests of Muscle Power Output Assess Rapid Movement Performance When Normalized for Body Size. J. Strength Cond. Res. 2009, 23, 1593–1605. [Google Scholar] [CrossRef]
  14. Prilutsky, B.I. Work, Energy Expenditure and Efficiency of the Stretch-Shortening Cycle. J. Appl. Biomech. 1997, 13, 466–471. [Google Scholar] [CrossRef]
  15. Baca, A. Application of computer animation techniques for presenting biomechanical research results. Comput. Biol. Med. 1998, 28, 449–454. [Google Scholar] [CrossRef]
  16. Baca, A. A comparison of methods for analyzing drop jump performance. Med. Sci. Sports Exerc. 1999, 31, 437–442. [Google Scholar] [CrossRef]
  17. Kornecki, S. Relazione tra gradi di liberta’ cinematici e forza muscolare durante l’esecuzione di esercizi dinamici per l’alle-namento. Atleticastudi 1988, 19, 285–288. [Google Scholar]
  18. Tenisci, T. Pendulum swing. Track Tech. 1980, 81, 2591–2592. [Google Scholar]
  19. Kaneko, M.; Komi, P.V.; Aura, O. Mechanical efficiency of concentric and eccentric exercises performed with medium to fast contraction rates. Scand. J. Sports Sci. 1984, 1, 15–20. [Google Scholar]
  20. Aura, O.; Komi, P.V. Mechanical Efficiency of Pure Positive and Pure Negative Work with Special Reference to the Work Intensity. Int. J. Sports Med. 1986, 07, 44–49. [Google Scholar] [CrossRef]
  21. Bosco, C.; Belli, A.; Astrua, M.; Tihanyi, J.; Pozzo, R.; Kellis, S.; Tsarpela, O.; Foti, C.; Manno, R.; Tranquilli, C. A dynamometer for evaluation of dynamic muscle work. Eur. J. Appl. Physiol. Occup. Physiol. 1995, 70, 379–386. [Google Scholar] [CrossRef] [PubMed]
  22. Karpilowski, B.; Nosarzewski, Z.; Iskra, L.; Staniak, Z.; Trzaskoma, Z. Pendulum training unit. Biol. Sport 1989, 6 (Suppl. S3), 309–310. [Google Scholar]
  23. Dick, F.W. Sports Training Principles, 2nd ed.; A & C Black: London, UK, 1992; p. 180. [Google Scholar]
  24. Trzaskoma, Z.; Wit, A.; Iskra, L.; Karpilowski, B. Application of an pendulum training simulator in training strength of lower extremities muscles. Biol. Sport 1989, 6 (Suppl. S3), 214–220. [Google Scholar]
  25. Eloranta, V. Effect of postural and load variation on the coordination of the leg muscles in rebound jumping movement. Electromyogr. Clin. Neurophysiol. 1997, 37, 79–88. [Google Scholar]
  26. Fowler, N.E.; Trzaskoma, Z.; Wit, A.; Iskra, L.; Lees, A. The effectiveness of a pendulum swing for the development of leg strength and counter-movement jump performance. J. Sports Sci. 1995, 13, 101–108. [Google Scholar] [CrossRef]
  27. Fowler, N.E.; Lees, A.; Reilly, T. Changes in stature following plyometric drop-jump and pendulum exercises. Ergonomics 1997, 40, 1279–1286. [Google Scholar] [CrossRef]
  28. Fowler, N.E.; Lees, A. A Comparison of the Kinetic and Kinematic Characteristics of Plyometric Drop-Jump and Pendulum Exercises. J. Appl. Biomech. 1998, 14, 260–275. [Google Scholar] [CrossRef] [PubMed]
  29. Trzaskoma, Z. Application of the pendulum training simulator to increasing the strength-speed potential of human lower limb muscles. Biol. Sport 1994, 11 (Suppl. S6), 3–119. [Google Scholar]
  30. Trzaskoma, L.; Tihanyi, J.; Trzaskoma, Z. The Effect of a Short-Term Combined Conditioning Training for the Development of Leg Strength and Power. J. Strength Cond. Res. 2010, 24, 2498–2505. [Google Scholar] [CrossRef]
  31. Trzaskoma, Z.; Wit, A. Comparison of three laboratory tests of short duration with respect to the mechanical power output by lower limbs of junior tennis players. Biol. Sport 1996, 13, 145–154. [Google Scholar]
  32. Trzaskoma, Z.; Wit, A.; Eliasz, J. Comparison of three laboratory tests of short duration with respect to the mechanical power output by lower limbs of athletes. Biol. Sport 1996, 13, 61–69. [Google Scholar]
  33. Trzaskoma, Z. Mechanical power output of lower limbs in advanced male tennis players. Biol. Sport 1997, 14, 55–63. [Google Scholar]
  34. Rodacki, A.L.F.; Fowler, N.E. Intermuscular coordination during pendulum rebound exercises. J. Sports Sci. 2001, 19, 411–425. [Google Scholar] [CrossRef] [PubMed]
  35. Rodacki, A.L.F.; Fowler, N.E.; Bennett, S. The Effect of Postural Variations in Movement Co-Ordination during Plyometric Rebound Exercises. J. Appl. Biomech. 2001, 17, 14–27. [Google Scholar] [CrossRef]
  36. Panoutsakopoulos, V.; Kollias, I.; Chomatas, D. Performance and variability of biomechanical parameters in consecutive plyometric pendulum rebound jumps. In Book of Abstracts of the 4th International Conference on Strength Training, Serres, Greece, 3–7 November 2004; Kellis, E., Amiridis, I., Vrabas, I., Eds.; Aristotle University of Thessaloniki: Serres, Greece, 2004; pp. 161–163. [Google Scholar]
  37. Wilder, J.N.; Riggins, E.R.; Noble, R.A.; Lelito, C.M.; Widenhoefer, T.L.; Almonroeder, T.G. The effects of drop vertical jump technique on landing and jumping kinetics and jump performance. J. Electromyogr. Kinesiol. 2021, 56, 102504. [Google Scholar] [CrossRef] [PubMed]
  38. Den Hartog, J.P. Mechanics; Dover Publications, Inc.: New York, NY, USA, 1961; pp. 247–248. [Google Scholar]
  39. Giatsis, G.; Panoutsakopoulos, V.; Kollias, I.A. Drop Jumping on Sand Is Characterized by Lower Power, Higher Rate of Force Development and Larger Knee Joint Range of Motion. J. Funct. Morphol. Kinesiol. 2022, 7, 17. [Google Scholar] [CrossRef] [PubMed]
  40. Panoutsakopoulos, V. Influence of kinetic energy on lower limb impact dynamics in the case of frontal collision during pendulum swing exercising. In Proceedings of the 3rd EMUNI Research Souk, Thessaloniki, Greece, 21 March 2011; Čurčić, D., Ed.; EMUNI University: Portorož, Slovenia, 2011; pp. 140–149. [Google Scholar]
  41. Dempster, W.T. Space Requirements of the Seated Operator; WADC-TR (55-159); Wright Patterson Air Force Base: Dayton, OH, USA, 1955. [Google Scholar]
  42. Winter, D.A. Biomechanics and Motor Control of Human Movement, 2nd ed.; John Wiley & Sons, Inc.: New York, NY, USA, 1990. [Google Scholar]
  43. Fleiss, J.L. The Design and Analysis of Clinical Experiments; John Wiley & Sons, Inc.: New York, NY, USA, 1986. [Google Scholar]
  44. Cohen, J. Statistical Power Analysis for the Behavioral Sciences, 2nd ed.; Lawrence Erlbaum Associates Publishers: Hillsdale, NJ, USA, 1988. [Google Scholar]
  45. Arampatzis, A.; Schade, F.; Walsh, M.; Brüggemann, G.-P. Influence of leg stiffness and its effect on myodynamic jumping performance. J. Electromyogr. Kinesiol. 2001, 11, 355–364. [Google Scholar] [CrossRef]
  46. Bobbert, M.F.; Huijing, P.A.; van Ingen Schenau, G.J. Drop jumping. II. The influence of dropping height on the biomechanics of drop jumping. Med. Sci. Sports Exerc. 1987, 19, 339–346. [Google Scholar] [CrossRef]
  47. Sanders, R.H.; Allen, J.B. Changes in net joint torques during accomodation to change in surface compliance in a drop jumping task. Hum. Mov. Sci. 1993, 12, 299–326. [Google Scholar] [CrossRef]
  48. Viitasalo, J.T.; Salo, A.; Lahtinen, J. Neuromuscular functioning of athletes and non-athletes in the drop jump. Eur. J. Appl. Physiol. Occup. Physiol. 1998, 78, 432–440. [Google Scholar] [CrossRef]
  49. Bubeck, D.; Gollhofer, A. Load induced changes of jump performance and activation patterns in free drop jump exercises and sledge jumps. Eur. J. Sport Sci. 2001, 1, 1–17. [Google Scholar] [CrossRef]
  50. Kibele, A. Technical Note: Possible errors in the comparative evaluation of drop jumps from different heights. Ergonomics 1999, 42, 1011–1014. [Google Scholar] [CrossRef] [PubMed]
  51. McMahon, J.J.; Lake, J.P.; Stratford, C.; Comfort, P. A Proposed Method for Evaluating Drop Jump Performance with One Force Platform. Biomechanics 2021, 1, 178–189. [Google Scholar] [CrossRef]
  52. Geraldo, G.F.; Bredt, S.T.; Menzel, H.J.; Peixoto, G.H.; Carvalho, L.A.; Lima, F.V.; Soares, J.S.; Andrade, A.G. Drop height is influenced by box height but not by individual stature during drop jumps. J. Phys. Educ. 2019, 30, e-3078. [Google Scholar] [CrossRef]
  53. Walsh, M.; Arampatzis, A.; Schade, F.; Brüggemann, G.P. The effect of drop jump starting height and contact time on power, work performed, and moment of force. J. Strength Cond. Res. 2004, 18, 561–566. [Google Scholar] [PubMed]
  54. Voigt, M.; Simonsen, E.; Dyhre-Poulsen, P.; Klausen, K. Mechanical and muscular factors influencing the performance in maximal vertical jumping after different prestretch loads. J. Biomech. 1995, 28, 293–307. [Google Scholar] [CrossRef] [PubMed]
  55. Avela, J.; Komi, P.V.; Santos, P.M. Effects of differently induced stretch loads on neuromuscular control in drop jump exercise. Eur. J. Appl. Physiol. Occup. Physiol. 1996, 72, 553–562. [Google Scholar] [CrossRef] [PubMed]
  56. Leukel, C.; Taube, W.; Gruber, M.; Hodapp, M.; Gollhofer, A. Influence of falling height on the excitability of the soleus H-reflex during drop-jumps. Acta Physiol. 2008, 192, 569–576. [Google Scholar] [CrossRef] [PubMed]
  57. Lafortune, M.A.; Lake, M.J.; Hennig, E.M. Differential shock transmission response of the human body to impact severity and lower limb posture. J. Biomech. 1996, 29, 1531–1537. [Google Scholar] [CrossRef] [PubMed]
  58. Pithioux, M.; Chavet, P.; St-Onge, N.; Nicol, C. Influence of muscle preactivation of the lower limb on impact dynamics in the case of frontal collision. Int. J. Crashworthiness 2005, 10, 557–565. [Google Scholar] [CrossRef]
  59. Guy-Cherry, D.; Alanazi, A.; Miller, L.; Staloch, D.; Ortiz-Rodriguez, A. Landing Styles Influences Reactive Strength Index without Increasing Risk for Injury. Sports Med. Int. Open 2018, 02, E35–E40. [Google Scholar] [CrossRef]
  60. You, C.-H.; Huang, C.-H. Effects of Leg Stiffness Regulated by Different Landing Styles on Vertical Drop Jump Performance. J. Hum. Kinet. 2022, 83, 29–37. [Google Scholar] [CrossRef] [PubMed]
  61. Young, W.B.; Pryor, J.F.; Wilson, G.J. Effect of instructions on characteristics of countermovement and drop jump performance. J. Strength Cond. Res. 1995, 9, 232–236. [Google Scholar]
  62. Arampatzis, A.; Brüggemann, G.P.; Klapsing, G.M. Leg stiffness and mechanical energetic processes during jumping on a sprung surface. Med. Sci. Sports Exerc. 2001, 33, 923–931. [Google Scholar] [CrossRef]
  63. Bassa, E.; Adamopoulos, I.; Panoutsakopoulos, V.; Xenofondos, A.; Yannakos, A.; Galazoulas, C.; Patikas, D.A. Optimal Drop Height in Prepubertal Boys Is Revealed by the Performance in Squat Jump. Sports 2023, 11, 1. [Google Scholar] [CrossRef]
  64. Moir, G.L.; Snyder, B.W.; Connaboy, C.; Lamont, H.S.; Davis, S.E. Using Drop Jumps and Jump Squats to Assess Eccentric and Concentric Force-Velocity Characteristics. Sports 2018, 6, 125. [Google Scholar] [CrossRef] [PubMed]
  65. Byrne, P.J.; Moran, K.; Rankin, P.; Kinsella, S. A Comparison of Methods Used to Identify ‘Optimal’ Drop Height for Early Phase Adaptations in Depth Jump Training. J. Strength Cond. Res. 2010, 24, 2050–2055. [Google Scholar] [CrossRef]
  66. Avela, J.; Santos, P.M.; Kyröläinen, H.; Komi, P.V. Effects of different simulated gravity conditions on neuromuscular control in drop jump exercises. Aviat. Space Environ. Med. 1994, 65, 301–308. [Google Scholar]
  67. Asmussen, E.; Bonde-Petersen, F. Storage of Elastic Energy in Skeletal Muscles in Man. Acta Physiol. Scand. 1974, 91, 385–392. [Google Scholar] [CrossRef]
  68. Rodacki, A.L.F.; Fowler, N.E. A movement pat tern repeatability approach during the eccentric ± concentric cycle in the pendulum swing. J. Sports Sci. 1998, 17, 549. [Google Scholar]
Biomechanics 03 00018 g001 550
Figure 1. Depiction of the experimental procedure: (a) execution of the vertical drop jump (VDJ); (b) execution of the horizontal plyometric rebound jump (HPRJ).
Figure 1. Depiction of the experimental procedure: (a) execution of the vertical drop jump (VDJ); (b) execution of the horizontal plyometric rebound jump (HPRJ).
Biomechanics 03 00018 g001
Biomechanics 03 00018 g002 550
Figure 2. Mean (n = 38) time–history curves for the examined vertical drop jump (VDJ; thick blue line) and horizontal plyometric rebound jump (HPRJ; thin green line) kinetic and kinematic parameters: (a) force output; (b) rate of force development; (c) work; (d) power; (e) body center of mass (BCM) velocity; (f) BCM displacement (0 = BCM position at the instant of touchdown); (g) vertical stiffness; (h) vertical stiffness depicted by plotting the BCM displacement vs. the force output. Abbreviations: F: force output; RFD: rate of force development; W: work; P: power; tC: contact time. NOTE: all curves are normalized with respect to tC; the curves in Figure 2g are depicted for the time period from touchdown to the maximum BCM displacement during the contact with the surface.
Figure 2. Mean (n = 38) time–history curves for the examined vertical drop jump (VDJ; thick blue line) and horizontal plyometric rebound jump (HPRJ; thin green line) kinetic and kinematic parameters: (a) force output; (b) rate of force development; (c) work; (d) power; (e) body center of mass (BCM) velocity; (f) BCM displacement (0 = BCM position at the instant of touchdown); (g) vertical stiffness; (h) vertical stiffness depicted by plotting the BCM displacement vs. the force output. Abbreviations: F: force output; RFD: rate of force development; W: work; P: power; tC: contact time. NOTE: all curves are normalized with respect to tC; the curves in Figure 2g are depicted for the time period from touchdown to the maximum BCM displacement during the contact with the surface.
Biomechanics 03 00018 g002
Biomechanics 03 00018 g003 550
Figure 3. Mean (n = 38) time–history curves for the examined vertical drop jump (VDJ; thick blue line) and horizontal plyometric rebound jump (HPRJ; thin green line) kinetic and kinematic parameters: (a) ankle joint angle; (b) ankle joint angular velocity; (c) knee joint angle; (d) knee joint angular velocity; (e) hip joint angle; (f) hip joint angular velocity; (g) leg length; (h) leg stiffness. Abbreviations: θ: angle; ω: angular velocity; ANK: ankle joint; KNEE: knee joint; HIP: hip joint; tC: contact time. NOTE: all curves are normalized with respect to tC.
Figure 3. Mean (n = 38) time–history curves for the examined vertical drop jump (VDJ; thick blue line) and horizontal plyometric rebound jump (HPRJ; thin green line) kinetic and kinematic parameters: (a) ankle joint angle; (b) ankle joint angular velocity; (c) knee joint angle; (d) knee joint angular velocity; (e) hip joint angle; (f) hip joint angular velocity; (g) leg length; (h) leg stiffness. Abbreviations: θ: angle; ω: angular velocity; ANK: ankle joint; KNEE: knee joint; HIP: hip joint; tC: contact time. NOTE: all curves are normalized with respect to tC.
Biomechanics 03 00018 g003
Table
Table 1. Mean ± standard deviation of the comparison for the spatiotemporal and kinematic parameters between the vertical drop jump (VDJ) and the horizontal plyometric rebound jump (HPRJ) test (n = 38).
Table 1. Mean ± standard deviation of the comparison for the spatiotemporal and kinematic parameters between the vertical drop jump (VDJ) and the horizontal plyometric rebound jump (HPRJ) test (n = 38).
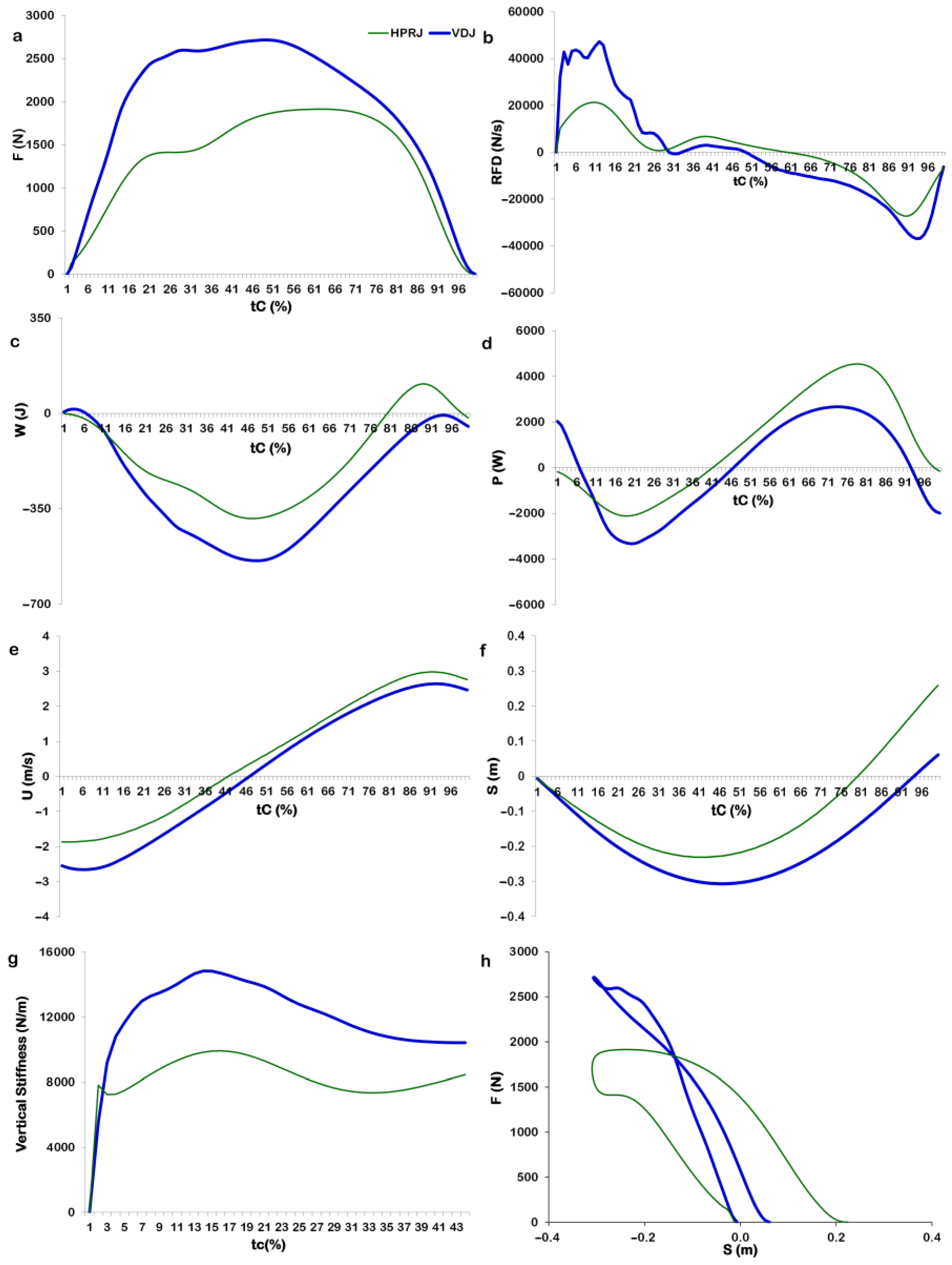
ParameterVDJHPRJtpd
KEI (J)240.6 ± 39.5243.9 ± 16.00.5410.5920.11
HJUMP (m)0.323 ± 0.0720.302 ± 0.0721.3990.1700.28
SBR (m)−0.301 ± 0.087−0.241 ± 0.0604.699<0.001 *0.80
SPR (m)0.370 ± 0.1050.454 ± 0.1100.3190.7540.78
tC (ms)408.8 ± 123.0426.7 ± 92.80.8190.4180.16
tBR (ms)192.5 ± 60.3185.6 ± 51.10.6470.5220.12
tFMAX (ms)131.4 ± 65.3269.1 ± 101.17.682<0.001 *1.62
tPMAX (ms)322.0 ± 117.0346.7 ± 94.31.1330.2650.23
VTD (m/s)−2.58 ± 0.15−1.90 ± 0.1021.416<0.001 *5.33
VTO (m/s)2.51 ± 0.292.73 ± 0.353.2620.002 *0.69
*: p < 0.05; KEI: body center of mass (BCM) kinetic energy at the instant of impact; HJUMP: jump height; SBR: BCM vertical displacement during the braking phase; SPR: BCM vertical displacement during the propulsion phase; tC: total contact time; tBR: duration of the braking phase; tFMAX: time to achieve peak vertical ground/horizontal wall reaction force for the VDJ and HPRJ, respectively; tPMAX: time to achieve peak power during the propulsion phase; VTD: BCM velocity at the instant of touchdown; VTO: BCM velocity at the instant of take-off.
Table
Table 2. Mean ± standard deviation of the comparison for the kinetic parameters between the vertical drop jump (VDJ) and the horizontal plyometric rebound jump (HPRJ) test (n = 38).
Table 2. Mean ± standard deviation of the comparison for the kinetic parameters between the vertical drop jump (VDJ) and the horizontal plyometric rebound jump (HPRJ) test (n = 38).
ParameterVDJHPRJtpd
F (kN)2.15 ± 0.912.74 ± 1.492.1680.037 *0.48
F (N/kg)3.68 ± 1.153.07 ± 0.982.9420.006 *0.57
RFD (kN/s)47.1 ± 23.833.7 ± 24.32.8850.006 *0.56
P (kW)2.93 ± 1.114.88 ± 0.929.188<0.001 *1.91
P (W/kg)35.9 ± 13.738.8 ± 7.31.2160.2320.26
KVERT (kN/m)14.84 ± 9.359.92 ± 6.932.5020.017 *0.60
KLEG (kN/m)4.23 ± 2.583.69 ± 1.640.6280.5340.25
*: p < 0.05; F: peak force output; P: peak power output during the propulsion phase; KVERT: vertical stiffness, KLEG: leg stiffness.
Table
Table 3. Mean ± standard deviation of the comparison for the joint angular kinematic parameters between the vertical drop jump (VDJ) and the horizontal plyometric rebound jump (HPRJ) test (n = 38).
Table 3. Mean ± standard deviation of the comparison for the joint angular kinematic parameters between the vertical drop jump (VDJ) and the horizontal plyometric rebound jump (HPRJ) test (n = 38).
ParameterVDJHPRJtpd
θANK-td (deg)100.9 ± 7.992.1 ± 9.35.300<0.001 *1.02
θANK-low (deg)66.4 ± 6.273.9 ± 10.34.356<0.001 *0.88
θANK-to (deg)136.2 ± 6.8127.0 ± 7.75.153<0.001 *1.27
ROMANK-BR (deg)−34.4 ± 8.8−18.2 ± 10.57.862<0.001 *1.67
ROMANK-PR (deg)69.8 ± 9.453.1 ± 11.07.106<0.001 *1.63
ωANK (rad/s)12.2 ± 2.211.5 ± 2.51.2170.2320.30
θKNEE-td (deg)140.1 ± 8.6121.2 ± 16.76.532<0.001 *1.42
θKNEE-low (deg)95.8 ± 14.496.0 ± 21.30.0520.9590.01
θKNEE-to (deg)175.2 ± 4.4165.4 ± 7.56.698<0.001 *1.59
ROMKNEE-BR (deg)−44.3 ± 17.1−25.1 ± 14.75.612<0.001 *1.20
ROMKNEE-PR (deg)79.3 ± 15.269.4 ± 19.02.8140.008 *0.58
ωKNEE (rad/s)11.4 ± 2.012.4 ± 2.91.7540.0890.40
θHIP-td (deg)135.9 ± 11.2121.0 ± 8.36.581<0.001 *1.51
θHIP-low (deg)106.9 ± 22.5111.8 ± 9.71.2430.2230.28
θHIP-to (deg)176.8 ± 4.8140.4 ± 5.930.456<0.001 *6.77
ROMHIP-BR (deg)−29.0 ± 22.0−9.2 ± 5.15.466<0.001 *1.24
ROMHIP-PR (deg)69.9 ± 22.828.5 ± 8.611.206<0.001 *2.40
ωHIP (rad/s)8.6 ± 1.55.1 ± 1.411.604<0.001 *2.41
*: p < 0.05; θ: angle; ω: angular velocity; ROM: range of motion; ANK: ankle joint; KNEE: knee joint; HIP: hip joint; td: instant of touchdown; low: instant of maximum body center of mass displacement during the contact phase; to: instant of take-off; BR: braking phase; PR: propulsion phase; NOTE: negative and positive ROM values indicate joint flexion and extension, respectively.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Panoutsakopoulos, V.; Kollias, I.A. Reliability of a Pendulum Apparatus for the Execution of Plyometric Rebound Exercises and the Comparison of Their Biomechanical Parameters with Load-Matching Vertical Drop Jumps. Biomechanics 2023, 3, 204-219. https://doi.org/10.3390/biomechanics3020018

AMA Style

Panoutsakopoulos V, Kollias IA. Reliability of a Pendulum Apparatus for the Execution of Plyometric Rebound Exercises and the Comparison of Their Biomechanical Parameters with Load-Matching Vertical Drop Jumps. Biomechanics. 2023; 3(2):204-219. https://doi.org/10.3390/biomechanics3020018

Chicago/Turabian Style

Panoutsakopoulos, Vassilios, and Iraklis A. Kollias. 2023. "Reliability of a Pendulum Apparatus for the Execution of Plyometric Rebound Exercises and the Comparison of Their Biomechanical Parameters with Load-Matching Vertical Drop Jumps" Biomechanics 3, no. 2: 204-219. https://doi.org/10.3390/biomechanics3020018

APA Style

Panoutsakopoulos, V., & Kollias, I. A. (2023). Reliability of a Pendulum Apparatus for the Execution of Plyometric Rebound Exercises and the Comparison of Their Biomechanical Parameters with Load-Matching Vertical Drop Jumps. Biomechanics, 3(2), 204-219. https://doi.org/10.3390/biomechanics3020018

Article Metrics

Back to TopTop