Next Article in Journal
Association of Foot Sole Sensibility with Quiet and Dynamic Body Balance in Morbidly Obese Women
Previous Article in Journal
Ballroom Dance as a Form of Rehabilitation: A Systematic Review
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Biomechanics
Volume 1
Issue 3
10.3390/biomechanics1030027
biomechanics-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Comparative Finite Element Analysis of Fixation Techniques for APC II Open-Book Injuries of the Pelvis

by
Andreas Lipphaus
*,
Matthias Klimek
and
Ulrich Witzel
Biomechanics Research Group, Department of Mechanical, Engineering, Ruhr-University Bochum, 44801 Bochum, Germany
*
Author to whom correspondence should be addressed.
Biomechanics 2021, 1(3), 321-333; https://doi.org/10.3390/biomechanics1030027
Submission received: 4 October 2021 / Revised: 2 November 2021 / Accepted: 3 November 2021 / Published: 5 November 2021
(This article belongs to the Section Injury Biomechanics and Rehabilitation)
Browse Figures
Versions Notes

Abstract

:
Open-book fractures are defined as the separation of the pubic symphysis or fractures of the rami and disruption of the anterior sacroiliac, sacrotuberous, and sacrospinal ligaments. They can be stabilized by fixation of the anterior arch. However, indications and advantages of additional placement of iliosacral screws remain unknown. A CT-based model of the healthy pelvis was created and ligaments were modeled as tension springs. Range of motion of the sacroiliac joint and the pubic symphysis, and bone and implant stresses were compared for the physiological model, anterior symphyseal plating alone, and additional posterior fixation using two iliosacral screws. The range of motion of the sacroiliac joint was reduced for anterior symphyseal plating alone and further decrease was noted with additional posterior fixation. Von Mises stresses acting on the symphyseal plate were 819.7 MPa for anterior fixation only and 711.56 MPa for additional posterior fixation equivalent with a safety factor of 1.1 and 1.26, respectively. Implant stresses were highest parasymphyseal. While bone stresses exhibited a more homogeneous distribution in the model of the healthy pelvis and the model with anterior and posterior fixation, pure symphyseal plating resulted in bending at the pelvic rami. The analysis does not indicate the superiority of either anterior plating alone or additional posterior fixation. In both cases, the physiological range of motion of the sacroiliac joint is permanently limited, which should be taken into account with regard to implant removal or more flexible techniques for stabilization of the sacroiliac joint.

1. Introduction

Although pelvic fractures make up only 3–8% of all fractures [1,2], fractures of the pelvic ring represent a clinical challenge and are associated with a high number of complications [3,4]. Pelvic fractures are mostly caused by accidents in young patients [5] and by falls in older patients [6]. The type of fracture depends on the direction of impact: The Young–Burgess classification differentiates between anterior–posterior compression, lateral compression, and vertical shear [7]. APC II defines an external rotation injury known as open-book injury, also classified as Tile B1 or B1.1 in the AO system. A separation of the pubic symphysis or fractures of the rami lead to instability of the anterior pelvic arch and, with sustained external rotation, to tearing of the anterior sacroiliac ligament, while the posterior sacroiliac ligament remains intact, resulting in a partial instability [8]. It has been reported that rupture of the sacrotuberous and sacrospinal ligament complex does not significantly increase pelvic instability [9].
The treatment of open-book injuries is controversial: recent biomechanical ex vivo studies have shown that solitary symphysis plating is not sufficient to reduce the movement of the sacroiliac joint [10] and that ring stability is best achieved by a combination of anterior and posterior ring fixation [11,12], questioning previous standard recommendations for the treatment of open-book injuries with sole plate fixation of the anterior ring [13]. However, implant failure has not been related to posterior pelvic fixation in an ex vivo study [14]. Some clinical studies found a lower rate of implant failure and malunion in patients treated with anterior and posterior fixation [15], while others reported no benefit with additional implantation of iliosacral screws and good outcome with stabilization of the anterior arch only [16]. In addition, the static immobilization of the sacroiliac joint or the pubic symphysis limits the physiological range of motion of these joints. Restrictions of movement are suspected as a possible cause of pain. Some 48.4% of all patients operated on for pelvic fractures suffer from chronic pain postoperatively [17]. More specifically, in one study, 18% of 250 patients treated with sacroiliac screw fixation for pelvic fractures had an implant removed for pain after an average of 6.7 months, resulting in a significant reduction in reported pain [18]. Residual pain with retained suprapubic implants was reported in 13.5% of the cases [19]. To preserve physiological joint mobility, Labitzke and Witzel suggested a dynamic fixation using a sleeve–cable tensioning [20]. In a recent in vitro study, Jordan et al. underlined the potential for trans-obturator cable fixation in open-book fractures [21]. In a similar fashion, minimally invasive tape suture osteosynthesis of the pubic symphysis was suggested [22]. Implant failure is not uncommon, but rates depend on the type of fracture and treatment and varies greatly between different studies. Breakage of the sacroiliac screw fixation was observed in 11.8% of the cases [23]. In suprapubic plating, broken screws only were reported in 5% of cases, a combination of loosened and broken screws in 17%, and broken plates in 7% [24]. Another aspect of retained implants is bone resorption through stress shielding, which further weakens the bone, making the maintenance of physiological stresses in the bone a major requirement for implants that remain in the body for a longer time [25].
Finite element (FE) models are widely used to noninvasively study the range of motion of joints and stresses in bone and implants. Several models have investigated the influence of fractures of the anterior ring alone or open-book fractures on the stability of the pelvic ring and loading of the pelvis or the attached ligaments with a high correlation between in vitro and in silico strains [26]. Böhme et al. found only single rotational instability of the sacroiliac joint if its interosseous and posterior ligaments remain intact. Otherwise, a second axis of rotation amplifies the rotational instability prompting the authors to suggest treatment by additional posterior fixation in these cases [27]. Ricci et al. reported higher stresses on the posterior structures caused by fractures of the rami [28]. Various computational studies analyzed implant stresses or joint displacement for different implants: Hu et al. compared fixation by iliosacral screws, tension band plates, and minimally invasive adjustable plates for Tile C fractures and reported good results for fractures stability with any implant, but inferior safety in the tension band plate [29]. Correlation of implant failure and stress peaks was found by Shim et al. using two patient-specific models with symphyseal plating and iliosacral screws [30]. Patient-specific finite models have also successfully been applied to treat a clinically challenging case of pelvic malunion [31]. In this fashion, preoperative simulations can assist treatment decisions to improve the stability of the osteosynthesis. There are some finite element models specifically comparing biomechanics of different implants used for open-book fractures, but with focus on anterior fixation [32] or external fixation [33].
So far there has been no consensus on the use of iliosacral screws in the treatment of open-book fractures and its advantages and potential complications are not fully understood. The questions about the necessity of screw implantation for posterior stabilization, movement restrictions in the sacroiliac joint, and the influence on the stresses in the bone and the sympyseal plate remain unanswered. Although there are several biomechanical experiments on body donors and clinical studies, the model presented here is the first in silico approach to compare stability after open-book injuries treated with and without additional iliosacral screws. Compared to other biomechanical models, in silico models can be easily adapted to different influencing variables and provide information about internal strains and stresses that are difficult to obtain through other experimental approaches [34]. The aim of the present study is to develop and validate a finite element model of the healthy pelvis and derive a model of an open-book injury. Range of motion of the sacroiliac joint and the pubic symphysis are compared for anterior pelvic ring fixation alone and combined anterior and posterior ring stabilization. Furthermore, implant and bone stresses are analyzed. Thereby, the need for posterior fixation can be assessed. Adequate stability and implant safety in anterior fixation only would support more careful consideration of sacroiliac screw implantation to reduce surgical time and avoid undesirable implant reactions. If stability and implant safety are unsatisfactory with pure symphyseal plating and can be improved with additional iliosacral screws, the use would be supported in order to avoid non-union and other complications.

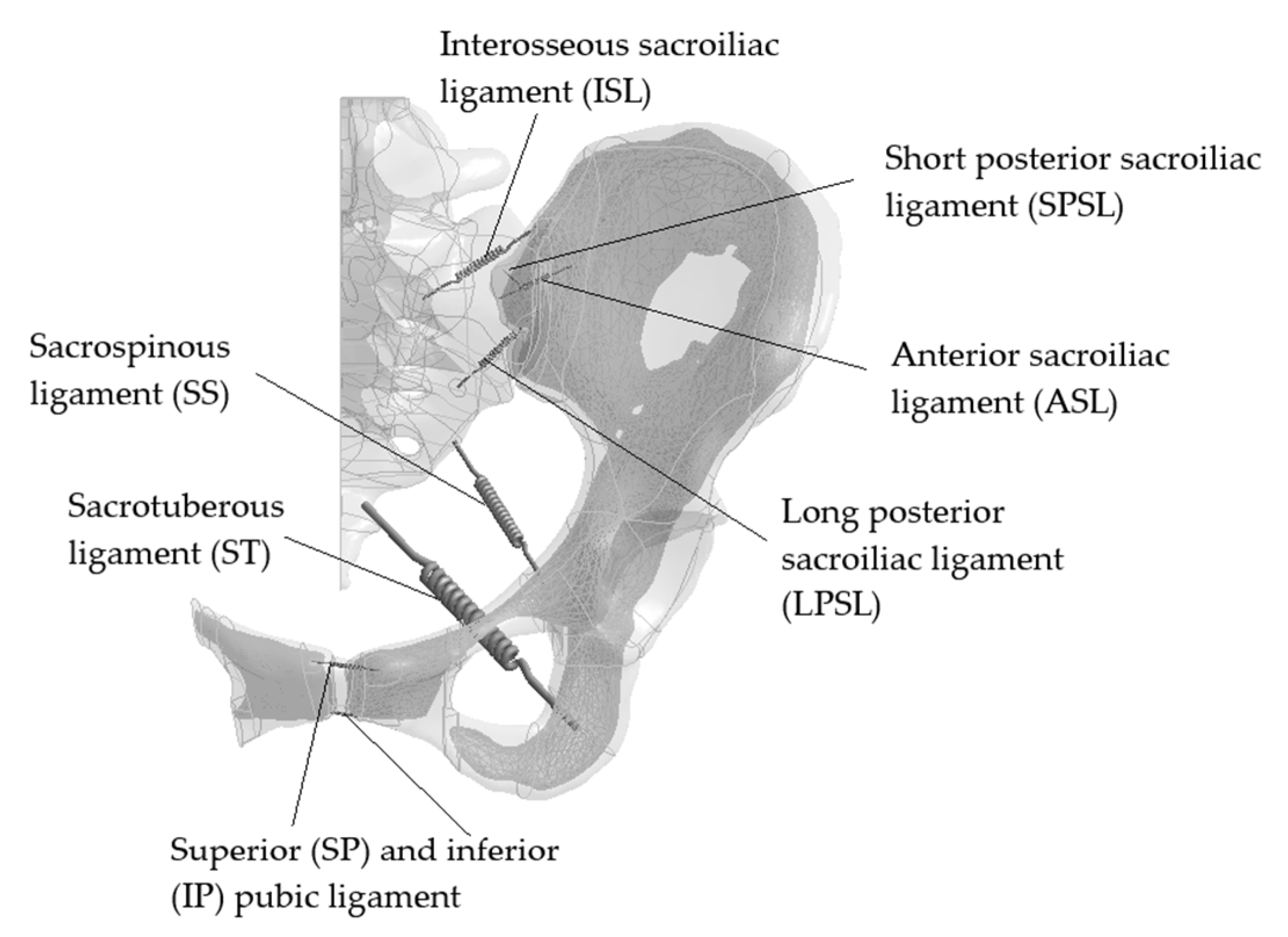
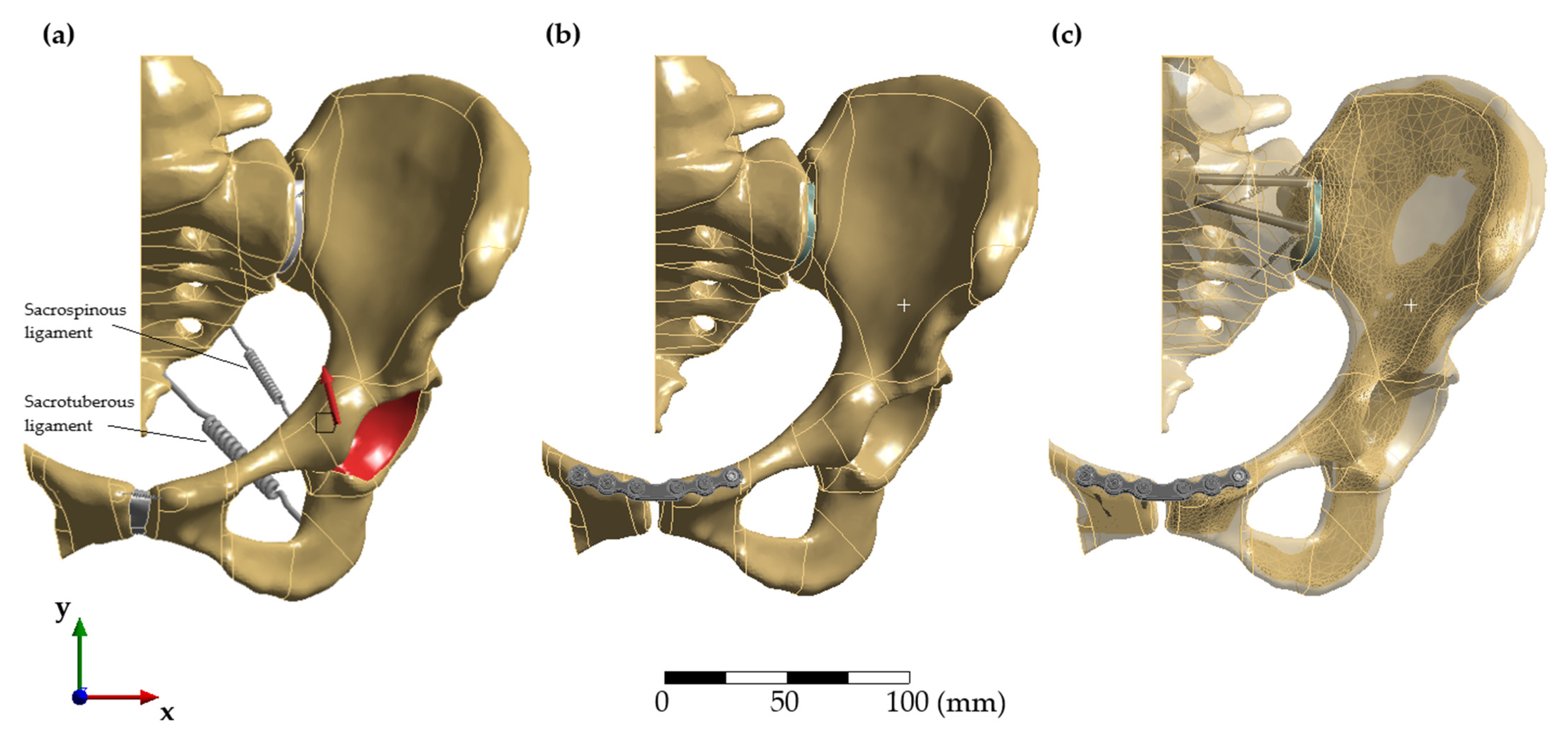
2. Materials and Methods

CT data of the female body from the Visible Human Project was imported into ScanIP (Version 14, Synopsys Inc, Mountain View, CA, USA). The data were composed of axial CT scans with a slice thickness of 1 mm and a resolution of 512 by 512 pixels. First, cortical bone with Hounsfield values of 250–2000 was selected [35]. Subsequently, the inner space was filled with cancellous bone. After manual smoothing, the CAD model was exported to Fusion 360 (Version 2.0.9642, Autodesk, CA, USA) for further optimization. A surface mesh was created and exported to ANSYS Workbench (Version 19.2, ANSYS Inc, Canonsburg, PA, USA). Facet bodies were patterned with non-uniform-rational-B-splines to minimize the number of surfaces and volumes were automatically created. Taking advantage of the symmetry of the pelvic ring [36,37], only the left side of the pelvis was included in the model. The sacrum was divided in the midsagittal plane [38] and, to be careful not to disturb the mechanical behavior of the pubic symphysis, a small part of the right side up to the rami was included in the model in a similar approach to Salzar et al. [39]. The volumes were meshed using 10-node tetrahedral elements (SOLID187) [31] to enable automated meshing of the complex curved geometries. A mesh convergence study was carried out, starting with an element size of 6 mm, which was successively reduced by 1 mm per step. A congruence of 95% was chosen as the termination criterion. Previous studies explained the need for flexible constraints [40] as two rigid bearings lead to artificial stress peaks. Therefore, the model was constraint using a frictionless support on the cut surface of the sacrum in order to allow rotational movements in the sagittal plane and with a fixed support on the cut surface of the right pelvic ring to ensure the stability of the analysis.
Bone was modeled as linear elastic material with a Young’s modulus of 17,000 MPa for cortical [41] and 150 MPa for cancellous bone [33] and a Poisson’s ratio of 0.3 for both. As stresses in the sacrum were not in the focus of this study and to minimize computational time, the sacrum was modeled as a homogeneous volume with a Young’s modulus of 4000 MPa matching its ratio of cortical and cancellous bone. A three-parameter Mooney–Rivlin material model with C10 = 0.1 MPa, C01 = 0.45 MPa and C11 = 0.6 MPa represented the hyperelastic properties of the fiber cartilage of the pubic symphysis [42]. The sacroiliac joint was modeled using a linear elastic material model with a Young´s modulus of 100 MPa and a Poisson’s ratio of 0.42 [43,44]. Implants were considered to be manufactured from TiAl6Nb7 with a Young´s modulus of 105 GPa, a Poisson’s ratio of 0.34, a fracture strength of 900 MPa, and a yield point of 795 MPa [45]. The sizing of the screws was adapted from ISO 5835:1991, and the plate was modeled with a radius of 60 mm, a widened middle bar, three screw holes on each side, and a plate height of 3.5 mm.
Philips et al. highlighted the importance of using spring elements for flexible boundary conditions to model the muscular and ligamentous apparatus because fixed boundary conditions lead to stress concentrations in the cortical bone unlikely to occur in vivo [46]. The anterior sacroiliac ligament (ASL), interosseous sacroiliac ligament (ISL), long posterior sacroiliac ligament (LPSL), short posterior sacroiliac ligament (SPSL), sacrospinous ligament (SS), sacrotuberous ligament (ST), superior pubic ligament (SP), and inferior pubic ligament (IP) were reconstructed based on anatomical information, as displayed in Figure 1.
Ligaments were modeled as tension springs without damping. As stiffness properties vary widely in literature, values taken from three different studies [47,48,49] were used, and displacement of the sacroiliac joint was compared to in vitro data [50] for each case. In this in vitro study, the ilium was constrained and the sacrum was loaded with 294 N at its upper surface for craniocaudal displacement and on the anterior surface for ventrodorsal movement. To validate the in silico model presented here, these loading conditions were replicated in the computational model. All further simulations were performed using the spring stiffness leading to the highest agreement with in vitro measurements and using the maximal hip joint contact forces of 238% body weight during gait, measured by Bergmann et al., which were transformed into the coordinate system of the model and applied to the acetabulum [51].
Contacts were modeled using a multi-point constraint (MPC) algorithm and augmented Lagrange method [52] with a maximal penetration of 10 µm. As with other established models, bounded contacts between bone and implant as well as between screws and plate, similar to locking screws, were used [30]. To create the model of the open-book injury, the anterior sacroiliac ligament, the sacrotuberous and sacrospinal ligament complex, and the superior and inferior pubic ligament, and the fiber cartilage of the pubic symphysis were removed following a similar model by Boehme et al. [53] based an ex vivo study [54]. Two different implant configurations were modeled: For anterior fixation, the plate and a total of six implant screws for fixation were virtually implanted superior to the pubic symphysis using Boolean operations [55]. In the second model, two iliosacral screws were added to stabilize the sacroiliac joint [56]. The final models are shown in Figure 2.
The range of motion was taken as mean displacement under gait load in all three spatial directions measured at the edge of the pubic symphysis and the sacroiliac joint. Von Mises stresses were analyzed for the implants and, with the fracture strength of titanium, the security factor was calculated. As bone has anisotropic material properties, principal stresses instead of von Mises stresses were evaluated for bone [57].

3. Results

3.1. Convergence Study and Validation

The mesh convergence study for the pelvis showed a deviation of congruence of 95% for element sizes of 5 mm and 4 mm. Cancellous bone and cartilage were further refined with an element size of 0.5 to 1 mm to avoid element distortion. The final model consistedof 836,429 elements for the model of the healthy pelvis, 698,197 elements for the open-book fracture model including the symphyseal plate, and 704,796 elements for the model with the sympyseal plate and two iliosacral screws.
The range of motion of the sacroiliac joint in the model of the healthy pelvis using three different sets of stiffness of the ligaments differed between each set. None matched exactly the in vitro measurements, as shown in Table 1. Consistency was high for all parameters for loading of the sacrum in the cranial direction. Using the stiffness values as reported by Shi et al. [47] in our model resulted in the highest consistency for caudal displacement. For ventrodorsal displacement, the best agreement between in vitro and in silico models was achieved using values by Zhao et al. [49]. Since the highest load occurred in the caudal direction due to the body weight, the stiffnesses as described by Shi et al. were used in the following simulations. The final values are 700 N/mm2 (ASL), 2800 N/mm2 (ISL), 1000 N/mm2 (LPSL), 400 N/mm2 (SPSL), 1400 N/mm2 (SS), 1500 N/mm2 (ST), 500 N/mm2 (SP), and 500 N/mm2 (IP).

3.2. Range of Motion of the Sacroiliac Joint and the Pubic Symphysis

Mean displacement of the sacroiliac joint and the pubic symphysis under gait load is given in Table 2 and Table S1. Displacement of the sacroiliac joint in the healthy pelvic ring was 0.07 mm in the mediolateral direction, 0.39 mm in craniocaudal direction, and −0.235 mm in anterio-posterior direction. In the model of the open-book fracture treated with pure anterior fixation, the range of motion was reduced to −0.03 mm, 0.12 mm, and 0.078 mm, respectively. Additional posterior fixation resulted in a further altering of the range of motion to 0.07 mm, 0.005 mm, and 0.03 mm.
For the pubic symphysis, gait loading resulted in a mediolateral displacement of 0.0135 mm, cranio-caudal displacement of 1.44 mm, and anterio-posterior displacement of 1.05 mm. A decrease was noted for symphyseal plating in craniocaudal and anterio-posterior direction their range of motion lowered to 0.33 mm and 0.365 mm. Displacement in mediolateral direction increased to 0.35 mm. In the model with two additional iliosacral screws, the range of motion was lowest in craniocaudal direction, 0.105 mm, and in anterio-posterior direction, 0.34 mm. In mediolateral direction, displacement of 0.165 mm was greater than in the model of the healthy pelvis but lower than in the model of anterior fixation only.

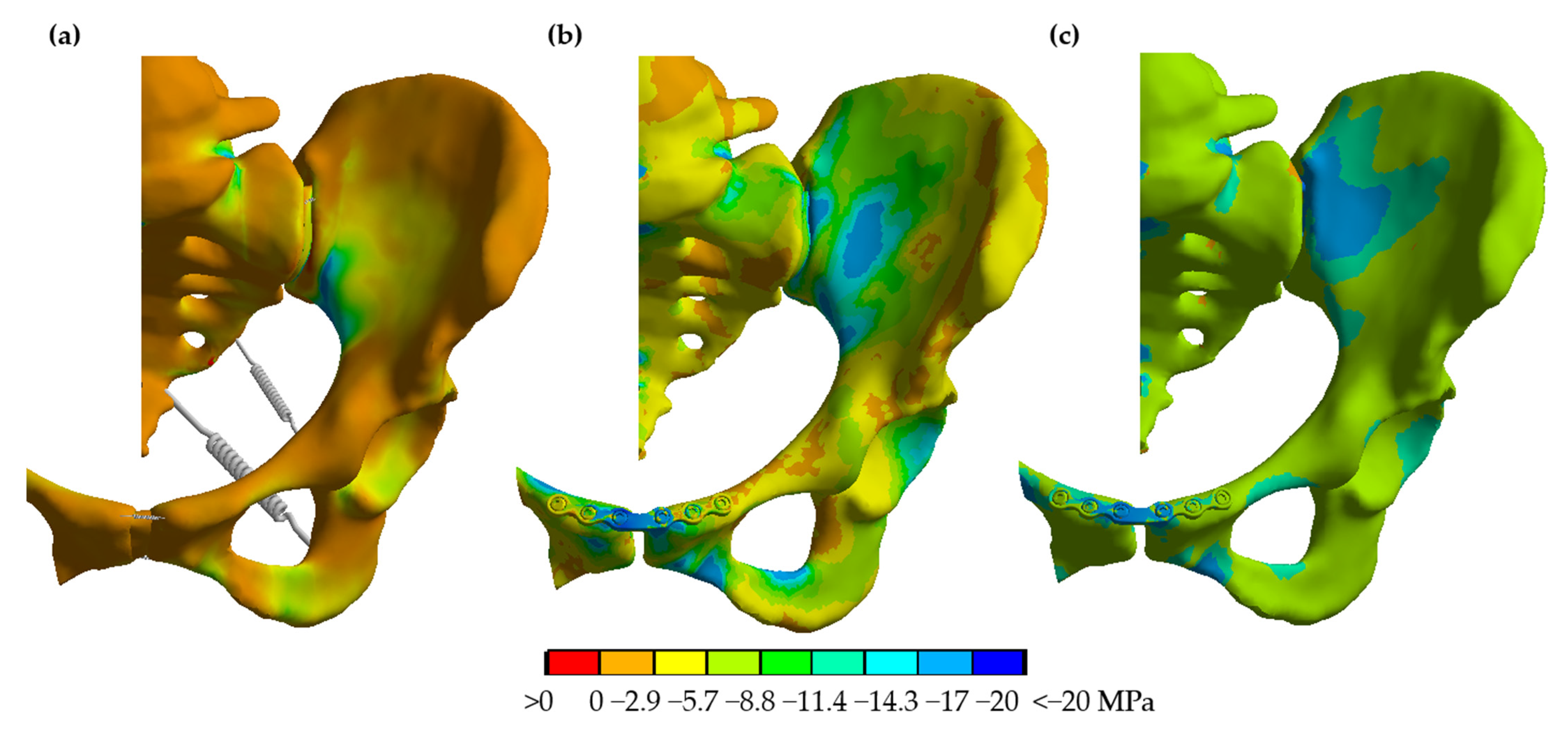
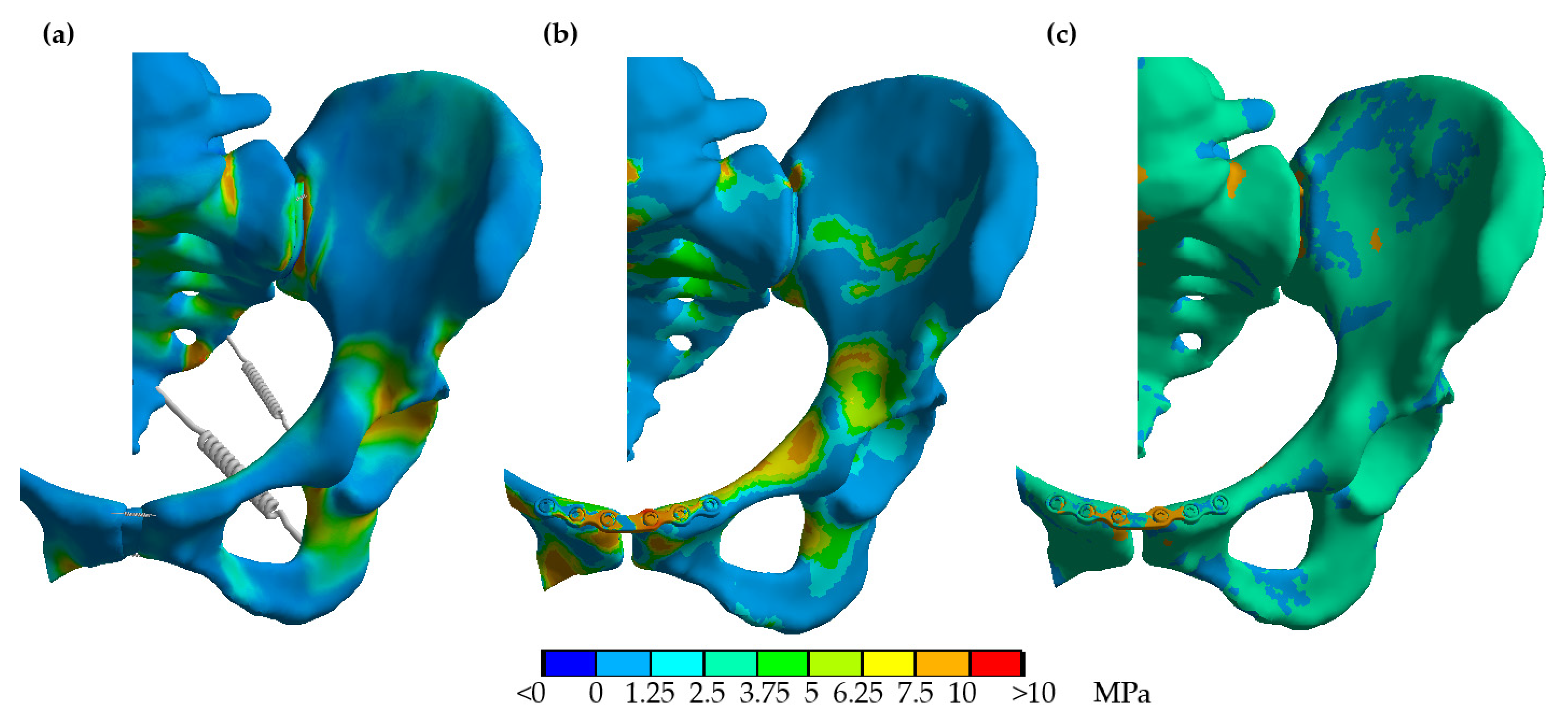
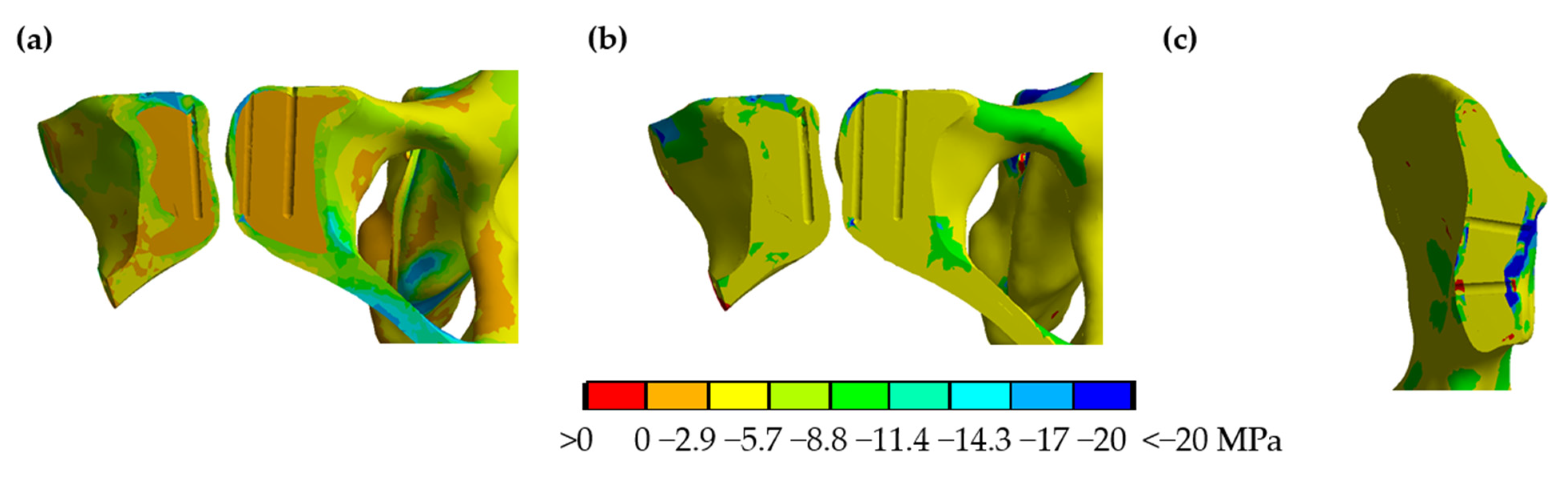
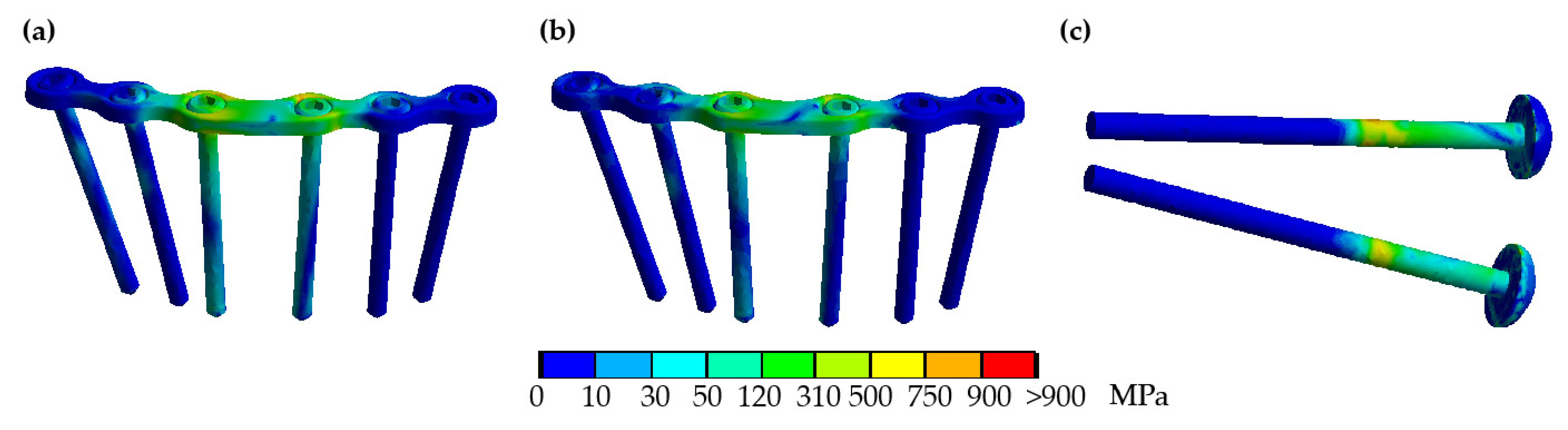
3.3. Implant and Bone Stresses

Compressive stresses in the model of the healthy pelvis were evenly distributed and mostly between 0 and −5.7 MPa (Figure 3a). For anterior fixation only, compression was unevenly distributed between the pubic rami resulting in bending loads (Figure 3b). Stresses were mostly between −2.9 and −8.8 MPa. Compressive stresses increased with additional posterior fixation but showed a homogeneous stress distribution without significant bending (Figure 3c). Most stresses were in the range of −5.7 to −8.8 MPa.
Tensile stresses were low in the model of the healthy pelvic ring, with most areas loaded with 1.25 MPa or less (Figure 4a). The homogeneous distribution shows that bending stresses were very low. In accordance with the compressive stresses, tensile stresses peaked at the superior pubic ramus in the model of the open-book fracture treated with implantation of the plate superior to the pubic symphysis indicating bending stresses (Figure 4b). With additional posterior fixation, bending was reduced, as displayed by the homogeneous stress distribution (Figure 4c). However, values were higher than in the model of the healthy pelvis and mostly between 2.5 and 3.75 MPa.
In the model with symphyseal fixation only, compressive stresses in the cancellous bone were between 0 to −2.9 MPa. Cross-sections of the bone surrounding the screws fixating the symphyseal plate and the iliosacral screws revealed a mean 3rd principal stress of −2 to −5.5 MPa (Figure 5). No stress shielding due to the implant screws was observed in either model.
Maximum von Mises stresses acting on the symphyseal plate were 819.7 MPa for fixation of the anterior arch alone (Figure 6a and Figure S1). The highest stresses were observed on the middle bar and the screws nearest to the disrupted pubic symphysis. The security factor for titanium with a fracture strength of 900 MPa was 1.1. Stresses decreased to 711.56 MPa and the security factor increased to 1.26 when the two iliosacral screws were added (Figure 6b). A peak stress of 871.42 MPa was calculated for the upper screw and 700.81 MPa for the lower screw (Figure 6c). The maximum stresses acted in the joint gap where the screws bridge the sacroiliac joint. The safety factor was calculated as 1.03 and 1.28, respectively.

4. Discussion

Optimal treatment of open-book fractures and the benefit of metal implant removal are a matter of debate due to frequent implant failure and chronic pain after surgery. In this study, a model of the healthy pelvis was developed. Validation of the model of the intact pelvic ring exhibited displacements of the sacroiliac joint comparable to previous studies. To compare the effect of pure anterior fixation or combined anterior and posterior fixation in APC II fractures, the anterior sacroiliac ligament and the sacrotuberous and the sacrospinal ligament complex, as well as the pubic symphysis, were removed from the model, with the posterior sacroiliac ligament remaining intact.
The range of motion calculated for the sacroiliac joint in the APC II fracture model under gait load showed that even with pure symphysis plating, the values in the cranial–caudal and anterior–posterior direction were lower than in the model of the healthy pelvis indicating adequate stability of the fixation. Indeed, the clinical experience of many trauma surgeons is that the fixation of the anterior pelvic ring alone often provides sufficient stability in open-book injuries to achieve favorable healing conditions [13]. However, iliosacral screw implantation resulted in further stability in the sacroiliac joint.
Von Mises stresses of the implants were below the strength of titanium for both configurations, indicating sufficient stability during gait. However, for maximal gait loads, the security factor for the iliosacral screws was only 1.03. Given that routine activities like climbing stairs likely create loads significantly larger than during gait, the results of the finite element model could explain the high rate of implant failure observed in clinical practice. Though, implant failure is unlikely to course complications during recovery [58].
Perhaps clinically of higher importance, the simulations revealed a persistent decrease of range of motion of the sacroiliac joint compared to the model of the healthy pelvic ring. This decrease was found in both treatment models but was more pronounced after implantation of the two additional iliosacral screws.
There is a high prevalence of chronic pain and functional limitations following pelvic fractures [17]. It is unclear if this relates to the fracture itself, injury-related damage or is caused by the fixation. In a cohort of patients undergoing surgery for pelvic fractures, improvement of pain levels after implant removal has been noted [18]. This indicates that retained implants might generate chronic pain. A decrease in the physiological range of motion of the sacroiliac joint might reduce the body’s ability to absorb impact loads during gait and therefore lead to lower back pain. The results of the in silico model presented in this study show that static fixation of the sacroiliac joint significantly reduces the physiological range of motion. A possible solution to achieve sufficient posterior stability while at the same time preserving the range of motion of the sacroiliac joint is the use of sleeve-cable tensioning for dynamic fixation [20]. On the other hand, Banierink et al. have found no difference in the quality of life and physical functioning between operatively and non-operatively treated patients [59]. However, so far, no clear evidence has been reported comparing long-term pain after open-book fractures treated with anterior fixation only and additional posterior fixation. Based on the results presented here, a hypothesis might be that chronic lower back pain following surgery for APC II fractures is lower when symphyseal plating is used without additional iliosacral screws while achieving the necessary stabilization at the same time. Using this indirect fixation of the sacroiliac joint physiological range of motion and rotation are more preserved than in rigid fixation using iliosacral screws.
Similar to other established finite element models of the pelvis [60], the implant screws were simplified as cylindrical solids with no threads to avoid singularities at sharp edges or notches with a very small radius. However, since the aim of this study is to compare the biomechanical performance of different fixation techniques and identical simplifications are applied, it is unlikely that modeling of the threads would change the outcome. The range of motion in the healthy pelvis is highly dependent on the ligamentous complex, while material properties of the articular cartilage are only of minor significance. The exact range of motion as reported in previous finite element models cannot be calculated even with the use of the respective stiffness due to differences in bone geometry, leverage, and spring length. Model-specific calibration of spring stiffness could therefore increase in accordance with in vitro or in vivo measurements. Material properties were adapted from healthy subjects reflecting the situation of a young patient after trauma. Since pelvic fractures are common in the elderly, future use of the in silico model presented here could investigate whether decreased bone stiffness due to osteoporosis influences the preferred treatment of APC II fractures of the pelvis. This, combined with modeling the screw thread, could also take into account the risk of screw loosening or secondary fractures in osteoporotic patients. Further limitations include the disregard of muscle forces and soft tissues in the present model. Indeed, muscles and soft tissues can provide stability to the pelvis, while on the other hand, muscle forces can also cause greater loading on the fractured pelvic ring. Especially with regard to stresses acting in the bone missing muscles, forces might cause significant deviations, as tension cording to minimize bending is not included [61]. Therefore, the compressive stresses presented in this study could underestimate the actual load. Indeed, stresses calculated for the model of the healthy pelvis are slightly lower than physiological values of −2 to −20 MPa [62]. Of note, in the analysis without implementation of muscle forces, pure anterior fixation resulted in bending loads, and it would be interesting to see if muscles act as tension cords to minimize bending and displacement. However, further knowledge about muscles forces acting in the fractured pelvic ring is necessary to include muscle forces. Further research should aim to create in silico models based on the specific anatomy of a clinical case or a body donor for better validation.
So far, the stability of symphyseal plates and iliosacral screws for open-book fractures has only been compared in in vitro studies. The results highly depend on the characteristics of the tested specimen. In contrast, in silico models can easily be adapted to material properties of osteoporotic bone or injuries of further ligaments. Thereby, unstable subtypes in open-book injuries which could benefit from additional posterior fixation can be identified. The finite element model presented here is the first to investigate the effect of additional implantation of iliosacral screws after symphyseal plating and supports careful consideration of the need for posterior fixation from a biomechanical perspective.

5. Conclusions

This comparative analysis of an APC II open-book fracture does not indicate the superiority of either anterior plating alone or additional posterior fixation. Symphyseal plating with locking screws might be sufficient in order to stabilize common open-book injuries, but implantation of sacroiliac screws can increase the stability of the sacroiliac joint in more complex cases. Implant stresses are below strength but with a low-security factor. This could explain implant failure commonly observed in clinical practice when activities creating loads higher than gait loads are performed. In both cases, the physiological range of motion of the sacroiliac joint is limited and might be associated with chronic pain. This should be considered when implant removal is discussed. The use of more flexible implants for posterior stabilization, such as cable fixation, should be the subject of further research.

Supplementary Materials

The following are available online at https://www.mdpi.com/article/10.3390/biomechanics1030027/s1, Figure S1: Von Mises stress acting in the symphyseal plate; Table S1: Minimal, maximal, and mean values of displacement of the sacroiliac joint and the pubic symphysis in mm.

Author Contributions

Conceptualization, A.L. and U.W.; methodology, A.L. and M.K.; software, M.K.; validation, A.L. and M.K.; formal analysis, M.K.; investigation, M.K.; writing—original draft preparation, A.L.; writing—review and editing, M.K. and U.W.; visualization, M.K.; supervision, U.W. All authors have read and agreed to the published version of the manuscript.

Funding

The authors received funding from the Deutsche Forschungsgesellschaft (DFG, German Research Foundation), grant number 445465815. The content is solely the responsibility of the authors and does not necessarily represent the official views of the DFG.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

All three finite element models of the human pelvis are available on Zenodo.org under the DOI 10.5281/zenodo.5522067.

Acknowledgments

The authors want to thank Beate Bender, Product Development, and the Institute of Product and Service Engineering, Ruhr-University Bochum, for the provision of computational equipment.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Pohlemann, T.; Tscherne, H.; Baumgärtel, F.; Egbers, H.J.; Euler, E.; Maurer, F.; Fell, M.; Mayr, E.; Quirini, W.W.; Schlickewei, W.; et al. Beckenverletzungen: Epidemiologie, Therapie und Langzeitverlauf. Übersicht über die multizentrische Studie der Arbeitsgruppe Becken. Unfallchirurg 1996, 99, 160–167. [Google Scholar]
  2. Hauschild, O.; Strohm, P.C.; Culemann, U.; Pohlemann, T.; Suedkamp, N.P.; Koestler, W.; Schmal, H. Mortality in patients with pelvic fractures: Results from the German pelvic injury register. J. Trauma 2008, 64, 449–455. [Google Scholar] [CrossRef]
  3. Culemann, U.; Oestern, H.J.; Pohlemann, T. Aktuelle Behandlung der Beckenringfraktur. Unfallchirurg 2014, 117, 145–159. [Google Scholar] [CrossRef] [PubMed]
  4. Hermans, E.; Edwards, M.J.R.; Goslings, J.C.; Biert, J. Open pelvic fracture: The killing fracture? J. Orthop. Surg. Res. 2018, 13, 83. [Google Scholar] [CrossRef]
  5. Durkin, A.; Sagi, H.C.; Durham, R.; Flint, L. Contemporary management of pelvic fractures. Am. J. Surg. 2006, 192, 211–223. [Google Scholar] [CrossRef] [PubMed]
  6. O’Brien, D.P.; Luchette, F.A.; Pereira, S.J.; Lim, E.; Seeskin, C.S.; James, L.; Miller, S.; Davis, K.; Hurst, J.M.; Johannigman, J.A.; et al. Pelvic fracture in the elderly is associated with increased mortality. Surgery 2002, 132, 710–714. [Google Scholar] [CrossRef] [PubMed]
  7. Burgess, A.R.; Eastridge, B.J.; Young, J.W.; Ellison, T.S.; Ellison, P.S.; Poka, A.; Bathon, G.H.; Brumback, R.J. Pelvic ring disruptions: Effective classification system and treatment protocols. J. Trauma 1990, 30, 848–856. [Google Scholar] [CrossRef] [PubMed]
  8. Tile, M. Fractures of the Pelvis. In The Rationale of Operative Fracture Care, 3rd ed.; Schatzker, J., Tile, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2005; pp. 239–290. [Google Scholar]
  9. Abdelfattah, A.; Moed, B.R. Ligamentous contributions to pelvic stability in a rotationally unstable open-book injury: A cadaver study. Injury 2014, 45, 1599–1603. [Google Scholar] [CrossRef]
  10. Stuby, F.M.; Lenz, M.; Doebele, S.; Agarwal, Y.; Skulev, H.; Ochs, B.G.; Zwingmann, J.; Gueorguiev, B. Symphyseal fixation in open book injuries cannot fully compensate anterior SI joint injury-A biomechanical study in a two-leg alternating load model. PLoS ONE 2017, 12, e0184000. [Google Scholar] [CrossRef] [Green Version]
  11. Dujardin, F.H.; Roussignol, X.; Hossenbaccus, M.; Thomine, J.M. Experimental study of the sacroiliac joint micromotion in pelvic disruption. J. Orthop. Trauma 2002, 16, 99–103. [Google Scholar] [CrossRef] [PubMed]
  12. Simonian, P.T.; Routt, M.L.; Harrington, R.M.; Mayo, K.A.; Tencer, A.F. Biomechanical simulation of the anteroposterior compression injury of the pelvis. An understanding of instability and fixation. Clin. Orthop. Relat. Res. 1994, 309, 245–256. [Google Scholar]
  13. Moed, B.R.; Barla, J.; Israel, H.A.; Tovar, S.; Joeris, A. Current Trends in the Surgical Treatment of Open-Book Pelvic Ring Injuries: An International Survey Among Experienced Trauma Surgeons. J. Orthop. Trauma 2019, 33, 61–65. [Google Scholar] [CrossRef]
  14. Metz, R.M.; Bledsoe, J.G.; Moed, B.R. Does Posterior Fixation of Partially Unstable Open-Book Pelvic Ring Injuries Decrease Symphyseal Plate Failure? A Biomechanical Study. J. Orthop. Trauma 2018, 32, 18–24. [Google Scholar] [CrossRef]
  15. Avilucea, F.R.; Whiting, P.S.; Mir, H. Posterior fixation of APC-2 pelvic ring injuries decreases rates of anterior plate failure and malunion. J. Bone Jt. Surg. Am. 2016, 98, 944–951. [Google Scholar] [CrossRef] [PubMed]
  16. Van Loon, P.; Kuhn, S.; Hofmann, A.; Hessmann, M.H.; Rommens, P.M. Radiological analysis, operative management and functional outcome of open book pelvic lesions: A 13-year cohort study. Injury 2011, 42, 1012–1019. [Google Scholar] [CrossRef] [PubMed]
  17. Meyhoff, C.S.; Thomsen, C.H.; Rasmussen, L.S.; Nielsen, P.R. High incidence of chronic pain following surgery for pelvic fracture. Clin. J. Pain 2006, 22, 167–172. [Google Scholar] [CrossRef] [PubMed]
  18. Quade, J.; Busel, G.; Beebe, M.; Auston, D.; Shah, A.R.; Infante, A.; Maxson, B.; Watson, D.; Sanders, R.W.; Mir, H.R. Symptomatic Iliosacral Screw Removal After Pelvic Trauma-Incidence and Clinical Impact. J. Orthop. Trauma 2019, 33, 351–353. [Google Scholar] [CrossRef]
  19. Giannoudis, P.V.; Chalidis, B.E.; Roberts, C.S. Internal fixation of traumatic diastasis of pubic symphysis: Is plate removal essential? Arch. Orthop. Trauma Surg. 2008, 128, 325–331. [Google Scholar] [CrossRef] [PubMed]
  20. Labitzke, R.; Witzel, U. Plattenfreie Synthese der ligamentären Beckenringverletzung (Malgaigne-Luxation). Langenbecks Arch. Chiv. 1983, 361, 781. [Google Scholar] [CrossRef] [Green Version]
  21. Jordan, M.C.; Jäckle, V.; Scheidt, S.; Gilbert, F.; Hölscher-Doht, S.; Ergün, S.; Meffert, R.H.; Heintel, T.M. Trans-obturator cable fixation of open book pelvic injuries. Sci. Rep. 2021, 11, 13463. [Google Scholar] [CrossRef] [PubMed]
  22. Cavalcanti Kußmaul, A.; Schwaabe, F.; Kistler, M.; Gennen, C.; Andreß, S.; Becker, C.A.; Böcker, W.; Greiner, A. Novel minimally invasive tape suture osteosynthesis for instabilities of the pubic symphysis: A biomechanical study. Arch. Orthop. Trauma Surg. 2021, 1–9, Epub ahead of print. [Google Scholar] [CrossRef]
  23. Kim, J.W.; Oh, C.W.; Oh, J.K.; Kyung, H.S.; Park, K.H.; Yoon, S.D.; Yoon, S.H. The incidence of and factors affecting iliosacral screw loosening in pelvic ring injury. Arch. Orthop. Trauma Surg. 2016, 136, 921–927. [Google Scholar] [CrossRef] [PubMed]
  24. Collinge, C.; Archdeacon, M.T.; Dulaney-Cripe, E.; Moed, B.R. Radiographic changes of implant failure after plating for pubic symphysis diastasis: An underappreciated reality? Clin. Orthop. Relat. Res. 2012, 470, 2148–2153. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  25. Witzel, U. Generelle Systematik und Beurteilung temporärer Implantate aus biomechanischer Sicht. In Generelle Beurteilungskriterien Für Die Wirksamkeit Temporärer Implantate, Proceedings of the DVM, Berlin, Germany; Deutscher Verband für Materialforschung: Berlin, Germany, 21 November 1989. [Google Scholar]
  26. Salo, Z.; Kreder, H.; Whyne, C.M. The Impact of an Open-Book Pelvic Ring Injury on Bone Strain: Validation of a Finite Element Model and Analysis Within the Gait Cycle. J. Biomech. Eng. 2021, 143, 071005. [Google Scholar] [CrossRef] [PubMed]
  27. Böhme, J.; Steinke, H.; Huelse, R.; Hammer, N.; Klink, T.; Slowik, V.; Josten, C. Komplexe ligamentäre Instabilitäten nach “open book“-Verletzungen des Beckenrings-Finite-Elemente-Computersimulation und Bruchversuch. Z. Orthop. Unf. 2011, 149, 83–89. [Google Scholar] [CrossRef]
  28. Ricci, P.L.; Maas, S.; Kelm, J.; Gerich, T. Finite element analysis of the pelvis including gait muscle forces: An investigation into the effect of rami fractures on load transmission. J. Exp. Orthop. 2018, 5, 33. [Google Scholar] [CrossRef] [Green Version]
  29. Hu, P.; Wu, T.; Wang, H.Z.; Qi, X.Z.; Yao, J.; Cheng, X.D.; Chen, W.; Zhang, Y.Z. Biomechanical Comparison of Three Internal Fixation Techniques for Stabilizing Posterior Pelvic Ring Disruption: A 3D Finite Element Analysis. Orthop. Surg. 2019, 11, 195–203. [Google Scholar] [CrossRef]
  30. Shim, V.; Höch, A.; Grunert, R.; Peldschus, S.; Böhme, J. Development of a Patient-Specific Finite Element Model for Predicting Implant Failure in Pelvic Ring Fracture Fixation. Comput. Math. Methods Med. 2017, 2017, 9403821. [Google Scholar]
  31. Kurz, S.; Pieroh, P.; Lenk, M.; Josten, C.; Böhme, J. Three-dimensional reduction and finite element analysis improves the treatment of pelvic malunion reconstructive surgery: A case report. Medicine 2017, 96, e8136. [Google Scholar] [CrossRef]
  32. Yu, K.H.; Hong, J.J.; Guo, X.S.; Zhou, D.S. Comparison of reconstruction plate screw fixation and percutaneous cannulated screw fixation in treatment of Tile B1 type pubic symphysis diastasis: A finite element analysis and 10-year clinical experience. J. Orthop. Surg. Res. 2015, 10, 151. [Google Scholar] [CrossRef] [Green Version]
  33. García, J.M.; Doblaré, M.; Seral, B.; Seral, F.; Palanca, D.; Gracia, L. Three-dimensional finite element analysis of several internal and external pelvis fixations. J. Biomech. Eng. 2000, 122, 516–522. [Google Scholar] [CrossRef]
  34. Carniel, E.L.; Toniolo, I.; Fontanella, C.G. Computational Biomechanics: In-Silico Tools for the Investigation of Surgical Procedures and Devices. Bioengineering 2020, 7, 48. [Google Scholar] [CrossRef]
  35. Rubio-Pérez, I.; Díaz Lantada, A. Surgical Planning of Sacral Nerve Stimulation Procedure in Presence of Sacral Anomalies by Using Personalized Polymeric Prototypes Obtained with Additive Manufacturing Techniques. Polymers 2020, 12, 581. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  36. Bakhshayesh, P.; Zaghloul, A.; Sephton, B.M.; Enocson, A. A novel 3D technique to assess symmetry of hemi pelvises. Sci. Rep. 2020, 10, 18789. [Google Scholar] [CrossRef]
  37. Ead, M.S.; Duke, K.K.; Jaremko, J.L.; Westover, L. Investigation of pelvic symmetry using CAD software. Med. Biol. Eng. Comput. 2020, 58, 75–82. [Google Scholar] [CrossRef] [PubMed]
  38. Bachtar, F.; Chen, X.; Hisada, T. Finite element contact analysis of the hip joint. Med. Bio. Eng. Comput. 2006, 44, 643–651. [Google Scholar] [CrossRef]
  39. Salzar, R.S.; Genovese, D.; Bass, C.R.; Bolton, J.R.; Guillemot, H.; Damon, A.M.; Crandall, J.R. Load path distribution within the pelvic structure under lateral loading. Int. J. Crashworth. 2009, 14, 99–110. [Google Scholar] [CrossRef]
  40. Watson, P.J.; Dostanpor, A.; Fagan, M.J.; Dobson, C.A. The effect of boundary conditions on finite element modelling of the human pelvis. Med. Eng. Phys. 2017, 43, 48–57. [Google Scholar] [CrossRef] [PubMed]
  41. Dalstra, M.; Huiskes, R. Load transfer across the pelvic bone. J. Biomech. 1995, 28, 715–724. [Google Scholar] [CrossRef] [Green Version]
  42. Li, Z.; Alonso, J.E.; Kim, J.E.; Davidson, J.S.; Etheridge, B.S.; Eberhardt, A.W. Three-dimensional finite element models of the human pubic symphysis with viscohyperelastic soft tissues. Ann. Biomed. Eng. 2006, 34, 1452–1462. [Google Scholar] [CrossRef]
  43. Xu, Z.; Li, Y.; Zhang, S.; Liao, L.; Wu, K.; Feng, Z.; Li, D. A finite element analysis of sacroiliac joint displacements and ligament strains in response to three manipulations. BMC Musculoskelet. Disord. 2020, 21, 709. [Google Scholar] [CrossRef]
  44. Hayes, W.C.; Mockros, L.F. Viscoelastic properties of human articular cartilage. J. Appl. Physiol. 1971, 31, 562–568. [Google Scholar] [CrossRef] [PubMed]
  45. ASTM F1295-16. Standard Specification for Wrought Titanium-6 Aluminum-7 Niobium Alloy for Surgical Implant Applications (UNS R56700); ASTM International: West Conshohocken, PA, USA, 2016. [Google Scholar]
  46. Phillips, A.T.; Pankaj, P.; Howie, C.R.; Usmani, A.S.; Simpson, A.H. Finite element modelling of the pelvis: Inclusion of muscular and ligamentous boundary conditions. Med. Eng. Phys. 2007, 29, 739–748. [Google Scholar] [CrossRef] [PubMed]
  47. Shi, D.; Wang, F.; Wang, D.; Li, X.; Wang, Q. 3-D finite element analysis of the influence of synovial condition in sacroiliac joint on the load transmission in human pelvic system. Med. Eng. Phys. 2014, 36, 745–753. [Google Scholar] [CrossRef] [PubMed]
  48. Yao, F.; He, Y.; Qian, H.; Zhou, D.; Li, Q. Comparison of Biomechanical Characteristics and Pelvic Ring Stability Using Different Fixation Methods to Treat Pubic Symphysis Diastasis: A Finite Element Study. Medicine 2015, 94, e2207. [Google Scholar] [CrossRef]
  49. Zhao, Y.; Zhang, S.; Sun, T.; Wang, D.; Lian, W.; Tan, J.; Zou, D.; Zhao, Y. Mechanical comparison between lengthened and short sacroiliac screws in sacral fracture fixation: A finite element analysis. Orthop. Traumatol. Surg. Res. 2013, 99, 601–606. [Google Scholar] [CrossRef] [Green Version]
  50. Miller, J.A.; Schultz, A.B.; Andersson, G.B. Load-displacement behavior of sacroiliac joints. J. Orthop. Res. 1987, 5, 92–101. [Google Scholar] [CrossRef] [Green Version]
  51. Bergmann, G.; Deuretzbacher, G.; Heller, M.; Graichen, F.; Rohlmann, A.; Strauss, J.; Duda, G.N. Hip contact forces and gait patterns from routine activities. J. Biomech. 2001, 34, 859–871. [Google Scholar] [CrossRef]
  52. Ghosh, R.; Pal, B.; Ghosh, D.; Gupta, S. Finite element analysis of a hemi-pelvis: The effect of inclusion of cartilage layer on acetabular stresses and strain. Comput. Methods Biomech. Biomed. Eng. 2015, 18, 697–710. [Google Scholar] [CrossRef]
  53. Böhme, J.; Hülse, R.; Slowik, V.; Hammer, N.; Steinke, H.; Josten, C. Computersimulation von ligamentären Instabilitäten bei anterior-posterioren Kompressionsverletzungen des Beckens. In Proceedings of the ANSYS Conference & 27th CADFEM Users’ Meeting, Leipzig, Germany, 18–20 November 2009. [Google Scholar]
  54. MacAvoy, M.C.; McClellan, R.T.; Goodman, S.B.; Chien, C.R.; Allen, W.A.; van der Meulen, M.C. Stability of open-book pelvic fractures using a new biomechanical model of single-limb stance. J. Orthop. Trauma 1997, 11, 590–593. [Google Scholar] [CrossRef]
  55. AO Surgery Reference. Available online: https://surgeryreference.aofoundation.org/orthopedic-trauma/adult-trauma/pelvic-ring/pubic-symphysis/orif-pubic-symphysis-plate (accessed on 30 October 2021).
  56. Gill, J.R.; Murphy, C.; Quansah, B.; Carrothers, A. Management of the open book APC II pelvis: Survey results from pelvic and acetabular surgeons in the United Kingdom. J. Orthop. 2017, 14, 530–536. [Google Scholar] [CrossRef]
  57. Witzel, U. Virtual synthesis of the skull in neanderthals by FESS. In Continuity and Discontinuity in the Peopling of Europe; Condemi, S., Weniger, G.C., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 203–212. [Google Scholar]
  58. Frietman, B.; Verbeek, J.; Biert, J.; Frölke, J.P. The Effect of Implant Failure After Symphyseal Plating on Functional Outcome and General Health. J. Orthop. Trauma 2016, 30, 336–339. [Google Scholar] [PubMed]
  59. Banierink, H.; Reininga, I.H.F.; Heineman, E.; Wendt, K.W.; Ten Duis, K.; IJpma, F.F.A. Long-term physical functioning and quality of life after pelvic ring injuries. Arch. Orthop. Trauma Surg. 2019, 139, 1225–1233. [Google Scholar] [CrossRef] [Green Version]
  60. Bakhtiarinejad, M.; Farvardin, A.; Murphy, R.J.; Grupp, R.B.; Tis, J.E.; Sponseller, P.D.; Armand, M. Comparative Biomechanical Study of Screw Fixation Techniques in Periacetabular Osteotomy. Biomechanics 2021, 1, 131–144. [Google Scholar] [CrossRef]
  61. Sverdlova, N.S.; Witzel, U. Principles of determination and verification of muscle forces in the human musculoskeletal system: Muscle forces to minimise bending stress. J. Biomech. 2010, 43, 387–396. [Google Scholar] [CrossRef]
  62. Witzel, U. Eine neue Methode zur virtuellen Schädelsynthese am Beispiel Camarasaurus. Hallesches Jahrb. Für Geowiss. 2007, 23, 73–78. [Google Scholar]
Biomechanics 01 00027 g001 550
Figure 1. Positioning of the ligaments in the finite element model.
Figure 1. Positioning of the ligaments in the finite element model.
Biomechanics 01 00027 g001
Biomechanics 01 00027 g002 550
Figure 2. Finite element models including bones, cartilage, and ligaments: (a) Model of the healthy pelvic ring including all ligaments modeled using tension springs. The gait load is applied to the acetabulum as shown in red. The red arrow illustrates the direction of the resultant hip force. (b) Model of the open-book fracture treated with a plate fixed superiorly to the pubic symphysis using six screws modeling anterior fixation only. Note that the anterior sacroiliac ligament, the sacrotuberous and sacrospinal ligament complex, and the fiber cartilage of the pubic symphysis were removed from the model of the injury. (c) Additional implantation of two iliosacral screws for posterior fixation. Bones are shown semitransparent to allow a view of the screws and the cancellous bone.
Figure 2. Finite element models including bones, cartilage, and ligaments: (a) Model of the healthy pelvic ring including all ligaments modeled using tension springs. The gait load is applied to the acetabulum as shown in red. The red arrow illustrates the direction of the resultant hip force. (b) Model of the open-book fracture treated with a plate fixed superiorly to the pubic symphysis using six screws modeling anterior fixation only. Note that the anterior sacroiliac ligament, the sacrotuberous and sacrospinal ligament complex, and the fiber cartilage of the pubic symphysis were removed from the model of the injury. (c) Additional implantation of two iliosacral screws for posterior fixation. Bones are shown semitransparent to allow a view of the screws and the cancellous bone.
Biomechanics 01 00027 g002
Biomechanics 01 00027 g003 550
Figure 3. Minimal principal stresses. (a) Model of the healthy pelvis. (b) Model of the open-book fracture treated with a plate fixed superior to the pubic symphysis. (c) Model with two additional iliosacral screws.
Figure 3. Minimal principal stresses. (a) Model of the healthy pelvis. (b) Model of the open-book fracture treated with a plate fixed superior to the pubic symphysis. (c) Model with two additional iliosacral screws.
Biomechanics 01 00027 g003
Biomechanics 01 00027 g004 550
Figure 4. Maximal principal stresses. (a) Model of the healthy pelvis. (b) Model of the open-book fracture treated with a plate fixed superior to the pubic symphysis. (c) Model with two additional iliosacral screws.
Figure 4. Maximal principal stresses. (a) Model of the healthy pelvis. (b) Model of the open-book fracture treated with a plate fixed superior to the pubic symphysis. (c) Model with two additional iliosacral screws.
Biomechanics 01 00027 g004
Biomechanics 01 00027 g005 550
Figure 5. Cross-sections display 3rd principal stresses in the bone surrounding the implants. (a) Pubic bone at the pubic symphysis next to the screws for fixing the plate in the model with symphyseal plating only. (b) Pubic bone at the pubic symphysis next to the screws for fixing the plate in the model with two iliosacral screws. (c) Sacrum and iliac bone at the sacroiliac joint next to the iliosacral screws.
Figure 5. Cross-sections display 3rd principal stresses in the bone surrounding the implants. (a) Pubic bone at the pubic symphysis next to the screws for fixing the plate in the model with symphyseal plating only. (b) Pubic bone at the pubic symphysis next to the screws for fixing the plate in the model with two iliosacral screws. (c) Sacrum and iliac bone at the sacroiliac joint next to the iliosacral screws.
Biomechanics 01 00027 g005
Biomechanics 01 00027 g006 550
Figure 6. Von Mises stresses acting in the implants: (a) For fixation of the anterior arch alone, a maximum stress of 819.7 MPa was observed in the symphyseal plate. (b) Additional posterior fixation decreases peak stresses of the symphyseal plate to 711.56 MPa. (c) Iliosacral screws are loaded with a peak stress of 871.42 MPa, confirming a factor of safety of 1.03.
Figure 6. Von Mises stresses acting in the implants: (a) For fixation of the anterior arch alone, a maximum stress of 819.7 MPa was observed in the symphyseal plate. (b) Additional posterior fixation decreases peak stresses of the symphyseal plate to 711.56 MPa. (c) Iliosacral screws are loaded with a peak stress of 871.42 MPa, confirming a factor of safety of 1.03.
Biomechanics 01 00027 g006
Table
Table 1. The range of motion of the sacroiliac joint of the three models using different spring stiffness compared to in vitro measurement. A load of 294 N was applied in craniocaudal direction for superior and inferior displacement and in ventrodorsal direction for anterior and posterior displacement.
Table 1. The range of motion of the sacroiliac joint of the three models using different spring stiffness compared to in vitro measurement. A load of 294 N was applied in craniocaudal direction for superior and inferior displacement and in ventrodorsal direction for anterior and posterior displacement.
Direction of DisplacementSuperiorInferiorAnteriorPosterior
in vitro Model [44]0.28 mm0.26 mm0.48 mm0.53 mm
FE model using ligament stiffness by Shi et al. [41]0.25 mm0.34 mm0.32 mm0.37 mm
FE model using ligament stiffness by Yao et al. [42]0.26 mm0.48 mm0.35 mm0.35 mm
FE model using ligament stiffness by Zhao et al. [43]0.26 mm0.5 mm0.49 mm0.48 mm
Table
Table 2. Range of motion of the healthy pelvis compared to the model of an open-book injury treated with symphyseal plating alone or symphyseal plating and iliosacral screw fixation. Positive values equal displacement in lateral, cranial, and anterior directions, respectively.
Table 2. Range of motion of the healthy pelvis compared to the model of an open-book injury treated with symphyseal plating alone or symphyseal plating and iliosacral screw fixation. Positive values equal displacement in lateral, cranial, and anterior directions, respectively.
Direction of DisplacementSacroiliac JointPubic Symphysis
Healthy pelvisSymphyseal platingSymphyseal plating andiliosacral screw fixationHealthy pelvisSymphyseal platingSymphyseal plating andiliosacral screw fixation
Mediolateral0.07 mm−0.03 mm0.07 mm0.0135 mm0.35 mm0.165 mm
Craniocaudal0.39 mm0.12 mm0.005 mm1.44 mm0.33 mm0.105 mm
Anterio-posterior−0.235 mm0.078 mm0.03 mm1.05 mm0.365 mm0.34 mm
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Lipphaus, A.; Klimek, M.; Witzel, U. Comparative Finite Element Analysis of Fixation Techniques for APC II Open-Book Injuries of the Pelvis. Biomechanics 2021, 1, 321-333. https://doi.org/10.3390/biomechanics1030027

AMA Style

Lipphaus A, Klimek M, Witzel U. Comparative Finite Element Analysis of Fixation Techniques for APC II Open-Book Injuries of the Pelvis. Biomechanics. 2021; 1(3):321-333. https://doi.org/10.3390/biomechanics1030027

Chicago/Turabian Style

Lipphaus, Andreas, Matthias Klimek, and Ulrich Witzel. 2021. "Comparative Finite Element Analysis of Fixation Techniques for APC II Open-Book Injuries of the Pelvis" Biomechanics 1, no. 3: 321-333. https://doi.org/10.3390/biomechanics1030027

APA Style

Lipphaus, A., Klimek, M., & Witzel, U. (2021). Comparative Finite Element Analysis of Fixation Techniques for APC II Open-Book Injuries of the Pelvis. Biomechanics, 1(3), 321-333. https://doi.org/10.3390/biomechanics1030027

Article Metrics

Back to TopTop