Effect of Degradation and Osteoarthritis on the Viscoelastic Properties of Human Knee Articular Cartilage: An Experimental Study and Constitutive Modeling
Abstract
:1. Introduction
2. Materials and Methods
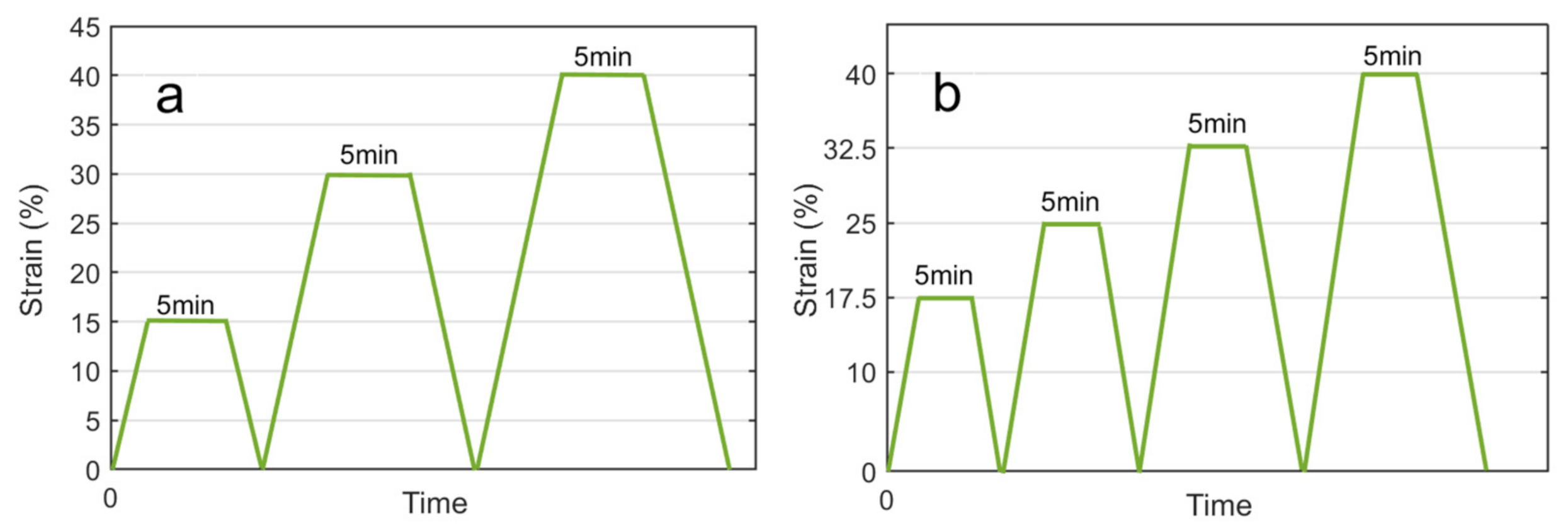
2.1. Experiments
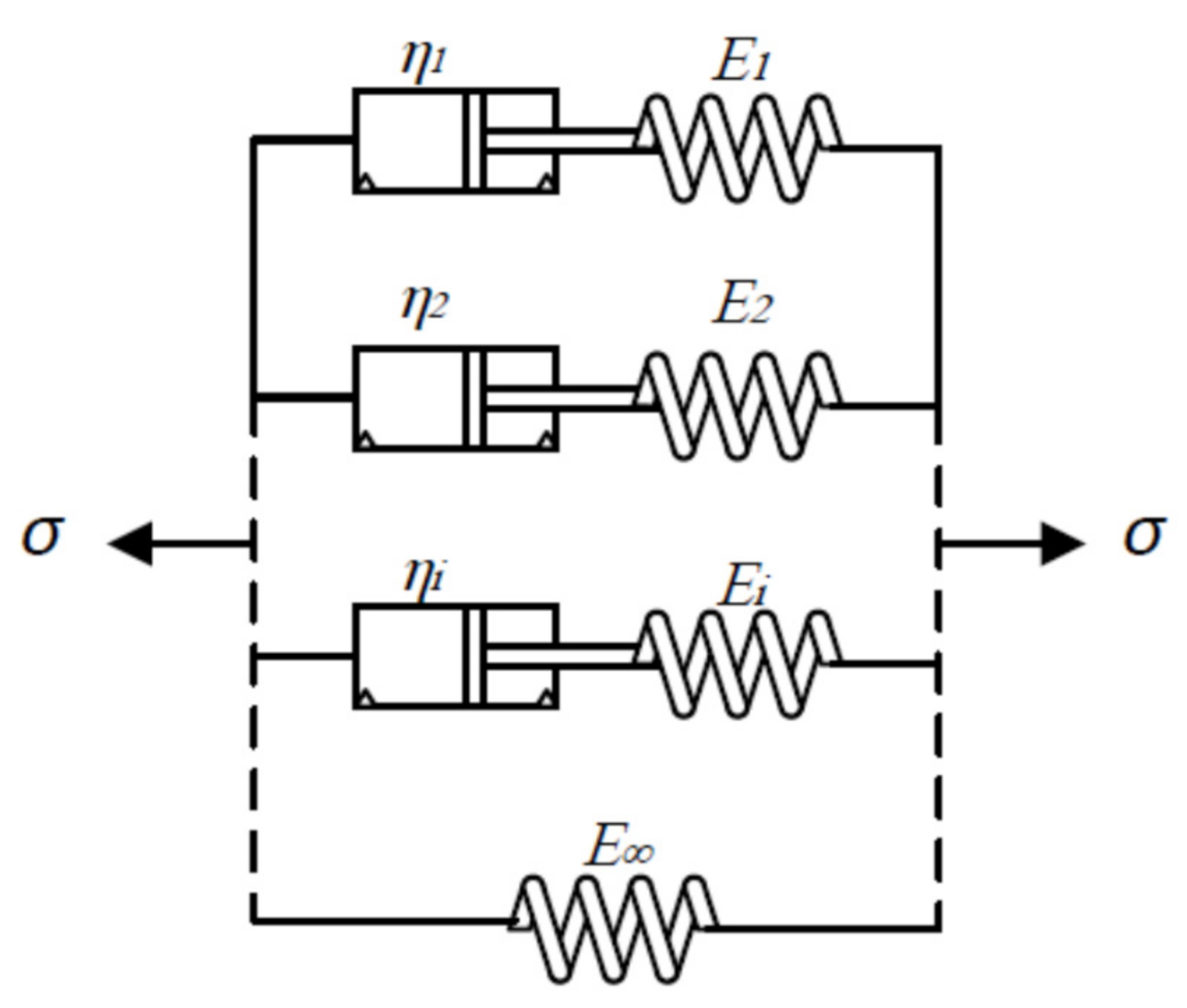
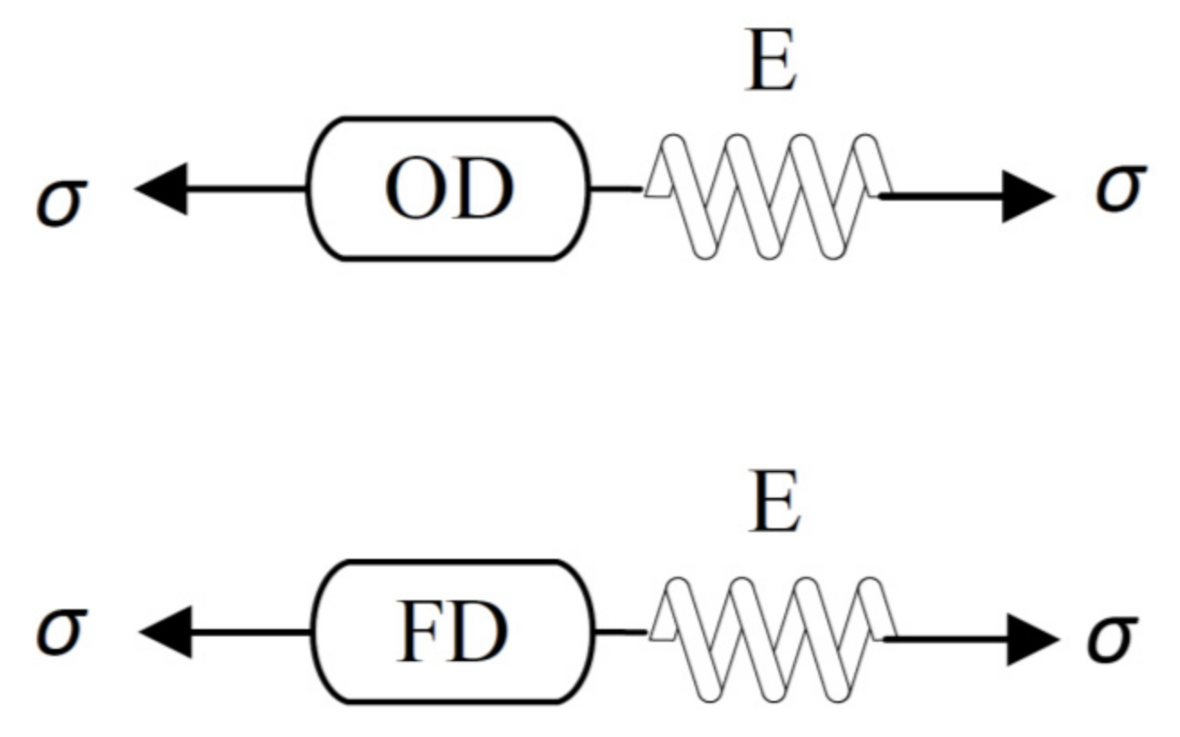
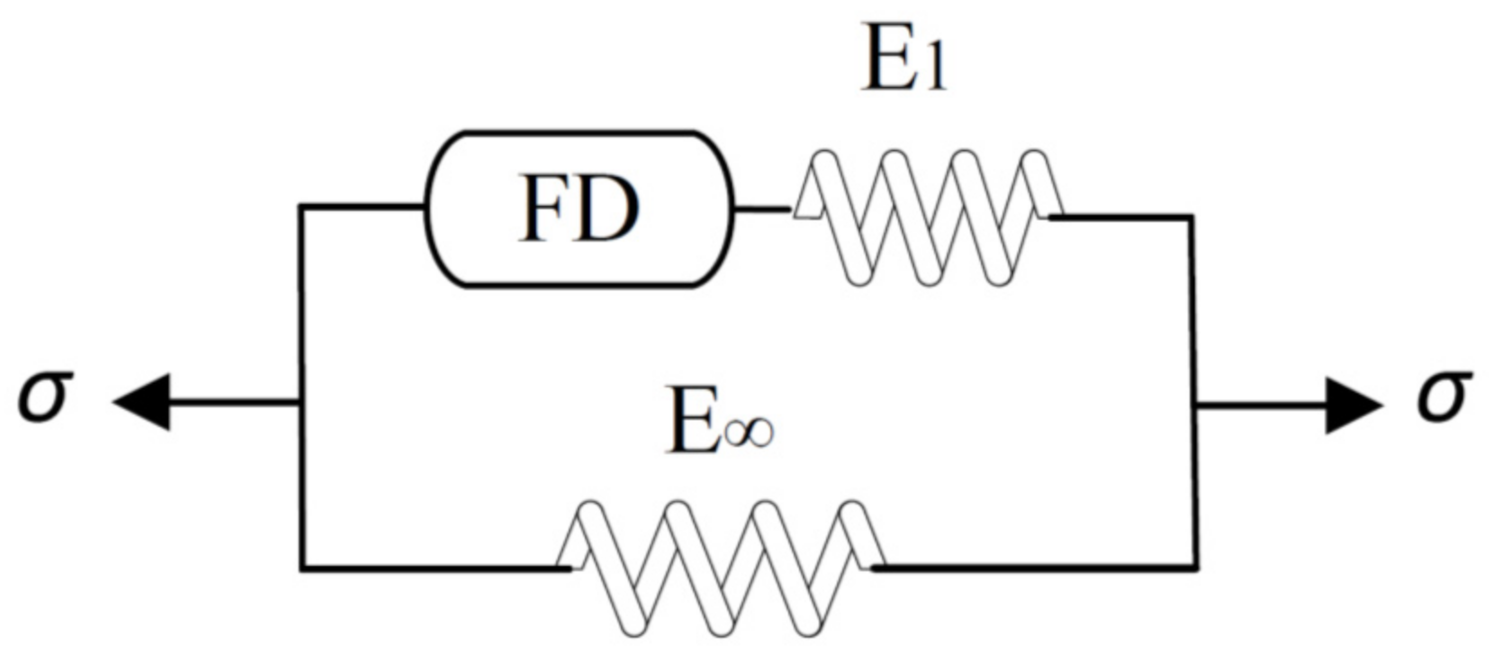
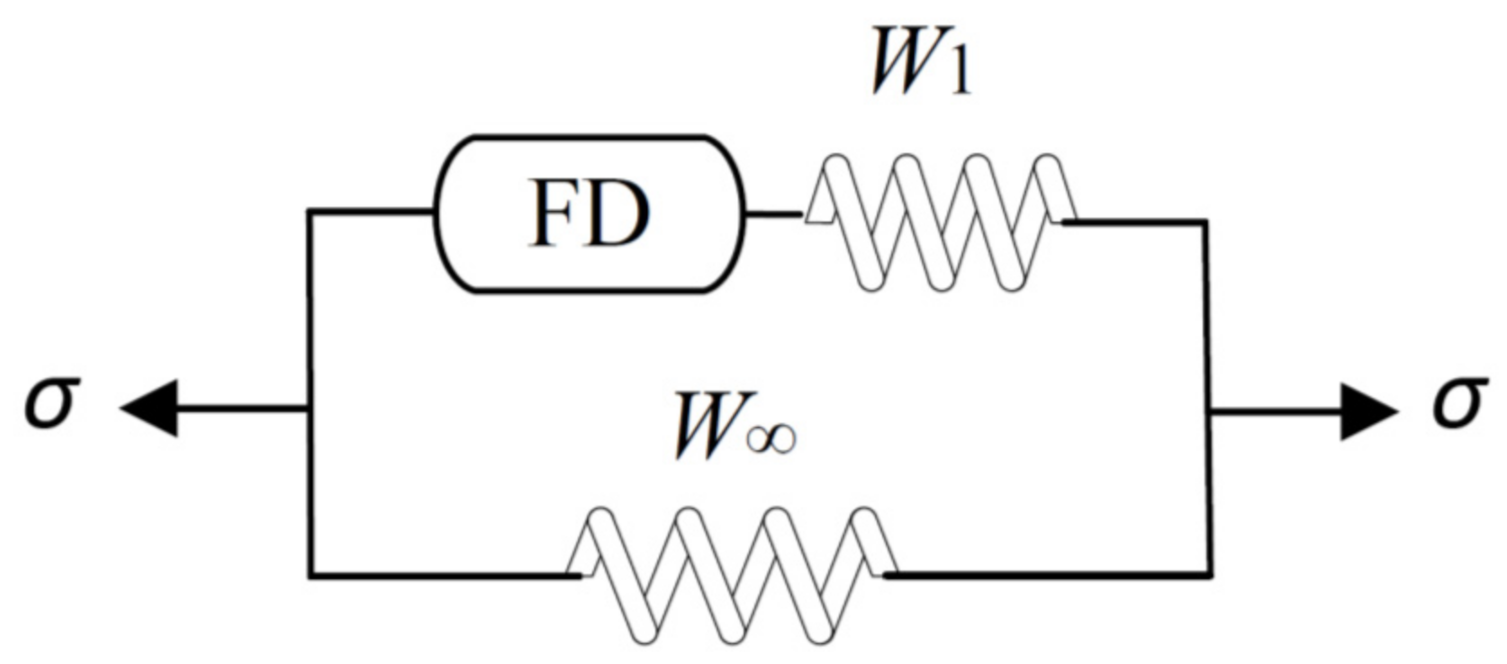
2.2. Modeling
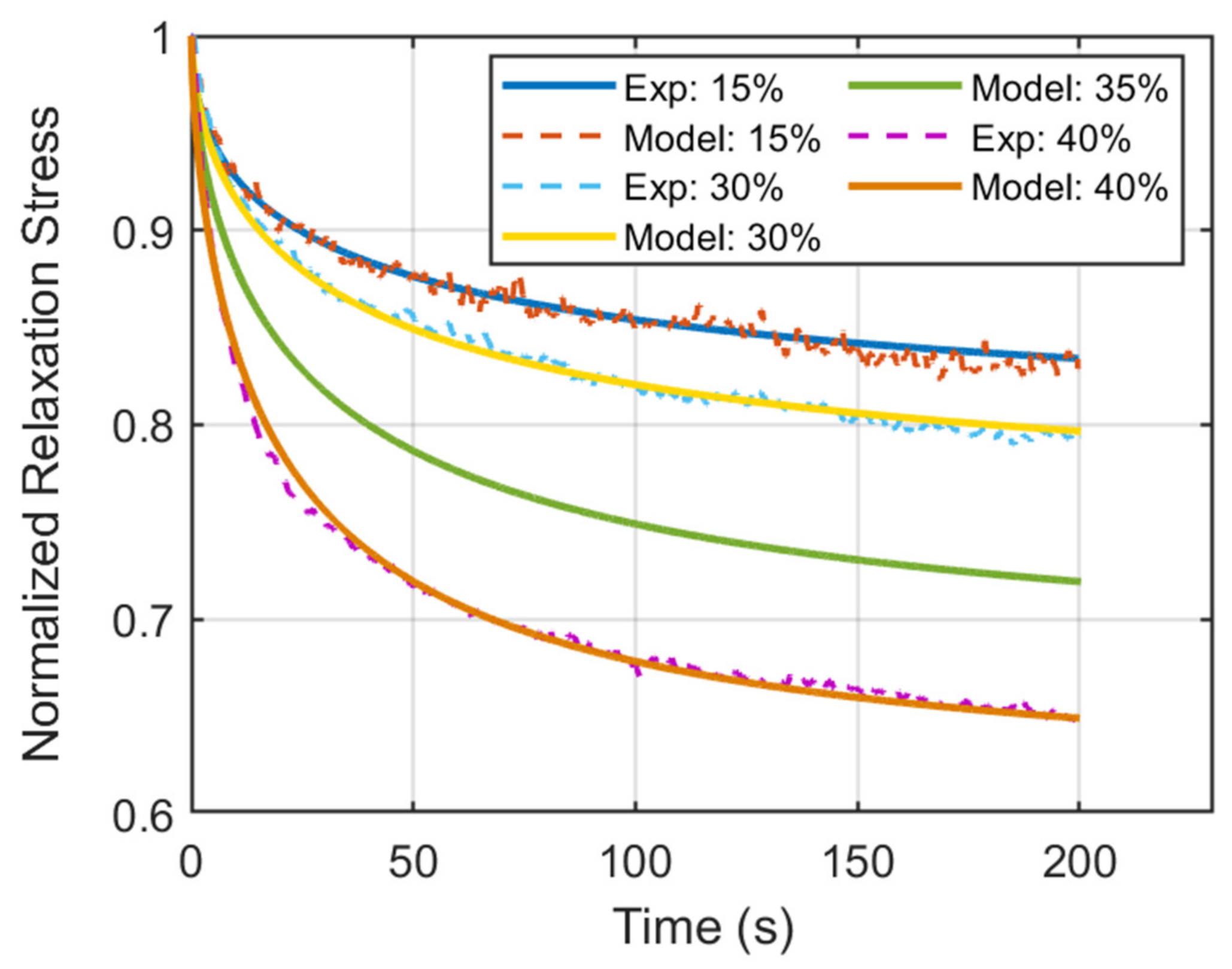
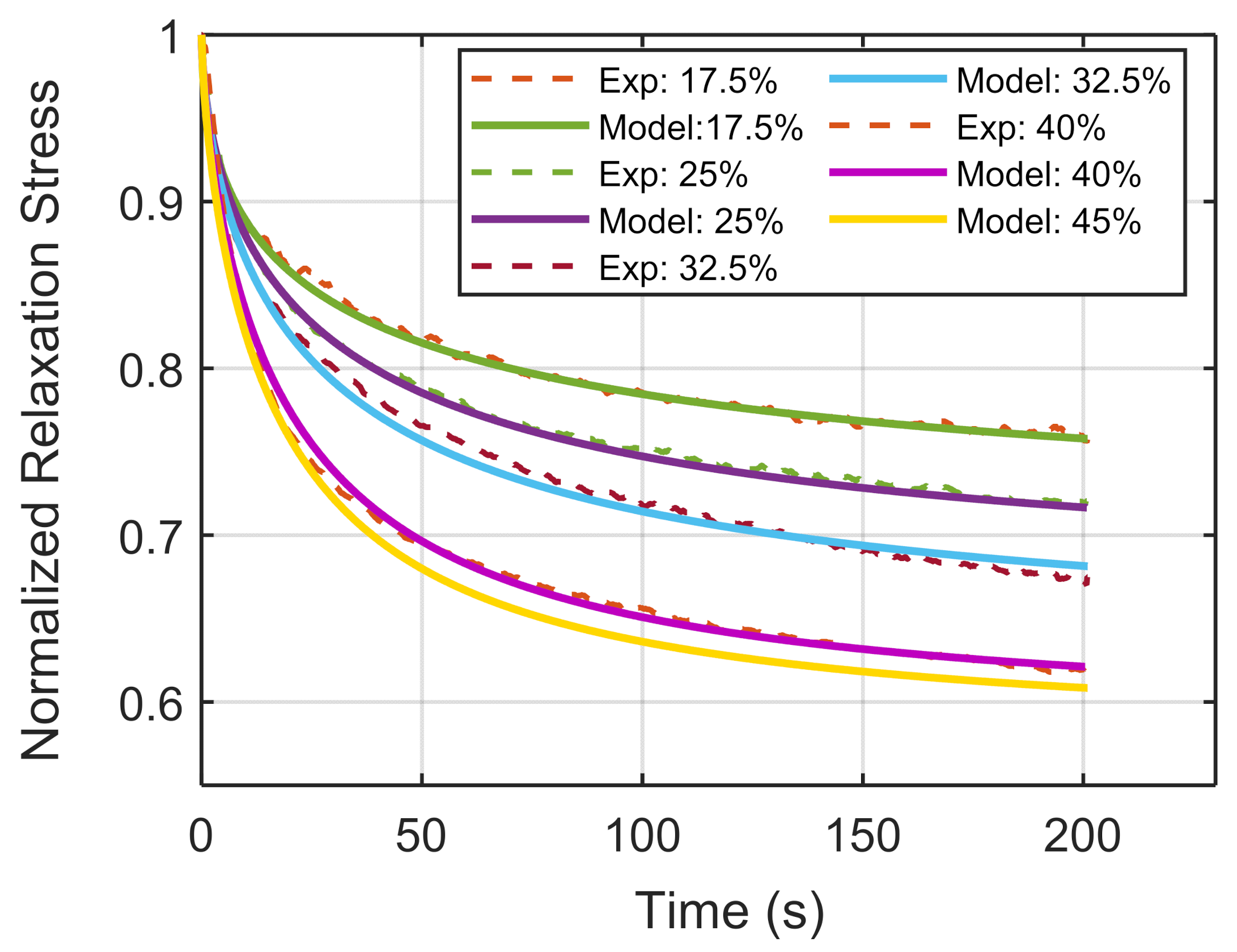
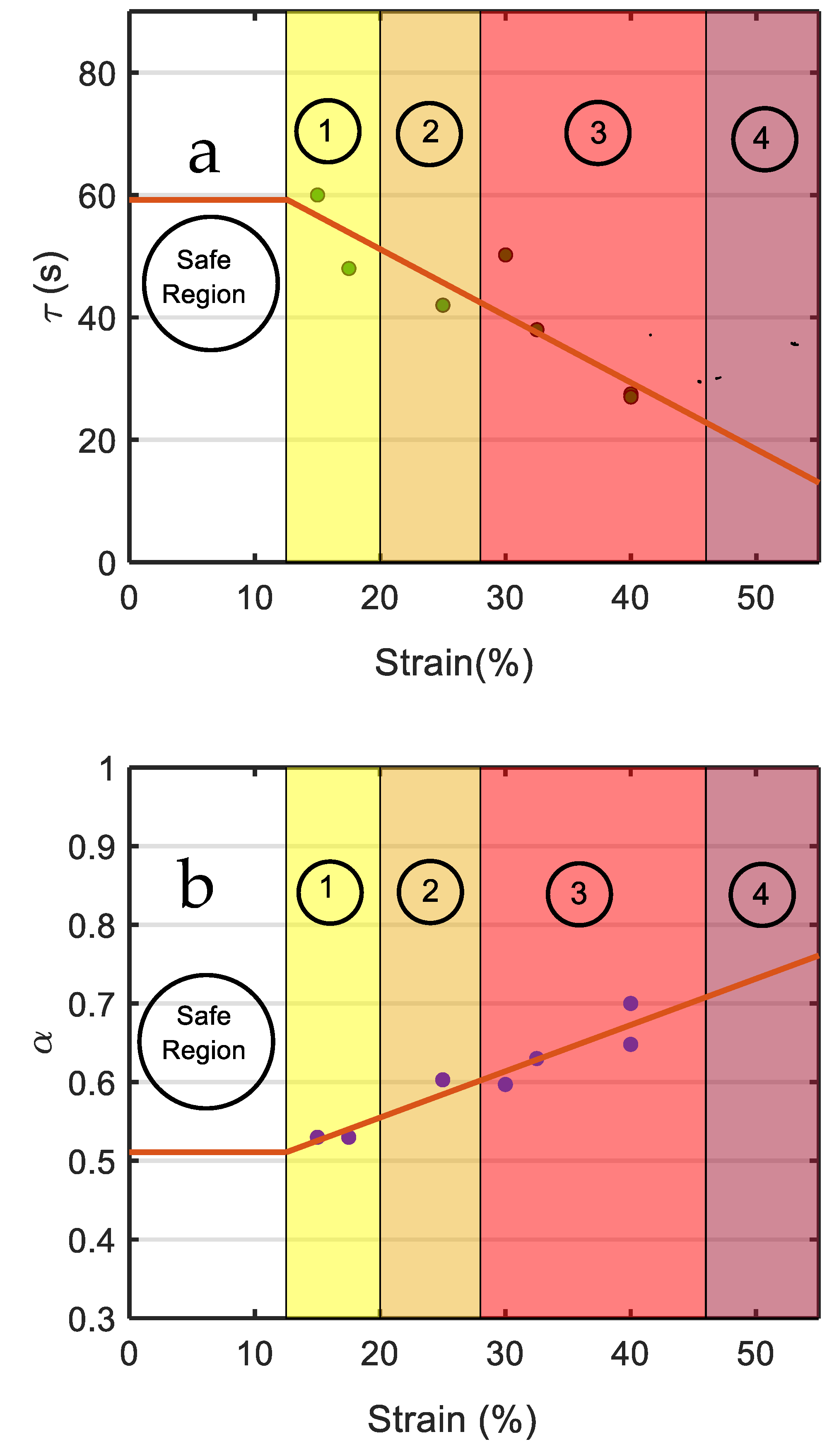
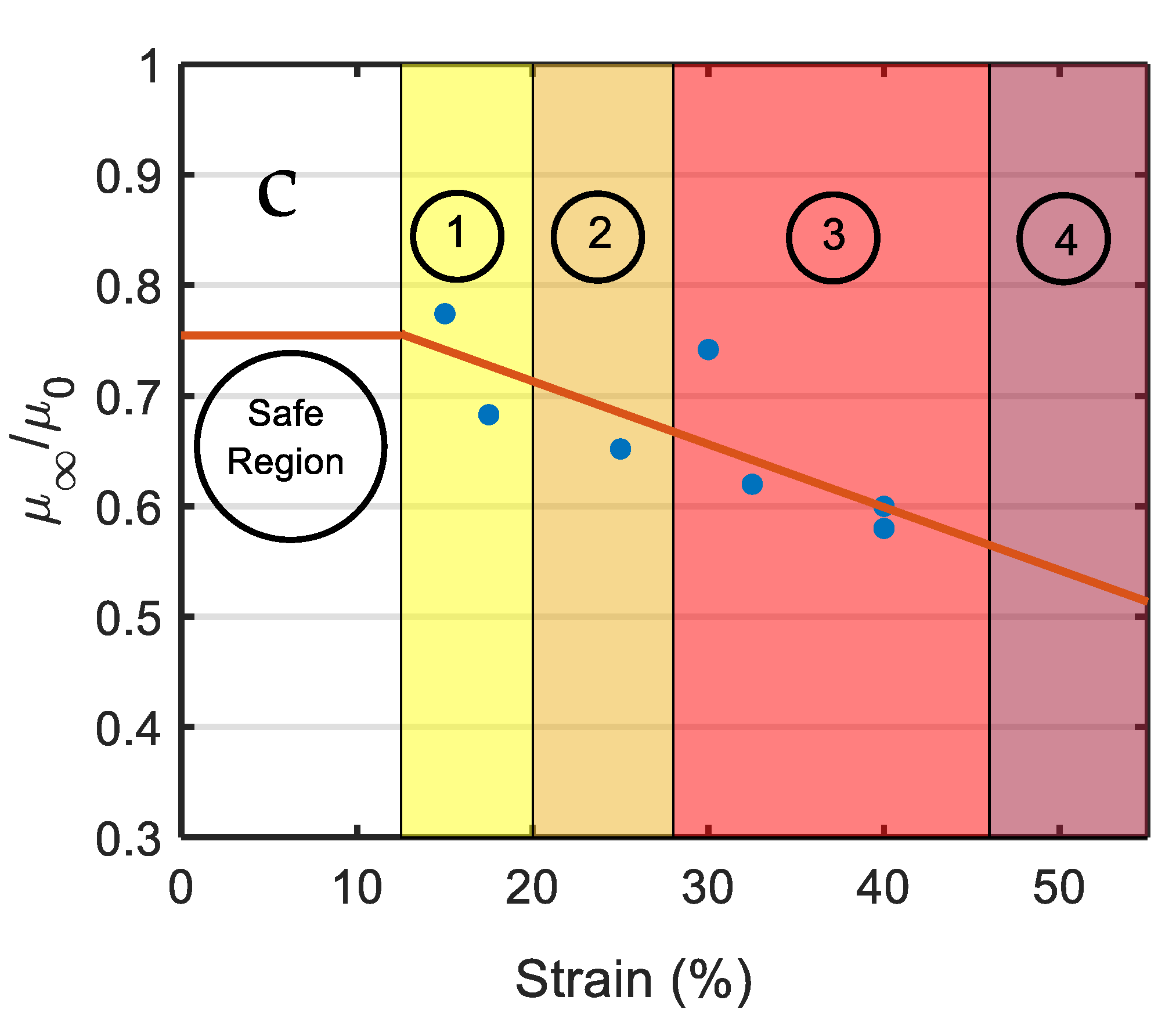
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mow, V.C.; Ateshian, G.A.; Spilker, R.L. Biomechanics of Diarthrodial Joints: A Review of Twenty Years of Progress. J. Biomech. Eng. 1993, 115, 460–467. [Google Scholar] [CrossRef]
- Pierce, D.M.; Ricken, T.; Holzapfel, G.A. Modeling sample/patient-specific structural and diffusional responses of cartilage using DT-MRI. Int. J. Numer. Methods Biomed. Eng. 2012, 29, 807–821. [Google Scholar] [CrossRef]
- Williamson, A.K.; Chen, A.C.; Masuda, K.; Thonar, E.J.-M.A.; Sah, R.L. Tensile mechanical properties of bovine articular cartilage: Variations with growth and relationships to collagen network components. J. Orthop. Res. 2003, 21, 872–880. [Google Scholar] [CrossRef]
- Ottani, V.; Raspanti, M.; Ruggeri, A. Collagen structure and functional implications. Micron 2001, 32, 251–260. [Google Scholar] [CrossRef]
- Hamerman, D. Clinical implications of osteoarthritis and ageing. Ann. Rheum. Dis. 1995, 54, 82–85. [Google Scholar] [CrossRef] [Green Version]
- Wilson, W.W.; Van Donkelaar, C.R.; Van Rietbergen, B.B.; Huiskes, H.R. The role of computational models in the search for the mechanical behavior and damage mechanisms of articular cartilage. Med. Eng. Phys. 2005, 27, 810–826. [Google Scholar] [CrossRef]
- Kleemann, R.; Krocker, D.; Cedraro, A.; Tuischer, J.; Duda, G. Altered cartilage mechanics and histology in knee osteoarthritis: Relation to clinical assessment (ICRS Grade). Osteoarthr. Cartil. 2005, 13, 958–963. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Khajehsaeid, H.; Abdollahpour, Z. Progressive deformation-induced degradation of knee articular cartilage and osteoarthritis. J. Biomech. 2020, 111, 109995. [Google Scholar] [CrossRef]
- Mow, V.C.; Gu, W.Y.; Chen, F.H. Structure and function of articular cartilage and meniscus. Basic Orthop. Biomech. Mechano-Biol. 2005, 3, 181–258. [Google Scholar]
- Charnley, J. The Lubrication of Animal Joints in Relation to Surgical Reconstruction by Arthroplasty. Ann. Rheum. Dis. 1960, 19, 10–19. [Google Scholar] [CrossRef] [Green Version]
- Ateshian, G.A. The role of interstitial fluid pressurization in articular cartilage lubrication. J. Biomech. 2009, 42, 1163–1176. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ateshian, G.; Warden, W.; Kim, J.; Grelsamer, R.; Mow, V. Finite deformation biphasic material properties of bovine articular cartilage from confined compression experiments. J. Biomech. 1997, 30, 1157–1164. [Google Scholar] [CrossRef]
- Mow, V.C.; Kuei, S.C.; Lai, W.M.; Armstrong, C.G. Biphasic Creep and Stress Relaxation of Articular Cartilage in Compression: Theory and Experiments. J. Biomech. Eng. 1980, 102, 73–84. [Google Scholar] [CrossRef] [PubMed]
- Lai, W.M.; Mow, V.C.; Roth, V. Effects of Nonlinear Strain-Dependent Permeability and Rate of Compression on the Stress Behavior of Articular Cartilage. J. Biomech. Eng. 1981, 103, 61–66. [Google Scholar] [CrossRef] [PubMed]
- Armstrong, C.G.; Lai, W.M.; Mow, V.C. An Analysis of the Unconfined Compression of Articular Cartilage. J. Biomech. Eng. 1984, 106, 165–173. [Google Scholar] [CrossRef]
- Huang, C.-Y.; Mow, V.C.; Ateshian, G.A. The Role of Flow-Independent Viscoelasticity in the Biphasic Tensile and Compressive Responses of Articular Cartilage. J. Biomech. Eng. 2001, 123, 410–417. [Google Scholar] [CrossRef]
- Coletti, J.M.; Akeson, W.H.; Woo, S.L.-Y. A Comparison of the Physical Behavior of Normal Articular Cartilage and the Arthroplasty Surface. J. Bone Jt. Surg. Am. Vol. 1972, 54, 147–160. [Google Scholar] [CrossRef]
- Parsons, J.; Black, J. The viscoelastic shear behavior of normal rabbit articular cartilage. J. Biomech. 1977, 10, 21–29. [Google Scholar] [CrossRef]
- Smyth, P.A.; Green, I. Fractional calculus model of articular cartilage based on experimental stress-relaxation. Mech. Time-Depend. Mater. 2015, 19, 209–228. [Google Scholar] [CrossRef]
- Ehlers, W.; Markert, B. A Linear Viscoelastic Two-Phase Model for Soft Tissues: Application to Articular Cartilage. ZAMM 2000, 80, 149–152. [Google Scholar] [CrossRef]
- Wilson, W.; van Donkelaar, C.; van Rietbergen, B.; Ito, K.; Huiskes, R. Stresses in the local collagen network of articular cartilage: A poroviscoelastic fibril-reinforced finite element study. J. Biomech. 2004, 37, 357–366. [Google Scholar] [CrossRef]
- Wilson, W.; van Donkelaar, C.; van Rietbergen, B.; Huiskes, R. A fibril-reinforced poroviscoelastic swelling model for articular cartilage. J. Biomech. 2005, 38, 1195–1204. [Google Scholar] [CrossRef]
- Julkunen, P.; Wilson, W.; Jurvelin, J.S.; Rieppo, J.; Qu, C.; Lammi, M.; Korhonen, R. Stress–relaxation of human patellar articular cartilage in unconfined compression: Prediction of mechanical response by tissue composition and structure. J. Biomech. 2008, 41, 1978–1986. [Google Scholar] [CrossRef]
- Stender, M.E.; Regueiro, R.; Klisch, S.M.; Ferguson, V.L. An Equilibrium Constitutive Model of Anisotropic Cartilage Damage to Elucidate Mechanisms of Damage Initiation and Progression. J. Biomech. Eng. 2015, 137, 081010. [Google Scholar] [CrossRef] [PubMed]
- Hosseini, S.; Wilson, W.; Ito, K.; van Donkelaar, C. A numerical model to study mechanically induced initiation and progression of damage in articular cartilage. Osteoarthr. Cartil. 2014, 22, 95–103. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Korhonen, R.K.; Laasanen, M.S.; Töyräs, J.; Lappalainen, R.; Helminen, H.J.; Jurvelin, J.S. Fibril reinforced poroelastic model predicts specifically mechanical behavior of normal, proteoglycan depleted and collagen degraded articular cartilage. J. Biomech. 2003, 36, 1373–1379. [Google Scholar] [CrossRef]
- Adams, M.E.; Brandt, K.D. Hypertrophic repair of canine articular cartilage in osteoarthritis after anterior cruciate ligament transection. J. Rheumatol. 1991, 18, 428–435. [Google Scholar]
- D’Lima, D.; Hashimoto, S.; Chen, P.; Colwell, C.; Lotz, M. Human chondrocyte apoptosis in response to mechanical injury. Osteoarthr. Cartil. 2001, 9, 712–719. [Google Scholar] [CrossRef] [Green Version]
- Sharma, G.; Saxena, R.; Mishra, P. Differential effects of cyclic and static pressure on biochemical and morphological properties of chondrocytes from articular cartilage. Clin. Biomech. 2007, 22, 248–255. [Google Scholar] [CrossRef]
- Liukkonen, M.K.; Mononen, M.E.; Klets, O.; Arokoski, J.P.; Saarakkala, S.; Korhonen, R. Simulation of Subject-Specific Progression of Knee Osteoarthritis and Comparison to Experimental Follow-up Data: Data from the Osteoarthritis Initiative. Sci. Rep. 2017, 7, 1–14. [Google Scholar] [CrossRef]
- Mononen, M.E.; Tanska, P.; Isaksson, H.; Korhonen, R. A Novel Method to Simulate the Progression of Collagen Degeneration of Cartilage in the Knee: Data from the Osteoarthritis Initiative. Sci. Rep. 2016, 6, 21415. [Google Scholar] [CrossRef] [Green Version]
- Khajehsaeid, H. A Comparison Between Fractional-Order and Integer-Order Differential Finite Deformation Viscoelastic Models: Effects of Filler Content and Loading Rate on Material Parameters. Int. J. Appl. Mech. 2018, 10, 1850099. [Google Scholar] [CrossRef]
- Wollscheid, D.; Lion, A. The benefit of fractional derivatives in modelling the dynamics of filler-reinforced rubber under large strains: A comparison with the Maxwell-element approach. Comput. Mech. 2013, 53, 1015–1031. [Google Scholar] [CrossRef]
- Khajehsaeid, H. Application of fractional time derivatives in modeling the finite deformation viscoelastic behavior of carbon-black filled NR and SBR. Polym. Test. 2018, 68, 110–115. [Google Scholar] [CrossRef]
- Simo, J.C.; Hughes, T.J.R. Computational Inelasticity; Springer Science and Business Media LLC: Berlin/Heidelberg, Germany, 1998; Volume 7. [Google Scholar]
- Khajehsaeid, H.; Naghdabadi, R.; Arghavani, J. A strain energy function for rubber-like materials. Const. Models Rubber VIII 2013, 8, 205–210. [Google Scholar]
- Khajehsaeid, H.; Arghavani, J.; Naghdabadi, R. A hyperelastic constitutive model for rubber-like materials. Eur. J. Mech.-A/Solids 2013, 38, 144–151. [Google Scholar] [CrossRef]
- Fereidoonnezhad, B.; O’Connor, C.; McGarry, J. A new anisotropic soft tissue model for elimination of unphysical auxetic behaviour. J. Biomech. 2020, 111, 110006. [Google Scholar] [CrossRef]
- Pucci, E.; Saccomandi, G. Some remarks about a simple history dependent nonlinear viscoelastic model. Mech. Res. Commun. 2015, 68, 70–76. [Google Scholar] [CrossRef]
- Soleymani, R.; Khajehsaeid, H. Theoretical and experimental study on silicone pneumatic artificial muscles. In Proceedings of the 8th Conference on Smart Structures and Materials, International Center for Numerical Methods in Engineering (CIMNE), Madrid, Spain, 5–8 June 2017. [Google Scholar]
- Gamonpilas, C.; McCuiston, R. A non-linear viscoelastic material constitutive model for polyurea. Polymer 2012, 53, 3655–3658. [Google Scholar] [CrossRef]
- Khajehsaeid, H.; Arghavani, J.; Naghdabadi, R.; Sohrabpour, S. A visco-hyperelastic constitutive model for rubber-like materials: A rate-dependent relaxation time scheme. Int. J. Eng. Sci. 2014, 79, 44–58. [Google Scholar] [CrossRef]
- Enelund, M.; Olsson, P. Damping described by fading memory—Analysis and application to fractional derivative models. Int. J. Solids Struct. 1999, 36, 939–970. [Google Scholar] [CrossRef]
- Robinson, D.L.; Kersh, M.E.; Walsh, N.C.; Ackland, D.; de Steiger, R.N.; Pandy, M. Mechanical properties of normal and osteoarthritic human articular cartilage. J. Mech. Behav. Biomed. Mater. 2016, 61, 96–109. [Google Scholar] [CrossRef] [Green Version]
- Khajehsaeid, H.; Tehrani, M.; Alaghehband, N. Anisotropic damage of soft tissues in supra-physiological deformations. J. Biomech. 2021, 124, 110548. [Google Scholar] [CrossRef] [PubMed]
- McDevitt, C.A.; Muir, H. Biochemical changes in the cartilage of the knee in experimental and natural osteoarthritis in the dog. J. Bone Jt. Surg. Br. 1976, 58, 94–101. [Google Scholar] [CrossRef] [PubMed]
- June, R.K.; Fyhrie, D.P. Enzymatic digestion of articular cartilage results in viscoelasticity changes that are consistent with polymer dynamics mechanisms. Biomed. Eng. Online 2009, 8, 32. [Google Scholar] [CrossRef] [Green Version]
- Van Wart, H.E.; Steinbrink, D.R. Complementary substrate specificities of class I and class II collagenases from Clostridium histolyticum. Biochemistry 1985, 24, 6520–6526. [Google Scholar] [CrossRef]
- Kumar, R.; Pierce, D.M.; Isaksen, V.; Davies, C.D.L.; Drogset, J.O.; Lilledahl, M.B. Comparison of Compressive Stress-Relaxation Behavior in Osteoarthritic (ICRS Graded) Human Articular Cartilage. Int. J. Mol. Sci. 2018, 19, 413. [Google Scholar] [CrossRef] [Green Version]
- Akbari, E.; Khajehsaeid, H. A continuum magneto-mechanical model for magnetorheological elastomers. Smart Mater. Struct. 2021, 30, 015008. [Google Scholar] [CrossRef]
- Kempson, G.; Muir, H.; Swanson, S.; Freeman, M. Correlations between stiffness and the chemical constituents of cartilage on the human femoral head. Biochim. Biophys. Acta (BBA) Gen. Subj. 1970, 215, 70–77. [Google Scholar] [CrossRef]
- Fadaiepour, A.; Khajehsaeid, H.; Ghanbari, A. Design and modeling of artificial arm muscle using shape memory alloys. Modares Mech. Eng. 2018, 17, 29–38. [Google Scholar]


| Strain (%) | |||
|---|---|---|---|
| 15 | 0.775 | 0.53 | 60 |
| 30 | 0.735 | 0.59 | 49 |
| 35 (Predicted) | 0.661 | 0.61 | 39 |
| 40 | 0.602 | 0.65 | 27 |
| Strain (%) | |||
|---|---|---|---|
| 17.5 | 0.683 | 0.53 | 48 |
| 25 | 0.652 | 0.60 | 42 |
| 32.5 | 0.621 | 0.63 | 38 |
| 40 | 0.580 | 0.69 | 27 |
| 45 (Predicted) | 0.572 | 0.71 | 24 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khajehsaeid, H.; Abdollahpour, Z.; Farahmandpour, H. Effect of Degradation and Osteoarthritis on the Viscoelastic Properties of Human Knee Articular Cartilage: An Experimental Study and Constitutive Modeling. Biomechanics 2021, 1, 225-238. https://doi.org/10.3390/biomechanics1020019
Khajehsaeid H, Abdollahpour Z, Farahmandpour H. Effect of Degradation and Osteoarthritis on the Viscoelastic Properties of Human Knee Articular Cartilage: An Experimental Study and Constitutive Modeling. Biomechanics. 2021; 1(2):225-238. https://doi.org/10.3390/biomechanics1020019
Chicago/Turabian StyleKhajehsaeid, Hesam, Zanko Abdollahpour, and Hedyeh Farahmandpour. 2021. "Effect of Degradation and Osteoarthritis on the Viscoelastic Properties of Human Knee Articular Cartilage: An Experimental Study and Constitutive Modeling" Biomechanics 1, no. 2: 225-238. https://doi.org/10.3390/biomechanics1020019
APA StyleKhajehsaeid, H., Abdollahpour, Z., & Farahmandpour, H. (2021). Effect of Degradation and Osteoarthritis on the Viscoelastic Properties of Human Knee Articular Cartilage: An Experimental Study and Constitutive Modeling. Biomechanics, 1(2), 225-238. https://doi.org/10.3390/biomechanics1020019







